Preliminary Study of Computational Time Steps in a Physically Based Distributed Rainfall–Runoff Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. GRM
2.2. CFL Condition
2.3. Virtual Rainfall Events, Virtual Catchments and Analysis Method
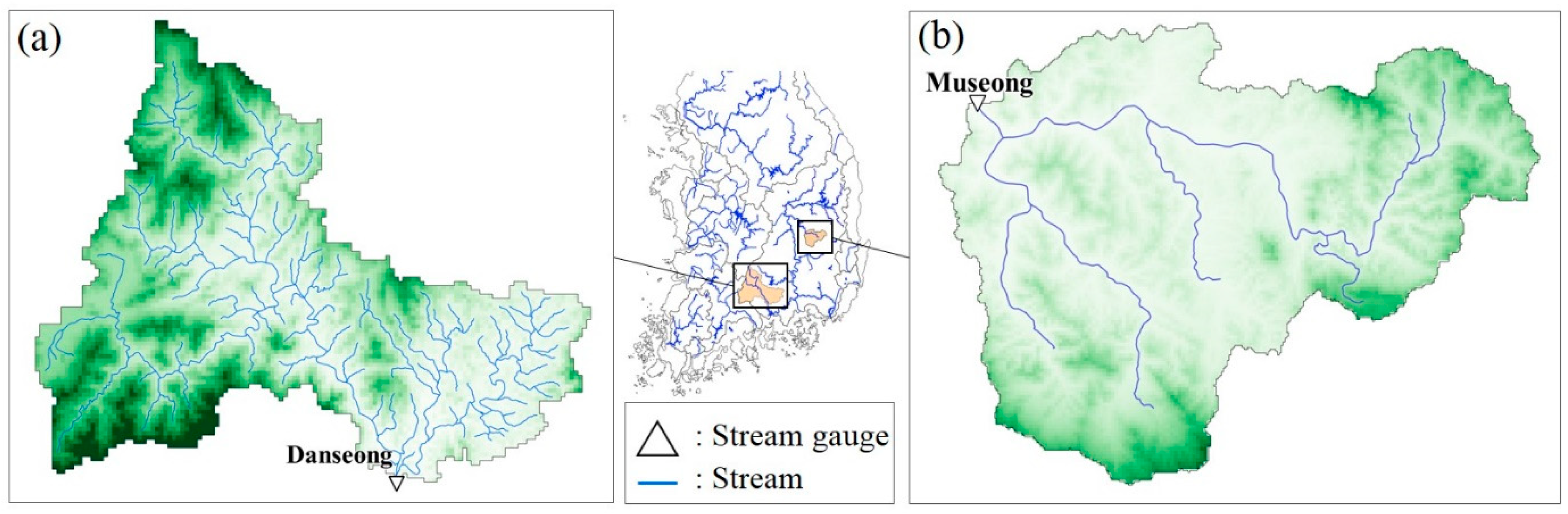
2.4. Real Catchments, Real Rainfall Events and Analysis Method
3. Results and Discussion
3.1. Comparison of How Peak Flow is Affected by the dt Setting for Rainfall Size in a Virtual Catchment
3.2. Comparison of How Peak Flow is Affected by the dt Setting for Stream Network Density In Virtual Catchments
3.3. Comparison of How Peak Flow is Affected by the dt Setting for Spatial Resolution in Virtual Catchments
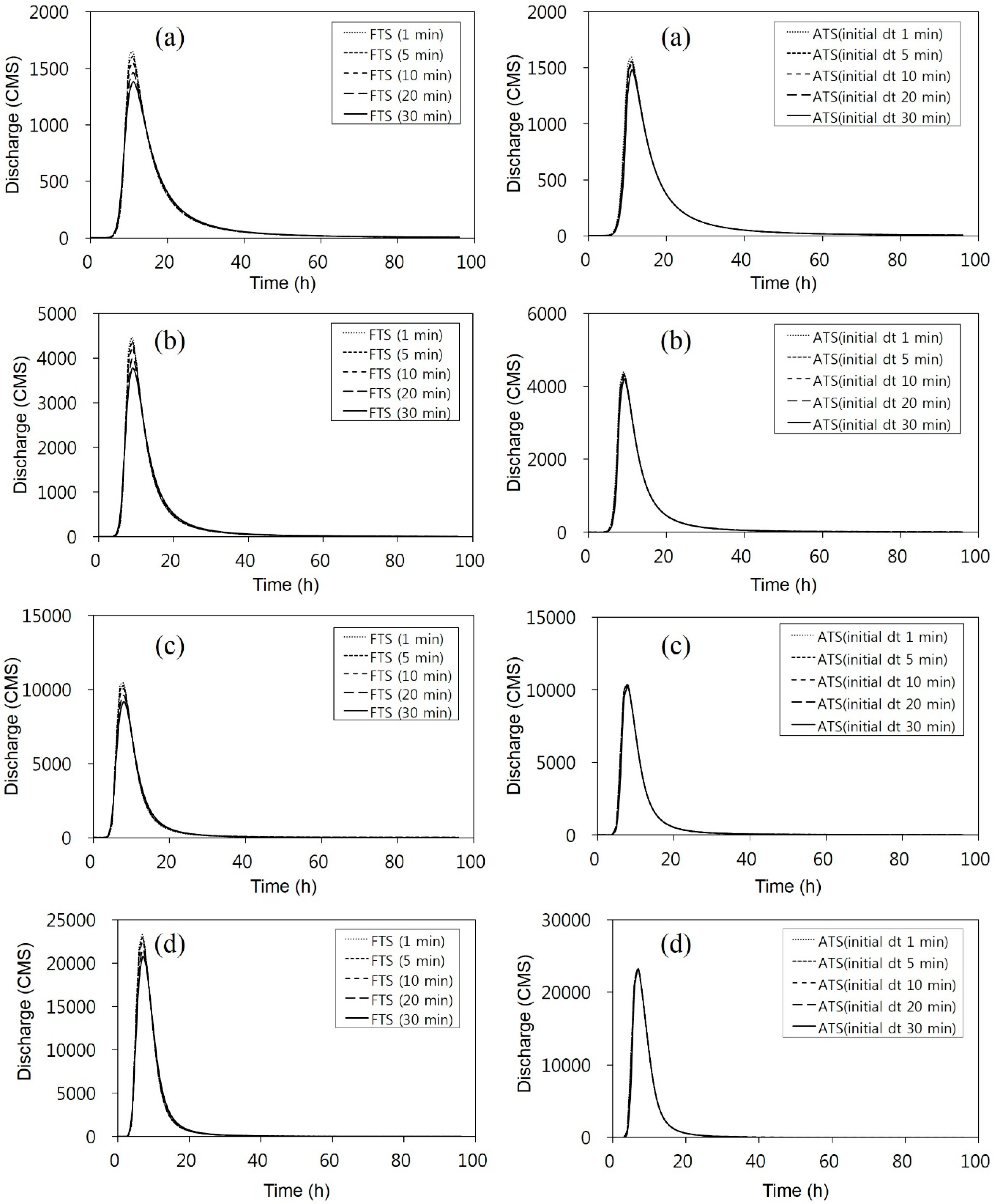
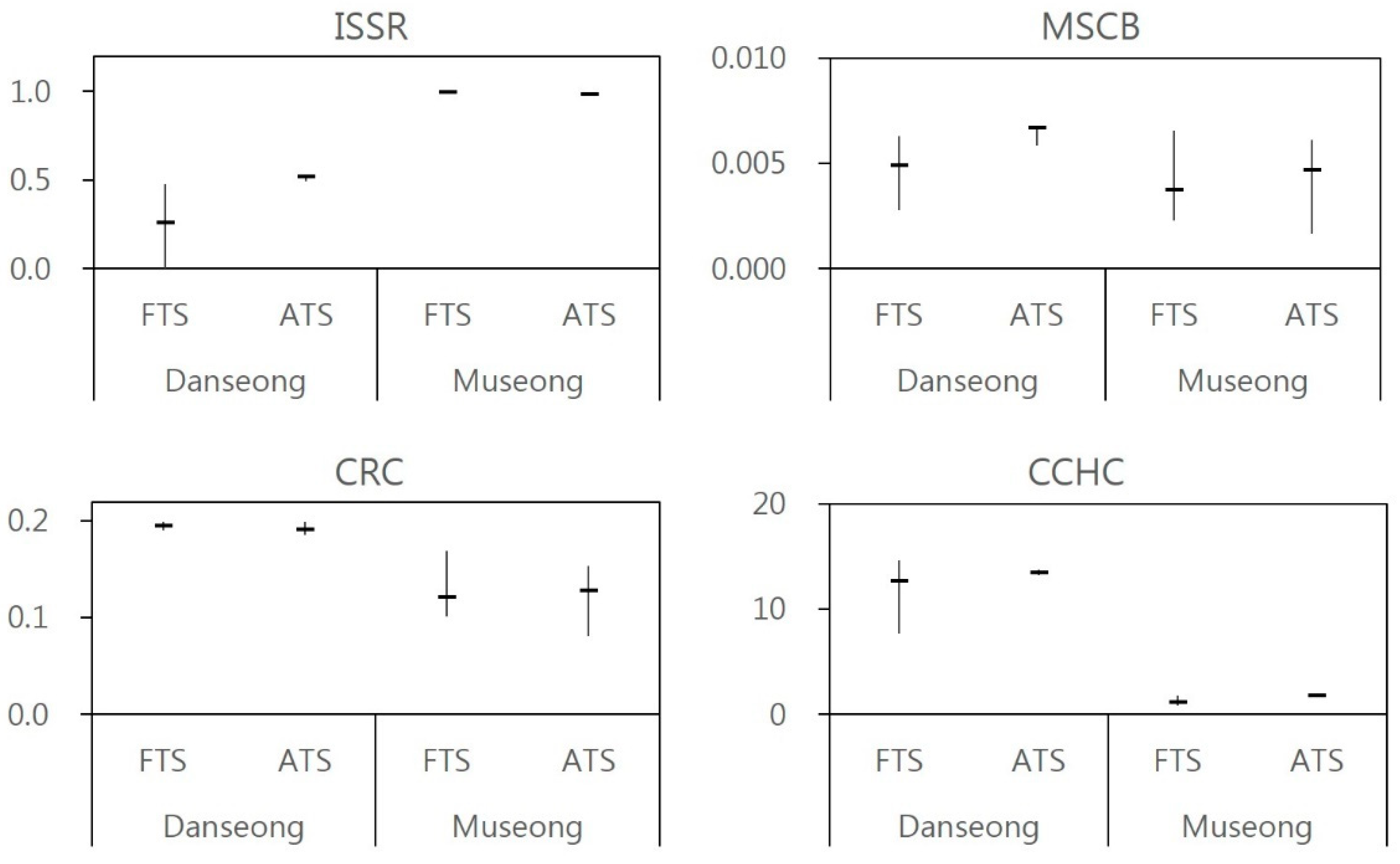
3.4. Evaluation of How Simulated Hydrographs and Parameters are Affected by dt Settings in Real Catchment
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hulbert, G.M.; Jang, I. Automatic time step control algorithms for structural dynamics. Comput. Methods Appl. Mech. 1995, 126, 155–178. [Google Scholar] [CrossRef]
- Hunter, N.M.; Horritt, M.S.; Bates, P.D.; Wilson, M.D.; Werner, M.G. An adaptive time step solution for raster-based storage cell modelling of floodplain inundation. Adv. Water. Resour. 2005, 28, 975–991. [Google Scholar] [CrossRef]
- Charney, J.G.; Fjörtoft, R.; von Neumann, J. Numerical integration of the barotropic vorticity equation. Tellus 1950, 2, 237–254. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of heat conduction type. Adv. Comput. Math. 1996, 6, 207–226. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the partial difference equations of mathematical physics. In AEC Research and Development Report, NYO-7689; AEC Computing and Applied Mathematics Centre: New York, NY, USA, 1956; pp. 63–76. [Google Scholar]
- Scott, F.B.; Brett, F.S. Finite-Volume Model for Shallow-Water Flooding of Arbitrary Topography. J. Hydraul. Eng. 2002, 128, 289–298. [Google Scholar]
- Kim, K.S.; Kim, J.S.; Kim, W. Estimation technique of computationally variable distance step in 1-D numerical model. KWRA 2011, 44, 363–376. (In Korean) [Google Scholar]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Haddeland, I.; Lettenmaier, D.P.; Skaugen, T. Reconciling simulated moisture fluxes resulting from alternate hydrologic model time steps and energy budget closure assumptions. J. Hydrometeorol. 2006, 7, 355–370. [Google Scholar] [CrossRef]
- Givoli, D.; Henigsberg, I. A simple time-step control scheme. Commun. Numer. Methods Eng. 1993, 9, 873–881. [Google Scholar] [CrossRef]
- Choi, Y.S.; Choi, C.K.; Kim, H.S.; Kim, K.T.; Kim, S. Multi-site calibration using a grid-based event rainfall–runoff model: A case study of the upstream areas of the Nakdong River basin in Korea. Hydrol. Process. 2015, 29, 2089–2099. [Google Scholar] [CrossRef]
- Choi, Y.S.; Kim, K.T. Grid Based Rainfall-Runoff Model User’s Manual; Korea Institute of Civil Engineering and Building Technology: Goyang-si, Gyeonggi-do, Korea, 2017; pp. 1–21. [Google Scholar]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Nicklow, J.; Reed, P.; Savic, D.; Dessalegne, T.; Harrell, L.; Chan-Hilton, A.; Karamouz, M.; Minsker, B.; Ostfeld, A.; Singh, A.; et al. State of the art for genetic algorithms and beyond in water resources planning and management. J. Water Res. Plan. Manag. 2010, 136, 412–432. [Google Scholar] [CrossRef]
- Moreno, H.A.; Vivoni, E.R.; Gochis, D.J. Utility of quantitative precipitation estimates for high resolution hydrologic forecasts in mountain watersheds of the Colorado Front Range. J. Hydrol. 2012, 438, 66–83. [Google Scholar] [CrossRef]
- Serrat-Capdevila, A.; Scott, R.L.; Shuttleworth, W.J.; Valdés, J.B. Estimating evapotranspiration under warmer climates: Insights from a semi-arid riparian system. J. Hydrol. 2011, 399, 1–11. [Google Scholar] [CrossRef]
- Shin, M.J.; Eum, H.I.; Kim, C.S.; Jung, I.W. Alteration of hydrologic indicators for Korean catchments under CMIP5 climate projections. Hydrol. Process. 2016, 30, 4517–4542. [Google Scholar] [CrossRef]
- Shin, M.J.; Guillaume, J.H.; Croke, B.F.; Jakeman, A.J. A review of foundational methods for checking the structural identifiability of models: Results for rainfall-runoff. J. Hydrol. 2015, 520, 1–16. [Google Scholar] [CrossRef]
- Shin, M.J.; Kim, C.S. Assessment of the suitability of rainfall–runoff models by coupling performance statistics and sensitivity analysis. Hydrol. Res. 2017, 48, 1192–1213. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]

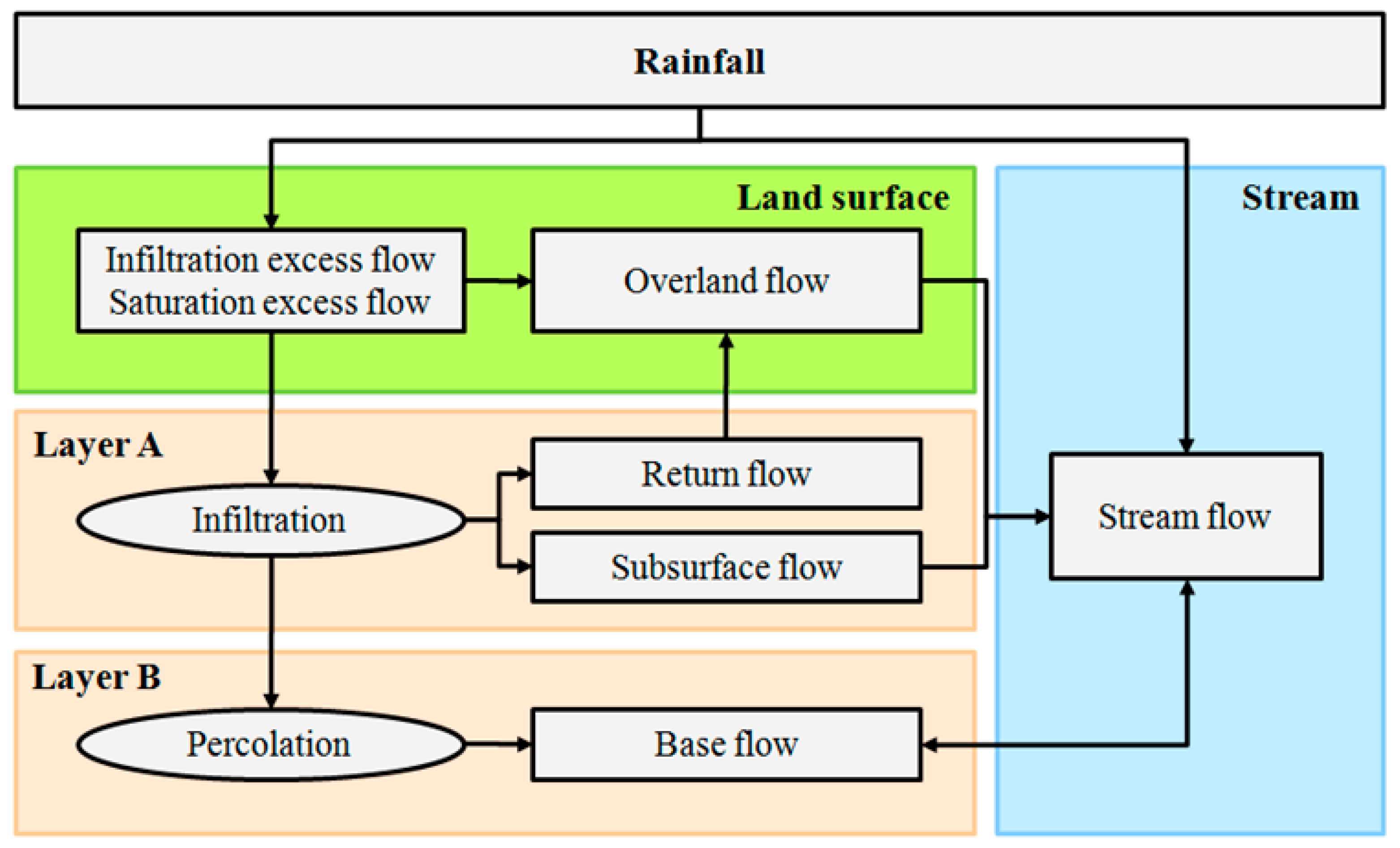

| Virtual Rainfall Event Name | Max. Rainfall Intensity (mm/h) | Min. Rainfall Intensity (mm/h) | Total Rainfall (mm) | Rainfall Duration (h) |
|---|---|---|---|---|
| VR5 | 5 | 1 | 25 | 9 |
| VR10 | 10 | 2 | 50 | |
| VR20 | 20 | 4 | 100 | |
| VR40 | 40 | 8 | 200 |
| Virtual Catchment Name | Catchment Area (km2) | Resolution | Slope (m/m) | Grid Number | Stream Grid | Applied Rainfall | |
|---|---|---|---|---|---|---|---|
| Number | Ratio * (%) | ||||||
| VD200_15 | 2540 | 200 m × 200 m | 0.005 | 63,503 | 9250 | 15 | VR20 |
| VD200_9 | 2540 | 200 m × 200 m | 63,503 | 5998 | 9 | VR5, VR10, VR20, VR40 | |
| VD200_6 | 2540 | 200 m × 200 m | 63,503 | 3744 | 6 | VR20 | |
| VD500_10 | 2540 | 500 m × 500 m | 10,201 | 996 | 10 | VR20 | |
| VD1000_12 | 2540 | 1000 m × 1000 m | 2550 | 295 | 12 | VR20 | |
| Catchment | Resolution | Rainfall | Observed Peak Flow (m3/s) | ||
|---|---|---|---|---|---|
| Name | Area (km2) | Period | Total Rainfall (mm) | ||
| Danseong | 1709 | 500 m × 500 m | 14 July 2012/15:00–21 July 2012/05:00 | 63 | 1213 |
| Museong | 472 | 200 m × 200 m | 31 August 2007/20:00–02 September 2007/21:00 | 100 | 981 |
| Rainfall Event | FTS | ATS | ||||
|---|---|---|---|---|---|---|
| dt (min) | Peak Flow (m3/s) | PPE * (%) | Initial dt (min) | Peak Flow (m3/s) | PPE * (%) | |
| VR5 | 1 | 1647 | 0 | 1 | 1596 | 0 |
| 5 | 1605 | 3 | 5 | 1556 | 3 | |
| 10 | 1555 | 6 | 10 | 1537 | 4 | |
| 20 | 1462 | 11 | 20 | 1556 | 3 | |
| 30 | 1380 | 16 | 30 | 1476 | 8 | |
| VR10 | 1 | 4471 | 0 | 1 | 4395 | 0 |
| 5 | 4367 | 2 | 5 | 4336 | 1 | |
| 10 | 4238 | 5 | 10 | 4276 | 3 | |
| 20 | 3995 | 11 | 20 | 4336 | 1 | |
| 30 | 3775 | 16 | 30 | 4186 | 5 | |
| VR20 | 1 | 10,427 | 0 | 1 | 10,354 | 0 |
| 5 | 10,256 | 2 | 5 | 10,345 | 0 | |
| 10 | 10,039 | 4 | 10 | 10,269 | 1 | |
| 20 | 9603 | 8 | 20 | 10,345 | 0 | |
| 30 | 9182 | 12 | 30 | 10,187 | 2 | |
| VR40 | 1 | 23,323 | 0 | 1 | 23,288 | 0 |
| 5 | 22,954 | 2 | 5 | 23,246 | 0 | |
| 10 | 22,497 | 4 | 10 | 23,202 | 0 | |
| 20 | 21,595 | 7 | 20 | 23,246 | 0 | |
| 30 | 20,720 | 11 | 30 | 23,129 | 1 | |
| Max. diff. PPE** | 1 | 0 | 1 | 0 | ||
| 5 | 1 | 5 | 2 | |||
| 10 | 2 | 10 | 4 | |||
| 20 | 4 | 20 | 3 | |||
| 30 | 5 | 30 | 7 | |||
| FTS | ATS | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dt (min) | VD200_15 | VD200_9 | VD200_6 | Max. diff. PPE * | Initial dt (min) | VD200_15 | VD200_9 | VD200_6 | Max. diff. PPE | ||||||
| Peak Flow (m3/s) | PPE | Peak Flow (m3/s) | PPE | Peak Flow (m3/s) | PPE | Peak Flow (m3/s) | PPE | Peak Flow (m3/s) | PPE | Peak Flow (m3/s) | PPE | ||||
| 1 | 10,762 | 0 | 10,427 | 0 | 9836 | 0 | 0 | 1 | 10,587 | 0 | 10,354 | 0 | 9663 | 0 | 0 |
| 5 | 10,434 | 3 | 10,256 | 2 | 9609 | 2 | 1 | 5 | 10,484 | 1 | 10,345 | 0 | 9579 | 1 | 1 |
| 10 | 10,193 | 5 | 10,039 | 4 | 9335 | 5 | 1 | 10 | 10,441 | 1 | 10,269 | 1 | 9489 | 2 | 1 |
| 20 | 9803 | 9 | 9603 | 8 | 8827 | 10 | 2 | 20 | 10,484 | 1 | 10,345 | 0 | 9579 | 1 | 1 |
| 30 | 9414 | 13 | 9182 | 12 | 8368 | 15 | 3 | 30 | 10,382 | 2 | 10,187 | 2 | 9281 | 4 | 2 |
| FTS | ATS | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dt (min) | VD200_9 | VD500_10 | VD1000_12 | Max. diff. PPE * | Initial dt (min) | VD200_9 | VD500_10 | VD1000_12 | Max. diff. PPE | ||||||
| Peak Flow (m3/s) | PPE | Peak Flow (m3/s) | PPE | Peak Flow (m3/s) | PPE | Peak Flow (m3/s) | PPE | Peak Flow (m3/s) | PPE | Peak Flow (m3/s) | PPE | ||||
| 1 | 10,427 | 0 | 8280 | 0 | 5619 | 0 | 0 | 1 | 10,354 | 0 | 8070 | 0 | 5379 | 0 | 0 |
| 5 | 10,256 | 2 | 8153 | 2 | 5546 | 1 | 1 | 5 | 10,345 | 0 | 7987 | 1 | 5338 | 1 | 1 |
| 10 | 10,039 | 4 | 7997 | 3 | 5456 | 3 | 1 | 10 | 10,269 | 1 | 7879 | 2 | 5108 | 5 | 4 |
| 20 | 9603 | 8 | 7693 | 7 | 5283 | 6 | 2 | 20 | 10,345 | 0 | 7987 | 1 | 5338 | 1 | 1 |
| 30 | 9182 | 12 | 7402 | 11 | 5115 | 9 | 3 | 30 | 10,187 | 2 | 7761 | 4 | 4999 | 7 | 5 |
| Event | Items | FTS | ATS | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Ave. | Standard dev. | Min. | Max. | Ave. | Standard dev. | |||
| Danseong | Performance evaluation statistics | NSE | 0.43 | 0.97 | 0.86 | 0.21 | 0.97 | 0.97 | 0.97 | 0.00 |
| nRMSE | 0.05 | 0.24 | 0.10 | 0.07 | 0.05 | 0.06 | 0.05 | 0.00 | ||
| PPE | 0.19 | 27.49 | 6.27 | 10.63 | 0.28 | 1.02 | 0.64 | 0.31 | ||
| Model parameters | ISSR | 0.00 | 0.48 | 0.30 | 0.21 | 0.50 | 0.55 | 0.52 | 0.02 | |
| MSCB | 0.003 | 0.006 | 0.005 | 0.001 | 0.006 | 0.007 | 0.007 | 0.000 | ||
| CRC | 0.191 | 0.200 | 0.196 | 0.003 | 0.185 | 0.199 | 0.193 | 0.005 | ||
| CCHC | 7.72 | 14.60 | 12.78 | 2.56 | 13.21 | 13.77 | 13.49 | 0.21 | ||
| Museong | Performance evaluation statistics | NSE | 0.97 | 0.99 | 0.98 | 0.01 | 0.99 | 0.99 | 0.99 | 0.00 |
| nRMSE | 0.03 | 0.04 | 0.04 | 0.00 | 0.03 | 0.03 | 0.03 | 0.00 | ||
| PPE | 0.54 | 6.74 | 2.45 | 2.27 | 2.87 | 3.70 | 3.40 | 0.30 | ||
| Model parameters | ISSR | 0.98 | 1.00 | 0.99 | 0.01 | 0.99 | 1.00 | 0.99 | 0.00 | |
| MSCB | 0.001 | 0.007 | 0.003 | 0.002 | 0.002 | 0.009 | 0.005 | 0.002 | ||
| CRC | 0.072 | 0.169 | 0.112 | 0.031 | 0.081 | 0.186 | 0.133 | 0.036 | ||
| CCHC | 0.87 | 1.84 | 1.31 | 0.40 | 1.64 | 1.86 | 1.79 | 0.08 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.S.; Shin, M.-J.; Kim, K.T. Preliminary Study of Computational Time Steps in a Physically Based Distributed Rainfall–Runoff Model. Water 2018, 10, 1269. https://doi.org/10.3390/w10091269
Choi YS, Shin M-J, Kim KT. Preliminary Study of Computational Time Steps in a Physically Based Distributed Rainfall–Runoff Model. Water. 2018; 10(9):1269. https://doi.org/10.3390/w10091269
Chicago/Turabian StyleChoi, Yun Seok, Mun-Ju Shin, and Kyung Tak Kim. 2018. "Preliminary Study of Computational Time Steps in a Physically Based Distributed Rainfall–Runoff Model" Water 10, no. 9: 1269. https://doi.org/10.3390/w10091269
APA StyleChoi, Y. S., Shin, M.-J., & Kim, K. T. (2018). Preliminary Study of Computational Time Steps in a Physically Based Distributed Rainfall–Runoff Model. Water, 10(9), 1269. https://doi.org/10.3390/w10091269





