Subdaily Rainfall Estimation through Daily Rainfall Downscaling Using Random Forests in Spain
Abstract
:1. Introduction
2. Study Area and Information Sources
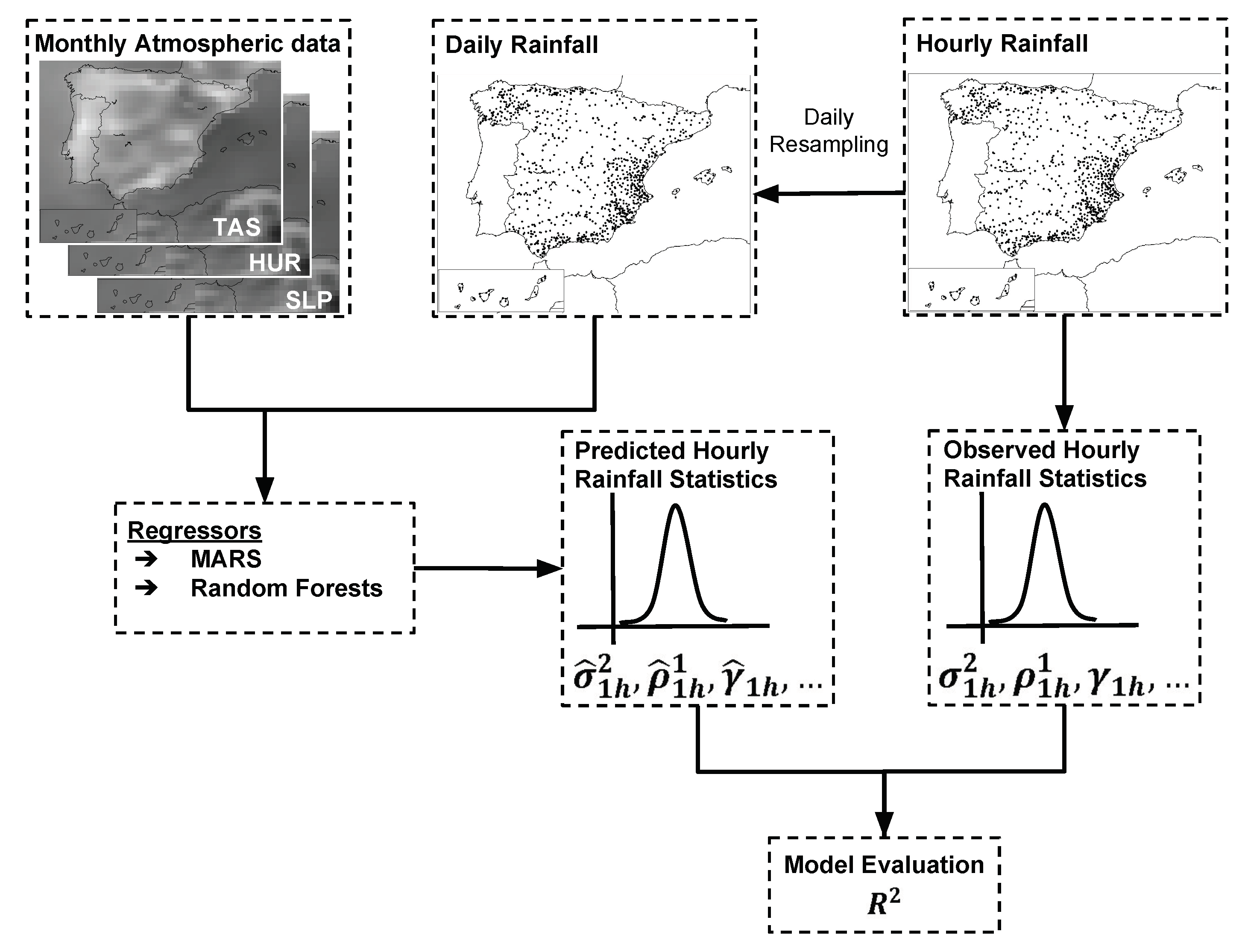
3. Methodology
3.1. Beuchat’s Model
3.2. RFB Model
3.3. Model Evaluation
3.4. Synthetic Rainfall Generation
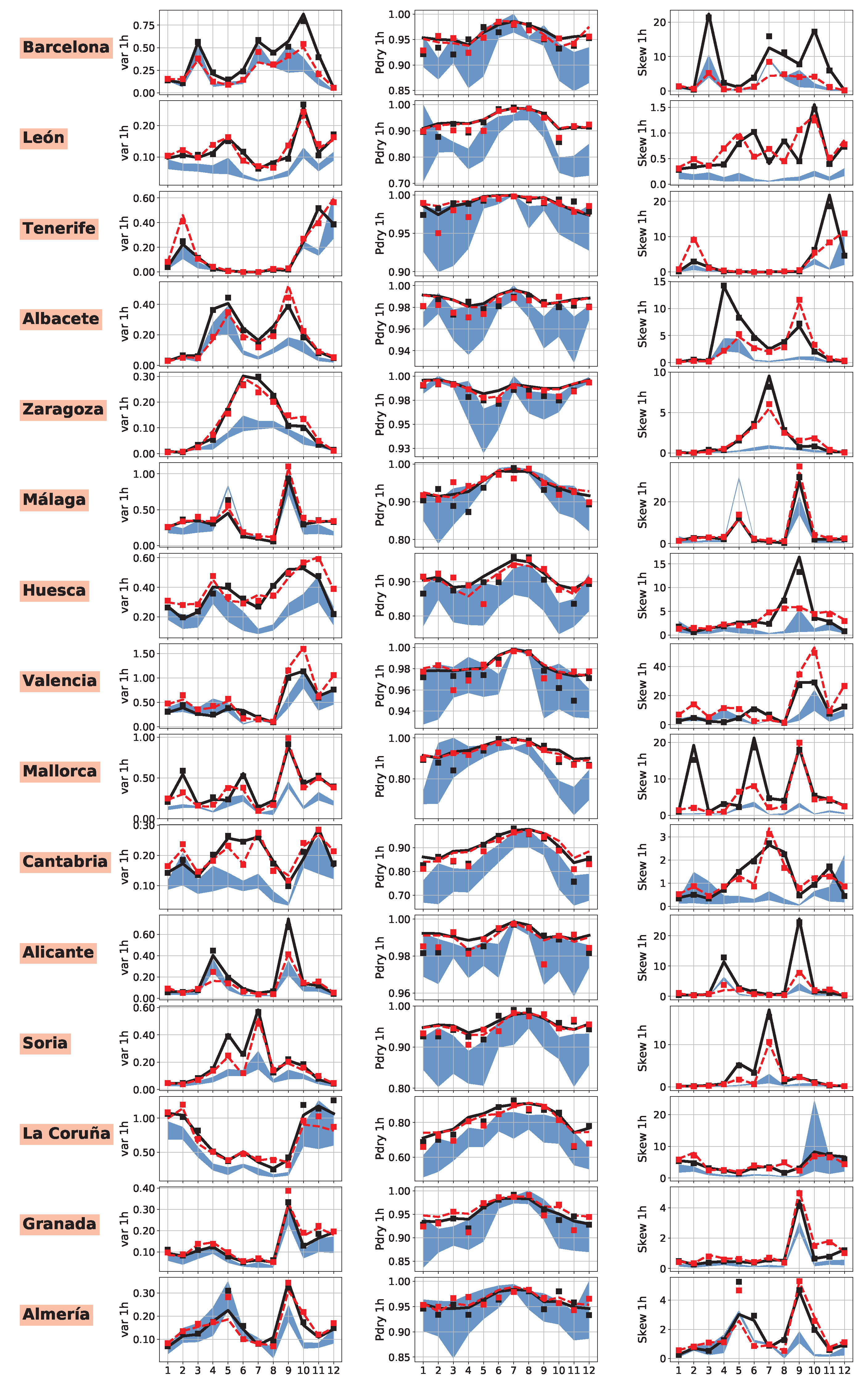
4. Results
4.1. Model Comparison
4.2. Performance Analysis of RFB
4.3. Performance of Simulated Rainfall
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Smith, J.; Baeck, M.; Meierdiercks, K.; Miller, A.; Krajewski, W. Radar rainfall estimation for flash flood forecasting in small urban watersheds. Adv. Water Resour. 2007, 30, 2087–2097. [Google Scholar] [CrossRef]
- Michaud, J.; Sorooshian, S. Effect of rainfall sampling errors on simulations of desert flash floods. Water Resour. Res. 1994, 30, 2765–2775. [Google Scholar] [CrossRef]
- Kun, Y.; Giuliano, D.B.; Florian, P. Flood Hazard Mapping in Data-Scarce Areas. In Global Flood Hazard; Schumann, G.J., Bates, P.D., Apel, H., Aronica, G.T., Eds.; American Geophysical Union: Washington, DC, USA, 2018. [Google Scholar]
- Cáceres, M.D.; Martin-StPaul, N.; Turco, M.; Cabon, A.; Granda, V. Estimating daily meteorological data and downscaling climate models over landscapes. Environ. Model. Softw. 2018, 108, 186–196. [Google Scholar] [CrossRef]
- Krajewski, W.; Smith, J. Radar hydrology: Rainfall estimation. Adv. Water Resour. 2002, 25, 1387–1394. [Google Scholar] [CrossRef]
- Noor, M.; Ismail, T.; Chung, E.S.; Shahid, S.; Sung, J.H. Uncertainty in Rainfall Intensity Duration Frequency Curves of Peninsular Malaysia under Changing Climate Scenarios. Water 2018, 10, 1750. [Google Scholar] [CrossRef]
- Pui, A.; Sharma, A.; Mehrotra, R.; Sivakumar, B.; Jeremiah, E. A comparison of alternatives for daily to sub-daily rainfall disaggregation. J. Hydrol. 2012, 470–471, 138–157. [Google Scholar] [CrossRef]
- Huffman, G.; Adler, R.; Bolvin, D.; Nelkin, E. The TRMM Multi-Satellite Precipitation Analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Pfeifroth, U.; Mueller, R.; Ahrens, B. Evaluation of satellite-based and reanalysis precipitation data in the tropical pacific. J. Appl. Meteorol. Climatol. 2013, 52, 634–644. [Google Scholar] [CrossRef]
- Austin, G.; Seed, A. Special issue on the hydrological applications of weather radar—Guest editors’ preface. Atmos. Sci. Lett. 2005, 6, 1. [Google Scholar] [CrossRef]
- Kim, J.E.; Joan Alexander, M. Tropical precipitation variability and convectively coupled equatorial waves on submonthly time scales in reanalyses and TRMM. J. Clim. 2013, 26, 3013–3030. [Google Scholar] [CrossRef]
- Del Jesus, M.; Rinaldo, A.; Rodríguez-Iturbe, I. Point rainfall statistics for ecohydrological analyses derived from satellite integrated rainfall measurements. Water Resour. Res. 2015, 51, 2974–2985. [Google Scholar] [CrossRef] [Green Version]
- Hershenhorn, J.; Woolhiser, D. Disaggregation of daily rainfall. J. Hydrol. 1987, 95, 299–322. [Google Scholar] [CrossRef] [Green Version]
- Glasbey, C.; Cooper, G.; McGechan, M. Disaggregation of daily rainfall by conditional simulation from a point-process model. J. Hydrol. 1995, 165, 1–9. [Google Scholar] [CrossRef]
- Cowpertwait, P. Further developments of the neyman-scott clustered point process for modeling rainfall. Water Resour. Res. 1991, 27, 1431–1438. [Google Scholar] [CrossRef]
- Burton, A.; Kilsby, C.; Fowler, H.; Cowpertwait, P.; O’Connell, P. RainSim: A spatial–temporal stochastic rainfall modelling system. Environ. Model. Softw. 2008, 23, 1356–1369. [Google Scholar] [CrossRef]
- Bennett, J.C.; Robertson, D.E.; Ward, P.G.; Hapuarachchi, H.P.; Wang, Q. Calibrating hourly rainfall-runoff models with daily forcings for streamflow forecasting applications in meso-scale catchments. Environ. Model. Softw. 2016, 76, 20–36. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Singh, V.P. Spatial Disaggregation of Areal Rainfall Using Two Different Artificial Neural Networks Models. Water 2015, 7, 2707–2727. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Meshgi, A.; Wang, X.; Zhang, J.; Tay, S.; Pijcke, G.; Manocha, N.; Ong, M.; Nguyen, M.; Babovic, V. Three resampling approaches based on method of fragments for daily-to-subdaily precipitation disaggregation. Int. J. Climatol. 2018, 38, e1119–e1138. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Eagleson, P. Mathematical models of rainstorm events in space and time. Water Resour. Res. 1987, 23, 181–190. [Google Scholar] [CrossRef]
- Cowpertwait, P. A spatial-temporal point process model of rainfall for the Thames catchment, UK. J. Hydrol. 2006, 330, 586–595. [Google Scholar] [CrossRef]
- Gupta, V.; Waymire, E. A statistical analysis of mesoscale rainfall as a random cascade. J. Appl. Meteorol. 1993, 32, 251–267. [Google Scholar] [CrossRef]
- Sharma, A.; Srikanthan, R. Continuous Rainfall Simulation: A Nonparametric Alternative. In Proceedings of the 30th Hydrology and Water Resources Symposium, Launceston, Tasmania, 4–7 December 2006. [Google Scholar]
- Lu, Y.; Qin, X. Multisite rainfall downscaling and disaggregation in a tropical urban area. J. Hydrol. 2014, 509, 55–65. [Google Scholar] [CrossRef]
- Cowpertwait, P.; Kilsby, C.; O’Connell, P. A space-time Neyman-Scott model of rainfall: Empirical analysis of extremes. Water Resour. Res. 2002, 38, 6. [Google Scholar] [CrossRef]
- Burton, A.; Fowler, H.; Blenkinsop, S.; Kilsby, C. Downscaling transient climate change using a Neyman-Scott Rectangular Pulses stochastic rainfall model. J. Hydrol. 2010, 381, 18–32. [Google Scholar] [CrossRef]
- Cowpertwait, P.; O’Connell, P.; Metcalfe, A.; Mawdsley, J. Stochastic point process modelling of rainfall. II. Regionalisation and disaggregation. J. Hydrol. 1996, 175, 47–65. [Google Scholar] [CrossRef]
- Marani, M.; Zanetti, S. Downscaling rainfall temporal variability. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Burlando, P.; Rosso, R. Scaling and multiscaling models of depth-duration-frequency curves for storm precipitation. J. Hydrol. 1996, 187, 45–64. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982; Volume 982. [Google Scholar]
- Beuchat, X.; Schaefli, B.; Soutter, M.; Mermoud, A. Toward a robust method for subdaily rainfall downscaling from daily data. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Agencia Estatal de Meteorología (AEMET). Iberian Climate Atlas; Agencia Estatal de Meteorología (España) and Instituto de Meteorología (Portugal): Madrid, Spain, 2011. [Google Scholar]
- Tullot, I.F. El clima de las Islas Canarias. Anuario de Estudios Atlánticos 1959, 1, 57–103. [Google Scholar]
- Herrera, R.G.; Puyol, D.G.; Martín, E.H.; Presa, L.G.; Rodríguez, P.R. Influence of the North Atlantic oscillation on the Canary Islands precipitation. J. Clim. 2001, 14, 3889–3903. [Google Scholar] [CrossRef]
- Diez-Sierra, J.; del Jesus, M. A rainfall analysis and forecasting tool. Environ. Model. Softw. 2017, 97, 243–258. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Herrera, S.; Gutiérrez, J.; Ancell, R.; Pons, M.; Frías, M.; Fernández, J. Development and analysis of a 50-year high-resolution daily gridded precipitation dataset over Spain (Spain02). Int. J. Climatol. 2012, 32, 74–85. [Google Scholar] [CrossRef]
- AEMET. Available online: http://www.aemet.es/en/portada (accessed on 4 July 2018).
- CMA. Available online: http://hispagua.cedex.es/instituciones/confederaciones/andalucia (accessed on 4 July 2018).
- CHS. Available online: https://www.chsegura.es/chs/index.html (accessed on 4 July 2018).
- CHMS. Available online: https://www.chminosil.es/es/ (accessed on 4 July 2018).
- CHC. Available online: https://www.chcantabrico.es/ (accessed on 4 July 2018).
- CHJ. Available online: https://www.chj.es/es-es/Organismo/Paginas/Organismo.aspx (accessed on 4 July 2018).
- CHE. Available online: http://www.chebro.es/ (accessed on 4 July 2018).
- OAPN. Available online: http://www.mapama.gob.es/es/parques-nacionales-oapn/ (accessed on 4 July 2018).
- SIAR. Available online: http://eportal.mapama.gob.es/websiar/SeleccionParametrosMap.aspx?dst=1 (accessed on 4 July 2018).
- SMC. Available online: http://en.meteocat.gencat.cat/?lang=en (accessed on 4 July 2018).
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 1–67. [Google Scholar]
- Friedman, J.; Roosen, C. An introduction to multivariate adaptive regression splines. Stat. Methods Med. Res. 1995, 4, 197–217. [Google Scholar] [CrossRef] [PubMed]
- Craven, P.; Wahba, G. Smoothing noisy data with spline functions. Numer. Math. 1978, 31, 377–403. [Google Scholar] [CrossRef]
- Alizadeh, Z.; Yazdi, J.; Kim, J.H.; Al-Shamiri, A.K. Assessment of Machine Learning Techniques for Monthly Flow Prediction. Water 2018, 10, 1676. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- He, X.; Chaney, N.; Schleiss, M.; Sheffield, J. Spatial downscaling of precipitation using adaptable random forests. Water Resour. Res. 2016, 52, 8217–8237. [Google Scholar] [CrossRef] [Green Version]
- Muñoz, P.; Orellana-Alvear, J.; Willems, P.; Célleri, R. Flash-Flood Forecasting in an Andean Mountain Catchment—Development of a Step-Wise Methodology Based on the Random Forest Algorithm. Water 2018, 10, 1519. [Google Scholar] [CrossRef]
- Sultana, Z.; Sieg, T.; Kellermann, P.; Müller, M.; Kreibich, H. Assessment of Business Interruption of Flood-Affected Companies Using Random Forests. Water 2018, 10, 1049. [Google Scholar] [CrossRef]
- Cowpertwait, P.; O’Connell, P.; Metcalfe, A.; Mawdsley, J. Stochastic point process modelling of rainfall. I. Single-site fitting and validation. J. Hydrol. 1996, 175, 17–46. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Markatou, M.; Tian, H.; Biswas, S.; Hripcsak, G. Analysis of variance of cross-validation estimators of the generalization error. J. Mach. Learn. Res. 2005, 6, 1127–1168. [Google Scholar]
- Cowpertwait, P. A generalized spatial-temporal model of rainfall based on a clustered point process. Proc. R. Soc. Lond. A 1995, 450, 163–175. [Google Scholar] [CrossRef]
- Leonard, M.; Lambert, M.; Metcalfe, A.; Cowpertwait, P. A space-time Neyman-Scott rainfall model with defined storm extent. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Cowpertwait, P.; Ocio, D.; Collazos, G.; De Cos, O.; Stocker, C. Regionalised spatiotemporal rainfall and temperature models for flood studies in the Basque Country, Spain. Hydrol. Earth Syst. Sci. 2013, 17, 479–494. [Google Scholar] [CrossRef] [Green Version]
- Cowpertwait, P. A Poisson-cluster model of rainfall: High-order moments and extreme values. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 885–898. [Google Scholar] [CrossRef]
- Hu, Z.; Hu, Q.; Zhang, C.; Chen, X.; Li, Q. Evaluation of reanalysis, spatially interpolated and satellite remotely sensed precipitation data sets in central Asia. J. Geophys. Res. 2016, 121, 5648–5663. [Google Scholar] [CrossRef]






| Organization | Number of Gauges |
|---|---|
| AEMET [38] | 38 |
| Cuenca Mediterránea Andaluza [39] | 109 |
| C.H.Segura [40] | 114 |
| C.H. Miño-Sil [41] | 89 |
| C.H. Cantábrico [42] | 56 |
| C.H. Jucar [43] | 185 |
| C.H. Ebro [44] | 69 |
| Organismo Autónomo Parques Nacionales [45] | 16 |
| Sistema de Información Agroclimática para el Regadio [46] | 237 |
| Servei Meteorològic de Catalunya [47] | 43 |
| Variance | Pdry | Skewness | ACF-lag1 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 h | 12 h | 1 h | 12 h | 1 h | 12 h | 1 h | 12 h | |||||||||
| B | RFB | B | RFB | B | RFB | B | RFB | B | RFB | B | RFB | B | RFB | B | RFB | |
| BWh | 0.79 | 0.65 | 0.96 | 0.96 | 0.84 | 0.89 | 0.99 | 0.99 | 0.59 | 0.62 | 0.91 | 0.91 | −0.13 | 0.40 | −12.16 | 0.04 |
| BWk | 0.65 | 0.72 | 0.98 | 0.98 | 0.53 | 0.75 | 0.98 | 0.98 | 0.62 | 0.68 | 0.94 | 0.93 | −0.54 | 0.00 | −52.59 | 0.32 |
| BSh | 0.73 | 0.63 | 0.96 | 0.96 | 0.92 | 0.94 | 0.99 | 0.99 | 0.69 | 0.65 | 0.91 | 0.92 | −0.68 | 0.33 | −7.89 | 0.34 |
| BSk | 0.72 | 0.75 | 0.97 | 0.97 | 0.92 | 0.93 | 0.99 | 0.99 | 0.65 | 0.65 | 0.93 | 0.93 | 0.14 | 0.49 | −13.83 | 0.38 |
| Csa | 0.80 | 0.81 | 0.98 | 0.98 | 0.92 | 0.94 | 0.98 | 0.99 | 0.73 | 0.74 | 0.92 | 0.92 | 0.26 | 0.57 | −11.51 | 0.53 |
| Csb | 0.84 | 0.85 | 0.99 | 0.99 | 0.93 | 0.97 | 0.98 | 0.99 | 0.65 | 0.65 | 0.92 | 0.91 | 0.14 | 0.67 | −8.11 | 0.65 |
| Cfa | 0.61 | 0.70 | 0.95 | 0.94 | 0.79 | 0.84 | 0.97 | 0.97 | 0.37 | 0.42 | 0.87 | 0.87 | 0.27 | 0.63 | −11.45 | 0.44 |
| Cfb | 0.69 | 0.72 | 0.97 | 0.97 | 0.93 | 0.95 | 0.99 | 0.99 | 0.59 | 0.62 | 0.93 | 0.93 | 0.29 | 0.65 | −7.16 | 0.57 |
| D | 0.66 | 0.77 | 0.94 | 0.97 | 0.73 | 0.69 | 0.92 | 0.88 | −0.56 | 0.21 | 0.78 | 0.79 | 0.26 | 0.43 | −13.77 | 0.03 |
| Total | 0.78 | 0.83 | 0.98 | 0.98 | 0.94 | 0.96 | 0.99 | 0.99 | 0.71 | 0.73 | 0.93 | 0.93 | 0.24 | 0.61 | −9.74 | 0.56 |
| Predictors | Predictands () | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| B | RFB | ||||||||
| TAS | |||||||||
| HUR | |||||||||
| Elevation | |||||||||
| 1 h | 12 h | 1 h | 12 h | |
|---|---|---|---|---|
| BWh | 0.97 | 0.99 | 0.59 | 0.72 |
| BWk | 0.97 | 0.97 | 0.12 | 0.83 |
| BSh | 0.96 | 0.98 | 0.59 | 0.85 |
| BSk | 0.98 | 0.99 | 0.67 | 0.87 |
| Csa | 0.97 | 0.99 | 0.75 | 0.86 |
| Csb | 0.96 | 0.99 | 0.80 | 0.90 |
| Cfa | 0.87 | 0.97 | 0.73 | 0.79 |
| Cfb | 0.95 | 0.98 | 0.8 | 0.90 |
| D | 0.61 | 0.93 | 0.04 | 0.20 |
| Total | 0.97 | 0.98 | 0.77 | 0.89 |
| Mean | Variance | Skewness | Proportion of Dry Intervals | Lag-1 Correlation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time scale | 1 d | 1 h | 1 d | 1 h | 1 d | 1 h | 1 d | 1 h | 1 d | 1 h | 1 d | 1 h | 1 d |
| Weights | 5 | 4 | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 4 | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diez-Sierra, J.; del Jesus, M. Subdaily Rainfall Estimation through Daily Rainfall Downscaling Using Random Forests in Spain. Water 2019, 11, 125. https://doi.org/10.3390/w11010125
Diez-Sierra J, del Jesus M. Subdaily Rainfall Estimation through Daily Rainfall Downscaling Using Random Forests in Spain. Water. 2019; 11(1):125. https://doi.org/10.3390/w11010125
Chicago/Turabian StyleDiez-Sierra, Javier, and Manuel del Jesus. 2019. "Subdaily Rainfall Estimation through Daily Rainfall Downscaling Using Random Forests in Spain" Water 11, no. 1: 125. https://doi.org/10.3390/w11010125
APA StyleDiez-Sierra, J., & del Jesus, M. (2019). Subdaily Rainfall Estimation through Daily Rainfall Downscaling Using Random Forests in Spain. Water, 11(1), 125. https://doi.org/10.3390/w11010125





