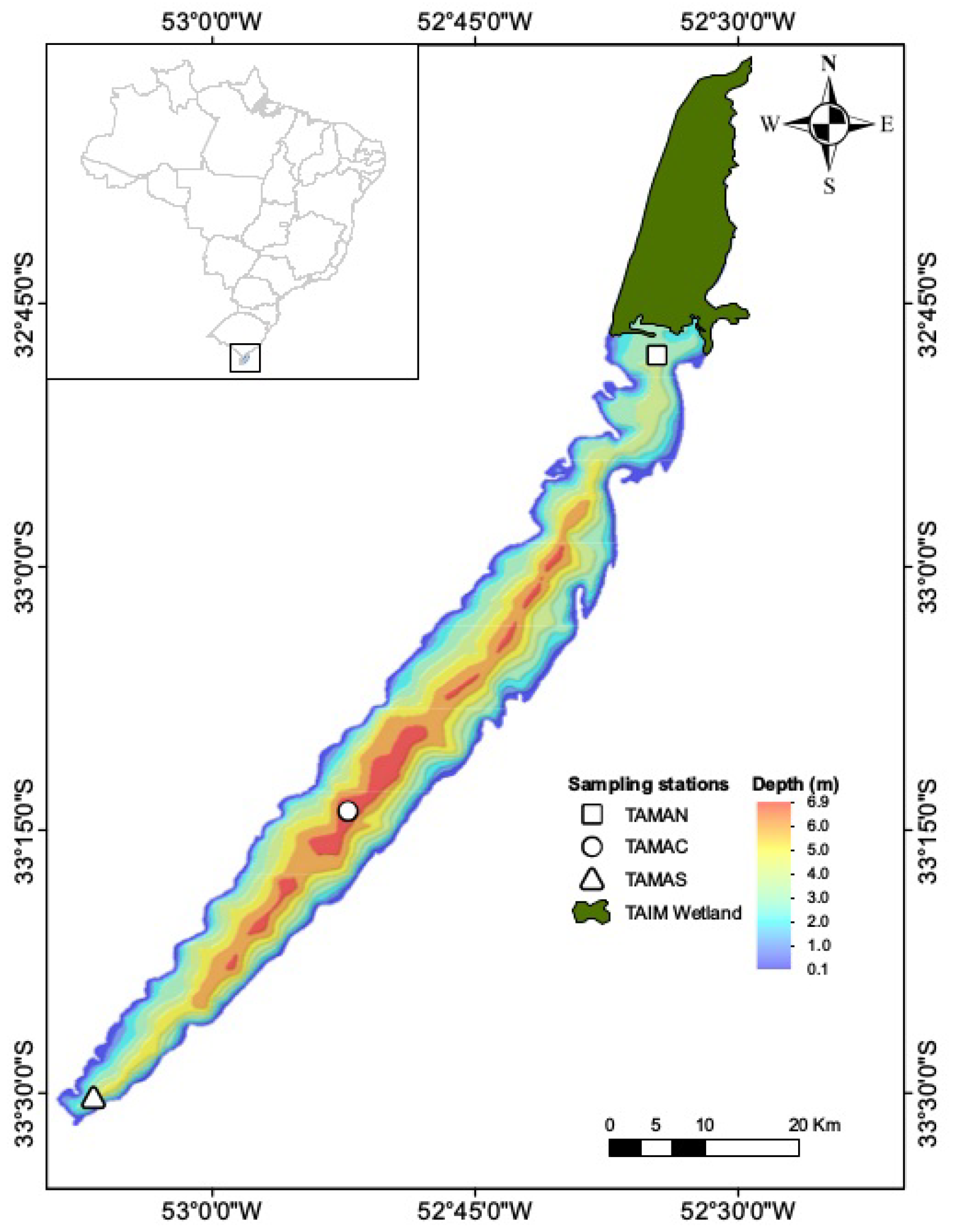
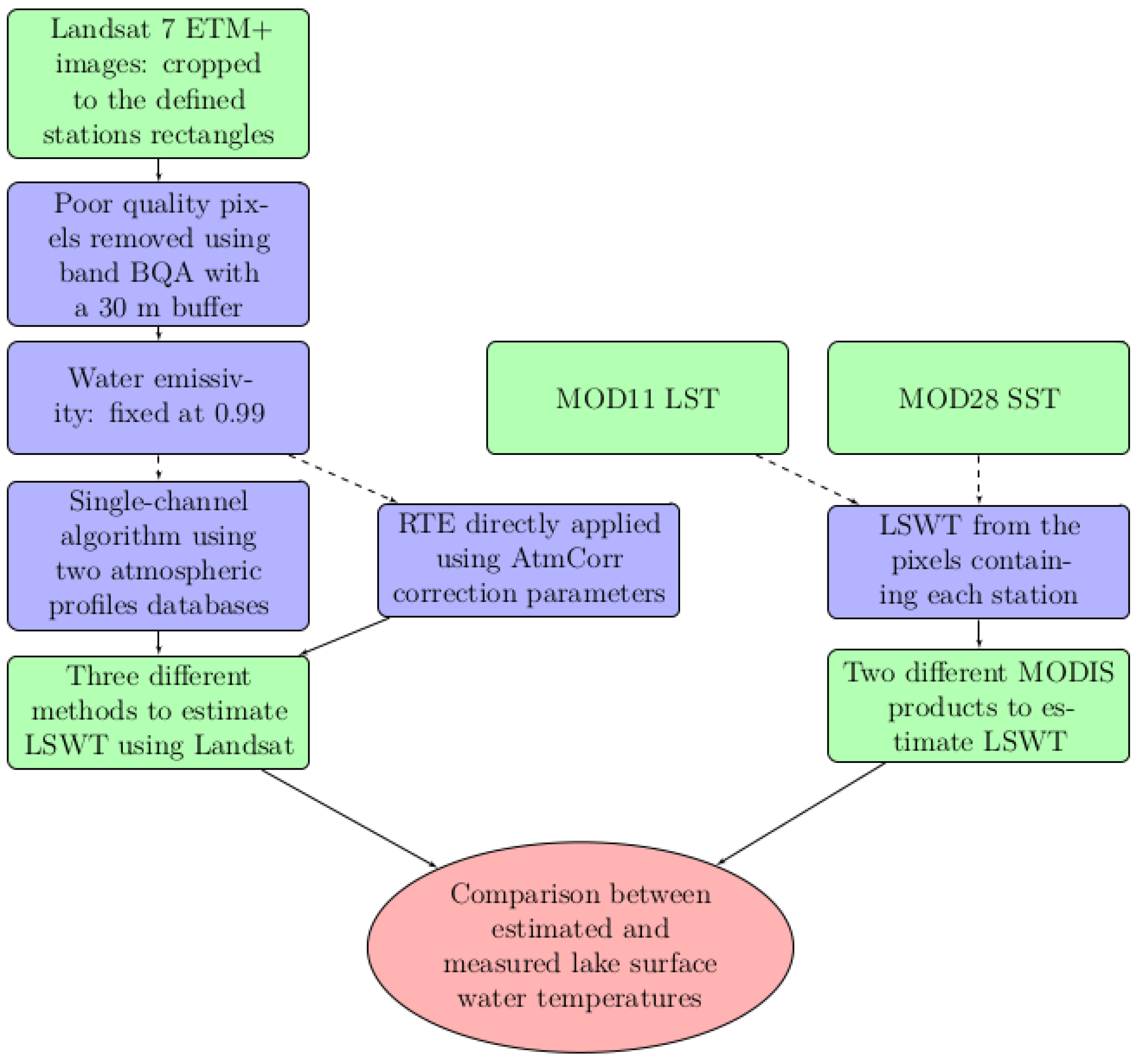
4.1. Comparison of Landsat 7 ETM+ and MODIS Performance
When using TIGR3 database constants, AtmCorr and the single-channel algorithm both showed good performance (with no statistical difference between their residual data), corroborating with similar studies found in the literature [
15,
24,
33]. TIGR3 outperforming SAFREE (
Table 3) for coastal-lake SWT estimation was previously reported [
35], suggesting that the SAFREE database should not be used in such studies.
The main limiting factor for LSWT estimates using Landsat imagery is the correction of the atmospheric effects. Using commercial radiative transfer codes to estimate these parameters and applying the RTE, Schneider and Mauser [
28] found an RMSE of 0.73
C when applying Lowtran with Landsat 5 images, and Allan et al. [
12] found an RMSE between 0.48
C and 0.94
C when applying MODTRAN with Landsat 7 ETM+. These studies showed how specific, more accurate atmospheric correction parameters can improve LSWT estimation. While AtmCorr is the best alternative (to the authors’ knowledge) for freely obtaining these parameters, it provides only a point estimate, which is interpolated from the closest nodes of parallels and meridians (1
× 1
grid). For large lakes, this can be a problem when estimating the temperature for its whole surface and, considering the operational limitation of AtmCorr, MOD07L2 may be the best option when using Landsat imagery in these cases, since it provides water vapour content with spatial variability. The main issue with the estimates using MOD07L2 with the single-channel algorithm in our study is the lower accuracy in some SWT estimates, reaching out to a
T of ±3
C in some cases. Many of these low-quality estimates are consistent with the results found by Jiménez-Muñoz et al. [
48], in which the error of the ST estimates increased considerably for atmospheric water vapour content higher than 3.0 g/cm
(
Figure 6).
The performance found for MODIS also compared well with the literature, with both products showing performance similar to what was found in most studies [
6,
10,
11,
14,
41]. Reinart and Reinhold [
23] used MOD28 to estimate the LSWT of two large lakes in Sweden, and found a mean absolute difference of 0.41
C and
of 0.993 for both lakes. In spite of the good performance found by the authors, LSWT estimates were compared with measured bulk temperatures, and so this may not be the case for the ST, since many of the data were from the summer months, when both lakes may have been thermally stratified.
Our findings showed higher similarity between LSWT estimations based on MOD11, AtmCorr, and SC-TIGR, different from LSWT estimations based on MOD28. Despite the similar performance shown by MOD28 and SC-TIGR (in terms of absolute error and RMSE), MOD28 showed more erratic behavior, with a smaller correlation coefficient and different linear regression (
Figure 4). Besides that, MOD28 showed a positive bias, while all other estimators showed a negative bias. Additionally, good agreement between the estimates using Landsat and MOD11 (
Table 3 and
Table 4) indicates that they are consistent estimators over this lake, while MOD28 is not, as there is a high correlation between the residuals for the Landsat methods and MOD11, but not between the former and MOD28. Even though high correlation was found between MOD11 and MOD28, it may be due to the fact that both MODIS products similarly overestimated small-to-medium temperatures and underestimated higher temperatures (despite MOD28 showing a positive bias), which was not observed in the Landsat estimates.
The lower performance obtained for MOD28 may be explained by its low spatial resolution of 4 km, which might be too coarse for Lake Mangueira due to its narrowness (5 km wide over the Northern station, and less than 4 km wide over the Southern station). In fact, errors in the estimates were considerably higher for the Southern station than for the Central and Northern stations, pointing to this. Considering that temperature varies more widely near the shores [
6,
8,
24], it can be inferred that this product is not recommended for applications to lakes with narrow widths (in comparison to its spatial resolution), as is the case for Lake Mangueira.
4.2. Sensitivity to Parameters and Source of Errors
As seen in the literature, error in lake-water temperatures derived from remote-sensing imagery can occur mainly due to poor correction of atmospheric effects [
30,
71], water-surface effects [
72], and due to the misrepresentation of water emissivity [
30,
45].
There is difficulty associated with estimating and removing atmospheric effects, which can promote substantial errors [
31,
70]. In fact, estimates tend to have lower accuracy when the water vapour content in the atmosphere is higher, since this increases the uncertainty regarding the effect of the atmosphere on the radiance measured by the sensor and, thus, in the correction parameters. Jiménez-Muñoz et al. [
48] showed that the error in ST estimates considerably increased for atmospheric water vapour content higher than 3.0 g/cm
. Here, Landsat-derived estimates using AtmCorr showed a similar (although less pronounced) pattern. As atmospheric water vapour content (from the MOD07L2 water vapour product) increases, so does the error in the estimates of both SC-TIGR and AtmCorr, although this is not the case for MOD11 and MOD28 (
Figure 6,
Table 5). Although in other studies the accuracy of MODIS products decreased with higher temperatures (e.g., Reference [
11]), which is related to higher water vapour content, this was not evident here (
p-value > 0.05 for both products,
Table 5). This may be due to the refined quality of the MODIS algorithm to remove these effects using its own band measurements [
31], and to directly apply it in its ST products.
Temperature estimates using the RTE are very sensitive to atmospheric parameters (
Figure 7), particularly to atmospheric transmissivity. For instance, a small change of 2.5% in atmospheric-transmissivity value implied an increase of about 2
C in the RMSE. The increase in errors is more pronounced when decreasing the values of the atmospheric parameters, showing that
(which decreases as atmospheric water vapour increases) has a more important effect on
than
and
(both increase as atmospheric water vapour increases), which is expected considering Equation (
6). In this case, negative bias also contributes to this sharp increase in errors, as it increased in magnitude when the atmospheric parameters negatively varied. This result highlights the importance of an accurate, precise source of estimation of the influence of the atmosphere on the radiance measured by the sensor, as has been shown in the literature by good results in estimation of LSWT when using in situ radiosonde data and radiative transfer models (e.g., Reference [
12]).
The single-channel algorithm is much less sensitive to changes in atmospheric parameters, i.e., atmospheric water vapour content. Prats et al. [
15] reported that a 50% decrease in water vapour content produced a decrease of 0.2–0.3
C in the estimated temperatures; in our sensitivity analysis, this decrease produced a (negative) increase of 0.3
C in the bias, and only marginally increased the RMSE (0.07
C). On the other hand, for increased
w values, the RMSE and maximum error increased by 0.5
C and 1
C, respectively, which is consistent with the report of Jiménez-Muñoz et al. [
48]. Considering the small size (in comparison to emissivity and the radiance measured by the sensor) of the contribution of the water vapour content to the temperature estimates in this algorithm, MOD07L2 can be used for retrievals of LSWT using Landsat images, since data are measured daily and are spatially distributed, and this product is ready to use.
In our study, only a few estimates were made when water vapour content was high (>3 g/cm
,
Figure 6), which limits further understanding of the performance of these methods under such conditions. However, as seen in these few estimates and in the literature (e.g., References [
11,
48]), studies estimating LSWT in areas with high atmospheric water vapour, such as tropical areas, should keep in mind that estimation is bound to produce higher errors, especially when using Landsat imagery (
Table 8). For the Landsat methods, other sources of atmospheric parameters, such as reanalysis products [
15,
31], should also be further studied in order to be used with the radiative transfer equation in an effort to increase the accuracy of the estimates.
The cool bias found in our study was also found in most LSWT studies (e.g., References [
6,
10,
11,
15,
73]). This can be a result of the cool-skin effect, when the few millimetres at the top of the water column are colder than the water underneath. Usually, this is not measured by in situ sensors but affects estimates made using remote sensing [
74]. The cool-skin effect reduces water temperature over a range of 0.1–0.6
C, occurring as a result of heat loss from water to air due to evaporation, and is affected mainly by wind speed [
72,
75]. A warm-layer effect can also be observed during calm sunny days in deeper lakes, where thermal stratification can occur, and can increase the ST up to several degrees [
76], but as observed here and in other studies (e.g., Reference [
36]), this is not the case for the shallow Lake Mangueira.
While this effect is different for each lake and depends on in situ lake-temperature measurements to be understood, techniques are available to address the cool-skin effect in sea water, which assume this to be a function of wind speed [
75]. Although we did not attempt to assess and remove the cool-skin effect in the estimations here, our study shows that it is important in LSWT studies using remote sensing. Prats et al. [
15] estimated the LSWT for French water bodies for a long time series using Landsat 5 TM and 7 ETM+ images, applying an adjusted sea-water algorithm to remove the effects of the cool-skin and warm-layer effects, and testing these approaches on a reservoir with in situ data to validate it. The estimated cool-skin effect reduced the LSWT by about 0.3 to 0.6
C for most of the data, and even though the authors concluded that the algorithm required further adaptations for use on continental waters, it demonstrated how techniques to remove these effects can be useful to improve the accuracy of remote sensing-derived SWT in lake studies.
In the case of emissivity, considering that MODIS products use a fixed value of emissivity for water, as was also used in our study for Landsat 7 ETM+ images (as well as in most studies of water-temperature estimations using remote sensing, e.g., References [
15,
24]), it can also be a source of considerable error. Emissivity varies with several parameters, such as salinity and turbidity, which can result in errors of estimation ranging from 0.2 to 0.5
C [
45]. Hulley et al. [
32] used an algorithm to improve the estimation of water emissivity and the coefficients for the split-window algorithm for MOD11, in order to improve its estimation of inland SWT. They found differences of emissivity in up to 0.01 for MODIS, which resulted in errors of 0.3–0.7
C.
As shown in the sensitivity analysis, emissivity has a significant impact on the estimated temperatures, and showed an optimal value of 0.98, reducing the RMSE and maximum absolute error by 10% and 20%, respectively, compared to our standard value of 0.99. This, however, can be a result of the balancing of the cool-skin effect: as the latter reduces water temperature at the surface, a lower value of emissivity (i.e., further from its physical, more-likely value) makes the surface appear warmer than it is, partially compensating for the cool-skin effect. Although this 0.98 emissivity value produced the best results, we assumed (taking into account that it was not measured) that the closest value, from 0.97 to 1, to its real value is 0.99, which was calculated by Masuda et al. [
69] and also found in MODIS product MOD11 (0.992 for band 31 and 0.988 for band 32) for Lake Mangueira. Due to the limitation of water emissivity estimation [
66], most approaches still use a fixed, tabulated value of emissivity, found in reflectivity and emissivity data available in spectral libraries such as MODIS’ [
77]. As emissivity and the removal of the cool-skin effect are limiting factors to be improved in LSWT estimations, the use of lower emissivity values can be tested in future studies to reduce errors resulting from the latter in an effort to improve the accuracy of LSWT estimates.