The Impact of Training Data Sequence on the Performance of Neuro-Fuzzy Rainfall-Runoff Models with Online Learning

Abstract

The learning algorithms in many of conventional Neuro-Fuzzy Systems (NFS) are based on batch or global learning where all parameters of the fuzzy system are optimized off-line. Although these models have frequently been used, they suffer from a reduced flexibility in their architecture as the number of rules need to be predefined by the user. This study uses a Dynamic Evolving Neural Fuzzy Inference System (DENFIS) in which an evolving, online clustering algorithm, the Evolving Clustering Method (ECM), is implemented. This study focused on evaluating the performance of this model in capturing the rainfall-runoff process and rainfall-water level relationship. The two selected study catchments are located in an urban tropical and in a semi-urbanized area, respectively. The first catchment, Sungai Kayu Ara (23.22 km²), is located in Malaysia, with 10-min rainfall-runoff time-series from which 30 major events are used. The second catchment, Dandenong (272 km²), is located in Victoria, Australia, with daily rainfall and river stage (water level) data from which 11 years of data is used. DENFIS results were then compared with two groups of benchmark models: a regression-based data-driven model known as the Autoregressive Model with Exogenous Inputs (ARX) for both study sites, and physical models Hydrologic Engineering Center–Hydrologic Modelling System (HEC–HMS) and Storm Water Management Model (SWMM) for Sungai Kayu Ara and Dandenong catchments, respectively. DENFIS significantly outperformed the ARX model in both study sites. Moreover, DENFIS was found comparable if not superior to HEC–HMS and SWMM in Sungai Kayu Ara and Dandenong catchments, respectively. A sensitivity analysis was then conducted on DENFIS to assess the impact of training data sequence on its performance. Results showed that starting the training with datasets that include high peaks can improve the model performance. Moreover, datasets with more contrasting values that cover wide range of low to high values can also improve the DENFIS model performance.

1. Introduction

Hydrological modelling includes a wide range of applications including rainfall-runoff (R-R) modelling [1], channel connectivity modelling [2,3], water quality modelling [4], etc. There has been growing research interest in R-R modelling in the past few decades due to the fact that understanding and capturing R-R process play an important role in water resources management. R-R models can generally be grouped into three main classes: (1) physically based models, which rely on a clear knowledge about the system mechanism, and its related parameters such as rainfall, runoff, soil moisture, evapotranspiration, land use, and etc. (e.g., Storm Water Management Model or SWMM [5]); (2) conceptual models that normally consider several conceptual stores (or buckets) to represent the water storage in soil, vegetation, groundwater, and surface water bodies within the catchment (e.g., Hydrologiska Byråns Vattenbalansavdelning (HBV) [6]); and (3) system theoretic or data-driven models which are more focused on the direct mapping between rainfall and runoff data rather than emphasizing on the physical processes of the system (e.g., Artificial Neural Networks (ANN) and Neuro-Fuzzy Systems (NFS)). To date, several studies have been reported in literature on successful usage of ANN in R-R modelling [7,8,9,10,11,12,13,14]. Although ANN has been widely used in R-R modelling, it is considered as a purely black-box tool. Since the early 2000s, NFS models have gained widespread interest in R-R modelling as they can provide some semantics about the physics of the problem. Neuro-Fuzzy Systems or NFS combine the reasoning capabilities of fuzzy logic with the connectionist strength of neural networks [15]. This hybridization provides a much faster modelling tool for capturing the relationship between the input and output data using the fuzzy inference systems (FIS). This type of models has been used in various hydrological modelling applications [16,17].

The FIS are generally categorized into two classes of linguistic and precise models. In the linguistic or Mamdani-type FIS [18], both antecedent and consequent of the rules are defined by fuzzy sets. On the other hand, in the precise or Takagi–Sugeno–Kang (TSK) FIS [19,20] only the rule antecedent is defined by fuzzy sets and the consequence is defined by crisp values which can be generated by a mathematical function (generally a linear function). TSK models have been generally preferred over Mamdani-type models in engineering applications due to their improved accuracy in modelling performance. NFS can be also classified based on its learning process to either global (offline) or local (online) learning. In local learning, the model parameters will be gradually updated by receiving any new data point from the flow of the training data to the model. In global learning, however, the model parameters will be optimized based on a static batch of training dataset. An Adaptive Network-based Fuzzy Inference System (ANFIS) [21], which has a global learning mechanism, is perhaps the most popular NFS model used in R-R modelling [22,23,24,25,26,27,28,29,30,31]. Due to its nature, global learning lacks adaptability when compared to the local learning [32]; therefore, models such as ANFIS are unable to capture the spatial and temporal changes of a dynamic environment except if they go through regular retraining processes. Moreover, models with global learning tend to exhibit a slower training process and higher sensitivity to data noise compared to the models with local learning [33]. Another drawback of the models with global learning (including ANFIS) is their fixed structure as the number of rules is predefined by the user [33]. This will make such models highly subjective to the experience and expertise of the users as the adopted number of rules may not be the best which reflects the complexity of R-R process in the system [34].

To date, several studies have promoted the transitions towards adopting local learning-based models for hydrological applications. For example, Luna et al. [35] proposed a recursive learning algorithm to develop a TSK fuzzy system based on the Expectation Maximization algorithm to forecast monthly stream flow for the Furnas hydroelectric plant in Brazil. The algorithm involves two stages, offline learning during initialization and online adaptation for adapting to new data. The model was compared against ANFIS, constructive fuzzy system model, and periodic autoregressive model. Despite all the models performing similarly, the proposed model was more efficient in terms of speed and structure due to its online adaptation. Hong and White [33] conducted a comparative study between the proposed Dynamic Neuro-Fuzzy Local Modelling System, a typical back-propagation multi-layer perceptron (MLP) and ANFIS. The models were employed to forecast the flow in Waikoropupu Springs in Taka Valley, New Zealand. The proposed model outperformed back-propagation MLP but was comparable against ANFIS; however, the training time required was far shorter than ANFIS. Hong [36] proposed a MLP with an improved sequential extended Kalman filter learning algorithm with updating the noise covariance. The proposed model was used to predict the temperature affected by discharge in the downstream of a power station cooling system in Waikato River, New Zealand. The results of the proposed model were comparable against back-propagation MLP and ANFIS; however, the proposed model performed faster due to the more efficient online learning implementation. Talei et al. [37] conducted a study on real-time flood forecasting using real-time dynamic evolving neural-fuzzy inference system. The model was developed for a Ronne basin sub-catchment in Sweden and was compared against ANFIS. The proposed model performed significantly better than ANFIS since inherits the ability to continuously update the model without retraining; whereas ANFIS needed a periodic retraining to maintain comparable performance. Nguyen et al. [38] conducted a comparative study on water level forecasting at Thakhek station on the Mekong River in China using a Dynamic Evolving Neural Fuzzy Inference System (DENFIS), ANFIS and unified runoff basin simulation (URBS). The study concluded that DENFIS [32] outperformed URBS while showing marginal improvements against ANFIS when applied on a 5-lead-day water level forecasting. However, DENFIS exhibits a lag-time error caused by having inputs of highly correlated lag data, a common issue faced in data driven modelling. More recently, Ashrafi et al. [39] proposed Generic Self-Evolving TSK (GSETSK) model and compared it against DENFIS and HBV models for river flow forecasting with limited data in two catchments located in Sweden and China. Authors concluded that GSETSK can perform comparably against both HBV and DENFIS with the added benefit of not requiring any priori-knowledge for model initialization unlike DENFIS where knowledge of the data domain is necessary for normalization.

The aforementioned studies signify the potential as well as the benefits of adopting models with local learning capability. Local learning allows a model to dynamically update its parameters for each new data tuple, an essential feature for real-time R-R applications with the added benefit of being highly efficient. Thus far, there has been very few studies on the application of NFS models with local learning in R-R modelling and the potential challenges in developing them such as training data sequences. This study aims to investigate the local learning capabilities of DENFIS [32] in both event-based and continuous rainfall-runoff modelling. The objectives of the present study are: (1) evaluating the DENFIS model performance when compared to two types of benchmark models, physically-based models and commonly-used data-driven techniques; (2) to assess the impact of sequential order of training data on the DENFIS model performance. For the first objective, the DENFIS model is applied for event-based rainfall-runoff modelling in an urban tropical catchment (23.22 km²), Sungai Kayu Ara, and rainfall-water level modelling in a semi-urban temperate catchment (272 km²), Dandenong. The results obtained from DENFIS are first compared against the Autoregressive Model with Exogenous Inputs (ARX), which is considered as the data-driven benchmark model. Then, DENFIS results are compared with physically-based benchmark models Hydrologic Engineering Center-Hydrologic Modelling System (HEC–HMS) [40] and Storm Water Management Model (SWMM) for the Sungai Kayu Ara and Dandenong catchments, respectively. It is worth mentioning that this study was originally on Dandenong catchment with SWMM model as the benchmark. However, Sungai Kayu Ara catchment was later added to extend the study in an event-based R-R modelling problem as well. Since a calibrated HEC–HMS model with results was readily available from a previous study on this catchment, the results were adopted for the sake of saving time. Therefore, the two catchments of this study have different benchmark models. However, as these two models are not fundamentally too different, no significant impact is expected on the validity of the comparisons presented in this article. For the second objective, the sequence of the training data was purposely manipulated for both catchments to evaluate the impact of training data sequence on DENFIS model performance.

2. Materials and Methods

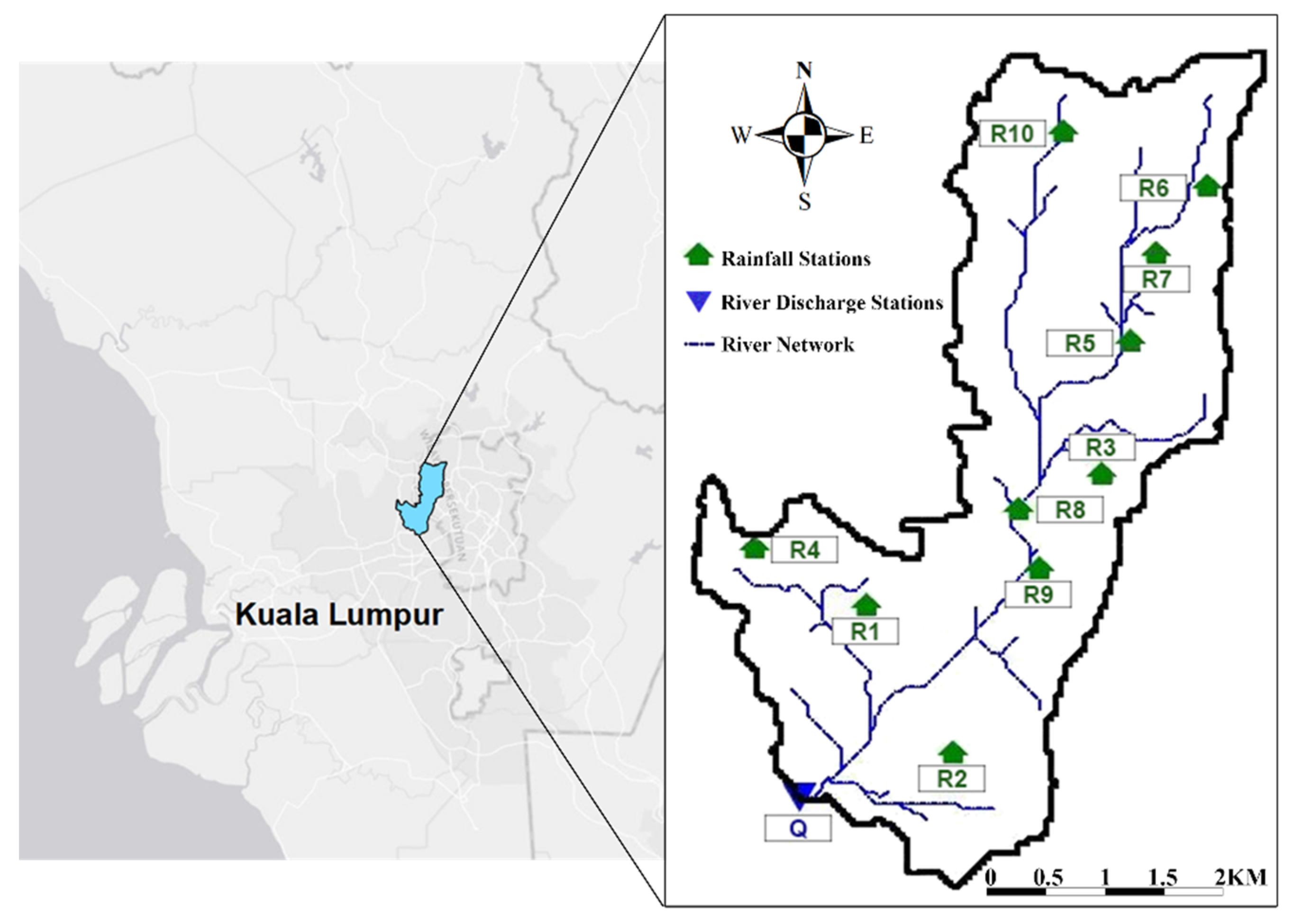
2.1. Study Sites

In this study, two different sites of different climate and degree of urbanization are investigated. The first site is the Sungai Kayu Ara river basin located in Selangor state, Malaysia. Sungai Kayu Ara basin covers an area of 23.22 km² as shown in Figure 1. The main river of this basin originates from the reserved highland area of Penchala and Segambut. Sungai Kayu Ara river basin is considered as tropical catchment, which is subjected to the Northeast Monsoon during December to March and the Southwest Monsoon during June to September [41]. Annual mean rainfall of this catchment is approximately 2000 mm as reported by Desa et al. [42]. The average daily temperature varies in the range of 25 °C to 33 °C while the mean monthly relative humidity falls within 70% to 90% depending upon the location and seasonal effect. The annual average evaporation rate is estimated between 4 to 5 mm/day. It is worth mentioning that the majority area of the catchment is flattened for development. Due to the specific characteristics of tropical rains which are normally short and intense, event-based R-R modelling is applicable for high-resolution data (5, 10, 15, 30, or 60 min R-R time series). Therefore, this catchment was chosen as the representative of an event-based R-R modelling in an urbanized tropical area, where high-resolution data (e.g., 10 min time steps) are required due to the nature of tropical R-R events. Moreover, this catchment has 10 rainfall stations, which makes the selection of inputs and model development quite challenging. The detail of rainfall and flow stations of Sungai Kayu Ara catchment and the period in which the data is considered are provided in Appendix A. In this study, a total of 30 rainfall-runoff events were extracted from 10-min rainfall-runoff time-series between March 1996 and July 2004. The event selection from the continuous time series was carried out by considering three main criteria. Firstly, the selected event must have been recorded in at least 6 rainfall stations (out of 10 rainfall stations). Secondly, the wetting front suction, which is one of the parameters used in the Green and Ampt infiltration method, is influenced by initial moisture content of the soil. Therefore, the inter-arrival time for selected rainfall events was decided to be greater than two days. Finally, to gain the optimum results for direct runoff values, rainfall events equal or greater than 3.0 mm were considered as the effective rainfall in this study.

As for the second study site, continuous daily rainfall and river water level data from the Dandenong catchment was used. As shown in Figure 2, Dandenong catchment is located in the South East of Melbourne, Australia, and covers an area of about 272 km². The primary creek in this catchment is the Dandenong creek which originates from the Dandenong Ranges National Park and discharges into Port Phillip Bay via both Mordialloc Creek and Patterson River. Although farmlands as well as some forest pockets remain in the catchment, approximately 45% of the land has been overcome by urbanization. The data used in this study is the mean daily rainfall and river level readings for the stations Dandenong, Rowville and Heathmont. Eleven years of daily data from January 2005 to December 2015 are available. Rowville and Heathmont are the two upstream stations with Heathmont having the highest elevation. This catchment was chosen as representative of a larger-sized catchment with multiple rainfall stations. Since this catchment is located in Australia, it was supposed that its rainfall regime could be significantly different as compared to the tropical catchment. The detail of rainfall and water level stations of Dandenong catchment and the period in which the data is considered are provided in Appendix A.

For further comparison of rainfall regimes in the two catchments, the average monthly rainfall records of Sungai Kayu Ara (over the period 1996–2004) and Dandenong (over the period 2005–2015) catchments are illustrated in Figure 3. In Sungai Kayu Ara catchment, November and June are the most wet and dry months of the year, respectively. However, in Dandenong catchment, November and December are the wettest months of the year while January and March are the driest.

2.2. Dynamic Evolving Neural-Fuzzy Inference System (DENFIS)

DENFIS is a TSK-type neuro-fuzzy system with local learning capability. The learning mechanism in DENFIS is based on incremental learning which has been implemented using an evolving, online clustering method known as Evolving Clustering Method (ECM). ECM, which is a fast one-pass algorithm, is a distance-based clustering method that can partition the input space through a dynamic estimation of cluster centers using the maximum distance between a point and an available cluster center. ECM is able to control the number of clusters by using a threshold parameter, D_thr, which defines the maximum allowable distance between a new data point and the center of existing clusters. In other words, if the calculated distance for a new data point exceeds this threshold, that point will become a new cluster center. The aforementioned distance in the ECM algorithm follows the typical Euclidean distance between two vectors x and y as it is denoted in Equation (1):

$$\Vert x-y\Vert ={\left(\frac{{\displaystyle \sum _{i=1}^q{\left|x_i-y_i\right|}^2}}{q}\right)}^{1/2}$$

(1)

where $x,y\in R^q$ and q is the number of input data points. Based on this mechanism, by receiving any new data point, either a new cluster may form, or an existing cluster may get updated by revising its center and size. Therefore, the process of updating for a specific cluster only stops when the cluster radius reaches a threshold value of D_thr. The visual demonstration of such a mechanism can be seen in Figure 4 for a 2-D input space.

The ECM algorithm can be summarized by the following steps:

Initialization: By entering the first training tuple, the first cluster $C_1{}^0$ will be created (Figure 4a) while this data point will be its cluster center $C_{C1}{}^0$ and its radius $R_1=0$.

Step 1.

Receiving a new data point x_i, its distance with the centers of all n existing clusters (created previously) need to be calculated using $D_{Cj}=\Vert x_i-C_{Cj}\Vert$ for $j=1,2,\dots ,n$ where j is the cluster index and C_Cj is the center of the jth cluster. If all examples of the data stream have been presented, the algorithm is complete.

Step 2.

The calculated distance D_ij will be compared against all existing cluster radius R_j. If any radius satisfies the condition $D_{ij}<R_j$, then x_i belongs to the closest cluster (denoted as C_m) with the minimum distance of $D_{im}=\Vert x_i-C_{Cm}\Vert =\min (\Vert x_i-C_{Cj}\Vert )$ for $D_{ij}\le R_j\left(j=1,2,\dots ,n\right)$. In this case, the new data point is adopted by an existing rule; therefore, no new cluster is created, and no existing cluster gets updated (the cases of x₄ and x₆ in Figure 4b,c). At this stage, the algorithm returns to Step 1. If D_ij > Rj, the algorithm continues to the next step.

Step 3.

For all n existing cluster centers, the parameter S_ij will be calculated for input data xi and clusters j = 1, 2, …, n, using S_ij = D_ij + R_ij. The cluster that gives the minimum S_ij will be denoted as cluster C_a with center C_Ca and parameter S_ia. Then algorithm goes to the next step.

Step 4.

If S_ia > 2 × D_thr, the input data xi does not belong to any existing clusters and a new cluster needs to be created similar to step 0 (the cases of x₃ and x₈ in Figure 4) and then the algorithm then returns to step 1. Else (i.e., S_ia ≤ 2× D_thr), algorithm goes to the next step.

Step 5.

Since S_ia ≤ 2× D_thr, the cluster C_a needs to be updated by revising the center location and increasing the cluster radius. In this process, the new radius will be set as R_{a (new)} = S_ia/2 while the new center will be located at the point on the line connecting x_i and C_Ca with a distance of R_{a (new)} from point x_i (the cases of x₂, x₅, x₇ and x₉ in Figure 4). The algorithm proceeds to the step 1.

The learning process in DENFIS follows typical TSK-type fuzzy inference system in which the antecedents of fuzzy rules will be defined by fuzzy sets using Gaussian membership functions. DENFIS employs the first-order TSK fuzzy inference system where the rule consequents will be defined by a linear function as given in Equation (2):

$$Y=a_0+a_1{x}_1+a_2{x}_2+ \dots +a_k{x}_k$$

(2)

where Y is the consequent (output); x₁, x₂, …, x_k are the antecedent variables (inputs); and a₀, a₁, a₂, …, a_k are the linear function parameters to be optimized during the learning process through training dataset. Further details on the learning mechanism in DENFIS can be found in Kasabov and Song [32].

DENFIS is selected due to several advantages that it has over conventional NFS models. The most important feature in DENFIS is its online learning that allows incremental learning from the flow of the data. Moreover, the number of nodes and rules in DENFIS are not predefined by the user. This allows the model to be flexible in dealing with different datasets. On the other hand, one major drawback of DENFIS is its progressive rule generation. In such a learning mechanism, no rule will be excluded even if it is outdated. Therefore, for future improvement, perhaps adding a rule pruning mechanism in the learning process could address this issue.

2.3. Benchmark Models

2.3.1. Hydrologic Engineering Center–Hydrologic Modelling System (HEC–HMS)

HEC–HMS [40] is a lumped conceptual model that can estimate the catchment response to a given precipitation by conceptualizing the entire river basin as a system which is interconnected by hydrologic and hydraulic components including river basins, streams, and reservoirs. From computational point of view, HEC–HMS is not a complex model while it is still a flexible tool for being used in a wide range of geographic and environmental conditions. Despite its successful usage in hydrological modelling, HEC–HMS has its own limitations due to its simplified model formulation. HEC–HMS requires pre-processing through HEC-GeoHMS (Geospatial Hydrologic Modelling) which is an extension of ArcGIS, specifically designed to provide surface delineation and geospatial data for HEC–HMS hydrologic modelling. In this study, HEC–HMS is developed for Sungai Kayu Ara catchment. For a better simulation of the watershed response to precipitation, the surface Digital Elevation Model (DEM) of the catchment with 10 m resolution was used to extract the drainage paths and watershed boundaries. The produced values by HEC-GeoHMS are then exported to HEC–HMS for hydrologic modelling.

2.3.2. Storm Water Management Model (SWMM)

SWMM is a dynamic R-R simulation model used in simulating runoff quantity and quality primarily from urban areas. SWMM was developed by the United States Environmental Protection Agency (US EPA) [5]. SWMM conceptualizes physical elements of a watershed system into a standard set of modelling objects. Rain gages and sub-catchments are the principal objects used to model the R-R process. Each sub-catchment area is comprised of a subdivision between impervious and pervious areas to simulate precipitation, evaporation and infiltration losses of each sub-catchment. SWMM uses kinematic wave equations to simulate the runoff based on the physical routing of discharge generated by precipitation through a system of pipes and channels originate from sub-catchments area. Kinematic equations are typically used in R-R modelling in which the model solves the continuity equation along with a simplified form of the momentum equation. This allows variations in spatial and temporal flows within a conduit. In this study, SWMM model is used for rainfall-river stage modelling in Dandenong catchment.

2.3.3. Autoregressive Model with Exogenous Inputs (ARX)

ARX is a linear regression model for input-output mapping where the simulated output Q(t) assumed to be related to the output antecedents Q(t − i) and input antecedents R(t − i) by the following formula:

$$Q\left(t\right)=-{\displaystyle \sum _{i=1}^{n_a}{a}_{i}Q(t-i)}+{\displaystyle \sum _{j=1}^{n_b}{b}_{j}R(t-n_k-j+1)+e(t)}$$

(3)

where n_a and n_b are the number of output and input antecedents, respectively; n_k is the delay associated with each input; e(t) is the true error term; and a_i and b_j are the model parameters to be optimized. This model is one of the most popular benchmarks for evaluating the performance of artificial intelligence (AI) techniques such as ANNs and NFS. Therefore, it is considered as the bottom-line benchmark of this study. In other words, any proposed AI-based data-driven model that cannot supersede ARX, is not worth practicing. This is due to the higher complexity of AI-based techniques compared to ARX.

2.4. Input Data Selection and Model Development

For Sungai Kayu Ara, a total of 30 rainfall-runoff events with 10-min data resolution were extracted from the available rainfall and runoff time series of Sungai Kayu Ara catchment. Talei et al. [27] showed that in event-based R-R modelling with ANFIS, it is not necessary to allocate a large number of events for training the model. It was shown that the model can be efficiently trained by few properly-selected events and reserve more events for the testing stage. In two separate studies it was found that factors such as hydrograph shape [27] and the lag time between rainfall and runoff [43] can be used to select the proper training events. The former, suggests that events with single discharge peaks are better choices for training the model compared to events with multiple peaks; the latter, however, suggests that events with the lag time close to the catchment’s time of concentration are good choices for training the model. Considering these two factors, from the 30 available R-R events, 12 were used as training events while the remaining 18 were reserved for testing. Although selection of R-R events for comprehensive analyses is expected to be in an independent and identically-distributed way [44], care was taken in selecting training and testing events so both datasets contain different range of events. Moreover, initial results also showed that training the model with a lesser number of events will deteriorate the model performance. A statistical analysis is conducted on the data used in Sungai Kayu Ara catchment and is presented in

Table 1. Statistical analysis of the data used for Sungai Kayu Ara and Dandenong catchments.

Sungai Kayu Ara (10-min Interval Data)
	Rainfall (mm)		Discharge (m³/s)
	Training	Testing	Training	Testing
Minimum	0	0	3.20	0.10
Maximum	26.5	48.0	135.00	180.90
Mean	0.7	0.6	17.81	12.33
Standard Deviation	2.2	2.5	21.85	22.15
Skewness	4.8	6.5	2.70	3.90
Dandenong (Daily Data)
	Rainfall (mm)		River Stage (m)
	Training	Testing	Training	Testing
Minimum	0	0	0	0
Maximum	149.0	84.0	6.80	3.00
Mean	2.0	1.9	0.18	0.16
Standard Deviation	6.0	5.1	0.44	0.27
Skewness	8.6	5.6	7.35	4.45

.

As can be seen, the maximum observed rainfall and runoff values in testing dataset are higher than the ones in training dataset. However, the mean and standard deviation values are almost similar. Rainfall antecedents from all 10 rainfall stations and runoff antecedents of the single runoff station in the catchment outlet were considered as the potential inputs during the input selection process. Rainfall antecedents were considered up to 10 lagged time steps as initial results showed that lags beyond this lag are not contributing much in R-R process. On the other hand, Dandenong catchment consists of 11 years of continuous rainfall and runoff time series. The first 8 years of the data was selected as training data while the remaining 3 years was kept for testing. Care was taken to have wide range of river stage values in both training and testing datasets. A statistical analysis on the data used in Dandenong catchment is conducted and the results are presented in Table 1. As can be seen, the maximum observed rainfall and water level values in training dataset are higher than the ones in testing dataset. However, the mean and standard deviation of both training and testing datasets are quite similar.

Choice of input remains as one of the main difficulties in the application of data-driven models [45]. It becomes very challenging when the high number of potential inputs increases the number of potential input combinations. In R-R modelling by data-driven models, for example, input selection will be focused on identifying the proper number of rainfall and/or runoff antecedents by which the model can be well-trained. To date, several input selection techniques are suggested for R-R data-driven models. Correlation analysis is perhaps one of the most commonly-used methods to identify proper inputs in hydrological data-driven models including NFS models [23,46,47,48]. On the other hand, mutual information analysis has been also used for inputs selection in several similar studies and is found to be a good choice in identifying appropriate inputs [49,50]. Talei and Chua [43] combined Correlation Coefficient (CC) and Mutual Information (MI) analyses to make an input selection technique for R-R modelling with ANFIS. The study showed that appropriate inputs should possess low mutual information while maintaining high correlations with the output. By definition, the correlation coefficient is expressed by:

$$CC\left(x,y\right)=\frac{{\displaystyle \sum _{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}}{\sqrt{{\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}}\times \sqrt{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}}$$

(4)

where CC(x,y) is correlation coefficient between variables x and y; $\overline{x}$ and $\overline{y}$ are average values of x and y variables, respectively; and n is the number of data points. In addition, mutual information is expressed by da Costa Couto [51]:

$$MI\left(x,y\right)=\frac{1}{2}\log \left(\frac{{\sigma }_x^2{\sigma }_y^2}{\left|{\sigma }_{xy}\right|}\right)$$

(5)

where MI(x,y) is the mutual information between variables x and y; σ_xy is the covariance between variables x and y; and ${\sigma }_x{}^2$ and ${\sigma }_y{}^2$ are the variance of variables x and y, respectively. To select the optimal combination between MI and CC, [43] proposed a ranking coefficient as:

$$R_k={\displaystyle \sum _{i=1}^n}{\widehat{C}}_i+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n}}{\widehat{I}}_{ij}$$

(6)

where ${\widehat{C}}_i$ is the normalized correlation coefficient between output (in this study discharge at present time Q(t)) and an input (e.g., rainfall) lead time in kth input combination; n is the number of inputs in a given input combination; and ${\widehat{I}}_{ij}$ is the normalized value for 1 − MI calculated for the ith and jth input lead times in the kth input combination. It is worth mentioning that MI is mutual information; hence, the 1 − MI represents the level of independency of two inputs. For an input combination with n inputs the second term of Equation (6) includes N number of mutual information terms where N can be obtained by Equation (7):

$$N=\frac{n!}{2!(n-2)!}$$

(7)

To better understand the procedure, a numerical example can be used as below:

If in an R-R modelling problem 4 inputs are involved, then 6 terms of mutual information are expected. Similarly for 5 inputs, 10 terms of mutual information are expected. Since the ideal normalized value of ${\widehat{C}}_i$ (for the maximum correlation) and 1 − MI (for the lowest mutual information) would be 1, the maximum value of R could be 3, 6, 10, … for input combinations with 2, 3, 4, … rainfall inputs, respectively. This method has been used successfully for input selection process in both continuous and event-based R-R modelling with NFS models in different catchment sizes [30,34,37]. Therefore, this method is also adopted for selecting the inputs in both catchments of the present study. In this study, the top five input combinations with 2, 3, 4, … inputs are used to develop the desired models. Preliminary results showed that the model performance does not improve or even may deteriorate where more than 4 inputs are involved. This is consistent with the findings by Talei and Chua [43] and Nayak et al. [22].

2.5. Performance Criteria

In order to evaluate the performance of R-R models, the observed and simulated discharge by R-R models are compared using several performance criteria including the Nash–Sutcliffe Coefficient of Efficiency (CE), Coefficient of Determination (R²), Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Relative Peak Error (RPE). The detailed formulation of these performance criteria is provided in

Table 2. Summary of performance criteria used to evaluate model performances.

Performance Criteria	Formula	Unit	Range
Nash-Sutcliffe Coefficient of Efficiency	$CE=1-\frac{{\displaystyle \sum _{i=1}^n{\left(Q_{Obs,i}-Q_{Sim,i}\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(Q_{Obs,i}-{\overline{Q}}_{Obs}\right)}^2}}$	Dimensionless	(−∞, 1]
Coefficient of Determination	$R^2={\left[\frac{{\displaystyle \sum _{i=1}^n\left(Q_{Obs,i}-{\overline{Q}}_{Obs}\right)\left(Q_{Sim,i}-{\overline{Q}}_{Sim}\right)}}{\sqrt{{\displaystyle \sum _{i=1}^n{\left(Q_{Obs,i}-{\overline{Q}}_{Obs}\right)}^2}}\times \sqrt{{\displaystyle \sum _{i=1}^n{\left(Q_{Sim,i}-{\overline{Q}}_{Sim}\right)}^2}}}\right]}^2$	Dimensionless	[0, 1]
Root Mean Square Error	$\mathrm{RMSE}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{\left(Q_{Sim,i}-Q_{Obs,i}\right)}^2}}{n}}$	m3s−1	[0, +∞)
Mean Absolute Error	$\mathrm{MAE}=\frac{{\displaystyle \sum _{i=1}^n\left|Q_{Sim,i}-Q_{Obs,i}\right|}}{n}$	m3s−1	[0, +∞)
Relative Peak Error	$\mathrm{RPE}=\frac{\left|\left(Q_{p,Obs}\right)-\left(Q_{p,Sim}\right)\right|}{Q_{p,Obs}}$	Dimensionless	[0, +∞)

Note: $Q_{Obs,i}$ = The ith observed discharge, ${\overline{Q}}_{Obs}$ = The average observed discharge, $Q_{p,Obs}$ = The observed peak discharge, n = total number of data points, $Q_{Sim,i}$ = The ith simulated discharge, ${\overline{Q}}_{Sim}$ = The average simulated discharge, $Q_{p,Sim}$ = The simulated peak discharge.

.

CE and R² are known as appropriate measures to assess the goodness-of-fitness between observed and simulated values [52] and have been successfully used in several similar studies [53,54,55,56]. The CE = 1 and R² = 1 indicate a perfect match between observed and simulated values. Although both CE and R² seem to have similar functionality, CE has been found a more sensitive measure in extreme values as it penalizes the errors in extreme values more than R² [57]. On the other hand, RMSE is also a useful measure that accords extra importance on the outliers in the data set; therefore, it is more biased towards the errors in simulating high values [52,58,59]. MAE computes all deviations between observed and simulated values regardless of the data point value. In other words, MAE is not giving any weight to errors on high or low values [57,60]. In addition to the overall goodness-of-fit, accurate prediction of peak flow is also important. Thus, RPE has been included in this study to evaluate the ability of the proposed models to accurately predict peak flows.

3. Result and Discussions

3.1. Input Selection Results

Applying the method discussed in Section 2.4, the best-performing inputs for both catchments were identified and are presented in

Table 3. Selected inputs for Sungai Kayu Ara and Dandenong catchments.

Catchment	Selected Inputs
Sungai Kayu Ara	R2(t − 2), R7(t − 1), R9(t − 8), Q(t − 1)
Dandenong	RD(t − 1), RSR(t − 1), RSH(t − 1)

. It is worth mentioning that for Catchment 1, R2, R7, and R9 refer to 2nd, 7th, and 9th rainfall stations, respectively. On the other hand, for Catchment 2, R_D, RS_R, and RS_H refer to the Dandenong rainfall station, upstream Rowville river stage station and upstream Heathmont river stage station, respectively. Moreover, t is considered as the present time; therefore, t − t₀ denotes t₀ time steps before the present time. For example, R(t − 1) in a daily dataset represents the rainfall data for 1-day before the present day.

3.2. DENFIS Performance on Event-Based R-R Modelling in Sungai Kayu Ara Catchment

As mentioned earlier in Section 2.4, from the 30 available R-R events in Sungai Kayu Ara catchment, 12 events were used for training the DENFIS model while the remaining 18 events were used for testing (validation) purposes. The desired output for Sungai Kayu Ara catchment was discharge at present time, Q(t). In calibrating DENFIS, the model parameter D_thr was considered 0.1 as recommended by [30]. A sensitivity analysis was conducted to explore whether increasing or decreasing the D_thr may improve model performance. As no significant improvement was observed, D_thr = 0.1 was fixed for Sungai Kayu Ara catchment. For comparison purposes, DENFIS was compared against two benchmark models: (1) a regression-based model, ARX, and (2) a HEC–HMS model. The ARX model was developed by using the same training events while the number of inputs was found based on trial and error to reach the best testing performance. In Sungai Kayu Ara catchment, the best performing ARX model was achieved by using 18 rainfall and 1 discharge antecedents. For HEC–HMS, however, the results are adopted from a previous study conducted by Alaghmand et al. [61,62]. In the aforementioned studies, HEC–HMS is calibrated with the same training events while all 10 rainfall stations are used as model inputs. Other parameters of the model such as catchment area, imperviousness, roughness, etc. were also set based on the available data from the catchment.

The average performance of DENFIS model across the 18 testing events was compared with those obtained by ARX and HEC–HMS modes as presented in

Table 4. Average CE, R², RMSE, MAE, and RPE values over the 18 testing events resulted by Dynamic Evolving Neural Fuzzy Inference System (DENFIS), Hydrologic Engineering Center-Hydrologic Modelling System (HEC–HMS), and Autoregressive Model with Exogenous Inputs (ARX) models for Sungai Kayu Ara catchment.

Model	CE (-)	R2 (-)	RMSE (m3/s)	MAE (m3/s)	RPE (-)
DENFIS	0.876	0.899	5.056	2.100	0.113
HEC–HMS	0.595	0.876	7.218	4.261	0.179
ARX	0.175	0.545	10.032	7.401	0.451

. DENFIS was able to significantly outperform ARX model in terms of all measures. Moreover, DENFIS significantly outperformed HEC–HMS in terms of all measures except for CE where the improvement was marginal. This could be due to the fact that CE penalty for errors in high flows is more significant. To investigate this hypothesis, the boxplots for RPE values across the 18 testing events simulated by DENFIS, HEC–HMS and ARX models are presented in Figure 5. As can be seen, despite the fact that the median RPE value for HEC–HMS model is smaller, the boxplot is more stretched compared to the DENFIS model. Moreover, there is an outlier in HEC–HMS boxplot while DENFIS has no outlier RPE value. This shows that DENFIS has been able to have a more consistent performance in peak estimation when compared to HEC–HMS. This is consistent with higher CE value for DENFIS compared to HEC–HMS. On the other hand, ARX was the worst model in peak estimation as it can be seen in Figure 5.

For further comparison, the observed versus simulated discharge values by DENFIS and HEC–HMS models for the testing dataset (all 18 events together) are presented by scatterplots as shown in Figure 6. As can be seen, DENFIS has managed to simulate both high and low flows (see Figure 6a) while HEC–HMS has several under/over estimations in simulating medium and high flow values (see Figure 6b). It is worth mentioning that DENFIS was able to produce comparable results against HEC–HMS by using 3 rainfall stations (see Table 3) while HEC–HMS is calibrated by using all 10 rainfall stations of the catchment; however, DENFIS was benefited by using runoff antecedent as input unlike HEC–HMS which only uses rainfall data and other catchment properties. In general, DENFIS also showed overestimation for some data points. Perhaps this could be attributed to the fact that in event-based R-R modelling the antecedent dry period is not directly considered in modelling. Therefore, the calibrated model may overestimate or underestimate the events due to the potential differences between the actual initial soil moisture conditions. Overall, DENFIS was found to be a reliable alternative model for event-based R-R modelling in Sungai Kayu Ara catchment. This was evident as DENFIS outperforms both HEC–HMS and ARX models in terms of all statistics.

3.3. DENFIS Performance on Continuous R-R Data Modelling in Dandenong Catchment

For Dandenong, 11 years of rainfall—river stage (water level) continuous time series was used from which the first 8 years were used to train the model and the remaining 3 years were left for testing (validation) the model. As presented in Table 3, rainfall at outlet station and river stage at upstream stations were used as inputs while the river stage in the outlet at present time RS(t) was the desired output. Similar to Sungai Kayu Ara catchment, the D_thr = 0.1 was adopted to develop DENFIS mode in the Dandenong catchment. In this case also, sensitivity analysis confirmed that the adopted value is efficient and can be fixed for this study. After calibrating (training) the DENFIS model, it was validated by testing dataset. For comparison purposes, two benchmark models ARX and SWMM were calibrated for the Dandenong catchment. The ARX model was calibrated for the same training dataset while the best performing combination was achieved by using 10 rainfall and 3 water level antecedents. The SWMM model was calibrated using 1 arc-second resolution DEM data alongside the data obtained from 9 rainfall stations distributed across the catchment. It is worth mentioning that, the extra 6 rainfall stations were not used in developing DENFIS and ARX models due to the discontinuity in their timeseries compared to the main 3 rainfall stations. Several parameters such as total area, slope inclination and pervious/impervious areas were loaded into the SWMM model. Moreover, other model parameters such as catchment width, infiltration rate, and Manning’s coefficients, were further adjusted using the Sensitivity-based Radio Tuning Calibration Tool (SRTC) [63], which allows parameter fine-tuning to improve the model performance. SRTC minimizes the uncertainty of the inferred model parameters [64]. In this approach, for each parameter an uncertainty value is assigned based the parameter type. The uncertainty values help to define the lower and upper limits of each parameter.

DENFIS results in simulating RS(t) for the testing dataset are compared with the ones obtained by SWMM and ARX models in

Table 5. CE, R², RMSE, and MAE values for testing river stage time series simulated by DENFIS, SWMM, and ARX models in Dandenong catchment.

Model	CE (-)	R2 (-)	RMSE (m)	MAE (m)	RPE (-)
DENFIS	0.803	0.808	0.121	0.056	0.159
SWMM	0.686	0.696	0.153	0.067	0.363
ARX	0.689	0.797	0.150	0.062	0.320

. As it can be seen, DENFIS significantly outperforms both ARX and SWMM models in terms of all performance indices. For example, the CE value obtained from DENFIS model is approximately 17% better than the one resulted by SWMM. However, it is worth mentioning that both DENFIS and ARX models are benefitting from water level antecedents, which contribute to their performances.

To assess the model performance in peak estimation, the top 10% percentile river stage values in the testing dataset (which selects 27 peaks) were used for RPE calculation based on the simulated river stage values by DENFIS, SWMM, and ARX models. This comparison is illustrated in terms of boxplots in Figure 7. As can be seen, the DENFIS model significantly outperforms both the SWMM and ARX models in peak estimation as DENFIS median RPE value of 0.159 is much lower than 0.363 and 0.320 resulted by SWMM and ARX models, respectively. Moreover, DENFIS was more consistent in simulating peak river stage values compared to SWMM and ARX models as DENFIS boxplot is less stretched compared to the ones obtained by SWMM and ARX. Overall, DENFIS managed to outperform the two benchmarks SWMM and ARX, in the Dandenong catchment, in terms of all performance indices.

Figure 8a,b show the scatterplots of observed and simulated river stage values by DENFIS and SWMM models, respectively. As can be seen in Figure 8a, DENFIS performs quite well in simulating the low water level values; however, few medium to high river stage values are underestimated. For SWMM, however, the model had several underestimations as well as overestimation for medium to high water level values (see Figure 8b). This perhaps matches with the RPE results in Figure 8 where the inaccuracy in peak estimation was greater in SWMM model compared to DENFIS. The poorer performance of SWMM can be attributed to the fact that, unlike DENFIS, SWMM does not use water level antecedents as input. Overall, DENFIS was found to be a competent model in simulating water level in the Dandenong catchment, since its performance in terms of all statistics was superior to those obtained by the SWMM and ARX models.

3.4. Impact of Training Data Sequence on DENFIS Performance

With the adoption of local learning in DENFIS, the sequence of data presented during model training would have some impact on the model learning process. Unlike batch learning models where model parameters are computed based on the training dataset as a whole, the change in training data sequence would affect the initialization and updating of the cluster parameters. Different training sequences would always result in some changes in model parameters. To investigate the impact of training data sequence on model performance, a systematic approach was formulated in which the training dataset for both catchments of this study were segmented into 3 categories of low (L), medium (M), and high (H) based on their peak values (i.e., peak discharge for Sungai Kayu Ara catchment and peak river stage for Dandenong catchment). For Sungai Kayu Ara catchment, events with peak value <40 m³/s were considered as L, between 40 to 70 m³/s were considered as M, larger than 70 m³/s were considered as H. DENFIS was then trained with various combinations of these 3 data categories (i.e., low, medium, high) and validated by the testing dataset used in Section 3.2 and Section 3.3 to evaluate the model performances for each combination. For Sungai Kayu Ara catchment, the 12 training events were distributed between the three categories of low, medium, and high based on their peak discharges while the testing events remained the same (i.e., 18 testing events). Whereas for Dandenong catchment, due to the uneven distribution of training data in the low, medium, and high categories, it was decided to choose a 1-year long representative dataset for each data category (i.e., low, medium, high) to avoid any potential impact of data length on this sensitivity analysis. In this way, only 3 out of 8 years of training dataset is used for this sensitivity analysis while the same testing dataset (last 3 years of the time series) is kept for validation. For selection of the three aforementioned years, peak values of 2 m and 2.9 m were considered as the thresholds to segregate L from M and M from H, respectively. A summary of the low, moderate, and high data categories for both catchments of this study is provided in

Table 6. Training data categories of low, moderate, and high for the Sungai Kayu Ara and Dandenong catchments.

Catchment	Data Category
	Low	Moderate	High
Sungai Kayu Ara (Events)	1, 3, 4, 8, 9	2, 5, 7, 10	6, 11, 12
Dandenong (Year)	2007	2012	2011

.

Table 7. Rules count and average DENFIS performance in simulating the 18 testing events of Sungai Kayu Ara catchment trained with Low (L), Medium (M), and High (H) datasets.

Parameters	Training Data Sequence
	LMH	LHM	MLH	MHL	HLM	HML
Rules Count	18	18	18	18	20	20
Rules Distribution	5, 3, 10	5, 10, 3	7, 4, 7	7, 11, 0	14, 0, 6	14, 6, 0
CE	0.805	0.779	0.810	0.781	0.845	0.819
R2	0.842	0.817	0.839	0.833	0.868	0.857
RMSE (m3/s)	5.635	5.860	5.557	5.835	5.248	5.319
MAE (m3/s)	2.462	2.711	2.400	2.697	2.335	2.434

shows the DENFIS performance in simulating testing dataset after being trained with different sequences of training data in Sungai Kayu Ara catchment. Moreover, the total number of generated rules and their distribution on training data is also provided. As can be seen, the maximum number of rules is generated by category H disregarding its location in training dataset followed by M and L. This means, data sets with higher peak values make a greater contribution to rule generation due to their new information in terms of extreme values. In Sungai Kayu Ara catchment, the top two performances were resulted for the cases that training started with H dataset (see HLM and HML performance in Table 7). The hydrograph for the best performing combination of the training dataset, HLM, is shown in Figure 9 for further visualization of the discussion. As can be seen, the hydrograph is plotted alongside the number of rules generated within the model as time progresses (see the grey shaded area in Figure 9). It can be observed that the model generated 14 rules upon training with the high peak flow data, while the remaining 6 rules were formed during training with moderate peak flow data. Moreover, no new rules were formed during training with low peak flow data which suggests that no novel information was learnt as sufficient information was captured beforehand. In general, Figure 9 shows the important role and crucial contribution of peaks in generating new rules in learning process. Over all, despite the fact that there were some differences in DENFIS performance for different combination in training dataset (example: approximately 8% difference between the worst and the best CE values), DENFIS was concluded to not be much sensitive to the sequence of training dataset in Sungai Kayu Ara catchment as the impact of this factor was insignificant. However, it is recommended to start the training process with the H dataset as it can initialize reasonable number of informative rules in the rule-base and enhance the general model performance in testing stage.

Following the same methodology, the impact of data sequence on DENFIS performance was assessed in Dandenong catchment and the results are tabulated in

Table 8. Rules count and overall DENFIS performance in simulating 3 years of testing dataset in Dandenong catchment trained with Low (L), Medium (M), and High (H) datasets.

Parameters	Training Data Sequence
	LMH	LHM	MLH	MHL	HLM	HML
Rule Count	15	15	14	13	15	14
Rules Distribution	5, 8, 2	5, 8, 2	8, 4, 2	8, 2, 3	9, 4, 2	9, 2, 3
CE	0.408	0.771	0.442	0.712	0.758	0.713
R2	0.524	0.784	0.527	0.714	0.778	0.750
RMSE (m)	0.276	0.172	0.268	0.193	0.177	0.192
MAE (m)	0.199	0.088	0.185	0.117	0.093	0.143

. Unlike the Sungai Kayu Ara catchment, the impact of data sequence on DENFIS performance in Dandenong catchment was substantial. For example, the best performing combination in terms of CE was LHM with an index of 0.771, whereas the worst performing data sequence was LMH with a CE = 0.408 which shows 89% improvement in model performance between these two cases. One of the major observations in Dandenong catchment was the contribution of each data category in rule generation. Unlike the Sungai Kayu Ara catchment, datasets H and M had competing roles in rule generation while they had almost similar knowledge for the system. It is evident as the one which comes earlier contributes the highest number of rules and limits the rule generation for the other one (the later one contributes maximum 2–3 rules only). Moreover, it can be observed that model performance was worst for the cases where the model was first trained with combinations LM and ML followed by H; whereas the model performs best in the cases when initially trained with combinations HL and LH followed by M. Therefore, it was concluded that the combinations with highly contrasting data of low and high peaks can provide the most informative knowledge for the system in Dandenong catchment.

For further visualization, Figure 10 shows the training river stage time series and rule number progression for the best performing training data combination of LHM in the Dandenong catchment. As it can be seen, at the end of the training process with low peak flow data, only 5 rules were generated in DENFIS while after training continues with high peak flow data, 8 new rules were created in DENFIS. Training the model for the last piece of training dataset, M, was able to add only 2 more rules to the system indicating that the majority of the useful knowledge is already provided by L and H data. Although the model was first trained with the low peak flow data, most of the information incorporated into the model was during training with high peak flow data. This is consistent with the finding in the Sungai Kayu Ara catchment, where the portion H of the training data provided the majority number of rules for the model.

Overall, this limited experiment on two catchments supports the idea that the sequence of data in the training process can have an impact on model performance. In general, it is recommended to starts the training with a diverse dataset in which high peaks are included. This will establish the rule-base with informative and inclusive rules which can potentially perform better in validation stage. It is also suggested to run sensitivity analysis whenever developing an online NFS model in a catchment, as the data characteristics could be different from one catchment to the other one. This study could be helpful for users who want to select the training dataset and calibrate an online data-driven R-R models which learn through the flow of data.

3.5. Study Limitations and Future Research Direction

This study evaluated the performance of DENFIS in simulating runoff and water level in the Sungai Kayu Ara and Dandenong catchments, respectively. Then the possibility of enhancing model performance through training data sequence was studied for both catchments. Although the two selected catchments are quite different, it is necessary to evaluate the effect of training data sequence on model performance in more catchment sizes and types. This will allow the users to draw a more generalized conclusion on such impact. Moreover, the comparative study between DENFIS and benchmark models was limited to HEC–HMS, SWMM, and ARX. As recently remarked by Onyutha [65], the type of the hydrological model chosen in a study could have an influence on simulating peak flow in that site. Therefore, further study on DENFIS is needed through comparative assessments with a different range of models, in order to better understand its capabilities in hydrological modelling. Moreover, the learning mechanism in DENFIS is incremental. In other words, its rule-base can gradually grow without any limitation. Considering the fact that some rules may become obsolete in time due to the potential temporal and spatial changes of the catchment, the lack of a rule pruning mechanism in its learning algorithm is evident. Further study is needed to enhance its algorithm toward such adaptability. One common criticism about AI-based models such as NFS is the point that they are not providing any equation that shows the relationship between inputs and outputs. However, it is important to acknowledge that these models are not meant to be a replacement for physical models. In physical models, many parameters are generally needed for calibrating the model; something that may not be available everywhere. In such cases, AI-based data-driven techniques (e.g., DENFIS) can be a very good complement as they can give reliable estimation of runoff by using rainfall as the only hydrological input. Therefore, despite the aforementioned limitations, the usage of AI-based hydrological models (e.g., DENFIS) could have a strong appeal, where there is a need.

4. Conclusions

The following can be concluded from this study:

• DENFIS performed well in both event-based rainfall-runoff modelling (Sungai Kayu Ara catchment) and continuous rainfall-river stage simulation (Dandenong catchment) in terms of several goodness-of-fit criteria including CE, R², RMSE, and MAE. Its results were significantly superior to those obtained from the benchmark model ARX (e.g., in Sungai Kayu Ara catchment, DENFIS result of CE = 0.876 was significantly higher than CE = 0.175 obtained by ARX) and were moderately better than the ones obtained by physically-based benchmark models HEC–HMS and SWMM in Sungai Kayu Ara and Dandenong catchments, respectively.
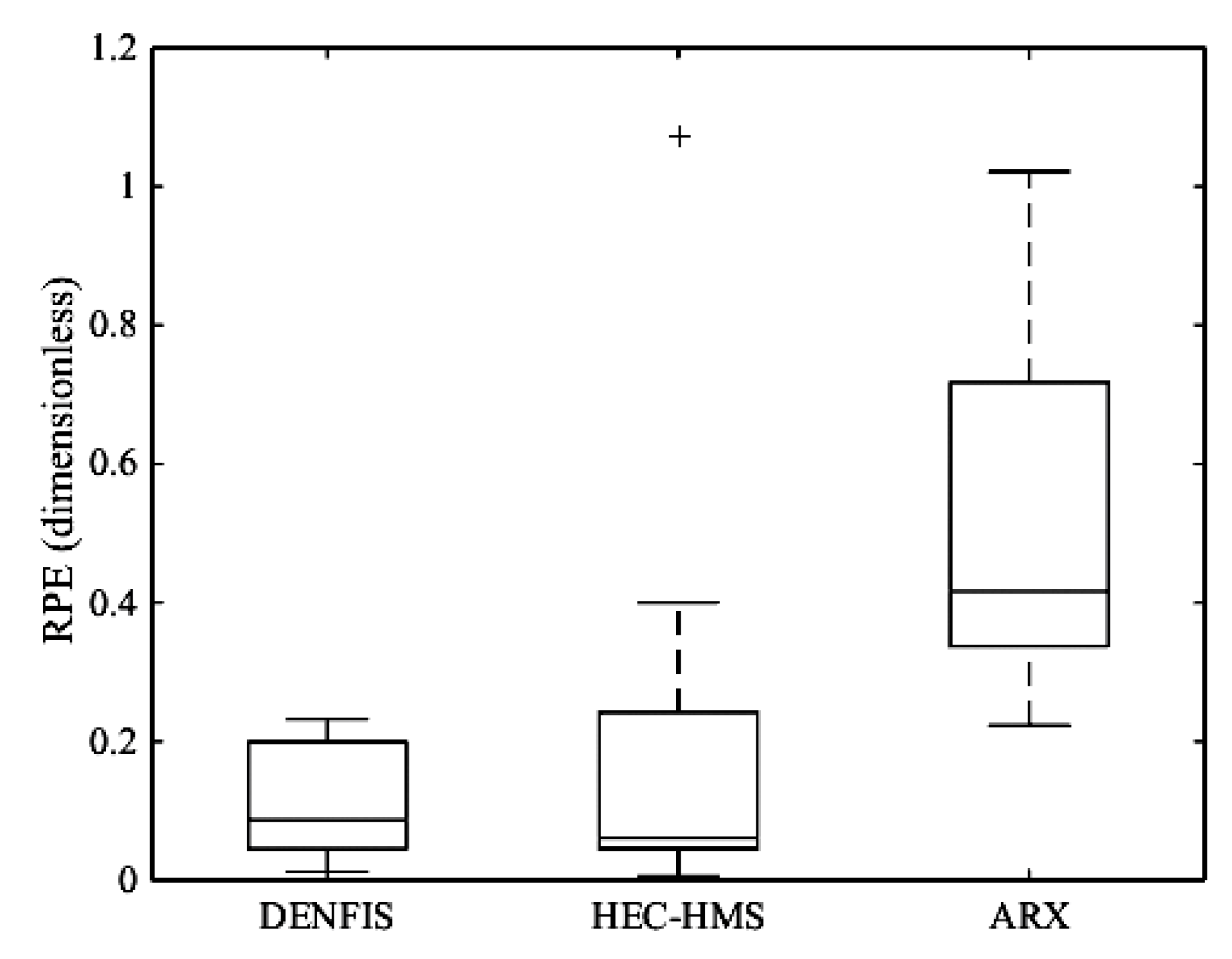
• In peak estimation in the Sungai Kayu Ara catchment, DENFIS produced comparable results in terms of RPE against HEC–HMS model (RPE = 0.113 for DENFIS against RPE = 0.179 for HEC–HMS); however, HEC–HMS had more scattered RPE values with few outliers. In Dandenong catchment, DENFIS (RPE = 0.159) significantly outperformed SWMM (RPE = 0.363) in peak estimation.
• The systematic investigation on the impact of data sequence with low (L), medium (M), and high (H) categories of output data showed that data category of high values, H, contributes to generation of more number of rules in both catchments. Moreover, in the Dandenong catchment, the combinations starting with contrasting categories (i.e., LH or HL) found to be successful in improving the model performance. This was attributed to the fact that the available contrasting data in early stage of training can result in an appropriate initialization of the model parameters. Moreover, this can contribute to generating more diverse rules in the rule-base which can eventually improve the model performance. This finding can be very useful when users choose the training data set.
• The findings of this study suggest the need for running sensitivity analysis on the training dataset during the development of NFS models with local learning. Moreover, the promising results of the proposed AI-based data-driven model, DENFIS, shows the potential advantages of this model in catchments with limited hydrological data.