Investigation on the Effect of Structural Parameters on Cavitation Characteristics for the Venturi Tube Using the CFD Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Physical Model
2.2. Mesh Generation
2.3. Numerical Approach
2.4. Testing System
3. Results and Discussion
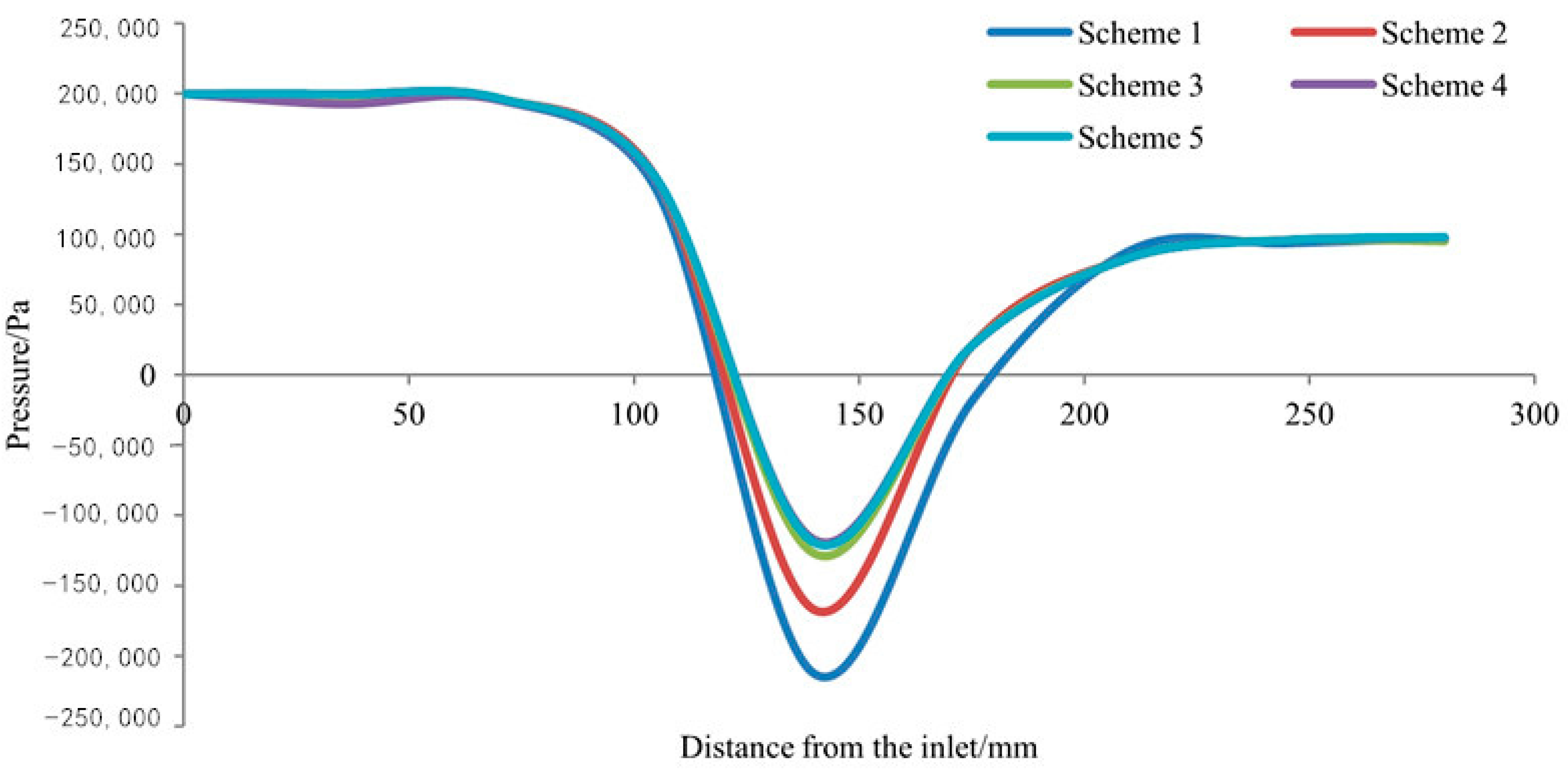
3.1. Verification of the Simulation Method
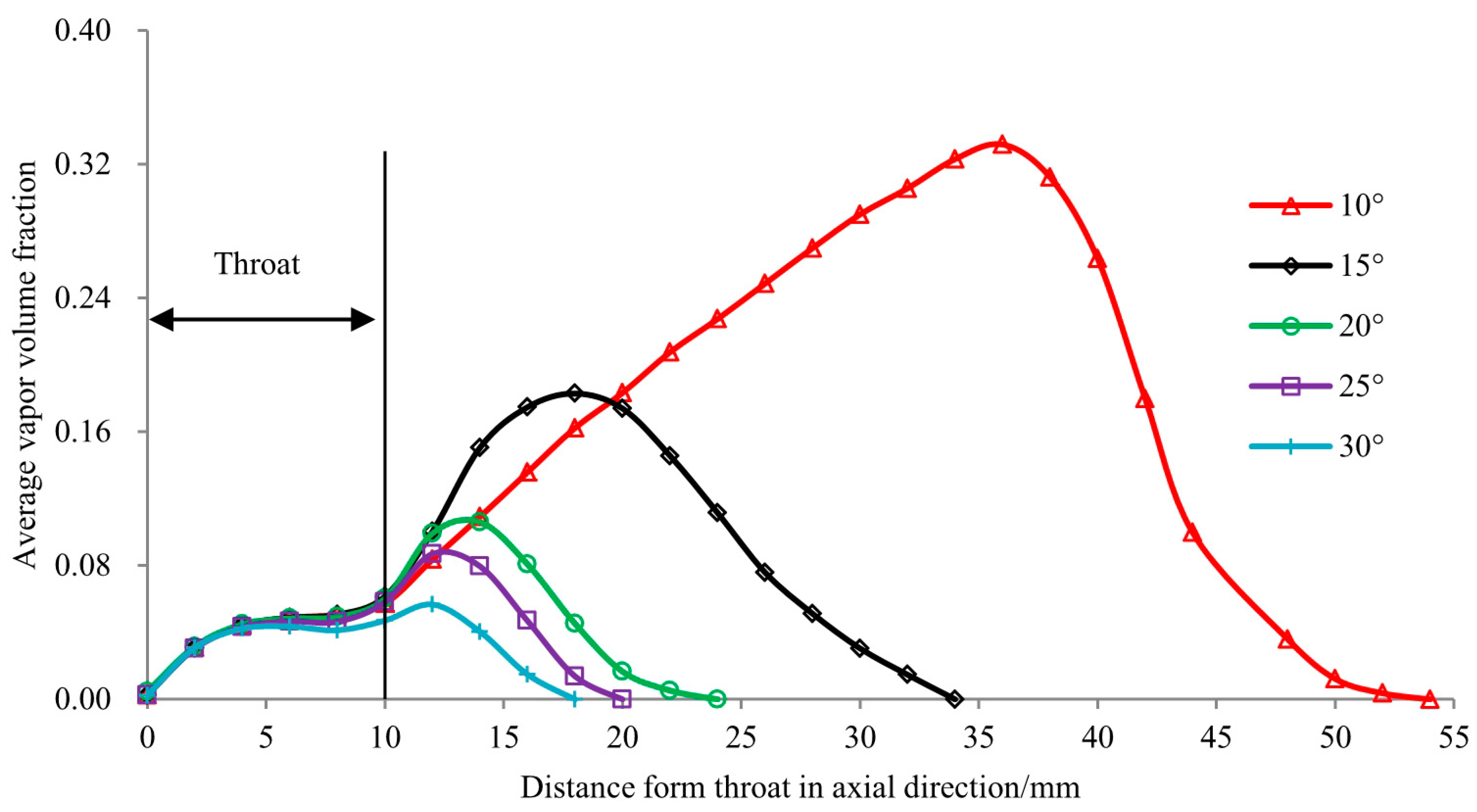
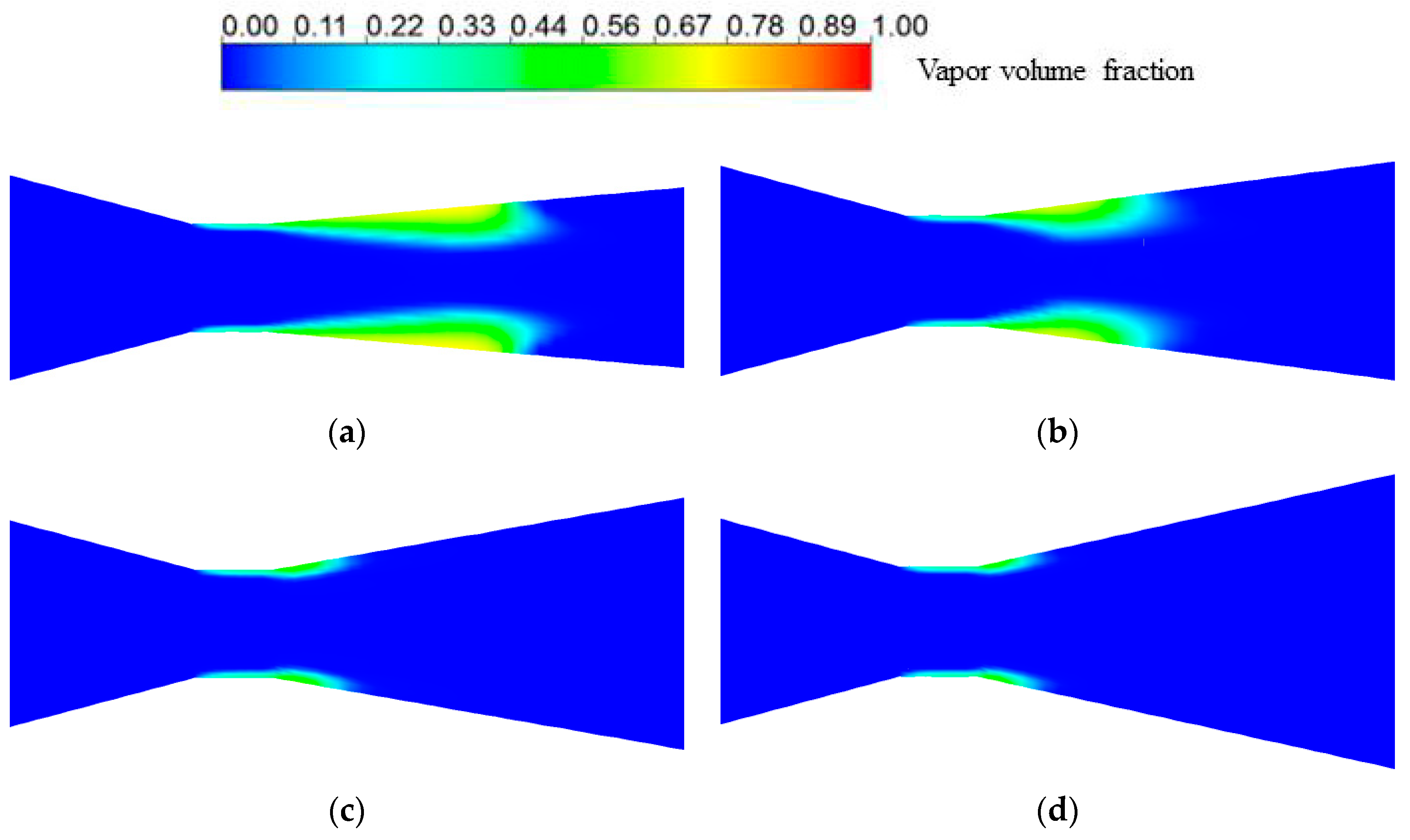
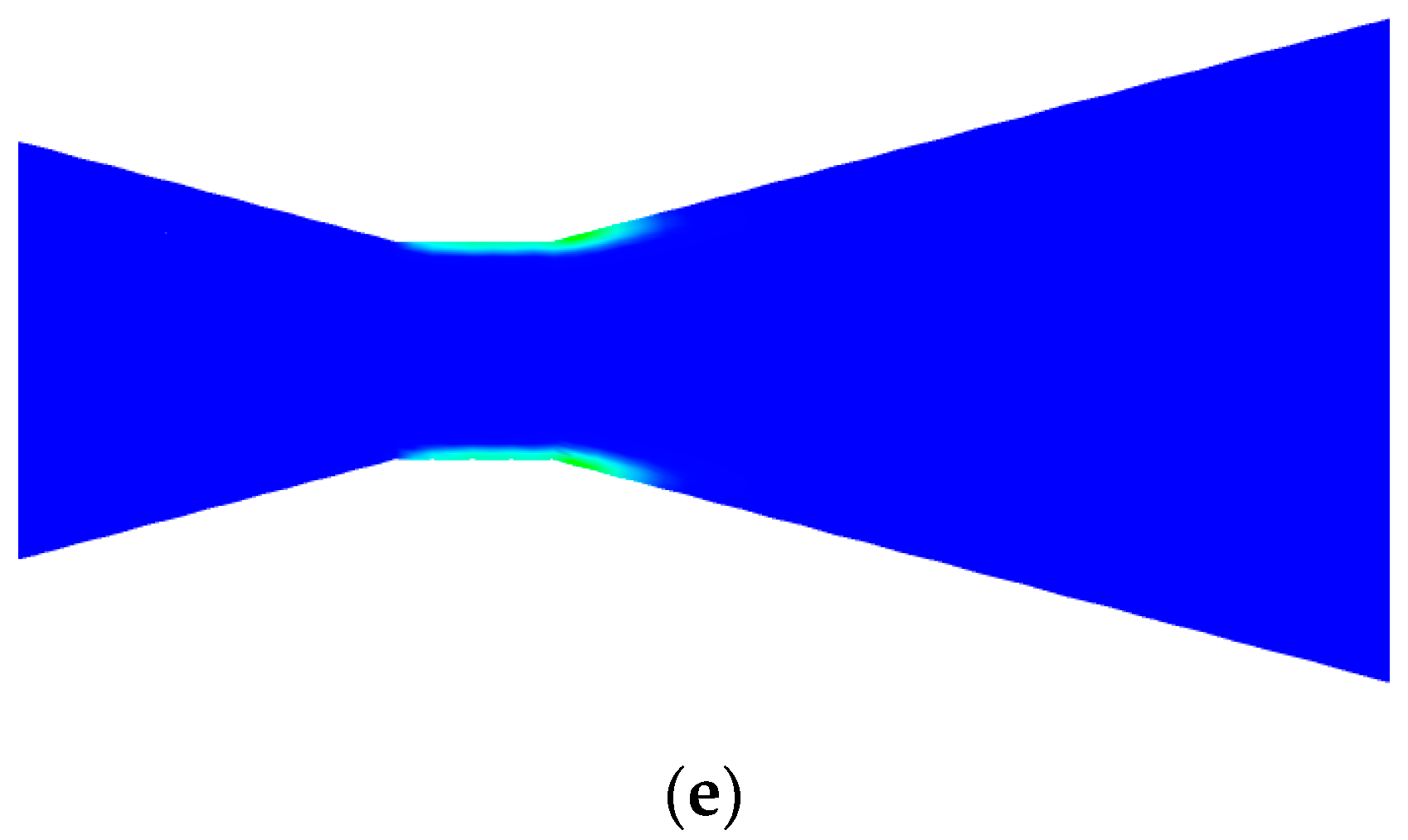
3.2. Effects of Contraction Angle on Cavitation Characteristics
3.3. Effects of Diffusion Angle on Cavitation Characteristics
3.4. Effects of Contraction Ratio on Cavitation Characteristics
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, J.X. Analysis on the effect of venturi tube structural parameters on fluid flow. AIP Adv. 2017, 7, 065315. [Google Scholar] [CrossRef] [Green Version]
- Simpson, A.; Ranade, V.V. Modeling hydrodynamic cavitation in venturi: Influence of venturi configuration on inception and extent of cavitation. AIChE J. 2019, 65, 421–433. [Google Scholar] [CrossRef]
- Pak, S.; Chang, K. Performance estimation of a Venturi scrubber using a computational model for capturing dust particles with liquid spray. J. Hazard. Mater. 2006, 138, 560–573. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zhu, Y.; Li, Y.; Liu, G.; Shang, T.; Zhu, J.A.; Jiao, T. Design and experimental of venturi in EGR system of turbocharged intercooled diesel engine. Trans. Chin. Soc. Agric. Eng. 2013, 29, 49–56. [Google Scholar]
- Wang, X.J.; Tang, L.; Jiang, Z. Numerical simulation of Venturi ejector reactor in yellow phosphorus purification system. Nucl. Eng. Des. 2014, 268, 18–23. [Google Scholar] [CrossRef]
- Quiroz-Pérez, E.; Vázquez-Román, R.; Lesso-Arroyo, R.; Barragán-Hernández, V.M. An approach to evaluate Venturi-device effects on gas wells production. J. Pet. Sci. Eng. 2014, 116, 8–18. [Google Scholar] [CrossRef]
- Ghassemi, H.; Fasih, H.F. Application of small size cavitating venturi as flow controller and flow meter. Flow Meas. Instrum. 2011, 22, 406–412. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Niu, W.Q. Simulating the effects of structural parameters on the hydraulic performances of Venturi tube. Model. Simul. Eng. 2012, 2012, 458368. [Google Scholar] [CrossRef]
- Ashrafizadeh, S.M.; Ghassemi, H. Experimental and numerical investigation on the performance of small-sized cavitating venturis. Flow Meas. Instrum. 2015, 42, 6–15. [Google Scholar] [CrossRef]
- Lu, H.; Guo, X.; Li, P.; Liu, K.; Gong, X. Design optimization of a venturi tube geometry in dense-phase pneumatic conveying of pulverized coal for entrained-flow gasification. Chem. Eng. Res. Des. 2017, 120, 208–217. [Google Scholar] [CrossRef]
- Manzano, J.; Palau, C.V.; Benito, M.D.A.; Guilherme, V.D.B.; Vasconcelos, D.V. Geometry and head loss in Venturi injectors through computational fluid dynamics. Eng. Agríc. 2016, 36, 482–491. [Google Scholar] [CrossRef] [Green Version]
- Bethi, B.; Sonawane, S.; Potoroko, I.; Bhanvase, B.A.; Sonawane, S.S. Novel hybrid system based on hydrodynamic cavitation for treatment of dye waste water: A first report on bench scale study. J. Environ. Chem. Eng. 2017, 5, 1874–1884. [Google Scholar] [CrossRef]
- Yi, C.; Lu, Q.; Wang, Y.; Wang, Y.; Yang, B. Degradation of organic wastewater by hydrodynamic cavitation combined with acoustic cavitation. Ultrason. Sonochemistry. 2018, 43, 156–165. [Google Scholar] [CrossRef] [PubMed]
- Rajoriya, S.; Bargole, S.; George, S.; Saharan, V.K. Treatment of textile dyeing industry effluent using hydrodynamic cavitation in combination with advanced oxidation reagents. J. Hazard. Mater. 2018, 344, 1109–1115. [Google Scholar] [CrossRef]
- Badmus, K.O.; Tijani, J.O.; Massima, E.; Petrik, L. Treatment of persistent organic pollutants in wastewater using hydrodynamic cavitation in synergy with advanced oxidation process. Environ. Sci. Pollut. Res. 2018, 25, 7299–7314. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.J.; Nguyen, D.X.; Bae, J.H. The performance of the sludge pretreatment system with venturi tubes. Water Sci. Technol. 2008, 57, 131–137. [Google Scholar] [CrossRef]
- Wang, X.; Jia, J.; Wang, Y. Combination of photocatalysis with hydrodynamic cavitation for degradation of tetracycline. Chem. Eng. J. 2017, 315, 274–282. [Google Scholar] [CrossRef]
- Boczkaj, G.; Gągol, M.; Klein, M.; Przyjazny, A. Effective method of treatment of effluents from production of bitumens under basic pH conditions using hydrodynamic cavitation aided by external oxidants. Ultrason. Sonochemistry. 2018, 40, 969–979. [Google Scholar] [CrossRef]
- Thanekar, P.; Murugesan, P.; Gogate, P.R. Improvement in biological oxidation process for the removal of dichlorvos from aqueous solutions using pretreatment based on Hydrodynamic Cavitation. J. Water Process Eng. 2018, 23, 20–26. [Google Scholar] [CrossRef]
- Hachino, K.; Sato, K.; Saito, Y. Inception and Dynamics of Traveling-Bubble-Type Cavitation in a Venturi. In Proceedings of the ASME/JSME 2003 4th Joint Fluids Summer Engineering Conference, Honolulu, HI, USA, 6–10 July 2003; pp. 279–285. [Google Scholar]
- Cai, J.; Huai, X.; Li, X. Dynamic behaviors of cavitation bubble for the steady cavitating flow. J. Therm. Sci. 2009, 18, 338–344. [Google Scholar] [CrossRef]
- Abdulaziz, A. Performance and image analysis of a cavitating process in a small type venturi. Exp. Therm. Fluid Sci. 2014, 53, 40–48. [Google Scholar] [CrossRef]
- Brinkhorst, S.; Von Lavante, E.; Wendt, G. Numerical investigation of cavitating Herschel Venturi-Tubes applied to liquid flow metering. Flow Meas. Instrum. 2015, 43, 23–33. [Google Scholar] [CrossRef]
- Chen, G.; Wang, G.; Hu, C.; Huang, B.; Gao, Y.; Zhang, M. Combined experimental and computational investigation of cavitation evolution and excited pressure fluctuation in a convergent–divergent channel. Int. J. Multiph. Flow. 2015, 72, 133–140. [Google Scholar] [CrossRef]
- Tomov, P.; Khelladi, S.; Ravelet, F.; Sarraf, C.; Bakir, F.; Vertenoeuil, P. Experimental study of aerated cavitation in a horizontal venturi nozzle. Exp. Therm. Fluid Sci. 2016, 70, 85–95. [Google Scholar] [CrossRef] [Green Version]
- Long, X.; Zhang, J.; Wang, J.; Xu, M.; Lyu, Q.; Ji, B. Experimental investigation of the global cavitation dynamic behavior in a venturi tube with special emphasis on the cavity length variation. Int. J. Multiph. Flow. 2017, 89, 290–298. [Google Scholar] [CrossRef]
- Zhu, J.; Xie, H.; Feng, K.; Zhang, X.; Si, M. Unsteady cavitation characteristics of liquid nitrogen flows through venturi tube. Int. J. Heat Mass Transf. 2017, 112, 544–552. [Google Scholar] [CrossRef]
- Tang, P.; Li, H.; Issaka, Z.; Chen, C. Impact forces on the drive spoon of a large cannon irrigation sprinkler: Simple theory, CFD numerical simulation and validation. Biosyst. Eng. 2017, 159, 1–9. [Google Scholar] [CrossRef]
- Brinkhorst, S.; Von Lavante, E.; Wendt, G. Experimental and numerical investigation of the cavitation-induced choked flow in a herschel venturi-tube. Flow Meas. Instrum. 2017, 54, 56–67. [Google Scholar] [CrossRef]
- Long, X.P.; Wang, J.; Zuo, D.; Zhang, J.Q.; Ji, B. Experimental investigation of the instability of cavitation in veturi tube under different cavitation stage. J. Mech. Eng. 2018, 54, 209–215. [Google Scholar] [CrossRef]








| Group | α (°) | β (°) | γ |
|---|---|---|---|
| 1 | 15, 30, 45, 60 | 20 | 0.28 |
| 2 | 30 | 10, 15, 20, 25, 30 | 0.28 |
| 3 | 30 | 20 | 0.2, 0.3, 0.4, 0.5 |
| Scheme | Scheme 1 | Scheme 2 | Scheme 3 | Scheme 4 | Scheme 5 |
|---|---|---|---|---|---|
| Grid number | 101,342 | 154,683 | 201,679 | 284,813 | 349,866 |
| Mass flow rate (kg s−1) | 2.41 | 2.46 | 2.49 | 2.50 | 2.50 |
| Inlet Pressure (MPa) | Outlet Pressure (MPa) | Mass Flow Rate | ||
|---|---|---|---|---|
| Measured (kg s−1) | Simulated (kg s−1) | Difference (%) | ||
| 0.15 | 0.10 | 1.64 | 1.70 | 3.66 |
| 0.20 | 0.10 | 2.38 | 2.49 | 4.62 |
| 0.25 | 0.10 | 2.43 | 2.53 | 4.12 |
| 0.30 | 0.10 | 2.42 | 2.54 | 4.96 |
| 0.35 | 0.10 | 2.43 | 2.55 | 4.94 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, P.; Juárez, J.M.; Li, H. Investigation on the Effect of Structural Parameters on Cavitation Characteristics for the Venturi Tube Using the CFD Method. Water 2019, 11, 2194. https://doi.org/10.3390/w11102194
Tang P, Juárez JM, Li H. Investigation on the Effect of Structural Parameters on Cavitation Characteristics for the Venturi Tube Using the CFD Method. Water. 2019; 11(10):2194. https://doi.org/10.3390/w11102194
Chicago/Turabian StyleTang, Pan, Juan Manzano Juárez, and Hong Li. 2019. "Investigation on the Effect of Structural Parameters on Cavitation Characteristics for the Venturi Tube Using the CFD Method" Water 11, no. 10: 2194. https://doi.org/10.3390/w11102194
APA StyleTang, P., Juárez, J. M., & Li, H. (2019). Investigation on the Effect of Structural Parameters on Cavitation Characteristics for the Venturi Tube Using the CFD Method. Water, 11(10), 2194. https://doi.org/10.3390/w11102194




