Long-Term Hydropower Generation Scheduling of Large-Scale Cascade Reservoirs Using Chaotic Adaptive Multi-Objective Bat Algorithm
Abstract
1. Introduction
2. Mathematical Modeling of the CHRO Problem
2.1. Objective Function
- (1)
- Maximizing the annual power generation of the hydropower system:
- (2)
- Maximizing the firm power output:where is the power output of the kth reservoir at tth period; is the synthetic output coefficient of the kth reservoir; is the hydraulic head of the kth reservoir at the tth period (m); is the generation flow of the kth reservoir at the tth period (m3/s); is the time duration of a single period.
2.2. Constraints
- (1)
- Reservoir water balance equation:
- (2)
- Reservoir storage conversion:
- (3)
- Reservoir water head:
- (4)
- Reservoir water level constraint:
- (5)
- Reservoir outflow constraint:
- (6)
- Power output constraint:where and are storage capacity of the kth reservoir at the tth and (t−1)th period, respectively (m3); and are inflow and outflow of the kth reservoir at the tth period, respectively (m3/s); is the water level of the kth reservoir at the tth period (m); is the storage-capacity curve of the kth reservoir; is the function between the outflow and tail water level of the kth reservoir; is the tail water level of the kth reservoir (m); and are the lowest and highest water level of the kth reservoir at the tth period, respectively (m); is the outflow of the kth reservoir at the tth period (m3/s); is the spillage of the kth reservoir at the tth period (m3/s); and are minimum and maximum outflow of the kth reservoir at the tth period, respectively (m3/s); is the function between the water level and maximum outflow of the kth reservoir; is the maximum power output of the kth reservoir at the tth period.
3. Overview of the Multi-Objective Bat Algorithm
4. Implementation of CAMOBA for solving the CHRO problem
4.1. External Archive Set Maintenance and Updating Operation
- (1)
- If EAS ( ) is vacant, put into EAS( ) directly.
- (2)
- Compare with other solutions in EAS( ). If is not dominated by any solution in EAS ( ), add into EAS ( ) and delete the solution dominated by in EAS( ).
- (3)
- If the number of individuals in EAS( ) exceeds the NE, a crowding distance comparison is performed for each new solution addition. In this process, the solution with the smallest crowding distance is eliminated. Non-dominated solutions are ranked based on one of the objective functions. The boundary solutions (the smallest and largest solutions of the function values) are given a larger distance value to maintain the diversity of the external archive set [23]. The crowding distance can be expressed as:where is the crowding distance of the jth solution; is the fitness of the jth solution of the mth objective; and are the minimum and maximum fitness of the mth objective, respectively.
4.2. Initial Population Generation
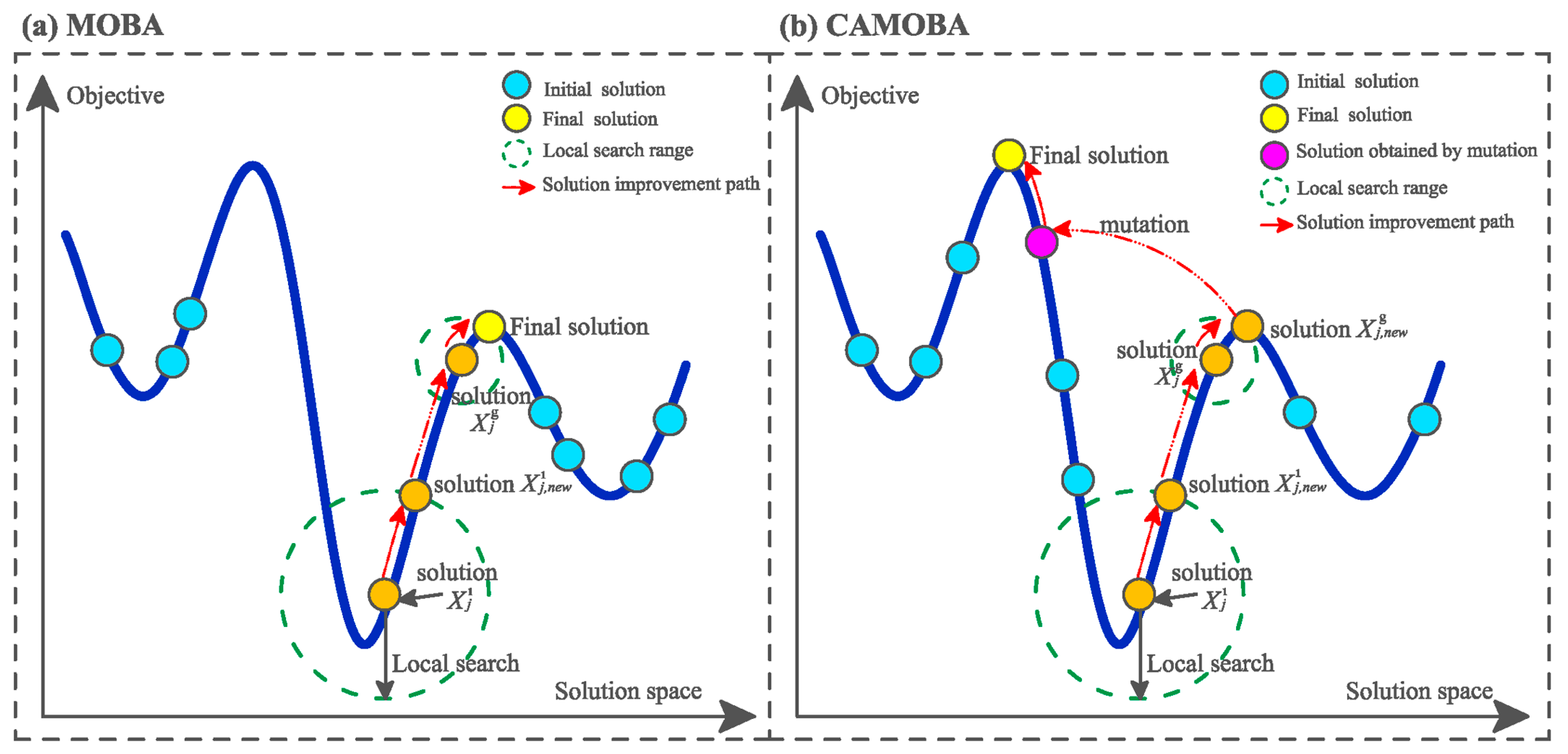
4.3. Self-Adaptive Local Search Strategy
4.4. Mutation Operation
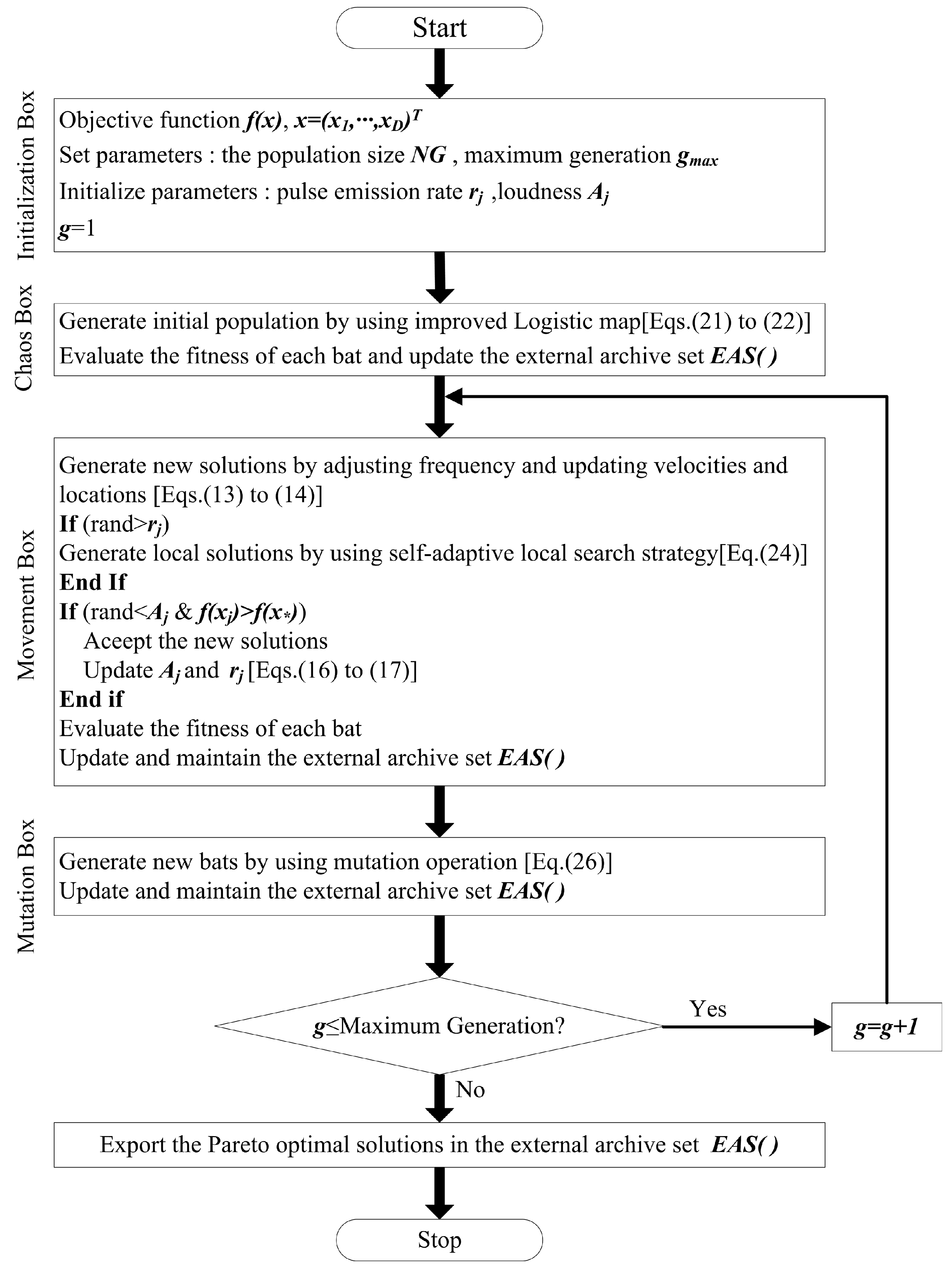
4.5. Procedures of CAMOBA for Solving the CHRO Problem
5. Case Study
5.1. Case Study Description
5.2. Parameter Settings
5.3. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, Z.-K.; Niu, W.-J.; Cheng, C.-T. Optimizing electrical power production of hydropower system by uniform progressive optimality algorithm based on two-stage search mechanism and uniform design. J. Clean Prod. 2018, 190, 432–442. [Google Scholar] [CrossRef]
- Madani, K.; Lund, J.R. Modeling California’s high-elevation hydropower systems in energy units. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Madani, K. Hydropower licensing and climate change: Insights from cooperative game theory. Adv. Water Resour. 2011, 34, 174–183. [Google Scholar] [CrossRef]
- Niu, W.-J.; Feng, Z.-K.; Cheng, C.-T.; Wu, X.-Y. A parallel multi-objective particle swarm optimization for cascade hydropower reservoir operation in southwest China. Appl. Soft Comput. 2018, 70, 562–575. [Google Scholar] [CrossRef]
- Reshma, T.; Reddy, K.V.; Pratap, D.; Agilan, V. Parameters Optimization using Fuzzy Rule Based Multi-Objective Genetic Algorithm for an Event Based Rainfall-Runoff Model. Water Resour. Manag. 2018, 32, 1501–1516. [Google Scholar] [CrossRef]
- Reddy, M.J.; Kumar, D.N. Optimal Reservoir Operation Using Multi-Objective Evolutionary Algorithm. Water Resour. Manag. 2006, 20, 861–878. [Google Scholar] [CrossRef]
- Wang, Y.; Hua, Z.; Wang, L. Parameter Estimation of Water Quality Models Using an Improved Multi-Objective Particle Swarm Optimization. Water 2018, 10, 32. [Google Scholar] [CrossRef]
- Sivasubramani, S.; Swarup, K.S. Multi-objective harmony search algorithm for optimal power flow problem. Int. J. Electr. Power 2011, 33, 745–752. [Google Scholar] [CrossRef]
- Hajibandeh, E.; Nazif, S. Pressure Zoning Approach for Leak Detection in Water Distribution Systems Based on a Multi Objective Ant Colony Optimization. Water Resour. Manag. 2018, 32, 2287–2300. [Google Scholar] [CrossRef]
- Sun, X.; Luo, J.; Xie, J. Multi-Objective Optimization for Reservoir Operation Considering Water Diversion and Power Generation Objectives. Water 2018, 10, 1540. [Google Scholar] [CrossRef]
- Li, F.F.; Qiu, J. Multi-Objective Reservoir Optimization Balancing Energy Generation and Firm Power. Energies 2015, 8, 6962–6976. [Google Scholar] [CrossRef]
- Yang, X.-S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NISCO 2010); Cruz, C., González, J.R., Krasnogor, N., Pelta, D.A., Terrazas, G., Eds.; Springer: Berlin, Germany, 2010; pp. 65–74. [Google Scholar]
- Bahmani-Firouzi, B.; Azizipanah-Abarghooee, R. Optimal sizing of battery energy storage for micro-grid operation management using a new improved bat algorithm. Int. J. Electr. Power 2014, 56, 42–54. [Google Scholar] [CrossRef]
- Zarei, A.; Mousavi, S.F.; Gordji, M.E.; Karami, H. Optimal Reservoir Operation Using Bat and Particle Swarm Algorithm and Game Theory Based on Optimal Water Allocation among Consumers. Water Resour. Manag. 2019, 33, 3071–3093. [Google Scholar] [CrossRef]
- Sathya, M.R.; Mohamed Thameem Ansari, M. Load frequency control using Bat inspired algorithm based dual mode gain scheduling of PI controllers for interconnected power system. Int. J. Electr. Power. 2015, 64, 365–374. [Google Scholar] [CrossRef]
- Niknam, T.; Azizipanah-Abarghooee, R.; Zare, M.; Bahmani-Firouzi, B. Reserve Constrained Dynamic Environmental/Economic Dispatch: A New Multiobjective Self-Adaptive Learning Bat Algorithm. IEEE Syst. J. 2013, 7, 763–776. [Google Scholar] [CrossRef]
- Yang, X.-S. Bat Algorithm for Multi-objective Optimisation. Int. J. Bio-Inspir. Comput. 2011, 3, 267–274. [Google Scholar] [CrossRef]
- Yang, N.-C.; Le, M.-D. Optimal design of passive power filters based on multi-objective bat algorithm and pareto front. Appl. Soft Comput. 2015, 35, 257–266. [Google Scholar] [CrossRef]
- Liang, H.; Liu, Y.; Li, F.; Shen, Y. A multiobjective hybrid bat algorithm for combined economic/emission dispatch. Int. J. Electr. Power 2018, 101, 103–115. [Google Scholar] [CrossRef]
- Bansal, S.; Singh, A.K.; Gupta, N. Optimal Golomb Ruler Sequences Generation for Optical WDM Systems: A Novel Parallel Hybrid Multi-objective Bat Algorithm. J. Inst. Eng. India Ser. B 2016, 98, 43–64. [Google Scholar] [CrossRef]
- Prakash, S.; Trivedi, V.; Ramteke, M. An elitist non-dominated sorting bat algorithm NSBAT-II for multi-objective optimization of phthalic anhydride reactor. Int. J. Syst. Assur. Eng. Manag. 2016, 7, 299–315. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the Strength Pareto approach. IEEE Trans. Evolut. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Aydin, I.; Karakose, M.; Akin, E. Chaotic-based hybrid negative selection algorithm and its applications in fault and anomaly detection. Expert Syst. Appl. 2010, 37, 5285–5294. [Google Scholar] [CrossRef]
- Parlitz, U.; Ergezinger, S. Robust communication based on chaotic spreading sequences. Phys. Lett. A 1994, 188, 146–150. [Google Scholar] [CrossRef]
- Li, D.; Cheung, D.; Shi, X.; Ng, V. Uncertainty reasoning based on cloud models in controllers. Comput. Math. Appl. 1998, 35, 99–123. [Google Scholar] [CrossRef]
- Li, R.; Jiang, Z.; Li, A.; Yu, S.; Ji, C. An improved shuffled frog leaping algorithm and its application in the optimization of cascade reservoir operation. Hydrol. Sci. J. 2019, 63, 2020–2034. [Google Scholar] [CrossRef]
- Bekele, E.G.; Nicklow, J.W. Multi-objective automatic calibration of SWAT using NSGA-II. J. Hydrol. 2007, 341, 165–176. [Google Scholar] [CrossRef]
- Kannan, S.; Baskar, S.; McCalley, J.D.; Murugan, P. Application of NSGA-II Algorithm to Generation Expansion Planning. IEEE Trans. Power Syst. 2009, 24, 454–461. [Google Scholar] [CrossRef]
- Schott, J.R. Fault Tolerant Design Using Single and Multicriteria Genetic Algorithm Optimization. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]





| Hydrological Years | Objective | Method | Max ↑ | Improve (%) | Mean ↑ | Improve (%) | Std ↓ | Improve (%) |
|---|---|---|---|---|---|---|---|---|
| Wet year | Annual power generation | CAMOBA | 115.6408 | 0.082% | 115.5407 | 0.048% | 0.0408 | 3.702% |
| MOBA | 115.5694 | 0.021% | 115.4885 | 0.003% | 0.0414 | 2.172% | ||
| NSGA-II | 115.5456 | - | 115.4851 | - | 0.0423 | - | ||
| Firm power output | CAMOBA | 560.6503 | 3.368% | 539.3225 | 5.774% | 22.6059 | 31.829% | |
| MOBA | 550.5622 | 1.508% | 525.0124 | 2.967% | 26.9268 | 18.798% | ||
| NSGA-II | 542.3833 | - | 509.8830 | - | 33.1604 | - | ||
| Normal year | Annual power generation | CAMOBA | 72.8236 | 0.005% | 72.8125 | 0.054% | 0.0173 | 67.544% |
| MOBA | 72.8227 | 0.004% | 72.7947 | 0.029% | 0.0415 | 22.043% | ||
| NSGA-II | 72.8199 | - | 72.7735 | - | 0.0532 | - | ||
| Firm power output | CAMOBA | 483.0351 | 7.237% | 431.6210 | 9.679% | 29.5803 | 19.650% | |
| MOBA | 461.8928 | 2.543% | 409.1474 | 3.968% | 30.5043 | 17.140% | ||
| NSGA-II | 450.4362 | - | 393.5319 | - | 36.8142 | - | ||
| Dry year | Annual power generation | CAMOBA | 56.0700 | 0.002% | 56.0621 | 0.046% | 0.0145 | 47.405% |
| MOBA | 56.0697 | 0.001% | 56.0582 | 0.040% | 0.0203 | 26.570% | ||
| NSGA-II | 56.0690 | - | 56.0360 | - | 0.0276 | - | ||
| Firm power output | CAMOBA | 338.1704 | 5.592% | 299.2050 | 4.398% | 20.4751 | 11.893% | |
| MOBA | 326.3672 | 1.906% | 288.7327 | 0.744% | 22.2445 | 4.279% | ||
| NSGA-II | 320.2625 | - | 286.6007 | - | 23.2388 | - |
| Hydrological Years | Algorithm | SP | HV | Time(s) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Max ↓ | Mean ↓ | Min ↓ | Std ↓ | Max ↑ | Mean ↑ | Min ↑ | Std ↓ | |||
| Wet year | CAMOBA | 0.0247 | 0.0220 | 0.0190 | 0.0017 | 0.8183 | 0.8114 | 0.7949 | 0.0075 | 511.2 |
| MOBA | 0.0729 | 0.0662 | 0.0618 | 0.0042 | 0.7367 | 0.7220 | 0.7124 | 0.0085 | 461.4 | |
| NSGA-II | 0.0245 | 0.0221 | 0.0165 | 0.0028 | 0.7320 | 0.7211 | 0.7057 | 0.0093 | 759.6 | |
| Normal year | CAMOBA | 0.0194 | 0.0148 | 0.0112 | 0.0027 | 0.8147 | 0.8038 | 0.7812 | 0.0107 | 515.4 |
| MOBA | 0.0681 | 0.0626 | 0.0519 | 0.0048 | 0.7821 | 0.7449 | 0.7123 | 0.0252 | 456.8 | |
| NSGA-II | 0.0398 | 0.0345 | 0.0298 | 0.0039 | 0.7414 | 0.7150 | 0.6968 | 0.0158 | 741.3 | |
| Dry year | CAMOBA | 0.0223 | 0.0204 | 0.0187 | 0.0011 | 0.8979 | 0.8852 | 0.8732 | 0.0080 | 509.7 |
| MOBA | 0.1940 | 0.1748 | 0.1658 | 0.0076 | 0.8165 | 0.8007 | 0.7826 | 0.0111 | 457.6 | |
| NSGA-II | 0.0384 | 0.0359 | 0.0317 | 0.0023 | 0.5525 | 0.5283 | 0.5213 | 0.0094 | 753.7 | |
| Scheme | f1 (108 kWh) | f2 (MW) | Scheme | f1 (108 kWh) | f2 (MW) | Scheme | f1 (108 kWh) | f2 (MW) |
|---|---|---|---|---|---|---|---|---|
| 1 | 72.8236 | 189.1719 | 11 | 72.7347 | 374.6256 | 21 | 72.5535 | 452.4976 |
| 2 | 72.8232 | 225.4624 | 12 | 72.7227 | 390.1868 | 22 | 72.5333 | 460.2505 |
| 3 | 72.8217 | 241.1590 | 13 | 72.7082 | 402.6378 | 23 | 72.5109 | 467.7229 |
| 4 | 72.8200 | 256.8327 | 14 | 72.6925 | 405.8924 | 24 | 72.4848 | 470.2905 |
| 5 | 72.8177 | 273.0836 | 15 | 72.6864 | 418.7940 | 25 | 72.4680 | 471.5678 |
| 6 | 72.8134 | 285.7809 | 16 | 72.6620 | 425.8439 | 26 | 72.4475 | 472.9724 |
| 7 | 72.8007 | 304.9514 | 17 | 72.6352 | 427.0217 | 27 | 72.4238 | 473.4131 |
| 8 | 72.7871 | 324.6124 | 18 | 72.6088 | 438.4034 | 28 | 72.3926 | 477.6139 |
| 9 | 72.7668 | 343.0365 | 19 | 72.5878 | 443.0313 | 29 | 72.3594 | 478.6686 |
| 10 | 72.7623 | 357.0580 | 20 | 72.5694 | 444.8507 | 30 | 72.3189 | 483.0351 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, L.; Yang, K.; Hu, H.; Yang, Z. Long-Term Hydropower Generation Scheduling of Large-Scale Cascade Reservoirs Using Chaotic Adaptive Multi-Objective Bat Algorithm. Water 2019, 11, 2373. https://doi.org/10.3390/w11112373
Su L, Yang K, Hu H, Yang Z. Long-Term Hydropower Generation Scheduling of Large-Scale Cascade Reservoirs Using Chaotic Adaptive Multi-Objective Bat Algorithm. Water. 2019; 11(11):2373. https://doi.org/10.3390/w11112373
Chicago/Turabian StyleSu, Lyuwen, Kan Yang, Hu Hu, and Zhe Yang. 2019. "Long-Term Hydropower Generation Scheduling of Large-Scale Cascade Reservoirs Using Chaotic Adaptive Multi-Objective Bat Algorithm" Water 11, no. 11: 2373. https://doi.org/10.3390/w11112373
APA StyleSu, L., Yang, K., Hu, H., & Yang, Z. (2019). Long-Term Hydropower Generation Scheduling of Large-Scale Cascade Reservoirs Using Chaotic Adaptive Multi-Objective Bat Algorithm. Water, 11(11), 2373. https://doi.org/10.3390/w11112373





