A Novel, Coupled CFD-DEM Model for the Flow Characteristics of Particles Inside a Pipe
Abstract
:1. Introduction
2. Coupled CFD-DEM Model
2.1. Mathematical Formulations
2.1.1. Governing Equations of the Fluid Phase
2.1.2. Governing Equations of the Particle Phase
2.1.3. Fluid–Particle Interaction Force
2.2. Implementation of the Coupled CFD-DEM Model
2.3. Benchmarking Examples
2.3.1. A Single Spherical Particle Settling in Still Water
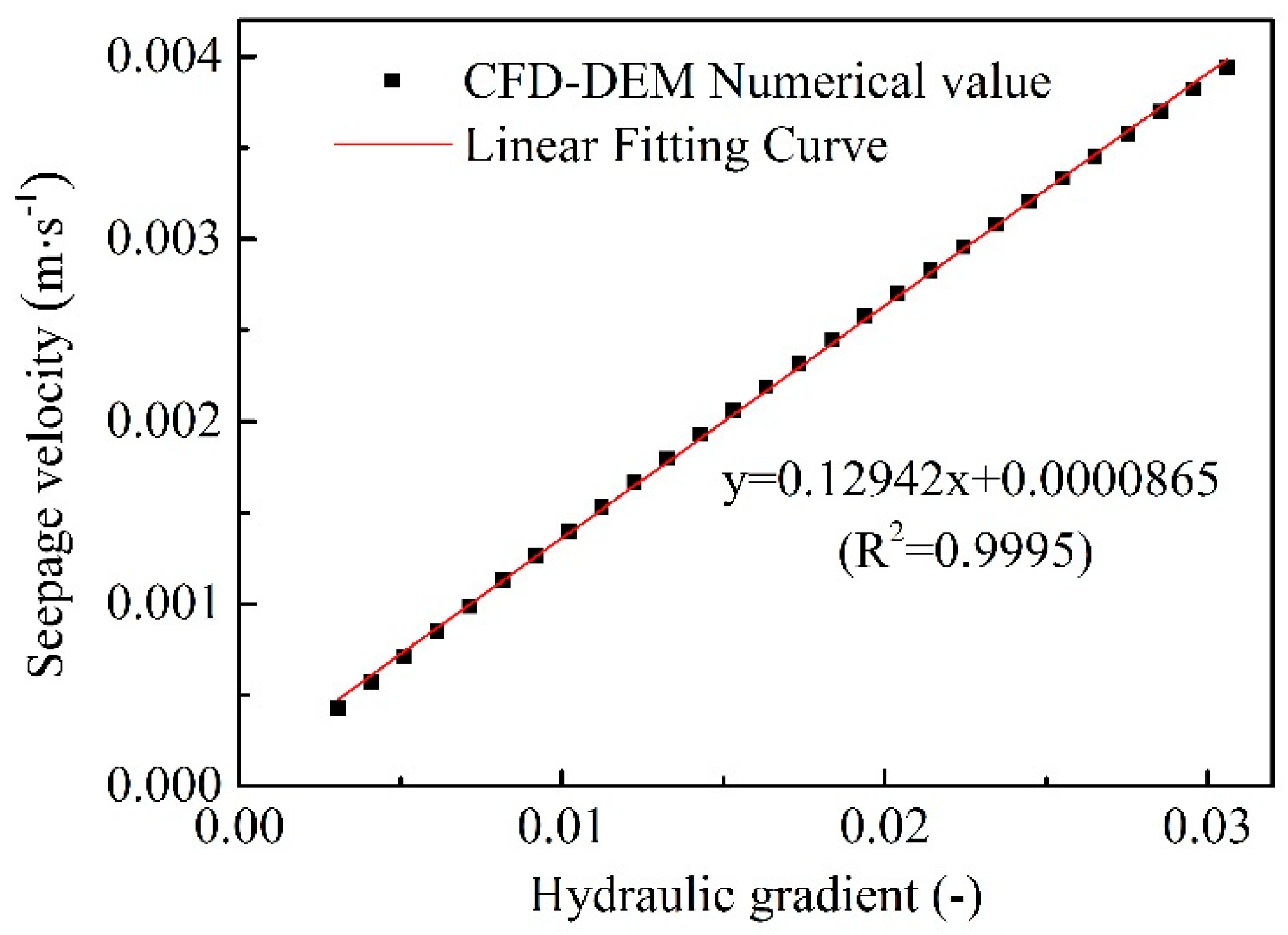
2.3.2. Darcy’s Law
3. Flow Characteristics of Particles Inside a Pipe
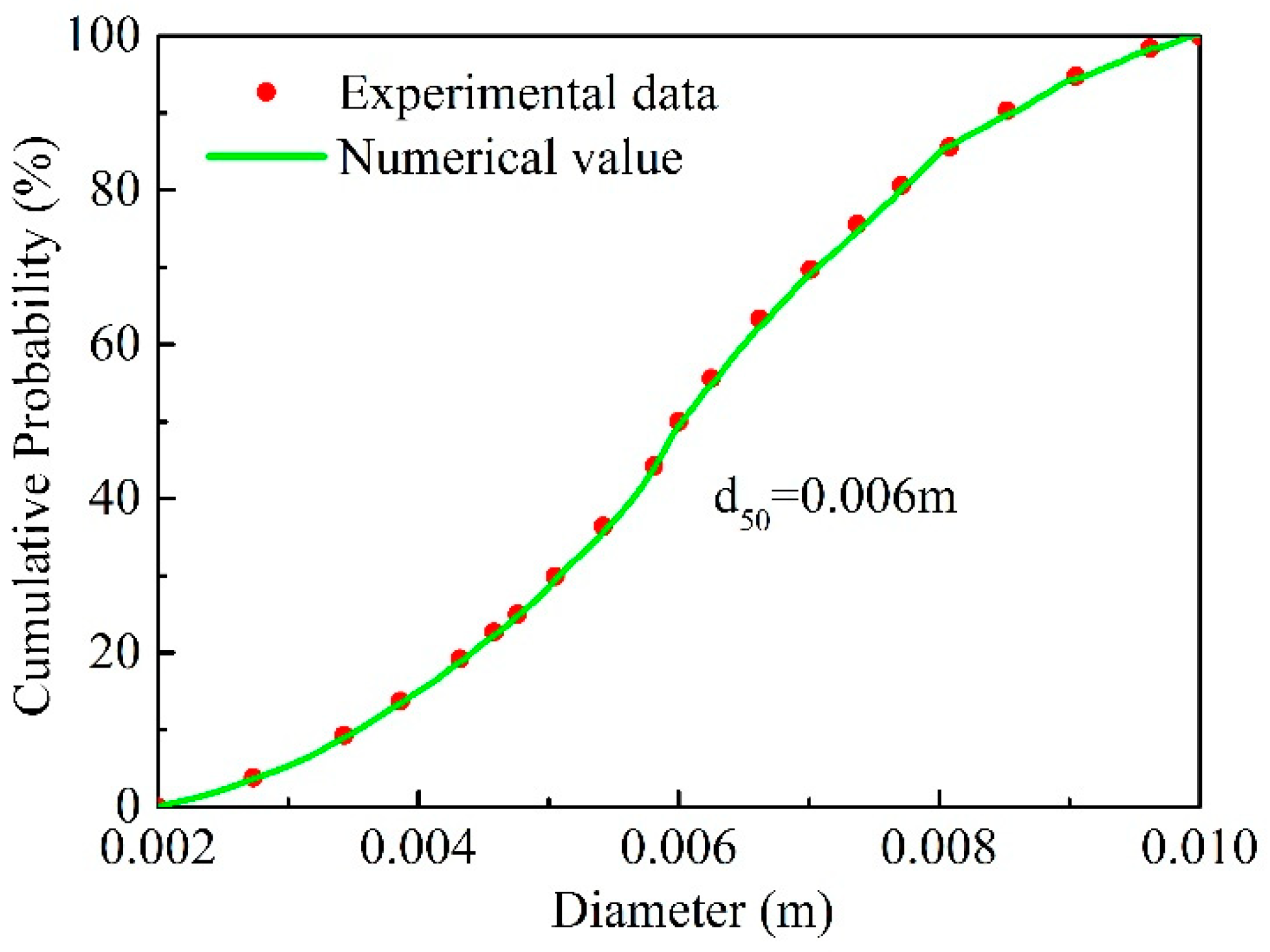
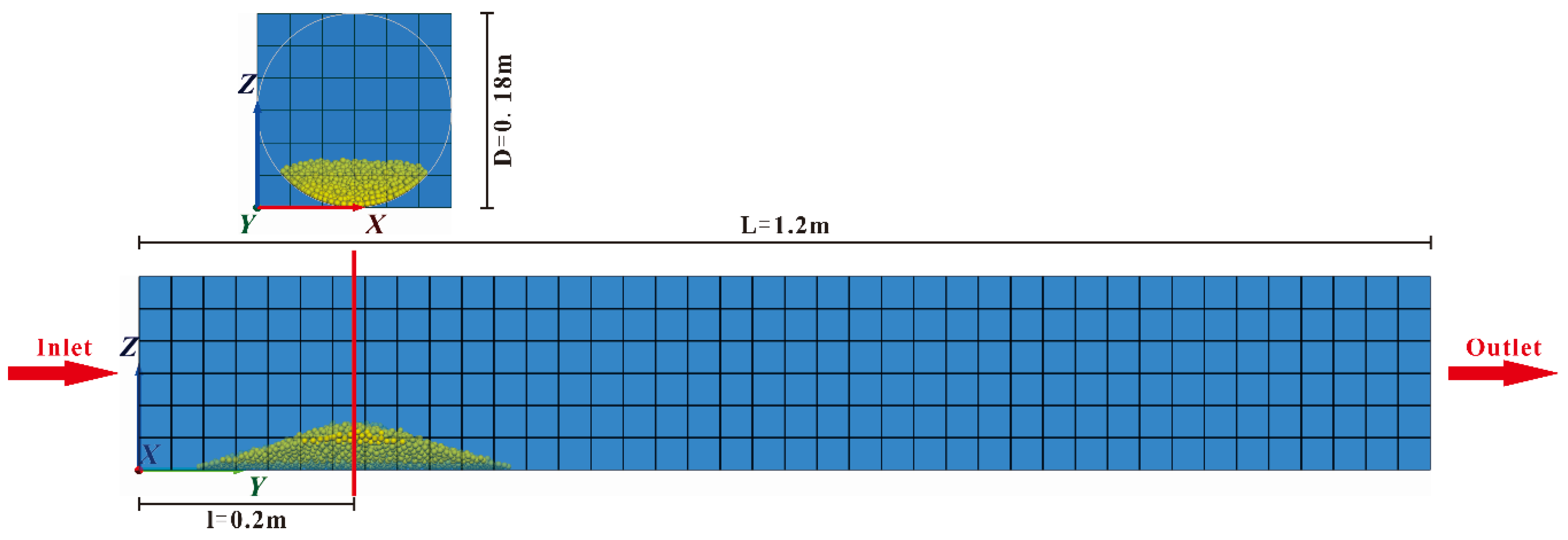
3.1. Model Description
3.2. Results
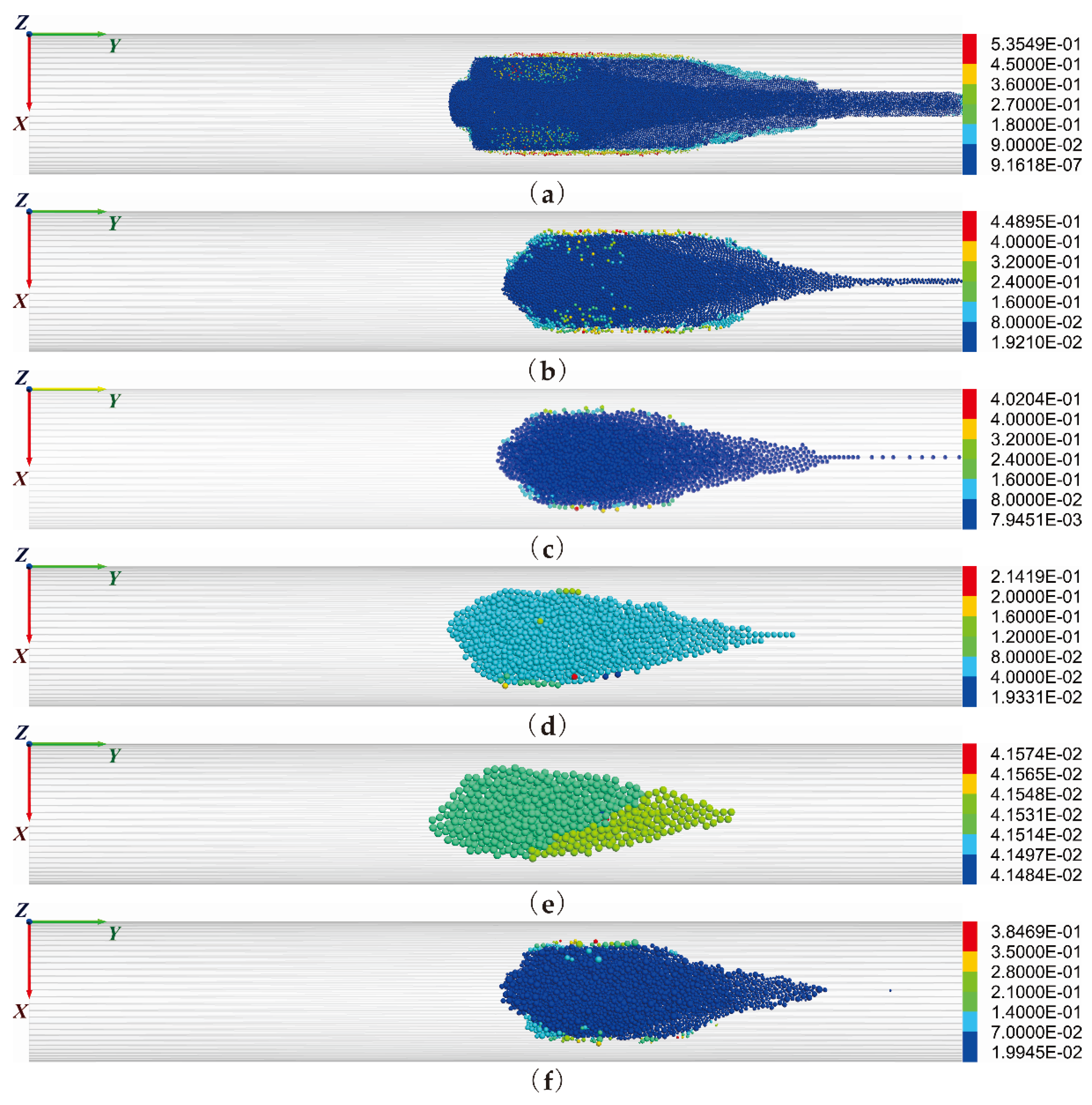
3.2.1. Particle Flow Patterns
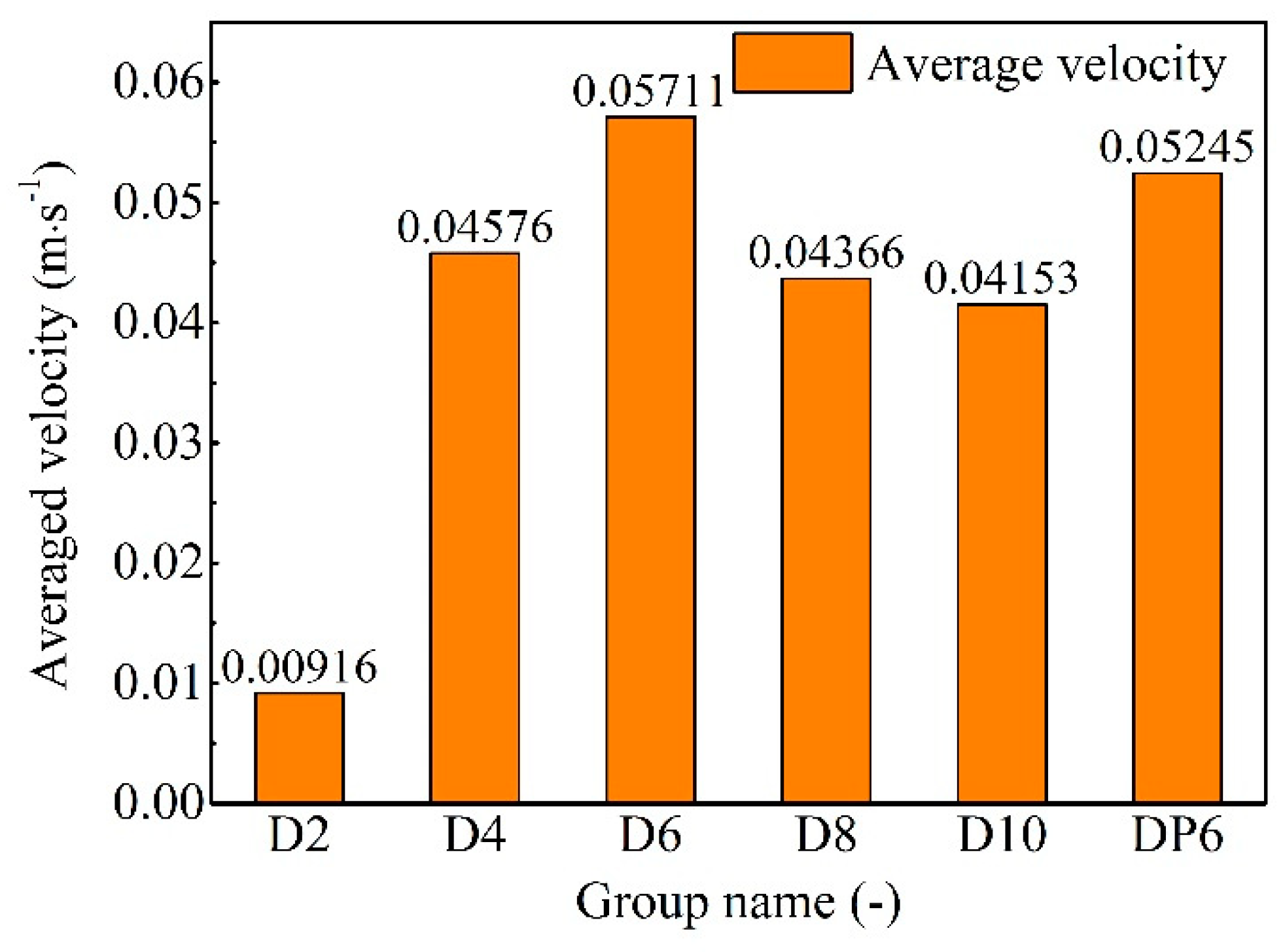
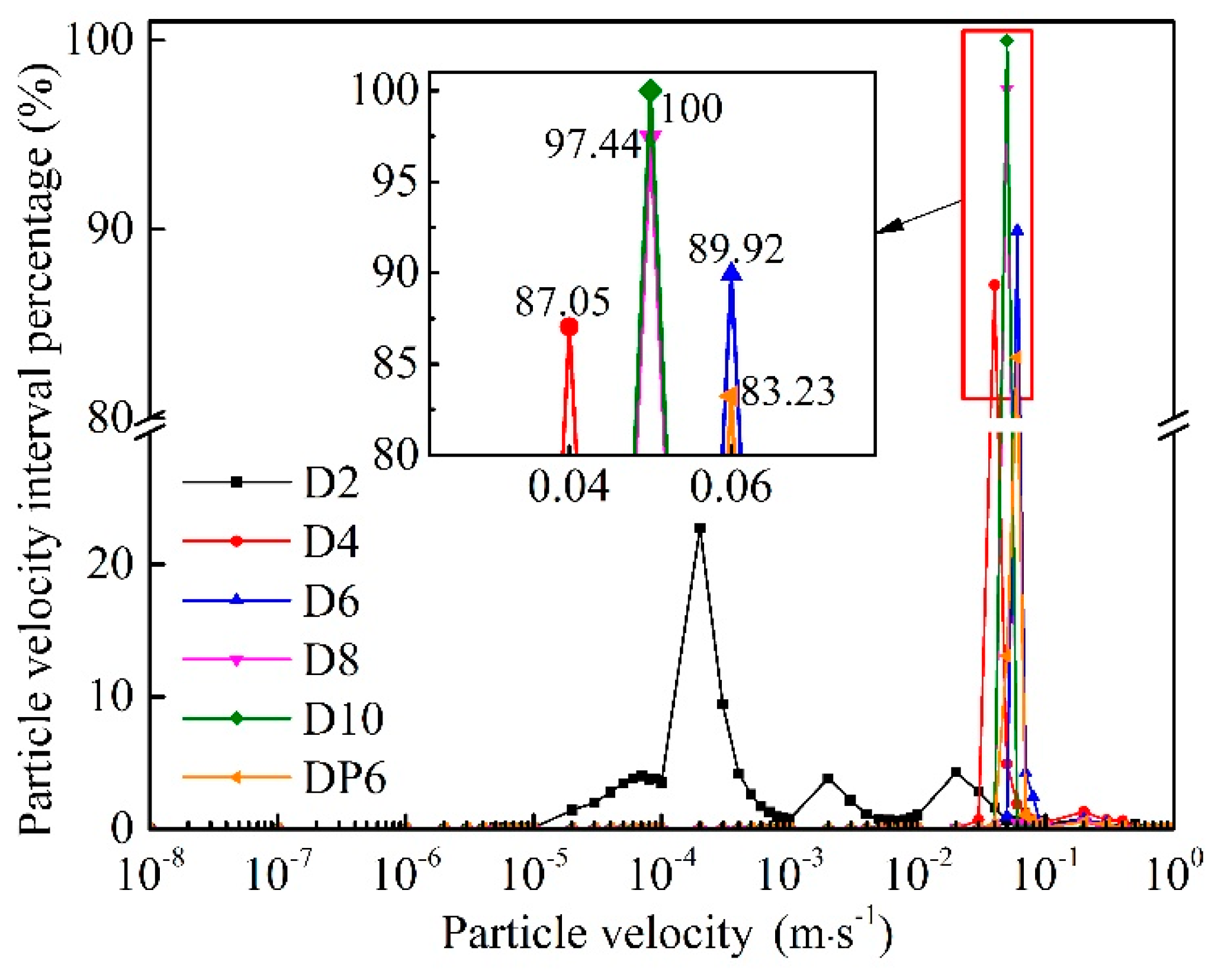
3.2.2. Particle Flow Velocity
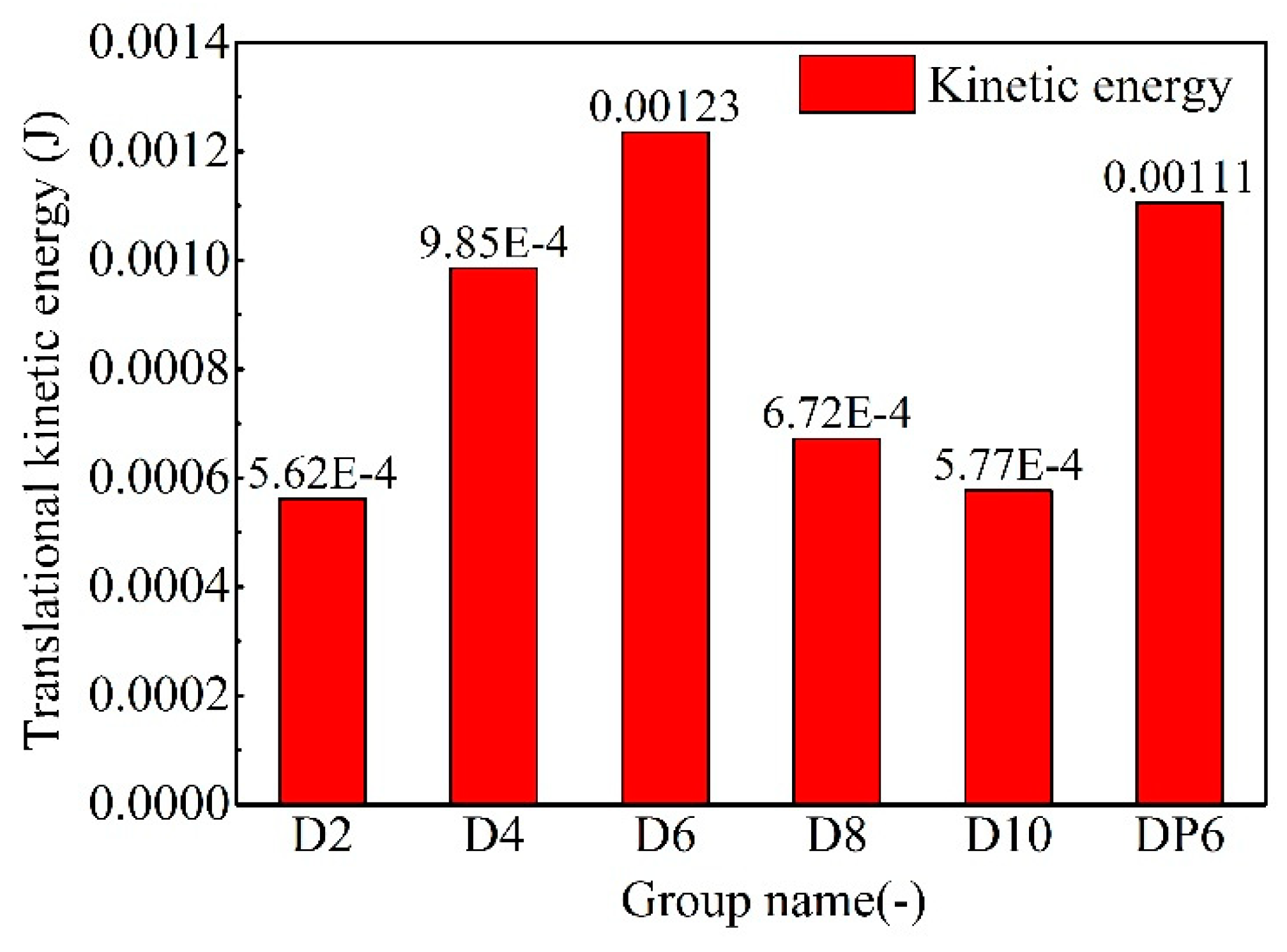
3.2.3. Particle Erosion Rate and Kinetic Energy
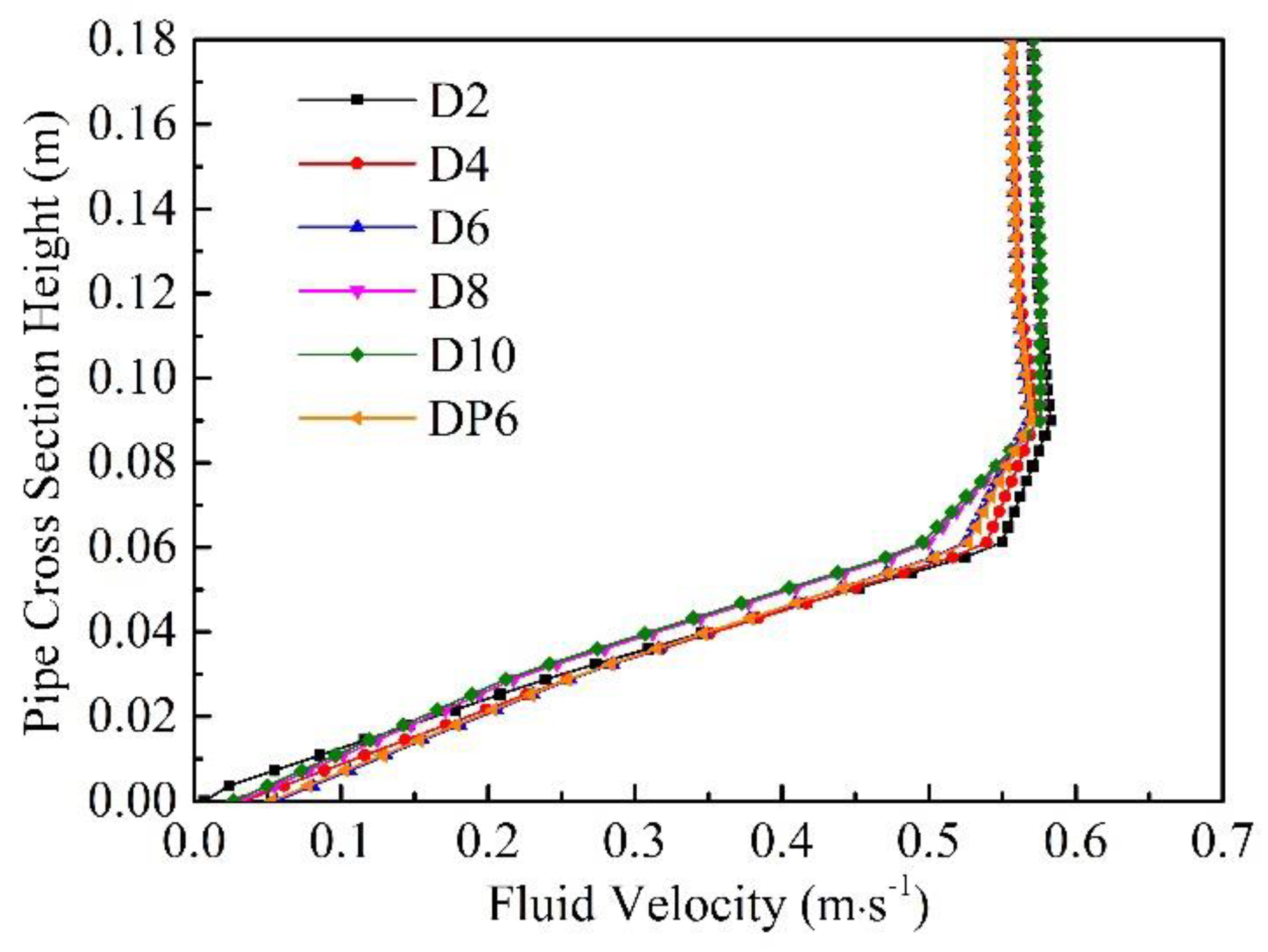
3.2.4. Fluid Flow Behaviours
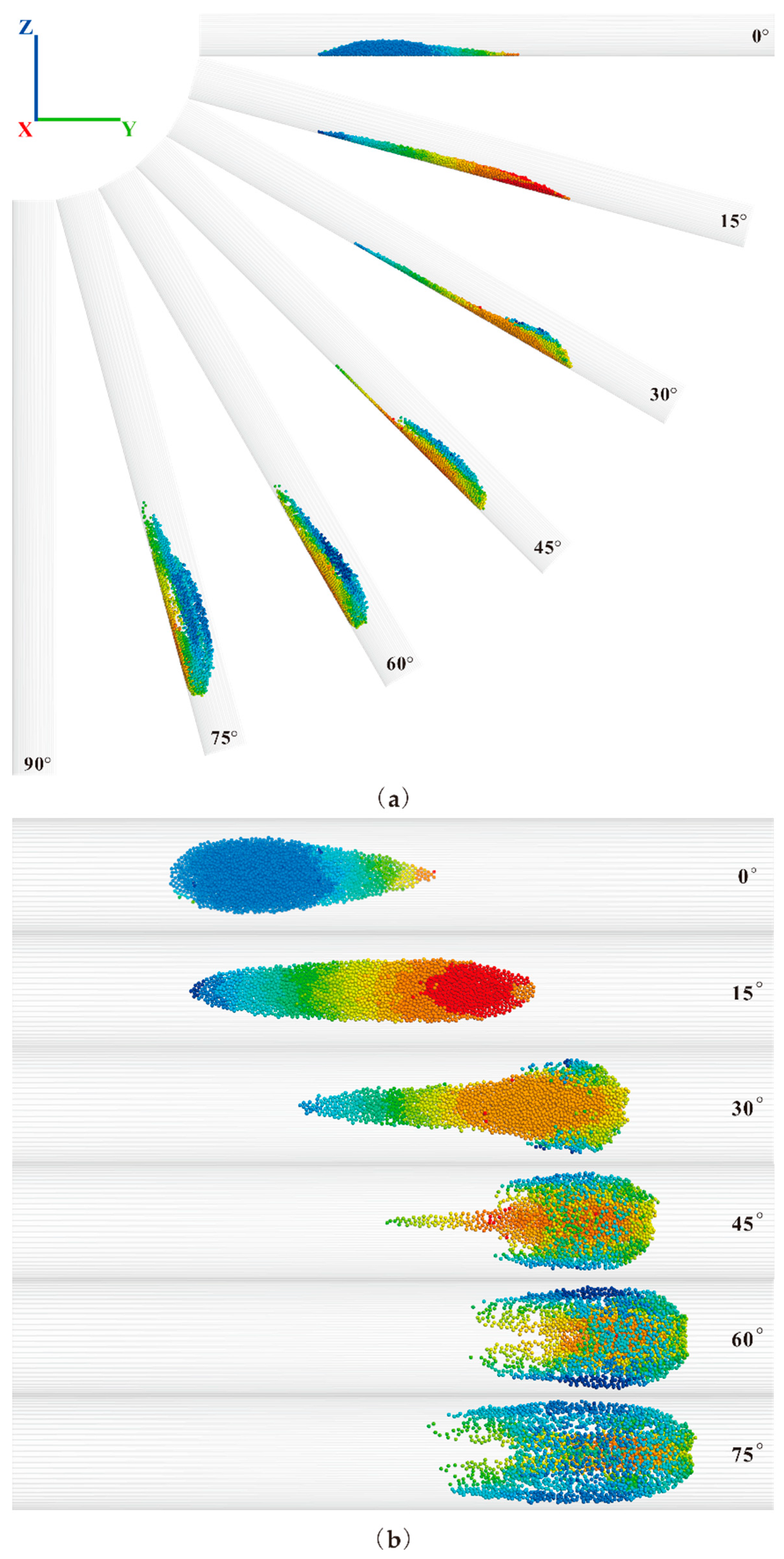
3.2.5. Pipe Inclination Angle
4. Discussion
4.1. Coupled CFD-DEM Model
4.2. Analysis of the Flow Characteristics of Particles Inside a Pipe
- Particle characteristics: (1) The particle position distribution and particle velocity distribution have symmetry, and the degree of symmetry is negatively correlated with the particle size. (2) The particle flow pattern has an obvious tip part and a main part, and the presence of the tip part is negatively correlated with the particle size. (3) The phenomenon of the particle outflow boundary and the volume fraction of outflow particles are negatively correlated with the particle size. (4) The maximum particle velocity and the particle velocity distribution range are negatively correlated with the particle size. (5) The percentage of the maximum velocity interval is positively correlated with the particle size. (6) The average particle velocity, particle erosion rate and kinetic energy all increased first and then decreased with an increase in the particle size.
- Fluid characteristics: The fluid field exhibits an uneven distribution. The presence of particles can impede the water flow and deflect the fluid velocity vector. The deflection mode adapts to the shape of the particle heap. The maximum fluid velocity is negatively correlated with the particle size. The flow velocity distribution along the centre line of the cross section shows the same trend and can be divided into three parts: a slow acceleration stage, fast acceleration stage and stabilization stage.
- The effects of the pipe inclination angles: There is a threshold for particle escape velocity inside a pipe. With an increase in the pipe inclination angle, the positive stress decreases, the friction force of the particles decreases, and the sliding force increases. Due to the combined action of the fluid drag force, the larger the inclination angle is, the smaller is the escape velocity threshold of the particle. As the inclination angle of the pipe gradually increases from 0° to 90°, the particles exhibit a significantly different performance. When the inclination angle is 0°, particles present the normal main and tip parts. When the inclination angle is 15°, particles appear as long strips that are evenly arranged along the bottom of the pipe. When the inclination angles are 30° and 45°, the particles present in the front part gradually lag behind the particles in the middle part and form the trailing part. When the inclination angles are 60° and 75°, the tailing part gradually disappears, forms an ellipsoidal particle group and exhibits a particle flying phenomenon. When the inclination angle is 90°, all of the particles leave the pipe.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| fluid density, | |
| particle density, | |
| t | time, s |
| m | particle mass, kg |
| fluid velocity, m/s | |
| particle translational velocity, m/s | |
| particle annular velocity, rad/s | |
| porosity, dimensionless | |
| fluid dynamic viscosity, | |
| fluid kinematic viscosity, | |
| r | particle radius, m |
| d | particle diameter, m |
| drag force coefficient, dimensionless | |
| Reynolds number of the particle, dimensionless | |
| drag force of the single particle, N | |
| drag force, N | |
| empirical coefficient to account for the local porosity, dimensionless | |
| buoyancy, N | |
| contact force exerted by the neighbouring particles, N | |
| externally applied force, N | |
| the sum of additional forces applied on the particle, N | |
| fluid pressure gradient force, N | |
| the total fluid–particle interaction force applied on the particle by the fluid, N | |
| p | fluid pressure, Pa |
| fluid pressure gradient, Pa/m | |
| G | gravitation, N |
| moment of contact force acting on the particle, | |
| moment of inertia for the particle, | |
| the body force per unit volume exerted on the fluid by the particle, N | |
| gravitational acceleration, | |
| volume of the particle, | |
| vertical velocity of the settling particle, m/s | |
| minimum width of the flow domain, m | |
| fluid element length, m | |
| coupling interval, s | |
| K | permeability coefficient, m/s |
| I | hydraulic gradient, dimensionless |
| pressure at the inlet, Pa | |
| pressure at the outlet, Pa | |
| L | length of flow path, m |
| k | intrinsic permeability coefficient, |
| v | seepage velocity, m/s |
References
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: A review of major applications and findings. Chem. Eng. Sci. 2008, 63, 5728–5770. [Google Scholar] [CrossRef]
- Peters, B.; Baniasadi, M.; Baniasadi, M. XDEM multi-physics and multi-scale simulation technology: Review of DEM-CFD coupling, methodology and engineering applications. Particuology 2019, 44, 176–193. [Google Scholar] [CrossRef]
- Manjula, E.V.P.J.; Ariyaratne, W.K.H.; Ratnayake, C. A review of CFD modelling studies on pneumatic conveying and challenges in modelling offshore drill cuttings transport. Powder Technol. 2017, 305, 782–793. [Google Scholar] [CrossRef]
- Kuang, S.B.; Zhou, M.M.; Yu, A.B. CFD-DEM modelling and simulation of pneumatic conveying: A review. Powder Technol. 2019, in press. [Google Scholar] [CrossRef]
- Guo, Y.; Yu, X.B. Comparison of the implementation of three common types of coupled CFD-DEM model for simulating soil surface erosion. Int. J. Multiph. Flow 2017, 91, 89–100. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Furtney, J.; Zhang, F.; Han, Y. Review of Methods and Applications for Incorporating Fluid Flow in the Discrete Element Method; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2013. [Google Scholar]
- Goniva, C.; Kloss, C.; Hager, A. An open source CFD-DEM perspective. In Proceedings of the Openfoam Workshop, Gothenburg, Sweden, 21–24 June 2010. [Google Scholar]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Han, Y.H. Construction of a LBM-DEM Coupling System and its Applications in Modeling Fluid Particle Interaction in Porous Media Flow. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2012. [Google Scholar]
- Shadloo, M.S.; Oger, G.; Touzé, D.L. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Hama, N.A.; Ouahbi, T.; Taibi, S. Analysis of mechanical behavior and internal stability of granular materials using discrete element method. Int. J. Numer. Anal. Meth. Geomech. 2016, 40, 1712–1729. [Google Scholar] [CrossRef]
- Akhshik, S.; Behzad, M.; Rajabi, M. CFD-DEM simulation of the hole cleaning process in a deviated well drilling: The effects of particle shape. Particuology 2016, 25, 72–82. [Google Scholar] [CrossRef]
- Chen, X.L.; Zhong, W.Q.; Zhou, X.G. CFD-DEM simulation of particle transport and deposition in pulmonary airway. Powder Technol. 2012, 228, 309–318. [Google Scholar] [CrossRef]
- Zhao, T.; Dai, F.; Xu, N.W. Coupled DEM-CFD investigation on the formation of landslide dams in narrow rivers. Landslides 2017, 14, 189–201. [Google Scholar] [CrossRef]
- Zhao, T.; Houlsby, G.T.; Utili, S. Investigation of granular batch sedimentation via DEM-CFD coupling. Granul. Matter 2014, 16, 921–932. [Google Scholar] [CrossRef]
- Gou, D.Z.; An, X.Z.; Yang, X.H. CFD-DEM modeling on air impact densification of equal spheres: Structure evolution, dynamics, and mechanism. Powder Technol. 2017, 322, 177–184. [Google Scholar] [CrossRef]
- Mondal, S.; Wu, C.; Sharma, M.M. Coupled CFD-DEM simulation of hydrodynamic bridging at constrictions. Int. J. Multiph. Flow 2016, 84, 245–263. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Y.; Ren, N.X.; Shi, W. A coupled CFD-DEM simulation of upward seepage flow in coarse sands. Mar. Georesour. Geotech. 2018, 37, 589–598. [Google Scholar] [CrossRef]
- Shan, T.; Zhao, J.D. A coupled CFD-DEM analysis of granular flow impacting on a water reservoir. Acta Mech. 2014, 225, 2449–2470. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Liu, D.Y.; Zhuang, Y.M. CFD-DEM modeling of CO2 capture using Alkali Metal-based sorbents in a bubbling fluidized bed. Int. J. Chem. React. Eng. 2014, 12, 441–449. [Google Scholar] [CrossRef]
- Lim, E.W.C.; Zhang, Y.; Wang, C. Effects of an electrostatic field in pneumatic conveying of granular materials through inclined and vertical pipes. Chem. Eng. Sci. 2006, 61, 7889–7908. [Google Scholar] [CrossRef]
- Tang, Z.J.; Yu, L.M.; Wang, F.H. Effect of particle size and shape on separation in a hydrocyclone. Water 2019, 11, 16. [Google Scholar] [CrossRef]
- Shamy, U.E.; Zeghal, M. A micro-mechanical investigation of the dynamic response and liquefaction of saturated granular soils. Soil Dyn. Earthq. Eng. 2007, 27, 712–729. [Google Scholar] [CrossRef]
- Zhao, J.D.; Shan, T. Coupled CFD-DEM simulation of fluid-particle interaction in geomechanics. Powder Technol. 2013, 239, 248–258. [Google Scholar] [CrossRef]
- Mao, H.T.; Wang, X.J.; Wang, Z.C. Seepage of saturated coarse soil multi-scale coupling simulation with dynamic water level. Chin. J. Rock. Mech. Eng. 2018, 37, 3797–3804. [Google Scholar]
- Dai, X.; Zheng, G.; Cheng, X.S. Numerical simulation of ground movement induced by leakage of groundwater and sand in excavations based on the DEM-CFD method. Chin. J. Rock. Mech. Eng. 2019, 38, 396–408. [Google Scholar]
- Shamy, U.E.; Aydin, F. Multiscale Modeling of Flood-Induced Piping in River Levees. J. Geotech. Geoenviron. 2008, 134, 1385–1398. [Google Scholar] [CrossRef]
- Climent, N.; Arroyo, M.; O’Sullivan, C.; Gens, A. Sand production simulation coupling DEM with CFD. Eur. J. Environ. Civ. En. 2014, 18, 983–1008. [Google Scholar] [CrossRef]
- Ren, L.B. A Parallel CFD-DEM Coupling Model and Numerical Simulation of Dense Particulate Two-phase Flows. Ph.D. Thesis, Shandong Universe, Jinan, China, 2015. [Google Scholar]
- Shao, B.; Yan, Y.F.; Bi, C.F. Migration of irregular cuttings particles in big size by CFD-DEM coupled simulation model. Sci. Technol. Eng. 2017, 17, 190–195. [Google Scholar]
- Zhang, F.; Huang, H. Coupled DEM-CFD Modeling of Fluid Injection into Granular Media. Aquac. Res. 2011, 31, 481–483. [Google Scholar]
- Zhou, J.; Yao, Z.X.; Zhang, G. Mesomechanical simulation of seepage flow in sandy soil. Chin. J. Geotech. Eng. 2007, 29, 977–981. [Google Scholar]
- Katagiri, J.; Konno, Y.; Yoneda, J. Pore-scale modeling of flow in particle packs containing grain-coating and pore-filling hydrates: Verification of a Kozeny—Carman-based permeability reduction model. J. Nat. Gas Sci. Eng. 2017, 45, 537–551. [Google Scholar] [CrossRef]
- Al-Arkawazi, S.; Marie, C.; Benhabib, K. Modeling the hydrodynamic forces between fluid-granular medium by coupling DEM-CFD. Chem. Eng. Res. Des. 2017, 117, 439–447. [Google Scholar] [CrossRef]
- Boyce, C.M.; Ozel, A.; Kolehmainen, J. Analysis of the effect of small amounts of liquid on gas-solid fluidization using CFD-DEM simulations. AIChE J. 2017, 63, 5290–5302. [Google Scholar] [CrossRef]
- Chen, F.; Drumm, E.C.; Guiochon, G. Coupled discrete element and finite volume solution of two classical soil mechanics problems. Comput. Geotech. 2011, 38, 638–647. [Google Scholar] [CrossRef]
- Li, P.C. Studies on Mechanism of Hydraulic Hoist of Coarse Particle in Vertical Pipe. Ph.D. Thesis, Tsinghua University, Beijing, China, 2007. [Google Scholar]
- Wu, L. Simulation of Liquid-Solid Two-Phase Flow with Coarse Particles in Pipes. Master’s Thesis, Hangzhou Dianzi University, Hangzhou, China, 2010. [Google Scholar]
- Anderson, T.B.; Jackson, R. A fluid mechanical description of fluidized beds: Equations of motion. Ind. End. Chem. Fundam. 1967, 6, 527–539. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. PFC 5.0 Documentation; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2018. [Google Scholar]
- Shi, C.; Zhang, Q.; Wang, S.N. Numerical Simulation Technology and Application with Particle Flow Code (PFC5.0), 1st ed.; China Architecture & Building Press: Beijing, China, 2018; pp. 404–415. [Google Scholar]
- Felice, R.D. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Xu, B.H.; Yu, A.B. Numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics. Chem. Eng. Sci. 1997, 52, 2785–2809. [Google Scholar] [CrossRef]
- Komiwes, V.; Mege, P.; Meimon, Y. Simulation of granular flow in a fluid applied to sedimentation. Granul. Matter 2006, 8, 41–54. [Google Scholar] [CrossRef]
- Stokes, G.G. Mathematical and Physical Papers; Cambridge University Press: Cambridge, UK, 1901. [Google Scholar]
- Schiller, L.; Naumann, A. A drag coefficient correlation. Vdi Zeitung 1935, 77, 318–320. [Google Scholar]
- DallaValle, J.M. Micromeritics: The Technology of Fine Particles, 2nd ed.; Pitman Publishing Corp.: Chicago, IL, USA, 1948. [Google Scholar]
- Brown, P.; Lawler, D. Sphere drag and settling velocity revisited. J. Environ. Eng. 2003, 129, 222–231. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretized fluid flow equations by operator splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
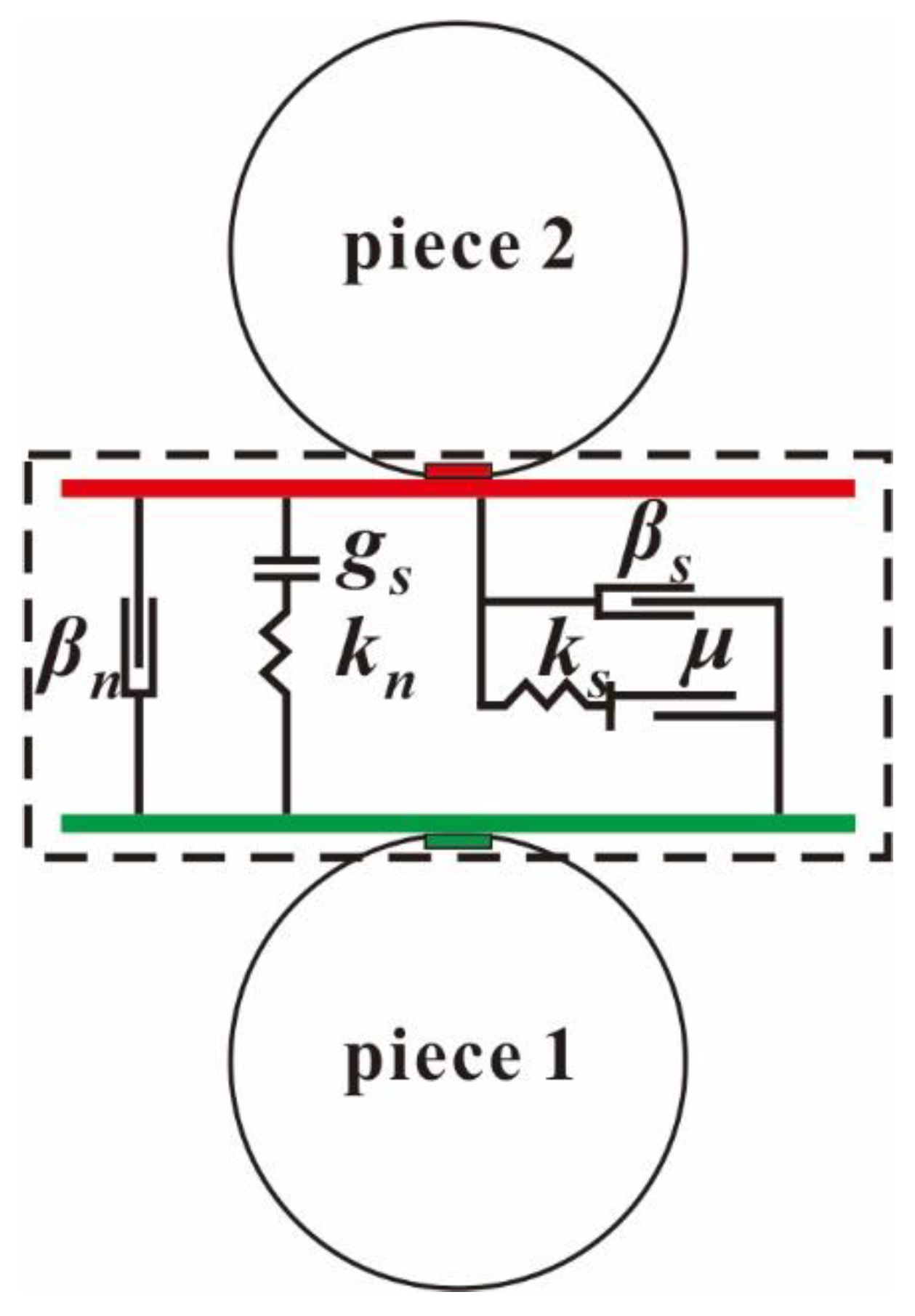

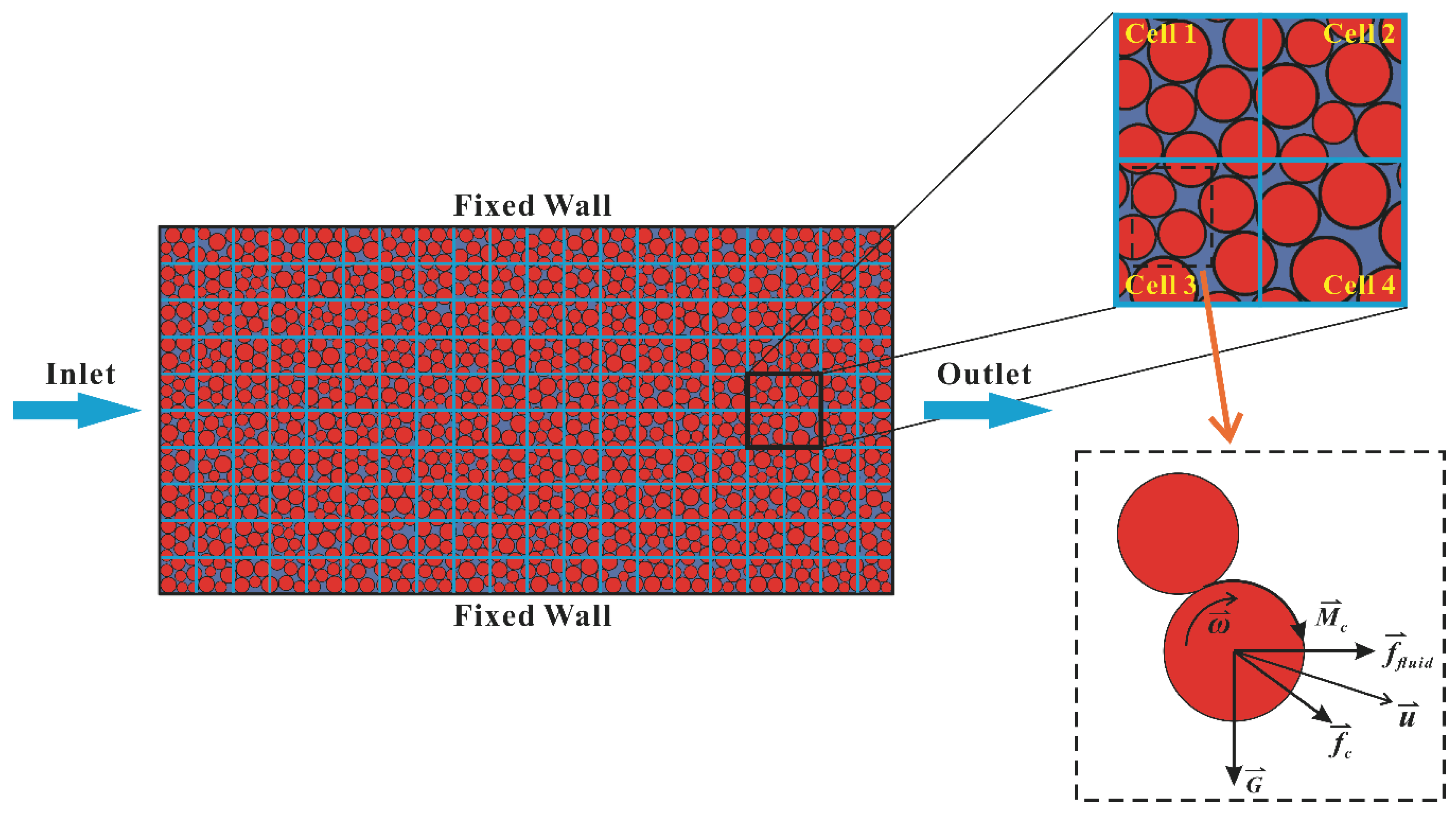
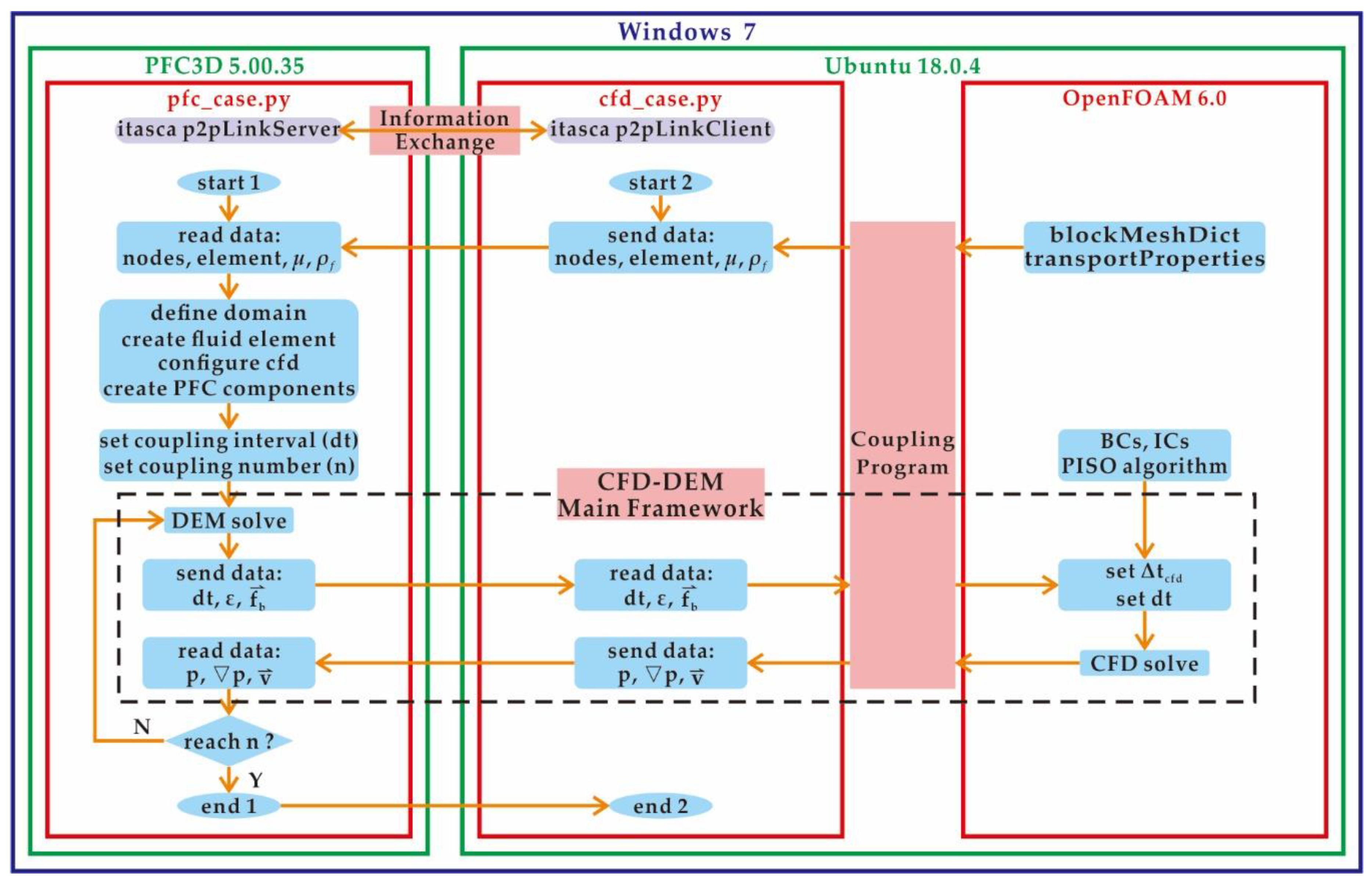
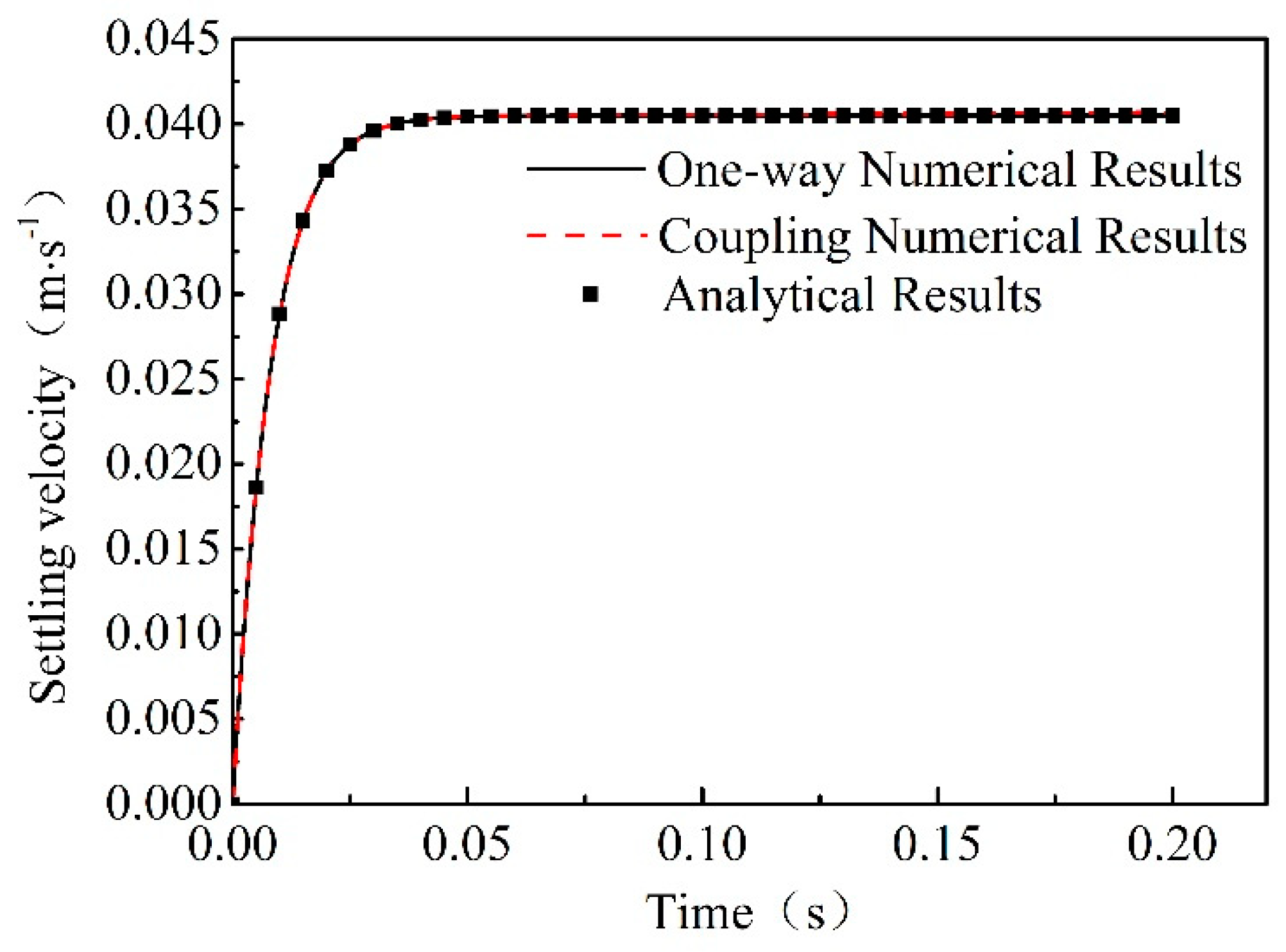




| Type | Specific Implementation Software | Practical Application |
|---|---|---|
| One commercial code | STAR CCM+ | Akhshik, S. [14] |
| Fluent | Ren, L.B. [31] | |
| Two commercial codes | Fluent-EDEM | Chen, X.L. [15,32] |
| CCFD-PFC3D | Hama, N. A. [13,33,34] | |
| COMSOL-PFC3D | Guo, Y. [3] | |
| One open source code and one commercial code | OpenFOAM-PFC3D | Katagiri, J. [35] |
| Code_Saturne 1-SIGRAME | Al-Arkawazi, S. [36] | |
| Two open source codes | OpenFOAM-LIGGGHTS | Ma, Z. [20,37] |
| OpenFOAM-YADE | Chen, F. [38] | |
| OpenFOAM-ESyS-Particle 2 | Zhao, T. [16,17] | |
| Programming language | C++ | Li, C.P. [39] |
| Fortune 77 | Wu, L. [40] |
| Name | Year | Correlation | |
|---|---|---|---|
| Newton [46] | 1687 | 0.44 | |
| Stokes [47] | 1880 | ||
| Schiller and Nauman [48] | 1935 | ||
| DallaValle [49] | 1948 | / | |
| Brown and Lawler [50] | 2003 | / | |
| Parameter | Value | ||||||
|---|---|---|---|---|---|---|---|
| Particle diameter (mm) | D2 | D4 | D6 | D8 | D10 | DP6 | |
| 2 | 4 | 6 | 8 | 10 | |||
| Particle density () | 2000 | ||||||
| Effective modulus (Pa) | |||||||
| Normal-to-shear stiffness ratio (-) | 2.0 | ||||||
| Particles friction coefficient (-, mm) | Sliding friction coefficient | Rolling friction coefficient | |||||
| 0.3 | 0.2 | ||||||
| Particle-wall friction coefficient (-, mm) | Sliding friction coefficient | Rolling friction coefficient | |||||
| 0.1 | 0.1 | ||||||
| Fluid density () | 1000 | ||||||
| Fluid dynamic viscosity () | 0.001 | ||||||
| DEM timestep (s) | |||||||
| CFD timestep (s) | |||||||
| Coupling interval (s) | 0.001 | ||||||
| Total simulation time (s) | 5.0, 1.0 | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Wang, G.; Jia, C.; Li, C. A Novel, Coupled CFD-DEM Model for the Flow Characteristics of Particles Inside a Pipe. Water 2019, 11, 2381. https://doi.org/10.3390/w11112381
Zhou H, Wang G, Jia C, Li C. A Novel, Coupled CFD-DEM Model for the Flow Characteristics of Particles Inside a Pipe. Water. 2019; 11(11):2381. https://doi.org/10.3390/w11112381
Chicago/Turabian StyleZhou, Haotong, Guihe Wang, Cangqin Jia, and Cheng Li. 2019. "A Novel, Coupled CFD-DEM Model for the Flow Characteristics of Particles Inside a Pipe" Water 11, no. 11: 2381. https://doi.org/10.3390/w11112381
APA StyleZhou, H., Wang, G., Jia, C., & Li, C. (2019). A Novel, Coupled CFD-DEM Model for the Flow Characteristics of Particles Inside a Pipe. Water, 11(11), 2381. https://doi.org/10.3390/w11112381




