Investigation of the Sloshing Behavior Due to Seismic Excitations Considering Two-Way Coupling of the Fluid and the Structure
Abstract
:1. Introduction
2. Numerical Models
2.1. Smoothed Particle Hydrodynamics
2.2. Finite Element Method
2.3. SPH-FEM Coupling
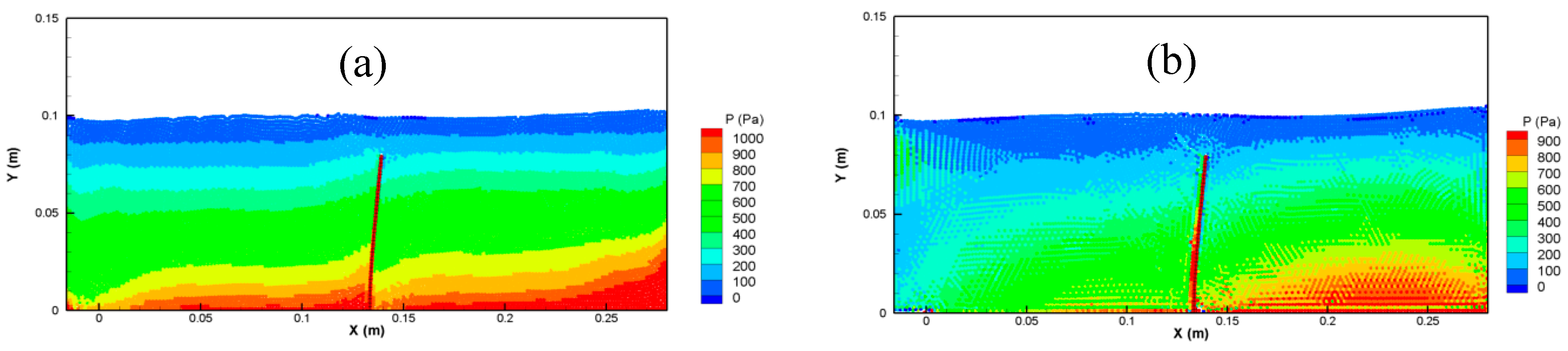
3. Numerical Results
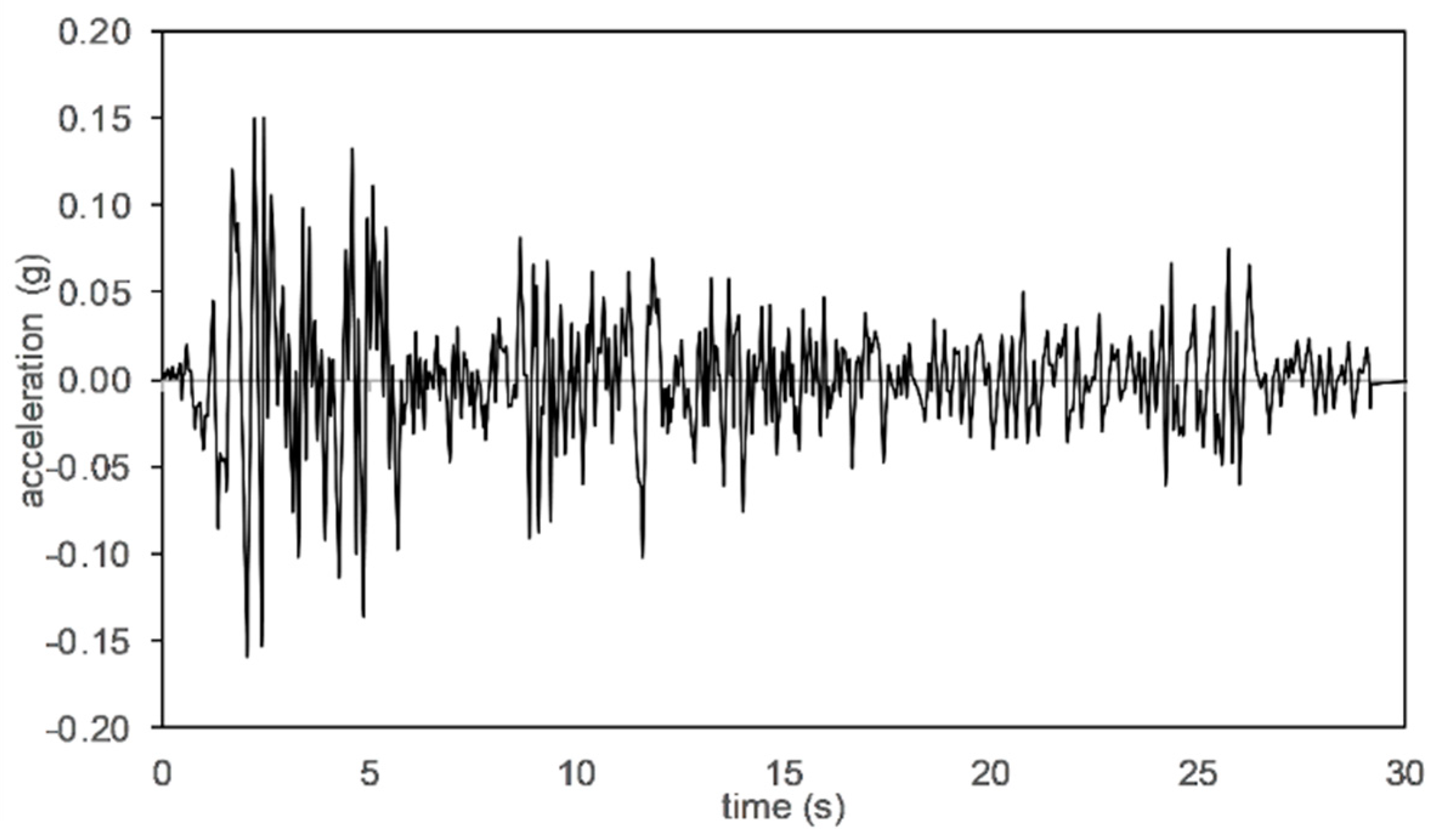
3.1. Near-Fault Type Excitation
3.2. Earthquake Excitation
4. Conclusions
Funding
Conflicts of Interest
References
- Stofan, A.J.; Sumner, I.E. Technical Note; Natl. Aeronaut. Sp. Adm. Ohio, Lowis Res. Center: Cleveland, OH, USA, 1963. [Google Scholar]
- Chiba, M. Nonlinear hydroelastic vibration of a cylindrical tank with an elastic bottom, containing liquid. Part I: Experiment. J. Fluids Struct. 1992, 6, 181–206. [Google Scholar] [CrossRef]
- Yalla, S.K.; Kareem, A.; Kantor, J.C. Semi-active tuned liquid column dampers for vibration control of structures. Eng. Struct. 2001, 23, 1469–1479. [Google Scholar] [CrossRef]
- Bredmose, H.; Brocchini, M.; Peregrine, D.H.; Thais, L. Experimental investigation and numerical modelling of steep forced water waves. J. Fluid Mech. 2003, 490, 217–249. [Google Scholar] [CrossRef]
- Akyildiz, H.; Ünal, E. Experimental investigation of pressure distribution on a rectangular tank due to the liquid sloshing. Ocean Eng. 2005, 32, 1503–1516. [Google Scholar] [CrossRef]
- Idelsohn, S.R.; Marti, J.; Souto-iglesias, A.; Oñate, E. Interaction between an elastic structure and free-surface flows: Experimental versus numerical comparisons using the PFEM. Comput. Mech. 2008, 43, 125–132. [Google Scholar] [CrossRef]
- Kim, Y. Numerical simulation of sloshing flows with impact load. Appl. Ocean Res. 2001, 23, 53–62. [Google Scholar] [CrossRef]
- Celebi, M.S.; Akyildiz, H. Nonlinear modeling of liquid sloshing in a moving rectangular tank. Ocean Eng. 2002, 29, 1527–1553. [Google Scholar] [CrossRef]
- Pal, P. Sloshing of Liquid in Partially Filled Container—An Experimental Study. Int. J. Recent Trends Eng. 2009, 1, 1–5. [Google Scholar]
- Chen, Y.; Xue, M.A. Numerical simulation of liquid sloshing with different filling levels using OpenFOAM and experimental validation. Water 2018, 10, 1752. [Google Scholar] [CrossRef] [Green Version]
- Serván-Camas, B.; Cercós-Pita, J.L.; Colom-Cobb, J.; García-Espinosa, J.; Souto-Iglesias, A. Time domain simulation of coupled sloshing–seakeeping problems by SPH–FEM coupling. Ocean Eng. 2016, 123, 383–396. [Google Scholar] [CrossRef] [Green Version]
- Hwang, S.C.; Park, J.C.; Gotoh, H.; Khayyer, A.; Kang, K.J. Numerical simulations of sloshing flows with elastic baffles by using a particle-based fluid-structure interaction analysis method. Ocean Eng. 2016, 118, 227–241. [Google Scholar] [CrossRef]
- Michael Isaacson, B.; Ryu, C.-S. Earthquake-Induced Sloshing in Vertical Container of Arbitrary Section. J. Eng. Mech. 1998, 124, 158–166. [Google Scholar] [CrossRef]
- Hernández-Barrios, H.; Heredia-Zavoni, E.; Aldama-Rodríguez, Á.A. Nonlinear sloshing response of cylindrical tanks subjected to earthquake ground motion. Eng. Struct. 2007, 29, 3364–3376. [Google Scholar] [CrossRef]
- Panigrahy, P.K.; Saha, U.K.; Maity, D. Experimental studies on sloshing behavior due to horizontal movement of liquids in baffled tanks. Ocean Eng. 2009, 36, 213–222. [Google Scholar] [CrossRef]
- Luo, H.; Zhang, R.; Weng, D. Mitigation of liquid sloshing in storage tanks by using a hybrid control method. Soil Dyn. Earthq. Eng. 2016, 90, 183–195. [Google Scholar] [CrossRef]
- Hashimoto, H.; Hata, Y.; Kawamura, K. Estimation of oil overflow due to sloshing from oil storage tanks subjected to a possible Nankai Trough earthquake in Osaka bay area. J. Loss Prev. Process Ind. 2017, 50, 337–346. [Google Scholar] [CrossRef]
- Cheng, X.; Cao, L.; Zhu, H. Liquid-solid Interaction Seismic Response of an Isolated Overground Rectangular Reinforced-concrete Liquid-storage Structure. J. Asian Archit. Build. Eng. 2015, 14, 175–180. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.-C.; Whittaker, A.; Coleman, J. Verification of a fluid-structure-interaction model for seismic analysis of Gen IV nuclear power plants. In Proceedings of the 11th National Conference in Earthquake Engineering, Earthquake Engineering Research Institute, Los Angeles, CA, USA, 25–29 June 2018. [Google Scholar]
- Waezi, Z.; Attari, N.K.A.; Rofooei, F.R. Controlling the seismic response of structures under near-field earthquakes with fluid/structure interaction of cylindrical liquid tanks. Eur. J. Environ. Civ. Eng. 2019, 23, 1–24. [Google Scholar] [CrossRef]
- Demir, A.; Dinçer, A.E. MPS ve FEM Tabanlı Akışkan-Yapı Etkileşimi Modelinin Çoruh Nehri Üzerindeki Ardıl Baraj-Yıkılma Problemine Uygulanması. Doğal Afetler ve Çevre Derg 2017, 90, 1–6. [Google Scholar] [CrossRef]
- Calderer, A.; Kang, S.; Sotiropoulos, F. Level set immersed boundary method for coupled simulation of air/water interaction with complex floating structures. J. Comput. Phys. 2014, 277, 201–227. [Google Scholar] [CrossRef] [Green Version]
- Pathak, A.; Raessi, M. A 3D, fully Eulerian, VOF-based solver to study the interaction between two fluids and moving rigid bodies using the fictitious domain method. J. Comput. Phys. 2016, 311, 87–113. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Currao, G.M.D.; Han, F.; Neely, A.J.; Young, J.; Tian, F.B. An immersed boundary method for fluid–structure interaction with compressible multiphase flows. J. Comput. Phys. 2017, 346, 131–151. [Google Scholar] [CrossRef] [Green Version]
- Nangia, N.; Patankar, N.A.; Bhalla, A.P.S. A DLM immersed boundary method based wave-structure interaction solver for high density ratio multiphase flows. arXiv 2019, arXiv:1901.07892. [Google Scholar] [CrossRef] [Green Version]
- Demir, A.; Dinçer, A.E.; Bozkus, Z.; Tijsseling, A.S. Numerical and experimental investigation of damping in a dam-break problem with fluid-structure interaction. J. Zhejiang Univ. Sci. A 2019, 20, 258–271. [Google Scholar] [CrossRef]
- Dinçer, A.E.; Demir, A.; Bozkus, Z.; Tijsseling, A.S. Fully Coupled Smoothed Particle Hydrodynamics-Finite Element Method Approach for Fluid-Structure Interaction Problems With Large Deflections. J. Fluids Eng. Trans. ASME 2019, 141, 1–13. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Dinçer, A.E. Numerical Investigation of Free Surface and Pipe Flow Problems by Smoothed Particle Hydrodynamics. Ph. D. Thesis, Middle East Technical University, Ankara, Turkey, 2017. [Google Scholar]
- Dinçer, A.E.; Bozkuş, Z.; Tijsseling, A.S. Prediction of Pressure Variation at an Elbow Subsequent to a Liquid Slug Impact by Using Smoothed Particle Hydrodynamics. J. Press. Vessel Technol. Trans. ASME 2018, 140, 031303. [Google Scholar] [CrossRef]
- Dinçer, A.E.; Bozkuş, Z.; Şahin, A.N. Effect of downstream channel slope on numerical modelling of dam break induced flows. In Proceedings of the Sustainable Hydraulics in the Era of Global Change—Proceedings of the 4th European Congress of the International Association of Hydroenvironment engineering and Research, IAHR, Granada, Spain, 4–9 July 2016. [Google Scholar]
- Attaway, S.W.; Heinstein, M.W.; Swegle, J.W. Coupling of smooth particle hydrodynamics with the finite element method. Nucl. Eng. Des. 1994, 150, 199–205. [Google Scholar] [CrossRef]
- Johnson, G.R. Linking of Lagrangian particle methods to standard finite element methods for high velocity impact computations. Nucl. Eng. Des. 1994, 150, 265–274. [Google Scholar] [CrossRef]
- Johnson, G.R.; Beissel, S.R. Normalized smoothing functions for sph impact computations. Int. J. Numer. Methods Eng. 1996, 39, 2725–2741. [Google Scholar] [CrossRef]
- De Vuyst, T.; Vignjevic, R.; Campbell, J.C. Coupling between meshless and finite element methods. Int. J. Impact Eng. 2005, 31, 1054–1064. [Google Scholar] [CrossRef]
- Fernández-Méndez, S.; Bonet, J.; Huerta, A. Continuous blending of SPH with finite elements. Comput. Struct. 2005, 83, 1448–1458. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Qiang, H.; Gao, W. Coupling of smoothed particle hydrodynamics and finite element method for impact dynamics simulation. Eng. Struct. 2010, 33, 255–264. [Google Scholar] [CrossRef]
- Hu, D.; Long, T.; Xiao, Y.; Han, X.; Gu, Y. Fluid-structure interaction analysis by coupled FE-SPH model based on a novel searching algorithm. Comput. Methods Appl. Mech. Eng. 2014, 276, 266–286. [Google Scholar] [CrossRef] [Green Version]
- Fourey, G.; Hermange, C.; Le Touzé, D.; Oger, G. An efficient FSI coupling strategy between Smoothed Particle Hydrodynamics and Finite Element methods. Comput. Phys. Commun. 2017, 217, 66–81. [Google Scholar] [CrossRef]
- Long, T.; Hu, D.; Wan, D.; Zhuang, C.; Yang, G. An arbitrary boundary with ghost particles incorporated in coupled FEM–SPH model for FSI problems. J. Comput. Phys. 2017, 350, 166–183. [Google Scholar] [CrossRef]
- Liu, G.; Liu, M.B. Smoothed Particle Hydrodynamics: A Mesh-Free Particle Method; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2003; ISBN 981-238-456-1. [Google Scholar]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Shao, J.R.; Li, H.Q.; Liu, G.R.; Liu, M.B. An improved SPH method for modeling liquid sloshing dynamics. Comput. Struct. 2012, 100, 18–26. [Google Scholar] [CrossRef] [Green Version]
- Randles, P.W.; Libersky, L.D. Smoothed Particle Hydrodynamics: Some recent improvements and applications. Comput. Methods Appl. Mech. Engrg. 1996, 7825, 375–408. [Google Scholar] [CrossRef]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling Low Reynolds Number Incompressible Flows Using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Anderson, J.D. Computational Fluid Dynamics: The Basics with Applications; McGraw-Hill: New York, NY, USA, 1995. [Google Scholar]
- Monaghan, J.J.; Kos, A. Solitary Waves on a Cretan Beach. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 145–155. [Google Scholar] [CrossRef]
- Bathe, K.-J. Finite Element Procedures; Prentice Hall, Pearson Education, Inc: Watertown, NY, USA, 2006; ISBN 9780979004957. [Google Scholar]
- Wilson, E.L. Three-Dimensional Static and Dynamic Analysis of Structures; Computers and Structures: Berkeley, CA, USA, 2002; Volume 90, ISBN 0923907009. [Google Scholar]
- Zhang, S.; Wang, G. Effects of near-fault and far-fault ground motions on nonlinear dynamic response and seismic damage of concrete gravity dams. Soil Dyn. Earthq. Eng. 2013, 53, 217–229. [Google Scholar] [CrossRef]
- Liao, W.I.; Loh, C.H.; Lee, B.H. Comparison of dynamic response of isolated and non-isolated continuous girder bridges subjected to near-fault ground motions. Eng. Struct. 2004, 26, 2173–2183. [Google Scholar] [CrossRef]

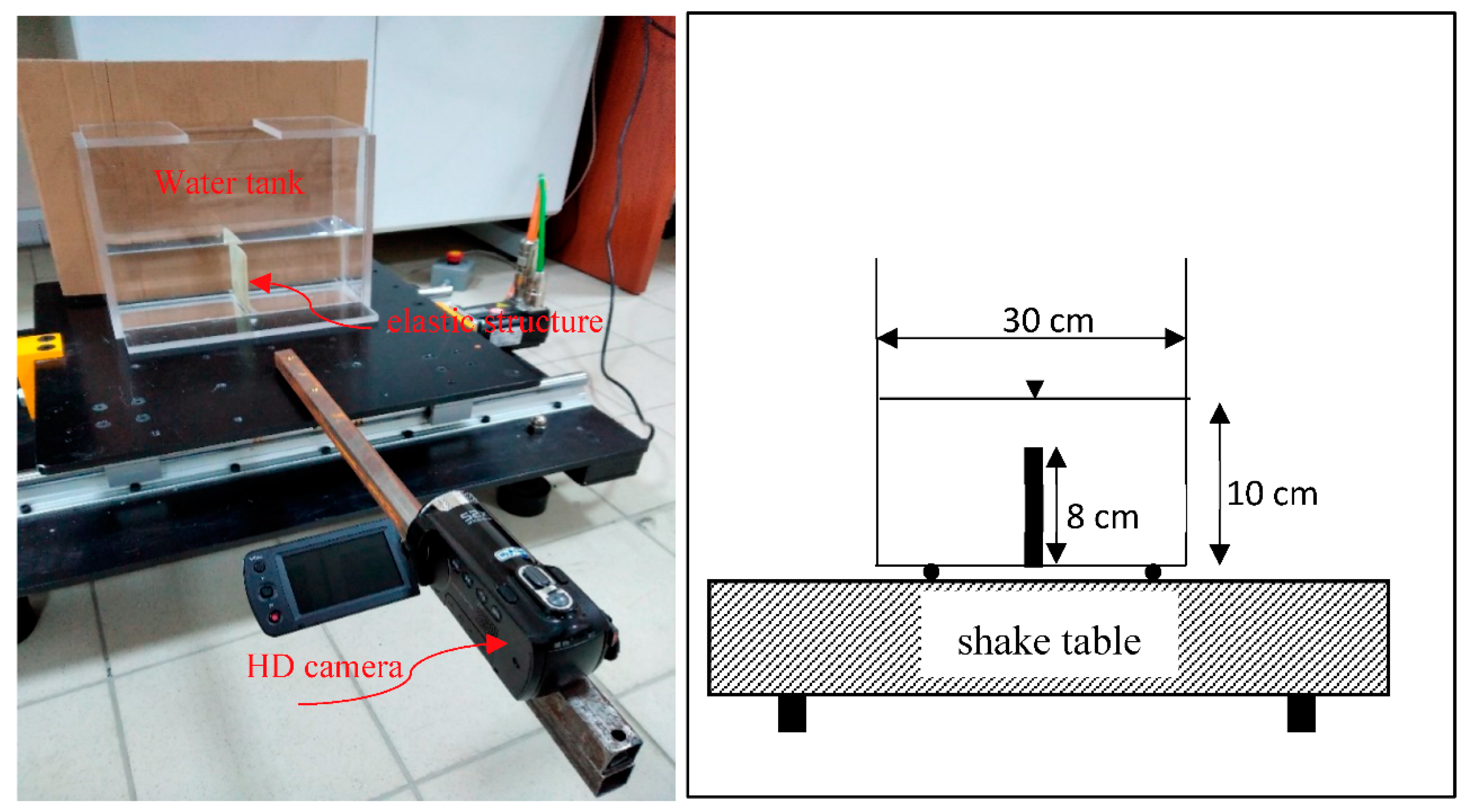











| The height of the plate (cm) | 8.0 |
| The width of the plate (cm) | 0.3 |
| Modulus of elasticity of the plate (MPa) | 10.0 |
| The initial distance between SPH particles (cm) | 0.15 |
| Max. time step (s) | 0.000016 |
| The number of SPH particles | 13,146 |
| The number of finite elements | 120 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dinçer, A.E. Investigation of the Sloshing Behavior Due to Seismic Excitations Considering Two-Way Coupling of the Fluid and the Structure. Water 2019, 11, 2664. https://doi.org/10.3390/w11122664
Dinçer AE. Investigation of the Sloshing Behavior Due to Seismic Excitations Considering Two-Way Coupling of the Fluid and the Structure. Water. 2019; 11(12):2664. https://doi.org/10.3390/w11122664
Chicago/Turabian StyleDinçer, A. Ersin. 2019. "Investigation of the Sloshing Behavior Due to Seismic Excitations Considering Two-Way Coupling of the Fluid and the Structure" Water 11, no. 12: 2664. https://doi.org/10.3390/w11122664
APA StyleDinçer, A. E. (2019). Investigation of the Sloshing Behavior Due to Seismic Excitations Considering Two-Way Coupling of the Fluid and the Structure. Water, 11(12), 2664. https://doi.org/10.3390/w11122664





