Investigation of Flow, Erosion, and Sedimentation Pattern around Varied Groynes under Different Hydraulic and Geometric Conditions: A Numerical Study
Abstract
:1. Introduction
2. Governing Equations
3. Numerical Simulation and Validation
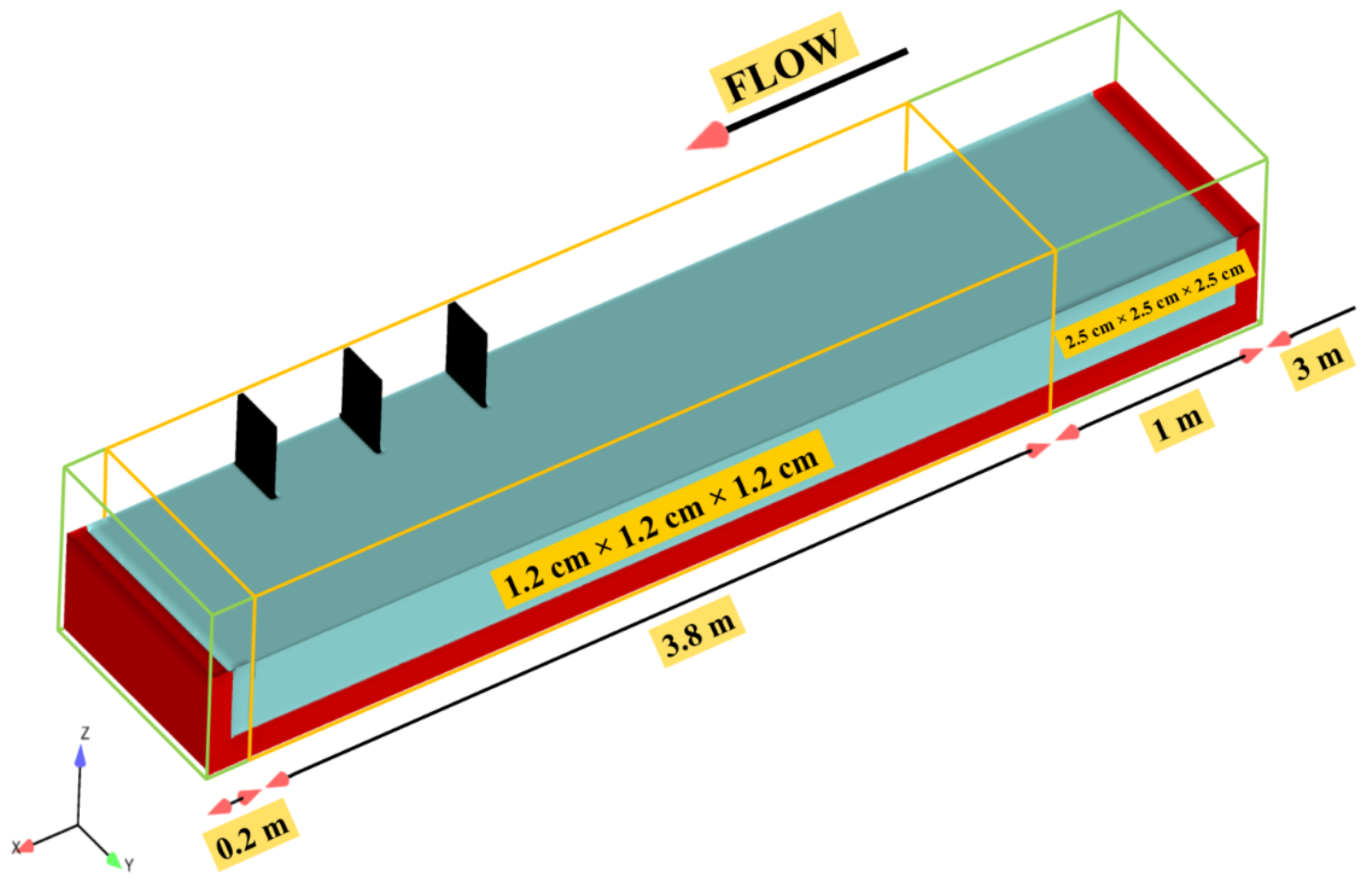
3.1. Laboratory Experiment
3.2. Numerical Setup
3.3. Data Validation
3.4. Numerical Simulations Description of Groynes with Different Length and Orientations
4. Results
5. Discussion
6. Conclusions
- -
- When groynes are arranged in an ascending order, more than 50% of scour occurs within 10% of the simulation time, while in a descending order, more than 70% of the scour occurred within a similar time.
- -
- Simulations with an orientation close to 90° had longer sediment scour equilibrium time.
- -
- Simulations with an ascending order have larger vortices after the third groyne than those of descending arrangement.
- -
- Under groynes of 135° with descending arrangement (first groyne: 40 cm; second groyne: 30 cm; third groyne: 20 cm), some small vortices are produced around the groynes.
- -
- Maximum deposition height when groynes are arranged in an ascending order is higher than in the reverse direction
- -
- An ascending arrangement produces a sediment line, contrary to a descending orientation
- -
- Arranging groynes in a descending order could reduce the maximum scour depth by 55%, and ascending arrangement by up to 72%.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zaid, B.A.; Tait, S. Development of Design Guidelines for Shallow Groynes; Technische Universität Carolo-Wilhelmina zu Braunschweig: Braunschweig, Germany. [CrossRef]
- Vaghefi, M.; Radan, P.; Akbari, M. Flow pattern around attractive, vertical, and repelling t-shaped spur dikes in a mild bend using cfd modeling. Int. J. Civ. Eng. 2018, 1–11. [Google Scholar] [CrossRef]
- Zaid, B.A.; Nardone, P.; Nones, M.; Gerstgraser, C.; Koll, K. Morphodynamic Effects of Stone and Wooden Groynes in a Restored River Reach. In Proceedings of the River Flow 2018-Ninth International Conference on Fluvial Hydraulics, Lyon-Villeurbanne, France, 5–8 September 2018. [Google Scholar]
- Uijttewaal, W.S. Effects of groyne layout on the flow in groyne fields: Laboratory experiments. J. Hydraul. Eng. 2005, 131, 782–791. [Google Scholar] [CrossRef]
- Garde, R.J.; Subramanya, K.S.; Nambudripad, K.D. Study of scour around spur-dikes. J. Hydraul. Div. 1961, 87, 23–37. [Google Scholar]
- Melville, B.W. Local scour at bridge abutments. J. Hydraul. Eng. 1992, 118, 615–631. [Google Scholar] [CrossRef]
- Saneie, M. Experimental Study on Effect of Minor Spur Dike to Reduce Main Spur Dike Scouring; The Food and Agriculture Organization (FAO): Rome, Italy, 2006; pp. 196–200. [Google Scholar]
- Zhang, H.; Nakagawa, H. Characteristics of local flow and bed deformation at impermeable and permeable spur dykes. Annu. J. Hydraul. Eng. 2009, 53, 145–150. [Google Scholar]
- Ghodsian, M.; Vaghefi, M. Experimental study on scour and flow field in a scour hole around a t-shape spur dike in a 90° bend. Int. J. Sediment Res. 2009, 24, 145–158. [Google Scholar] [CrossRef]
- Al-Khateeb, H.M.M.; AL-Thamiry, H.A.K.; Hassan, H.H. Evaluation of local scour development around curved non-submerged impermeable groynes. Int. J. Sci. Technol. Res. 2016, 5, 83–89. [Google Scholar]
- Radan, P.; Vaghefi, M. Flow and scour pattern around submerged and non-submerged t-shaped spur dikes in a 90° bend using the ssiim model. Int. J. River Basin Manag. 2016, 14, 219–232. [Google Scholar] [CrossRef]
- Gualtieri, C. Numerical Simulation of Flow Patterns and Mass Exchange Processes in Dead Zones. In Proceedings of the 4th International Congress on Environmental Modelling and Software, Barcelona, Spain, 6–10 July 2008. [Google Scholar]
- Uijttewaal, W.S.J.; Lehmann, D.; Mazijk, A.V. Exchange processes between a river and its groyne fields: Model experiments. J. Hydraul. Eng. ASCE 2001, 127, 928–936. [Google Scholar] [CrossRef]
- Karami, H.; Basser, H.; Ardeshir, A.; Hosseini, S.H. Verification of numerical study of scour around spur dikes using experimental data. Water Environ. J. 2014, 28, 124–134. [Google Scholar] [CrossRef]
- Acharya, A.; Duan, J.G. Three dimensional simulation of flow field around series of spur dikes. In Proceedings of the World Environmental and Water Resources Congress 2011, Palm Springs, CA, USA, 22–26 May 2011. [Google Scholar]
- Koken, M.; Gogus, M. Effect of spur dike length on the horseshoe vortex system and the bed shear stress distribution. J. Hydraul. Res. 2015, 53, 196–206. [Google Scholar] [CrossRef]
- McCoy, A.; Constantinescu, G.; Weber, L.J. Numerical investigation of flow hydrodynamics in a channel with a series of groynes. J. Hydraul. Eng. 2008, 134, 157–172. [Google Scholar] [CrossRef]
- Yossef, M.F.M.; Vriend, H.J.D. Sediment exchange between a river and its groyne fields: Mobile-bed experiment. J. Hydraul. Eng. ASCE 2010, 136, 610–625. [Google Scholar] [CrossRef]
- Ning, J.; Li, G.D.; Ma, M. 3D Numerical Simulation for Flow and Local Scour Around Spur Dike. In Proceedings of the IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017. [Google Scholar]
- Abdulmajid, M.; Mohammad, H.; Javad, A. Effect of changes in the hydraulic conditions on the velocity distribution around a l-shaped spur dike at the river bend using flow-3d model. Tech. J. Eng. Appl. Sci. 2013, 3, 1862–1868. [Google Scholar]
- Vaghefi, M.; Ahmadi, A.; Faraji, B. The effect of support structure on flow patterns around t-shape spur dike in 90° bend channel. Arab. J. Sci. Eng. 2015, 40, 1299–1307. [Google Scholar] [CrossRef]
- Giglou, A.N.; McCorquodale, J.A.; Solari, L. Numerical study on the effect of the spur dikes on sedimentation pattern. Ain Shams Eng. J. 2017, 9, 2057–2066. [Google Scholar] [CrossRef]
- Flow Science. Flow-3d User Manual: V10.1; Flow Science, Inc.: Santa Fe, NM, USA, 2012. [Google Scholar]
- Gualtieri, C.; Angeloudis, A.; Bombardelli, F.; Jha, S.; Stoesser, T. On the values for the turbulent schmidt number in environmental flows. Fluids 2017, 2, 17. [Google Scholar] [CrossRef]
- van Rijn, L.C. Mathematical Modelling of Morphological Processes in the Case of Suspended Sediment Transport; Delft University of Technology: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Dodaro, G.; Tafarojnoruz, A.; Sciortino, G.; Adduce, C.; Calomino, F.; Gaudio, R. Modified einstein sediment transport method to simulate the local scour evolution downstream of a rigid bed. J. Hydraul. Eng. 2016, 142, 04016041. [Google Scholar] [CrossRef]
- Dodaro, G.; Tafarojnoruz, A.; Stefanucci, F.; Adduce, C.; Calomino, F.; Gaudio, R.; Sciortino, G. An experimental and numerical study on the spatial and temporal evolution of a scour hole downstream of a rigid bed. In Proceedings of the International Conference on Fluvial Hydraulics, River Flow, Lausanne, Switzerland, 3–5 September 2014; pp. 3–5. [Google Scholar]
- Zhang, H. Study on Flow and Bed Deformation in Channels with Spur Dike; Kyoto University: Kyoto, Japan, 2005. [Google Scholar]
- Gisonni, C.; Hager, W.H.; Unger, J. Spurs in river engineering—A preliminary study. In Proceedings of the 31 IAHR Congress, Seoul, Korea, 11–17 September 2005; pp. 1894–1901. [Google Scholar]
- Chiew, Y.M. Scour protection at bridge piers. J. Hydraul. Eng. 1992, 118, 1260–1269. [Google Scholar] [CrossRef]
- Jahangirzadeh, A.; Basser, H.; Akib, S.; Karami, H.; Naji, S.; Shamshirband, S. Experimental and numerical investigation of the effect of different shapes of collars on the reduction of scour around a single bridge pier. PLoS ONE 2014, 9, e98592. [Google Scholar] [CrossRef] [PubMed]
- Calomino, F.; Tafarojnoruz, A.; Marchis, M.D.; Gaudio, R.; Napoli, E. Experimental and numerical study on the flow field and friction factor in a pressurized corrugated pipe. J. Hydraul. Eng. 2015, 141, 04015027. [Google Scholar] [CrossRef]
- Calomino, F.; Alfonsi, G.; Gaudio, R.; D’Ippolito, A.; Lauria, A.; Tafarojnoruz, A.; Artese, S. Experimental and numerical study of free-surface flows in a corrugated pipe. Water 2018, 10, 638. [Google Scholar] [CrossRef]














| Test Number. | Q (m3/s) | Y (m) | U (m/s) | U/Ucr | Fr | ds1 (m) | ds2 (m) | ds3 (m) | V (m3) |
|---|---|---|---|---|---|---|---|---|---|
| E1 | 0.035 | 0.150 | 0.233 | 0.650 | 0.190 | 0.156 | 0.000 | 0.026 | 0.0165 |
| Test Number | Coarser Mesh Size (m) | Finer Mesh Size (m) | Total Number of Cells | Numerical Simulation | Laboratory Experiment | Computational Time (hour) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| ds1 (m) | ds2 (m) | ds3 (m) | ds1 (m) | ds2 (m) | ds3 (m) | |||||
| 1 | 0.030 | 0.020 | 395880 | 0.091 | 0.016 | 0.020 | 0.156 | 0.000 | 0.026 | 71 |
| 2 | 0.025 | 0.012 | 1507550 | 0.133 | 0.005 | 0.023 | 0.156 | 0.000 | 0.026 | 146 |
| Cross Section | FLOW-3D | SSIIM 2.0 | FLOW-3D | SSIIM 2.0 |
|---|---|---|---|---|
| * R2 | R2 | ** RMSE | RMSE | |
| X = 5.65m | 0.776 | 0.790 | 0.031 | 0.022 |
| X = 5.95m | 0.960 | 0.970 | 0.055 | 0.019 |
| X = 6.16m | 0.428 | 0.157 | 0.117 | 0.078 |
| X = 6.41m | 0.819 | 0.858 | 0.071 | 0.066 |
| X = 6.66m | 0.897 | 0.967 | 0.038 | 0.051 |
| ds3(m) | ds2(m) | ds1(m) | |
|---|---|---|---|
| Experimental | 0.026 | 0.0 | 0.156 |
| FLOW-3D | 0.023 | 0.005 | 0.133 |
| Simulation Number. | Simulation Description | Groynes Orientation (with Respect to Flow Direction) in (°) | First Groyne Length (cm) | Second Groyne Length (cm) | Third Groyne Length (cm) | Constriction Ratio (%) |
|---|---|---|---|---|---|---|
| 1 | 90D.30.30.30 | 90 | 30 | 30 | 30 | 30 |
| 2 | 45D.20.30.40 | 45 | 20 | 30 | 40 | 28 |
| 3 | 60D.20.30.40 | 60 | 20 | 30 | 40 | 35 |
| 4 | 75D.20.30.40 | 75 | 20 | 30 | 40 | 37 |
| 5 | 90D.20.30.40 | 90 | 20 | 30 | 40 | 40 |
| 6 | 105D.20.30.40 | 105 | 20 | 30 | 40 | 37 |
| 7 | 120D.20.30.40 | 120 | 20 | 30 | 40 | 35 |
| 8 | 135D.20.30.40 | 135 | 20 | 30 | 40 | 28 |
| 9 | 45D.40.30.20 | 45 | 40 | 30 | 20 | 28 |
| 10 | 60D.40.30.20 | 60 | 40 | 30 | 20 | 35 |
| 11 | 75D.40.30.20 | 75 | 40 | 30 | 20 | 37 |
| 12 | 90D.40.30.20 | 90 | 40 | 30 | 20 | 40 |
| 13 | 105D.40.30.20 | 105 | 40 | 30 | 20 | 37 |
| 14 | 120D.40.30.20 | 120 | 40 | 30 | 20 | 35 |
| 15 | 135D.40.30.20 | 135 | 40 | 30 | 20 | 28 |
| Simulation Number. | Simulation Description | Maximum Scour Depth (cm) | Maximum Scour Depth (cm) | Maximum Deposition Depth (cm) | ||
|---|---|---|---|---|---|---|
| S | First Groyne | Second Groyne | Third Groyne | |||
| 1 | 90D.30.30.30 | 17.2 | 2.78 | 4.61 | 17.2 | 5.80 |
| 2 | 45D.20.30.40 | 5.96 | 4.27 | 5.42 | 5.96 | 2.19 |
| 3 | 60D.20.30.40 | 7.00 | 4.77 | 6.96 | 7.00 | 2.51 |
| 4 | 75D.20.30.40 | 8.20 | 4.48 | 7.51 | 8.20 | 2.22 |
| 5 | 90D.20.30.40 | 10.90 | 4.77 | 6.15 | 10.90 | 3.00 |
| 6 | 105D.20.30.40 | 9.70 | 3.79 | 6.82 | 9.70 | 1.95 |
| 7 | 120D.20.30.40 | 7.30 | 2.68 | 5.96 | 7.30 | 2.96 |
| 8 | 135D.20.30.40 | 4.77 | 2.08 | 3.66 | 4.77 | 1.67 |
| 9 | 45D.40.30.20 | 7.70 | 2.41 | 2.50 | 7.70 | 2.93 |
| 10 | 60D.40.30.20 | 10.20 | 2.12 | 2.51 | 10.20 | 3.73 |
| 11 | 75D.40.30.20 | 12.40 | 0.35 | 2.37 | 12.40 | 5.39 |
| 12 | 90D.40.30.20 | 15.30 | 0.10 | 1.90 | 15.30 | 4.53 |
| 13 | 105D.40.30.20 | 12.80 | −0.10 | 2.56 | 12.80 | 4.23 |
| 14 | 120D.40.30.20 | 11.20 | 0.00 | 1.72 | 11.20 | 4.59 |
| 15 | 135D.40.30.20 | 9.20 | 0.65 | 1.80 | 9.20 | 2.26 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choufu, L.; Abbasi, S.; Pourshahbaz, H.; Taghvaei, P.; Tfwala, S. Investigation of Flow, Erosion, and Sedimentation Pattern around Varied Groynes under Different Hydraulic and Geometric Conditions: A Numerical Study. Water 2019, 11, 235. https://doi.org/10.3390/w11020235
Choufu L, Abbasi S, Pourshahbaz H, Taghvaei P, Tfwala S. Investigation of Flow, Erosion, and Sedimentation Pattern around Varied Groynes under Different Hydraulic and Geometric Conditions: A Numerical Study. Water. 2019; 11(2):235. https://doi.org/10.3390/w11020235
Chicago/Turabian StyleChoufu, Liang, Saeed Abbasi, Hanif Pourshahbaz, Poorya Taghvaei, and Samkele Tfwala. 2019. "Investigation of Flow, Erosion, and Sedimentation Pattern around Varied Groynes under Different Hydraulic and Geometric Conditions: A Numerical Study" Water 11, no. 2: 235. https://doi.org/10.3390/w11020235
APA StyleChoufu, L., Abbasi, S., Pourshahbaz, H., Taghvaei, P., & Tfwala, S. (2019). Investigation of Flow, Erosion, and Sedimentation Pattern around Varied Groynes under Different Hydraulic and Geometric Conditions: A Numerical Study. Water, 11(2), 235. https://doi.org/10.3390/w11020235






