2D PIV Measurement of Twin Buoyant Jets in Wavy Cross-Flow Environment
Abstract
:1. Introduction
2. Materials and Methods
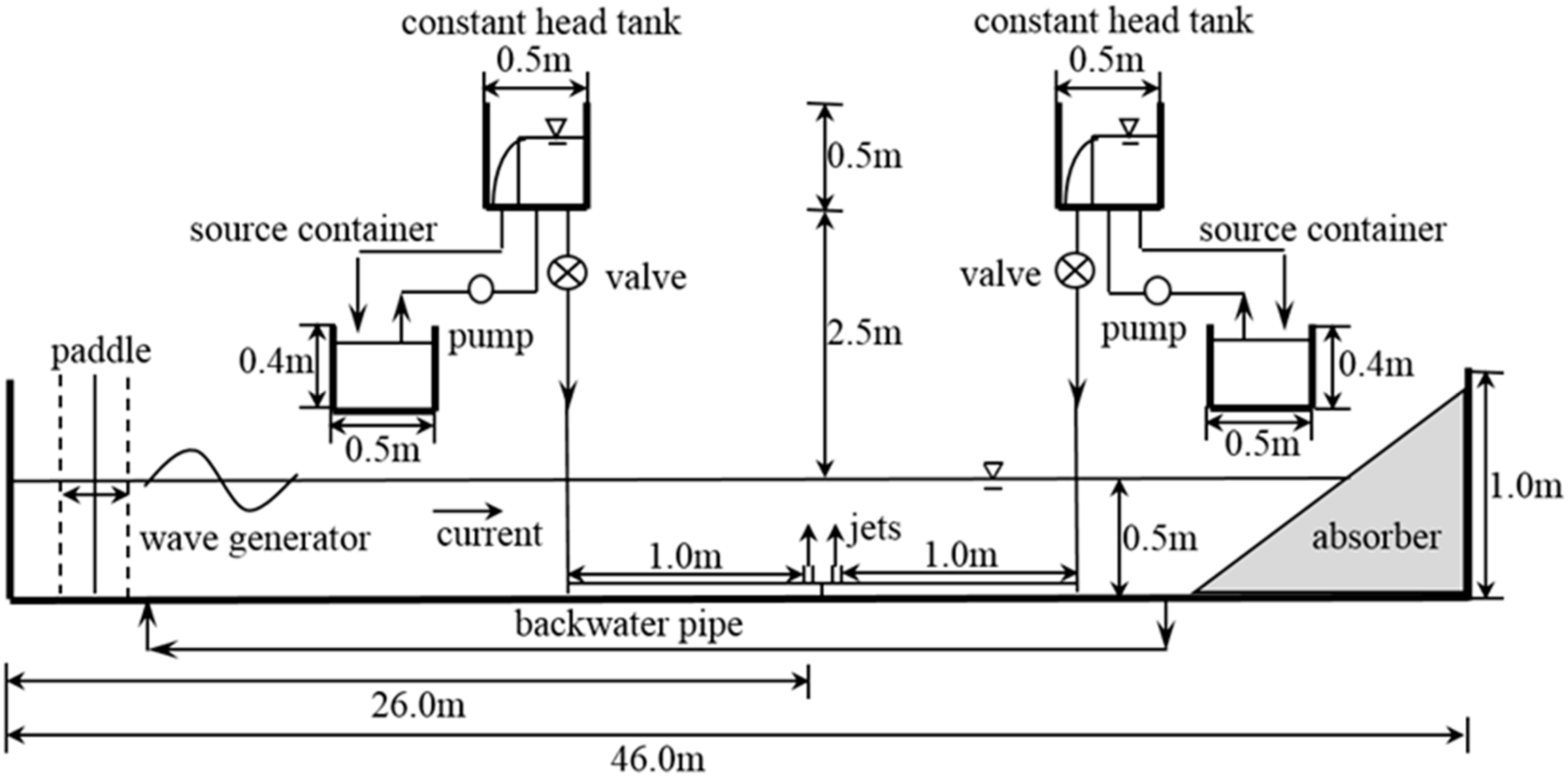
2.1. Experimental Setup
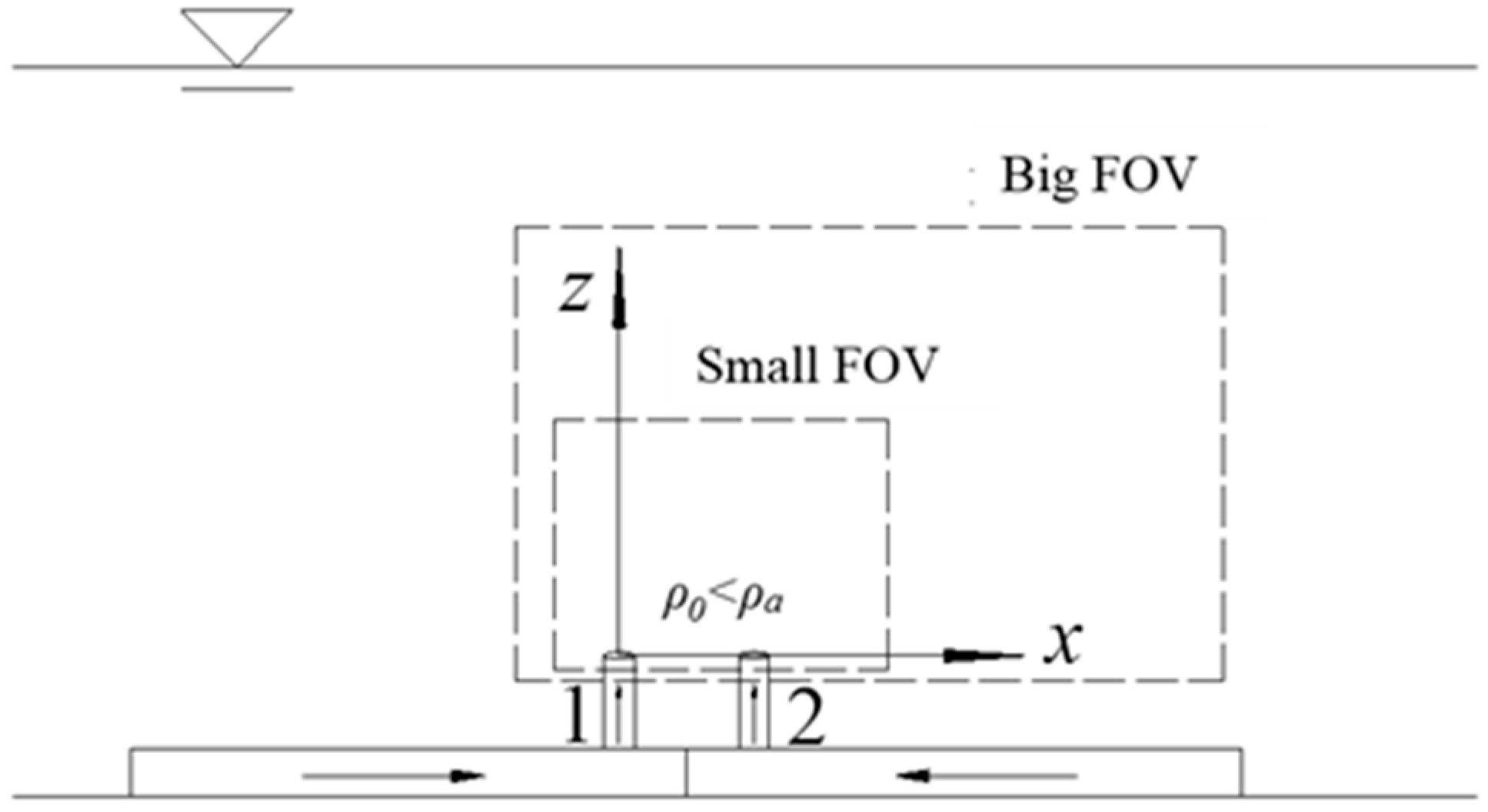
2.2. PIV Measurements
2.3. Experimental Cases
3. Results and Discussion
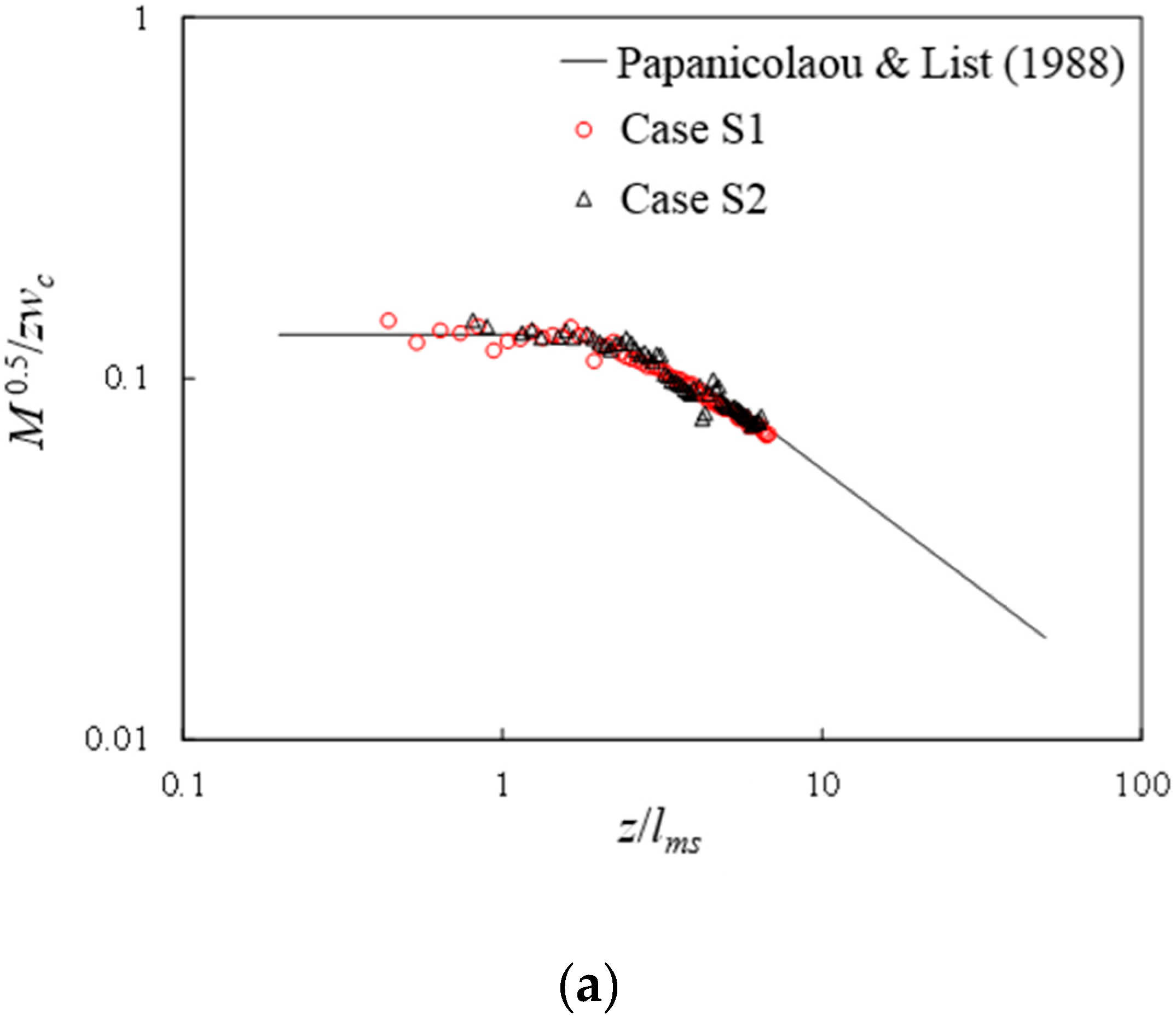
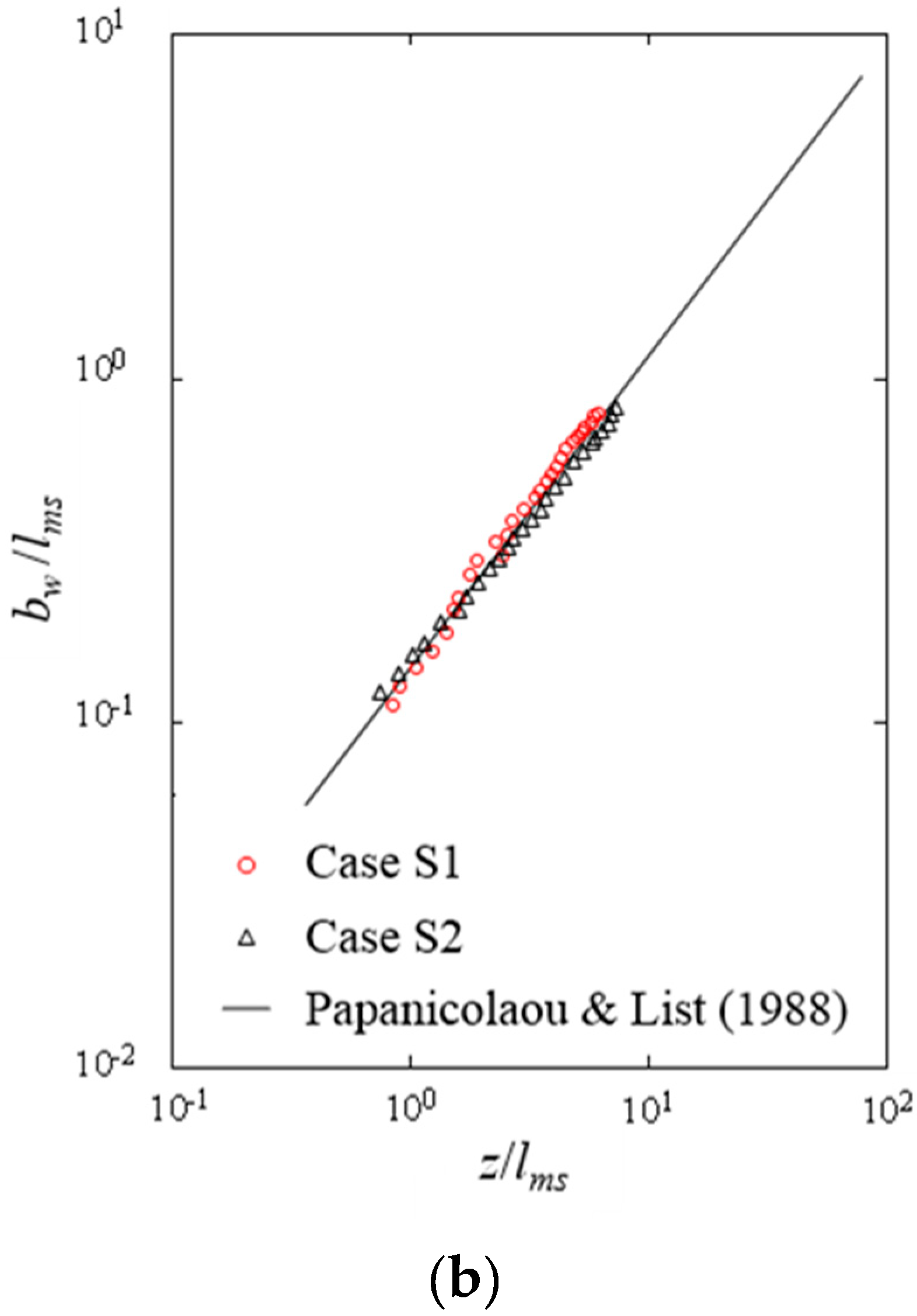
3.1. Single Buoyant Jet in Stagnant Water
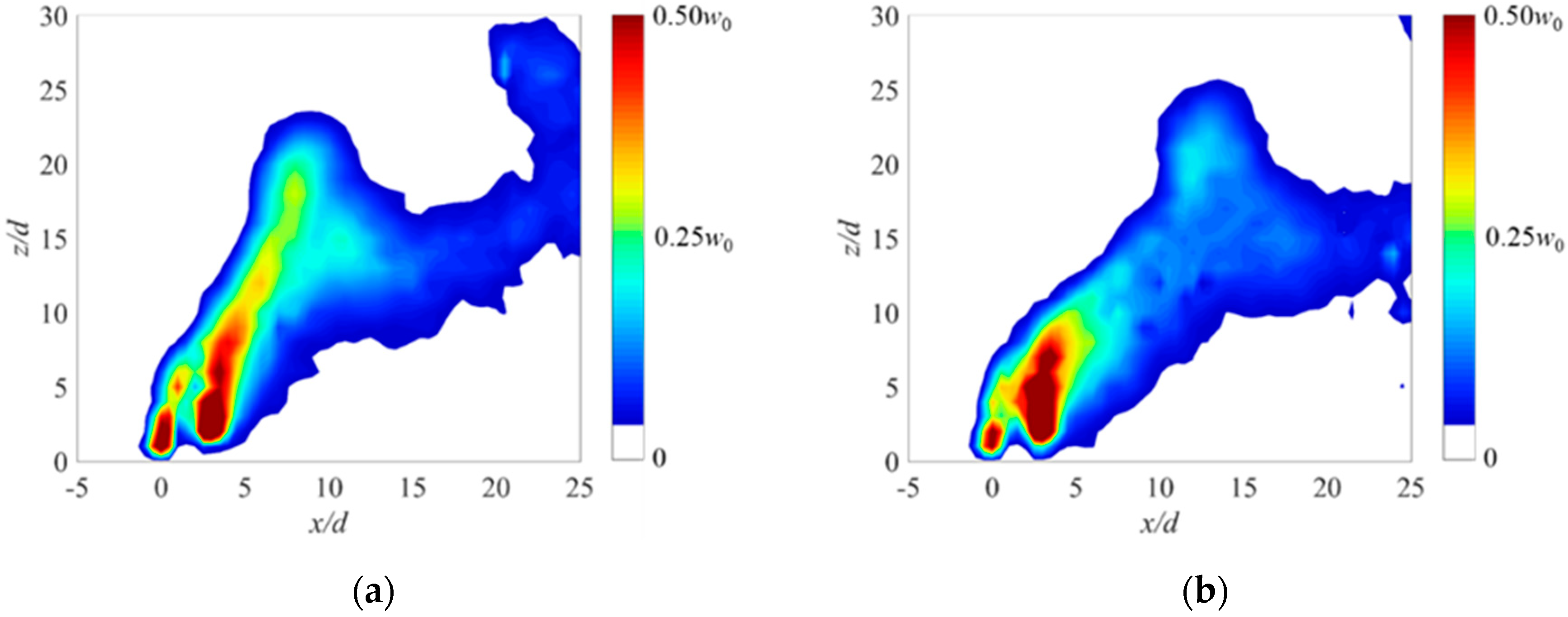
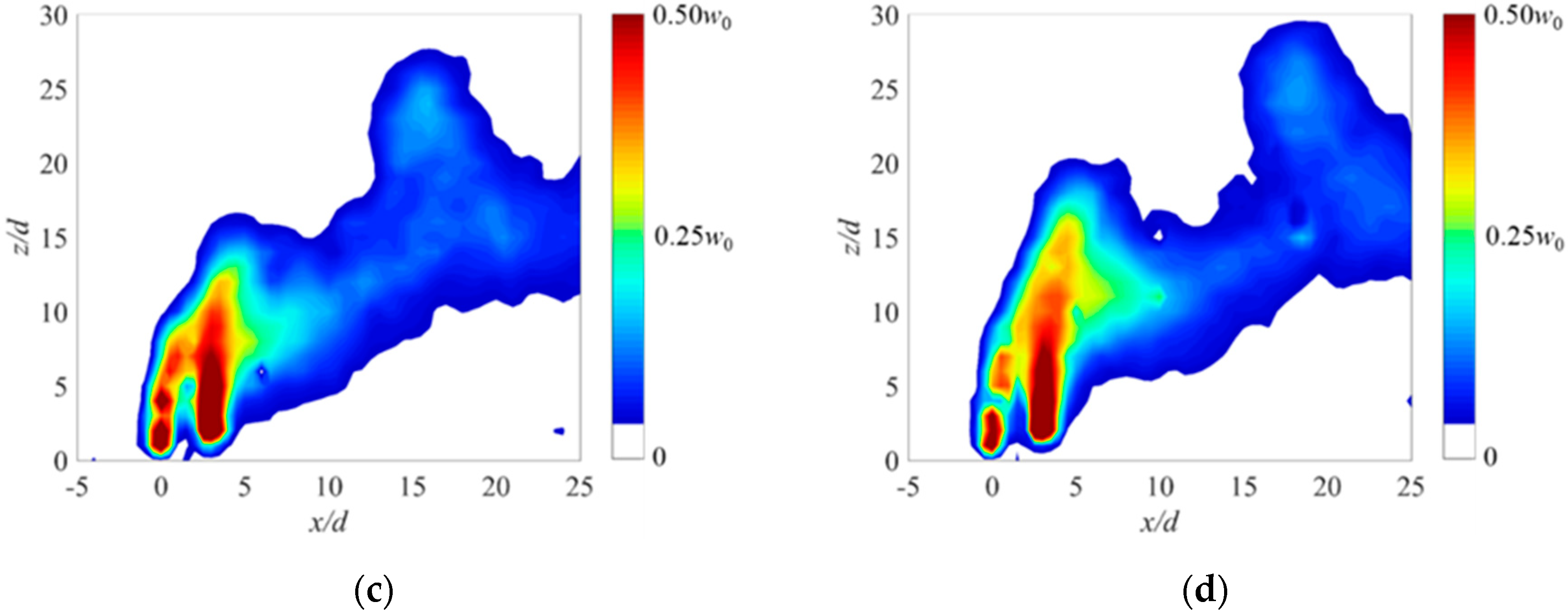
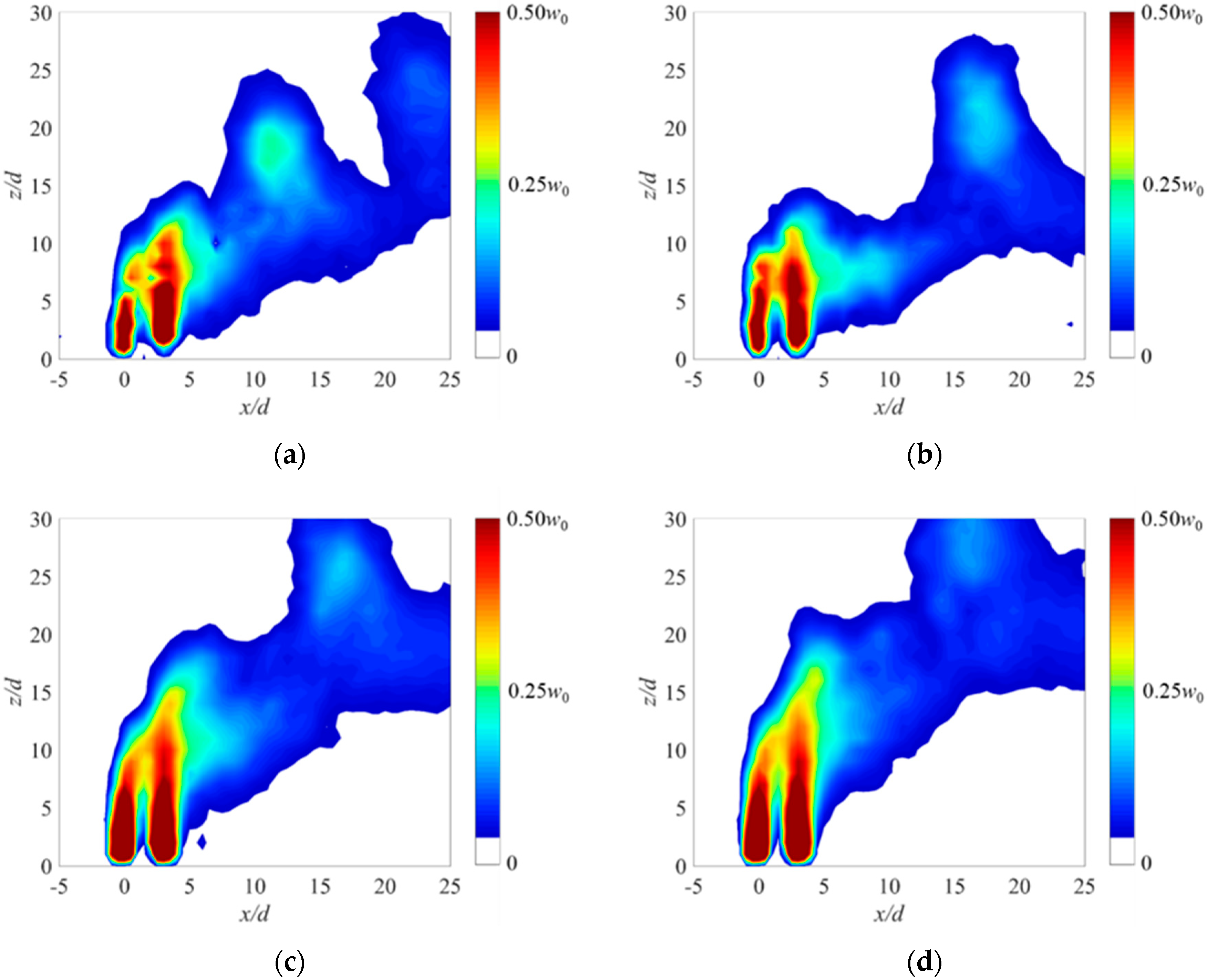
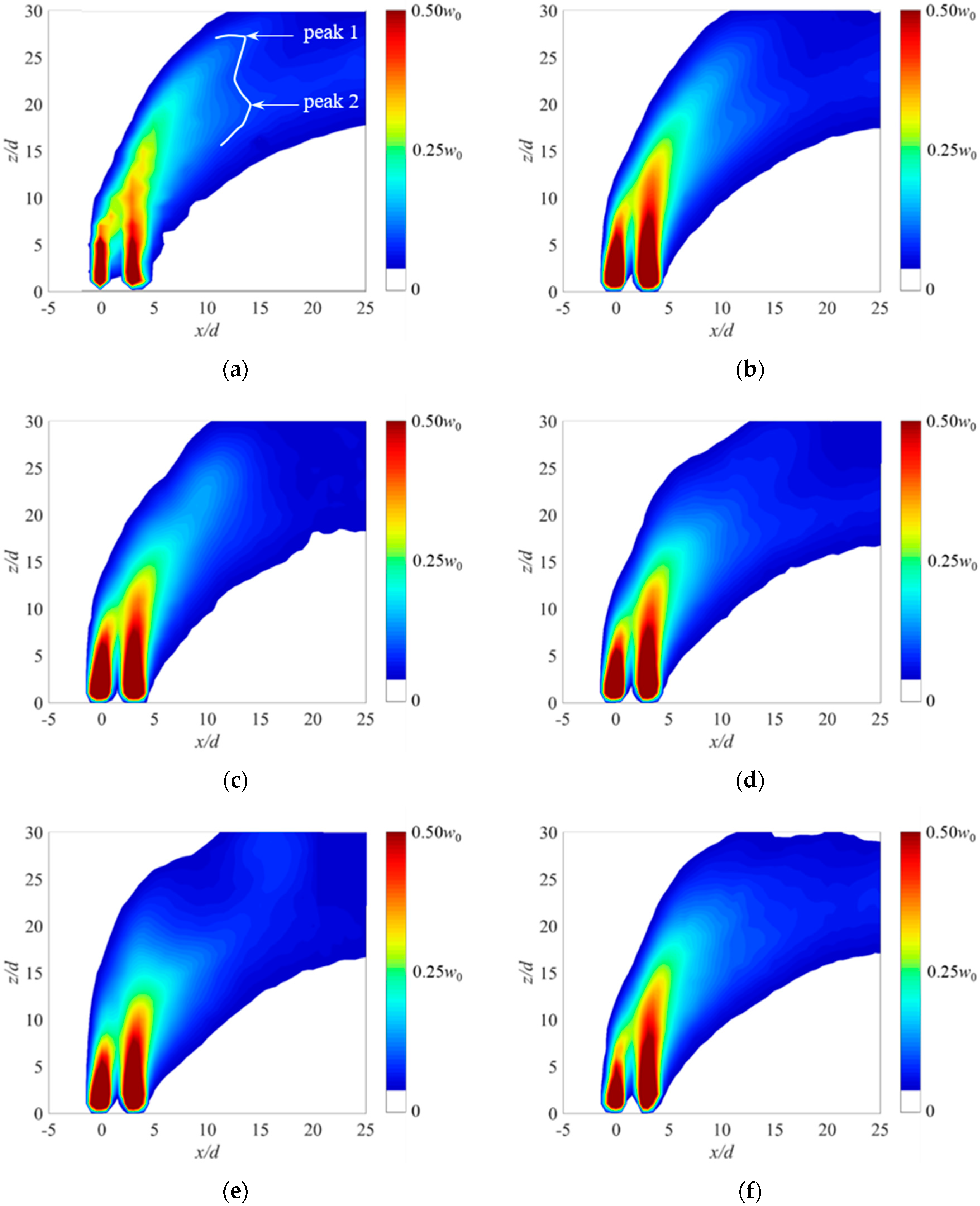
3.2. Phase-Averaged Flow Structure
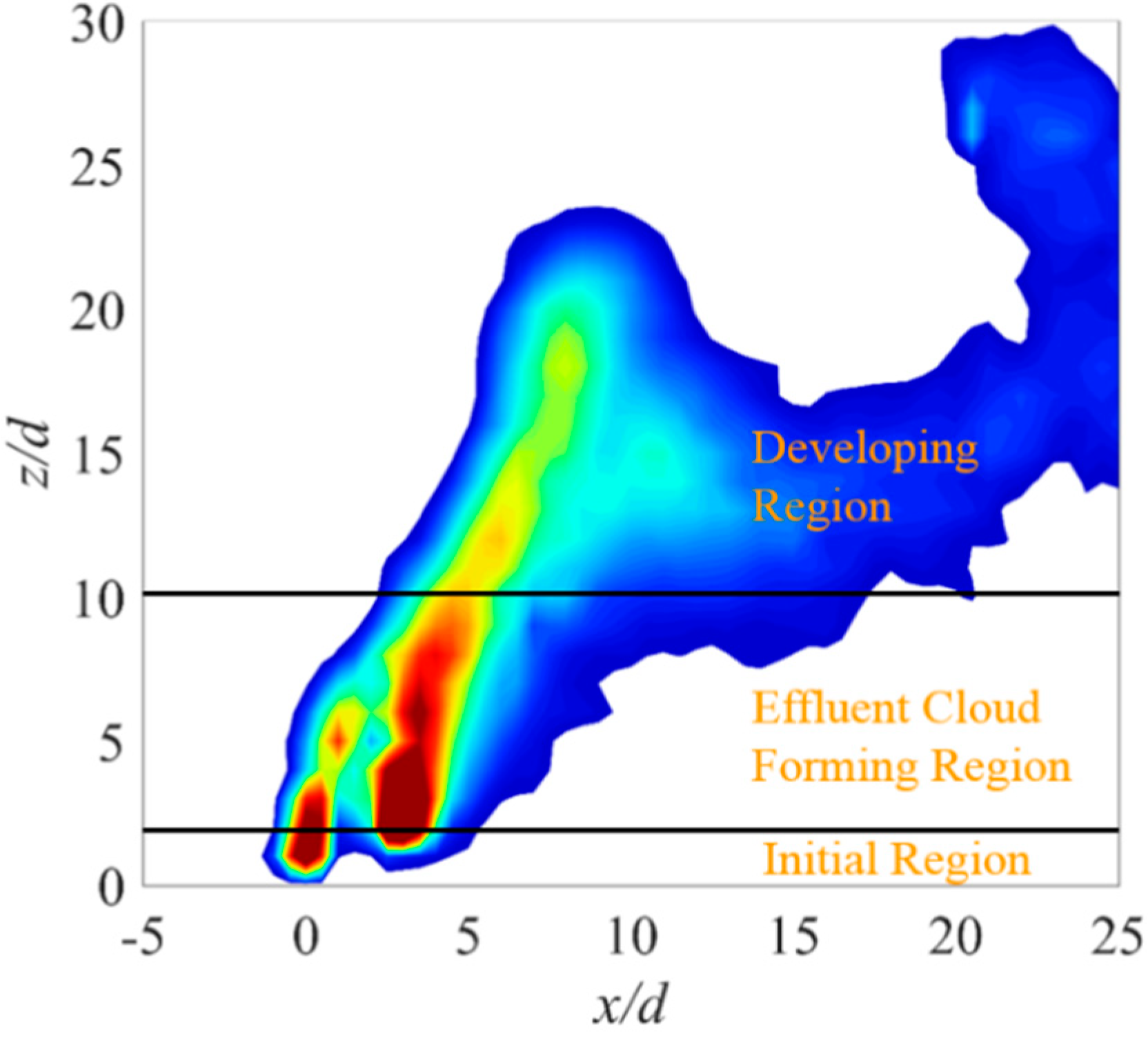
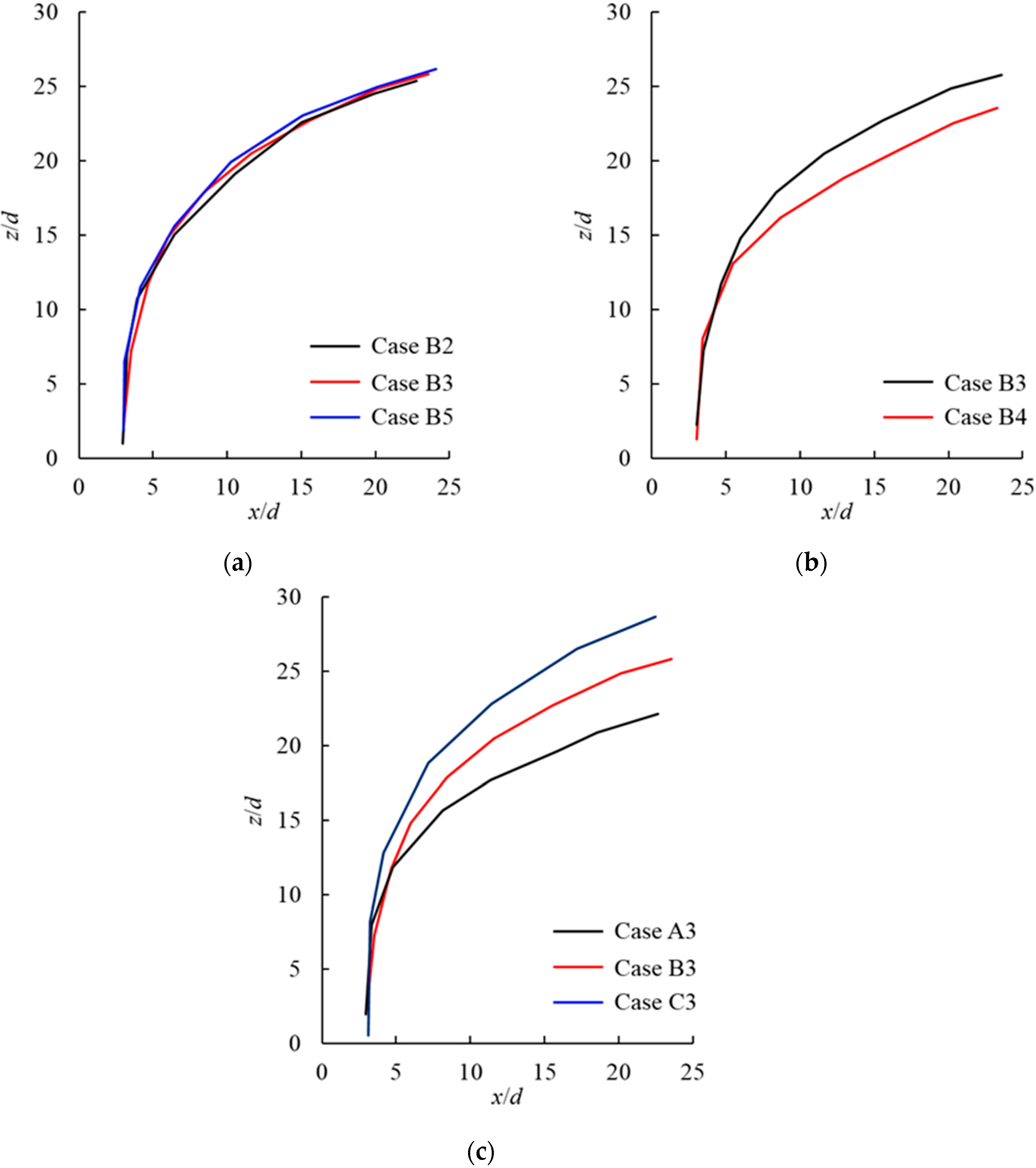
3.3. Mean Flow Structure
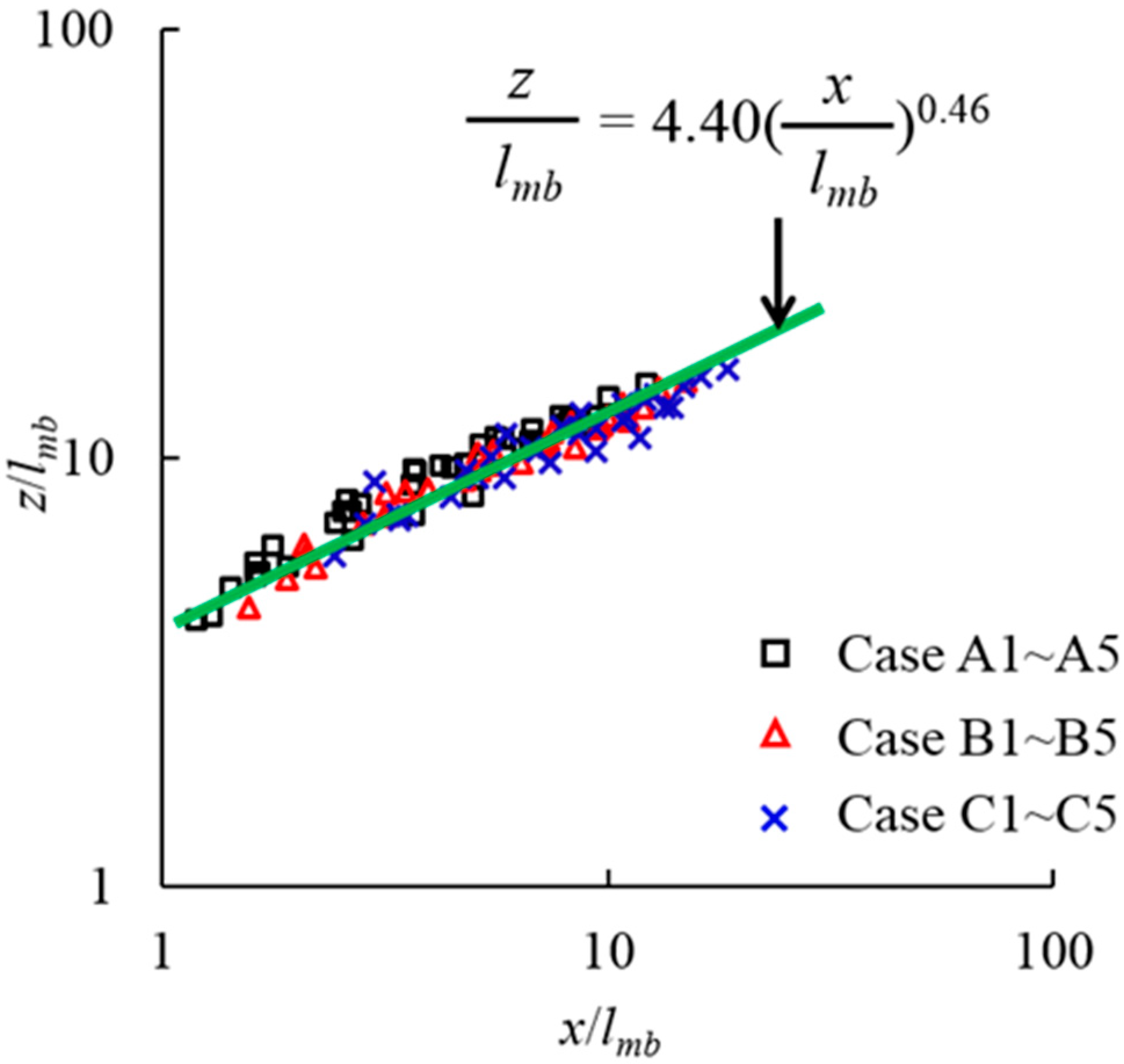
3.4. Dimensional Analysis
3.5. Empirical Formula of Trajectory
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Roberts, D.A.; Johnston, E.L.; Knott, N.A. Impacts of desalination plant discharges on the marine environment: A critical review of published studies. Water Res. 2010, 44, 5117–5128. [Google Scholar] [CrossRef] [PubMed]
- Binelli, A.; Magni, S.; Torre, C.D.; Parolini, M. Science of the total environment toxicity decrease in urban wastewaters treated by a new bio filtration process. Sci. Total Environ. 2015, 537, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Mennaa, F.Z.; Arbib, Z.; Perales, J.A. Urban wastewater treatment by seven species of microalgae and an algal bloom: Biomass production, N and P removal kinetics and harvestability. Water Res. 2015, 83, 42–51. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.Y.; Liu, C.B.; Chu, L.; Tang, Y.H.; Luo, S.L. Rapid and efficient treatment of wastewater with high-concentration heavy metals using a new type of hydrogel-based adsorption process. Bioresour. Technol. 2016, 219, 451–457. [Google Scholar] [CrossRef] [PubMed]
- Fan, L. Turbulent Buoyant Jets into Stratified or Flowing Ambient Fluids; California Institute of Technology: Pasadena, CA, USA, 1967. [Google Scholar]
- Papanicolaou, P.N.; List, E.J. Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 1988, 195, 341–391. [Google Scholar] [CrossRef]
- Jiang, M.T.; Law, A.W.K.; Lai, A.C.H. Turbulence characteristics of 45° inclined dense jets. Environ. Fluid Mech. 2018, 1–28. [Google Scholar] [CrossRef]
- Shao, D.; Huang, D.; Jiang, B.; Law, A.W.K. Flow patterns and mixing characteristics of horizontal buoyant jets at low and moderate Reynolds numbers. Int. J. Heat Mass Trans. 2017, 105, 831–846. [Google Scholar] [CrossRef]
- Kotsovinos, N.E. A Study of the Entrainment and Turbulence in a Plane Buoyant Jet; University of California: Berkeley, CA, USA, 1975. [Google Scholar]
- Davis, R.M.A.; Siegel, L.; Shirazi, D. Measurement of buoyant jet entrainment from single and multiple sources. J. Heat Transf. 2010, 100, 442–447. [Google Scholar] [CrossRef]
- Ahmad, N.; Baddour, R.E.; Asce, M. Dilution and penetration of vertical negatively buoyant thermal jets. J. Hydraul. Eng. 2012, 138, 850–857. [Google Scholar] [CrossRef]
- Chen, H. Turbulent Buoyant Jets and Plumes in Flowing Ambient Environments; University of Aalborg: Aalborg, Denmark, 1991. [Google Scholar]
- Gutmark, E.J.; Ibrahim, I.M.; Murugappan, S. Dynamics of single and twin circular jets in cross flow. Exp. Fluids 2011, 50, 653–663. [Google Scholar] [CrossRef]
- Yu, D.; Ali, M.S.; Lee, J.H.W. Multiple tandem jets in cross-flow. J. Hydraul. Eng. 2006, 132, 971–982. [Google Scholar] [CrossRef]
- Li, Z.W.; Huai, W.X.; Qian, Z.D. Study on the flow field and concentration characteristics of the multiple tandem jets in crossflow. Sci. China Technol. Sci. 2012, 55, 2778–2788. [Google Scholar] [CrossRef]
- Ziegler, H.; Wooler, P.T. Multiple jets exhausting into a crossflow. J. Aircr. 1971, 8, 414–420. [Google Scholar] [CrossRef]
- Makihata, T.; Miyai, Y. Trajectories of single and double jets injected into a crossflow of arbitrary velocity distribution. J. Fluids Eng. 1979, 101, 217–223. [Google Scholar] [CrossRef]
- Roberts, P. Inclined dense jets in flowing current. J. Hydraul. Eng. 1987, 113, 323–340. [Google Scholar] [CrossRef]
- Lee, J.H.W. Note on Ayoub’s data of horizontal round buoyant jet in current. J. Hydraul. Eng. 1989, 115, 969–975. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Malcangio, D.; De Serio, F.; Mossa, M. Vertical dense jet in flowing current. Environ. Fluid Mech. 2017, 18, 75–96. [Google Scholar] [CrossRef]
- Malcangio, D.; Ben Meftah, M.; Chiaia, G.; De Serio, F.; Mossa, M.; Petrillo, A.F. Experimental studies on vertical dense jets in a crossflow. In Proceedings of the River Flow 2016, St. Louis, MO, USA, 12–15 July 2016; pp. 890–897. [Google Scholar]
- Keramaris, E.; Pechlivanidis, G. The behaviour of a turbulent buoyant jet into flowing environment. Procedia Eng. 2016, 162, 120–127. [Google Scholar] [CrossRef]
- Chen, Y.L.; Hsiao, S.C. Numerical modeling of a buoyant round jet under regular waves. Ocean Eng. 2018, 161, 154–167. [Google Scholar] [CrossRef]
- Ger, A.M. Wave effects on submerged buoyant jets. In Proceedings of the 18th IAHR, Cagliari, Italy, 10–14 September 1979; pp. 295–300. [Google Scholar]
- Sharp, J.J. The effects of waves on buoyant jets. Proc. Inst. Civ. Eng. Part 2 1986, 81, 471–475. [Google Scholar]
- Chin, D.A. Influence of surface waves on outfall dilution. J. Hydraul. Eng. 1987, 113, 1006–1018. [Google Scholar] [CrossRef]
- Chin, D.A. Model of buoyant jet-surface-wave interaction. J. Waterw. Port Coast. Ocean Eng. 1988, 114, 331–345. [Google Scholar] [CrossRef]
- Kwan, K.H.; Swan, C. Near-field measurements of a buoyant jet in waves and currents. In Proceedings of the 25th Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996; pp. 4569–4582. [Google Scholar]
- Mori, N.; Chang, K.A. Experimental study of a horizontal jet in a wavy environment. J. Eng. Mech. 2003, 129, 1149–1155. [Google Scholar] [CrossRef]
- Ferrari, S.; Badas, M.G.; Querzoli, G. On the effect of regular waves on inclined negatively buoyant jets. Water 2018, 10, 726. [Google Scholar] [CrossRef]
- Mossa, M.; Davies, P.A. Some aspects of turbulent mixing of jets in the marine environment. Water 2018, 10, 522. [Google Scholar] [CrossRef]
- Ryu, Y.; Chang, K.A.; Mori, N. Dispersion of neutrally buoyant horizontal round jet in wave environment. J. Hydraul. Eng. 2005, 131, 1088–1097. [Google Scholar] [CrossRef]
- Chang, K.A.; Ryu, Y.; Mori, N. Parameterization of neutrally buoyant horizontal round jet in wave environment. J. Waterw. Port Coast. Ocean Eng. 2009, 135, 100–107. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Hsu, T.W.; Lin, J.F.; Chang, K.A. Mean and turbulence properties of a neutrally buoyant round jet in a wave environment. J. Waterw. Port Coast. Ocean Eng. 2011, 137, 109–122. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, Y.P.; Tao, J.F.; Pan, Y.; Sowa, D.M.A.; Li, C.W. Three-dimensional flow structure of a non-buoyant jet in a wave-current coexisting environment. Ocean. Eng. 2016, 116, 42–54. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, Y.P.; Wang, Y.N.; Zhang, C.K. Near-field dilution of a turbulent jet discharged into coastal waters: Effect of regular waves. Ocean Eng. 2017, 140, 29–42. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, Y.P.; Pan, Y. Initial dilution equations for wastewater discharge: Example of non-buoyant jet in wave-following-current environment. Ocean Eng. 2018, 164, 139–147. [Google Scholar] [CrossRef]
- Keane, R.; Adrian, R.J. Optimization of particle image velocimeters. Part I: Double plused system. Meas. Sci. Technol. 1990, 1, 1202–1215. [Google Scholar] [CrossRef]
- Prasad, A.K.; Adrian, R.J.; Landreth, C.C.; Offutt, P.W. Effect of resolution on the speed and accuracy of particle image velocimetry interrogations. Exp. Fluids 1992, 13, 105–116. [Google Scholar] [CrossRef]
- Oshima, Y.; Kinoshita, O. Coanda Effect of Water Jet. Trans. Soc. Instrum. Control Eng. 2009, 11, 491–496. [Google Scholar]
- Su, L.K.; Mungal, M.G. Simultaneous measurements of scalar and velocity field evolution in turbulent crossflowing jets. J. Fluid Mech. 2004, 513, 1–45. [Google Scholar] [CrossRef]


| Case | Jet-to-Current Velocity Ratio Rjc | Wave-to-Current Velocity Ratio Rwc | Strouhal Number St | Initial Flow Flux Q0 (L/h) | Initial Velocity w0 (m/s) | Wave Period T (s) | Wave Height H (cm) | Cross-Flow Velocity uc (m/s) |
|---|---|---|---|---|---|---|---|---|
| A0 | 8.75 | — | — | 200 | 0.70 | — | — | — |
| A1 | 8.75 | 0.17 | 0.125 | 200 | 0.70 | 1 | 2 | 0.08 |
| A2 | 8.75 | 0.35 | 0.125 | 200 | 0.70 | 1 | 4 | 0.08 |
| A3 | 8.75 | 0.32 | 0.083 | 200 | 0.70 | 1.5 | 2 | 0.08 |
| A4 | 8.75 | 0.63 | 0.083 | 200 | 0.70 | 1.5 | 4 | 0.08 |
| A5 | 8.75 | 0.37 | 0.063 | 200 | 0.70 | 2 | 2 | 0.08 |
| B0 | 11.00 | — | — | 250 | 0.88 | — | — | — |
| B1 | 11.00 | 0.17 | 0.125 | 250 | 0.88 | 1 | 2 | 0.08 |
| B2 | 11.00 | 0.35 | 0.125 | 250 | 0.88 | 1 | 4 | 0.08 |
| B3 | 11.00 | 0.32 | 0.083 | 250 | 0.88 | 1.5 | 2 | 0.08 |
| B4 | 11.00 | 0.63 | 0.083 | 250 | 0.88 | 1.5 | 4 | 0.08 |
| B5 | 11.00 | 0.37 | 0.063 | 250 | 0.88 | 2 | 2 | 0.08 |
| C0 | 13.25 | — | — | 300 | 1.06 | — | — | — |
| C1 | 13.25 | 0.17 | 0.125 | 300 | 1.06 | 1 | 2 | 0.08 |
| C2 | 13.25 | 0.35 | 0.125 | 300 | 1.06 | 1 | 4 | 0.08 |
| C3 | 13.25 | 0.32 | 0.083 | 300 | 1.06 | 1.5 | 2 | 0.08 |
| C4 | 13.25 | 0.63 | 0.083 | 300 | 1.06 | 1.5 | 4 | 0.08 |
| C5 | 13.25 | 0.37 | 0.063 | 300 | 1.06 | 2 | 2 | 0.08 |
| Case | Water Depth h (m) | Flow Flux Q0 (L/h) | Density Difference Δρ | Initial Velocity w0 (m/s) |
|---|---|---|---|---|
| S1 | 0.60 | 50 | 0.73% | 0.18 |
| S2 | 0.70 | 100 | 0.73% | 0.36 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Otoo, E.; Chen, Y.; Ding, H. 2D PIV Measurement of Twin Buoyant Jets in Wavy Cross-Flow Environment. Water 2019, 11, 399. https://doi.org/10.3390/w11020399
Xu Z, Otoo E, Chen Y, Ding H. 2D PIV Measurement of Twin Buoyant Jets in Wavy Cross-Flow Environment. Water. 2019; 11(2):399. https://doi.org/10.3390/w11020399
Chicago/Turabian StyleXu, Zhenshan, Ebenezer Otoo, Yongping Chen, and Hongwei Ding. 2019. "2D PIV Measurement of Twin Buoyant Jets in Wavy Cross-Flow Environment" Water 11, no. 2: 399. https://doi.org/10.3390/w11020399
APA StyleXu, Z., Otoo, E., Chen, Y., & Ding, H. (2019). 2D PIV Measurement of Twin Buoyant Jets in Wavy Cross-Flow Environment. Water, 11(2), 399. https://doi.org/10.3390/w11020399





