A Simple Early Warning System for Flash Floods in an Ungauged Catchment and Application in the Loess Plateau, China
Abstract
:1. Introduction
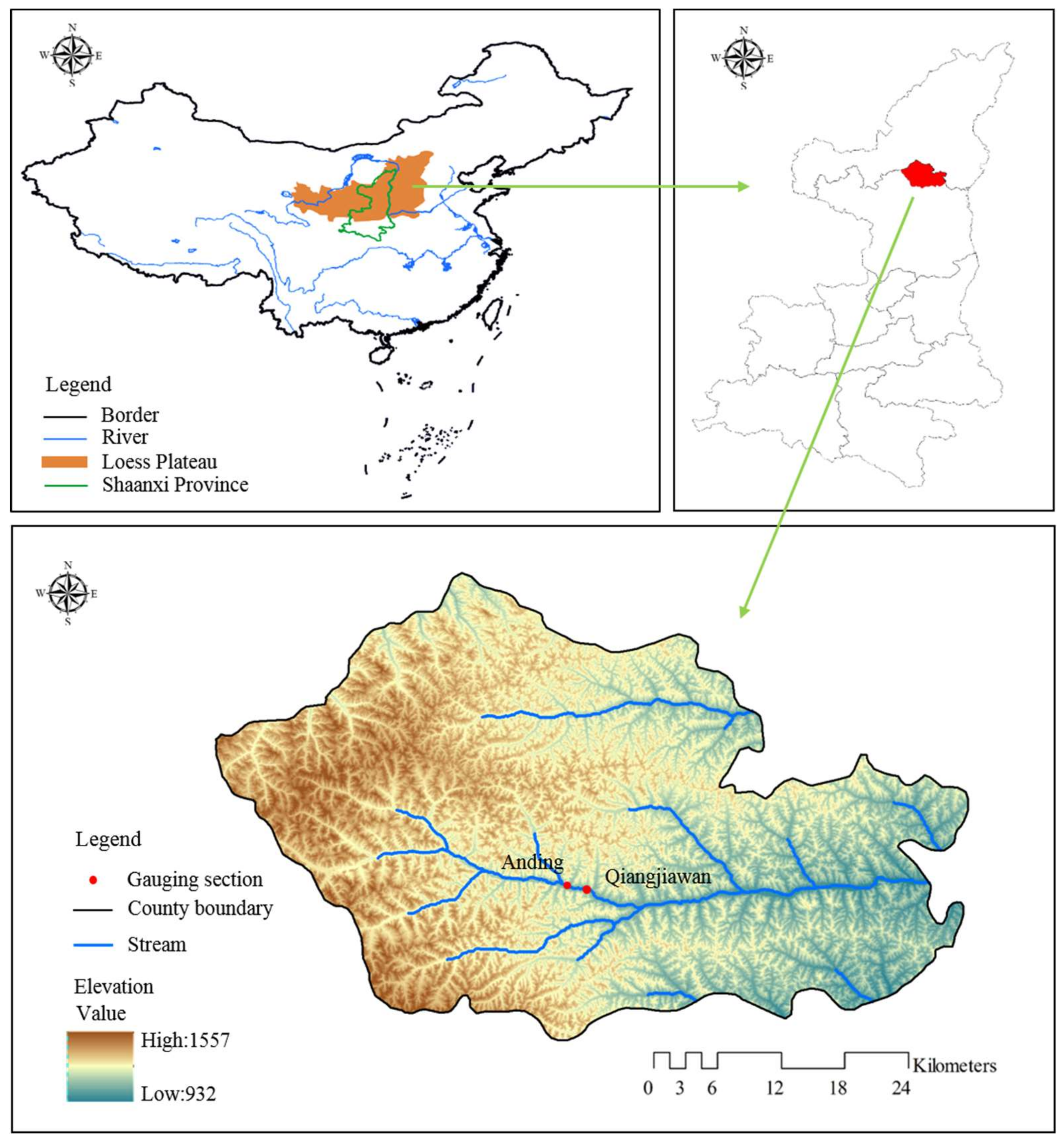
2. Study Area
3. Early Warning System for Flash Flood Disasters
3.1. Key Concepts
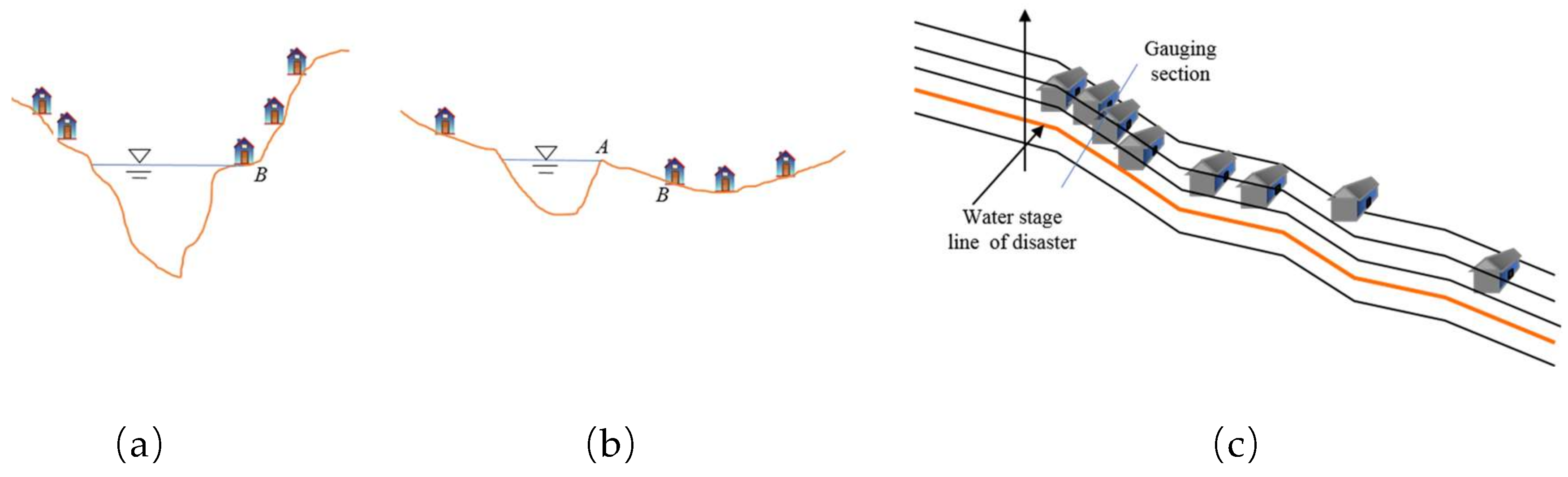
3.1.1. Water Stage of a Disaster
3.1.2. Critical Water Stage/Flow
3.1.3. Critical Rainfall
3.2. Design Flood Calculation
3.2.1. Design Rainstorm Calculation
3.2.2. Design Flood
3.3. Critical Rainfall Calculation by Rating Curve
3.3.1. The Rating Curve
3.3.2. Calculation Method for Critical Rainfall
- a. Critical flow calculation. The water stage of a disaster (critical water stage, Ec) in the gauging section is converted into the critical flow (Qc) based on the rating curve representing the relationship of the water stage-flow in the gauging section.
- b. Design flood calculation. The design flood is obtained with different frequencies (1%, 2%, 5%, 10% and 20%) via the method mentioned in Section 3.2., and the peak flow of the flood with different frequencies can be obtained.
- c. Setup the relationship between frequency and flow (Q~P). The curve of flow frequency (Q~P) is drawn, based on the peak flow of the design flood with different frequencies.
- d. Frequency calculation of critical rainfall. The frequency of the critical rainfall can be calculated through the critical flow and the frequency curve, based on the hypothesis that the frequency of critical rainfall is equal to the frequency of critical flow.
- e. Critical rainfall calculation with a given duration (one hour). The method of calculation of critical rainfall with the duration of one hour, is the same as the design point rainstorm. After lookup, the Kp value based on the frequency of critical rainfall and the value of Cv1, the critical rainfall value with 1-hour duration can be calculated with the following formula:
- f. Critical rainfall calculation with different durations:
3.4. Early Warning Index in Water Stage/Flow
3.5. Early Warning Index in Rainfall
3.6. Early Warning System
4. Results
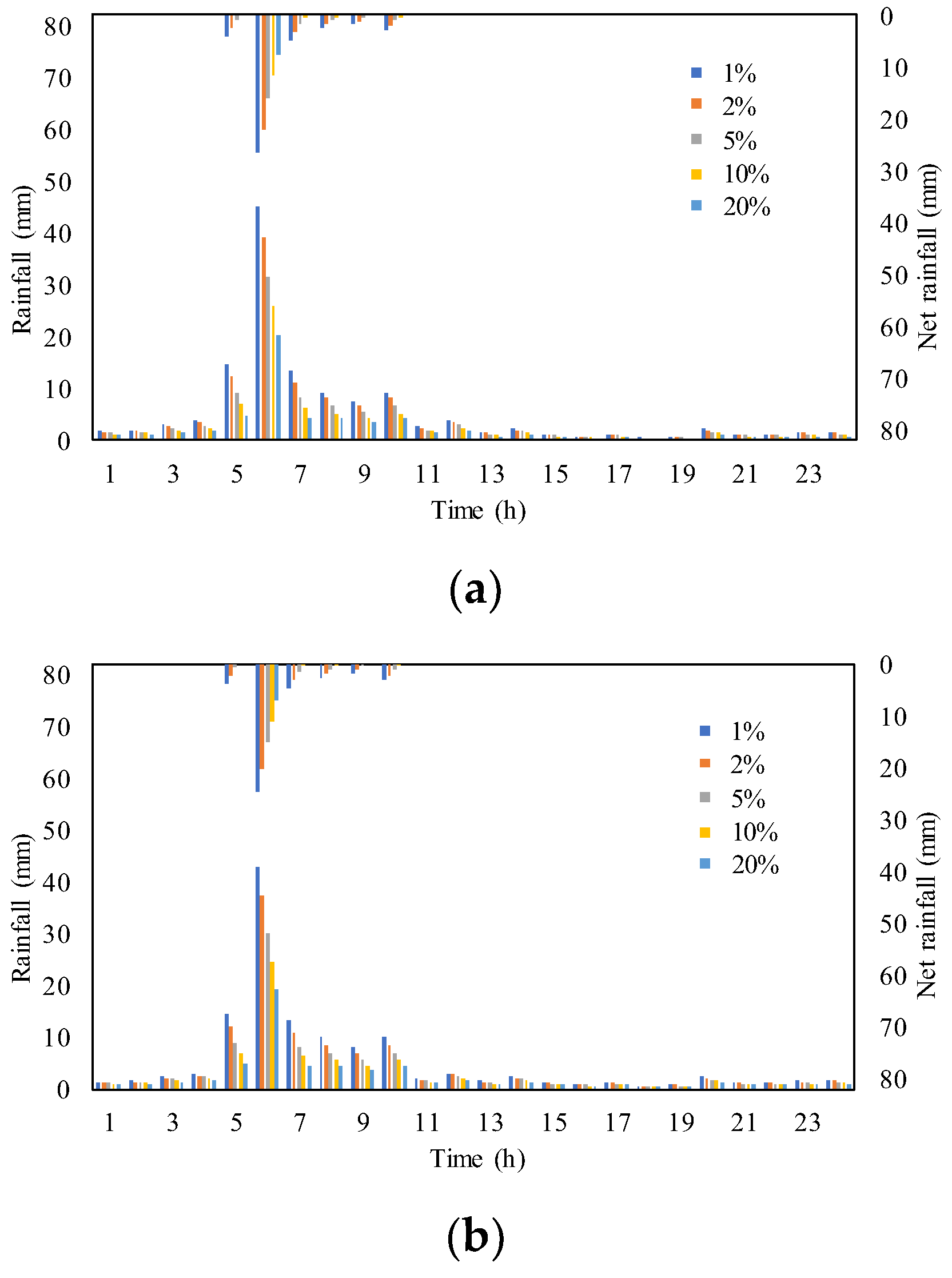
4.1. Design Rainstorm and Floods
4.2. Rating Curve
4.3. Early Warning Index in Water Stage/Flow
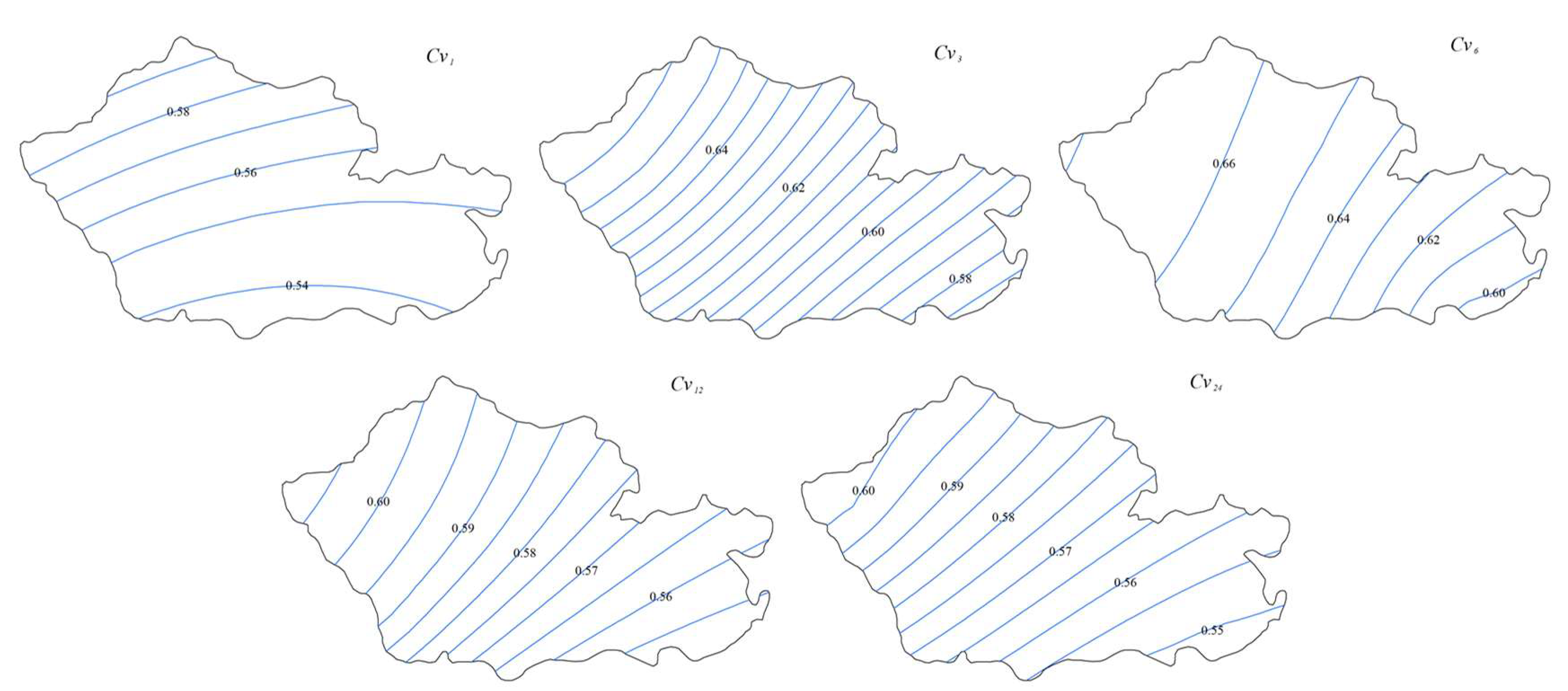
4.4. Critical Rainfall
4.5. Early Warning Index in Rainfall
5. Application
5.1. Application Steps
- Data collection. The observed data of current floods and rainstorms should be collected in the flash flood event, and the flood marks as well as relevant hydraulic parameters should be measured at the gauging section after the flood.
- Flood peak flow simulation. The observed rainstorm data are used to simulate the peak flow (Qa) with the instantaneous unit hydrograph.
- Simulation test. The river water stage Ea corresponding to the peak flow Qa is calculated via the plotted rating curve at the gauging section. Then the Ea is compared with the elevation of flood marks (Em) to assess the simulation performance of the early warning system, and the error can be calculated with the following formula:
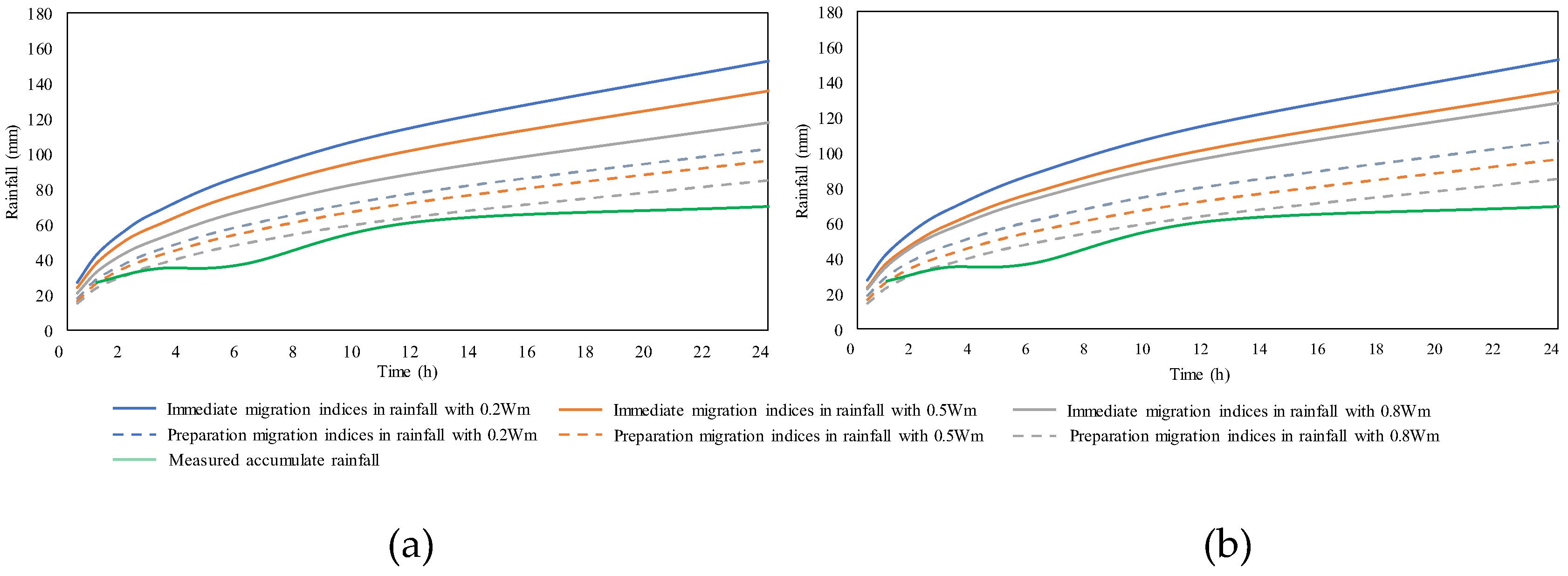
- Warning signal test. The issue of warning signal is determined by the relation between the measured rainfall cumulative curve and the cumulative curve of migration index in rainfall. We can draw the measured rainfall cumulative curve and the cumulative curves of rainfall indices for preparation and immediate migration in a figure. The corresponding warning signal should be issued once the measured curve exceeds the rainfall index for the preparation of immediate migration.
5.2. Application Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Borga, M.; Boscolo, P.; Zanon, F.; Sangati, M. Hydrometeorological analysis of the 29 August 2003 flash flood in the Eastern Italian Alps. J. Hydrometeorol. 2007, 8, 1049–1067. [Google Scholar] [CrossRef]
- Desilets, S.; Ferré, T.; Ekwurzel, B. Flash flood dynamics and composition in a semiarid mountain watershed. Water Resour. Res. 2008, 44, 5121–5127. [Google Scholar] [CrossRef]
- Nieland, C.; Mushtaq, S. The effectiveness and need for flash flood warning systems in a regional inland city in Australia. Nat. Hazards 2016, 80, 1–19. [Google Scholar] [CrossRef]
- Borga, M.; Stoffel, M.; Marchi, L.; Marra, F.; Jakob, M. Hydrogeomorphic response to extreme rainfall in headwater systems: Flash floods and debris flows. J. Hydrol. 2014, 518, 194–205. [Google Scholar] [CrossRef]
- Miao, Q.; Yang, D.; Yang, H.; Li, Z. Establishing a rainfall threshold for flash flood warnings in China’s mountainous areas based on a distributed hydrological model. J. Hydrol. 2016, 541, 371–386. [Google Scholar] [CrossRef] [Green Version]
- Chang, J.; Zhang, H.; Wang, Y.; Zhu, Y. Assessing the impact of climate variability and human activities on streamflow variation. Hydrol. Earth Syst. Sci. 2016, 20, 1547–1560. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Hou, B.; Chang, J.; Huang, Q.; Chen, Y. Copulas-based probabilistic characterization of the combination of dry and wet conditions in the Guanzhong Plain, China. J. Hydrol. 2014, 519, 3204–3213. [Google Scholar] [CrossRef]
- Luo, P.; Mu, D.; Xue, H.; Ngo-Duc, T.; Dang-Dinh, K.; Takara, K.; Nover, D.; Schladow, G. Flood inundation assessment for the Hanoi Central Area, Vietnam under historical and extreme rainfall conditions. Sci. Rep. 2018, 8, 12623. [Google Scholar] [CrossRef] [PubMed]
- Hill, L. More-than-representational geographies of the past and the affectivity of sound: Revisiting the Lynmouth flood event of 1952. Soc. Cult. Geogr. 2015, 16, 1–23. [Google Scholar] [CrossRef]
- Gaume, E.; Livet, M.; Desbordes, M.; Villeneuve, J. Hydrological analysis of the river Aude, France, flash flood on 12 and 13 November 1999. J. Hydrol. 2004, 286, 135–154. [Google Scholar] [CrossRef]
- He, Y.; He, S.; Hu, Z.; Qin, Y.; Zhang, Y. The devastating 26 July 2017 Floods in Yulin City, northern Shaanxi, China. Geomat. Nat. Hazards Risk 2018, 9, 70–78. [Google Scholar] [CrossRef]
- Hapuarachchi, H.; Wang, Q.; Pagano, T. A review of advances in flash flood forecasting. Hydrol. Process. 2011, 25, 2771–2784. [Google Scholar] [CrossRef]
- Chen, M.; Pang, J.; Wu, P. Flood routing model with particle filter-based data assimilation for flash flood forecasting in the micro-model of lower Yellow river, China. Water 2018, 10, 1612. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Wang, Q.J. A Review of Methods and Systems Available for Flash Flood Forecasting; CSIRO: Canberra, Australia, 2008; pp. 30–39. [Google Scholar]
- Reed, S.; Schaake, J.; Zhang, Z. A distributed hydrologic model and threshold frequency-based method for flash flood forecasting at ungauged locations. J. Hydrol. 2007, 337, 402–420. [Google Scholar] [CrossRef]
- Martina, M.; Todini, E.; Libralon, A. A Bayesian decision approach to rainfall thresholds based flood warning. Hydrol. Earth Syst. Sci. 2006, 2, 413–426. [Google Scholar] [CrossRef]
- Vincendon, B.; Ducrocq, V.; Nuissier, O.; Viè, B. Perturbation of convection-permitting NWP forecasts for flash-flood ensemble forecasting. Nat. Hazards Earth Syst. 2011, 11, 1529–1544. [Google Scholar] [CrossRef] [Green Version]
- Ntelekos, A.; Georgakakos, K.; Krajewski, W. On the uncertainties of flash flood guidance: Toward probabilistic forecasting of flash floods. J. Hydrometeorol. 2006, 7, 896–915. [Google Scholar] [CrossRef]
- Na, W.; Yoo, C. A bias correction method for rainfall forecasts using backward storm tracking. Water 2018, 10, 1728. [Google Scholar] [CrossRef]
- Zhang, H.; Singh, P.V.; Wang, B.; Yu, Y. CEREF: A hybrid data-driven model for forecasting annual streamflow in socio-hydrological system. J. Hydrol. 2016, 540, 246–256. [Google Scholar] [CrossRef]
- Chiang, Y.; Hsu, K.; Chang, F.; Hong, Y.; Sorooshian, S. Merging multiple precipitation sources for flash flood forecasting. J. Hydrol. 2007, 340, 183–196. [Google Scholar] [CrossRef]
- Kobold, M.; Brilly, M. The use of HBV model for flash flood forecasting. Nat. Hazards Earth Syst. Sci. 2006, 6, 407–417. [Google Scholar] [CrossRef] [Green Version]
- Sirdas, S.; Şen, Z. Determination of flash floods in western Arabian Peninsula. J. Hydrol. Eng. 2007, 12, 676–681. [Google Scholar] [CrossRef]
- Lincoln, W.; Franz, K. A Modeling Approach for Flash Flood Forecasting For Small Watersheds in Iowa; American Geophysical Union Fall Meeting: San Francisco, CA, USA, 2008. [Google Scholar]
- Borrell, V.E.; Dartus, D.; Ababou, R. Flash flood modeling with the MARINE hydrological distributed model. Hydrol. Earth Syst. Sci. 2006, 3, 3397–3438. [Google Scholar] [CrossRef]
- England, J.; Velleux, M.; Julien, P. Two-dimensional simulations of extreme floods on a large watershed. J. Hydrol. 2007, 347, 229–241. [Google Scholar] [CrossRef]
- Saber, M.; Yilmaz, K.K. Evaluation and bias correction of satellite-based rainfall estimates for modelling flash floods over the Mediterranean region: Application to Karpuz river basin, Turkey. Water 2018, 10, 657. [Google Scholar] [CrossRef]
- Norbiato, D.; Borga, M.; Esposti, S.; Gaume, E.; Anquetin, S. Flash flood warning based on rainfall thresholds and soil moisture conditions: An assessment for gauged and ungauged basins. J. Hydrol. 2008, 362, 274–290. [Google Scholar] [CrossRef]
- Zhai, X.; Guo, L.; Liu, R.; Zhang, Y. Rainfall threshold determination for flash flood warning in mountainous catchments with consideration of antecedent soil moisture and rainfall pattern. Nat. Hazards 2018, 94, 605–625. [Google Scholar] [CrossRef]
- Yan, W.; Deng, L.; Zhong, Y.; Shangguan, Z. The characters of dry soil layer on the Loess Plateau in China and their influencing factors. PLoS ONE 2015, 10, e0134902. [Google Scholar] [CrossRef] [PubMed]
- Ren, C.; Li, Z.; Zhang, H. Integrated multi-objective stochastic fuzzy programming and AHP method for agricultural water and land optimization allocation under multiple uncertainties. J. Clean Prod. 2019, 2101, 12–24. [Google Scholar] [CrossRef]
- Liu, D.; Tian, F.; Hu, H.; Hu, H. The role of run-on for overland flow and the characteristics of runoff generation in the Loess Plateau, China. Hydrol. Sci. J. 2012, 57, 1107–1117. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H. The characteristics of hard rain and its distribution over the loess plateau. Acta Geogr. Sin. 1983, 4, 416–425. [Google Scholar]
- Yu, Y.; Zhang, H.; Singh, V.P. Forward prediction of runoff data in data-scarce basins with an improved ensemble empirical mode decomposition (EEMD) model. Water 2018, 10, 388. [Google Scholar] [CrossRef]
- Wang, T.; Kou, X.; Xiong, Y.; Mou, P.; Wu, J.; Ge, J. Temporal and spatial patterns of NDVI and their relationship to precipitation in the Loess Plateau of China. Int. J. Remote Sens. 2010, 31, 1943–1958. [Google Scholar] [CrossRef]
- Zhao, W.; Fu, B.; Men, Q.; Zhang, Q.; Zhang, Y. Effects of land-use pattern change on rainfall-runoff and runoff-sediment relations: A case study in Zichang watershed of the Loess Plateau of China. J. Environ. Sci. 2004, 16, 436–442. [Google Scholar]
- Song, S.; Schmalz, B.; Zhang, J.; Li, G.; Fohrer, N. Application of modified manning formula in the determination of vertical profile velocity in natural rivers. Hydrol. Res. 2017, 48, 133–146. [Google Scholar] [CrossRef]
- Chow, C.N. Open Channel Hydraulics; McGraw Hill Book Company: New York, NY, USA, 1959. [Google Scholar]
- Cao, Q.; Guan, K. Analysis on different forms of manning formula in stage—Discharge relation calculation for compound cross section channel. Ground Water 2015, 37, 156–169. (In Chinese) [Google Scholar]
- Xie, X.; Wang, L. Changes of potential evaporation in northern China over the past 50 years. J. Nat. Resour. 2007, 22, 683–691. (In Chinese) [Google Scholar]










| Duration | Distribution of Design Rainstorm (%) | ||||
|---|---|---|---|---|---|
| (H) | Hs1,p | Hs3,p–Hs1,p | Hs6,p–Hs3,p | Hs12,p–Hs6,p | Hs24,p–Hs12,p |
| 1 | 10.6 | ||||
| 2 | 11.9 | ||||
| 3 | 17.9 | ||||
| 4 | 21.9 | ||||
| 5 | 52.2 | ||||
| 6 | 100 | ||||
| 7 | 47.8 | ||||
| 8 | 35.5 | ||||
| 9 | 29 | ||||
| 10 | 35.5 | ||||
| 11 | 15.2 | ||||
| 12 | 22.5 | ||||
| 13 | 9.4 | ||||
| 14 | 14.5 | ||||
| 15 | 7.6 | ||||
| 16 | 5 | ||||
| 17 | 7.6 | ||||
| 18 | 3.1 | ||||
| 19 | 4.4 | ||||
| 20 | 13.8 | ||||
| 21 | 7.6 | ||||
| 22 | 7.5 | ||||
| 23 | 9.4 | ||||
| 24 | 10.1 | ||||
| Total | 100 | 100 | 100 | 100 | 100 |
| Time (h) | Unit hydrograph u(t, △t) | Net rainfall (Hnett, mm) | Total Net Rainfall (mm) | |||
|---|---|---|---|---|---|---|
| Hnet1 | Hnet2 | … | Hnett | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | u(1,1) | u(1,1) × Hnet1 | 0 | 0 | 0 | Hnetsum1 |
| 2 | u(2,1) | u(2,1) × Hnet2 | u(1,1) × Hnet2 | 0 | 0 | Hnetsum2 |
| 3 | u(3,1) | u(3,1) × Hnet3 | u(2,1) × Hnet2 | … | … | Hnetsum3 |
| . | … | … | u(3,1) × Hnet2 | … | … | … |
| . | … | … | … | … | u(1,1) × Hnett | … |
| . | … | … | … | … | u(2,1) × Hnett | … |
| 23 | … | … | … | … | u(3,1) × Hnett | … |
| 24 | … | … | … | … | … | … |
| Disaster Prevention Objects | Duration (h) | Annual Maximum Rainfall and Statistical Parameters | Design Point Rainfall WITH Different Frequency | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Hmaxd (mm) | Cvd | Cs/Cvd | 1% | 2% | 5% | 10% | 20% | ||
| Anding | 1 | 30.8 | 0.56 | 3.5 | 92.7 | 80.7 | 65.3 | 53.3 | 41.6 |
| 3 | 35.8 | 0.64 | 3.5 | 121.4 | 103.8 | 81.6 | 65.2 | 48.7 | |
| 6 | 43.0 | 0.62 | 3.5 | 141.5 | 121.7 | 96.3 | 77.0 | 58.5 | |
| 12 | 49.6 | 0.59 | 3.5 | 156.2 | 135.4 | 108.1 | 87.3 | 67.0 | |
| 24 | 56.0 | 0.57 | 3.5 | 171.4 | 148.4 | 119.8 | 97.4 | 75.6 | |
| Qiangjiawan | 1 | 31.5 | 0.56 | 3.5 | 94.8 | 82.5 | 66.7 | 54.4 | 42.5 |
| 3 | 36.5 | 0.64 | 3.5 | 123.7 | 105.8 | 83.2 | 66.4 | 49.6 | |
| 6 | 44.5 | 0.62 | 3.5 | 146.4 | 125.9 | 99.6 | 79.6 | 60.5 | |
| 12 | 50.2 | 0.58 | 3.5 | 155.6 | 135.1 | 108.4 | 87.8 | 67.7 | |
| 24 | 57.5 | 0.56 | 3.5 | 173.1 | 150.6 | 121.9 | 99.4 | 77.6 | |
| Disaster Prevention Objects | Duration (h) | Parameters | Point-to-Surface Conversion Parameter | Design Surface Rainfall with Different Frequency | |||||
|---|---|---|---|---|---|---|---|---|---|
| ad | bd | αd | 1% | 2% | 5% | 10% | 20% | ||
| Anding | 1 | 0.018 | 0.313 | 0.484 | 44.9 | 39.1 | 31.6 | 25.8 | 20.1 |
| 3 | 0.014 | 0.247 | 0.599 | 72.8 | 62.2 | 48.9 | 39.1 | 29.2 | |
| 6 | 0.009 | 0.209 | 0.698 | 98.8 | 85 | 67.2 | 53.7 | 40.8 | |
| 12 | 0.007 | 0.197 | 0.739 | 115.4 | 100 | 79.9 | 64.5 | 49.5 | |
| 24 | 0.007 | 0.187 | 0.763 | 130.7 | 113.2 | 91.4 | 74.3 | 57.7 | |
| Qiangjiawan | 1 | 0.018 | 0.313 | 0.453 | 42.9 | 37.3 | 30.2 | 24.6 | 19.2 |
| 3 | 0.018 | 0.313 | 0.569 | 70.4 | 60.2 | 47.3 | 37.8 | 28.2 | |
| 6 | 0.014 | 0.247 | 0.670 | 98.1 | 84.3 | 66.7 | 53.3 | 40.5 | |
| 12 | 0.009 | 0.209 | 0.712 | 110.7 | 96.1 | 77.1 | 62.5 | 48.2 | |
| 24 | 0.007 | 0.197 | 0.737 | 127.5 | 111 | 89.8 | 73.3 | 57.2 | |
| Section | Simulated Water Stage Ea (m) | Measured Flood Mark Em (m) | Relative Error ε (%) |
|---|---|---|---|
| Anding | 1104.93 | 1104.87 | 0.005 |
| Qiangjiawan | 1070.36 | 1070.58 | 0.021 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, H.; Singh, V.P.; Yu, R.; Zhang, S. A Simple Early Warning System for Flash Floods in an Ungauged Catchment and Application in the Loess Plateau, China. Water 2019, 11, 426. https://doi.org/10.3390/w11030426
Li Z, Zhang H, Singh VP, Yu R, Zhang S. A Simple Early Warning System for Flash Floods in an Ungauged Catchment and Application in the Loess Plateau, China. Water. 2019; 11(3):426. https://doi.org/10.3390/w11030426
Chicago/Turabian StyleLi, Zhehao, Hongbo Zhang, Vijay P. Singh, Ruihong Yu, and Shuqi Zhang. 2019. "A Simple Early Warning System for Flash Floods in an Ungauged Catchment and Application in the Loess Plateau, China" Water 11, no. 3: 426. https://doi.org/10.3390/w11030426
APA StyleLi, Z., Zhang, H., Singh, V. P., Yu, R., & Zhang, S. (2019). A Simple Early Warning System for Flash Floods in an Ungauged Catchment and Application in the Loess Plateau, China. Water, 11(3), 426. https://doi.org/10.3390/w11030426








