A Mesh Reduced Method for Speeding Up Structured Grid-Based Water Quantity and Quality Models in Large-Scale River Networks
Abstract
:1. Introduction
2. Model Settings and Framework
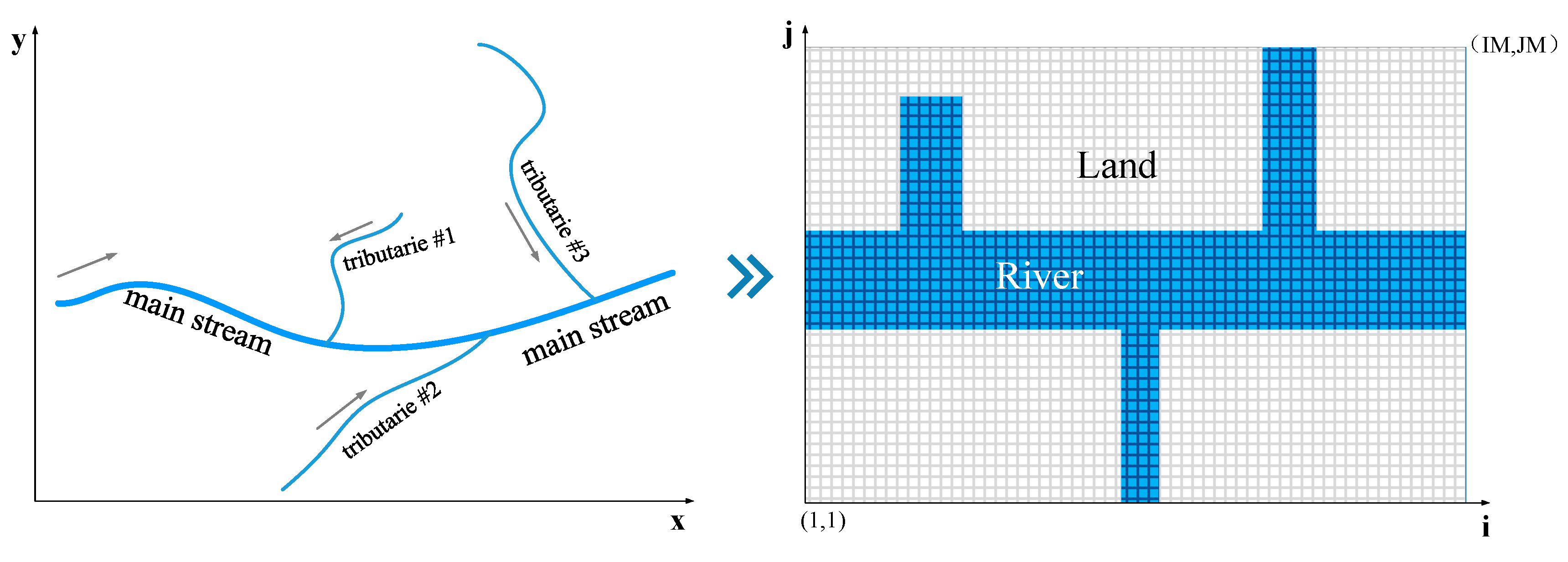
2.1. Structured Grids Settings for Models
2.2. Problems of Models with Structure Grids Used in River Network Areas
Do j=1, JM
…
End Do
End Do
2.3. Framework of the Mesh Reduced Method
Do i=1,IM
Do j=1,JM
IF(FSM(I,j)=0) THEN
IJM=IJM+1
x(IJM)=x(i,j)
y(IJM)=y(i,j)
zb(IJM)=zb(i,j)
i0(IJM)=i
j0(IJM)=j
End if
End Do
End Do
i=i0(ij)
j=j0(ij)
Do k=1,IJM
if(i-1>0)then
if(i-1.eq.i0(k).and.j.eq.j0(k))then
ij1(ij)=k
end if
end if
if(i+1<IM)then
if(i+1.eq.i0(k).and.j.eq.j0(k))then
ij2(ij)=k
end if
end if
if(j-1>0)then
if(i.eq.i0(k).and.j-1.eq.j0(k))then
ij3(ij)=k
end if
end if
if(j+1<JM)then
if(i.eq.i0(k).and.j+1.eq.j0(k))then
ij4(ij)=k
end if
end if
End Do
End Do
3. Results and Discussion
3.1. The Improvement of ECOMSED
3.2. Application Areas and Model Setup
3.3. Grid Making and Grids One-Dimensioned
3.4. Accuracy Verification
- (1)
- The girds of ALB should be dry grids, which are close to wet grids.
- (2)
- Grids removed from the original computing zone (IM × JM) should be dry girds, where water can never cover in the real world.
- (3)
- The spatial relationship of all wet girds should be absolutely the same as in the original model.
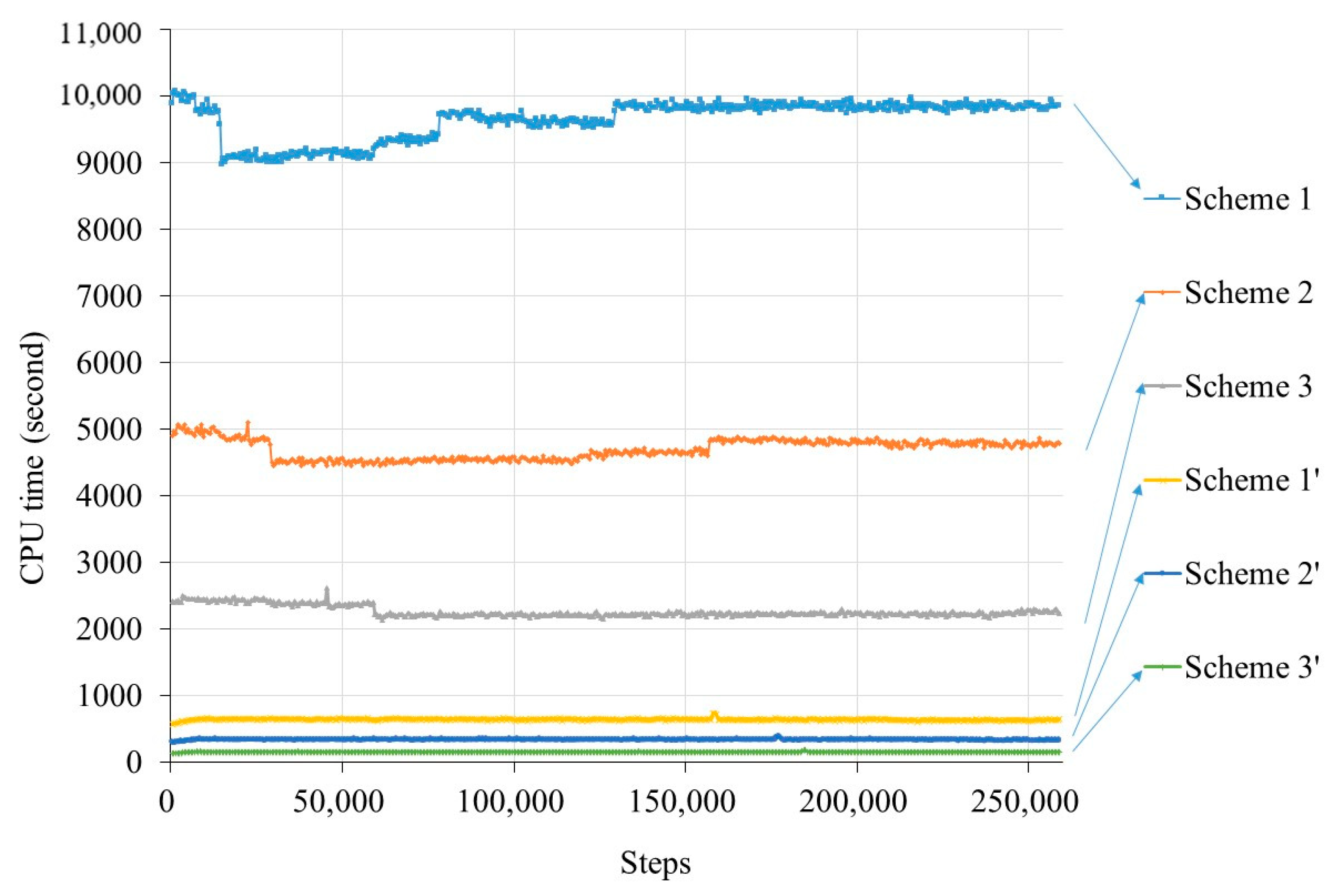
3.5. Improvement of Computational Efficiency
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Mattiussi, C. An Analysis of Finite Volume, Finite Element, and Finite Difference Methods Using Some Concepts from Algebraic Topology. J. Comput. Phys. 1997, 133, 289–309. [Google Scholar] [CrossRef] [Green Version]
- Bu, W.; Tang, Y.; Wu, Y.; Yang, J. Finite difference/finite element method for two-dimensional space and time fractional Bloch–Torrey equations. J. Comput. Phys. 2014, 293, 264–279. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C.; Hsu, M.H. Water quality modeling in a tidal estuarine system using a three-dimensional model. Environ. Eng. Sci. 2011, 28, 443–459. [Google Scholar] [CrossRef]
- Rathnayaka, K.; Malano, H.; Maheepala, S.; George, B.; Nawarathna, B.; Arora, M.; Roberts, P. Seasonal demand dynamics of residential water end-uses. Water 2015, 7, 202–216. [Google Scholar] [CrossRef]
- Mohajeri, S.H.; Righetti, M.; Wharton, G.; Romano, G.P. On the structure of turbulent gravel bed flow: Implications for sediment transport. Adv. Water Resour. 2016, 92, 90–104. [Google Scholar] [CrossRef]
- Fischer, C.; Nana, G.; Selberherr, S. Finite difference, boundary-fitted grid generation for arbitrarily shaped two-dimensional simulation areas. Comput. Methods Appl. Mech. Eng. 1993, 110, 17–24. [Google Scholar] [CrossRef]
- Velho, P.; Schnorr, L.M.; Casanova, H.; Legrand, A. On the validity of flow-level tcp network models for grid and cloud simulations. Acm Trans. Model. Comput. Simul. 2013, 23, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Jorgenson, P.C.E.; Pletcher, R.H. An implicit numerical scheme for the simulation of internal viscous flow on unstructured grids. Comput. Fluids 1996, 25, 447–466. [Google Scholar] [CrossRef]
- Hou, J.; Simons, F.; Mahgoub, M.; Hinkelmann, R. A robust well-balanced model on unstructured grids for shallow water flows with wetting and drying over complex topography. Comput. Methods Appl. Mech. Eng. 2013, 257, 126–149. [Google Scholar] [CrossRef]
- And, C.H.K.W.; Govardhan, R. Vortex-induced vibrations. Annu. Mech. 2004, 36, 413–455. [Google Scholar]
- Ezer, T.; Mellor, G.L. Sensitivity studies with the north atlantic sigma coordinate princeton ocean model. Dyn. Atmos. Ocean. 2000, 32, 185–208. [Google Scholar] [CrossRef]
- Blumberg, A.F. A Primer for ECOMSED User Manual: Versionl; Hydroqual. Inc.: Mahwah, NJ, USA, 2002; pp. 1–188. [Google Scholar]
- Irvine, K.N.; Pettibone, G.W. Dynamics of indicator bacteria populations in sediment and river water near a combined sewer outfall. Environ. Technol. Lett. 1993, 14, 531–542. [Google Scholar] [CrossRef]
- Quirk, J.J. An alternative to unstructured grids for computing gas dynamic flows around arbitrarily complex two-dimensional bodies. Comput. Fluids 1994, 23, 125–142. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.; Chandler-Wilde, S.N. A depth-tntegrated 2d coastal and estuarine model with conformal boundary-fitted mesh generation. Int. J. Numer. Methods Fluids 2015, 23, 819–846. [Google Scholar] [CrossRef]
- Medeiros, S.C.; Hagen, S.C.; Weishampel, J.F. Comparison of floodplain surface roughness parameters derived from land cover data and field measurements. J. Hydrol. 2012, 452–453, 139–149. [Google Scholar] [CrossRef]
- Cao, W.; Xu, C.F.; Wang, Z.H.; Yao, L.; Liu, H.Y. CPU/GPU computing for a multi-block structured grid based high-order flow solver on a large heterogeneous system. Clust. Comput. 2014, 17, 255–270. [Google Scholar] [CrossRef]
- Navarro, C.A.; Hitschfeldkahler, N.; Mateu, L.A. A Survey on Parallel computing and its applications in data-parallel problems using GPU architectures. Commun. Comput. Phys. 2014, 15, 285–329. [Google Scholar] [CrossRef]
- Xu, S.; Huang, X.; Zhang, Y.; Oey, L.Y.; Xu, F.; Fu, H.; Yang, G. gpuPOM: A GPU-based princeton ocean model. Geosci. Model Dev. Discuss. 2014, 7, 7651–7691. [Google Scholar] [CrossRef]
- Medeiros, S.C.; Hagen, S.C. Review of wetting and drying algorithms for numerical tidal flow models. Int. J. Numer. Methods Fluids 2013, 71, 473–487. [Google Scholar] [CrossRef]
- Schmalz, R. ROMS high resolution hindcasts for delaware river and bay. Am. Soc. Civ. Eng. 2014, 67–88. [Google Scholar]
- Srinivas, G.; Gowda, B.P.M. Aerodynamic Performance Comparison of Airfoils by Varying Angle of Attack Using Fluent and Gambit. Appl. Mech. Mater. 2014, 592–594, 1889–1896. [Google Scholar] [CrossRef]
- Kong, X.; Wu, D.J.; Cai, C.S.; Liu, Y.Q. New strategy of substructure method to model long-span hybrid cable-stayed bridges under vehicle-induced vibration. Eng. Struct. 2012, 34, 421–435. [Google Scholar] [CrossRef]
- Litrico, X.; Fromion, V.; Baume, J.P.; Arranja, C.; Rijo, M. Experimental validation of a methodology to control irrigation canals based on Saint-Venant equations. Control Eng. Pract. 2005, 13, 1425–1437. [Google Scholar] [CrossRef] [Green Version]
- Equation, N.S. Navier-Stokes equations. Acta Appl. Math. 1989, 28, 295–296. [Google Scholar]
- Aoki, K.I.; Sato, D. Solving the QCD non-perturbative flow equation as a partial differential equation and its application to dynamical chiral symmetry breaking. Prog. Theor. Exp. Phys. 2013, 4, 5834–5838. [Google Scholar] [CrossRef]
- Larsen, S.E. The Atmospheric Boundary Layer over Land and Sea: Focus on the Offshore Southern Baltic and Southern North Sea Region; DTU Wind Energy: Roskilde, Denmark, 2013; pp. 1–36. [Google Scholar]
- Yuan, S.; Lin, L.; Amini, F.; Tang, H. Numerical Study of Turbulence and Erosion of an HPTRM-Strengthened Levee under Combined Storm Surge Overflow and Wave Overtopping. J. Coast. Res. 2014, 30, 142–157. [Google Scholar]
- Wang, Y.G.; Yang, Y.Q.; Chen, X.L.; Engel, B.A.; Zhang, W.S. The moving confluence route technology with wad scheme for 3D hydrodynamic simulation in high altitude inland waters. J. Hydrol. 2018, 559, 411–427. [Google Scholar] [CrossRef]
- Shi, Y.Y.; Xu, G.H.; Wang, Y.G.; Engel, B.A.; Peng, H.; Zhang, W.S.; Cheng, M.L.; Dai, M.L. Modelling hydrology and water quality processes in the Pengxi River basin of the Three Gorges Reservoir using the soil and water assessment tool. Agric. Water Manag. 2017, 182, 24–38. [Google Scholar] [CrossRef]
- Kaazempur-Mofrad, M.R.; Ethire, C.R. An efficient characteristic galerkin scheme for the advection equation in 3-D. Comput. Methods Appl. Mech. Eng. 2002, 191, 5345–5363. [Google Scholar] [CrossRef]
- Allcock, B.; Bester, J.; Bresnahan, J.; Chervenak, A.L.; Foster, I.; Kesselman, C.; Tuecke, S. Data management and transfer in high-performance computational grid environments. Parallel Comput. 2002, 28, 749–771. [Google Scholar] [CrossRef] [Green Version]
- Itoh, T.; Yamaguchi, A.; Kyotani, T.; Hanaoka, T.A.; Mizukami, F. High-performance bio-sensor with enzymes immobilized on mesoporous membranes: Nanosized pores just corresponding to the size of an enzyme improve the stability of the sensor drastically. Adv. Porous Mater. 2016, 4, 157–165. [Google Scholar] [CrossRef]
- Zounmevo, J.A.; Afsahi, A. A fast and resource-conscious MPI message queue mechanism for large-scale jobs. Future Gener. Comput. Syst. 2014, 30, 265–290. [Google Scholar] [CrossRef]
- Kressler, B.; Spincemaille, P.; Prince, M.R.; Yi, W. Reduction of reconstruction time for time-resolved spiral 3D contrast-enhanced magnetic resonance angiography using parallel computing. Magn. Reson. Med. 2006, 56, 704–708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Efremenko, D.S.; Loyola, D.G.; Doicu, A.; Spurr, R.J.D. Multi-core-CPU and GPU-accelerated radiative transfer models based on the discrete ordinate method. Comput. Phys. Commun. 2014, 185, 3079–3089. [Google Scholar] [CrossRef]
- Johan, Z.; Mathur, K.K.; Johnsson, S.L.; Hughes, T.J.R. An efficient communications strategy for finite element methods on the Connection Machine CM-5 system. Comput. Methods Appl. Mech. Eng. 1994, 113, 363–387. [Google Scholar] [CrossRef]
- Kennedy, G.J.; Martins, J.R.R.A. A parallel finite-element framework for large-scale gradient-based design optimization of high-performance structures. Finite Elem. Anal. Des. 2014, 87, 56–73. [Google Scholar] [CrossRef]
- Pettit, J.R.; Waiker, A.E.; Lowe, M.J.S. Improved detection of rough defects for ultrasonic NDE inspections based on finite element modeling of elastic wave scattering. AIP Conf. Proc. 2014, 1581, 521–528. [Google Scholar]
- Chen, C.H.; Chu, W.C.; Lu, C.W.; Chung, Y.C.; Yang, D.L. A Parallel Program Generation Environment for Solving PDEs on Distributed Memory Computing Environments. Asian J. Inf. Technol. 2012, 11, 1025–1038. [Google Scholar]


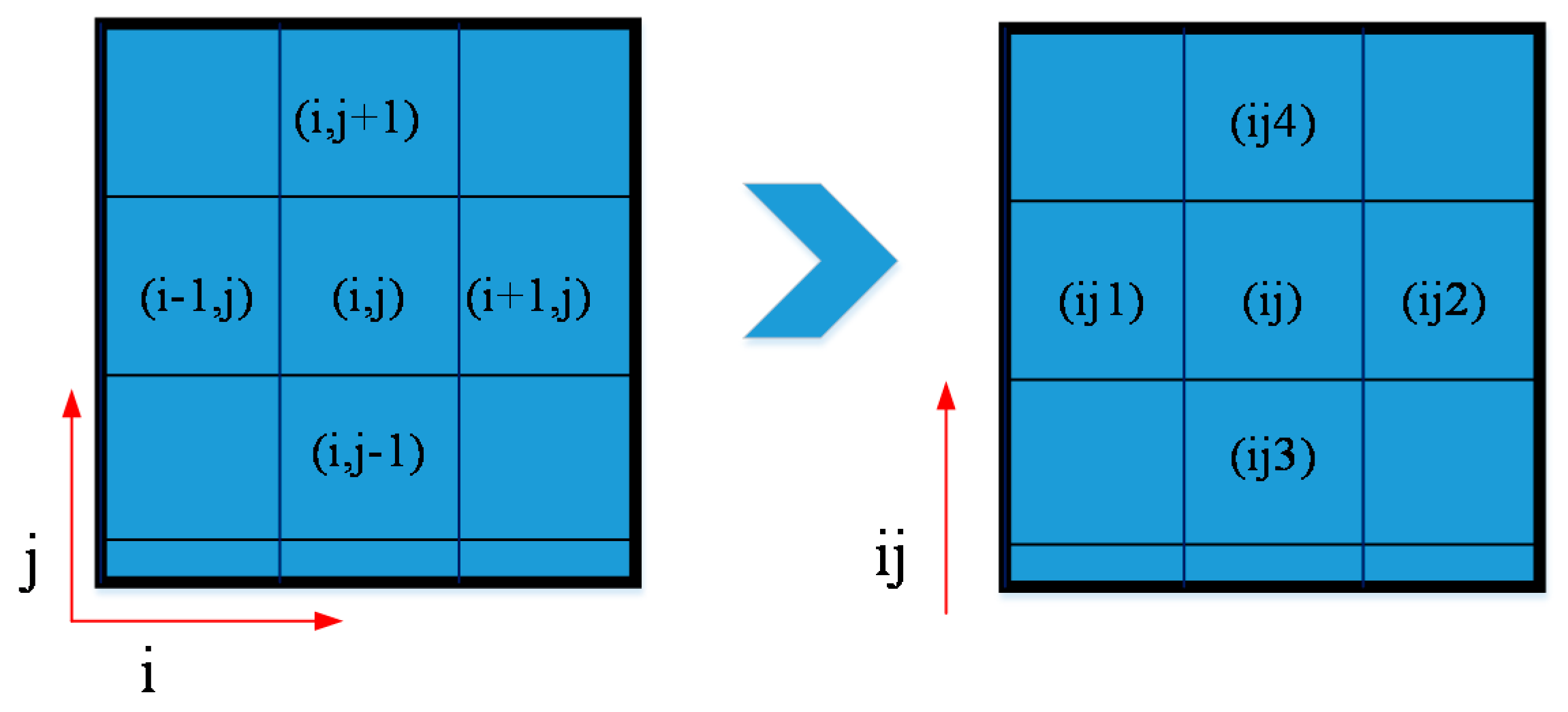


| Original Variables | Replaced Variables |
|---|---|
| do i=1, IM do j=1, JM do j=1, JM or do i=1, IM | do ij=1, IJM |
| i, j | (ij) |
| i−1, j | ij1(ij) |
| i+1, j | ij2(ij) |
| i, j−1 | ij3(ij) |
| i, j+1 | ij4(ij) |
| i−2, j | ij1(ij1(ij)) |
| i+2, j | ij2(ij2(ij)) |
| … | … |
| Contents | Relative Errors |
|---|---|
| flow velocity in u direction | 0.002% |
| flow velocity in v direction | 0.001% |
| water level | 0.000% |
| sediment concentration | 0.006% |
| Schemes | IM | JM | IM × JM | Schemes | IJM | Grids Reduction Rate |
|---|---|---|---|---|---|---|
| Scheme 1 | 1064 | 232 | 246,848 | Scheme 1′ | 26,069 | 89.44% |
| Scheme 2 | 532 | 232 | 123,424 | Scheme 2′ | 13,115 | 89.37% |
| Scheme 3 | 532 | 116 | 61712 | Scheme 3′ | 6492 | 89.48% |
| Efficiency Index | Schemes | 1 day | 10 days | 20 days | 30 days |
|---|---|---|---|---|---|
| Sip (105) | Scheme 1 | 1.11 | 1.22 | 1.22 | 1.22 |
| Scheme 2 | 1.13 | 1.25 | 1.26 | 1.26 | |
| Scheme 3 | 1.03 | 1.14 | 1.14 | 1.14 | |
| Scheme 1’ | 0.90 | 0.88 | 0.93 | 0.95 | |
| Scheme 2’ | 0.91 | 0.87 | 0.88 | 0.90 | |
| Scheme 3’ | 0.87 | 0.88 | 0.84 | 0.83 | |
| Sp | Scheme 1’-1 | 16.26 | 14.62 | 14.90 | 15.09 |
| Scheme 2’-2 | 15.91 | 14.10 | 14.08 | 14.23 | |
| Scheme 3’-3 | 17.05 | 15.58 | 15.20 | 15.07 |
| Schemes | 1 day | 10 days | 20 days | 30 days | Average |
|---|---|---|---|---|---|
| Scheme 1’-1 | 18.92% | 27.87% | 23.77% | 22.13% | 23.17% |
| Scheme 2’-2 | 19.47% | 30.40% | 30.16% | 28.57% | 27.15% |
| Scheme 3’-3 | 15.53% | 22.81% | 26.32% | 27.19% | 22.96% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.; Wang, Y.; Xu, J.; Yang, S.; Hou, H. A Mesh Reduced Method for Speeding Up Structured Grid-Based Water Quantity and Quality Models in Large-Scale River Networks. Water 2019, 11, 437. https://doi.org/10.3390/w11030437
Kang J, Wang Y, Xu J, Yang S, Hou H. A Mesh Reduced Method for Speeding Up Structured Grid-Based Water Quantity and Quality Models in Large-Scale River Networks. Water. 2019; 11(3):437. https://doi.org/10.3390/w11030437
Chicago/Turabian StyleKang, Jin, Yonggui Wang, Jing Xu, Shuihua Yang, and Haobo Hou. 2019. "A Mesh Reduced Method for Speeding Up Structured Grid-Based Water Quantity and Quality Models in Large-Scale River Networks" Water 11, no. 3: 437. https://doi.org/10.3390/w11030437
APA StyleKang, J., Wang, Y., Xu, J., Yang, S., & Hou, H. (2019). A Mesh Reduced Method for Speeding Up Structured Grid-Based Water Quantity and Quality Models in Large-Scale River Networks. Water, 11(3), 437. https://doi.org/10.3390/w11030437





