Comparative Study of Regional Frequency Analysis and Traditional At-Site Hydrological Frequency Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Methods
2.2.1. Regional Frequency Analysis
2.2.2. Data Preparation
2.2.3. Identification of Homogeneous Regions
- (1)
- The discordancy measure. The discordancy measure is mentioned in 2.2.2. In addition to being used to detect whether the original data is reasonable or not, the discordancy measure can also be used to test whether each site in the initially formed homogeneous region is a discordant point of the region. If the discordance statistic Di of a site exceeds the critical value, moving the site to another adjacent homogeneous region may be considered.
- (2)
- The heterogeneity measure. Hosking et al. [31] recommended the use of a heterogeneity measure to determine whether the region formed by preliminary division is a homogeneous region. The calculation formula for the heterogeneity measure is as follows:where ni is the length of the rainfall data series of the i-th station in the homogeneous region, ti is the L-Cv of the i-th station in the homogeneous region, N is the total number of stations in the homogeneous region, and μv and σv are the mean and mean square error of V1 obtained by Monte Carlo simulations, respectively. H1 < 1 indicated that the area was an acceptable homogeneous region, 1 ≤ H1 < 2 indicated that the area was a possible heterogeneous area, and H1 ≥ 2 indicated that the area was a heterogeneous area. If the value of H1 did not meet the standard, the site within the region needed to be adjusted until it met the criteria to become an acceptable homogeneous region. According to experience, there were several useful ways to adjust the sites: (1) move a site or few sites from one region to the adjacent one; (2) subdivide the region; (3) merge two or more regions and redefine groups; and (4) break up the region by reassigning its sites to other regions.
2.2.4. The Optimal Frequency Distribution
2.2.5. Rainfall Estimation
- (1)
- The annual maximum daily rainfall data of each station in the homogeneous region is averaged to generate a new rainfall data sequence. The calculation expression is as follows:where j = 1,2,……; i = 1,2,……N; Qij represents the measured rainfall data sequence of the i-th site; and is the average rainfall value of the measured rainfall data sequence of the i-th site.
- (2)
- The L-moment parameters L-Cv, L-Cs, and L-Ck, and the weighted average of the L-moment parameters of each station in each homogeneous region are obtained, that is, the regional average L-moment parameters of the homogeneous region is obtained. Its calculation expression is:where tR and trR are the weighted average of the L-moment parameters of each station in each homogeneous region. N is the number of sites in the region, ni is the measured rain data sequence length for the i-th site.
- (3)
- Estimate the distribution function parameters of the optimal frequency distribution of the region determined by the goodness-of-fit test, and then the quantiles under different return periods are obtained by the quantile functions of the chosen frequency distribution.
- (4)
- The principle of the index flood method is to treat the rainfall at each site as two components, one representing the rainfall unique to the site and the other representing the rainfall that reflects the rainfall characteristics common to the homogeneous region. The quantiles under different return periods represent the rainfall characteristics shared by the reaction area and the unique rainfall characteristics of the site, that is, the multi-year average rainfall of the site. The expression of the rainfall estimation is as follows:where QT,i,j is the estimation of the rainstorm in which the return period of the j-th station is in the i-th region. qT,i is the quantile corresponding to the return period of the i-th region. is the average annual maximum daily rainfall for site j.
2.2.6. Traditional At-Site Hydrological Frequency Analysis
3. Results
3.1. The Differences of Optimal Frequency Distributions
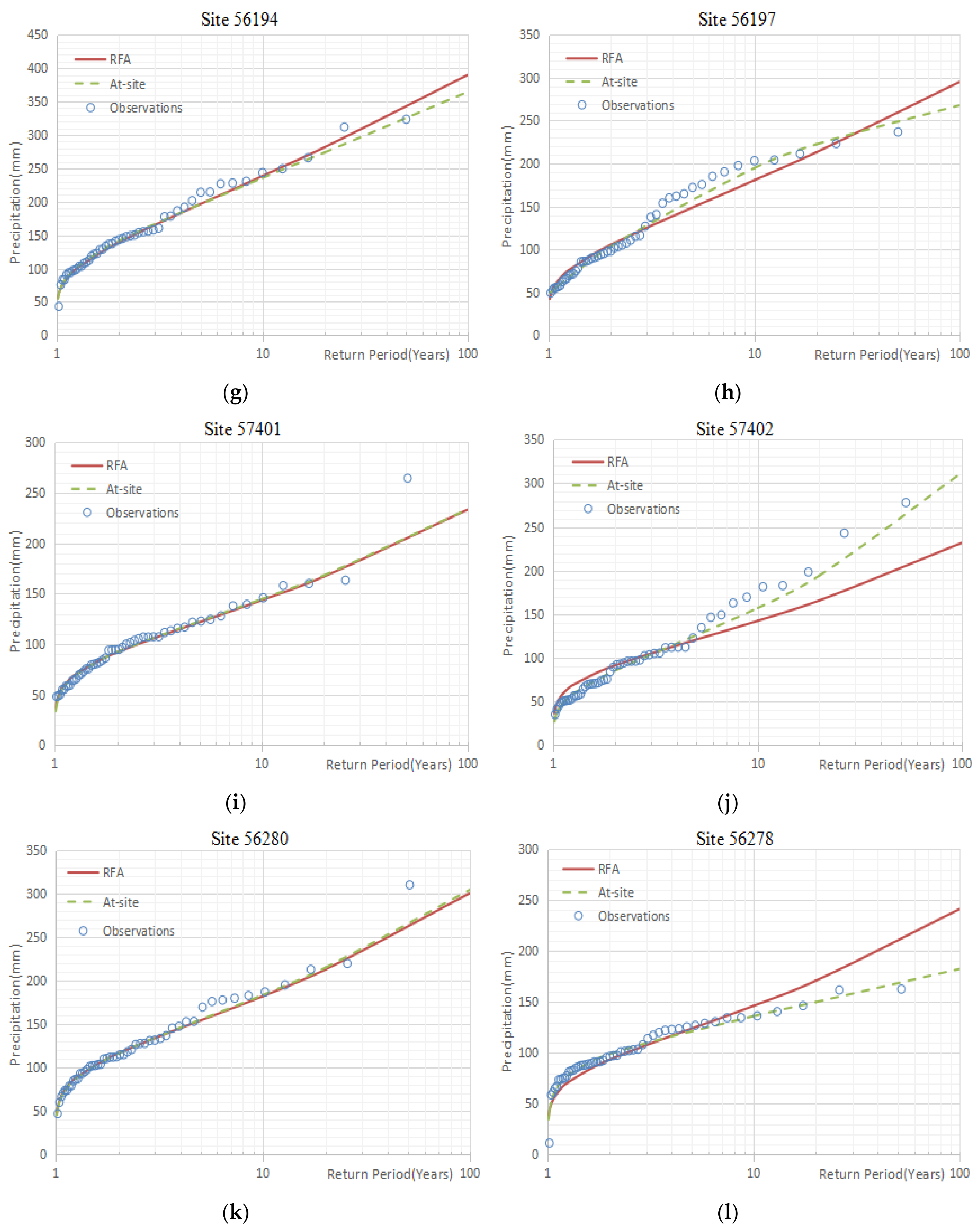
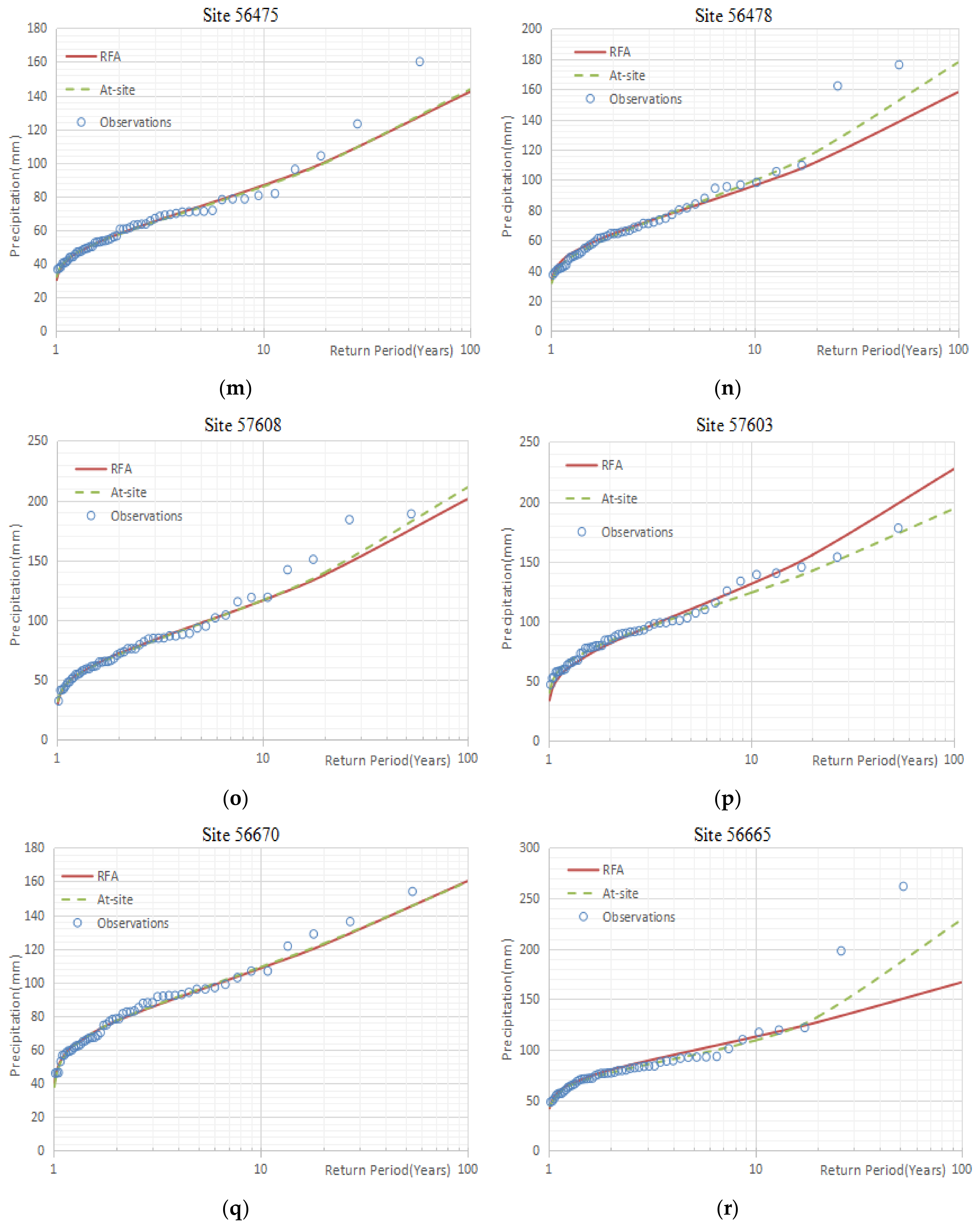
3.2. Comparison of Fitting Results
3.3. The Differences between the Estimations
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kysely, J.; Picek, J.; Huth, R. Formation of homogeneous regions for regional frequency analysis of extreme precipitaion events in the Czech Republic. Stud. Geophys. Geod. 2006, 51, 327–344. [Google Scholar] [CrossRef]
- Okada, N.; Kusaka, T.; Sassa, K.; Takayama, T.; Sakakibara, H. Water Hazards Caused by Naturally-Occurring Hydrologic Extremes. Knowledge for Sustainable Development: An Insight into the Encyclopedia of Life Support Systems; UNESCO, EOLSS: Oxford, UK, 2002; pp. 243–263. [Google Scholar]
- Shabri, A.B.; Daud, Z.M.; Ariff, N.M. Regional analysis of annual maximum rainfall using TL-moments method. Theor. Appl. Climatol. 2011, 104, 561–570. [Google Scholar] [CrossRef]
- Ngongondo, C.S.; Xu, C.Y.; Tallaksen, L.M. Regional frequency analysis of rainfall extremes in Southern Malawi using the index rainfall and L-moments approaches. Stoch. Environ. Res. Risk Assess. 2011, 25, 939–955. [Google Scholar] [CrossRef]
- Wang, J.Q.; Gu, W.Y.; Yao, H.M. Seasonal variations of precipitation and rainstorm in China. Adv. Water Sci. 1997, 8, 108–116. [Google Scholar]
- Khan, S.A.; Hussain, I.; Hussain, T.; Faisal, M.; Muhammad, Y.S.; Shoukry, A.M. Regional frequency analysis of extremes precipitation using L-moments and partial L-moments. Adv. Meteorol. 2017, 2017, 6954902. [Google Scholar] [CrossRef]
- Hossein, M.; Arash, Z.G. Regional frequency analysis of daily rainfall extremes using L-moments approach. Atmósfera 2014, 27, 411–427. [Google Scholar]
- Zhang, Q.; Xiao, M.; Singh, V.P.; Li, J. Regionalization and spatial changing properties of droughts across the Pearl River Basin, China. J. Hydrol. 2012, 472–473, 355–366. [Google Scholar] [CrossRef]
- Abolverdi, J.; Khalili, D. Development of regional rainfall annual maxima for southwestern Iran by L-moments. Water Resour. Manag. 2010, 24, 2501–2526. [Google Scholar] [CrossRef]
- Smithers, J.C.; Schulze, R.E. A methodology for the estimation of short duration design storms in South Africa using a regional approach based on L-moments. J. Hydrol. 2001, 241, 42–52. [Google Scholar] [CrossRef]
- Lin, B.; Bonnin, G.M.; Martin, D.L. Regional Frequency Studies of Annual Extreme Precipitation in the United States Based on Regional L-Moments Analysis; ASCE Proceedings: Omaha, NE, USA, 2006. [Google Scholar]
- Haddad, K.; Rahman, A. Regional flood frequency analysis in eastern Australia: Bayesian GLS regression-based methods within fixed region and ROI framework—Quantile regression vs. parameter regression technique. J. Hydrol. 2012, 430–431, 142–161. [Google Scholar] [CrossRef]
- Durocher, M.; Burn, D.H.; Zadeh, S.M. A nationwide regional flood frequency analysis at ungauged sites using ROI/GLS with copulas and super regions. J. Hydrol. 2018, 567, 191–202. [Google Scholar] [CrossRef]
- Abdi, A.; Hassanzadeh, Y.; Talatahari, S.; Fakheri-Fard, A.; Mirabbasi, R.; Ouarda, T.B.M.J. Multivariate regional frequency analysis: Two new methods to increase the accuracy of measures. Adv. Water Resour. 2017, 107, 290–300. [Google Scholar] [CrossRef]
- Chen, Y.F.; Wang, Q.R.; Sha, Z.G. Application of L-moment based regional flood frequency analysis method to middle and lower Yangtze River. J. Hohei Univ. Nat. Sci. 2002, 31, 207–211. [Google Scholar]
- Wu, J.M.; Lin, B.Z.; Shao, Y.H. Application of regional L-moments analysis method in precipitation frequency analysis for Taihu Lake Basin. J. China Hydrol. 2015, 35, 15–22. [Google Scholar]
- Shao, Y.H.; Wu, J.M.; Li, M. Frequency analysis of extreme precipitation in Huaihe River Basin based on hydrometeorological regional L-moments method. J. China Hydrol. 2016, 36, 16–23. [Google Scholar]
- Xiong, L.H.; Guo, S.L.; Wang, C.J. Advance in regional flood frequency analysis from abroad. Adv. Water Sci. 2004, 15, 261–267. [Google Scholar]
- Li, M.; Lin, B.Z.; Shao, Y.H. Study on spatial continuity of precipitation quantile estimates based on regional L-moments analysis. J. China Hydrol. 2015, 35, 14–19. [Google Scholar]
- Liang, Y.Y.; Liu, S.G.; Zhong, G.H. Comparison between conventional moments and L-moments in rainfall frequency analysis for Taihu Lake Basin. J. China Hydrol. 2013, 33, 16–21. [Google Scholar]
- Hassan, B.G.H.; Ping, F. Regional rainfall frequency analysis for the luanhe basin—By using L-moments and cluster techniques. APCBEE Procedia 2012, 1, 126–135. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, S.; Guo, Y. L-moment-based regional frequency analysis of annual extreme precipitation and its uncertainty analysis. Water Resour. Manag. 2017, 31, 3899–3919. [Google Scholar] [CrossRef]
- Yang, T.; Chen, X.; Yang, H.W.; Xie, H.W. Regional flood frequency analysisin in Pearl River Delta region based on L-moments approach. J. Hohei Univ. Nat. Sci. 2009, 37, 615–619. [Google Scholar]
- State Environmental Protection Administration. National Ecological Status Survey and Assessment; China Environmental Science Press: Beijing, China, 2006. [Google Scholar]
- Chen, C.; Pang, Y.M.; Pan, X.B.; Wang, C.Y. Analysis on change of reference crop evapotranspiration and climatic influence factors in Sichuan. Chin. J. Agrometeorol. 2011, 32, 35–40. [Google Scholar]
- Zhou, C.Y.; Cen, S.X.; Li, Y.Q. Precipitation variation and its impacts in Sichuan in the last 50 years. Acta Geogr. Sin. 2011, 66, 619–630. [Google Scholar]
- Du, H.M.; Yan, J.P. Climatic change and drought-flood regional responses in Sichuan. Resour. Sci. 2013, 35, 2491–2500. [Google Scholar]
- Li, M.R.; Ao, T.Q.; Li, X.D. Regional L-moments analysis-based study on hydrological frequency analysis of Sichuan Province. Water Resour. Hydropower Eng. 2018, 49, 54–61. [Google Scholar]
- Hosking, J.R.M. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. B Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Dalrymple, T. Flood Frequency Analysis. Manual of Hydrology: Part 3. Flood-Flow Techniques. Water Supply Paper 1543-A; United States Geological Survey: Reston, VA, USA, 1960; 8p. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Hemin, S.; Wang, G.J.; Li, X.C.; Chen, J.; Su, B.D.; Jiang, T. Regional frequency analysis of observed sub-daily rainfall maxima over Eastern China. Adv. Atmos. Sci. 2017, 34, 209–225. [Google Scholar]
- Burn, D.H. Cluster analysis as applied to regional flood frequency. J. Water Resour. Plan. Manag. 1989, 115, 567–582. [Google Scholar] [CrossRef]
- Jin, G.Y. General extreme value distribution and its application to hydrology. J. China Hydrol. 1998, 2, 10–16. [Google Scholar]
- Jin, G.Y. Principles and Methods of Hydrology Statistics, 2nd ed.; China Industry Press: Beijing, China, 1964; pp. 1–338. [Google Scholar]
- Department of Hydrology, Ministry of Water Resources. Chinese Hydrology Journal; China Water Resources and Hydropower Press: Beijing, China, 1997; pp. 214–216. [Google Scholar]
- Ministry of Water Resources; Ministry of Power Industry. Specification for Design Flood Calculation of Water Conservancy and Hydropower Projects: SDJ22-79 (Trial); Water Power Press: Beijing, China, 1980. [Google Scholar]
- Liang, Z.M.; Zhong, P.A.; Hua, J.P. Hydrology and Water Calculation, 2nd ed.; China Water & Power Press: Beijing, China, 2008; p. 27. [Google Scholar]
- Guo, S.L.; Liu, Z.J.; Xiong, L.H. Advances and assessment on design flood estimation methods. J. Hydraul. Eng. 2016, 47, 302–314. [Google Scholar]
- Ministry of Water Resources; Ministry of Power Industry. Specification for Design Flood Calculation of Water Conservancy and Hydropower Projects: SL44-2006; Water Power Press: Beijing, China, 2006. [Google Scholar]





| Region | Name | Number | Discordancy | Length (Years) | Average (mm) | Cv | Cs | Ck |
|---|---|---|---|---|---|---|---|---|
| 1 | Litang | 56,257 | 0.16 | 57 | 35.68 | 0.1338 | 0.1562 | 0.1660 |
| Xinlong | 56,251 | 1.96 | 50 | 28.38 | 0.1167 | 0.0577 | 0.2052 | |
| 2 | Jiuzhaigou | 56,097 | 0.2 | 50 | 30.83 | 0.1440 | 0.1723 | 0.1747 |
| A’ba | 56,171 | 1.93 | 55 | 33.22 | 0.1631 | 0.3773 | 0.3467 | |
| 3 | Liangzhong | 57,306 | 0.02 | 51 | 100.65 | 0.2101 | 0.1757 | 0.1748 |
| Xichong | 57,309 | 1.75 | 49 | 92.22 | 0.2042 | 0.1660 | 0.2385 | |
| 4 | Beichuan | 56,194 | 0.19 | 49 | 153.43 | 0.2218 | 0.1998 | 0.1557 |
| Shifang | 56,197 | 2.37 | 49 | 116.17 | 0.2531 | 0.2122 | 0.0773 | |
| 5 | Shehong | 57,401 | 0.05 | 50 | 98.34 | 0.2074 | 0.1931 | 0.1840 |
| Pengxi | 57,402 | 2.86 | 52 | 97.71 | 0.2757 | 0.2967 | 0.1890 | |
| 6 | Minshan | 56,280 | 0.06 | 50 | 125.29 | 0.2081 | 0.2135 | 0.1950 |
| Tianquan | 56,278 | 2.8 | 51 | 100.42 | 0.1591 | 0.0583 | 0.1662 | |
| 7 | Yuexi | 56,475 | 0.38 | 56 | 61.97 | 0.1732 | 0.2695 | 0.2384 |
| Xide | 56,478 | 1.58 | 50 | 68.88 | 0.2017 | 0.2868 | 0.2440 | |
| 8 | Xuyong | 57,608 | 0.11 | 52 | 78.60 | 0.2175 | 0.2795 | 0.2333 |
| Hejiang | 57,603 | 2.02 | 52 | 88.77 | 0.1752 | 0.2042 | 0.1831 | |
| 9 | Miyi | 56,670 | 0.07 | 53 | 80.44 | 0.1573 | 0.1627 | 0.1650 |
| Yanbian | 56,665 | 2.65 | 51 | 83.73 | 0.1794 | 0.3564 | 0.3705 |
| Number of Sites in Region | Critical Value |
|---|---|
| 5 | 1.333 |
| 6 | 1.648 |
| 7 | 1.917 |
| 8 | 2.14 |
| 9 | 2.329 |
| 10 | 2.491 |
| 11 | 2.632 |
| 12 | 2.757 |
| 13 | 2.869 |
| 14 | 2.971 |
| ≥15 | 3 |
| Region | Site | ZDIST | At-Site Optimal Frequency Distribution | Regional Optimal Frequency Distribution | ||||
|---|---|---|---|---|---|---|---|---|
| GLO | GEV | GNO | PE3 | GPD | ||||
| 1 | 56257 | −0.83 | −1.41 | −1.39 | −1.47 | −2.57 | GLO | GLO |
| 56251 | −1.38 | −2.37 | −2.2 | −2.23 | −4.25 | GLO | ||
| 2 | 56097 | 0.21 | −0.46 | −0.55 | −0.78 | −1.95 | GLO | GLO |
| 56171 | −1.36 | −1.54 | −1.83 | −2.32 | −2.14 | GLO | ||
| 3 | 57306 | 0.25 | −0.43 | −0.52 | −0.76 | −1.91 | GLO | GLO |
| 57309 | −1.59 | −2.24 | −2.3 | −2.51 | −3.65 | GLO | ||
| 4 | 56194 | 0.8 | 0.11 | −0.04 | −0.38 | −1.46 | GNO | GEV |
| 56197 | 2.99 | 2.15 | 1.92 | 1.45 | 0.21 | GPD | ||
| 5 | 57401 | 0.14 | −0.46 | −0.58 | −0.85 | −1.81 | GLO | GLO |
| 57402 | 0.67 | 0.28 | −0.02 | −0.53 | −0.77 | GNO | ||
| 6 | 56280 | 0.05 | −0.47 | −0.63 | −0.92 | −1.7 | GLO | GLO |
| 56278 | 0.02 | −0.98 | −0.81 | −0.85 | −2.88 | GLO | ||
| 7 | 56475 | −0.41 | −0.79 | −1.01 | −1.39 | −1.75 | GLO | GLO |
| 56478 | −0.35 | −0.67 | −0.89 | −1.27 | −1.51 | GLO | ||
| 8 | 57608 | −0.16 | −0.5 | −0.72 | −1.09 | −1.38 | GLO | GLO |
| 57603 | 0.23 | −0.35 | −0.49 | −0.78 | −1.68 | GLO | ||
| 9 | 56670 | 0.36 | −0.37 | −0.43 | −0.65 | −1.94 | GLO | GLO |
| 56665 | −2.08 | −2.29 | −2.56 | −3.03 | −2.93 | Wakeby | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Li, X.; Ao, T. Comparative Study of Regional Frequency Analysis and Traditional At-Site Hydrological Frequency Analysis. Water 2019, 11, 486. https://doi.org/10.3390/w11030486
Li M, Li X, Ao T. Comparative Study of Regional Frequency Analysis and Traditional At-Site Hydrological Frequency Analysis. Water. 2019; 11(3):486. https://doi.org/10.3390/w11030486
Chicago/Turabian StyleLi, Mengrui, Xiaodong Li, and Tianqi Ao. 2019. "Comparative Study of Regional Frequency Analysis and Traditional At-Site Hydrological Frequency Analysis" Water 11, no. 3: 486. https://doi.org/10.3390/w11030486
APA StyleLi, M., Li, X., & Ao, T. (2019). Comparative Study of Regional Frequency Analysis and Traditional At-Site Hydrological Frequency Analysis. Water, 11(3), 486. https://doi.org/10.3390/w11030486




