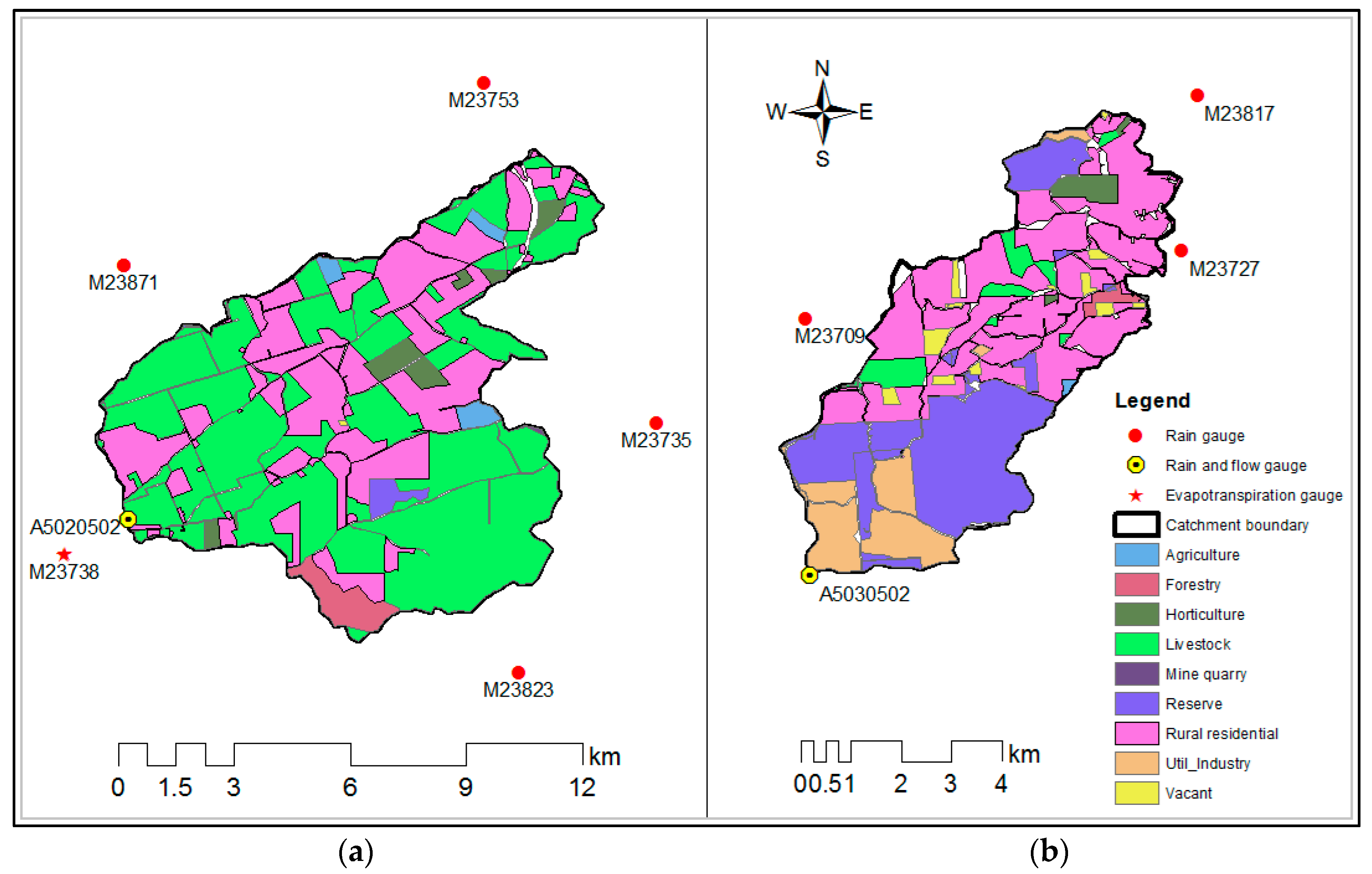
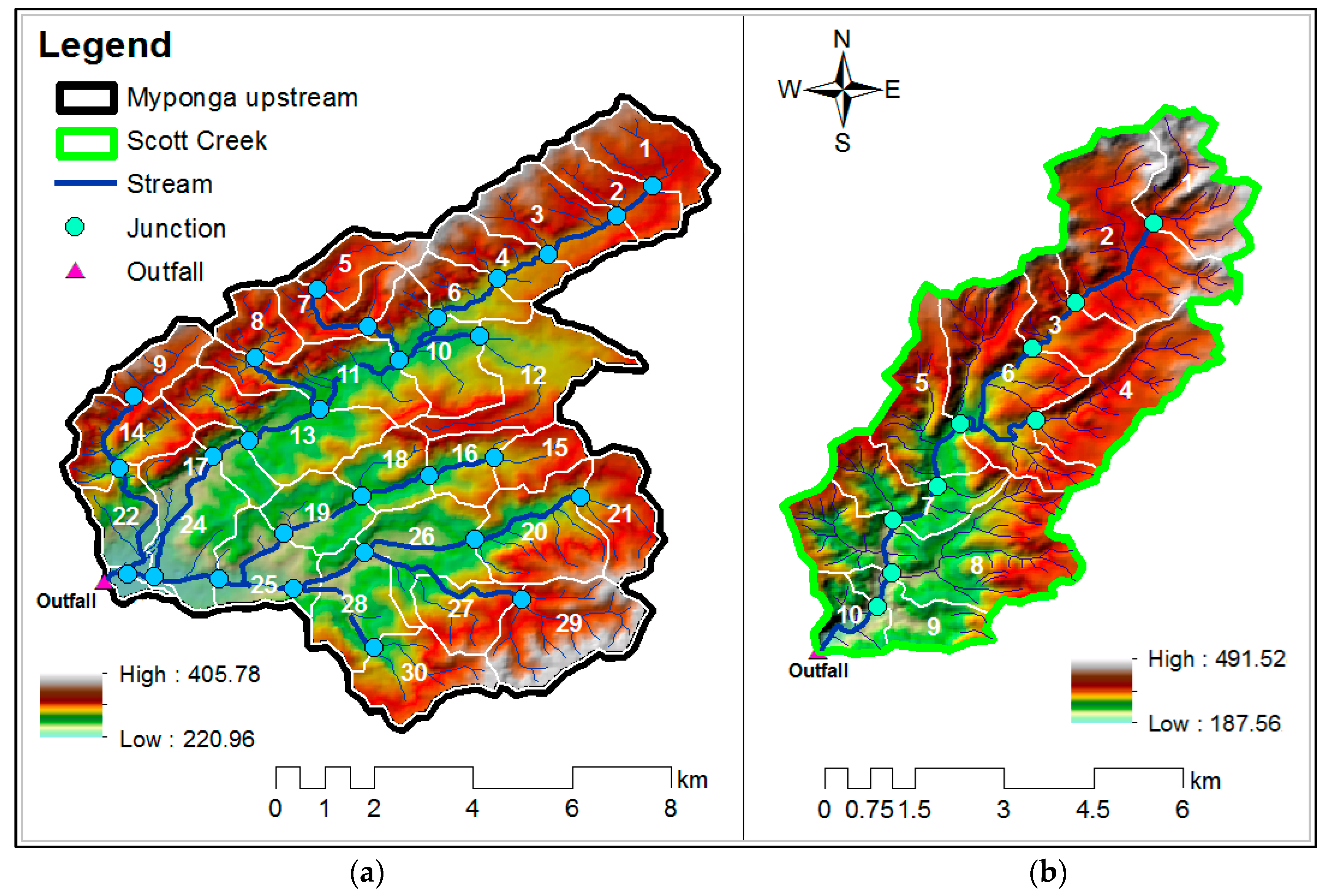
1. Introduction
Rainfall–runoff (RR) models are important tools for planning, design and management of water resource systems. These models are used in a wide range of hydrological applications ranging from the estimation of catchment runoff to analyzing the impact of land-use change on runoff [
1]. The methods of synthesizing the rainfall–runoff process in these models differ from one model to another, consequently a variety of model classifications exist. According to Brocca et al. [
2], RR models can be classified based on their spatial structure (lumped versus semi-distributed or distributed), time representation (continuous time versus event-based) or process description (physically meaningful versus data-driven). Daniel et al. [
3] adopted four different classifications for RR models based on: (i) parameter specification (deterministic or stochastic); (ii) the nature of the basic algorithms (empirical, conceptual or physically-based); (iii) spatial representation (lumped, semi-distributed or distributed); and (iv) the temporal representation (event-based or continuous time). Similar classifications can be found in Elga et al. [
4], Singh [
5] and Wheater et al. [
6]. Of the available models, spatial and temporal representations are the most commonly adopted model types [
7,
8], while event-based (EB) and continuous simulation (CS) models are the most recognized category within the temporal domain [
4,
5]. In EB modelling, the rainfall–runoff process in a catchment is simulated for a single rainfall or streamflow event with durations ranging from several hours to several days. Whereas in CS modelling the rainfall–runoff process is simulated for a long time period ranging from a couple of months to several years, including both dry and wet seasons. Generally, in EB modelling, only the infiltration process is modelled in order to account for losses, while in CS modelling, the evapotranspiration loss is also accounted for [
9].
CS and EB models both have advantages and limitations. One major advantage of CS modelling is that it is capable of accounting for antecedent conditions such as initial soil-moisture status, stream and reservoir level, water table depth, etc. [
10,
11]. In contrast, EB models are unable to account for antecedent conditions, instead values are subjectively assigned by the user and then calibrated using an observed hydrograph [
12,
13]. The great disadvantage of CS modelling is that it requires a long period of hydrological observations making its application challenging in case of a limited data availability [
14,
15]. EB modelling offers more flexibility in this case as it does not require a long period of hydrological data [
14,
16].
Catchment urbanization, land-use and land-cover are some dominant factors affecting the performance of RR modelling [
1,
14,
15,
17]. Hydrological processes can greatly alter due to land use change and therefore runoff generation process in a rural catchment is different to that of an urban catchment. [
14,
15,
16,
17]. In rural catchments, runoff patterns and paths on the soil surface evolve from natural conditions such as topography and land use, whereas in urbanized catchments, flow paths are mainly predefined by the sewer and stormwater management system and hence the runoff is not obstructed by any significant retention process [
14,
15,
18]. Hydrographs generated from urban catchments are more likely to have spikey shapes because during a storm event runoff reaches a peak quickly by following the sewerage path and falls quickly, once rainfall ceases [
1,
15]. On the other hand, streamflow hydrographs generated in rural catchments are more likely to have gentle shapes, with streamflows peaking relatively slowly during a storm event and falling gradually over a long period after the storm is over [
15,
17]. Generally, rural catchments are dominated by pervious surfaces with a wide range of vegetation cover and hence, are subject to more substantial runoff losses and flow peaks are delayed [
1,
14,
16,
17]. On the other hand, urban catchments are dominated by impervious areas that are directly connected to the sewerage or stormwater systems, thereby resulting in a quick peak during a storm event. Therefore, depending on the catchment condition, there is a clear distinction between hydrographs generated by urban and rural catchments, consequently the performance of EB and CS models can vary from one catchment to another.
Many researchers have found that an EB approach performed better than the CS approach for their case study catchments. For example, Chu et al. [
8] compared continuous and EB approaches on Mona Lake Watershed in West Michigan and obtained a better fit using an EB model. Similarly, De Silva et al. [
19] studied the hydrology of the Kelani River basin in Sri Lanka and found that the EB model performed better when simulating extreme events. Sampath et al. [
20] used continuous and EB approaches to predict streamflow hydrographs from Tittawella tank catchment in Sri Lanka and found that the EB model performed better over the relatively short study period. Azmat et al. [
21] studied a high-altitude watershed using continuous and EB modelling and found the EB model was more accurate. In contrast, Cunderlik and Simonovic [
22] found that CS was able to produce more reliable hydrographs. In the recent review of ARR 2016 (Australian rainfall–runoff) [
16], CS model is reported to have limited ability to represent rural catchment behavior, which contrasts with other researchers including Brocca et al. [
2], Boughton and Droop [
23], Paquet et al. [
24], who have successfully used the CS approach to estimate design floods and carry out real time flood forecasting. Furthermore, Kemp and Hewa [
25] have recently found that EB modelling performed by RORB (run-off routing burroughs) [
12], as recommended by ARR 2016, was unable to produce reliable flood quantiles at more frequent events. Therefore, it is both timely and important to explore the ability of EB and CS modelling approaches to accurately estimate runoff hydrographs and design floods resulting from more frequent events. The focus of the above cited studies has been to assess the performance of EB and CS modelling in reproducing the observed streamflow hydrograph (also known as total runoff hydrograph), while the current study considered both total runoff hydrograph (TRH) as well as direct runoff hydrograph (DRH).
The DRH is the hydrograph that remains after removing baseflow from the TRH. Baseflow represents the usual day to day flow that appears in a stream because of groundwater seepage. The separation of baseflow from the total hydrograph is an inexact science because the direct runoff and baseflow are distinct processes and are partially interrelated [
26,
27,
28]. However, various graphical and filtering techniques have been developed to perform baseflow separation (see
Section 2.5 for details) [
28,
29,
30,
31,
32,
33]. The study of DRHs is important in order to understand the influence of the various hydrological processes that govern flow generation from a catchment [
26] and because the timing, duration and magnitude of groundwater flows is quite distinct from that of direct runoff [
27], understanding these distinct processes is the key to identifying the likely hydrologic response characteristics of a catchment [
34].
Nowadays, several computer-based RR modelling tools have been developed that frequently used in hydrological studies across worldwide. Among them, RORB [
12], WBNM (watershed bounded network model) [
35], RAFTS (runoff analysis and flow training simulation) [
36] and ILSAX [
37] are EB modelling tools commonly used in Australia. In contrast, some RR modelling tools have been developed that can conduct both EB and CS modelling. Examples of widely used such modelling tools include: HEC-HMS (RR model developed by US Army Corp of Engineers-Hydrologic Engineering Centre) [
38], PRMS (precipitation-runoff modelling system developed by U.S. Geological Survey) [
39], EPA-SWMM (storm water management model developed by the Environmental Protection Agency, USA) [
11,
40,
41,
42,
43], AWBM (Australian water balance model) [
44], XP-SWMM (storm water management model developed by XP Software Inc.).
While each modelling tool has its own strengths and weaknesses, EPA-SWMM is a catchment scale model capable of simulating single events as well as continuous time series, water quality, storage and treatment, in both urban and rural catchments [
11,
41]. This model is available in the public domain and has been successfully applied across a wide range of geographical areas [
10,
45,
46,
47] and because of its high potentiality, this model is widely adopted in Australian context for hydrological studies [
15,
48,
49]. For instance, Wella-Hewage [
15] used the EPA-SWMM model to assess the performance of water-sensitive urban design (WSUD) systems for greenfield catchments in South Australia. Choi and Ball [
48] used the EPA-SWMM model to study the runoff characteristics of Centennial Park catchments in Sydney in order to develop a more efficient parameter estimation methodology for urban catchments. Chowdhury et al. [
49] also used the EPA-SWMM model to run a series of stormwater harvesting and urbanization scenarios on a number of catchments located in southeast Queensland. Hence, it is evident that EPA-SWMM can be used in a wide range of hydrological applications and therefore, it is a suitable modelling tool for assessing the performance of EB and CS modelling.
The aim of this study is to explore the ability of EB and CS modelling approaches to accurately estimate runoff hydrographs and design floods resulting from more frequent events in semi-rural catchments in a semi-arid environment. More specifically the study explores the ability of the models to accurately reproduce both the TRH and the DRH. The outcomes of this study will act as a decision-making tool in areas including but not limited to: (i) the understanding of the hydrologic response of these types of catchments; (ii) design flood estimation; and (iii) further planning and development. Considering the capabilities of EPA-SWMM, its publicly availability and wider acceptance in Australian context, this modelling tool will be adopted for this investigation.
This paper presents the details of the investigation and its outcome in the following order: (i) a description of the study catchments; (ii) EPA-SEMM model architecture; (iii) data used in the study; (iv) model setup, calibration and validation procedure; (v) results and discussion; and (vi) summary of the findings, modelling assumptions, limitations and conclusions.
4. Discussion
4.1. Summary and Outcome of the Study
Stormwater management model, EPA-SWMM was used to study the performance of EB and CS modelling at the Myponga upstream and Scott Creek catchment. While setting up the model, some parameter values were obtained from GIS and DEM, some using the recommended values in the EPA-SWMM manual and the others were assumed either realistic or default values.
Model calibrations were conducted using rainfall, evapotranspiration and observed runoff time series from 2001 to 2004. While the complete time series during the calibration period was reproduced by CS method, several events (20 at the Myponga upstream catchment and 16 at Scott Creek catchment) were reproduced through EB modeling. In order to compare results of the two methods, corresponding events from the simulated time series by the CS model was also extracted. Following the calibration, these models were validated and modelling performance in reproducing both TRHs and DRHs were assessed.
Performances of the EB modelling and CS modelling were assessed using a total of 8 goodness-of-fit measure. The scores of each goodness-of-fit criterion was averaged, and a single score was defined for each catchment for using the framework proposed by Ritter and Muñoz-Carpena [
76] to classify performance levels. The four levels of performance are: (i) very good (NSE, ANSE, KGE > 0.75); (ii) good (0.65 < NSE, ANSE, KGE < 0.75); (iii) satisfactory (0.50 < NSE, ANSE, KGE < 0.65); and (iv) unsatisfactory (NSE, ANSE, KGE < 0.50). The results are summarized in
Table 7.
The above observations and remarks made based on the average scores of goodness-of-fit measures were further validated by comparing the percentage events of the two modelling methods that fall into each performance grades (
Figure 10 and
Figure 15) as well as by comparing the percentage events that each model type outperformed the other in terms of all eight selected goodness-of-fit measures (
Figure 11 and
Figure 16). Based on the above analysis and observations, it can be summarizing that EB modelling has better capability in estimating both TRH and DRH at the Myponga upstream and Scott Creek catchments. In specific to the selected study catchments, it is suggested to employ EB modelling approach to estimate runoff hydrographs, design flood and further planning and management of these catchments.
4.2. Modelling Errors, Limitations and Future Directions
During the model development, a number of assumptions and simplifications were made to simplify complex hydrological processes which can contribute to have increased errors in the model output. According to Coon and Reddy [
83], errors in a hydrological model can arise from various sources including: (i) errors in precipitation and streamflow data; (ii) limitations in model structure; (iii) errors in model calibration; (iv) inaccurate estimation and interpretation of land-use and land-cover data; and (v) changes in land-use during the simulation period.
While developing the model, the precipitation data used were obtained from point-based rainfall gauge stations and then applied uniformly over a specified area around the gauging stations defined by the Thiessen-polygon method. In case of a large Thiessen-polygon boundary, spatial variation of rainfall becomes significant and the actual rainfall in the subcatchments could be significantly different to the rainfall measured at the gauging stations. This may add errors to the model output.
Limitations in model structure can affect the model output and therefore can lead to inaccurate estimation by the model. For instance, during the model setup, infiltration into soil and unsaturated zone moisture content was assumed to be uniform over the entire subcatchment. These assumptions can have a significant impact on soil moisture characteristics. In the EPA-SWMM model, the soil moisture content in the unsaturated zone controls flow from the unsaturated zone to the saturated zone. Therefore, such simplifications can lead to estimation errors. While groundwater flow is a complex process, EPA-SWMM represents the groundwater flow process by a simple groundwater module which considers the total groundwater flow into a stream as a sum of interflow and baseflow. During dry periods, when all the groundwater from catchment discharges into streams, the system becomes empty and EPA-SWMM assumes that there is no input from groundwater and it does not allow water entering to catchment from another groundwater zone.
Another major source of error in RR modelling is the error arise through improper model calibration. While in automatic calibration, either local optimization routine or global optimization routine can be chosen to use, this study used local optimization procedure where parameters were assigned some initial values and a possible range. It has been found that different initial values can affect the objective function, which affects the overall calibration. This is a limitation of local optimization. In contrast, global optimization does not require initial start points, rather all possible start points are considered. Therefore, the use of global optimization may reduce the optimization error, thereby increasing the modelling performance.
In this study, land-use information was obtained from aerial photographs and GIS which can be open to misinterpretation and misclassification. It was assumed that land-use would remain unchanged during the study period. However, this assumption is not realistic and land-use can change with time. For future studies it is recommended to explore possible options that allows to input a variable land-use data in the model during the modelling and the validation period. In fact, it is suggested that a land transformation model be integrated into EPA-SWMM model in order to allow more realistic representation of land-use changes.
There are a range of recommendations that can be made for the future to improve the modelling performance. During the setup of the EPA-SWMM model, daily time step data was used due to the lack of sub-daily data. For future studies, it is recommended to use sub-daily data if possible. While due to the unavailability of concurrent continuous data for the selected gauging stations, this study used only eight years of time series data, future studies should consider longer periods of time series data to come up with a more representative result. Due to the unavailability of the grid-based data, this study was conducted using point-based data, in future studies, it is recommended to use grid-based rainfall data that is more accurate than point-based data. Due to the time limitation, this study was limited to two catchments only, in future, it is recommended to assess modelling performance using more catchments before results can be generalised as RR modelling performance can vary from one catchment to another.