Experimental Investigation on Characteristics of Sand Waves with Fine Sand under Waves and Currents
Abstract
:1. Introduction
2. Experimental Installation and Methods
2.1. Experimental Set-Up
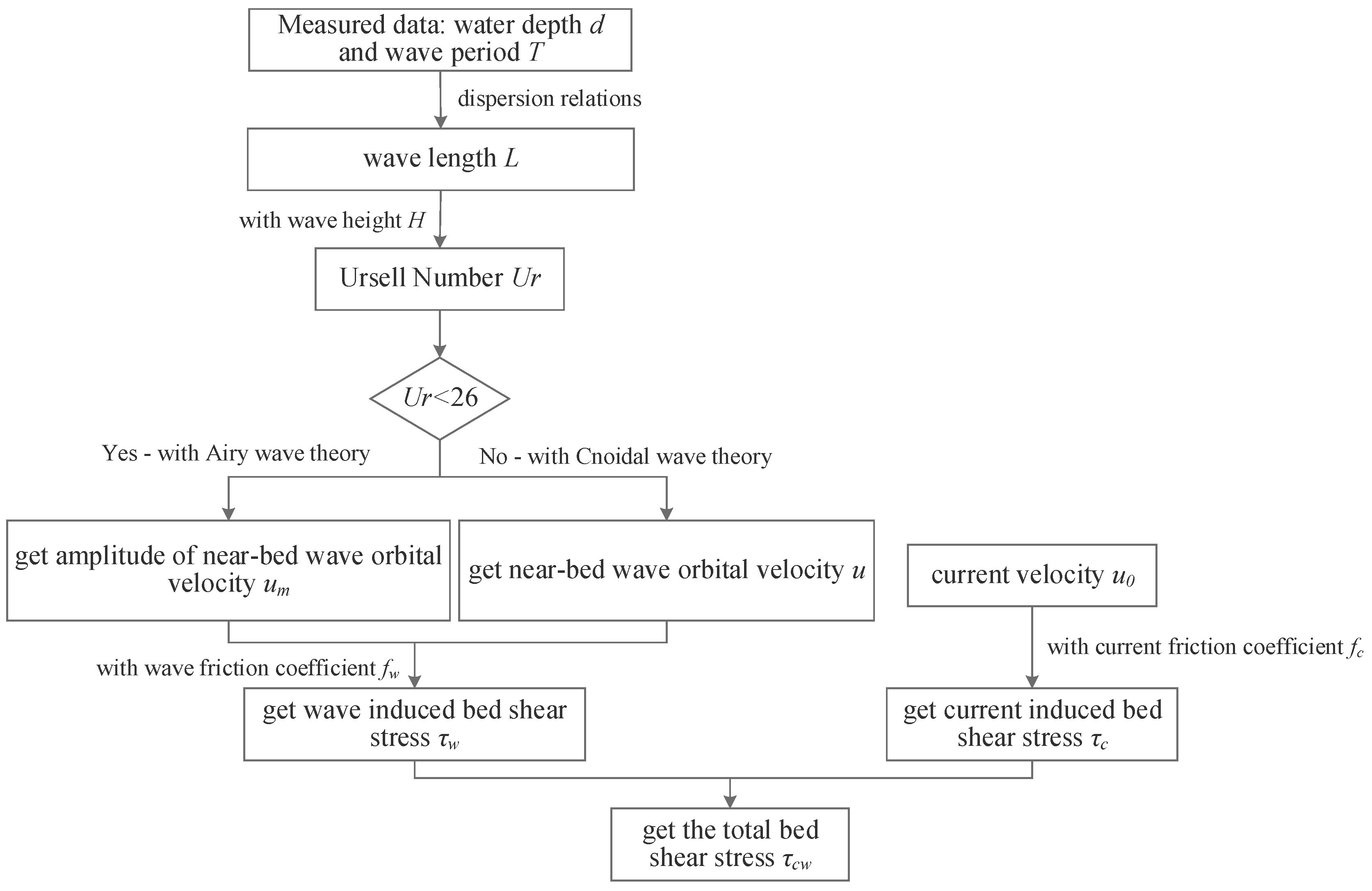
2.2. Water Characteristics Calculation
3. Results
3.1. Dynamic Growth of Sand Waves
3.2. Geometry Characteristics of Sand Waves
4. Discussion
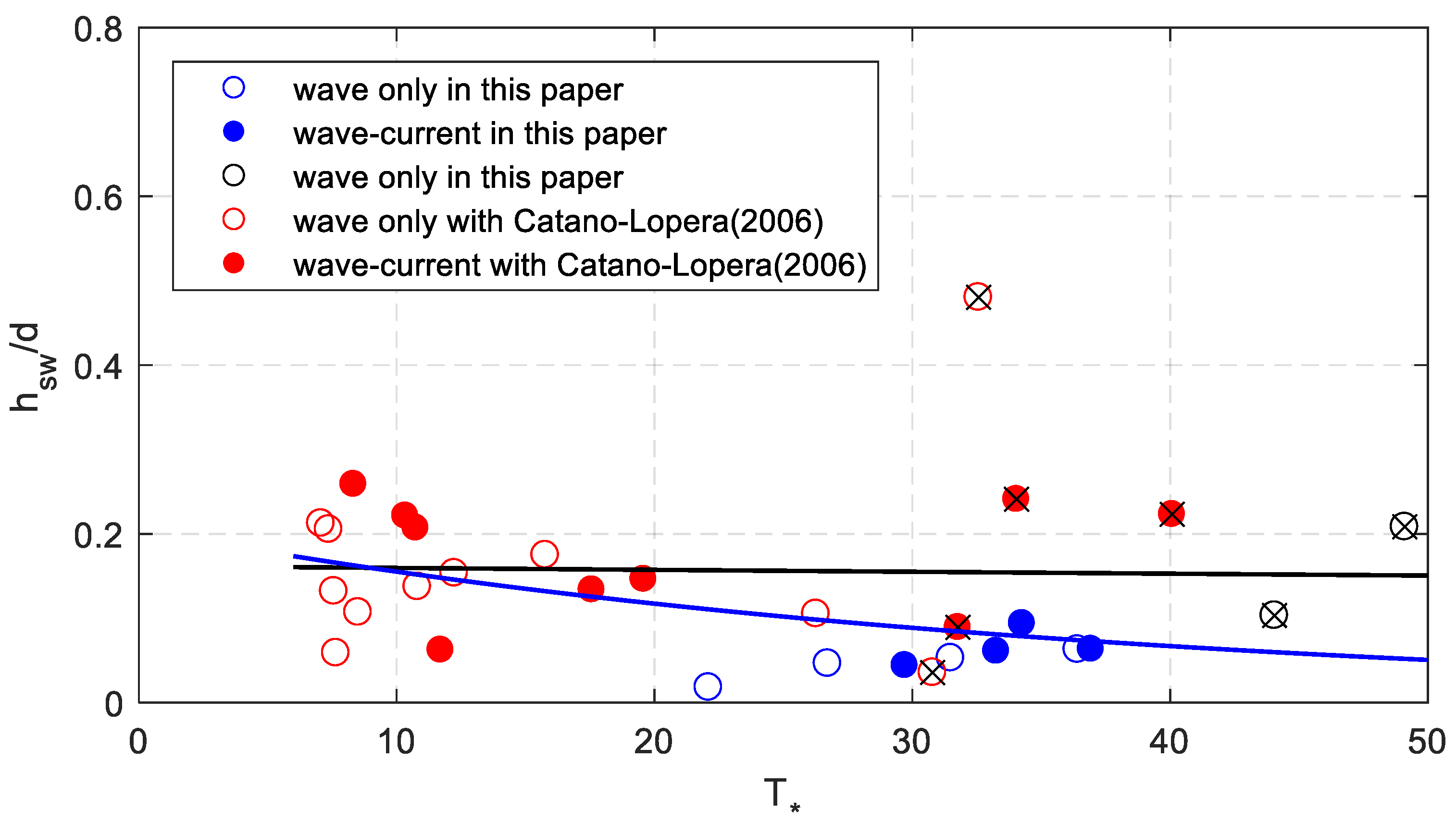
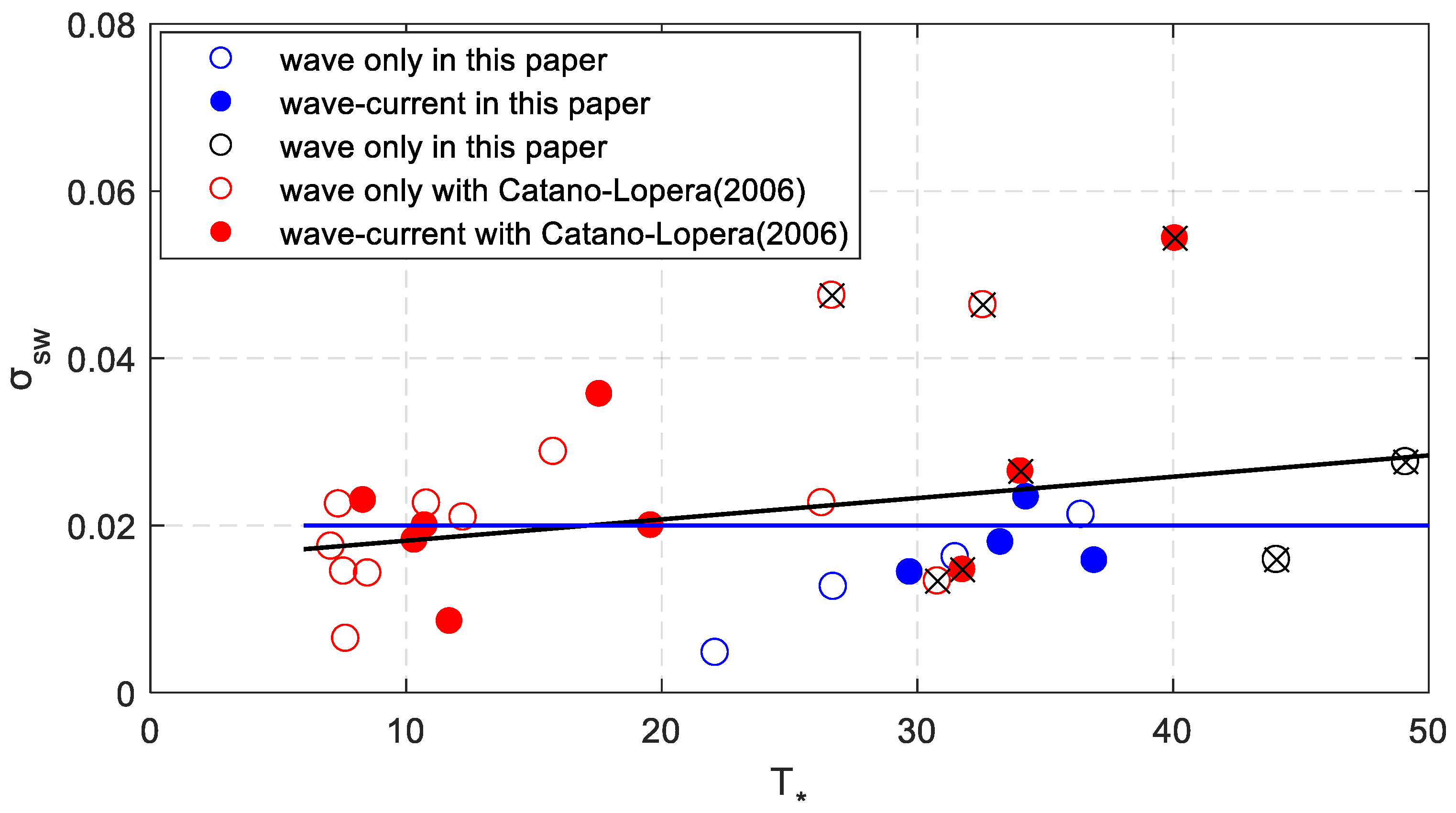
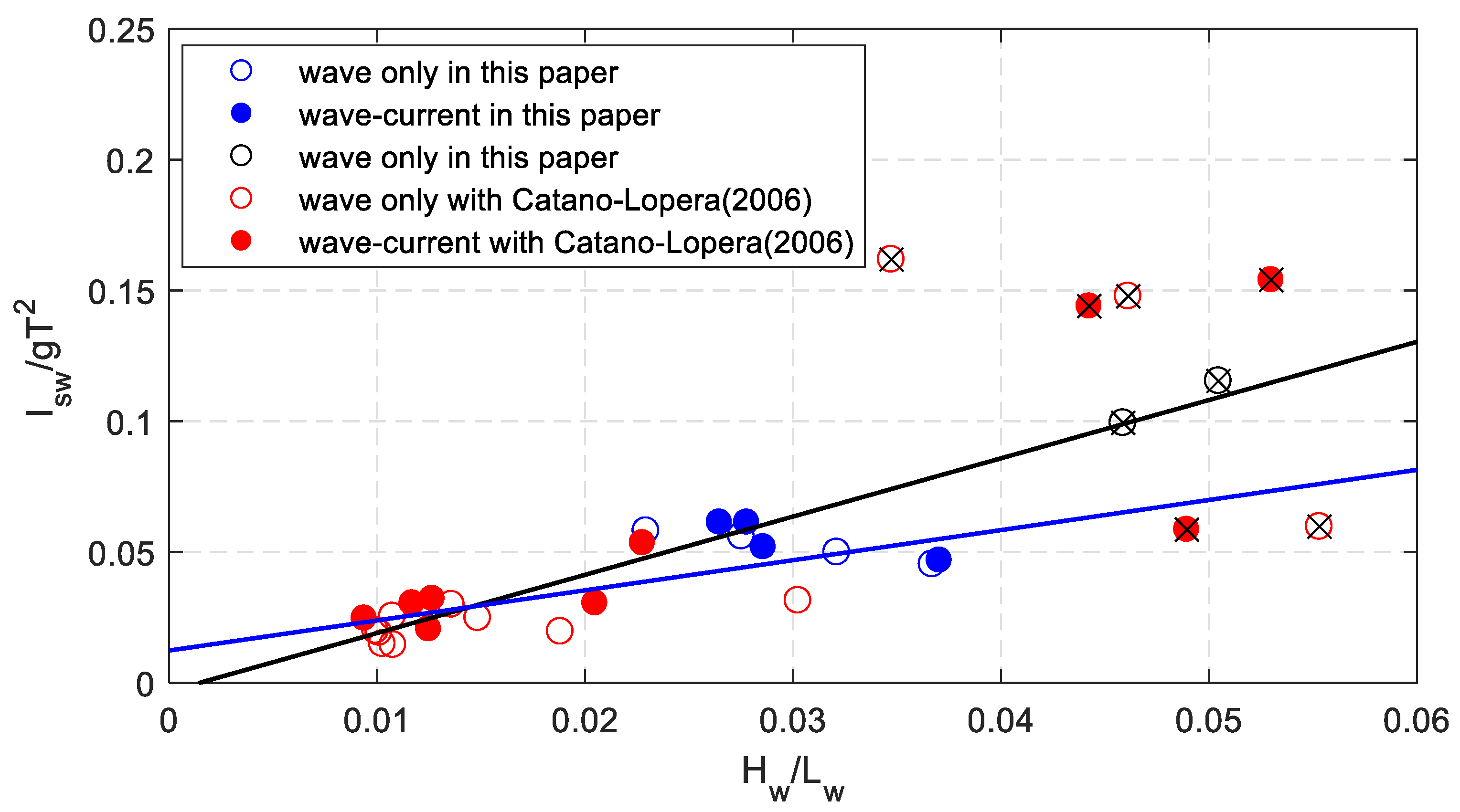
4.1. Comparison with the Results of Cataño-Lopera et al. [1]
4.2. Bedforms with Dimensionless Shear Stress
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notation
| = wave height |
| = wave period |
| = depth-averaged current velocity |
| = water depth |
| = median diameter of sediment |
| = Ursell number |
| = wave length |
| = dimensionless bed-shear stress |
| = mean bed shear stress due to current and waves |
| = critical bed shear stress |
| = density of sediment |
| = density of water |
| = gravitational acceleration |
| = critical Shields number |
| = dimensionless particle diameter |
| = viscosity coefficient of water |
| = amplitude of the near-bottom wave orbital velocity |
| = wave friction factor |
| = current friction factor |
| = wave-averaged bed shear stress due to waves only |
| = bed shear stress due to current only |
| = wave number |
| = near-bed peak orbital excursion |
| = wave related roughness |
| = ripple height |
| = modulus of elliptic integral |
| = the first kind complete elliptic integral |
| = the second kind complete elliptic integral |
| = near-bed instantaneous velocity due to waves |
| = Jacobian elliptic sinusoid function |
| = Jacobian elliptic cosine function |
| = Jacobian elliptic delta function |
| = distance from the wave trough to the sea bed |
| = distance from the wave crest to the sea bed |
| = sand wave height |
| = sand wave length |
| = sand wave steepness |
References
- Cataño-Lopera, Y.A.; García, M.H. Geometry and migration characteristics of bedforms under waves and currents. Part 1: Sandwave morphodynamics. Coast. Eng. 2006, 53, 767–780. [Google Scholar] [CrossRef]
- Cataño-Lopera, Y.A.; García, M.H. Geometry and migration characteristics of bedforms under waves and currents: Part 2: Ripples superimposed on sandwaves. Coast. Eng. 2006, 53, 781–792. [Google Scholar] [CrossRef]
- Terwindt, J.H.J. Sand waves in the southern bight of the North Sea. Mar. Geol. 1971, 10, 51–67. [Google Scholar] [CrossRef]
- Mccave, I.N. Sand waves in the North Sea off the coast of Holland. Mar. Geol. 1971, 10, 199–225. [Google Scholar] [CrossRef]
- Campmans, G.H.P.; Roos, P.C.; de Vriend, H.J.; Hulshcher, S.J.M.H. Modeling the influence of storms on sand wave formation: A linear stability approach. Cont. Shelf Res. 2017, 137, 103–116. [Google Scholar] [CrossRef]
- Van Dijk, T.A.G.P.; Kleinhans, M.G. Processes controlling the dynamics of compound sand waves in the North Sea, Netherlands. J. Geophys. Res. Earth Surf. 2005, 110, 1–15. [Google Scholar] [CrossRef]
- Besio, G.; Blondeaux, P.; Brocchini, M.; Hulshcer, S.J.M.H.; Idier, D.; Knaapen, M.A.F.; Németh, A.; Roos, P.C.; Vittori, G. The morphodynamics of tidal sand waves: A model overview. Coast. Eng. 2017, 55, 657–670. [Google Scholar] [CrossRef]
- Berg, J.V.D.; Sterlini, F.; Hulscher, S.J.M.H.; Damme, R.V. Non-linear process based modelling of offshore sand waves. Cont. Shelf Res. 2012, 37, 26–35. [Google Scholar] [CrossRef]
- Knaapen, M.A.F.; Hulscher, S.J.M.H.; Tiessen, M.C.H.; Berg, J.V.D.; Parker, G.; García, M.H. Using a sand wave model for optimal monitoring of a navigation depth. In Proceedings of the Forth IAHR Symposium on River, Coastal and Estuarine Morphodynamics, Urbana, IL, USA, 4–7 October 2005; pp. 999–1007. [Google Scholar]
- Németh, A.; Hulscher, S.J.M.H.; de Vriend, H.J. Offshore sand wave dynamics, engineering problems and future solutions. Pipeline Gas J. 2003, 230, 67–69. [Google Scholar]
- Roos, P.C.; Blondeaux, P.; Hulscher, S.J.M.H.; Vittor, G. Linear evolution of sandwave packets. J. Geophys. Res. Earth Surf. 2005, 110, 1–10. [Google Scholar] [CrossRef]
- Ma, X.; Yan, J.; Fan, F. Morphology of submarine barchans and sediment transport in barchans fields off the Dongfang coast in Beibu Gulf. Geomorphology 2014, 213, 213–224. [Google Scholar] [CrossRef]
- Li, Y.; Lin, M.; Jiang, W.; Fan, F. Process control of the sand wave migration in Beibu Gulf of the South China Sea. J. Hydrodyn. 2011, 23, 439–446. [Google Scholar] [CrossRef]
- Dodd, N.; Blondeaux, P.; Calvete, D.; Swart, H.E.D.; Falqués, A.; Hulscher, S.J.M.H.; Różyński, G.; Vittori, G. Understanding coastal morphodynamics using stability methods. J. Coast. Res. 2003, 19, 849–865. [Google Scholar]
- Belderson, R.H. Offshore tidal and non-tidal sand ridges and sheets: Differences in morphology and hydrodynamic setting. In Shelf Sands and Sandstones—Memoir 11; CSPG Special Publications: Calgary, AB, Canada, 1986. [Google Scholar]
- Hulscher, S.J.M.H. Tidal-induced large-scale regular bed form patterns in a three-dimensional shallow water model. J. Geophys. Res. Oceans 1996, 101, 20727–20744. [Google Scholar] [CrossRef]
- Borsje, B.W.; Roos, P.C.; Kranenburg, W.M.; Hulscher, S.J.M.H. Modeling tidal sand wave formation in a numerical shallow water model: The role of turbulence formulation. Cont. Shelf Res. 2013, 60, 17–27. [Google Scholar] [CrossRef]
- Németh, A.A.; Hulscher, S.J.M.H.; de Vriend, H.J. Modelling sand wave migration in shallow shelf seas. Cont. Shelf Res. 2002, 22, 2795–2806. [Google Scholar] [CrossRef]
- Besio, G.; Blondeaux, P.; Brocchini, M.; Vittori, G. On the modeling of sand wave migration. J. Geophys. Res. Oceans 2004, 109, 1–13. [Google Scholar] [CrossRef]
- Campmans, G.H.P.; Roos, P.C.; de Vriend, H.J.; Hulscher, S.J.M.H. The influence of storms on sand wave evolution: A nonlinear idealized modeling approach. J. Geophys. Res. Earth Surf. 2018, 123, 2070–2086. [Google Scholar] [CrossRef]
- Campmans, G.H.P.; Roos, P.C.; Schrijen, E.; Hulscher, S.J.M.H. Modeling wave and wind climate effects on tidal sand wave dynamics: A North Sea case study. Estuar. Coast. Shelf Sci. 2018, 213, 137–147. [Google Scholar] [CrossRef]
- Borsje, B.W.; de Vries, M.B.; Bouma, T.J.; Besio, G.; Hulscher, S.J.M.H.; Herman, P.M.J. Modelling biogeomorphological influences for offshore sandwaves. Cont. Shelf Res. 2009, 29, 1289–1301. [Google Scholar] [CrossRef]
- Borsje, B.W.; Hulscher, S.J.M.H.; Herman, P.M.J.; de Vries, M.B. On the parameterization of biological influences on offshore sandwave dynamics. Ocean Dyn. 2009, 59, 659–670. [Google Scholar] [CrossRef]
- Roos, P.C.; Wemmenhove, R.; Hulscher, S.J.M.H.; Hoeijmakers, H.W.M.; Kruyt, N.P. Modeling the effect of nonuniform sediment on the dynamics of offshore tidal sandbanks. J. Geophys. Res. Earth Surf. 2007, 112, 1–11. [Google Scholar] [CrossRef]
- Van Oyen, T.; Blondeaux, P. Grain sorting effects on the formation of tidal sand waves. J. Fluid Mech. 2009, 629, 311–342. [Google Scholar] [CrossRef]
- Van Oyen, T.; Blondeaux, P. Tidal sand wave formation: Influence of graded suspended sediment transport. J. Geophys. Res. Oceans 2009, 114, 1–18. [Google Scholar] [CrossRef]
- Blondeaux, P. Sediment mixtures, coastal bedforms and grain sorting phenomena: An overview of the theoretical analyses. Adv. Water Resour. 2012, 48, 113–124. [Google Scholar] [CrossRef]
- Borsje, B.W.; Kranenburg, W.M.; Roos, P.C.; Matthieu, J.; Hulscher, S.J.M.H. The role of suspended load transport in the occurrence of tidal sand waves. J. Geophys. Res. Earth Surf. 2014, 119, 701–716. [Google Scholar] [CrossRef]
- Van Gerwen, W.; Borsje, B.W.; Damveld, J.H.; Hulscher, S.J.M.H. Modelling the effect of suspended load transport and tidal asymmetry on the equilibrium tidal sand wave height. Coast. Eng. 2018, 136, 56–64. [Google Scholar] [CrossRef]
- Chou, Y.J.; Shao, Y.C.; Sheng, Y.H.; Cheng, C.J. Stabilized formulation for modeling the erosion/deposition flux of sediment in circulation/CFD models. Water 2019, 11, 197. [Google Scholar] [CrossRef]
- Williams, J.J.; Bell, P.S.; Thorne, P.D. Unifying large and small wave-generated ripples. J. Geophys. Res. Oceans 2005, 110, 1–18. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, Z.; Wu, Z.; Liu, F.; Liang, B.; He, Y.; Huang, F. Experiment research on geometry and evolution characteristics of sand wave bedforms generated by waves and currents. In 5th International Conference on Coastal and Ocean Engineering, Shanghai, China, 2018; IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; pp. 9–15. [Google Scholar]
- Van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua Publications: Blokzijl, The Netherlands, 1993. [Google Scholar]
- Swart, D.H. Offshore Sediment Transport and Equilibrium Beach Profiles. Ph.D. Thesis, Civil Engineering and Geosciences, Delft, The Netherlands, December 1974. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of stationary waves. Lond. Edinb. Dublin Philos. Magazine J. Sci. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Keller, J.B. The solitary wave and periodic waves in shallow water. Commun. Appl. Math. 1984, 1, 323–339. [Google Scholar] [CrossRef]
- Zou, Z.L. Coastal Dynamics; China Communications Press: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Van Rijn, L.C. Sediment transport, part III: Bed forms and alluvial roughness. J. Hydraul. Eng. ASCE 1984, 110, 1733–1754. [Google Scholar] [CrossRef]
- Yalin, M.S. River Mechanics; Pergamon Press: Oxford, UK, 1992. [Google Scholar]
- Julien, P.Y. Erosion and Sedimentation; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Wiberg, P.L.; Sherwood, C.R. Calculating wave-generated bottom orbital velocities from surface-wave parameters. Comput. Geosci. 2008, 34, 1243–1262. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, Y.P.; Gao, S.; Du, J.; Yang, Y.; Tang, J.; Gao, J. On estimation of coastal wave parameters and wave-induced shear stresses. Limnol. Oceanogr. Meth. 2018, 16, 594–606. [Google Scholar] [CrossRef]
- Boyd, R.; Forbes, D.L.; Heffler, D.E. Time-sequence observations of wave-formed sand ripples on an ocean shoreface. Sedimentology 1988, 35, 449–464. [Google Scholar] [CrossRef]
- Allen, J.R.L. Physical Processes of Sedimentation; American Elsevier Pub. Co.: New York, NY, USA, 1970. [Google Scholar]
- Zhao, N.; Liu, X.J.; Lu, G. Characteristics and evolution process and their modeling of sand ripples on Dongtai tidal flats, Jiangsu province China. J. Sediment. Res. 2012, 3, 4, (In Chinese with English abstract). [Google Scholar]







| Scenarios | H (m) | T (s) | u0 (m/s) | d (m) | D50 (mm) |
|---|---|---|---|---|---|
| 1 | 0.10 | 2 | 0 | 0.6 | 0.17 |
| 2 | 0.12 | 2 | 0 | 0.6 | 0.17 |
| 3 | 0.14 | 2 | 0 | 0.6 | 0.17 |
| 4 | 0.16 | 2 | 0 | 0.6 | 0.17 |
| 5 | 0.14 | 2 | −0.2 | 0.6 | 0.17 |
| 6 | 0.14 | 2 | 0.2 | 0.6 | 0.17 |
| 7 | 0.14 | 2 | 0.25 | 0.6 | 0.17 |
| 8 | 0.14 | 2 | 0.35 | 0.6 | 0.17 |
| 9 | 0.20 | 2 | 0 | 0.6 | 0.18 |
| 10 | 0.22 | 2 | 0 | 0.6 | 0.18 |
| Scenarios a | H (cm) | T (s) | u0 (m/s) | d (m) | D50 (mm) | hsw (cm) | lsw (m) | Ur | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10.0 | 2 | 0 | 0.6 | 0.17 | 1.09 | 2.28 | 8.81 | 3.49 | 0.00 | 0.15 | 22.10 |
| 2 | 12.0 | 2 | 0 | 0.6 | 0.17 | 2.79 | 2.2 | 10.57 | 4.19 | 0.00 | 0.15 | 26.72 |
| 3 | 14.0 | 2 | 0 | 0.6 | 0.17 | 3.18 | 1.96 | 12.33 | 4.92 | 0.00 | 0.15 | 31.49 |
| 4 | 16.0 | 2 | 0 | 0.6 | 0.17 | 3.79 | 1.78 | 14.09 | 5.66 | 0.00 | 0.15 | 36.41 |
| 5 | 14.0 | 2 | −0.2 | 0.6 | 0.17 | 2.65 | 1.84 | 12.33 | 4.92 | −0.27 | 0.15 | 29.71 |
| 6 | 14.0 | 2 | 0.2 | 0.6 | 0.17 | 3.67 | 2.04 | 12.33 | 4.92 | 0.27 | 0.15 | 33.26 |
| 7 | 14.0 | 2 | 0.25 | 0.6 | 0.17 | 5.64 | 2.41 | 12.33 | 4.92 | 0.42 | 0.15 | 34.26 |
| 8 | 14.0 | 2 | 0.35 | 0.6 | 0.17 | 3.81 | 2.41 | 12.33 | 4.92 | 0.82 | 0.15 | 36.93 |
| 9 | 20.0 | 2 | 0 | 0.6 | 0.18 | 6.2 | 3.9 | 17.62 | 7.22 | 0.00 | 0.16 | 44.05 |
| 10 | 22.0 | 2 | 0 | 0.6 | 0.18 | 12.5 | 4.53 | 19.38 | 8.03 | 0.00 | 0.16 | 49.10 |
| 11 | 19.6 | 2 | 0 | 0.56 | 0.25 | 26.9 | 5.8 | 20.12 | 7.47 | 0.00 | 0.22 | 32.57 |
| 12 b | 12.8 | 5.2 | 0 | 0.56 | 0.25 | 3.3 | 5.1 | 117.19 | 1.93 | 0.00 | 0.22 | 7.65 |
| 13 | 19.2 | 6.9 | 0 | 0.56 | 0.25 | 11.9 | 6.8 | 347.56 | 1.80 | 0.00 | 0.22 | 7.07 |
| 14 | 19.7 | 4.2 | 0 | 0.56 | 0.25 | 9.8 | 3.4 | 123.08 | 3.73 | 0.00 | 0.22 | 15.77 |
| 15 | 17.7 | 1.6 | 0 | 0.56 | 0.25 | 2 | 1.5 | 10.32 | 7.08 | 0.00 | 0.22 | 30.79 |
| 16 | 20.9 | 2.9 | 0 | 0.56 | 0.25 | 5.9 | 2.6 | 56.76 | 6.07 | 0.00 | 0.22 | 26.27 |
| 17 | 10.7 | 3.4 | 0 | 0.56 | 0.25 | 7.7 | 3.4 | 37.88 | 2.63 | 0.00 | 0.22 | 10.81 |
| 18 | 17.4 | 2.3 | 0 | 0.56 | 0.25 | 39.9 | 8.4 | 24.83 | 6.16 | 0.00 | 0.22 | 26.66 |
| 19 | 15.1 | 5.9 | 0 | 0.56 | 0.25 | 11.5 | 5.1 | 186.26 | 1.86 | 0.00 | 0.22 | 7.37 |
| 20 | 10.4 | 4.1 | 0 | 0.56 | 0.25 | 6 | 4.2 | 55.46 | 2.12 | 0.00 | 0.22 | 8.51 |
| 21 | 14.7 | 4.1 | 0 | 0.56 | 0.25 | 8.6 | 4.1 | 82.12 | 2.95 | 0.00 | 0.22 | 12.24 |
| 22 | 12.3 | 5.1 | 0 | 0.56 | 0.25 | 7.4 | 5.1 | 107.38 | 1.91 | 0.00 | 0.22 | 7.57 |
| 23 | 19.6 | 1.9 | 0.17 | 0.56 | 0.25 | 13.5 | 5.1 | 17.75 | 7.60 | 0.20 | 0.22 | 34.04 |
| 24 | 19.2 | 5.8 | 0.17 | 0.56 | 0.25 | 12.4 | 6.8 | 240.36 | 2.32 | 0.20 | 0.22 | 10.34 |
| 25 | 19.7 | 3.7 | 0.17 | 0.56 | 0.25 | 8.2 | 4.1 | 92.73 | 4.38 | 0.20 | 0.22 | 19.58 |
| 26 | 17.7 | 1.5 | 0.17 | 0.56 | 0.25 | 5 | 3.4 | 8.65 | 7.10 | 0.20 | 0.22 | 31.77 |
| 27 | 11.3 | 3.6 | 0.17 | 0.56 | 0.25 | 3.5 | 4.1 | 45.68 | 2.63 | 0.20 | 0.22 | 11.71 |
| 28 | 10.7 | 2 | 0.17 | 0.56 | 0.25 | 7.5 | 2.1 | 10.98 | 3.93 | 0.20 | 0.22 | 17.57 |
| 29 | 12.1 | 5.1 | 0.17 | 0.56 | 0.25 | 14.5 | 6.3 | 105.38 | 1.88 | 0.20 | 0.22 | 8.33 |
| 30 | 13 | 4.4 | 0.17 | 0.56 | 0.25 | 11.6 | 5.8 | 83.15 | 2.41 | 0.20 | 0.22 | 10.74 |
| 31 | 23 | 2 | 0.17 | 0.56 | 0.25 | 12.5 | 2.3 | 23.61 | 8.95 | 0.20 | 0.22 | 40.08 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liang, B.; Wu, G. Experimental Investigation on Characteristics of Sand Waves with Fine Sand under Waves and Currents. Water 2019, 11, 612. https://doi.org/10.3390/w11030612
Wang Z, Liang B, Wu G. Experimental Investigation on Characteristics of Sand Waves with Fine Sand under Waves and Currents. Water. 2019; 11(3):612. https://doi.org/10.3390/w11030612
Chicago/Turabian StyleWang, Zhenlu, Bingchen Liang, and Guoxiang Wu. 2019. "Experimental Investigation on Characteristics of Sand Waves with Fine Sand under Waves and Currents" Water 11, no. 3: 612. https://doi.org/10.3390/w11030612
APA StyleWang, Z., Liang, B., & Wu, G. (2019). Experimental Investigation on Characteristics of Sand Waves with Fine Sand under Waves and Currents. Water, 11(3), 612. https://doi.org/10.3390/w11030612





