Evaluation of the Effect of Channel Geometry on Streamflow and Water Quality Modeling and Modification of Channel Geometry Module in SWAT: A Case Study of the Andong Dam Watershed

Abstract

The impact of the channel geometry on water quantity and quality simulation of the Soil and Water Assessment Tool (SWAT) was evaluated for the Andong Dam watershed. The new equations to determine the bankfull width of the channels and the bottom width of the floodplains were developed using aerial photographs, and its performance was compared with the current equations of SWAT. The new equations were more exact than the current equations since the current equations tended to overestimate the widths of the channel and floodplain. When compared with the observed data, the streamflow of the scenario 2 (S2, applying the new equations) showed lower deviation and higher accuracy than scenario 1 (S1, applying the current equations) because the peak flow of S2 captured the observed data better due to the impact of the change geometry. Moreover, the water quality results of S2 outperformed S1 regarding suspended solid, total nitrogen, and dissolved oxygen. This is attributed to the variables, such as flow travel time, which is directly related to the channel geometry. Additionally, SWAT was modified to consider the various channel cross-sectional shapes. The results of this study suggest that the channel geometry information for the water quantity and quality estimation should be carefully applied, which could improve the model performance regarding streamflow and water quality simulations.

1. Introduction

Various studies have been conducted to predict the hydrology and water quality for river and watershed management in ungauged watersheds. As a result of these efforts, various watershed-scale hydrological models have been developed, such as the Precipitation Runoff Modeling System (PRMS), Hydrologic Simulation Program—Fortran (HSPF), Better Assessment Science Integrating Point and Nonpoint Sources (BASINS), and Soil and Water Assessment Tool (SWAT) [1]. These hydrological models generally simulate the streamflow and water quality by calculating various parameters based on input data such as topographic and meteorological data [2,3].

In addition to the parameters calculated using the topographic and meteorological data (e.g., curve numbers, elevation, slope, and soil properties), the hydraulic characteristics of the channels in watersheds also play a crucial role in the water quantity and quality simulation as well as habitat evaluation since they are important influential factors [4,5]. For this reason, in most hydrological models, the channel shape parameters (e.g., channel width, depth, slope, length, and floodplain width) are required as input parameters [6]. Among these parameters, channel width and the water depth of channels are used to apply Manning’s equation for flow routing in channels in watersheds [7]. Due to the valid influence of channel width and depth, they are essential input parameters in hydrological modeling. The channel length and slope can be accurately estimated by digital elevation models (DEMs) and channel extraction algorithms; however, the channel width and depth are difficult to estimate accurately [6]. Thus, in most hydrological models, the channel width and depth are estimated using the regression equations for the upstream watershed area [8,9,10,11].

The current and typically used regression equations were developed only from large-scale studies over multiple regions in the United States. Ames [6] and Staley et al. [12] suggested that those equations may not be applicable to small-scale watershed studies. Thus, it is essential to evaluate the applicability of the current regression equations of SWAT in small or middle-scale watersheds with different characteristics. Moreover, although natural channels have various cross-sectional shapes, most hydrological models assume channel cross-sections as simplified forms such as rectangles, trapezoids, and triangles [13,14,15]. Similar to other commonly used hydrological models (e.g., PRMS, HSPF, and BASINS), SWAT, one of the most widely used models worldwide [16,17,18,19,20], also considers channel geometry through simplification with a predefined geometric shape, i.e., a compound channel composed of two trapezoids [21]. Thus, the current channel geometry estimation module in SWAT needs to be modified as it is limited in terms of taking into account multiple channel cross-section shapes.

Therefore, the objectives of this study were to evaluate the current regression equations of SWAT for channel geometry estimation by comparing with the new regression equations for a middle-scale watershed in Korea, to modify SWAT for application to various channels with different cross-section shapes, and to investigate the impact of channel geometry on the model simulation results and water quantity and quality.

2. Materials and Methods

2.1. Overview of SWAT

SWAT is a physically-based and long-term continuous time model. SWAT is used to predict the impact of management practices, land use and land cover change, and climate change on hydrology and water quality at a watershed scale [22]. Weather, soil properties, topography, and land management practices are the main inputs for simulating hydrologic and water quality processes in a watershed [23]. The model divides a watershed into a number of sub-watersheds according to the threshold values; the sub-watersheds are further divided into main channels and hydrologic response units (HRUs), a unique combination of land use, soil, and slope classes within each sub watershed. A HRU is the smallest computational unit in SWAT. Surface runoff, soil water content, baseflow, nutrient cycles, and erosion are simulated for each HRU, and then the HRUs are combined and calculated for a sub-watershed by a weighted value [7].

SWAT regards channels as compound channels that have a double trapezoidal shape as shown in Figure 1 [6,7,8]. The lower part of the trapezoid shape of the channels is the main channel, and the upper part is the floodplain. The floodplain dimension is considered when the volume of water in the channel exceeds the maximum amount of water that can be stored by the channel.

SWAT currently uses Equations (1) and (2) for estimating the width and depth of the main channel at the bankfull stage, which means that the channel is filled up to the top of the bank. Equation (3) is used to estimate the bottom width of the floodplain. These equations were developed using the methodology based on Muttiah et al. [8], Allen et al. [9], and Leopold and Maddock [10].

$$W_{bnkfull}=1.29·A^{0.6},$$

(1)

$$D_{bnkfull}=0.13·A^{0.4},$$

(2)

$$W_{btm,fld}=5·W_{bnkful},$$

(3)

where $W_{bnkfull}$ and $D_{bnkfull}$ are the bankfull stage width and depth, respectively, of the main channel (m); $A$ is the upstream drainage area (km²); and $W_{btm,fld}$ is the bottom width of the floodplain (m). Moreover, SWAT assumes that the slopes of the main channel and floodplain have a 2:1 and 4:1 run to the rise, respectively. Based on these assumptions, SWAT computes the bottom width of the main channel using the bankfull width and depth using Equation (4).

$$W_{btm}=W_{bnkfull}-2·z_{ch}·D_{bnkfull},$$

(4)

where $W_{btm}$ is the bottom width of the main channel (m) and $z_{ch}$ is the inverse of the channel side slope. Then, SWAT calculates other variables including the cross-section area of flow, the wetted perimeter, and the hydraulic radius using channel geometry data to calculate the flow velocity and simulate the flow and water quality over time (Equations (5)–(7)).

$$P_{ch}=W_{btm}+2·depth·\sqrt{1+z_{ch}^2},$$

(5)

$$R_{ch}=\frac{A_{ch}}{P_{ch}},$$

(6)

$$v_c=\frac{R_{ch}^{2/3}·sl{p}_{ch}^{1/2}}{n},$$

(7)

where $P_{ch}$ is the wetted perimeter of flow (m), $W_{btm}$ is the bottom width of the channel (m), $z_{ch}$ is the inverse of the channel slope, depth is the depth of water in the channel (m), $R_{ch}$ is the hydraulic radius (m), $A_{ch}$ is the cross-sectional area of flow (m²), $P_{ch}$ is the wetted perimeter of flow (m), $v_c$ is the flow velocity (m/s), $sl{p}_{ch}$ is the slope along the channel length (m/m), and n is Manning’s coefficient for the channel.

SWAT uses the five different stream power equations for sediment routing in stream channels; simplified Bagnold equation, simplified Bagnold model, Kodatie model, Molinas and Wu model, and Yang sand and gravel model [7]. All these models predict the maximum concentration of bed load using a non-linear function of peak velocity, where the channel geometry-related variables such as flow velocity, bottom width of the channel, and flow depth are used.

The outflow of water quality related to nitrogen and phosphorus from a channel, such as organic nitrogen, ammonia, nitrite, nitrate, and organic P, is estimated by subtracting the amount of change in each item’s concentration from the total amount in the channel and adjusting travel time in the reach segment that is decided by the flow rate and the volume of the channel. Similar to the nitrogen and phosphorus simulation processes in the channel, the dissolved oxygen (DO) is estimated by subtracting the variation of DO from the total amount of DO in the channel considering the flow travel time.

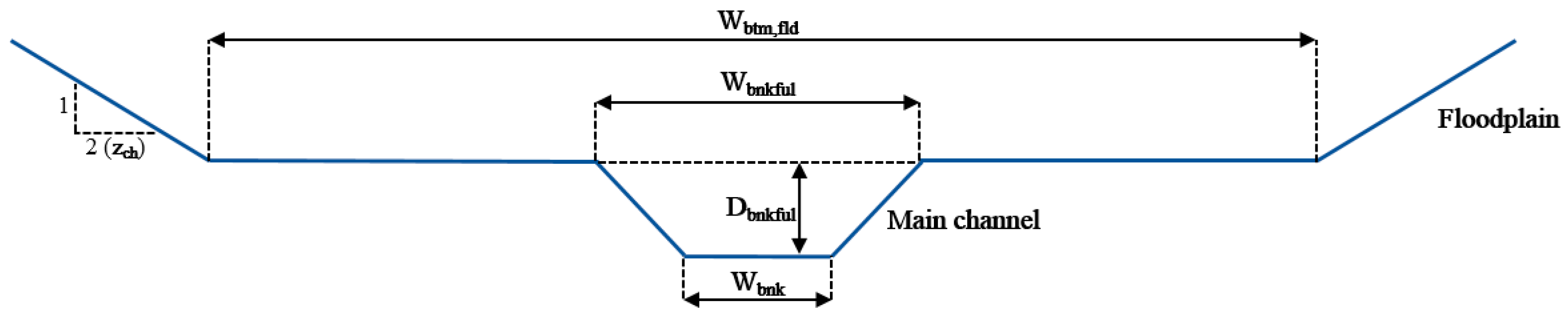
2.2. Development of New Regression Equations for Estimating Channel Geometries

2.2.1. Study Area

This study was carried out for the Andong Dam watershed located upstream of the Nakdong River, which is one of the four major rivers in South Korea. Figure 2 shows the location and other information for the study area. The dam was built in 1976, and it has a total watershed area of 1584 km², which corresponds to a middle-scale watershed according to the standard of watershed classification by size [24]. The recent 10-year average temperature is 10.25 °C, and average annual precipitation is 1258 mm. Most of the watershed consists of forest areas, showing that the well-formed, narrow river valley is naturally distributed in both the main channels and tributaries from upstream to downstream.

2.2.2. Development of New Regression Equations to Reflect Real Channel Geometry Information

The regression equations to determine the bankfull width of the main channels and floodplain bottom width in middle-scale watersheds were developed as follows. First, the sub-watersheds of the study area were delineated, and the areas of each sub-watershed including the upstream area were calculated. Then, using aerial photographs provided by Google Earth Pro and the sub-watershed shape file formed by SWAT, the bankfull stage width of the main channels and the bottom width of the floodplain were measured at a constant distance (i.e., approximately 500 m intervals) for each sub-watershed. However, the distance was flexibly changed considering the condition of the sub-watersheds such as the sub-watershed area, hydraulic structures, and topographic characteristics.

According to Cinotto [25], a bankfull stage occurs within a range of 1~2 years, and there are primary indicators identifying a bankfull width stage: topography (a change in the slope from the channel bank to a flat valley bottom), vegetation (a change in vegetation species or its presence), and sediment texture (the size distribution of surface sediments). However, these indicators are not fully applicable when using aerial photographs without a field investigation. Thus, as an alternative, the distance with the widest water surface through various aerial photographs was assumed as the bankfull stage because the bankfull stage means that the channel is filled with water up to the top of the bank.

To determine the widest water surface, the aerial photographs provided by Google Earth Pro at different shooting times from 2012 to 2017 were compared for the entire study area because the shooting time was different depending on the region. To guarantee the reliability of the data, it was confirmed that there had been no extreme flood that could cause changes in the morphological changes of the study area during this period. Figure 3 shows an example of this process. In this process, no measurements were made in sub-watersheds where hydraulic structures affecting the surface area of the water, such as weirs, were located. This is because the new regression equations were only for the channel widths of natural rivers, not those regulated or affected by human activities.

The average widths were calculated from the measured bankfull stage widths of the main channels and the measured bottom width of the floodplain for each sub-watershed, and these were used as data for developing the new regression equations.

Table 1. Measured channel and floodplain geometry data for the study area.

No.	Area (km2)	Ch_w (m)	Fld_w (m)	No.	Area (km2)	Ch_w (m)	Fld_w (m)
1	54.1	8.1	20.0	18	545.2	34.2	68.4
2	41.5	8.3	17.9	19	104.4	18.3	37.1
3	134.8	14.4	30.2	20	141.0	22.0	37.4
4	59.2	7.8	18.8	22	661.4	43.8	66.9
5	201.2	15.7	39.9	25	169.9	17.7	32.6
6	49.3	8.5	21.1	26	702.0	45.6	75.2
8	42.9	8.2	18.8	27	754.7	39.2	82.6
9	260.8	21.5	43.6	28	90.8	9.3	24.6
11	50.4	12.4	19.8	30	197.6	19.4	35.7
12	28.6	9.3	21.4	33	41.0	6.1	12.8
13	362.1	23.8	54.1	34	85.2	15.4	31.2
14	35.9	7.1	21.8	35	39.3	9.6	23.3
15	404.7	26.4	56.2	40	1187.5	62.5	89.0
16	57.0	13.2	27.6

Note: No.: sub-watershed number. Ch_w: bankfull width of the main channel. Fld_w: bottom width of Floodplain.

summarizes the channel geometry data measured by Google Earth Pro in the sub-watersheds.

In this study, the new regression equation for estimating the bankfull width of the main channels was developed as a power function of the upstream drainage area (the same as the current equation in SWAT). To estimate the bottom width of the floodplain, the current SWAT model exploits the regression equation expressed as a function of the bankfull width of the main channels, while this study developed a new power regression equation as a function of the upstream drainage area.

The optimal coefficients for each regression equation were derived by using CurveExpert Professional (v.2.2.0). CurveExpert is a cross-platform program that provides the curve fitting results and data analysis at the same time, providing various linear regression models and nonlinear regression models. CurveExpert basically provides more than 60 regression models and also has the advantage of allowing users to enter their desired regression models [26].

2.3. Modification of Channel Geometry Estimation Module in SWAT

Due to meteorological and geographical characteristics, natural rivers have various cross-section shapes as shown in Figure 4. For example, as shown in Figure 4a–d, there are many different shapes of cross-sections in natural rivers with a symmetric floodplain, including a floodplain biased to one side as well as no floodplain. Additionally, the slope of both sides of the stream is commonly not symmetrical. Therefore, this study adjusted the SWAT 2012 code (v.664) written in FORTRAN language to allow users to apply various cross-section shapes of rivers.

2.4. Input Data for SWAT

The SWAT input data were constructed to simulate the Andong Dam watershed to analyze the effect of channel geometry data on the hydrological and water quality simulation. The model was run using two scenarios. Scenario 1 (S1) used current regressions in SWAT for channel geometry estimation, and Scenario 2 (S2) used the regression equations developed in this study. These two scenarios used the same input data except for the channel geometry data, i.e., bankfull width of the main channel, and the bottom width of the floodplain.

The elevation data were rasterized as a 30-m resolution digital elevation model (DEM) from 1:5000 vector maps obtained from the Korea National Geography Institute. The soil data pertinent to texture, depth, and chemical attributes, which were supplied by the Korea Rural Development Administration, were rasterized from 1:25,000 vector maps. The land use and land cover (LULC) map for 24 classes for 2010 was obtained from the Korea Ministry of Environment. The dominant land use of the Andong Dam watershed is forest (81%), followed by cultivated croplands (6.5%), including both rice paddy fields and upland crops. Eight years (2008–2015) of daily weather data were collected from three weather stations of the Korea Meteorological Administration (Andong, Bonghwa, and Taebaek) containing precipitation, maximum and minimum temperature, relative humidity, wind speed, and solar radiation (Figure 2).

2.5. Streamflow and Water Quality Simulation Using SWAT

The Andong Dam watershed was divided into 34 sub-watersheds and 1799 HRUs based on the DEM, LULC map, and soil map. Among the two water-routing options (variable storage routing method and Muskingum routing method), the Muskingum routing method was applied in this study. The first 3 years (2008–2010) over the whole period were set as the warm-up period. The calibration for streamflow and water quality was carried out from 2011 to 2013 for 3 years, and the validation was performed from 2014 to 2015. This study used the daily dam inflow data of Andong Dam, monitored by the Korea Water Resources Corporation (lower yellow point in Figure 2). Additionally, the streamflow data of Dosan Station were used to improve the accuracy of the model simulation results; Dosan Station is at the outlet of the 25^th sub-watershed as shown in Figure 2. However, the calibration and validation for water quality was carried out for only one observation station, Nakbon B Station which is located nearby Dosan Station, due to the absence of available observed water quality data for Andong Dam Station. This study analyzed sediment, total nitrogen (TN), and DO among various water quality items.

2.6. Model Calibration and its Evaluation

To guarantee the objectivity of the calibration, the SWAT Calibration and Uncertainty Program (SWAT-CUP) [27] was used instead of manual calibration. SWAT-CUP is one of the most popular auto-calibration programs as it can produce parameter estimation by uncertainty analysis and simultaneously reduce labor on the part of the user [23,27,28]. SWAT-CUP provides five calibration procedures for the SWAT calibration: Sequential Uncertainty Fitting algorithm version 2 (SUFI-2), Generalized Likelihood Uncertainty Estimation (GLUE), Parameter Solution (ParaSol), Markov chain Monte Carlo (MCMC), and Particle Swarm Optimization (PSO). In this study, calibration was performed using SUFI-2, which has been used to optimize the SWAT parameters in many studies [23,29,30]. For the streamflow and water quality calibration, the sensitivity analysis for the selected parameters based on the previous studies (16 parameters for the streamflow calibration and 22 parameters for the water quality calibration) was initially carried out [30]. Through the sensitivity analysis, 12 parameters for streamflow and 15 parameters for water quality were selected (

Table 2. Calibrated parameters for streamflow.

Parameter	Definition	Variation Method	Fitted Value
			Dosan		Andong Dam
			S1	S2	S1	S2
ALPHA_BF	Baseflow alpha factor	Replace	0.61	0.61	0.83	0.83
CH_K2	Effective hydraulic conductivity in main channel alluvium	Replace	13.34	13.47	0.77	0.78
CN2	SCS runoff curve number	Multiply	0.82	0.83	0.75	0.76
ESCO	Soil evaporation compensation factor	Replace	0.45	0.46	0.09	0.09
GW_DELAY	Groundwater delay time	Replace	113	114	269	271
GWQMN	Threshold depth of water in the shallow aquifer required for return flow to occur	Replace	2451	2476	822	830
LAT_TTIME	Lateral flow travel time	Replace	3.16	3.19	1.45	1.47
MSK_CO1	Calibration coefficient used to control impact of the storage time constant for normal flow	Replace	4.03	4.03	4.03	4.03
MSK_CO2	Calibration coefficient used to control impact of the storage time constant from low flow	Replace	3.94	3.94	3.94	3.94
MSK_X	Weighting factor controlling relative importance of inflow rate and outflow rate in determining water storage in a reach	Replace	0.01	0.01	0.01	0.01
SOL_AWC	Available water capacity of the soil layer	Multiply	0.83	0.84	1.24	1.25
SURLAG	Surface runoff lag time	Replace	6.65	6.72	6.65	6.72

and

Table 3. Calibrated parameters for water quality of Nakbon B Station.

Parameter	Definition	Variation Method	VALUES
			S1	S2
CDN	Denitrification exponential rate coefficient	Replace	2.63	2.51
N_UPDIS	Nitrogen uptake distribution parameter	Replace	16.70	38.10
PRF_BSN	Peak rate adjustment factor for sediment routing in the main channel	Replace	0.46	0.21
ADJ_PKR	Peak rate adjustment factor for sediment routing in tributary	Replace	1.13	0.62
RSDCO	Residue decomposition coefficient	Replace	0.06	0.07
SOL_NO3	Initial NO3 concentration in the soil layer	Replace	7.90	27.50
LAT_ORGN	Organic N in the baseflow	Replace	0.05	0.45
HLIFE_NGW	Half-life of nitrate in the shallow aquifer	Replace	56.66	77.80
SLSUBBSN	Average slope length	Multiply	1.23	0.86
HRU_SLP	Average slope steepness	Multiply	1.03	1.24
USLE_P	USLE equation support practice	Replace	0.35	0.84
BIOMIX	Biological mixing efficiency	Replace	0.14	0.16
USLE_C	Min value of USLE C factor applicable to the land cover/plant	Multiply	1.19	1.03
USLE_K	USLE equation soil erodibility (K) factor	Multiply	1.45	1.30
AI1	Fraction of algal biomass that is nitrogen	Replace	0.07	0.08

), and these selected parameters were identically applied to S1 and S2; the same ranges were set for each parameter’s value. In the calibration process, the channel-related parameters were excluded to prevent the interpretation of the effect of channel geometry information on the model simulations.

To evaluate the model performance, this study used a graphical technique. According to Legates and McCabe [31], the graphical techniques are essential to appropriate the model evaluation because they provide a visual comparison of the simulated and measured constituent data and a first overview of model performance. This study conducted the model evaluation using a hydrograph. A hydrograph is beneficial to identify the model bias and differences in timing, the magnitude of peak flows, as well as the shape of the recession curves [32,33].

In addition to the graphical model evaluation, various statistical techniques are concurrently used, and the following statistic criteria were selected: coefficient of determination (R²), Nash-Sutcliffe efficiency (NSE), root mean square error (RMSE)-observations standard deviation ratio (RSR), and percent bias (PBIAS). R² is the square of the coefficient of correlation between the simulated and observed values and it ranges from 0 to 1. When R² is 1, it means that the simulated data are perfect. NSE indicates the fit of the data to a linear 1:1 measured versus the simulated best-fit line [34], and it ranges from minus infinity (poor model) to 1.0 (perfect model). A limitation of NSE is the fact that larger values in a time series are significantly overestimated while lower ones are neglected because the differences between the observed and simulated values are computed as squared values [31].

The RMSE summarizes the average error between the observed and predicted variables using the same units as those variables, and RSR is estimated as the ratio of the RMSE and standard deviation of the measured data. The optimal value of RSR is 0, which signifies the perfect model simulation [33]. PBIAS measures the average tendency of the simulated data to be larger or smaller than their corresponding measured values. PBIAS is the deviation of values being evaluated and is expressed as a percentage. The optimal value of PBIAS is 0, and positive values mean model underestimation bias whereas negative values indicate model overestimation [35].

Table 4. The SWAT performance evaluation classification.

Performance Rating	R2, NSE	RSR	PBIAS
			Streamflow	Sediment	N, P
Very good	0.75$–$1.00	0.00$–$0.50	$–\pm$10	$–\pm$15	$–\pm$25
Good	0.50$–$0.75	0.50$–$0.60	$\pm$10 $–\pm$15	$\pm$15 $–\pm$30	$\pm$25 $–\pm$40
Satisfactory	0.25$–$0.50	0.60$–$0.70	$\pm$15 $–\pm$25	$\pm$30 $–\pm$55	$\pm$40 $–\pm$70
Unsatisfactory	0.00$–$0.25	0.70$–$	$\pm$25 $–$	$\pm$55 $–$	$\pm$70 $–$

is the classification of the model efficiencies suggested by Moriasi et al. [33]. However, this study applied the standards of TN to DO due to the absence of reference for DO.

3. Results and Discussion

3.1. Comparison between Current and New Regression Equations for Applicability Assessment of the Middle-Scale Watershed

The average channel bankfull width and the average floodplain bottom width data for each sub-watershed, which were calculated from the channel geometry data measured by Google Earth Pro, were applied to the CurveExpert program to develop the regression equations. The new regression equations were expressed as a function of the upstream watershed area. Equations (8) and (9) are the new regression equations for the bankfull stage width of the main channel, and for the flood width for the Andong Dam basin, respectively.

$$W_{bnkfull}=1.0768·A^{0.5519}$$

(8)

$$W_{btm,fld}=3.4986·A^{0.4611}$$

(9)

where $W_{bnkfull}$ is the bankfull stage width of the main channel (m); $A$ is the upstream drainage area (km²); and $W_{btm,fld}$ is the bottom width of the floodplain (m). Figure 5 shows the comparisons of the average measured bankfull width of the main channels and the floodplain bottom width of each sub-watershed constructed through Google Earth Pro, the regression equations of the current SWAT model, and the new regression equations. Figure 6 shows the bar graphs that indicate the results of the calculated main channel width and floodplain bottom width for each sub-watershed using the current SWAT regression equations and the new regression equations. It can be seen in Figure 5 that SWAT tended to slightly overestimate the bankfull width of the main channels. In particular, the bottom width of the floodplain was significantly overestimated when compared to the measured data. On the contrary, the new regression equations showed a high degree of accuracy for both results compared with the current regression equations in SWAT. According to the analysis of the channel geometry estimation results of S1 (current regression equations) and S2 (new regression equations), the channel bankfull width and the floodplain bottom width of S1 were estimated to be 35% and 73% larger, respectively, than those of S2, for all of the sub-watersheds. These results reflect that the current regression equations in SWAT are inappropriate for middle-scale watersheds such as the Andong Dam because of overestimation as Ames et al. [6] stated. Specifically, the current regression equation of SWAT for estimating floodplain widths was found to be considerably inaccurate.

3.2. Model Performance Evaluation and Analysis of the Effect of Channel Geometry Data on Model Simulation

3.2.1. Comparison of Flow Velocity Estimation Results from Current and New Regression Equations.

Figure 7 indicates the results of the flow velocity calculations in the #25 (Dosan Station) and #34 (Andong Dam Station) sub-watersheds where the streamflow and water quality calibration were performed. As shown in Figure 7a,b, the flow velocity of S1 (current regression equations) was smaller than that of S2 (new regression equations) at both stations. When peak flow occurred, the gap of the flow velocity between S1 and S2 tended to increase. The average percentage of the difference in the flow velocity of S1 and S2 for 5 years was 48% and 50%, respectively.

This result suggests that the impact of channel geometry caused such a difference in the flow velocity. According to Neitsch et al. [7], the flow velocity is proportional to the hydraulic radius in SWAT (Equation (7)). The hydraulic radius is the value of the cross-sectional area divided by the wetted perimeter (Equation (6)), which is proportional to the channel width (Equation (5)). Due to these relationships between the channel width, wetted perimeter, hydraulic radius, and flow velocity, the flow velocity decreases when the channel width increases under the condition of an identical cross-sectional area of flow in the channel, which means that the amount of water flowing into the channel is the same (combining surface runoff, lateral flow, and baseflow). Therefore, when considering the flow velocity estimation procedure, the results where S1 showed a lower value for flow velocity than S2 were due to the fact that the channel width of S1 was more extensive than that of S2.

3.2.2. Comparison of Simulated Streamflow for Scenarios 1 and 2

The calibration and validation were carried out during the periods from 2011 to 2013 and from 2014 to 2015, respectively. The optimal values of the parameters for Dosan and Andong Dam Stations are presented in Table 2, and the calibrated values for S1 and S2 were similar. Figure 8 shows the streamflow calibration and validation results for Dosan and Andong Dam Stations. The simulated streamflow adequately captured the observed data during the peak flow and recession limb, while the low flow or baseflow was underestimated at both stations. This is because the streamflow calibration was carried out focusing on the high flow (peak flow) periods due to the fact that channel geometry information primarily had an impact on the high flow. In Figure 8, spring and winter were omitted because there were few rainfall events. In these hydrographs, one point of interest was that the simulated peak flow and recession limb tended to be relatively higher in S2 (red lines) than in S1 (blue lines) for both stations. This was due to the channel-routing method, the Muskingum routing method. The Muskingum routing method is based on an assumed linear relationship between a channel’s storage and inflow and outflow (Equation (10)) [36,37].

$$V_{stored}=K·\left(X·q_{in}+\left(1-X\right)·q_{out}\right),$$

(10)

$$K=1000·L_{ch}·\frac{3}{5v_c},$$

(11)

where V_stored is the storage volume, K is the storage time constant, X is the weighting factor, q_in is the inflow, q_out is the flow out, $L_{ch}$ is the channel length (km), and $v_c$ is the flow velocity. Here, K is inversely proportional to the flow velocity and is proportional to the channel length (Equation (11)) [7]. Therefore, if the channel width is relatively larger like in S1, the flow velocity will be estimated to be smaller, and thus, K will be calculated to be larger so that the amount of water stored in the channel will increase. This means that the streamflow or outflow from the channel decreases because more water is stored by the channel when the channel width increases. This trend, where the peak flow as well as the falling limb of S1 showed that the higher values were smaller than those of S2 due to the difference between the channel widths, can be easily seen in all hydrographs in Figure 8.

Table 5. Statistical criteria for the streamflow calibration and validation results.

Criteria	Dosan Station				Andong Dam Station
	Calibration		Validation		Calibration		Validation
	S1	S2	S1	S2	S1	S2	S1	S2
R2	0.79	0.78	0.61	0.62	0.78	0.77	0.69	0.70
NSE	0.77	0.77	0.52	0.54	0.74	0.74	0.67	0.69
RSR	0.51	0.48	0.68	0.69	0.51	0.51	0.57	0.56
PBIAS	29.7	16.3	36.0	31.2	24.9	14.8	35.0	20.7

shows the values of R², NSE, RSR, and PBIAS for the calibration and validation periods. According to the classification of model efficiencies (Table 4), the values of R² and NSE during the calibration periods at both stations were ‘very good’ and those during the validation periods were ‘good’. The values of the RSR of S1 and S2 during the calibration period at Dosan Station were ‘good’ and ‘very good’, respectively, and those values were ‘satisfactory’ during validation. At Andong Dam Station, all values of RSR of S1 and S2 during the calibration and validation were ‘good’. Overall, although there was a slight difference in R², NSE, and RSR between S1 and S2 at both stations, no specific differences were indicated. This is because the amount of water flowing into the channel was calculated as the sum of the surface runoff, lateral flow, and baseflow at the watershed scales, which was estimated using meteorological and topographical data before flowing into the channel. In other words, the parameters related to the cross-sectional shape of the channel had little effect on the flow rate calculation for the channel.

Unlike the previous three criteria, however, the values of PBIAS showed distinct differences between S1 and S2 during the calibration and validation periods at both stations. The values of S2 for the calibration and validation results were much greater than those of S1 at both stations. This means that the channel geometry of S2 estimated by the new regression equations reduced the deviation and improved the accuracy of the streamflow simulation. This can be seen in Figure 8.

3.2.3. Comparison of Simulated Water Quality for Scenarios 1 and 2

Compared to the analysis results of streamflow simulation, the distinct differences appeared in the water quality simulation results for S1 and S2. The adjusted parameters for S1 and S2 showed distinctly different values for all parameters as shown in Table 3. For example, the calibrated values of N_UPDIS (ranges from 0 to 100) were 16.70 and 38.10 for S1 and S2, respectively, and SOL_NO3 (ranges from 0 to 100) were 7.90 and 27.50, respectively.

The results of model performance evaluations also reveal that the channel geometry-related parameters affected water quality simulation. According to the performance ratings in Table 4, R², NSE, RSR, and PBIAS of S2 for the calibration results improved more compared with ‘satisfactory’ for Sediment, TN, and DO as shown in

Table 6. Statistical criteria for the water quality calibration and validation results.

Criteria	Sediment				TN				DO
	Calibration		Validation		Calibration		Validation		Calibration		Validation
	S1	S2	S1	S2	S1	S2	S1	S2	S1	S2	S1	S2
R2	0.65	0.87	0.84	0.84	0.65	0.76	0.71	0.72	0.79	0.79	0.21	0.32
NSE	0.65	0.87	0.78	0.80	0.41	0.65	0.32	0.41	0.59	0.62	−0.49	0.21
RSR	0.59	0.36	0.46	0.44	0.77	0.59	0.46	0.31	0.64	0.62	1.03	1.00
PBIAS	−7.7	−9.9	37.6	22.6	75.3	57.4	18.8	14.4	62.3	49.9	95.8	66.6

. On the other hand, NSE, RSR, and PBIAS of S1 for TN during the calibration period were within the ‘unsatisfactory’ range. During the validation periods, the simulation results of S1 and S2 improved more than the ‘satisfactory’ ranges apart from DO. Although the DO simulation results indicated unsatisfactory, S2 showed the higher values for all model evaluation indicators compared to S1. This suggests that the water quality simulation was influenced by the channel geometry information when considering the same parameters and ranges were identically applied to S1 and S2 for calibration.

The same results were also demonstrated by the graphical comparisons between the observed and simulated water quality for S1 and S2 during the calibration and validation periods. As shown in Figure 9, even though some peak and low water quality values were underestimated in both scenarios, S2 tended to estimate water quality to be higher than S1 (closer to observation) concerning all water quality items, i.e., sediment, TN and DO. When comparing the total amount of sediment, TN and DO for five years between S1 and S2, the 5-year sum of S2 for sediment, TN and DO were higher with 20.8%, 81.1% and 28.6% respectively (

Table 7. Total amount of the simulated water quality for 5 years.

Values	Sediment		TN		DO
	S1	S2	S1	S2	S1	S2
5-year sum (tons)	256,000	309,000	2427	4396	11,142	14,334
Percent difference	20.8%		81.1%		28.6%

).

Figure 10a,b shows the sediment simulation results. The simulated sediment from S2 was higher than in S1, especially when peak flow occurred. The difference between the two scenarios was due to the way that SWAT simulates the instream transportation for sediment. SWAT estimates the maximum concentration of sediment that can be transported by water in each sub-watershed depending on the flow velocity. Then, based on the maximum concentration of sediment, the deposition and degradation are determined. Accordingly, as the maximum concentration of sediment of S2 with a faster flow velocity was estimated to be larger, the amount of sediment at the sub-watershed outlet would be larger. Consequently, if the incorrect channel cross-section information is applied, the uncertainty in sediment simulation could be increased.

The results of TN were akin to the sediment results (in Figure 9c,d); TN of S2 was higher than that of S1 during peak flow periods and this tendency was also caused by the effect of the channel geometry. The amount of TN at an outlet includes the values of organic nitrogen, ammonia, nitrite, as well as nitrate, and each nitrogen-related item is estimated by subtracting the change in nitrate concentration. The amount of change in the nitrate concentration is a function of nitrite, algae, biomass concentration, and flow travel time. Here, the travel time is inversely proportional to the flow rate and is proportional to the volume of the channel. That is, the larger the cross-sectional area, the longer the flow travel time. For this reason, the TN for S1 with a large cross-sectional area was smaller than that of S2.

The DO simulation results showed a similar trend with the TN results; S2 predicted higher DO than S1 for the calibration and validation periods. This is due to the same reason as the TN estimation process. Here, the DO was computed by an equation related to atmospheric reaeration, algal biomass concentration, CBOD, channel depth, ammonium concentration, nitrite concentration, and flow travel time. As a result, because of the effect of travel time on the DO outflow, S1 with a large amount of change of DO in the channel discharged a smaller amount of DO at the watershed outlet.

From the analysis above, it seems that inaccurate channel geometry data could increase uncertainty in the water quality simulation. This misinterpretation, caused by the uncertainty of the simulation results, could eventually impede the proper establishment of watershed management. Figure 10 gives an example pertaining to this situation. Figure 10 is the load duration curve (LDC) for the sediment. The LDC is a graphical analytical tool that describes the relationships between streamflow and water quality. The LDC can assist in decision making regarding this relationship and provides basic information for the total maximum daily load (TMDL) [38], one of the most used watershed management approaches.

Although the LDCs in Figure 10a,b were made for the same station, each LDC shows different tendencies for all flow duration intervals. In the case of Figure 10a, S1 exceeded the standard load under all flow duration intervals except the moist condition. S2, on the other hand, did not exceed the standard load under dry conditions and low flows, which means that the water quality for S2 met the target water quality under these duration intervals. Likewise, in Figure 10b, S1 and S2 showed a difference where the exceedance frequency of S1 was much higher under all conditions except for low flows. Consequently, S1 and S2 could result in different judgments on whether the current water quality of the target river was acceptable. Based on the example of Figure 10, this suggests that if the LDC is developed by erroneously simulated results derived from inaccurate channel geometry information, it could lead to misjudgments in determining the water quality status of a target river.

3.3. Modification of the SWAT 2012 Code to Apply Various Shapes of Channel Cross-Sections

The channel geometry, as a symmetrical trapezoid, of the current SWAT model was improved so that various cross-sectional shapes of a channel could be considered (Figure 11). In Figure 11, the red letters are newly added input variables in order to take into account the various channel cross-sectional shapes. The inclination of each side of both the channel and floodplain were divided into independent input variables to consider different slopes. Additionally, in the present SWAT model, the floodplain width is automatically calculated by the model when the model is running, so it cannot be adjusted by the user. However, in the improved module, the floodplain bottom width is added and divided into two sides (left and right) as new input variables, which helps the user to adjust the floodplain bottom width.

In Figure 11, W_fld,left and W_fld,right are the left and right side width of the floodplain; slp_fld,left and slp_fld,right are the side slope of the floodplain; and slp_ch,left and slp_ch,right are the slope of the main channel. The cross-sectional shape input table should use the new improved channel geometry module. If the user has actual channel data on the cross section, the channel shape can be accurately reflected through the newly added variables. Furthermore, the convenience, when exploiting the modified module, was improved by adjusting the SWAT so that the user could select the current module or an improved one. In addition, the SWAT 2012 code was modified to display the sub-watershed name where the river cross-section data that users generated were applied when using the modified SWAT, which helps the user to see if cross-section information is applied to each sub-watershed.

4. Conclusions

Using multiple aerial photographs, the new regression equations were developed for estimating the bankfull stage width of the main channels and the bottom width of the floodplain in the middle-scale watershed, the Andong Dam watershed. Through a comparison with the new regression equations, the applicability of the current regression equations in SWAT were evaluated for the middle-scale watershed. Then, it was assessed how the channel geometry information affected the flow and water quality simulation. Finally, the channel geometry estimation module in the current SWAT model was improved by modifying SWAT to consider various cross-sectional shapes of channels.

The new regression equations developed using aerial photographs showed higher accuracy than the current regression equations in the SWAT modeling. The current regression equations are likely to overestimate both the main channel width and the floodplain bottom width. Consequently, the current regression equations in SWAT showed poor applicability to the middle-scale watershed as mentioned by Ames et al. [6].

The flow velocity, streamflow, and water quality results estimated in two different scenarios, S1 (using current equations) and S2 (using new equations), were compared to assess the impact of the channel geometry information. While the flow velocity of S1 with the larger channel width showed smaller values than S2, the streamflow simulation results showed no significant differences in general. However, the peak flow rate and falling limb of S2 were estimated to be somewhat higher (closer to observations). Such results occurred because the variation in the channel geometry had an effect on the storage time constant and then caused the outflow from the channel to be diminished by increasing the amount of water stored in the channel. The water quality simulation results (e.g., sediment, TN, and DO) showed the obvious improvement of model performances when the new regression equations were applied; all statistic criteria (R², NSE, RSR, and PBIAS) indicated greater values than those applying the current equations. The simulation results of S2 replicated the observed water quality data better by predicting peak values to be higher than those of S1. Moreover, the analysis of LDCs developed by the results of S1 and S2 suggested that the application of faulty channel geometry information to the channel not only leads to the uncertainty of the water quality simulation but also to the erroneous analysis of water quality condition. Therefore, it was confirmed that the accurate channel cross-section data are as critical as meteorological and topographical input data.

However, this study has a limitation as the new regression equations were developed targeting only one region, the Andong Dam watershed; it is premature to conclude whether the results from this study can be applicable worldwide. Thus, further research applying this study’s approach should be conducted with respect to other middle- and small-scale watersheds with different characteristics. Nonetheless, this study demonstrated that channel geometry could increase the accuracy of modeling water quality simulations by changing the hydraulic characteristics of the channel, although it does not substantially affect streamflow simulation. The demonstration derived in this study is also critical in other fields, as the hydraulic properties of a channel are one of the significant factors determining the aquatic ecosystem or hydrological component.