Modeling the Application Depth and Water Distribution Uniformity of a Linearly Moved Irrigation System
Abstract
:1. Introduction
2. Materials and Methods
2.1. LMIS and Spray Sprinkler
2.2. Modeling for Calculation of Application Depth
- = peak water application rate (mm h−1)
- t = water application time (h).
2.3. Modeling for Calculation of Uniformity
2.4. Setup and Procedures of Indoor Experiment
3. Results and Discussion
3.1. Coefficient of Discharge
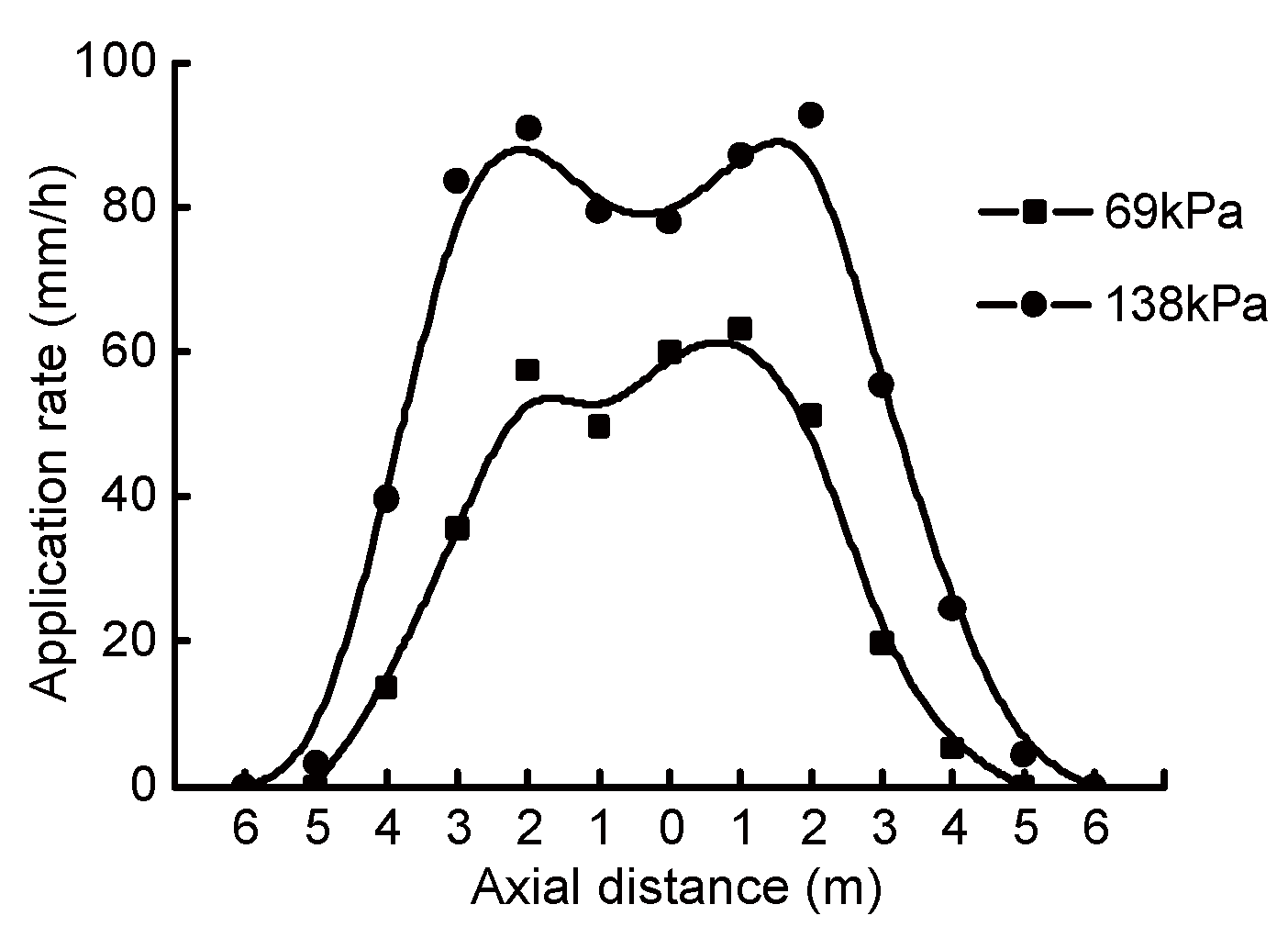
3.2. Measured Water Distributions
3.3. Comparison of Application Depth and CU Values between Experimental Measured Data and Modeling Simulations
3.3.1. Application Depth
3.3.2. Coefficient of Uniformity
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yuan, S.Q.; Li, H.; Wang, X.K. Status, problems, trends and suggestions for water-saving irrigation equipment in China. J. Drain. Irrig. Mach. Eng. (JDIME) 2015, 33, 78–92. [Google Scholar]
- Zhu, X.Y.; Chikangaise, P.; Shi, W.D.; Chen, W.H.; Yuan, S.Q. Review of intelligent sprinkler irrigation technologies for remote autonomous system. Int. J. Agric. Biol. Eng. 2018, 11, 23–30. [Google Scholar] [CrossRef]
- Xu, D.; Li, Y.N.; Gong, S.H.; Zhang, B.Z. Experiment on sweet pepper nitrogen detection based on near infrared reflectivity spectral ridge regression. J. Drain. Irrig. Mach. Eng. (JDIME) 2019, 37, 63–72. [Google Scholar]
- Hart, W.E. Sprinkler distribution analysis with a digital computer. Trans ASAE 1963, 6, 206–208. [Google Scholar]
- Vories, E.D.; Von Bernuth, R.D. Single nozzle sprinkler performance in wind. Trans. ASAE 1986, 29, 1325–1330. [Google Scholar]
- Li, J.; Kawano, H. Sprinkler rotation nonuniformity and water distribution. Trans. ASAE 1996, 39, 2027–2031. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Yuan, S.Q.; Jiang, J.Y.; Liu, J.P.; Liu, X.F. Comparison of fluidic and impact sprinklers based on hydraulic performance. Irrig. Sci. 2015, 33, 367–374. [Google Scholar] [CrossRef]
- Liu, J.P.; Yuan, S.Q.; Li, H.; Zhu, X.Y. Experimental and combined calculation of variable fluidic sprinkler in agriculture irrigation. AMA-Agr. Mech. Asia Afr. Lat. Am. 2016, 47, 82–88. [Google Scholar]
- Xiang, Q.J.; Xu, Z.D.; Chen, C. Experiments on air and water suction capability of 30PY impact sprinkler. J. Drain. Irrig. Mach. Eng. (JDIME) 2018, 36, 82–87. [Google Scholar]
- Hu, G.; Zhu, X.Y.; Yuan, S.Q.; Zhang, L.G.; Li, Y.F. Comparison of ranges of fluidic sprinkler predicted with BP and RBF neural network models. J. Drain. Irrig. Mach. Eng. (JDIME) 2019, 37, 263–269. [Google Scholar]
- Christiansen, J.E. Irrigation by Sprinkling; Bulletin 670; California Agricultural Experiment Station, University of California: Berkeley, CA, USA, 1942. [Google Scholar]
- Solomon, K. Variability of sprinkler coefficient of uniformity test results. Trans. ASAE 1979, 22, 1078–1080. [Google Scholar] [CrossRef]
- Fukui, Y.; Nakanishi, K.; Okamura, S. Computer evaluation of sprinkler irrigation uniformity. Irrig. Sci. 1980, 2, 23–32. [Google Scholar] [CrossRef]
- Seginer, I.; Kantz, D.; Bernuth, R.D. Indoor measurement of single-radius sprinkler patterns. Trans. ASAE 1992, 35, 523–533. [Google Scholar] [CrossRef]
- Tarjuelo, J.M.; Montero, J.; Valiente, M.; Honrubia, F.T.; Ortiz, J. Irrigation uniformity with medium size sprinklers. Part I: Characterization of water distribution in no-wind conditions. Trans. ASAE 1999, 42, 665–675. [Google Scholar] [CrossRef]
- Michael, J.L.; John, S.S. Sprinkler head maintenance effects on water application uniformity. J. Irrig. Drain. Eng. ASCE 2000, 126, 142–148. [Google Scholar]
- Playán, E.; Zapata, N.; Faci, J.M.; Tolosa, D.; Lacueva, J.L.; Pelegrin, J.; Salvador, R.; Sanchez, I.; Lafita, A. Assessing sprinkler irrigation uniformity using a ballistic simulation model. Agric. Water Manag. 2006, 84, 89–100. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Yuan, S.Q.; Liu, J.P. Effect of sprinkler head geometrical parameters on hydraulic performance of fluidic sprinkler. J. Irrig. Drain. Eng. ASCE 2012, 138, 1019–1026. [Google Scholar] [CrossRef]
- Zhang, L.; Merkley, G.P.; Pinthong, K. Assessing whole-field sprinkler irrigation application uniformity. Irrig. Sci. 2013, 31, 87–105. [Google Scholar] [CrossRef]
- Liu, J.P.; Yuan, S.Q.; Darko, R.O. Characteristics of water and droplet size distributions from fluidic sprinklers. Irrig. Drain. 2016, 65, 522–529. [Google Scholar] [CrossRef]
- Yuan, S.Q.; Darko, R.O.; Zhu, X.Y.; Liu, J.P.; Tian, K. Optimization of movable irrigation system and performance assessment of distribution uniformity under varying conditions. Int. J. Agric. Biol. Eng. 2017, 10, 72–79. [Google Scholar]
- Tang, L.D.; Yuan, S.Q.; Qiu, Z.P. Development and research status of water turbine for hose reel irrigator. J. Drain. Irrig. Mach. Eng. (JDIME) 2018, 36, 963–968. [Google Scholar]
- Lu, M.Y.; Lu, K.J.; Hu, G.; Zhu, X.Y. Experiment on hydraulic performance of type SD-03 pop-up sprinkler. J. Drain. Irrig. Mach. Eng. (JDIME) 2018, 36, 1120–1124. [Google Scholar]
- Buchleiter, G.W. Performance of LEPA equipment on center pivot machines. Appl. Eng. Agric. 1992, 8, 631–637. [Google Scholar] [CrossRef]
- King, B.A.; Kincaid, D.C. Optimal performance from center pivot sprinkler systems. Trans. ASABE 1995, 38, 1737–1747. [Google Scholar]
- Luz, P.B. A graphical solution to estimate potential runoff in center-pivot irrigation. Trans. ASABE 2011, 54, 81–92. [Google Scholar] [CrossRef]
- Martin, D.L.; Kranz, W.L.; Thompson, A.L.; Liang, H. Selecting sprinkler packages for center pivots. Trans. ASABE 2012, 55, 513–523. [Google Scholar] [CrossRef]
- Lu, J.; Cheng, J. Numerical simulation analysis of energy conversion in hydraulic turbine of hose reel irrigator JP75. J. Drain. Irrig. Mach. Eng. (JDIME) 2018, 36, 448–453. [Google Scholar]
- Zhu, X.Y.; Peters, T.; Neibling, H. Hydraulic performance assessment of LESA at low pressure. Irrig. Drain. 2016, 65, 530–536. [Google Scholar] [CrossRef]
- Tian, K.; Zhu, X.Y.; Wan, J.H.; Bao, Y. Development and performance test of lateral move irrigation system. J. Drain. Irrig. Mach. Eng. (JDIME) 2017, 35, 357–361. [Google Scholar]
- Yan, H.J.; Jin, H.Z. Study on the discharge coefficient of nonrotatable sprays for center-pivot system. J. Irrig. Drain. Eng. ASCE 2004, 23, 55–58. [Google Scholar]
- Dogana, E.; Kirnaka, H.; Dogan, Z. Effect of varying the distance of collectors below a sprinkler head and travel speed on measurements of mean water depth and uniformity for a linear move irrigation sprinkler system. Biosyst. Eng. 2008, 99, 190–195. [Google Scholar] [CrossRef]
- Yan, H.J.; Jin, H.Z.; Qian, Y.C. Characterizing center pivot irrigation with fixed spray plate sprinklers. Sci. Chin. 2010, 53, 1398–1405. [Google Scholar] [CrossRef]
- ASAE Standards. Procedure for Sprinkler Distribution Testing for Research Purposes, 32nd ed.; S330.1; ASAE: St. Joseph, MI, USA, 1985. [Google Scholar]
- ASAE Standards. Procedure for Sprinkler Testing and Performance Reporting, 32nd ed.; S398.1; ASAE: St. Joseph, MI, USA, 1985. [Google Scholar]
- ASAE. Test Procedure for Determining the Uniformity of Water Distribution of Center Pivot and Lateral Move Irrigation Machines Equipped with Spray or Sprinkler Nozzles; ANSI/ASAE S436.1 MAR01; ASAE Standards: St. Joseph, MI, USA, 2001. [Google Scholar]
- MOD GB/T 19795.2. Agricultural Irrigation Equipment—Rotating Sprinklers—Part 2: Uniformity of Distribution and Test Methods; International Organization for Standardization: Geneva, Switzerland, 2005. [Google Scholar]
- Schneider, A.D. Efficiency and uniformity of the LEPA and spray sprinkler methods: A review. Trans. ASAE 2000, 43, 937–944. [Google Scholar] [CrossRef]
- Kohl, K.D.; Kohl, R.A.; DeBoer, D.W. Measurement of low pressure sprinkler evaporation loss. Trans. ASAE 1987, 30, 1071–1074. [Google Scholar] [CrossRef]
- Dechmi, F.; Playán, E.; Cavero, J.; Faci, J.M.; Martínez-Cob, A. Wind effects on solid set sprinkler irrigation depth and yield of maize (Zea mays). Irrig. Sci. 2003, 22, 67–77. [Google Scholar] [CrossRef]
- Playán, E.; Salvador, R.; Faci, J.M. Day and night wind drift and evaporation losses in sprinkler solid-sets and moving laterals. Agric. Water Manag. 2005, 76, 139–159. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, W.X.; Li, J.S.; Li, Y.F. Fertigation uniformity and evaporation drift losses of center pivot irrigation system. J. Drain. Irrig. Mach. Eng. (JDIME) 2018, 36, 1125–1130. [Google Scholar]









| 69 kPa | 138 kPa | ||||||
|---|---|---|---|---|---|---|---|
| Flow Rate, m3 h−1 | Nozzle I | Nozzle II | Nozzle III | Nozzle I | Nozzle II | Nozzle III | |
| Replications | |||||||
| 1 | 0.8 | 0.79 | 0.8 | 1.16 | 1.21 | 1.22 | |
| 2 | 0.84 | 0.83 | 0.81 | 1.18 | 1.17 | 1.15 | |
| 3 | 0.77 | 0.8 | 0.83 | 1.21 | 1.16 | 1.19 | |
| Mean | 0.80 | 0.81 | 0.81 | 1.18 | 1.18 | 1.19 | |
| Operating Pressure (kPa) | LMIS Speed (m min−1) | Application Depth (mm) | CU (%) | Standard Deviation |
|---|---|---|---|---|
| 69 kPa | 1.5 | 4.2 | 86.0 | 0.15 |
| 2.3 | 2.8 | 84.5 | 0.26 | |
| 3.3 | 2.0 | 88.7 | 0.12 | |
| 4.0 | 1.6 | 88.9 | 0.12 | |
| 4.7 | 1.3 | 84.8 | 0.15 | |
| Mean | 2.38 | 86.58 | 0.16 | |
| 138 kPa | 1.5 | 7.7 | 87.0 | 0.75 |
| 2.3 | 4.2 | 89.8 | 0.82 | |
| 3.3 | 3.1 | 87.2 | 1.00 | |
| 4.0 | 2.8 | 85.9 | 0.47 | |
| 4.7 | 2.6 | 86.5 | 0.36 | |
| Mean | 4.08 | 87.28 | 0.68 |
| 69 kPa | 138 kPa | |||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | R2 | A | B | C | R2 | |
| Measured data | 0.186 | 1.814 | 5.780 | 0.9954 | 0.529 | 4.331 | 11.26 | 0.9698 |
| Elliptical prediction | 0.231 | 2.140 | 6.461 | 0.9946 | 0.389 | 3.605 | 10.88 | 0.9946 |
| Parabolic prediction | 0.196 | 1.818 | 5.487 | 0.9946 | 0.330 | 3.061 | 9.240 | 0.9946 |
| Triangular prediction | 0.147 | 1.363 | 4.115 | 0.9946 | 0.248 | 2.300 | 6.930 | 0.9946 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhu, X.; Yuan, S.; Fordjour, A. Modeling the Application Depth and Water Distribution Uniformity of a Linearly Moved Irrigation System. Water 2019, 11, 827. https://doi.org/10.3390/w11040827
Liu J, Zhu X, Yuan S, Fordjour A. Modeling the Application Depth and Water Distribution Uniformity of a Linearly Moved Irrigation System. Water. 2019; 11(4):827. https://doi.org/10.3390/w11040827
Chicago/Turabian StyleLiu, Junping, Xingye Zhu, Shouqi Yuan, and Alexander Fordjour. 2019. "Modeling the Application Depth and Water Distribution Uniformity of a Linearly Moved Irrigation System" Water 11, no. 4: 827. https://doi.org/10.3390/w11040827
APA StyleLiu, J., Zhu, X., Yuan, S., & Fordjour, A. (2019). Modeling the Application Depth and Water Distribution Uniformity of a Linearly Moved Irrigation System. Water, 11(4), 827. https://doi.org/10.3390/w11040827





