A Multidisciplinary Approach for Evaluating Spatial and Temporal Variations in Water Quality
Abstract
1. Introduction
2. Methods
2.1. AI Techniques
2.1.1. Multilayer Perceptron (MLP) Network
2.1.2. Radial Basis Function (RBF) Network
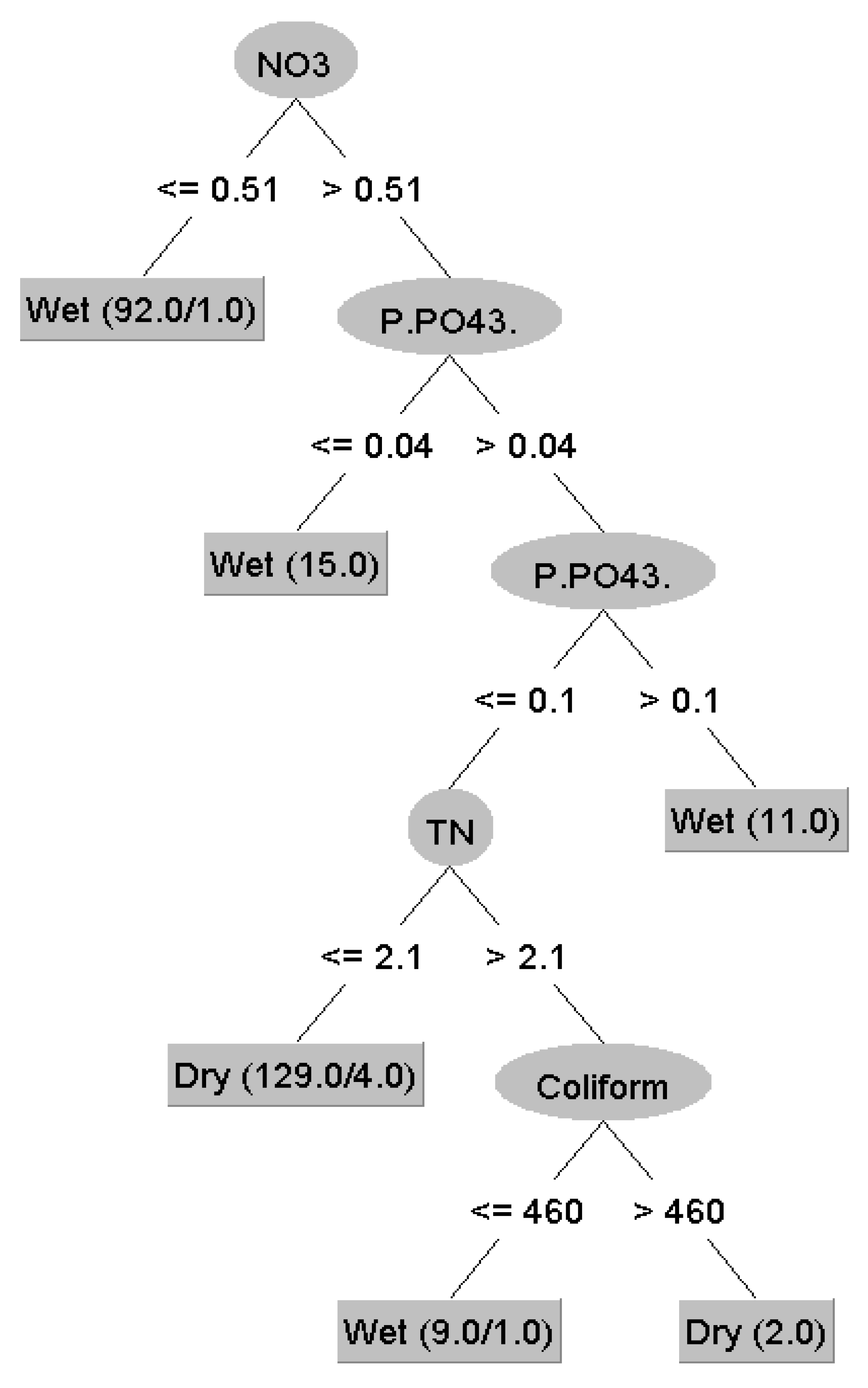
2.1.3. Decision Tree (DT)
2.1.4. Support Vector Machine (SVM)
2.2. Dataset
- The wet season (November to April): three times (26–27 August 2015; 29–30 September 2015; and 26–27 October 2015);
- The dry season (November to April): three times (28–29 March 2016; 28–29 April 2016; and 26–27 May 2016).
3. Results and Discussion
3.1. Preliminary Assessment of Water Quality
3.2. Spatial Variation
3.3. Temporal Variation
3.4. Methodological Implications
3.5. Water Quality Management
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goncharuk, V.V.; Pshinko, G.N.; Rudenko, A.V.; Pleteneva, T.V.; Syroeshkin, A.V.; Uspenskaya, E.V.; Zlatskiy, I.A. Genetically Safe Drinking Water. Requirements and Methods of Its Quality Control. J. Water Chem. Technol. 2018, 40, 16–20. [Google Scholar] [CrossRef]
- Tabari, H.; Hosseinzadeh, T.P. Reconstruction of river water quality missing data using artificial neural networks. Water Qual. Res. J. Can. 2015, 5, 326–335. [Google Scholar] [CrossRef]
- Palani, S.; Liong, S.-Y.; Tkalich, P. An ANN application for water quality forecasting. Mar. Pollut. Bull. 2008, 56, 1586–1597. [Google Scholar] [CrossRef] [PubMed]
- Swain, R.; Sahoo, B. Improving river water quality monitoring using satellite data products and a genetic algorithm processing approach. Sustainabil. Water Qual. Ecol. 2007, 9–10, 88–114. [Google Scholar] [CrossRef]
- Jolk, C.; Greassidis, S.; Jaschinski, S.; Stolpe, H.; Zindler, B. Planning and Decision Support Tools for the Integrated Water Resources Management in Vietnam. Water 2011, 711–725. [Google Scholar] [CrossRef]
- Quan, N.H.; Meon, G. Nutrient Dynamics during Flood Events in Tropical Catchments: A Case Study in Southern Vietnam. Clean Soil Air Water 2014, 43, 652–661. [Google Scholar] [CrossRef]
- Meon, G.; Pätsch, M.; Phuoc, N.V.; Quan, N.H. EWATEC-COAST: Technologies for Environmental and Water Protection of Coastal Zones in Vietnam. In Proceedings of the 4th International Conference for Environment and Natural Resources—ICENR, Göttingen, Germany, 17–18 June 2014. [Google Scholar]
- Keen, B.; Chu, T.H.; Slavich, P.; Bell, R.; Hoang, M.T. Opportunities to Improve the Sustainable Utilisation and Management of Water and Soil Resources for Coastal Agriculture in Vietnam and Australia; Report FR2013-12; Australian Centre for International Agricultural Research (ACIAR): Canberra, Australia, 2013; ISBN 978-1-922137-60-9.
- Binh Thuan Department of Agriculture and Rural Development. Irrigation Development Plan of Binh Thuan Province 2011–2020; Binh Thuan Department of Agriculture and Rural Development: Bình Thuận, Vietnam, 2011. [Google Scholar]
- Mirauda, D.; Ostoich, M. Assessment of Pressure Sources and Water Body Resilience: An Integrated Approach for Action Planning in a Polluted River Basin. Int. J. Environ. Res. Public Health 2018, 15, 390. [Google Scholar] [CrossRef]
- Mirauda, D.; Ostoich, M.; Di Maria, F.; Benacchio, S.; Saccardo, I. Integrity Model Application: A Quality Support System for Decision-makers on Water Quality Assessment and Improvement. IOP Con. Ser. Earth Environ. Sci. 2018, 120. [Google Scholar] [CrossRef]
- Kulishenko, A.E.; Ostapenko, V.T.; Kravchenko, T.B.; Kvasnitsa, E.A.; Ostapenko, R.V. The statistical analysis of quality indicators of the Dnieper river water and directions for reconstruction of water treatment facilities of the Dnieper waterworks in Kiev. J Water Chem. Technol. 2011, 3, 117. [Google Scholar] [CrossRef]
- Mishra, A. Assessment of water quality using principal component analysis: A case study of the river Ganges. J Water Chem. Technol. 2010, 32, 227–234. [Google Scholar] [CrossRef]
- Nnaji, C.C.; Agunwamba, J.C. The environmental impact of crude oil formation water: A multivariate approach. J Water Chem. Technol. 2013, 35, 222–232. [Google Scholar] [CrossRef]
- Wu, W.; Dandy, G.; Maier, H. Protocol for developing ANN models and its application to the assessment of the quality of the ANN model development process in drinking water quality modelling. Environ. Modell. Softw. 2014, 54, 108–127. [Google Scholar] [CrossRef]
- Arain, M.B.; Ullah, I.; Niaz, A.; Shah, N.; Shah, A.; Hussain, Z.; Muhammad, T.; Hassan, I.A.; Jameel, A.B.; Tasneem, K. Evaluation of water quality parameters in drinking water of district Bannu, Pakistan: Multivariate study. Sustainabil. Water Qual. Ecol. 2014, 3–4, 114–123. [Google Scholar] [CrossRef]
- Kikuchi, T.; Furuichi, T.; Hai, H.T.; Tanaka, S. Assessment of Heavy Metal Pollution in River Water of Hanoi Using Multivariate Analyses. Bull. Environ. Contam. Toxicol. 2009, 85, 575–582. [Google Scholar] [CrossRef] [PubMed]
- Loc, H.H.; Hong Diep, N.T.; Can, N.T.; Irvine, K.N.; Shimizu, Y. Integrated evaluation of Ecosystem Services in Prawn-Rice rotational crops, Vietnam. Ecosyst. Serv. 2017, 26, 377–387. [Google Scholar] [CrossRef]
- Shrestha, S.; Fazama, F. Assessment of surface water quality using multivariate statistical techniques: A case study of the Fuji river basin, Japan. Environ. Modell. Softw. 2007, 22, 464–475. [Google Scholar] [CrossRef]
- Funahashi, K. On the approximate realization of continuous mappings by neural networks. Neural Netw. 1989, 2, 183–192. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feed-forward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Norgaard, M.R.; Poulsen, N.K.; Hansen, L.K. Neural Networks for Modelling and Control of Dynamic Systems; A Practitioner’s Handbook; Springer: London, UK, 2000. [Google Scholar]
- Caruana, R.; Lawrence, S.; Giles, L. Overfitting in neural nets: Backpropagation, conjugate gradient, and early stopping. 2001. Available online: https://papers.nips.cc/paper/1895-overfitting-in-neural-nets-backpropagation-conjugate-gradient-and-early-stopping.pdf (accessed on 25 October 2018).
- Jiang, J.; Chao, D.; Chen, H. Boundary value problems for fractional differential equation with causal operators. Appl. Math. Nonlinear Sci. 2016, 1, 11–22. [Google Scholar] [CrossRef]
- Batool, F.; Adeel, S.; Azeem, M.; Khan, A.A.; Bhatti, I.A.; Ghaffar, A.; Iqbal, N. Gamma radiations induced improvement in dyeing properties and colorfastness of cotton fabrics dyed with chicken gizzard leaves extracts. Radiat. Phys. Chem. 2013, 89, 33–37. [Google Scholar] [CrossRef]
- Guan, X.; Zhu, Y.; Song, W. Application of RBF neural network improved by peak density function in intelligent color matching of wood dyeing. Chaos, Solitons Fractals 2016, 89, 485–490. [Google Scholar] [CrossRef]
- Myles, A.J.; Feudale, R.N.; Liu, Y.; Woody, N.A.; Brown, S.D. An introduction to decision tree modeling. J. Chemomet. Soc. 2004, 18, 275–285. [Google Scholar] [CrossRef]
- Debeljak, M.; Džeroski, S. Decision trees in ecological modelling. In Modelling Complex Ecological Dynamics; Springer: Heidelberg, Germany, 2011; pp. 197–209. [Google Scholar]
- Abe, S. Support Vector Machines for Pattern Classification; Springer: London, UK, 2005. [Google Scholar]
- Han, J.; Jian, P.; Micheline, K. Data Mining: Concepts and Techniques; Elsevier: New York, NY, USA, 2011. [Google Scholar]
- International Standard ISO Document 5667—1: Guidance on the Design of Sampling Programmes and Sampling Techniques. Available online: https://www.iso.org/obp/ui/#iso:std:iso:5667:-1:ed-2:v1:en (accessed on 15 December 2018).
- International Standard ISO Document 5667—3: Preservation and Handling of Water Samples. Available online: https://www.iso.org/obp/ui/#iso:std:iso:5667:-1:ed-2:v1:en (accessed on 15 December 2018).
- International Standard ISO Document 5667—4: Guidance on Sampling from Lakes, Natural and Man-made. Available online: https://www.iso.org/obp/ui/#iso:std:iso:5667:-1:ed-2:v1:en (accessed on 15 December 2018).
- International Standard ISO Document 5667—1: Guidance on Sampling of Rivers and Streams. Available online: https://www.iso.org/obp/ui/#iso:std:iso:5667:-1:ed-2:v1:en (accessed on 15 December 2018).
- Ministry of Natural Resources and Environment, QCVN 08 –MT: 2015. National Technical Regulation on Surface Water Quality. Available online: http://moitruong.com.vn/Upload/48/Nam_2017/Thang_3/Ngay_17/QCVN08-2015_Quy_chuan_ky_thuat_quoc_gia_ve_chat_luong_nuoc_mat.pdf (accessed on 15 December 2018).
- Hoang, D.T. Environmental Monitoring in Vietnam: Current Status and Perspective; Vietnam Environment Administration: Nanoi, Vietnam, 2011.







| Classifier | Advantages | Limitations |
|---|---|---|
| MLP Network | + Easy to design + Few parameters | - Requiring high computational time - The training period may be slow - Difficult to identify the number of neurons and layers |
| RBF Network | + Easy to design + Good generalization + More fast learning | - Sensitive to the dimensionality of data - Necessary of the preliminary setting of neurons and basic functions |
| DT | + DT-based models are easily interpreted. + Easy to produce the model. + Can be used for both discrete and continuous values | - Not working well on the small training dataset - Overfitting problem. - A dataset with a small variation can produce different decision trees |
| SVM | + High accuracy performance capability + Working well even if the dataset is not linearly separable | - The high cost of computation - High memory usage |
| Naïve Bayes Classifier | + Simple to implement. + Providing accurate results in most of classification and prediction problems. + High computational efficiency | - The precision will decrease when the size of the dataset is small. |
| Observed Variables | Minimum | Maximum | Mean | Standard Deviation | QCVN 08-MT: 2015/BTNMT |
|---|---|---|---|---|---|
| pH | 6.75 | 8.9 | 7.57 | 0.315 | 6–8.5 |
| DO | 5 | 5.82 | 5.221 | 0.131 | ≥5 |
| BOD | 3 | 9 | 5.159 | 1.052 | ≤6 |
| COD | 8.3 | 17.1 | 10.819 | 1.802 | ≤15 |
| TSS | 2 | 32 | 11.28 | 5.342 | ≤50 |
| NH4 | 0.05 | 0.17 | 0.089 | 0.019 | ≤0.3 |
| NO2 | 0.01 | 0.04 | 0.012 | 0.005 | ≤0.05 |
| NO3 | 0.27 | 1.2 | 0.608 | 0.194 | ≤5 |
| TN | 0 | 4.2 | 0.815 | 0.999 | Not Applicable |
| TP | 0 | 0.33 | 0.111 | 0.071 | Not Applicable |
| P.PO43 | 0 | 0.3 | 0.064 | 0.049 | ≤0.2 |
| Coliform | 3 | 24,000 | 429.938 | 1938.732 | ≤5000 |
| Parameters | QCVN 08-MT:2015/BTNMT | Site C1 | Site C11 | Site C14 | Site SA2 | Site SA4 | Site R19 | |
|---|---|---|---|---|---|---|---|---|
| Arsenic (mg/L) | ≤0.02 | Range | 0–2.5 | 0–3.1 | 0–2.6 | 0–4 | 1.8–12 | 0–3.5 |
| Mean | 0.417 | 0.52 | 0.437 | 1.6 | 4.317 | 1.25 | ||
| S.D. | 1.02 | 1.264 | 1.06 | 1.367 | 3.837 | 1.184 | ||
| Mercury (mg/L) | ≤0.001 | UNDETECTED | ||||||
| Cadmium (mg/L) | ≤0.005 | |||||||
| Lead (mg/L) | ≤0.02 | |||||||
| Zinc (mg/L) | ≤1.0 | Range | 0–0.02 | 0–0.03 | 0–0.02 | 0–0.05 | 0–0.06 | 0–0.03 |
| Mean | 0.007 | 0.012 | 0.01 | 0.013 | 0.023 | 0.01 | ||
| S.D. | 0.103 | 0.013 | 0.011 | 0.02 | 0.023 | 0.013 | ||
| Manganese (mg/L) | ≤0.2 | Range | 0–0.04 | 0.02–0.09 | 0.02–0.05 | 0–0.07 | 0–0.14 | 0–0.02 |
| Mean | 0.023 | 0.042 | 0.03 | 0.022 | 0.058 | 0.01 | ||
| S.D. | 0.014 | 0.026 | 0.011 | 0.026 | 0.054 | 0.011 | ||
| Chrome VI (mg/L) | ≤0.02 | Range | 0–0.05 | 0–0.04 | 0–0.05 | 0–0.09 | 0–0.05 | 0–0.05 |
| Mean | 0.0083 | 0.006 | 0.008 | 0.015 | 0.008 | 0.008 | ||
| S.D. | 0.02 | 0.016 | 0.021 | 0.037 | 0.021 | 0.021 | ||
| Nickel (mg/L) | ≤0.1 | UNDETECTED | ||||||
| Iron (mg/L) | ≤1.0 | Range | 0.26–1.61 | 0.25–2.22 | 0.27–1.3 | 0.26–1.33 | 0.28–5.33 | 0–0.52 |
| Mean | 0.731 | 1.13 | 0.802 | 0.673 | 1.57 | 0.33 | ||
| S.D. | 0.470 | 0.867 | 0.369 | 0.381 | 1.9 | 0.211 | ||
| Model | Correctly Classified Samples | Incorrectly Classified Samples |
|---|---|---|
| DT (J48) | 221 (85.66%) | 37 (14.34%) |
| MLP | 217 (84.11%) | 41 (15.89%) |
| Naïve Bayes | 206 (79.84%) | 52 (20.16%) |
| RBF | 224 (86.82%) | 34 (13.18%) |
| SVM | 199 (77.13%) | 59 (22.87%) |
| Model | MAE | RMSE | RAE | RRSE |
|---|---|---|---|---|
| DT (J48) | 0.11 | 0.29 | 27.64% | 67.23% |
| MLP | 0.11 | 0.28 | 29.16% | 64.92% |
| Naïve Bayes | 0.13 | 0.30 | 34.50 % | 68.57% |
| RBF | 0.20 | 0.28 | 52.98% | 63.97% |
| SVM | 0.15 | 0.39 | 39.44% | 88.90% |
| Model | Correctly Classified Samples | Incorrectly Classified Samples |
|---|---|---|
| DT (J48) | 244 (94.57%) | 14 (5.43%) |
| MLP | 244 (94.57%) | 14 (5.43%) |
| Naïve Bayes | 244 (94.57%) | 14 (5.43%) |
| RBF | 243 (94.19%) | 15 (5.81%) |
| SVM | 198 (76.74%) | 60 (23.25%) |
| Model | MAE | RMSE | RAE | RRSE |
|---|---|---|---|---|
| DT (J48) | 0.069 | 0.23 | 13.68% | 45.69% |
| MLP | 0.062 | 0.2 | 12.33% | 41.41% |
| Naïve Bayes | 0.085 | 0.22 | 16.98% | 44.49% |
| RBF | 0.133 | 0.22 | 26.49% | 43.42% |
| SVM | 0.233 | 0.48 | 46.51% | 96.44% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, V.T.; Quan, N.H.; Loc, H.H.; Thanh Duyen, N.T.; Dung, T.D.; Nguyen, H.D.; Do, Q.H. A Multidisciplinary Approach for Evaluating Spatial and Temporal Variations in Water Quality. Water 2019, 11, 853. https://doi.org/10.3390/w11040853
Le VT, Quan NH, Loc HH, Thanh Duyen NT, Dung TD, Nguyen HD, Do QH. A Multidisciplinary Approach for Evaluating Spatial and Temporal Variations in Water Quality. Water. 2019; 11(4):853. https://doi.org/10.3390/w11040853
Chicago/Turabian StyleLe, Viet Thang, Nguyen Hong Quan, Ho Huu Loc, Nguyen Thi Thanh Duyen, Tran Duc Dung, Hiep Duc Nguyen, and Quang Hung Do. 2019. "A Multidisciplinary Approach for Evaluating Spatial and Temporal Variations in Water Quality" Water 11, no. 4: 853. https://doi.org/10.3390/w11040853
APA StyleLe, V. T., Quan, N. H., Loc, H. H., Thanh Duyen, N. T., Dung, T. D., Nguyen, H. D., & Do, Q. H. (2019). A Multidisciplinary Approach for Evaluating Spatial and Temporal Variations in Water Quality. Water, 11(4), 853. https://doi.org/10.3390/w11040853






