Application Research of an Efficient and Stable Boundary Processing Method for the SPH Method
Abstract
:1. Introduction
2. SPH Methodology and Fixed Particle Interpolation Method
2.1. SPH Methodology
2.2. Fixed Ghost Boundary Method
- (1)
- Arrange the fixed ghost particles on the normal unit vector (out of the fluid domain) and distribute mirror particles (i.e., interpolation points) on the opposite direction according to the shape of the surface,
- (2)
- The physical properties of mirror particles are evaluated through performing interpolation among the fluid particles,
- (3)
- The physical properties of fixed ghost particles are duplicated from the mirror particles according to the laws of mirror.
3. Boundary Interpolation Method
3.1. Moving Least Squares (MLS) Method
3.2. Simplified Finite Difference Interpolation (SFDI) Method
3.3. Normalized Interpolation Method
3.4. Improved Shepard Interpolation Method
4. Numerical Results
4.1. Hydrostatic Tank Test
4.2. Dam-Breaking Problem
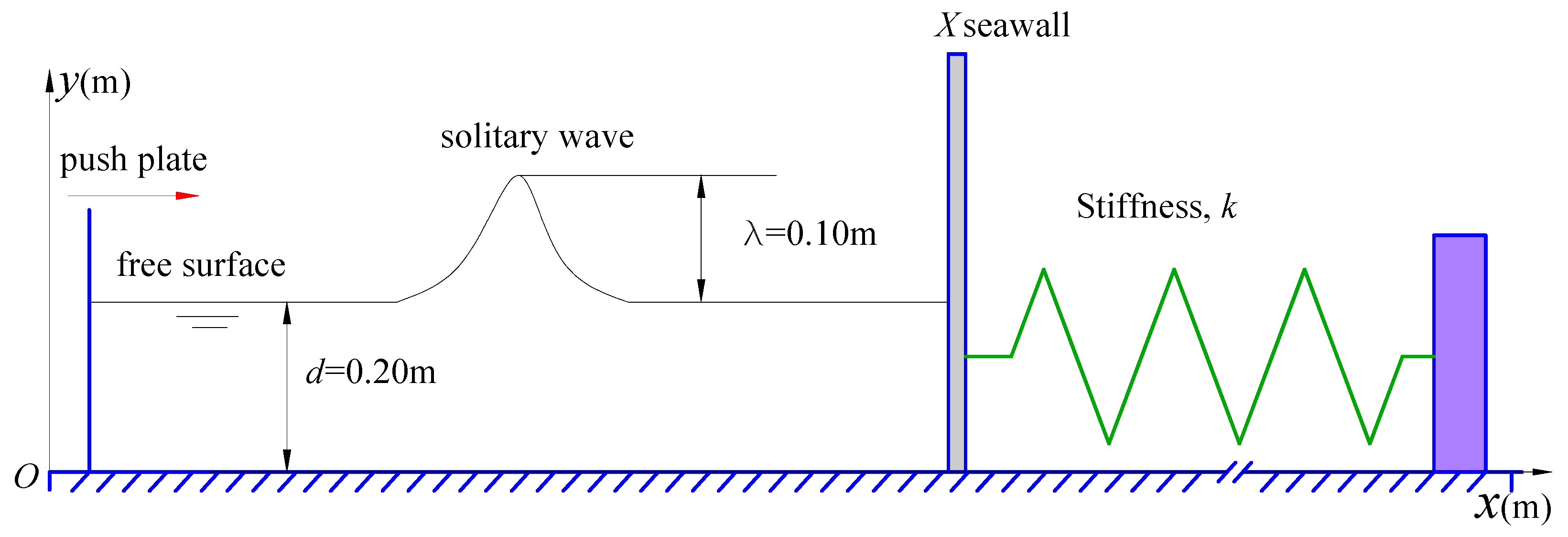
4.3. Solitary Wave Impact on Fixed Seawalls
4.4. Solitary Wave Impact on Movable Seawalls
5. Conclusions and Discussions
Author Contributions
Funding
Conflicts of Interest
References
- Lucy, L.B. A numerical approach to testing of fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 45–58. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1758. [Google Scholar] [CrossRef]
- Chen, Y.S.; Zheng, X.; Jin, S.Q.; Duan, W.Y. A corrected solid boundary treatment method for Smoothed Particle Hydrodynamics. China Ocean Eng. 2017, 31, 238–247. [Google Scholar] [CrossRef]
- Padova, D.D.; Mossa, M.; Sibilla, S. SPH numerical investigation of characteristics of hydraulic jumps. Environ. Fluid Mech. 2018, 18, 849–870. [Google Scholar] [CrossRef]
- Padova, D.D.; Brocchini, M.; Buriani, F.; Corvaro, S.; Serio, D.F.; Mossa, M.; Sibilla, S. Experimental and numerical investigation of pre-breaking and breaking vorticity within a plunging breaker. Water 2018, 10, 387. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Padova, D.D.; Mossa, M.; Sibilla, S. SPH modelling of hydraulic jump oscillations at an abrupt drop. Water 2017, 9, 790. [Google Scholar] [CrossRef]
- Padova, D.D.; Mossa, M.; Sibilla, S. SPH numerical investigation of the characteristics of an oscillating hydraulic jump at an abrupt drop. J. Hydrodyn. 2018, 30, 106–113. [Google Scholar] [CrossRef]
- Zheng, X.; Duan, W.Y.; Ma, Q.W. Comparison of improved meshless interpolation schemes for SPH method and accuracy analysis. J. Mar. Sci. Appl. 2010, 9, 223–230. [Google Scholar] [CrossRef]
- Sun, P.; Ming, F.; Zhang, A. Numerical simulation of interactions between free surface and rigid body using a robust SPH method. Ocean Eng. 2015, 98, 32–49. [Google Scholar] [CrossRef]
- Hashemi, M.R.; Fatehi, R.; Manzari, M.T. A modified SPH method for simulating motion of rigid bodies in Newtonian fluid flows. Int. J. Non-Linear Mech. 2012, 47, 626–638. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Kajtar, J.B. SPH particle boundary forces for arbitrary boundaries. Comput. Phys. Commun. 2009, 180, 1811–1820. [Google Scholar] [CrossRef]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Bouscasse, B.; Colagrossi, A.; Marrone, S.; Antuono, M. Nonlinear water wave interaction with floating bodies in SPH. J. Fluid Struct. 2013, 42, 112–129. [Google Scholar] [CrossRef]
- Zheng, X. An Investigation of Improved SPH and Its Application for Free Surface Flow. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2010. [Google Scholar]
- Ma, Q.W. A New Meshless Interpolation Scheme for MLPG_R Method. CMES 2008, 23, 75–89. [Google Scholar]
- Sriram, V.; Ma, Q.W. Improved MLPG_R method for simulating 2D interaction between violent waves and elastic structures. J. Comput. Phys. 2012, 231, 7650–7670. [Google Scholar] [CrossRef]
- Zheng, X.; Ma, Q.W.; Shao, S.D.; Khayyer, A. Modelling of Violent Water Wave Propagation and Impact by Incompressible SPH with First-Order Consistent Kernel Interpolation Scheme. Water 2017, 9, 400. [Google Scholar] [CrossRef]
- Zhang, N.B.; Zheng, X.; Ma, Q.W.; Duan, W.Y.; Khayyer, A.; Lv, X.P.; Shao, S.D. A hybrid stabilization technique for simulating water wave—Structure interaction by incompressible Smoothed Particle Hydrodynamics (ISPH) method. J. Hydro-Environ. Res. 2018, 18, 77–94. [Google Scholar] [CrossRef]
- Chen, J.; Beraun, J.; Carney, T. A corrective smoothed particle method for boundary value problems in heat conduction. Int. J. Numer. Methods Eng. 1999, 46, 231–252. [Google Scholar] [CrossRef]
- Wen, H.J.; Ren, B.; Dong, P.; Wang, Y.X. A SPH numerical wave basin for modeling wave-structure interactions. Appl. Ocean Res. 2016, 59, 366–377. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.; Stansby, P.; Laurence, D. Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J. Comput. Phys. 2009, 228, 6703–6725. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Jian, G.Y.; Zhao, L.; Ding, F.X. Improved Shepard Method and Its Application in Gravity Field Data Interpolation. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 477–480. [Google Scholar]
- Kang, Z.; Wang, Y.Q. Structural topology optimization based on non-local Shepard interpolation of density field. Comput. Methods Appl. Mech. Eng. 2011, 200, 3515–3525. [Google Scholar] [CrossRef]
- Kang, Z.; Wang, Y.Q. A nodal variable method of structural topology optimization based on Shepard interpolant. Int. J. Numer. Methods Eng. 2012, 90, 329–342. [Google Scholar] [CrossRef]
- Monaghan, J.; Kos, A. Solitary waves on a Cretan beach. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 145–154. [Google Scholar] [CrossRef]
- Molteni, D.; Colagrossi, A.; Colicchio, G. On the use of an alternative water state equation in SPH. In Proceedings of the SPHERIC, 2nd International Workshop, Universidad Politécnica de Madrid, Getafe, Spain, 23–25 May 2007. [Google Scholar]
- Antuono, M.; Colagrossi, A.; Marrone, S.; Molteni, D. Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput. Phys. Commun. 2010, 181, 532–549. [Google Scholar] [CrossRef]
- Morris, J.P. Analysis of Smoothed Particle Hydrodynamics with Applications. Ph.D. Dissertation Thesis, Department of Mathematics, Monash University, Victoria, Australia, 1996. [Google Scholar]
- Kolerski, T.; Shen, H.T.; Kioka, S. A numerical model study on ice boom in a coastal lake. J. Coast. Res. 2013, 29, 177–186. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 23rd National Conference, New York, NY, USA, 27–29 August 1968; ACM: New York, NY, USA, 1968; pp. 517–523. [Google Scholar]
- Lodha, S.K.; Franke, R. Scattered data techniques for surfaces. In Proceedings of the Scientific Visualization Conference, Dagstuhl, Germany, 9–13 June 1997; pp. 189–230. [Google Scholar]
- Farwig, R. Rate of convergence of Shepard’s global interpolation formula. Math. Comput. 1986, 46, 577–590. [Google Scholar]
- Franke, R.; Nielson, G.M. Smooth interpolation of large sets of scattered data. Int. J. Numer. Methods Eng. 1980, 15, 1691–1704. [Google Scholar] [CrossRef]
- Chen, Z.; Zong, Z.; Liu, M.B.; Zou, L.; Li, H.T.; Shu, C. An SPH model for multiphase flows with complex interfaces and large density differences. J. Comput. Phys. 2015, 283, 169–188. [Google Scholar] [CrossRef]
- Buchner, B. Green Water on Ship-type Offshore Structures. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Ren, B.; Wen, H.; Dong, P.; Wang, Y. Improved SPH simulation of wave motions and turbulent flows through porous media. Coast. Eng. 2016, 107, 14–27. [Google Scholar] [CrossRef]
- Philip, L.-F.; Lin, P.Z.; Chang, K.A.; Sakakiyama, T. Numerical modeling of wave interaction with porous structures. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 322–330. [Google Scholar]
- Lin, P.Z.; Liu, X.; Zhang, J. The simulation of a landside-induced surge wave and its overtopping of a dam using a coupled ISPH model. Eng. Appl. Comput. Fluid Mech. 2015, 9, 432–444. [Google Scholar]
- Zheng, X.; Hu, Z.H.; Ma, Q.W.; Duan, W.Y. Incompressible SPH based on rankine source solution for water wave impact simulation. Proced. Eng. 2015, 126, 650–654. [Google Scholar] [CrossRef]
- Pimanmas, A.; Joyklad, P.; Warnitchal, P. Structural design guideline for Tsunami evacuation shelter. J. Earthq. Tsunami 2010, 4, 269–284. [Google Scholar] [CrossRef]
- Liang, D.F.; Wei, J.; Shao, S.D.; Chen, R.D.; Yang, K.J. Incompressible SPH simulation of solitary wave interaction with movable seawalls. J. Fluid Struct. 2017, 69, 72–88. [Google Scholar] [CrossRef]


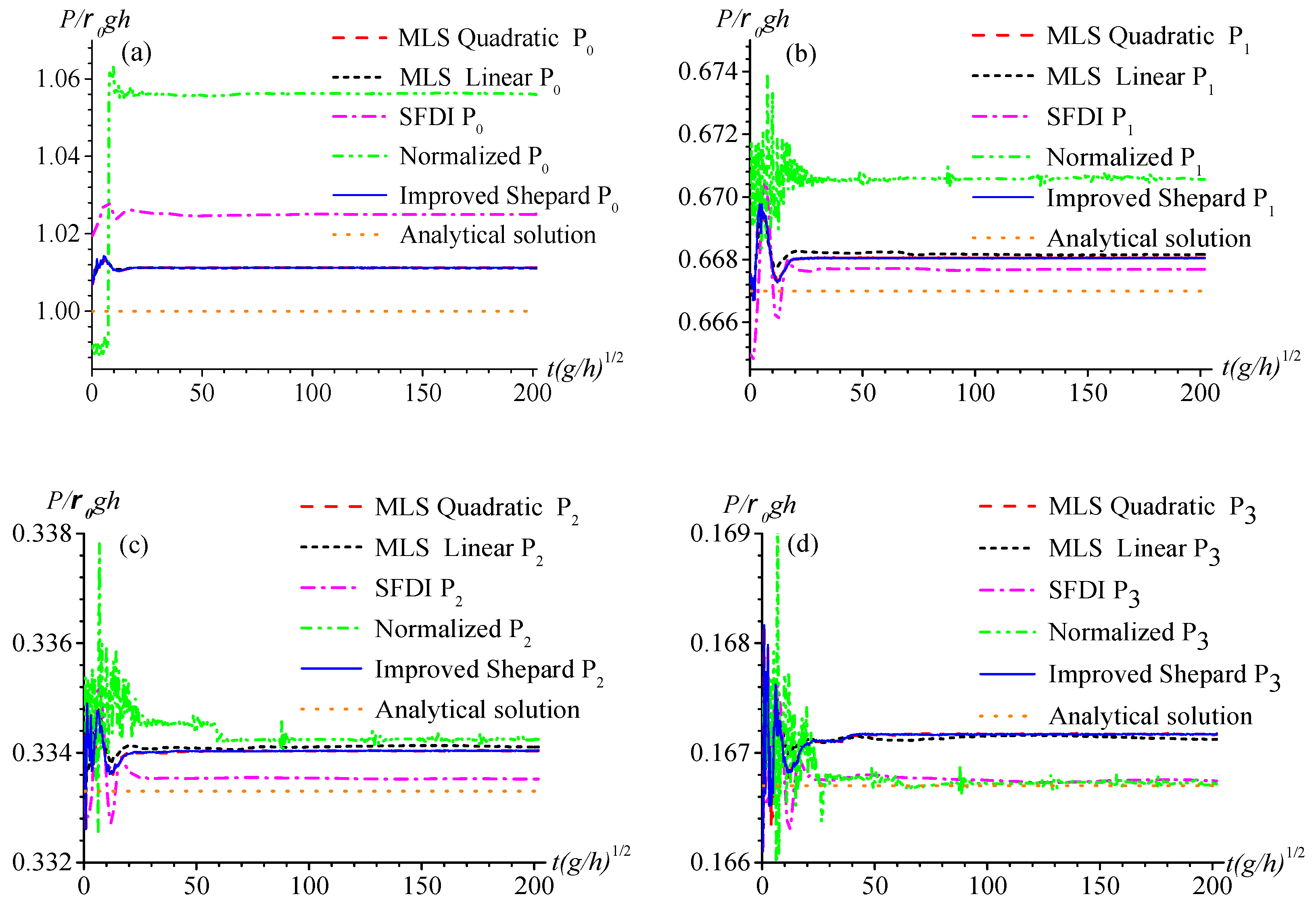
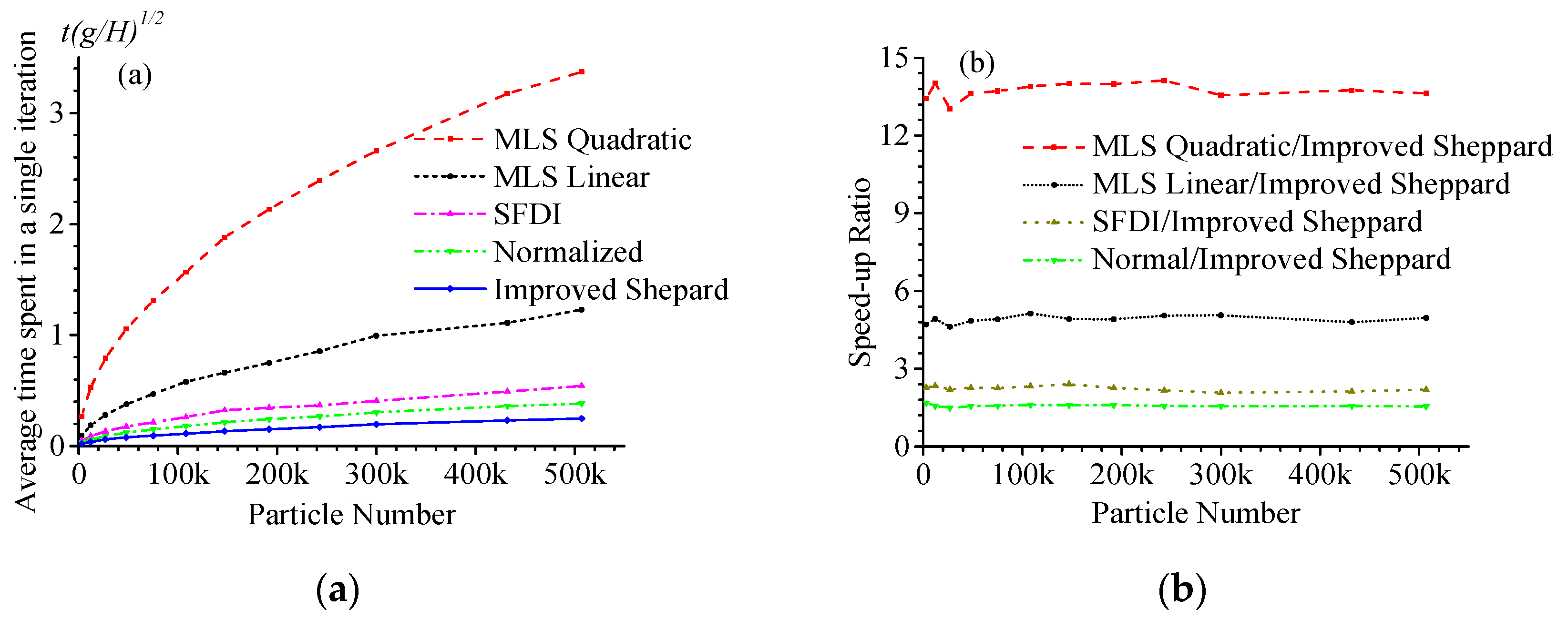

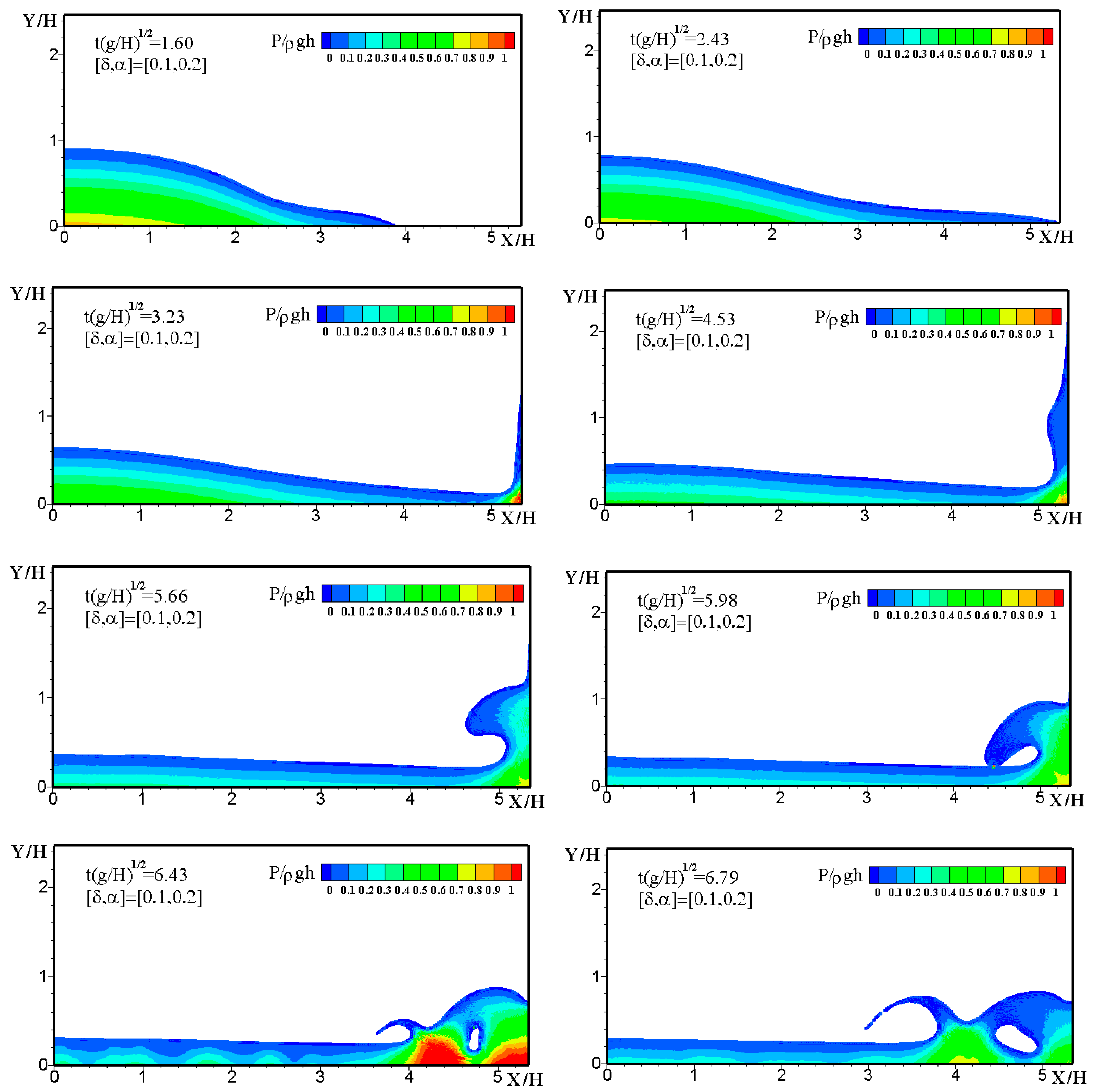



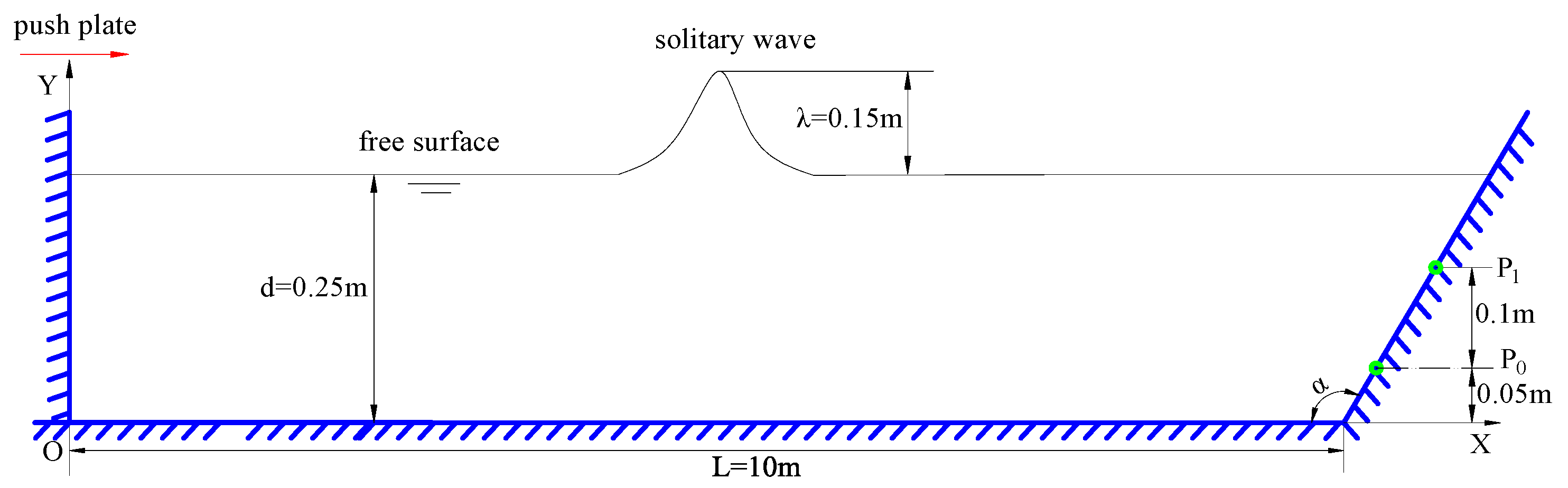




| Interpolation Method | Calculated Amount (Relationship with Neighboring Particles) |
|---|---|
| Moving Least Squares method | Quadratic |
| Simplified Finite Difference Interpolation method | Quadratic |
| Normalized interpolation method | Linear |
| Improved Shepard method | Linear |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Chen, W.; Hu, Z.; Zheng, X.; Jin, S.; Zhang, X. Application Research of an Efficient and Stable Boundary Processing Method for the SPH Method. Water 2019, 11, 1110. https://doi.org/10.3390/w11051110
Huang X, Chen W, Hu Z, Zheng X, Jin S, Zhang X. Application Research of an Efficient and Stable Boundary Processing Method for the SPH Method. Water. 2019; 11(5):1110. https://doi.org/10.3390/w11051110
Chicago/Turabian StyleHuang, Xing, Wu Chen, Zhe Hu, Xing Zheng, Shanqin Jin, and Xiaoying Zhang. 2019. "Application Research of an Efficient and Stable Boundary Processing Method for the SPH Method" Water 11, no. 5: 1110. https://doi.org/10.3390/w11051110
APA StyleHuang, X., Chen, W., Hu, Z., Zheng, X., Jin, S., & Zhang, X. (2019). Application Research of an Efficient and Stable Boundary Processing Method for the SPH Method. Water, 11(5), 1110. https://doi.org/10.3390/w11051110





