Causal Reasoning: Towards Dynamic Predictive Models for Runoff Temporal Behavior of High Dependence Rivers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study
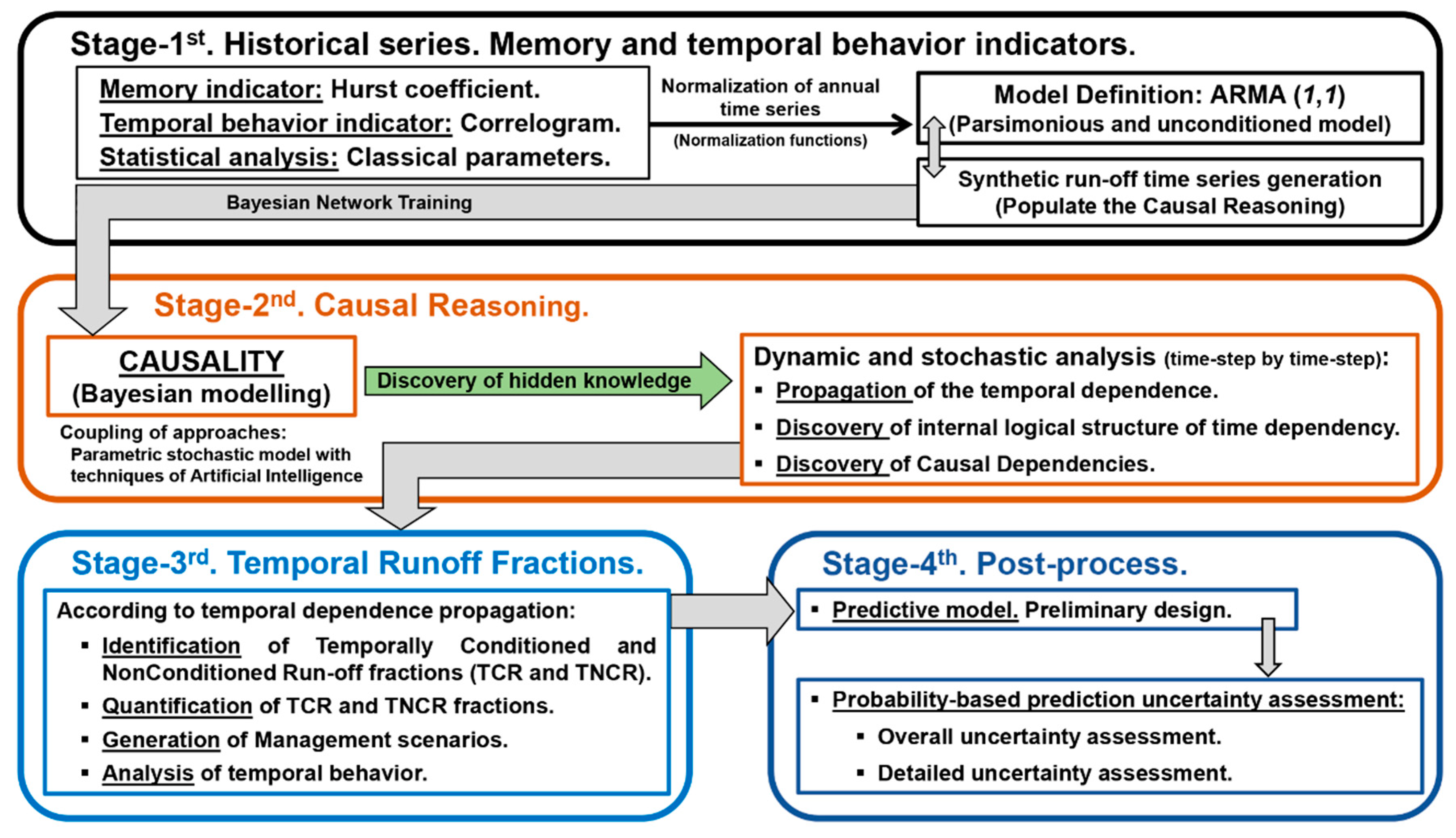
2.2. Methodololy
2.2.1. Stage-1. Historical Series. Memory and Temporal Behavior Indicators
2.2.2. Stage-2. Causal Reasoning
2.2.3. Stage-3. Temporal Runoff Fractions
2.2.4. Stage-4. Post-Process.
3. Results
3.1. Statistical Analysis
3.2. Analysis of the Temporal Conditionality through Causal Reasoning
3.3. Management Scenarios
3.4. Predictive Model. Probability-Based Assessment
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Allan, R.P.; Soden, B.J. Atmospheric Warming and the Amplification of Precipitation Extremes. Science 2008, 321, 1481–1484. [Google Scholar] [CrossRef]
- Berg, P.; Moseley, C.; Haerter, J.O. Strong Increase in Convective Precipitation in Response to Higher Temperatures. Nat. Geosci. 2013, 6, 181–185. [Google Scholar] [CrossRef]
- Trenberth, K.E. Changes in Precipitation with Climate Change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Lepori, F.; Pozzoni, M.; Pera, S. What Drives Warming Trends in Streams? A Case Study from the Alpine Foothills. River Res. Appl. 2015, 31, 663–675. [Google Scholar] [CrossRef]
- Reihan, A.; Kriauciuniene, J.; Meilutyte-Barauskiene, D.; Kolcova, T. Temporal Variation of Spring Flood in Rivers of the Baltic States. Hydrol. Res. 2012, 43, 301–314. [Google Scholar] [CrossRef]
- Praskievicz, S. Impacts of Projected Climate Changes on Streamflow and Sediment Transport for Three Snowmelt-Dominated Rivers in the Interior Pacific Northwest. River Res. Appl. 2016, 32, 4–17. [Google Scholar] [CrossRef]
- Botai, J.O.; Botai, C.M.; de Wit, J.P.; Muthoni, M.; Adeola, A.M. Analysis of Drought Progression Physiognomies in South Africa. Water 2019, 11, 299. [Google Scholar] [CrossRef]
- IPCC. Intergovernmental Panel on Climate Change. Fifth Assessment Report (AR5). Available online: http://www.ipcc.ch (accessed on 3 January 2016).
- O’Gorman, P.A. Precipitation Extremes Under Climate Change. Curr. Clim. Chang. Rep. 2015, 1, 49–59. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pfahl, S.; O’Gorman, P.A.; Fischer, E.M. Understanding the Regional Pattern of Projected Future Changes in Extreme Precipitation. Nat. Clim. Chang. 2017, 7, 423–427. [Google Scholar] [CrossRef]
- Marotzke, J.; Jakob, C.; Bony, S.; Dirmeyer, P.A.; O’Gorman, P.A.; Hawkins, E.; Perkins-Kirkpatrick, S.; Le Quere, C.; Nowicki, S.; Paulavets, K.; et al. Climate Research Must Sharpen its View. Nat. Clim. Chang. 2017, 7, 89–91. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wan, H.; Zwiers, F.W.; Hegerl, G.C.; Min, S. Attributing Intensification of Precipitation Extremes to Human Influence. Geophys. Res. Lett. 2013, 40, 5252–5257. [Google Scholar] [CrossRef]
- Min, S.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human Contribution to More-Intense Precipitation Extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More Extreme Precipitation in the World’s Dry and Wet Regions. Nat. Clim. Chang. 2016, 6, 508. [Google Scholar] [CrossRef]
- Drobinski, P.; Alonzo, B.; Bastin, S.; Da Silva, N.; Muller, C. Scaling of Precipitation Extremes with Temperature in the French Mediterranean Region: What Explains the Hook Shape? J. Geophys. Res. Atmos. 2016, 121, 3100–3119. [Google Scholar] [CrossRef]
- Wasko, C.; Sharma, A. Steeper Temporal Distribution of Rain Intensity at Higher Temperatures within Australian Storms. Nat. Geosci. 2015, 8, 527. [Google Scholar] [CrossRef]
- Guinard, K.; Mailhot, A.; Caya, D. Projected Changes in Characteristics of Precipitation Spatial Structures Over North America. Int. J. Climatol. 2015, 35, 596–612. [Google Scholar] [CrossRef]
- Molina, J.L.; Zazo, S. Assessment of Temporally Conditioned Runoff Fractions in Unregulated Rivers. J. Hydrol. Eng. 2018, 23, 04018015. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Review of Dependence Modeling in Hydrology and Water Resources. Prog. Phys. Geogr. 2016, 40, 549–578. [Google Scholar] [CrossRef]
- Van den Berg, M.J.; Vandenberghe, S.; De Baets, B.; Verhoest, N.E.C. Copula-Based Downscaling of Spatial Rainfall: A Proof of Concept. Hydrol. Earth Syst. Sci. 2011, 15, 1445–1457. [Google Scholar] [CrossRef]
- Molina, J.L.; Pulido-Velazquez, D.; Luis Garcia-Arostegui, J.; Pulido-Velazquez, M. Dynamic Bayesian Networks as a Decision Support Tool for Assessing Climate Change Impacts on Highly Stressed Groundwater Systems. J. Hydrol. 2013, 479, 113–129. [Google Scholar] [CrossRef]
- Nourani, V.; Kisi, O.; Komasi, M. Two Hybrid Artificial Intelligence Approaches for Modeling Rainfall-Runoff Process. J. Hydrol. 2011, 402, 41–59. [Google Scholar] [CrossRef]
- Bianucci, P.; Sordo-Ward, A.; Moralo, J.; Garrote, L. Probabilistic-Multiobjective Comparison of User-Defined Operating Rules. Case Study: Hydropower Dam in Spain. Water 2015, 7, 956–974. [Google Scholar] [CrossRef] [Green Version]
- Uysal, G.; Alvarado-Montero, R.; Schwanenberg, D.; Sensoy, A. Real-Time Flood Control by Tree-Based Model Predictive Control Including Forecast Uncertainty: A Case Study Reservoir in Turkey. Water 2018, 10, 340. [Google Scholar] [CrossRef]
- Recio Villa, I.; Martinez Rodriguez, J.B.; Molina, J.L.; Pino Tarrago, J.C. Multiobjective Optimization Modeling Approach for Multipurpose Single Reservoir Operation. Water 2018, 10, 427. [Google Scholar] [CrossRef]
- Romano, E.; Del Bon, A.; Petrangeli, A.B.; Preziosi, E. Generating Synthetic Time Series of Springs Discharge in Relation to Standardized Precipitation Indices. Case Study in Central Italy. J. Hydrol. 2013, 507, 86–99. [Google Scholar] [CrossRef]
- Wang, W.; Chau, K.; Cheng, C.; Qiu, L. A Comparison of Performance of several Artificial Intelligence Methods for Forecasting Monthly Discharge Time Series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef]
- Molina, J.L.; Zazo, S.; Rodriguez-Gonzalvez, P.; Gonzalez-Aguilera, D. Innovative Analysis of Runoff Temporal Behavior through Bayesian Networks. Water 2016, 8, 484. [Google Scholar] [CrossRef]
- Molina, J.L.; Zazo, S. Causal Reasoning for the Analysis of Rivers Runoff Temporal Behavior. Water Resour. Manag. 2017, 31, 4669–4681. [Google Scholar] [CrossRef]
- Zazo, S. Analysis of the Hydrodynamic Fluvial Behaviour through Causal Reasoning and Artificial Vision. Ph.D. Thesis, University of Salamanca, Ávila, Spain, 12 May 2017. [Google Scholar]
- Molina, J.L.; Zazo, S.; Martín, A. Causal Reasoning: An Adaptive/Predictive Approach for Runoff Temporal Behaviour of High Dependences Rivers. In Proceedings of the 3rd International Electronic Conference on Water Sciences (ECWS-3), 15–30 November 2018; https://ecws-3.sciforum.net/.
- Sang, Y.; Shang, L.; Wang, Z.; Liu, C.; Yang, M. Bayesian-Combined Wavelet Regressive Modeling for Hydrologic Time Series Forecasting. Chin. Sci. Bull. 2013, 58, 3796–3805. [Google Scholar] [CrossRef]
- Mohammadi, K.; Eslami, H.R.; Kahawita, R. Parameter Estimation of an ARMA Model for River Flow Forecasting using Goal Programming. J. Hydrol. 2006, 331, 293–299. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Parameters Estimate of Autoregressive Moving Average and Autoregressive Integrated Moving Average Models and Compare their Ability for Inflow Forecasting. J. Math. Stat. 2012, 8, 330–338. [Google Scholar]
- Kong, X.; Huang, G.; Fan, Y.; Li, Y.; Zeng, X.; Zhu, Y. Risk Analysis for Water Resources Management Under Dual Uncertainties through Factorial Analysis and Fuzzy Random Value-at-Risk. Stoch. Environ. Res. Risk Assess. 2017, 31, 2265–2280. [Google Scholar] [CrossRef]
- MITECO. Ministerio Para la Transición Ecológica. Gobierno de España. Available online: https://www.miteco.gob.es/es/agua/temas/seguridad-de-presas-y-embalses/desarrollo/ (accessed on 30 October 2018).
- De Castro, M.; Martín-Vide, J.; Alonso, S. El Clima de España: Pasado, Presente y Escenarios de Clima Para el Siglo XXI. Evaluación Preliminar de los Impactos en España por Efecto del Cambio Climático; Ministerio de Medio Ambiente y Universidad de Castilla-La Mancha: Madrid, Spain, 2005; pp. 1–64. ISBN 84-8320-303-0. [Google Scholar]
- Cortesi, N. Variabilidad de la Precipitación en la Península Ibérica. Ph.D. Thesis, University of Zaragoza, Zaragoza, Spain, 12 January 2013. [Google Scholar]
- Vallarino, E.; Bravo Guillén, G.; Girón Caro, F.; Salate Díaz, E. Tratado Básico de Presas. Tomo I: Generalidades—Presas de Hormigón y de Materiales Sueltos; Colegio de Ingenieros de Caminos, Canales y Puertos: Madrid, Spain, 2001. [Google Scholar]
- CHJ. Confederación Hidrográfica del Júcar. Ministerio Para la Transición Ecológica. Gobierno de España. Available online: https://www.chj.es/es-es/medioambiente/cuencahidrografica/ (accessed on 8 January 2019).
- Macian-Sorribes, H.; Pulido-Velazquez, M.; Tilmant, A. Definition of Efficient Scarcity-Based Water Pricing Policies through Stochastic Programming. Hydrol. Earth Syst. Sci. 2015, 19, 3925–3935. [Google Scholar] [CrossRef]
- EU Directive. EU Directive of the European Parliament and of the Council Establishing a Framework for Community Action in the Field of Water Policy (2000/60/EC) 2000. Off. J. Eur. Union 2000, 22, 2000. [Google Scholar]
- MFOM. Ministerio de Fomento. Gobierno de España. Confederación Hidrográfica del Júcar. Norma 5.2—IC Drenaje Superficial de la Instrucción de Carreteras. Available online: https://www.fomento.gob.es/recursos_mfom/ordenfom_298_2016.pdf (accessed on 10 January 2019).
- IGME. Instituto Geológico y Minero de España. Available online: http://igme.maps.arcgis.com/home/webmap/viewer.html?webmap=036292dc5b8946bd979a7dc47d2f8561 (accessed on 23 January 2019).
- MITECO. Ministerio para la Transición Ecológica. Gobierno de España. Available online: https://sig.mapama.gob.es/redes-seguimiento/ (accessed on 30 October 2018).
- Salas, J.; Delleur, J.; Yevjevich, V.; Lane, W.L. Applied Modeling of Hydrologic Time Series, 1st ed.; Water Resources Publications: Littleton, CO, USA, 1980; p. 484. [Google Scholar]
- Tyralis, H.; Koutsoyiannis, D. Simultaneous Estimation of the Parameters of the Hurst-Kolmogorov Stochastic Process. Stoch. Environ. Res. Risk Assess. 2011, 25, 21–33. [Google Scholar] [CrossRef]
- TRASERO. Tratamiento y Gestión de Series Temporales Hidrológicas; Diputación Provincial de Alicante—Departamento de Ciclo Hídrico: Alicante, Spain, 2015; pp. 28–30. ISBN 978-84-15327-28-8. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning and Inference, 2nd ed.; Cambridge University Press: New York, NY, USA, 2009; p. 484. ISBN 978-0-521-89560-6. [Google Scholar]
- HUGIN. Hugin Expert A/S. 2010. 7.3. Available online: http://www.hugin.com (accessed on 17 December 2018).
- Cain, J. Planning Improvements in Natural Resources Management; Centre for Ecology and Hydrology: Wallingford, UK, 2001. [Google Scholar]
- Sperotto, A.; Molina, J.L.; Torresan, S.; Critto, A.; Marcomini, A. Reviewing Bayesian Networks Potentials for Climate Change Impacts Assessment and Management: A Multi-Risk Perspective. J. Environ. Manag. 2017, 202, 320–331. [Google Scholar] [CrossRef]
- Jensen, F.V. An Introduction to Bayesian Networks; UCL Press: London, UK, 1996. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Francisco, CA, USA, 1988; p. 552. [Google Scholar]
- Adarnowski, J.F. Development of a Short-Term River Flood Forecasting Method for Snowmelt Driven Floods Based on Wavelet and Cross-Wavelet Analysis. J. Hydrol. 2008, 353, 247–266. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Teshnehlab, M. Using Adaptive Neuro-Fuzzy Inference System for Hydrological Time Series Prediction. Appl. Soft Comput. 2008, 8, 928–936. [Google Scholar] [CrossRef]
- Aqil, M.; Kita, I.; Yano, A.; Nishiyama, S. A Comparative Study of Artificial Neural Networks and Neuro-Fuzzy in Continuous Modeling of the Daily and Hourly Behaviour of Runoff. J. Hydrol. 2007, 337, 22–34. [Google Scholar] [CrossRef]
- Castelletti, A.; Soncini-Sessa, R. Bayesian Networks and Participatory Modelling in Water Resource Management. Environ. Model. Softw. 2007, 22, 1075–1088. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Díaz Caballero, F.F. Selección de Modelos Mediante Criterios de Información en Análisis Factorial: Aspectos Teóricos y Computacionales. Ph.D. Thesis, University of Granada, Granada, Spain, 27 January 2011. [Google Scholar]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Comparison of Stochastic and Machine Learning Methods for Multi-Step Ahead Forecasting of Hydrological Processes. Stoch. Environ. Res. Risk Assess. 2019, 33, 481–514. [Google Scholar]
- Tyralis, H.; Koutsoyiannis, D. A Bayesian Statistical Model for Deriving the Predictive Distribution of Hydroclimatic Variables. Clim. Dyn. 2014, 42, 2867–2883. [Google Scholar] [CrossRef]
- Iglesias, A.; Estrela, T.; Gallart, F. Impactos Sobre Los Recursos Hídricos. In Evaluación Preliminar de los Impactos en España por Efecto del Cambio Climático; Ministerio de Agricultura, Pesca y Alimentación: Madrid, Spain, 2005; pp. 303–353. https://www.miteco.gob.es/es/cambio-climatico/temas/impactos-vulnerabilidad-y-adaptacion/plan-nacional-adaptacion-cambio-climatico/evaluacion-preliminar-de-los-impactos-en-espana-del-cambio-climatico/eval_impactos.aspx.
- CEDEX. Informe Técnico: Evaluación del Impacto del Cambio Climático en los Recursos Hídricos y Sequías en España; Centro de Estudios y Experimentación de Obras Públicas, Ministerio de Fomento. Ministerio de Agricultura y Pesca, Alimentación y Medio Ambiente; Gobierno de España: Madrid, Spain, 2017; pp. 15–19. [Google Scholar]
- Garrote, L.; de Lama, B.; Martín-Carrasco, F. Previsiones para España según los últimos estudios de Cambio Climático. In El Cambio Climático en España y sus Consecuencias en el Sector Agua; Universidad Rey Juan Carlos: Madrid, Spain, 2007; pp. 3–15. [Google Scholar]
- Jiménez Álvarez, A. Desarrollo de Metodologías para mejorar la estimación de los Hidrogramas de Diseño para el cálculo de los órganos de desagüe de las presas. Ph.D. Thesis, Polytechnical University of Madrid, Madrid, Spain, 22 January 2016. [Google Scholar]








| Intervals | Classes | ||
|---|---|---|---|
| Range | Color Code | Description | |
| [1.00, 0.95] | Totally dependent | DR ≥ 0.50. A lot of evidence of relevant dependencies | |
| (0.95, 0.90] | Highly dependent | ||
| (0.90, 0.75] | Dependent | ||
| (0.75, 0.50] | Slightly dependent | ||
| (0.50, 0.00] | DR < 0.50. Little or null evidence of significant dependencies | ||
| Parameters | Historical Runoff Series | Average of All Annual Synthetic Series |
|---|---|---|
| Mean: | 27.06 Hm³ | 26.75 Hm³ |
| Standard deviation: | 15.23 Hm³ | 16.12 Hm³ |
| Skewness coefficient 1: | 1.05 | 1.58 |
| Variation coefficient: | 56% | 59% |
| Dependence Propagation (time-lags) | Analysis of Peaks | Analysis of Valleys | Average Behavior | |||
|---|---|---|---|---|---|---|
| % TCR | % TNCR | % TCR | % TNCR | % TCR | % TNCR | |
| Dependence 1 year | 84.8 | 15.2 | 87.4 | 12.6 | 86.1 | 13.9 |
| Dependence 2 year | 78.1 | 21.9 | 76.7 | 23.3 | 77.4 | 22.6 |
| Dependence 3 year | 73.5 | 26.5 | 72.4 | 27.6 | 73.0 | 27.0 |
| Dependence 4 year | 70.1 | 29.9 | 67.2 | 32.8 | 68.7 | 31.3 |
| Dependence 5 year | 66.9 | 33.1 | 68.8 | 31.2 | 67.9 | 32.1 |
| Dependence 6 year | 65.4 | 34.6 | 67.9 | 32.1 | 66.7 | 33.3 |
| Parameters | TCR Fraction | |||||
|---|---|---|---|---|---|---|
| Dependence Propagation (time-lags) | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Mean (Hm³) | 23.50 | 21.24 | 20.18 | 19.26 | 18.04 | 17.26 |
| Standard deviation (Hm³) | 14.86 | 13.76 | 13.62 | 13.05 | 11.39 | 10.64 |
| Maximum (Hm³) | 72.05 | 70.67 | 70.63 | 69.08 | 66.27 | 62.96 |
| Minimum (Hm³) | 4.11 | 3.75 | 3.73 | 0.65 | 3.46 | 2.96 |
| Range (Hm³) | 67.94 | 66.92 | 66.90 | 68.43 | 62.81 | 60.00 |
| Skewness coefficient 1 | 1.47 | 1.42 | 1.50 | 1.48 | 1.70 | 1.78 |
| Variation coefficient (%) | 63 | 65 | 68 | 68 | 63 | 62 |
| Kurtosis | 2.05 | 2.08 | 2.43 | 2.75 | 4.30 | 4.83 |
| ARMA Model (p, q) | AIC | ||||||
| Historical records | (1, 0) | −5.8705 | |||||
| (1, 1) | −5.8704 | 0.9985 | 0.0007 | ||||
| (1, 2) | −5.8703 | 0.0007/0.0007 | |||||
| (2, 0) | −5.8704 | ||||||
| (2, 1) | −5.8703 | 0.9992/−0.0007 | 0.0001 | ||||
| (2, 2) | −5.8702 | 0.0001/0.0007 | |||||
| TCR Fraction | TNCR Fraction | ||||||
| AIC | AIC | ||||||
| Dep-1 | (1, 0) | −5.8267 | −5.8469 | ||||
| (1, 1) | −5.8266 | 0.9984 | 0.0007 | −5.8468 | 0.9986 | 0.0007 | |
| (1, 2) | −5.8266 | 0.0007/0.0007 | −5.8467 | 0.0007/0.0007 | |||
| (2, 0) | −5.8266 | −5.8468 | |||||
| (2, 1) | −5.8266 | 0.9992/−0.0008 | 0.0001 | −5.8467 | 0.9993/−0.0007 | 0.0001 | |
| (2, 2) | −5.8265 | 0.0001/0.0007 | −5.8466 | 0.0001/0.0007 | |||
| Dep-2 | (1, 0) | −5.9146 | −5.4748 | ||||
| (1, 1) | −5.9145 | 0.9985 | 0.0007 | −5.4747 | 0.9979 | 0.0010 | |
| (1, 2) | −5.9144 | 0.0007/0.0007 | −5.4746 | 0.0010/0.0010 | |||
| (2, 0) | −5.9145 | −5.4748 | |||||
| (2, 1) | −5.9144 | 0.9993/−0.0008 | −0.0001 | −5.4747 | 0.9990/−0.0010 | 0.0001 | |
| (2, 2) | −5.9143 | −0.0001/0.0007 | −5.4746 | 0.0001/0.0010 | |||
| Dep-3 | (1, 0) | −5.8417 | −5.5094 | ||||
| (1, 1) | −5.8416 | 0.9984 | 0.0007 | −5.5093 | 0.9980 | 0.0010 | |
| (1, 2) | −5.8415 | 0.0007/0.0007 | −5.5093 | 0.0010/0.0010 | |||
| (2, 0) | −5.8416 | −5.5093 | |||||
| (2, 1) | −5.8415 | 0.9992/−0.0008 | −0.0001 | −5.5093 | 0.9990/−0.0010 | 0.0001 | |
| (2, 2) | −5.8414 | −0.0001/0.0007 | −5.5092 | 0.0001/0.0010 | |||
| Dep-4 | (1, 0) | −5.8236 | −5.5015 | ||||
| (1, 1) | −5.8235 | 0.9984 | 0.0007 | −5.5014 | 0.9980 | 0.0010 | |
| (1, 2) | −5.8234 | 0.0007/0.0007 | −5.5013 | 0.0010/0.0010 | |||
| (2, 0) | −5.8235 | −5.5014 | |||||
| (2, 1) | −5.8234 | 0.9992/−0.0008 | −0.0001 | −5.5013 | 0.9990/−0.0010 | 0.0001 | |
| (2, 2) | −5.8233 | −0.0001/0.0007 | −5.5012 | 0.0001/0.0010 | |||
| Dep-5 | (1, 0) | −5.8776 | −5.5647 | ||||
| (1, 1) | −5.8776 | 0.9984 | 0.0007 | −5.5646 | 0.9981 | 0.0010 | |
| (1, 2) | −5.8776 | 0.0007/0.0007 | −5.5645 | 0.0010/0.0010 | |||
| (2, 0) | −5.8776 | −5.5646 | |||||
| (2, 1) | −5.8776 | 0.9992/−0.0008 | −0.0001 | −5.5645 | 0.9990/−0.0010 | 0.0001 | |
| (2, 2) | −5.8776 | −0.0001/0.0007 | −5.5644 | 0.0001/0.0010 | |||
| Dep-6 | (1, 0) | −5.9128 | −5.5902 | ||||
| (1, 1) | −5.9127 | 0.9985 | 0.0007 | −5.5901 | 0.9981 | 0.0009 | |
| (1, 2) | −5.9126 | 0.0007/0.0007 | −5.5900 | 0.0009/0.0009 | |||
| (2, 0) | −5.9127 | −5.5901 | |||||
| (2, 1) | −5.9126 | 0.9992/−0.0008 | −0.0001 | −5.5900 | 0.9991/−0.0009 | 0.0001 | |
| (2, 2) | −5.9125 | −0.0001/0.0007 | −5.5899 | 0.0001/0.0009 | |||
| Probability | TCR | TNCR 3 | Runoff Prediction | ||
|---|---|---|---|---|---|
| Overall | Detailed | ||||
| 0.50 | 14.68 | 2.06 | 16.74 | 14.68 ± 2.06 | [12.62, 16.74] |
| 0.60 | 16.82 | 2.62 | 19.44 | 16.82 ± 2.62 | [14.20, 19.44] |
| 0.70 | 19.38 | 3.37 | 22.75 | 19.38 ± 3.37 | [16.01, 22.75] |
| 0.80 | 22.67 | 4.30 | 26.97 | 22.67 ± 4.30 | [18.37, 26.97] |
| 0.85 | 25.17 | 5.06 | 30.23 | 25.17 ± 5.06 | [20.11, 30.23] |
| 0.90 | 28.38 | 6.12 | 34.50 | 28.38 ± 6.12 | [22.26, 34.50] |
| 0.95 | 34.46 | 8.03 | 26.43 | 34.46 ± 8.03 | [26.43, 42.49] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina, J.-L.; Zazo, S.; Martín, A.-M. Causal Reasoning: Towards Dynamic Predictive Models for Runoff Temporal Behavior of High Dependence Rivers. Water 2019, 11, 877. https://doi.org/10.3390/w11050877
Molina J-L, Zazo S, Martín A-M. Causal Reasoning: Towards Dynamic Predictive Models for Runoff Temporal Behavior of High Dependence Rivers. Water. 2019; 11(5):877. https://doi.org/10.3390/w11050877
Chicago/Turabian StyleMolina, José-Luis, Santiago Zazo, and Ana-María Martín. 2019. "Causal Reasoning: Towards Dynamic Predictive Models for Runoff Temporal Behavior of High Dependence Rivers" Water 11, no. 5: 877. https://doi.org/10.3390/w11050877
APA StyleMolina, J.-L., Zazo, S., & Martín, A.-M. (2019). Causal Reasoning: Towards Dynamic Predictive Models for Runoff Temporal Behavior of High Dependence Rivers. Water, 11(5), 877. https://doi.org/10.3390/w11050877







