Intelligent Control/Operational Strategies in WWTPs through an Integrated Q-Learning Algorithm with ASM2d-Guided Reward
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup and Operation
2.2. Q-Learning Algorithm
3. Development with an ASM2d-QL Algorithm for AAO System
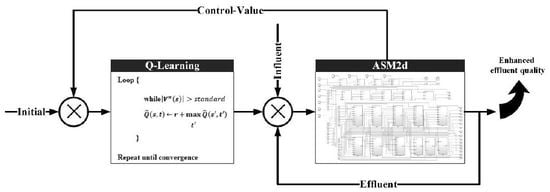
3.1. ASM2d-QL Algorithm Architecture
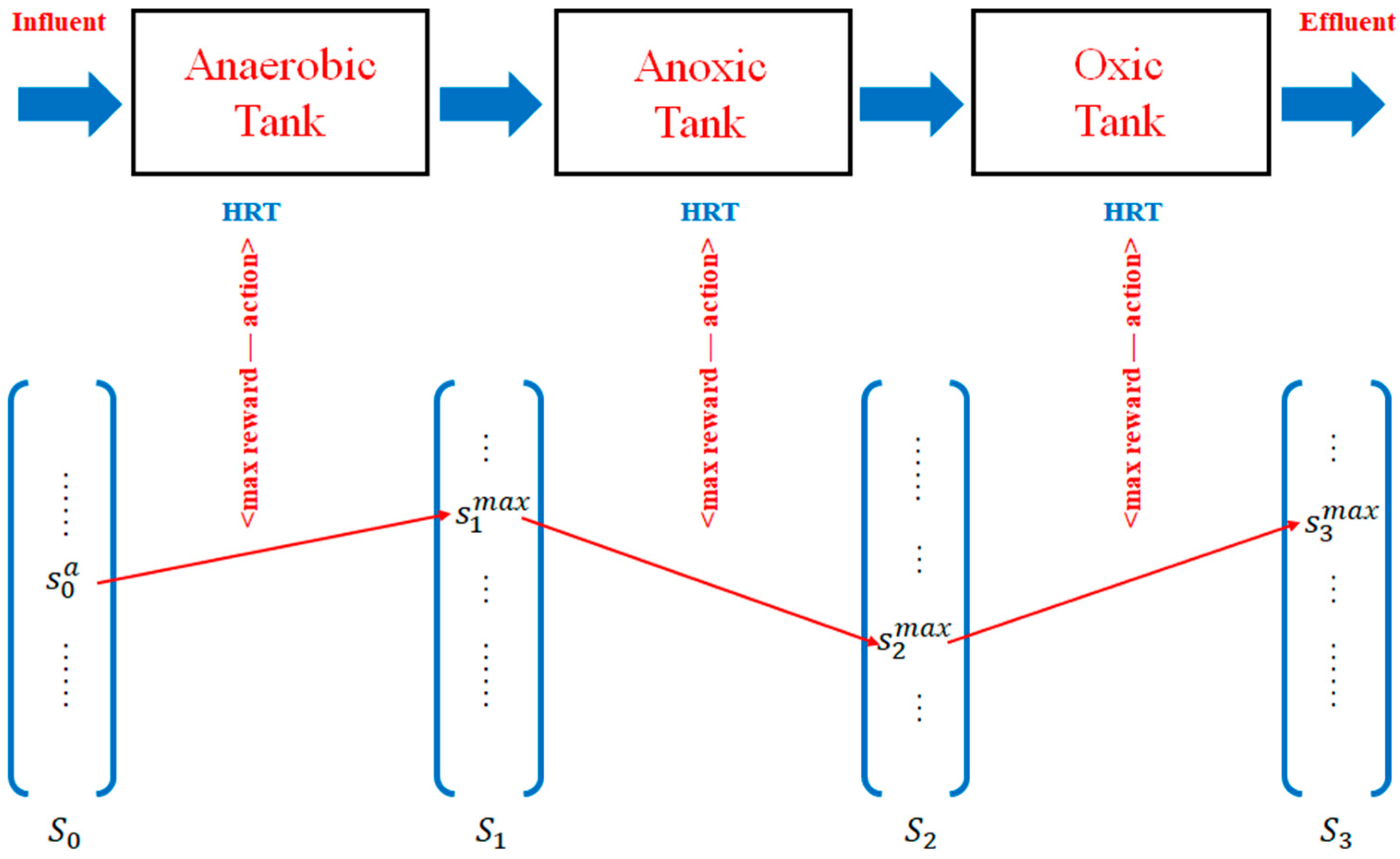
3.2. HRT Optimization Based on ASM2d-Guided Reward
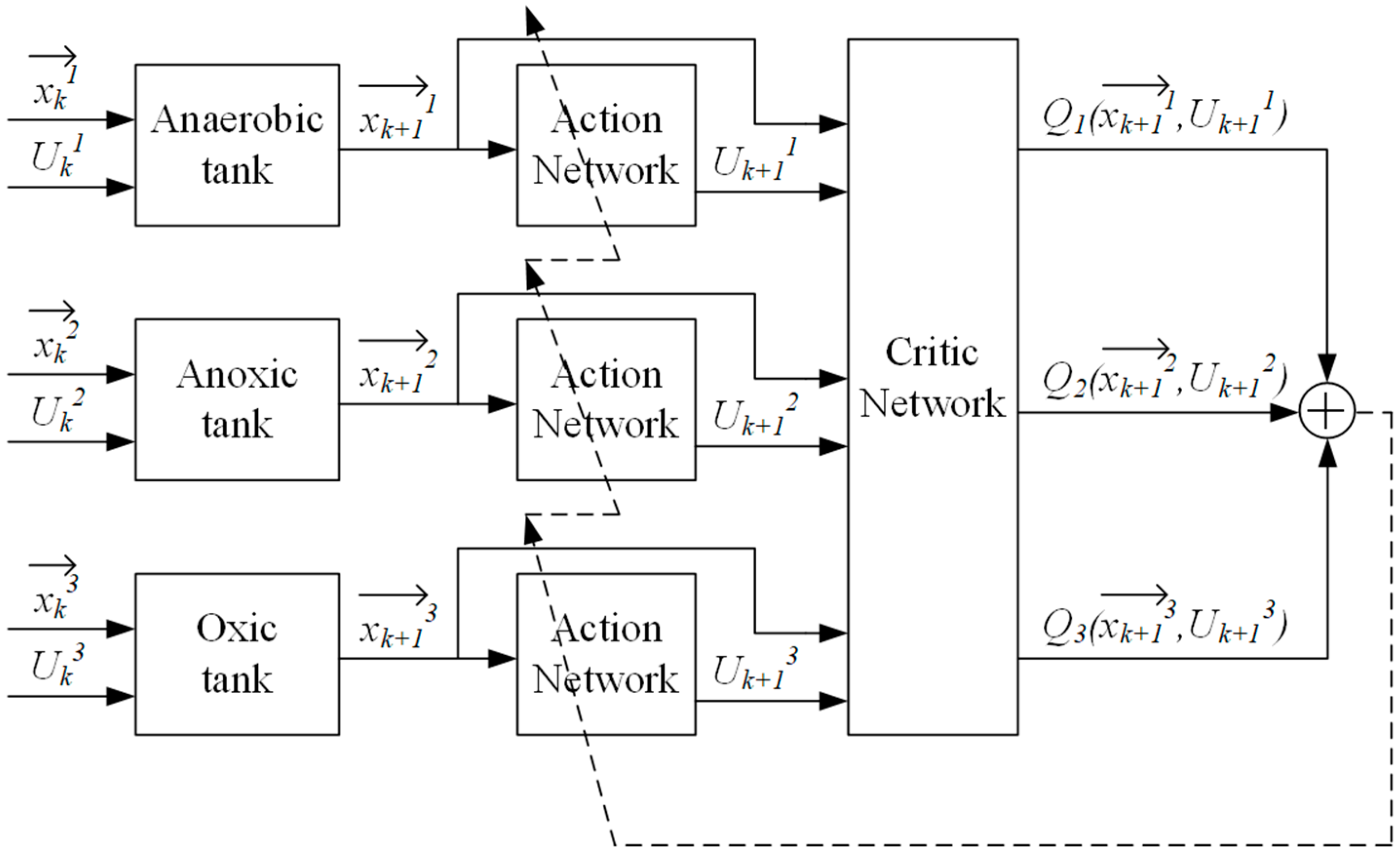
3.2.1. QL Modeling for HRT Optimization
3.2.2. ASM2d-Guided Reward Setting in QL Algorithm
3.3. IRR Optimization Based on ASM2d-Guided Reward
4. Results
4.1. Model Description
4.2. Model Validation
5. Discussion
5.1. Advantages of the Integrated ASM2d-QL Algorithm
5.2. Limitations of the Integrated ASM2d-QL Algorithm
5.3. Future Developments
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Abbassi, B.E.; Abuharb, R.; Ammary, B.; Almanaseer, N.; Kinsley, C. Modified Septic Tank: Innovative Onsite Wastewater Treatment System. Water 2018, 10, 578. [Google Scholar] [CrossRef]
- Angelakis, A.N.; Snyder, S.A. Wastewater Treatment and Reuse: Past, Present, and Future. Water 2015, 7, 4887–4895. [Google Scholar] [CrossRef]
- Jover-Smet, M.; Martín-Pascual, J.; Trapote, A. Model of Suspended Solids Removal in the Primary Sedimentation Tanks for the Treatment of Urban Wastewater. Water 2017, 9, 448. [Google Scholar] [CrossRef]
- Longo, S.; Mirko d’Antoni, B.; Bongards, M.; Chaparro, A.; Cronrath, A.; Fatone, F.; Lema, J.M.; Mauricio-Iglesias, M.; Soares, A.; Hospido, A. Monitoring and diagnosis of energy consumption in wastewater treatment plants. A state of the art and proposals for improvement. Appl. Energy. 2016, 179, 1251–1268. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Yang, W.N.; Ngo, H.H.; Guo, W.S.; Jin, P.K.; Dzakpasu, M.; Yang, S.J.; Wang, Q.; Wang, X.C.; Ao, D. Current status of urban wastewater treatment plants in China. Environ. Int. 2016, 92–93, 11–22. [Google Scholar] [CrossRef]
- Jin, L.Y.; Zhang, G.M.; Tian, H.F. Current state of sewage treatment in China. Water Res. 2014, 66, 85–98. [Google Scholar] [CrossRef]
- Lu, B.; Huang, S.; Grossmann, I.E. Optimal Synthesis and Operation of Wastewater Treatment Process with Dynamic Influent. Ind. Eng. Chem. Res. 2017, 56, 8663–8676. [Google Scholar] [CrossRef]
- Jiang, Y.; Dinar, A.; Hellegers, P. Economics of social trade-off: Balancing wastewater treatment cost and ecosystem damage. J. Environ. Manag. 2018, 211, 42–52. [Google Scholar] [CrossRef]
- Zuluaga-Bedoya, C.; Ruiz-Botero, M.; Ospina-Alarcón, M.; Garcia-Tirado, J. A dynamical model of an aeration plant for wastewater treatment using a phenomenological based semi-physical modeling methodology. Comput. Chem. Eng. 2018, 117, 420–432. [Google Scholar] [CrossRef]
- Nourani, V.; Elkiran, G.; Abba, S.I. Wastewater treatment plant performance analysis using artificial intelligence-an ensemble approach. Water Sci. Technol. 2018, 78, 2064–2076. [Google Scholar] [CrossRef] [PubMed]
- Han, H.G.; Qian, H.H.; Qiao, J.F. Nonlinear multiobjective model-predictive control scheme for wastewater treatment process. J. Process Contr. 2014, 24, 47–59. [Google Scholar] [CrossRef]
- Henze, M.; Gujer, W.; Mino, T.; van Loosedrecht, M. Activated Sludge Models ASM1, ASM2, ASM2d and ASM3; IWA Scientific and Technical Report No. 9; IWA Publishing: London, UK, 2000. [Google Scholar]
- Drewnowski, J.; Makinia, J.; Szaja, A.; Łagód, G.; Kopeć, Ł.; Aguilar, J.A. Comparative Study of Balancing SRT by Using Modified ASM2d in Control and Operation Strategy at Full-Scale WWTP. Water 2019, 11, 485. [Google Scholar] [CrossRef]
- Wu, X.H.; Yang, Y.; Wu, G.M.; Mao, J.; Zhou, T. Simulation and optimization of a coking wastewater biological treatment process by activated sludge models (ASM). J. Environ. Manag. 2016, 165, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.S.; Pang, J.W.; Guo, W.Q.; Yang, X.Y.; Wu, Z.Y.; Ren, N.Q.; Zhao, Z.Q. Biological phosphorus removal in an extended ASM2 model: Roles of extracellular polymeric substances and kinetic modeling. Bioresour. Technol. 2017, 232, 412–416. [Google Scholar] [CrossRef] [PubMed]
- Harrou, F.; Dairi, A.; Sun, Y.; Senouci, M. Statistical monitoring of a wastewater treatment plant: A case study. J. Environ. Manag. 2018, 223, 807–814. [Google Scholar] [CrossRef] [PubMed]
- Chow, C.; Saint, C.; Zappia, L.; Henderson, R.; Roeszler, G.; Dexter, R.; Nguyen, T.; Stuetz, R.; Byrne, A.; Trolio, R.; et al. Online water quality monitoring-the voice of experience, meeting the challenges and removing barriers to implementing online monitoring schemes. AWA Water J. 2014, 41, 60–67. [Google Scholar]
- Chow, C.W.K.; Liu, J.; Li, J.; Swain, N.; Reid, K.; Saint, C.P. Development of smart data analytics tools to support wastewater treatment plant operation. Chemometr. Intell. Lab. 2018, 177, 140–150. [Google Scholar] [CrossRef]
- Van den Broeke, J.; Carpentier, C.; Moore, C.; Carswell, L.; Jonsson, J.; Sivil, D.; Rosen, J.S.; Cade, L.; Mofidi, A.; Swartz, C.; et al. Compendium of Sensors and Monitors and Their Use in the Global Water Industry; Water Environment Research Foundation: Alexandria, VA, USA; Global Water Research Coalition: Unley, SA, Australia, 2014. [Google Scholar]
- Hernández-del-Olmo, F.; Llanes, F.H.; Gaudioso, E. An emergent approach for the control of wastewater treatment plants by means of reinforcement learning techniques. Expert Syst. Appl. 2012, 39, 2355–2360. [Google Scholar] [CrossRef]
- Hreiz, R.; Latifi, M.A.; Roche, N. Optimal design and operation of activated sludge processes: State-of-the-art. Chem. Eng. J. 2015, 281, 900–920. [Google Scholar] [CrossRef]
- Al Jibouri, A.K.H.; Upreti, S.R.; Wu, J. Optimal control of continuous ozonation of non-biodegradable pollutants. J. Process Contr. 2018, 66, 1–11. [Google Scholar] [CrossRef]
- De Araújo, A.C.B.; Gallani, S.; Mulas, M.; Olsson, G. Systematic approach to the design of operation and control policies in activated sludge systems. Ind. Eng. Chem. Res. 2011, 50, 8542–8557. [Google Scholar] [CrossRef]
- Machado, V.C.; Gabriel, D.; Lafuente, J.; Baeza, J.A. Cost and effluent quality controllers design based on the relative gain array for a nutrient removal WWTP. Water Res. 2009, 43, 5129–5141. [Google Scholar] [CrossRef] [PubMed]
- Gopakumar, V.; Tiwari, S.; Rahman, I. A deep learning based data driven soft sensor for bioprocesses. Biochem. Eng. J. 2018, 136, 28–39. [Google Scholar] [CrossRef]
- Han, H.G.; Liu, Z.; Guo, Y.N.; Qiao, J.F. An intelligent detection method for bulking sludge of wastewater treatment process. J. Process Contr. 2018, 68, 118–128. [Google Scholar] [CrossRef]
- Shi, S.; Xu, G. Novel performance prediction model of a biofilm system treating domestic wastewater based on stacked denoising auto-encoders deep learning network. Chem. Eng. J. 2018, 347, 280–290. [Google Scholar] [CrossRef]
- Torregrossa, D.; Leopold, U.; Hernández-Sancho, F.; Hansen, J. Machine learning for energy cost modelling in wastewater treatment plants. J. Environ. Manag. 2018, 223, 1061–1067. [Google Scholar] [CrossRef]
- Zhu, J.; Kang, L.; Anderson, P.R. Predicting influent biochemical oxygen demand: Balancing energy demand and risk management. Water Res. 2018, 128, 304–313. [Google Scholar] [CrossRef]
- Guo, H.; Jeong, K.; Lim, J.; Jo, J.; Kim, Y.M.; Park, J.P.; Kim, J.H. Prediction of effluent concentration in a wastewater treatment plant using machine learning models. J. Environ. Sci. China 2015, 32, 90–101. [Google Scholar] [CrossRef]
- Guerrini, A.; Romano, G.; Indipendenza, A. Energy Efficiency Drivers in Wastewater Treatment Plants: A Double Bootstrap DEA Analysis. Sustainability 2017, 9, 1126. [Google Scholar] [CrossRef]
- Turunen, V.; Sorvari, J.; Mikola, A. A decision support tool for selecting the optimal sewage sludge treatment. Chemosphere 2018, 193, 521–529. [Google Scholar] [CrossRef]
- Marvuglia, A.; Kanevski, M.; Benetto, E. Machine learning for toxicity characterization of organic chemical emissions using USEtox database: Learning the structure of the input space. Environ. Int. 2015, 83, 72–85. [Google Scholar] [CrossRef] [PubMed]
- Mesbah, M.; Soroush, E.; Rezakazemi, M. Development of a least squares support vector machine model for prediction of natural gas hydrate formation temperature. Chin. J. Chem. Eng. 2017, 25, 1238–1248. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G.; Mojoodi, A.; Ferraz, H. Event-triggered optimal tracking control of nonlinear systems. Int. J. Robust Nonlin. 2017, 27, 598–619. [Google Scholar] [CrossRef]
- Wei, Q.L.; Liu, D.R.; Shi, G. A Novel Dual Iterative Q-Learning Method for Optimal Battery Management in Smart Residential Environments. IEEE Trans. Ind. Electron. 2015, 62, 2509–2518. [Google Scholar] [CrossRef]
- Wei, Q.L.; Song, R.Z.; Sun, Q.Y. Nonlinear neuro-optimal tracking control via stable iterative Q-learning algorithm. Neurocomputing 2015, 168, 520–528. [Google Scholar] [CrossRef]
- Kiumarsi, B.; Lewis, F.L.; Modares, H.; Karimpour, A.; Naghibi-Sistani, M.B. Reinforcement-learning for optimal tracking control of linear discrete-time systems with unknown dynamics. Automatica 2014, 50, 1167–1175. [Google Scholar] [CrossRef]
- Wang, K.; Chai, T.Y.; Wong, W.C. Routing, power control and rate adaptation: A Q-learning-based cross-layer design. Comput. Netw. 2016, 102, 20–37. [Google Scholar] [CrossRef]
- Syafiie, S.; Tadeo, F.; Martinez, E.; Alvarez, T. Model-free control based on reinforcement learning for a wastewater treatment problem. Appl. Soft Comput. 2011, 11, 73–82. [Google Scholar] [CrossRef]
- Zhang, W.T.; Hou, F.; Peng, Y.Z.; Liu, Q.S.; Wang, S.Y. Optimizing aeration rate in an external nitrification–denitrifying phosphorus removal (ENDPR) system for domestic wastewater treatment. Chem. Eng. J. 2014, 245, 342–347. [Google Scholar] [CrossRef]
- Fang, F.; Qiao, L.L.; Cao, J.S.; Li, Y.; Xie, W.M.; Sheng, G.P.; Yu, H.Q. Quantitative evaluation of A2O and reversed A2O processes for biological municipal wastewater treatment using a projection pursuit method. Sep. Purific. Tech. 2016, 166, 164–170. [Google Scholar] [CrossRef]
- APHA (American Public Health Association). Standard Methods for the Examination of Water and Wastewater, 21st ed.; APHA: Washington, DC, USA, 2005. [Google Scholar]
- Watkins, C. Learning from Delayed Rewards. Ph.D. Thesis, Cambridge University, Cambridge, UK, 1989. [Google Scholar]
- Watkins, C.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Arin, A.; Rabadi, G. Integrating estimation of distribution algorithms versus Q-learning into Meta-RaPS for solving the 0–1 multidimensional knapsack problem. Comput. Ind. Eng. 2017, 112, 706–720. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; McGraw-Hill Science/Engineering/Math: New York, NY, USA, 1997; pp. 367–379. ISBN 0070428077. [Google Scholar]







| Systems | COD (mg/L) | NH4+-N (mg/L) | TP (mg/L) |
|---|---|---|---|
| #1 | 264.54 | 13.12 | 2.38 |
| #2 | 244.62 | 22.78 | 1.82 |
| #3 | 288.84 | 18.12 | 3.21 |
| #4 | 300.39 | 25.15 | 2.14 |
| #5 | 326.26 | 24.34 | 3.96 |
| #6 | 335.80 | 22.78 | 2.09 |
| #7 | 345.35 | 14.03 | 1.06 |
| #8 | 385.26 | 22.45 | 2.66 |
| Parameters | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 |
|---|---|---|---|---|---|---|---|---|
| Effective volume of anaerobic tank (L) | 2.50 | 1.25 | 3.75 | 2.50 | 5.00 | 2.50 | 1.25 | 3.75 |
| Effective volume of anoxic tank (L) | 5.00 | 8.75 | 5.00 | 8.75 | 6.25 | 7.50 | 5.00 | 6.25 |
| Effective volume of oxic tank (L) | 6.25 | 5.00 | 7.50 | 8.75 | 8.75 | 7.50 | 8.75 | 8.75 |
| DO in anaerobic tank (mg/L) | – | – | – | – | – | – | – | – |
| DO in anoxic tank (mg/L) | – | – | – | – | – | – | – | – |
| DO in oxic tank (mg/L) | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 |
| HRT in anaerobic tank (h) | 1.0 | 0.5 | 1.5 | 1.0 | 2.0 | 1.0 | 0.5 | 1.5 |
| HRT in anoxic tank (h) | 2.0 | 3.5 | 2.0 | 3.5 | 2.5 | 3.0 | 2.0 | 2.5 |
| HRT in oxic tank (h) | 2.5 | 2.0 | 3.0 | 3.5 | 3.5 | 3.0 | 3.5 | 3.5 |
| HRT in settling tank (h) | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| Influent flow (L/h) | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 |
| IRR (%) | 260 | 310 | 240 | 320 | 290 | 280 | 230 | 250 |
| Sludge return rate (%) | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 | 0–100 |
| MLSS in the main reactor (mg/L) | 3500 ± 500 | 3500 ± 500 | 3500 ± 500 | 3500 ± 500 | 3500 ± 500 | 3500 ± 500 | 3500 ± 500 | 3500 ± 500 |
| For each s, t initialize the table entry to zero. Observe the current state s While For circulation equals 3 to simulate the whole AAO treatment, do the following:
|
| Parameters | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 |
|---|---|---|---|---|---|---|---|---|
| HRT in anaerobic tank (h) | 1.0 | 0.5 | 1.5 | 1.0 | 2.0 | 1.0 | 0.5 | 1.5 |
| HRT in anoxic tank (h) | 2.0 | 3.5 | 2.0 | 3.5 | 2.5 | 3.0 | 2.0 | 2.5 |
| HRT in oxic tank (h) | 2.5 | 2.0 | 3.0 | 3.5 | 3.5 | 3.0 | 3.5 | 3.5 |
| q (%) | 260 | 310 | 240 | 320 | 290 | 280 | 230 | 250 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, J.; Yang, S.; He, L.; Chen, Y.; Ren, N. Intelligent Control/Operational Strategies in WWTPs through an Integrated Q-Learning Algorithm with ASM2d-Guided Reward. Water 2019, 11, 927. https://doi.org/10.3390/w11050927
Pang J, Yang S, He L, Chen Y, Ren N. Intelligent Control/Operational Strategies in WWTPs through an Integrated Q-Learning Algorithm with ASM2d-Guided Reward. Water. 2019; 11(5):927. https://doi.org/10.3390/w11050927
Chicago/Turabian StylePang, Jiwei, Shanshan Yang, Lei He, Yidi Chen, and Nanqi Ren. 2019. "Intelligent Control/Operational Strategies in WWTPs through an Integrated Q-Learning Algorithm with ASM2d-Guided Reward" Water 11, no. 5: 927. https://doi.org/10.3390/w11050927
APA StylePang, J., Yang, S., He, L., Chen, Y., & Ren, N. (2019). Intelligent Control/Operational Strategies in WWTPs through an Integrated Q-Learning Algorithm with ASM2d-Guided Reward. Water, 11(5), 927. https://doi.org/10.3390/w11050927