The Effect of Climatic and Non-climatic Factors on Groundwater Levels in the Jinghuiqu Irrigation District of the Shaanxi Province, China
Abstract
:1. Introduction
2. Materials and Method
2.1. Study Area
2.2. Research Method
2.2.1. Climatic Phases Defined by Rainfall Anomalies
2.2.2. Mann–Kendall Test
2.2.3. The Optimized Well–Canal Irrigation Ratio
2.2.4. Data Standardization
2.3. The Data Source
2.4. Data Pre-Analysis
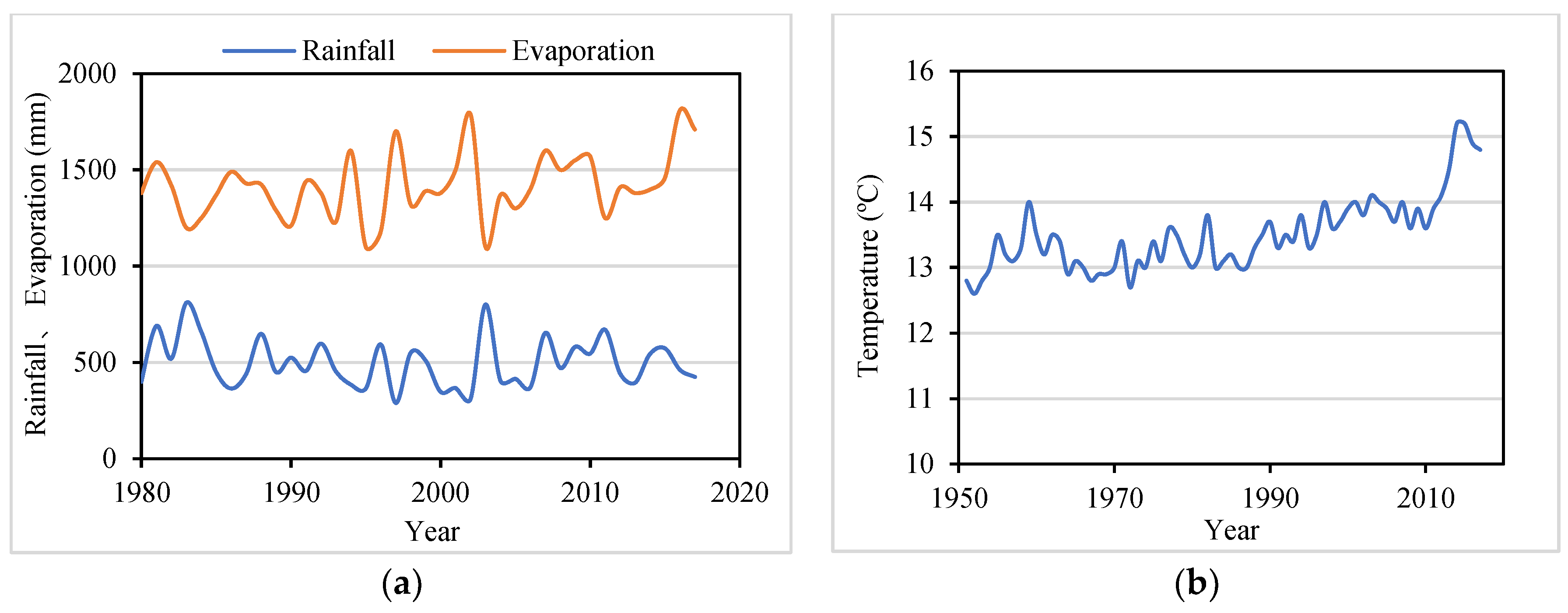
2.4.1. Meteorological Data
2.4.2. Climatic Phases Defined
3. Result
3.1. Climate Change and Abrupt Change Detection
3.2. Variation Trend of Groundwater Levels in Distinct Climatic Phases
3.3. The Influence of Groundwater Extraction and the Well–Canal Ratio Factors on Groundwater Levels in Distinct Climate Phases
4. Discussion
4.1. Influence of Distinct Climate Phases on Groundwater Levels
4.2. The Influence of Other Factors on the Groundwater Level
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Wilby, R.L.; Whitehead, P.G.; Wade, A.J.; Butterfield, D.; Davis, R.J.; Watts, G. Integrated modelling of climate change impacts on water resources and quality in a lowland catchment: River Kennet, UK. J. Hydrol. 2006, 330, 204–220. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: The Physical Science Basis; Contribution of Working Group 1 to the Forth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- IPCC. Summary for Policymakers. In Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Touhami, I.; Chirino, J.M.; Andreu, J.R.; Sánchez, H.; Moutahir, J.B. Assessment of climate change impacts on soil water balance and aquifer recharge in a semiarid region in south east Spain. J. Hydrol. 2015, 527, 619–629. [Google Scholar] [CrossRef] [Green Version]
- Treidel, H.; Martin-Bordes, J.J.; Gurdak, J.J. Climate Change Effects on Groundwater Resources: A Global Synthesis of Findings and Recommendations, International Association of Hydrologists (IAH)—International Contributions to Hydrogeology; Taylor & Francis: Abingdon, UK, 2012; 414p. [Google Scholar]
- Stavig, L.; Collins, L.; Hager, C.; Herring, M.; Brown, E.; Locklar, E. The Effects of Climate Change on Cordova, Alaska on the Prince William Sound. Alaska Tsunami Papers. 2005. Available online: https://seagrant.uaf.edu/nosb/papers/2005/cordova-nurds.html (accessed on 1 November 2018).
- Hiscock, K.; Sparkes, R.; Hodgens, A. Evaluation of Future Climate Change impacts on European Groundwater Resources. Climate Change Effects on Groundwater Resources: A Global Synthesis of Findings and Recommendations; International Association of Hydrogeologists (IAH)—International Contributions to Hydrogeology; Treidel, H., Martin-Bordes, J.J., Gurdak, J.J., Eds.; Taylor & Francis: London, UK, 2012; pp. 351–366. [Google Scholar]
- Gandhi, V.P.; Bhamoriya, V. Groundwater Irrigation in India; India Infrastructure Report 90; Oxford University Press: New Delhi, India, 2011. [Google Scholar]
- Pengra, B.A. A Glass Half Empty: Regions at Risk Due to Groundwater Depletion. Environ. Dev. 2012, 2, 117–127. [Google Scholar] [CrossRef]
- Salem, G.S.A.; Kazama, S.; Nepal, C.D. Impacts of climate change on groundwater level and irrigation cost in a groundwater dependent irrigated region. Agric. Water Manag. 2018, 208, 33–42. [Google Scholar] [CrossRef]
- Simmons, C.T. Groundwater down under. Groundwater 2016, 54, 459–460. [Google Scholar] [CrossRef] [PubMed]
- Mehrdad, J.; Ara, T.; Seyed, K.A.; Saeid, H.; Petter, P. Long term groundwater balance and water quality monitoring in the eastern plains of Urmia Lake, Iran: A novel GIS based low cost approach. J. Afr. Earth Sci. 2018, 147, 11–19. [Google Scholar] [CrossRef]
- Prasad, Y.S.; Rao, B.V. Groundwater depletion and groundwater balance studies of Kandivalasa River Sub Basin, Vizianagaram District, Andhra Pradesh, India. Groundw. Sustain. Dev. 2018, 6, 71–78. [Google Scholar] [CrossRef]
- Hafmann, N.; Mortsch, L.; Donner, S.; Dunacan, K.; Kreutzwiser, R.; Kulshreshtha, S.; Piggott, A.; Schellenberg, S.; Schertzer, B.; Slivizky, M. Climate Change and Variability: Impacts on Canadian Water; Environmental Adaptation Research Group, Environment Canada, Faculty of Environment Studies, University of Waterloo: Waterloo, ON, Canada, 2000; p. 120. [Google Scholar]
- Chen, Z.; Grasby, S.; Osadetz, K.G. Relation between climate variability and groundwater level in the upper carbonate aquifer, south Manitoba, Canada. J. Hydrol. 2004, 290, 43–62. [Google Scholar] [CrossRef]
- Zektser, S.; Loáiciga, H.A.; Wolf, J.T. Environmental impacts of groundwater overdraft: Selected case studies in the southwestern United States. Environ. Geol. 2005, 47, 396–404. [Google Scholar] [CrossRef]
- Panda, K.; Mishra, A.; Jena, S.K.; James, B.K.; Kumar, A. The influence of drought and anthropogenic effects on groundwater levels in Orissa, India. J. Hydrol. 2007, 343, 140–153. [Google Scholar] [CrossRef]
- Al-Ruwaih, F.; Almedeij, J. Periodic behavior of groundwater level fluctuations in residential areas. J. Hydrol. 2006, 328, 677–684. [Google Scholar] [CrossRef]
- Shahid, S.; Hazarika, M.K. Groundwater drought in the north-western districts of Bangladesh. Water Res. Manag. 2010, 24, 1989–2006. [Google Scholar] [CrossRef]
- Daneshvar, V.F.; Dinpashoh, Y.; Aalami, M.T.; Jhajharia, D. Trend analysis of groundwater using non-parametric methods (case study: Ardabil plain). Stoch. Environ. Res. Risk Assess. 2013, 27, 547–559. [Google Scholar] [CrossRef]
- Weider, K.; Boutt, D. Heterogeneous water table response to climate revealed heterogeneous water table response to climate revealed by 60 years of ground water data. Geophys. Res. Lett. 2010, 37, L24405. [Google Scholar] [CrossRef]
- Huang, Y.F.; Liu, J.M.; Jiang, P.; Zhang, B. Study on groundwater dynamics and prediction of Jinghuiqu based on Modflow. Res. Soil Water Conserv. 2014, 21, 273–278. [Google Scholar] [CrossRef]
- Jiang, P.; Liu, J.M.; Huang, Y.F.; Zhang, Y.Q. Groundwater in Jinghuiqu responds to climate change and human activities. Yellow River 2014, 36, 45–47, 51. (In Chinese) [Google Scholar] [CrossRef]
- Wada, Y. Modeling groundwater depletion at regional and global scales: Present state and future prospects. Surv. Geophys. 2016, 37, 419–451. [Google Scholar] [CrossRef]
- Döll, P.; Müller Schmied, H.; Schuh, C.; Portmann, F.T.; Eicker, A. Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites. Water Resour. Res. 2014, 50, 5698–5720. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, S.; Russo, T.; Lall, U. Comment on “Quantifying renewable groundwater stress with GRACE” by Alexandra, S. Richey et al. Water Resour. Res. 2016, 52, 4184–4187. [Google Scholar] [CrossRef]
- Gurdak, J.J.; Hanson, R.T.; McMahon, P.B.; Bruce, B.W.; McCray, J.E.; Thyne, G.D.; Reedy, R.C. Climate variability controls on unsaturated water and chemical movement, high plains aquifer, USA. Vadose Zone J. 2007, 6, 533–547. [Google Scholar] [CrossRef]
- Russo, T.A.; Lall, U. Depletion and response of deep groundwater to climate-induced pumping variability. Nat. Geosci. 2017, 10, 105–108. [Google Scholar] [CrossRef]
- Sen, Z. Hydrological trend analysis with innovative and over-whitening procedures. Hydrol. Sci. J. 2017, 62, 294–305. [Google Scholar] [CrossRef]
- Tirogo, J.; Jost, A.; Biaou, A.; Valdes-Lao, D.; Koussoubé, Y.; Ribstein, P. Climate variability and groundwater response: A case study in Burkina Faso (West Africa). Water 2016, 8, 171. [Google Scholar] [CrossRef]
- Tabari, H.; Nikbakht, J.; Shifteh Some’e, B. Investigation of groundwater level fluctuations in the north of Iran. Environ. Earth Sci. 2012, 66, 231–243. [Google Scholar] [CrossRef]
- Abdullahi, M.G.; Toriman, M.E.; Gasim, M.B.; Garba, I. Trends analysis of groundwater: Using non-parametric methods in Terengganu Malaysia. J. Earth Sci. Clim. 2015, 6. [Google Scholar] [CrossRef]
- Bronaugh, D.; Werner, A. zyp: Zhang + Yue-Pilon Trends Package. R Package Version 0. 2013, 10-1. Available online: http://CRAN.R-project.org/package=zyp (accessed on 17 March 2019).
- Jia, Z.F.; Wang, Z.; Wang, H. Characteristics of Dew Formation in the Semi-Arid Loess Plateau of Central Shaanxi Province, China. Water 2019, 11, 126. [Google Scholar] [CrossRef]
- Liu, X.H.; Li, L.; Hu, A.Y. Hydrochemical characterization of a groundwater aquifer and its water quality suitability for irrigation in Jinghuiqu Irrigation District of China. Water Environ. Res. 2013, 85, 245–258. [Google Scholar] [CrossRef]
- Bellier, O.; Mercier, J.L.; Vergely, P.; Long, C.; Ning, C. Evolution Sédimentaire et Tectonique du Graben Cénozoïque de la Wei He (province du Shaanxi, Chine du Nord). Bull. Soc. Géol. Fr. 1988, 8, 979–994. [Google Scholar] [CrossRef]
- Le Brocque, A.F.; Jarrod, K.; Kathryn, R.S. Chronic groundwater decline: A multi-decadal analysis of groundwater trends under extreme climate cycles. J. Hydrol. 2018, 561, 976–986. [Google Scholar] [CrossRef]
- Wang, C.X.; Su, Z.L.; Jiang, Y.C.; Wu, C.B. Disaster analysis of Sanming city based on Mann-Kendall method in Excel. J. Qinghai Meteorol. 2017, 3, 82–85. [Google Scholar]
- Wei, F.Y. Modern Climate Statistical Diagnosis and Prediction Technology; China Meteorological Press: Beijing, China, 2003; pp. 69–72.
- Chen, Z.P.; Xu, Q. Mann-Kendall test method for analysis of precipitation time-history variation characteristics. Sci. Technol. Bull. 2016, 32, 47–50. [Google Scholar] [CrossRef]
- Dai, F.G.; Cai, H.J.; Liu, X.M.; Liu, X.; Liang, H.W. The proportion of suitable well and canal irrigation was simulated and analyzed by the groundwater model in the irrigated area. Trans. Chin. Soc. Agric. Eng. 2012, 28, 45–51. [Google Scholar] [CrossRef]
- Anysz, H.; Zbiciak, A.; Ibadov, N. The Influence of Input Data Standardization Method on Prediction Accuracy of Artificial Neural Networks. Procedia Eng. 2016, 153, 66–70. [Google Scholar] [CrossRef] [Green Version]
- Niu, Y. Standardized Data Processing for Comprehensive Evaluation of Crop Yield Indicators. Rural Econ. Sci.-Technol. 2017, 28, 16–19. [Google Scholar] [CrossRef]
- Liu, J.Y.; Zhang, K.; Wang, G.H. A comparative study of data standardization methods in comprehensive evaluation. Dig. Technol. Appl. 2018, 36, 84–85. [Google Scholar] [CrossRef]
- Hundecha, Y.; Bárdossy, A. Trends in daily precipitation and temperature extremes across western Germany in the second half of the 20th century. Int. J. Climatol. 2005, 25, 1189–1202. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.Y.; Liu, Y.; Yao, A.M. Dynamic Analysis of Groundwater Level in Jinghuiqu irrigation district. J. Irrig. Drain. 2015, 34, 67–70. [Google Scholar] [CrossRef]
- Wang, J.Y.; Zhang, P.P.; Liu, Y. Relationship between Groundwater Level Dynamics and Irrigation Agriculture in Jinghuiqu irrigation district. Agric. Res. Arid Areas 2016, 34, 247–251. [Google Scholar]
- Guobin, F.; Russell, S.; Crosbie, O.B.; Stephen, P.; Charles, W.D.; Xiaogang, S.; Tom, V.N.; Chris, L. Attributing variations of temporal and spatial groundwater recharge: A statistical analysis of climatic and non-climatic factors. J. Hydrol. 2019, 568, 816–834. [Google Scholar] [CrossRef]
- Crosbie, R.S.; McCallum, J.L.; Walker, G.R.; Chiew, F.H.S. Modelling climate-change impacts on groundwater recharge in the Murray-Darling Basin, Australia. Hydrogeol. J. 2010, 18, 1639–1656. [Google Scholar] [CrossRef]
- Smerdon, B.D. A synopsis of climate change effects on groundwater recharge. J. Hydrol. 2017, 555, 125–128. [Google Scholar] [CrossRef]
- Crosbie, R.S.; McCallum, J.L.; Walker, G.R.; Chiew, F.H.S. Episodic recharge and climate change in the Murray-Darling Basin, Australia. Hydrogeol. J. 2012, 20, 245–261. [Google Scholar] [CrossRef]
- Li, X.Y. Analysis and Evaluation of Ecological Environment Quality in Jinghuiqu Irrigation District. Master’s Thesis, Chang’an University, Xi’an, China, 2008. [Google Scholar] [CrossRef]
- Ye, Y.C.; Li, L. Jinghuiqu Chorography; Sanqin Publishing: Xi’an, China, 1991; pp. 207–210. [Google Scholar]
- Richey, A.S.; Thomas, B.F.; Lo, M.H.; Reager, J.T.; Famiglietti, J.S.; Voss, K.; Swenson, S.; Rodell, M. Quantifying renewable groundwater stress with GRACE. Water Resour. Res. 2015, 51, 5217–5238. [Google Scholar] [CrossRef] [Green Version]










| Average Annual Rainfall (mm) | Canal Irrigation Water (108 m3) | Well Irrigation Water (108 m3) | Groundwater Depth (m) | Ratio | Water Balance |
|---|---|---|---|---|---|
| 390 | 4.1 | 2.1 | 3–5 | 0.52 | balanced |
| 600–700 | 3.7–4.0 | 1.4–1.9 | 3–5 | 0.35–0.55 | fundamental |
| 540 | 1.5–2.0 | 1.0–1.4 | >8 | 0.5–0.7 | possible |
| 450 | 1.2–1.7 | >1.5 | >8 | >1 | imbalanced |
| Weather Station | Longitude (N) | Latitude (E) | Weather Station No. |
|---|---|---|---|
| Sanyuan | 108.78° | 34.60° | 57041 1 |
| Jingyang | 108.82° | 34.55° | 57033 1 |
| Lintong | 109.26° | 34.40° | - |
| Fuping | 109.18° | 34.78° | 57042 1 |
| Gaoling | 109.11° | 34.52° | - |
| Trend (Response) | Mean Sen’s Slope (year−1) | Over Phase | Number of MWS | Z Absolute Value | Groundwater Level Change (m year−1) | Standard Error |
|---|---|---|---|---|---|---|
| Wet (1980–1984) | ||||||
| Rising | 0.16 | 0.31 | 37 | 0.76 | 0.12 | 0.02 |
| Declining | −0.25 | −0.24 | 48 | 1.35 * | −0.15 | 0.01 |
| Stable | 0.02 | 0.07 | 34 | 0.33 | 0.05 | 0.02 |
| Normal (1985–1996) | ||||||
| Rising | 0.08 | 0.11 | 11 | 0.71 | 0.19 | 0.02 |
| Declining | −0.21 | −0.33 | 63 | 1.49 * | −0.54 | 0.02 |
| Stable | −0.01 | −0.12 | 45 | 1.15 | −0.13 | 0.02 |
| Dry (1997–2002) | ||||||
| Rising | 0.13 | 0.17 | 16 | 0.51 | 0.15 | 0.02 |
| Declining | −0.56 | −0.39 | 71 | 1.79 ** | −0.62 | 0.01 |
| Stable | −0.17 | −0.13 | 32 | 0.65 | −0.23 | 0.01 |
| Wet (2003–2011) | ||||||
| Rising | 0.23 | 1.02 | 28 | 1.12 | 0.21 | 0.02 |
| Declining | −0.42 | −0.52 | 50 | 1.51 * | −0.29 | 0.04 |
| Stable | 0.05 | 0.43 | 41 | 0.81 | 0.11 | 0.03 |
| Normal (2012–2017) | ||||||
| Rising | 0.11 | 0.59 | 13 | 0.64 | 0.07 | 0.03 |
| Declining | −0.28 | −0.32 | 69 | 1.68 ** | −0.69 | 0.03 |
| Stable | −0.03 | −0.55 | 37 | 1.24 | −0.06 | 0.02 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Jia, Z.; Guan, Z.; Xu, C. The Effect of Climatic and Non-climatic Factors on Groundwater Levels in the Jinghuiqu Irrigation District of the Shaanxi Province, China. Water 2019, 11, 956. https://doi.org/10.3390/w11050956
Zhao Z, Jia Z, Guan Z, Xu C. The Effect of Climatic and Non-climatic Factors on Groundwater Levels in the Jinghuiqu Irrigation District of the Shaanxi Province, China. Water. 2019; 11(5):956. https://doi.org/10.3390/w11050956
Chicago/Turabian StyleZhao, Zhiqiang, Zhifeng Jia, Zilong Guan, and Chunyan Xu. 2019. "The Effect of Climatic and Non-climatic Factors on Groundwater Levels in the Jinghuiqu Irrigation District of the Shaanxi Province, China" Water 11, no. 5: 956. https://doi.org/10.3390/w11050956
APA StyleZhao, Z., Jia, Z., Guan, Z., & Xu, C. (2019). The Effect of Climatic and Non-climatic Factors on Groundwater Levels in the Jinghuiqu Irrigation District of the Shaanxi Province, China. Water, 11(5), 956. https://doi.org/10.3390/w11050956





