Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Correction for Pixel Scale Error
2.3. Method Development
3. Application and Results
- (1)
- Applying Equation (1), a correction of the pixel scale error is performed. Results are shown for selected durations in Figure 3 and Table 1. It is evident that the error between rain gauge intensities and radar intensities are significantly larger for short rainfall durations. This is a result of the daily mean-field bias adjustment and leads to a bias factor of 1 for the 1440 min durations (1 day). As shown in Figure 3, there is a considerable scatter between maximum rain gauge intensities and the corresponding radar intensities, which is also explained by the Nash–Sutcliffe Efficiency (NSE)-values in Table 1 and Figure 3. Furthermore, the scatter is larger for the shorter durations indicating high uncertainties. However, as the study aims for a mean pixel scale error, the dispersion of the pixel scale error is not considered any further.
- (2)
- (3)
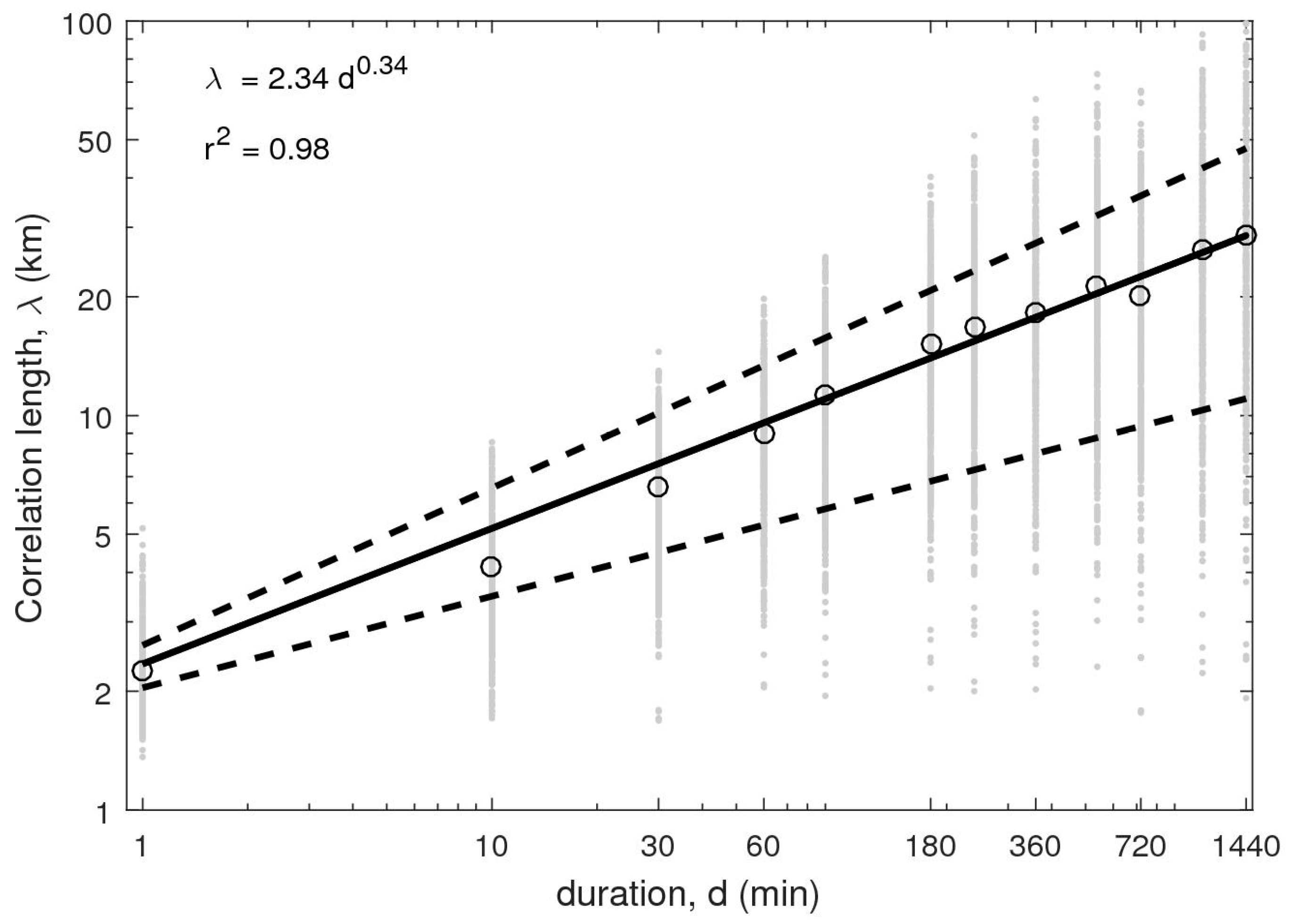
- The correlation lengths, λ are fitted (Equation (6)) as a function of duration (Figure 6). From Figure 6, it is evident that there is a large variability from storm to storm, but that the mean fit well to the power function with r2 of 0.98. It shows that the power-law function in Equation (6) can be further used to derive a relationship of the storm-centred ARF as a function of area and duration. In addition to the mean relationship, the uncertainty corresponding to mean plus/minus one standard deviation (assuming a Gaussian distribution) is investigated. This uncertainty will provide insight into the variability from storm to storm.
- (4)
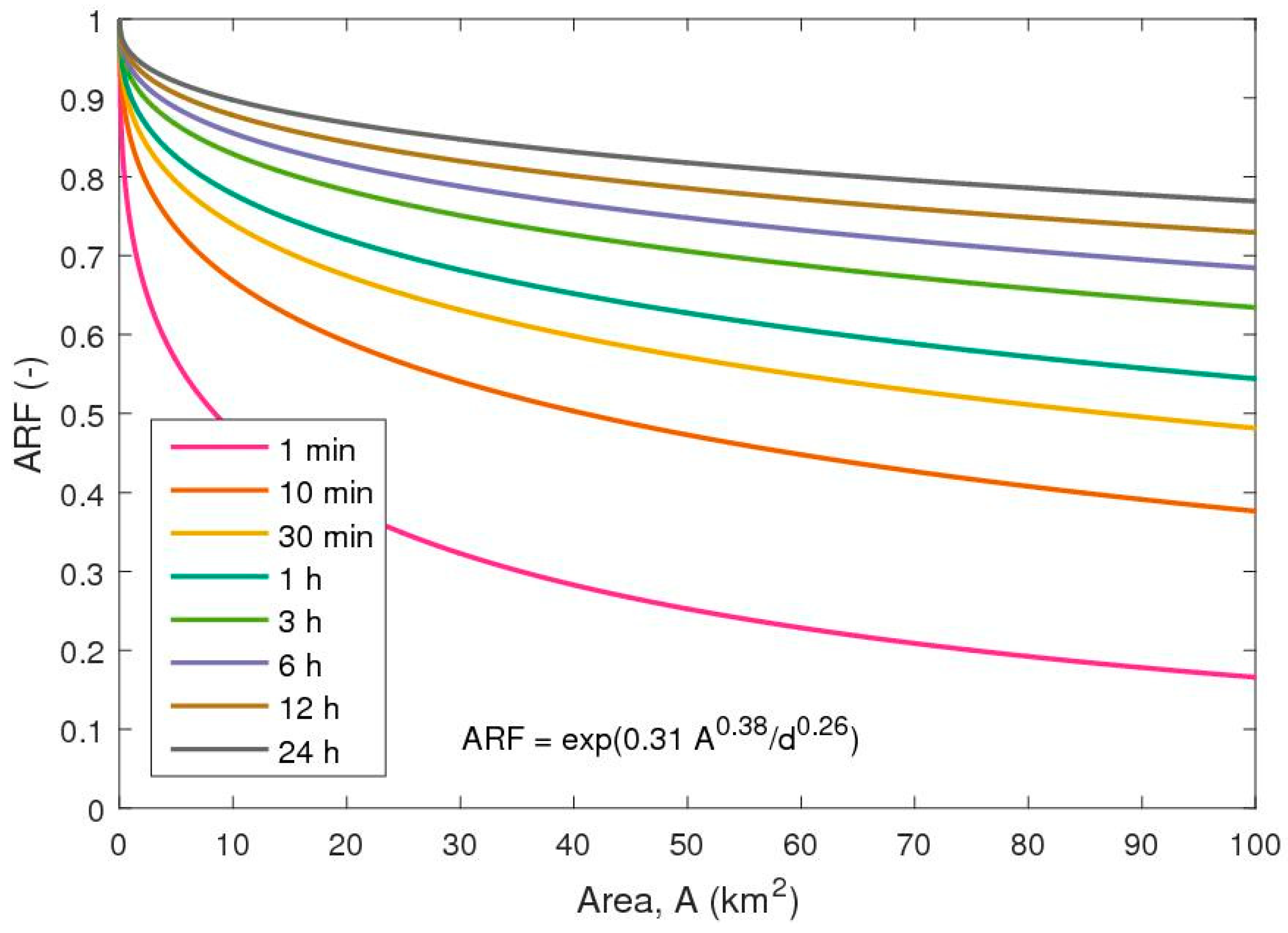
- Applying the obtained function of correlation length and duration, each storm is re-fitted by the relationship in Equation (7) to derive an ARF function. Examples of this fit are shown in Figure 4 and Figure 5 for durations of 60 and 360 min, respectively. Comparing with the mean ARF functions, the fitted relationships show a slight overestimation for the small areas and correspondingly an underestimation for large areas. For some durations, the opposite case occurs (not shown). This uncertainty is a trade-off of fitting a fixed parameter relationship to all durations.
- (5)
4. Discussion
4.1. Comparison with Previous Studies
4.2. Implementation in Urban Drainage Design
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Willems, P. Compound intensity/duration/frequency-relationships of extreme precipitation for two seasons and two storm types. J. Hydrol. 2000, 233, 189–205. [Google Scholar] [CrossRef]
- Madsen, H.; Arnbjerg-Nielsen, K.; Mikkelsen, P.S. Update of regional intensity-duration-frequency curves in Denmark: Tendency towards increased storm intensities. Atmos. Res. 2009, 92, 343–349. [Google Scholar] [CrossRef]
- WPC Funktionspraksis for afløbssystemer under regn, skrift nr. 27 (Practice for drainage systems during rain, Guideline no. 27); The Water Pollution Committee of the Society of Danish Engineers; IDA: Copenhagen, Denmark, 2007. [Google Scholar]
- Rodriguez-Iturbe, I.; Mejía, J.M. On the transformation of point rainfall to areal rainfall. Water Resour. Res. 1974, 10, 729–735. [Google Scholar] [CrossRef]
- Sivapalan, M.; Blöschl, G. Transformation of point rainfall to areal rainfall: Intensity-duration-frequency curves. J. Hydrol. 1998, 204, 150–167. [Google Scholar] [CrossRef]
- Villarini, G.; Serinaldi, F.; Krajewski, W.F. Modeling radar-rainfall estimation uncertainties using parametric and non-parametric approaches. Adv. Water Resour. 2008, 31, 1674–1686. [Google Scholar] [CrossRef]
- U.S. Weather Bureau. Rainfall Intensity-Frequency Regime Part 2-Southeastern United States, Technical Paper No. 29; Department of Commerce: Washington, DC, USA, 1958.
- NERC (Natural Environment Research Council, UK). Flood Studies Report; Natural Environment Research Council: Swindon, UK, 1975; Volume II. [Google Scholar]
- Asquith, W.H.; Famiglietti, J.S. Precipitation areal-reduction factor estimation using an annual-maxima centered approach. J. Hydrol. 2000, 230, 55–69. [Google Scholar] [CrossRef] [Green Version]
- De Michele, C.; Kottegoda, N.T.; Rosso, R. The derivation of areal reduction factor of storm rainfall from its scaling properties. Water Resour. Res. 2001, 37, 3247–3252. [Google Scholar] [CrossRef]
- Vaes, G.; Willems, P.; Berlamont, J. Areal rainfall correction coefficients for small urban catchments. Atmos. Res. 2005, 77, 48–59. [Google Scholar] [CrossRef]
- Veneziano, D.; Langousis, A. The areal reduction factor: A multifractal analysis. Water Resour. Res. 2005, 41, 1–15. [Google Scholar] [CrossRef]
- Mineo, C.; Ridolfi, E.; Napolitano, F.; Russo, F. The areal reduction factor: A new analytical expression for the Lazio Region in central Italy. J. Hydrol. 2018, 560, 471–479. [Google Scholar] [CrossRef]
- Durrans, S.R.; Julian, L.T.; Yekta, M. Estimation of Depth-Area Relationships using Radar-Rainfall Data. J. Hydrol. Eng. 2007, 7, 356–367. [Google Scholar] [CrossRef]
- Allen, R.J.; DeGaetano, A.T. Considerations for the use of radar-derived precipitation estimates in determining return intervals for extreme areal precipitation amounts. J. Hydrol. 2005, 315, 203–219. [Google Scholar] [CrossRef]
- Lombardo, F.; Napolitano, F.; Russo, F. On the use of radar reflectivity for estimation of the areal reduction factor. Nat. Hazards Earth Syst. Sci. 2006, 6, 377–386. [Google Scholar] [CrossRef] [Green Version]
- Overeem, A.; Buishand, T.A.; Holleman, I.; Uijlenhoet, R. Extreme value modeling of areal rainfall from weather radar. Water Resour. Res. 2010, 46, 1–10. [Google Scholar] [CrossRef]
- Wright, D.B.; Smith, J.A.; Baeck, M.L. Critical Examination of Area Reduction Factors. J. Hydrol. Eng. 2014, 19, 769–776. [Google Scholar] [CrossRef]
- Pavlovic, S.; Perica, S.; St Laurent, M.; Mejía, A. Intercomparison of selected fixed-area areal reduction factor methods. J. Hydrol. 2016, 537, 419–430. [Google Scholar] [CrossRef]
- Svensson, C.; Jones, D.A. Review of methods for deriving areal reduction factors. J. Flood Risk Manag. 2010, 3, 232–245. [Google Scholar] [CrossRef] [Green Version]
- Omolayo, A.S. On the transposition of areal reduction factors for rainfall frequency estimation. J. Hydrol. 1993, 145, 191–205. [Google Scholar] [CrossRef]
- Schilling, W. Rainfall data for urban hydrology: what do we need? Atmos. Res. 1991, 27, 5–21. [Google Scholar] [CrossRef]
- Einfalt, T.; Arnbjerg-Nielsen, K.; Golz, C.; Jensen, N.-E.; Quirmbach, M.; Vaes, G.; Vieux, B. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; ten Veldhuis, M.-C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef] [Green Version]
- Bengtsson, L.; Niemczynowicz, J. Areal reduction factors from rain movement. Nord. Hydrol. 1986, 17, 65–82. [Google Scholar] [CrossRef]
- Thorndahl, S.; Beven, K.J.; Jensen, J.B.; Schaarup-Jensen, K. Event based uncertainty assessment in urban drainage modelling, applying the GLUE methodology. J. Hydrol. 2008, 357, 421–437. [Google Scholar] [CrossRef] [Green Version]
- Thorndahl, S.; Willems, P. Probabilistic modelling of overflow, surcharge and flooding in urban drainage using the first-order reliability method and parameterization of local rain series. Water Res. 2008, 42, 455–466. [Google Scholar] [CrossRef]
- Thorndahl, S.; Schaarup-Jensen, K.; Rasmussen, M.R. On hydraulic and pollution effects of converting combined sewer catchments to separate sewer catchments. Urban Water J. 2013, 12, 120–130. [Google Scholar] [CrossRef]
- Thorndahl, S.; Nielsen, J.E.; Rasmussen, M.R. Bias adjustment and advection interpolation of long-term high resolution radar rainfall series. J. Hydrol. 2014, 508, 214–226. [Google Scholar] [CrossRef]
- Nielsen, J.E.; Thorndahl, S.; Rasmussen, M.R. A numerical method to generate high temporal resolution precipitation time series by combining weather radar measurements with a nowcast model. Atmos. Res. 2014, 138, 1–12. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M. The distribution of raindrops with size. J. Meteor 1945, 5, 165–166. [Google Scholar] [CrossRef]
- Smith, J.A.; Krajewski, W.F. Estimation of the Mean Field Bias of Radar Rainfall Estimates. J. Appl. Meteorol. 2002, 30, 397–412. [Google Scholar] [CrossRef]
- Kitchen, M.; Blackall, R.M. Representativeness errors in comparisons between radar and gauge measurements of rainfall. J. Hydrol. 1992, 134, 13–33. [Google Scholar] [CrossRef]
- Habib, E.; Ciach, G.J.; Krajewski, W.F. A method for filtering out raingauge representativeness errors from the verification distributions of radar and raingauge rainfall. Adv. Water Resour. 2004, 27, 967–980. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Villarini, G.; Smith, J.A. Radar-Rainfall Uncertainties: Where are We after Thirty Years of Effort? Bull. Am. Meteorol. Soc. 2010, 91, 87–94. [Google Scholar] [CrossRef]
- Peleg, N.; Ben-Asher, M.; Morin, E. Radar subpixel-scale rainfall variability and uncertainty: Lessons learned from observations of a dense rain-gauge network. Hydrol. Earth Syst. Sci. 2013, 17, 2195–2208. [Google Scholar] [CrossRef]
- Peleg, N.; Marra, F.; Fatichi, S.; Paschalis, A.; Molnar, P.; Burlando, P. Spatial variability of extreme rainfall at radar subpixel scale. J. Hydrol. 2018, 556, 922–933. [Google Scholar] [CrossRef] [Green Version]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Madsen, H.; Gregersen, I.B.; Rosbjerg, D.; Arnbjerg-Nielsen, K. Regional frequency analysis of short duration rainfall extremes using gridded daily rainfall data as co-variate. Water Sci. Technol. 2017, 75, 1971–1981. [Google Scholar] [CrossRef] [PubMed]
- Keifer, C.J.; Chu, H.H. Synthetic Storm Pattern for Drainage Design. J. Hydraul. Div. 1957, 83, 1–25. [Google Scholar]






| Duration, d (min) | 1 | 10 | 30 | 60 | 180 | 360 | 720 | 1440 |
| Bias, B (-) | 1.63 | 1.36 | 1.21 | 1.15 | 1.07 | 1.04 | 1.03 | 1.00 |
| Nash–Sutcliffe Efficiency, NSE (-) | 0.21 | 0.40 | 0.52 | 0.60 | 0.63 | 0.62 | 0.62 | 0.61 |
| Root mean square error, RMSE (mm/h) | 22.47 | 9.82 | 4.61 | 2.65 | 1.12 | 0.66 | 0.38 | 0.21 |
| b1 | b2 | b3 | |
|---|---|---|---|
| mean | 0.31 | 0.38 | 0.26 |
| mean – 1 × std. dev. | 0.21 | 0.45 | 0.36 |
| mean + 1 × std. dev. | 0.47 | 0.37 | 0.17 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thorndahl, S.; Nielsen, J.E.; Rasmussen, M.R. Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology. Water 2019, 11, 1120. https://doi.org/10.3390/w11061120
Thorndahl S, Nielsen JE, Rasmussen MR. Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology. Water. 2019; 11(6):1120. https://doi.org/10.3390/w11061120
Chicago/Turabian StyleThorndahl, Søren, Jesper Ellerbæk Nielsen, and Michael R. Rasmussen. 2019. "Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology" Water 11, no. 6: 1120. https://doi.org/10.3390/w11061120
APA StyleThorndahl, S., Nielsen, J. E., & Rasmussen, M. R. (2019). Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology. Water, 11(6), 1120. https://doi.org/10.3390/w11061120






