Impact of Vegetation Density on the Wake Structure
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
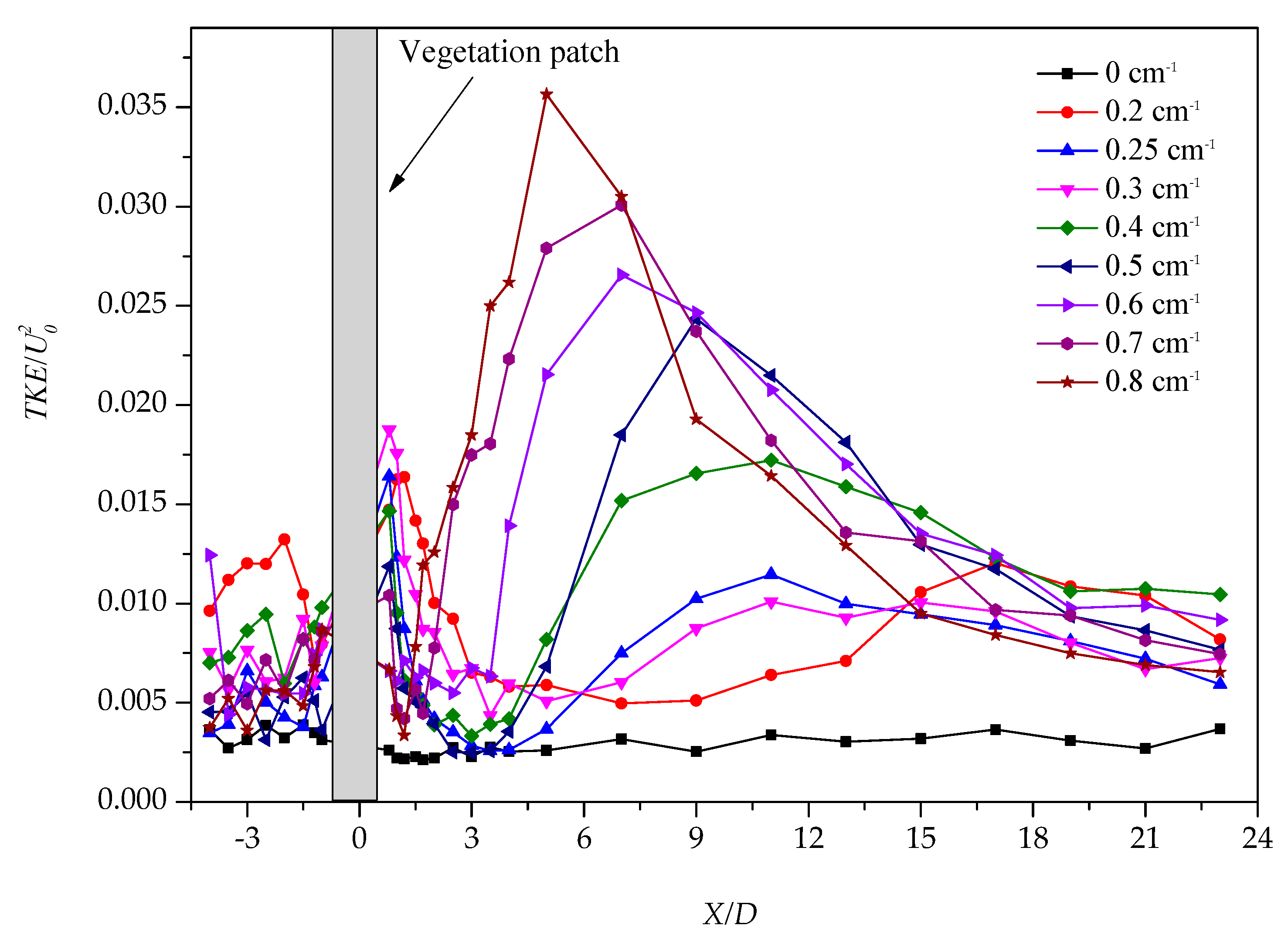
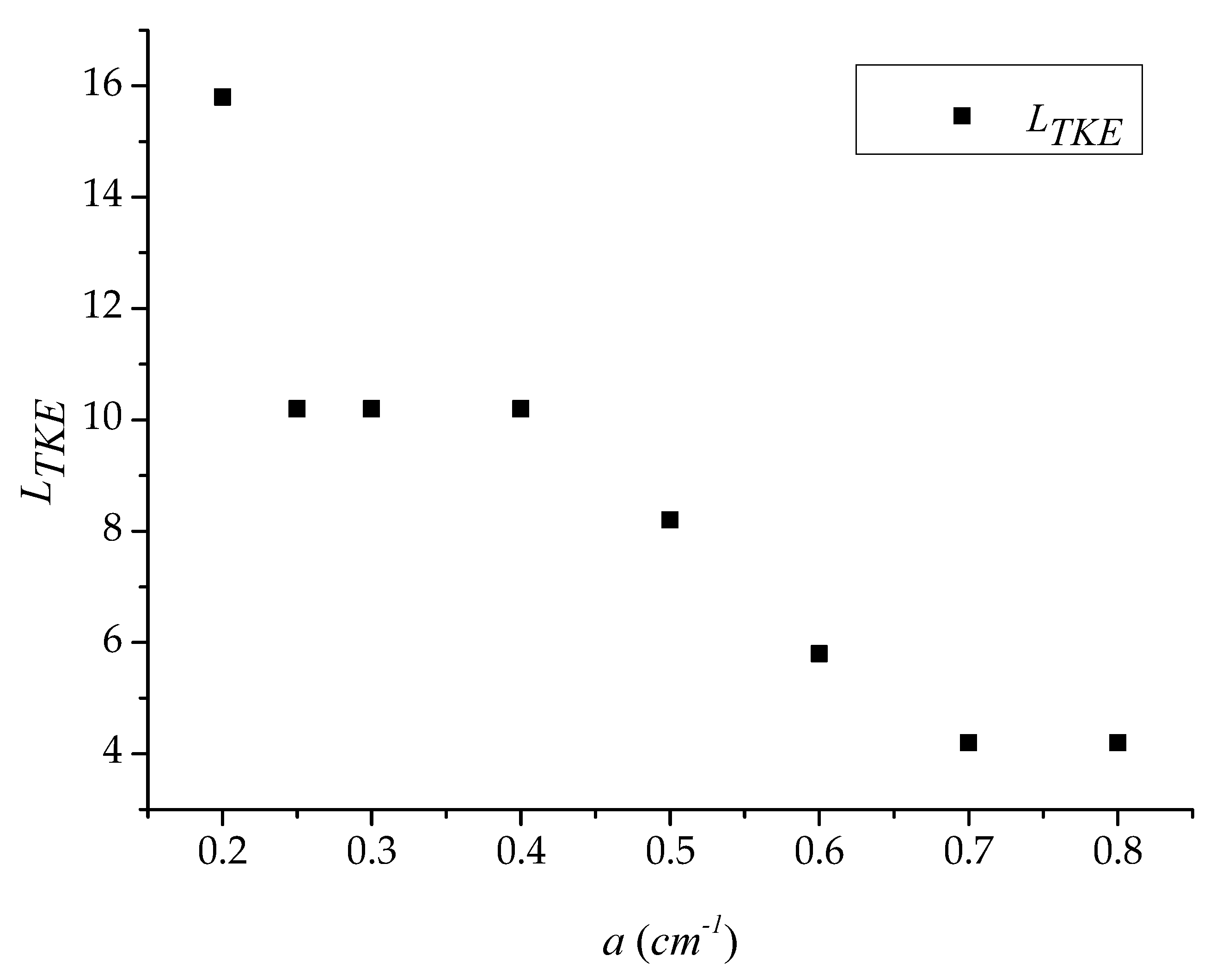
3.1. Longitudinal Distribution of the Turbulent Kinetic Energy with Different Vegetation Density
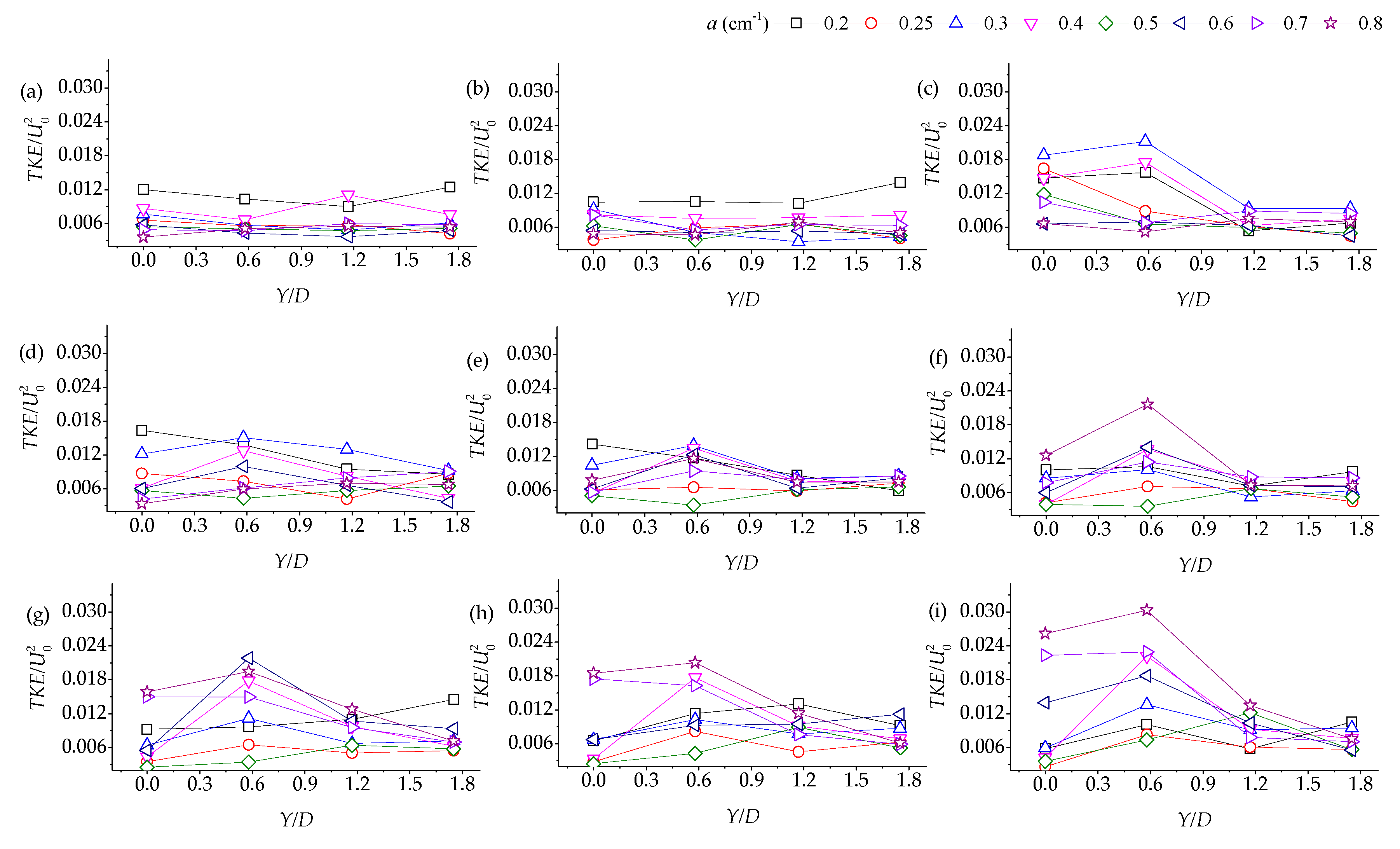
3.2. Lateral Distribution of Stream-Wise TKE with Different Vegetation Densities
3.3. Vertical Distribution of the Turbulent Intensity with Altered Plant Patch Density
3.4. Reynolds Stress Distribution of Different Vegetation Density
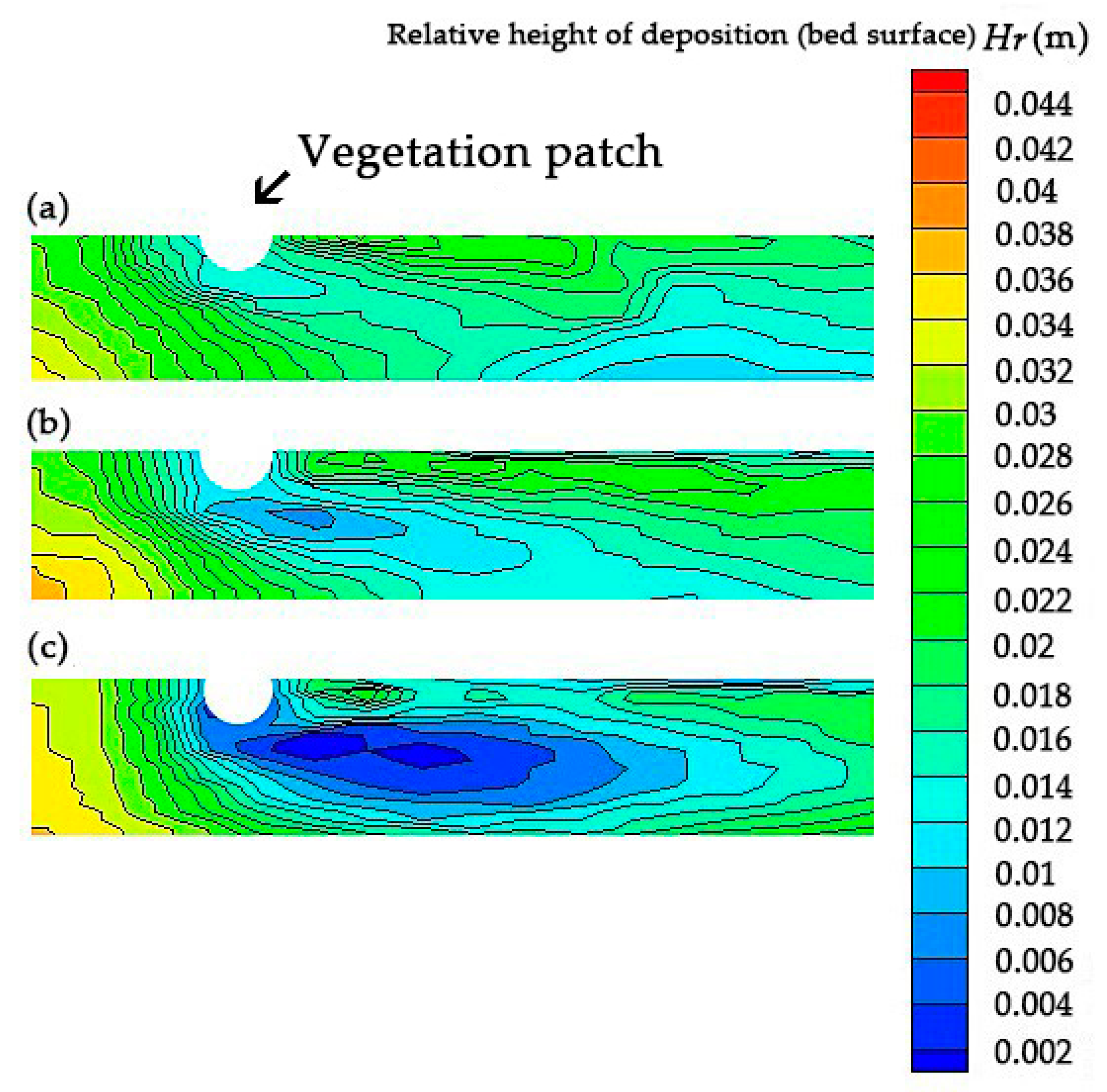
4. Impact of Turbulence with Altered Vegetation Densities on the Sedimentation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, S.; Chan, H.; Li, Y. Observations on flow and local scour around submerged flexible vegetation. Adv. Water Resour. 2012, 43, 28–37. [Google Scholar] [CrossRef]
- Corenblit, D.; Tabacchi, E.; Steiger, J.; Gurnell, A.M. Reciprocal interactions and adjustments between fluvial landforms and vegetation dynamics in river corridors: A review of complementary approaches. Earth-Sci. Rev. 2007, 84, 56–86. [Google Scholar] [CrossRef]
- Vandenbruwaene, W.; Temmerman, S.; Bouma, T.J.; Klaassen, P.C.; De Vries, M.B.; Callaghan, D.P.; van Steeg, P.; Dekker, F.; van Duren, L.A.; Martini, E.; et al. Flow interaction with dynamic vegetation patches: Implications for bio-geomorphic evolution of a tidal land-scape. J. Geophys. Res. 2011, 116, F01008. [Google Scholar] [CrossRef]
- Bouma, T.J.; De Vries, M.B.; Low, E.; Peralta, G.; Tanczos, I.C.; Van De Koppel, J.; Herman, P.M.J. Trade-offs related to ecosystem engineering: A case study on stiffness of emerging macrophytes. Ecology 2005, 86, 2187–2199. [Google Scholar] [CrossRef]
- Zong, L.; Nepf, H. Vortex development behind a finite porous obstruction in a channel. J. Fluid Mech. 2011, 691, 368–391. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Dai, L.; Xu, W. Influence of vegetation on turbulence characteristics and Reynolds shear stress in partly vegetated channel. J. Fluids Eng. 2015, 137, 061201. [Google Scholar] [CrossRef]
- Nezu, I.; Onitsuka, K. Turbulent structures in partly vegetated open-channel flows with LDA and PIV measurements. J. Hydraul. Res. 2001, 39, 629–642. [Google Scholar] [CrossRef]
- Balke, T.; Klaassen, P.C.; Garbutt, A.; van der Wal, D.; Herman, P.M.J.; Bouma, T.J. Conditional outcome of ecosystem engineering: A case study on tussocks of the salt marsh pioneer Spartina anglica. Geomorphology 2012, 153, 232–238. [Google Scholar] [CrossRef]
- Ortiz, A.C.; Ashton, A.; Nepf, H.M. Mean and turbulent velocity fields near rigid and flexible plants and the implications for deposition. J. Geophys. Res. Earth Surf. 2013, 118, 2585–2599. [Google Scholar] [CrossRef]
- Chang, K.; Constantinescu, G. Numerical investigation of flow and turbulence structure through and around a circular array of rigid cylinders. J. Fluid Mech. 2015, 776, 161–199. [Google Scholar] [CrossRef]
- Hu, Z.H.; Lei, J.R.; Liu, C.; Nepf, H. Wake structure and sediment deposition behind models of submerged vegetation with and without flexible leaves. Adv. Water Resour. 2018, 118, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Castro, I.P. Wake characteristics of two-dimensional perforated plates normal to an air-stream. J. Fluid Mech. 1971, 46, 599–609. [Google Scholar] [CrossRef]
- Chen, Z.; Ortiz, A.; Zong, L.J.; Nepf, H. The wake structure downstream of a porous obstruction with implications for deposition near a finite patch of emergent vegetation. Water Resour. Res. 2012, 48, W09517. [Google Scholar] [CrossRef]
- Liu, C.; Nepf, H. Sediment deposition within and around a finite patch of model vegetation over a range of channel velocity. Water Resour. Res. 2016, 51, 600–612. [Google Scholar] [CrossRef]
- Bouma, T.J.; Van Duren, L.A.; Temmerman, S.; Claverie, T.; Blanco-Garcia, A.; Ysebaert, T.; Herman, P. Spatial flow and sedimentation patterns within patches of epibenthic structures: Combining field, flume and modeling experiments. Cont. Shelf Res. 2007, 27, 1020–1045. [Google Scholar] [CrossRef]
- Rominger, J.; Nepf, H.M. Flow adjustment and interior flow associated with a rectangular porous obstruction. J. Fluid Mech. 2011, 680, 636–659. [Google Scholar] [CrossRef]
- Dimotakis, P.E. Turbulent free shear layer mixing and combustion. In High-Speed Flight Propulsion Systems; Murthy, S.N.B., Curran, E.T., Eds.; AIAA: Reston, VA, USA, 1991; pp. 265–340. [Google Scholar]
- Graf, W.H.; Istiarto, I. Flow pattern in the scour hole around a cylinder. J. Hydraul. Res. 2012, 40, 13–20. [Google Scholar] [CrossRef]
- Lopez, F.; Garcia, M. Open-channel flow through simulated vegetation: Suspended sediment transport modeling. Water Resour. Res. 1998, 34, 2341–2352. [Google Scholar] [CrossRef]
- Scott, M.; Friedman, J.; Auble, G. Fluvial process and the establishment of bottomland trees. Geomorphology 1996, 14, 327–339. [Google Scholar] [CrossRef]
- Gurnell, A.M.; Petts, G.E.; Hannah, D.M.; Smith, B.P.G.; Edwards, P.J.; Kollmann, J.; Ward, J.V.; Tockner, K. Riparian vegetation and island formation along the gravel-bed Fiume Tagliamento, Italy. Earth Surf. Process. Landf. 2001, 26, 31–62. [Google Scholar] [CrossRef]
- Schnauder, I.; Moggridge, H.L. Vegetation and hydraulic-morphological interactions at the individual plant, patch and channel scale. Aquat. Sci. 2009, 71, 318–330. [Google Scholar] [CrossRef]
- Gurnell, A.M.; Bertoldi, W.; Corenblit, D. Changing river channels: The roles of hydrological processes, plants and pioneer fluvial land-forms in humid temperate, mixed load, gravel bed rivers. Earth-Sci. Rev. 2012, 111, 129–141. [Google Scholar] [CrossRef]
- Gurnell, A.M. Plants as river system engineers. Earth Surf. Process. Landf. 2014, 39, 4–25. [Google Scholar] [CrossRef]
- Crosato, A.; Saleh, M.S. Numerical study on the effects of floodplain vegetation on river planform style. Earth Surf. Process. Landf. 2011, 36, 711–720. [Google Scholar] [CrossRef]
- Chen, D.; Jirka, G. Experimental study of plane turbulent wakes in a shallow water layer. Fluid Dyn. Res. 1995, 16, 11–41. [Google Scholar] [CrossRef]
- Valiela, I.; Teal, J.M.; Deuser, W.G. The nature of growth forms in the salt marsh grass spartina alterniflora. Am. Nat. 1978, 112, 461–470. [Google Scholar] [CrossRef]
- Leonard, L.A.; Luther, M.E. Flow hydrodynamics in tidal marsh canopies. Limnol. Oceanogr. 1995, 40, 1474–1484. [Google Scholar] [CrossRef]
- Chien, N.; Wan, Z. Mechanics of Sediment Transport; American Society of Civil Engineers: Reston, VA, USA, 1999; pp. 317–326. [Google Scholar]
- Nepf, H.M. Drag, turbulence and diffusivity in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Wood, C.J. Visualization of an incompressible wake with base bleed. J. Fluid Mech. 1967, 29, 259–272. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, H.B. Laboratory measurements of velocity and turbulence field behind porous fences. J. Wind Eng. Ind. Aerodyn. 1999, 80, 311–326. [Google Scholar] [CrossRef]
- Takemura, T.; Tanaka, N. Flow structures and drag characteristics of a colony-type emergent roughness model mounted on a flat plate in uniform flow. Fluid Dyn. Res. 2007, 39, 694–710. [Google Scholar] [CrossRef]
- Townsend, A.A. Measurements in the turbulent wake of a cylinder. Proc. R. Soc. Lond. 1947, 190, 551–561. [Google Scholar]
- Lyn, D.A.; Einav, S.; Rodi, W.; Park, J.-H. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. J. Fluid Mech. 1995, 304, 285–319. [Google Scholar] [CrossRef]
- Ricardo, A.M.; Koll, K.; Franca, M.J. The terms of turbulent kinetic energy budget within random arrays of emergent cylinders. Water Resour. Res. 2014, 50, 4131–4148. [Google Scholar] [CrossRef]
- Church, M. Bed material transport and the morphology of alluvial river channels. Annu. Rev. Earth Planet. Sci. 2006, 34, 325–354. [Google Scholar] [CrossRef]
- Boyer, C.; Roy, A.G.; Best, J.L. Dynamics of a river channel confluence with discordant beds: Flow turbulence, bed load sediment transport, and bed morphology. J. Geophys. Res. 2006, 111, F04007. [Google Scholar] [CrossRef]
- Celik, A.; Diplas, P.; Dancey, C.; Valyrakis, M. Impulse and particle dislodgement under turbulent flow conditions. Phys. Fluids 2010, 22, 046601. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.C.; Friedrichs, C.T.; Maa, J.P.Y.; Wright, L.D. Estimating bottom stress in tidal boundary layer from acoustic Doppler velocimeter data. J. Hydraul. Eng. 2000, 126, 399–406. [Google Scholar] [CrossRef]
- Nino, Y.; Garcia, M.H. Experiments on particle-turbulence interactions in the near-wall region of an open channel flow: Implications for sediment transport. J. Fluid Mech. 1996, 326, 285–319. [Google Scholar] [CrossRef]
- Williams, J.J.; Thorne, P.D.; Heathershaw, A.D. Measurements of turbulence in the benthic boundary layer over a gravel bed. Sedimentology 1989, 36, 959–971. [Google Scholar] [CrossRef]
- Zong, L.; Nepf, H. Flow and deposition in and around a finite patch of vegetation. Geomorphology 2010, 116, 363–372. [Google Scholar] [CrossRef]
- Follett, E.M.; Nepf, H.M. Sediment patterns near a model patch of reedy emergent vegetation. Geomorphology 2012, 179, 141–151. [Google Scholar] [CrossRef] [Green Version]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef] [Green Version]
- Sukhodolov, A.N.; Sukhodolova, T.A. Morphodynamics and Hydraulics of Vegetated River Reaches: A Case Study on the Müggelspree in Germany. In River Coastal and Estuarine Morphodynamics; Parker, G., Garcia, M., Rhoads, B., Eds.; Taylor & Francis: London, UK, 2005; Volume 1, pp. 229–236. [Google Scholar]
- Van Wesenbeeck, B.K.; Van de Koppel, J.; Herman, P.M.J.; Bouma, T.J. Does scale-dependent feedback explain spatial complex-ity in salt-marsh ecosystems? Oikos 2008, 117, 152–159. [Google Scholar] [CrossRef]
- Hajdukiewicz, H.; Wyżga, B.; Mikuś, P.; Zawiejska, J.; Radecki-Pawlik, A. Impact of a large flood on mountain river habitats, channel morphology, and valley infrastructure. Geomorphology 2016, 272, 55–67. [Google Scholar] [CrossRef]
- Mikuś, P.; Wyżga, B.; Walusiak, E.; Radecki-Pawlik, A.; Liro, M.; Hajdukiewicz, H.; Zawiejska, J. Island development in a mountain river subjected to passive restoration: The Raba River, Polish Carpathians. Sci. Total Environ. 2019, 660, 406–420. [Google Scholar] [CrossRef]
- Jones, C.; Lawton, J.H.; Shachak, M. Organisms as ecosystems engineers. Oikos 1994, 69, 373–386. [Google Scholar] [CrossRef]








| Condition | a (cm−1) | n (cm−2) |
|---|---|---|
| A1 | 0 | 0 |
| A2 | 0.2 | 0.5 |
| A3 | 0.25 | 0.625 |
| A4 | 0.3 | 0.75 |
| A5 | 0.4 | 1 |
| A6 | 0.5 | 1.25 |
| A7 | 0.6 | 1.5 |
| A8 | 0.7 | 1.75 |
| A9 | 0.8 | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Wang, D.; Liu, X. Impact of Vegetation Density on the Wake Structure. Water 2019, 11, 1266. https://doi.org/10.3390/w11061266
Yu Z, Wang D, Liu X. Impact of Vegetation Density on the Wake Structure. Water. 2019; 11(6):1266. https://doi.org/10.3390/w11061266
Chicago/Turabian StyleYu, Zijian, Dan Wang, and Xingnian Liu. 2019. "Impact of Vegetation Density on the Wake Structure" Water 11, no. 6: 1266. https://doi.org/10.3390/w11061266
APA StyleYu, Z., Wang, D., & Liu, X. (2019). Impact of Vegetation Density on the Wake Structure. Water, 11(6), 1266. https://doi.org/10.3390/w11061266




