Analysis of the Hydraulic Properties of Undisturbed Layered Loess in Northwest China
Abstract
1. Introduction
- Exploring the variation in the water content profile in the layered loess–palaeosol sequence through the field undisturbed soil column infiltration test;
- Studying the variation in cumulative infiltration with time in the layered soils and infiltration models through the laboratory soil column experiment;
- Deriving the hydraulic properties of different soils through direct and indirect methods and further discussing the impact of the layered structure on hydrological processes under infiltration conditions.
2. Materials and Methods
2.1. Experimental Materials and Methods
2.1.1. Geological Environmental Conditions at the Study Area
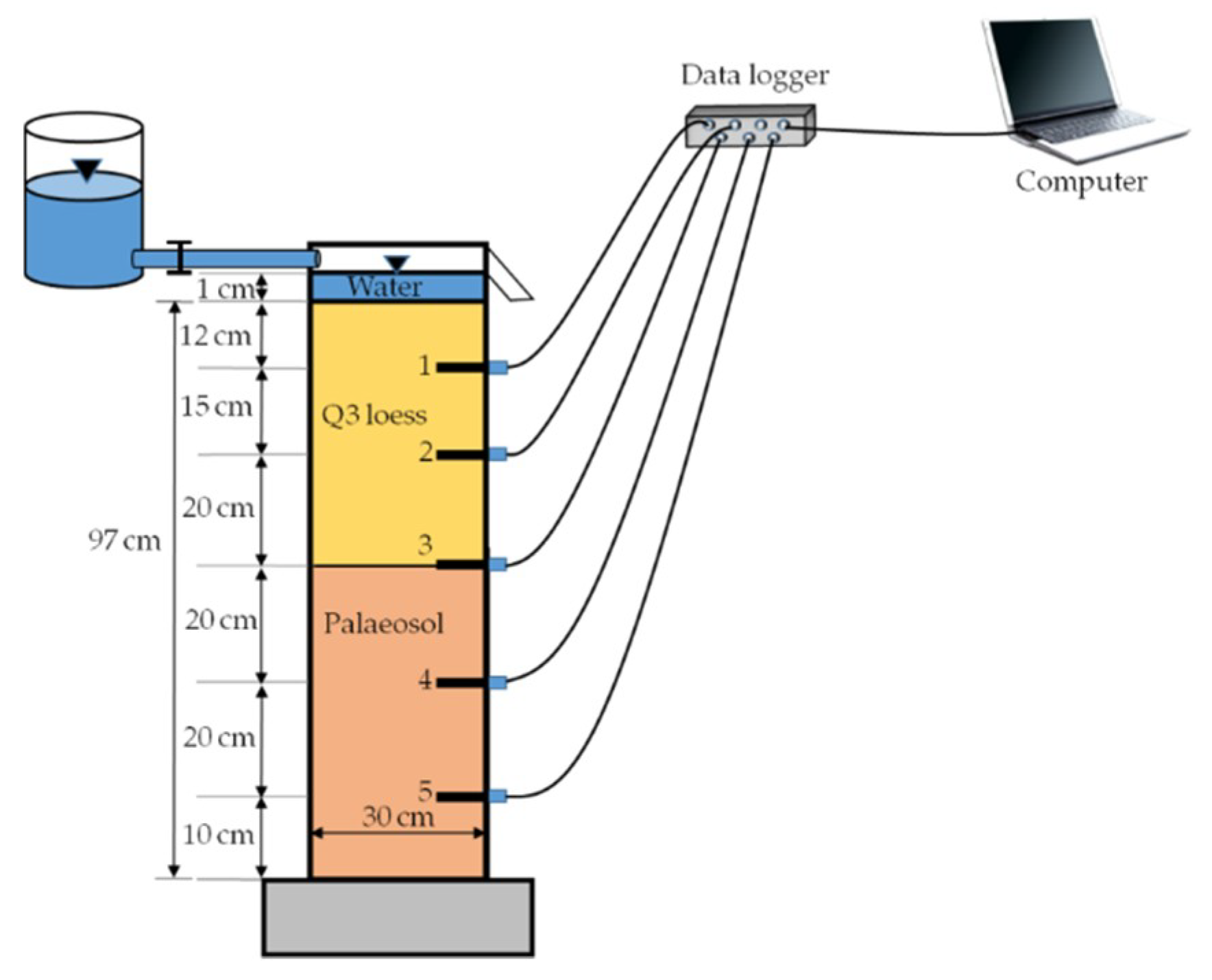
2.1.2. The Field Irrigation Experiment
2.1.3. Large Laboratory Soil Column Infiltration Experiment
2.1.4. Test of the Basic Physical and Hydraulic Properties of the Study Soil
2.2. Theory of the Soil Hydraulic Properties
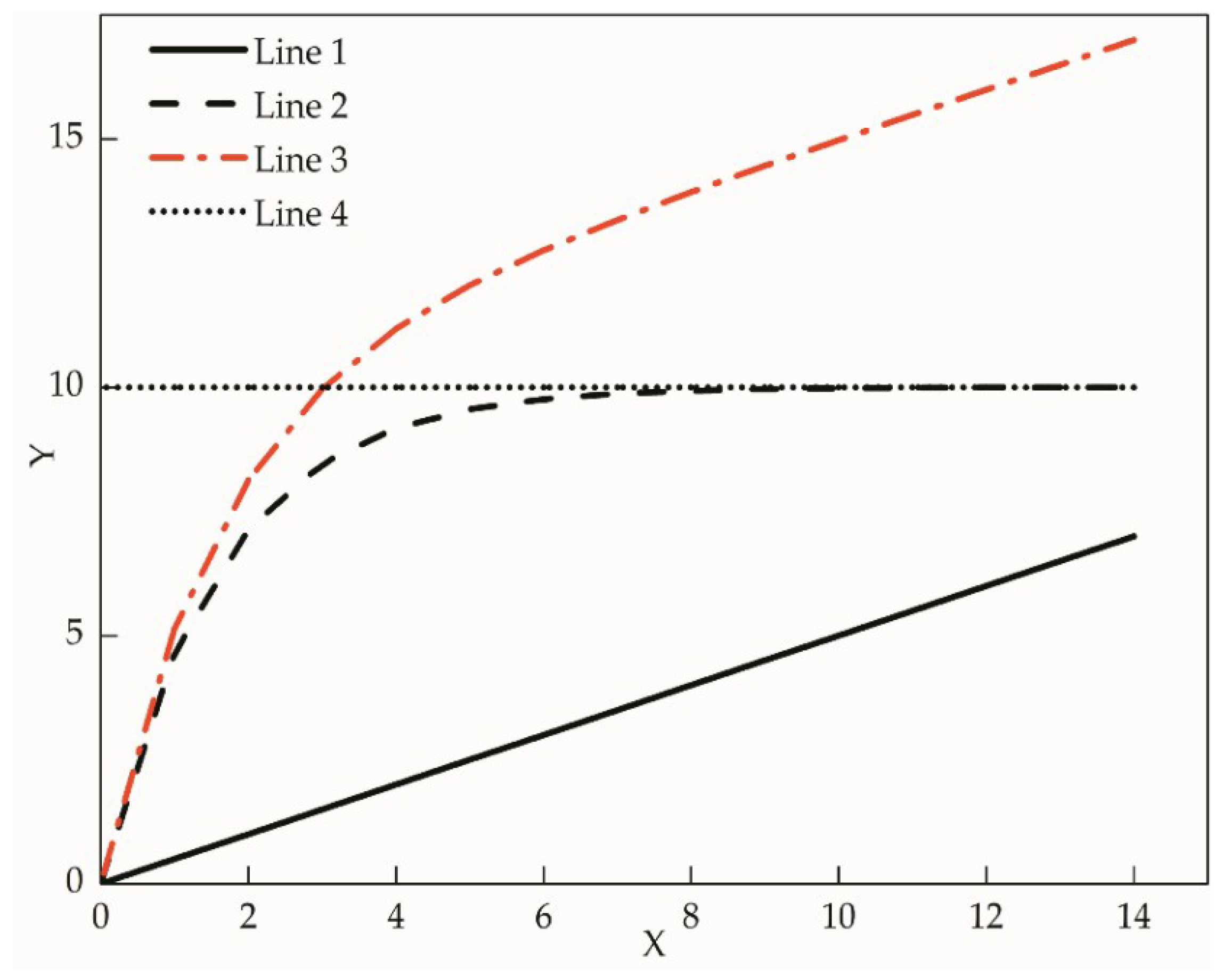
2.2.1. Infiltration Model of the Layered Soil
2.2.2. Description of the Basic Soil Hydraulic Properties
3. Results and Discussion
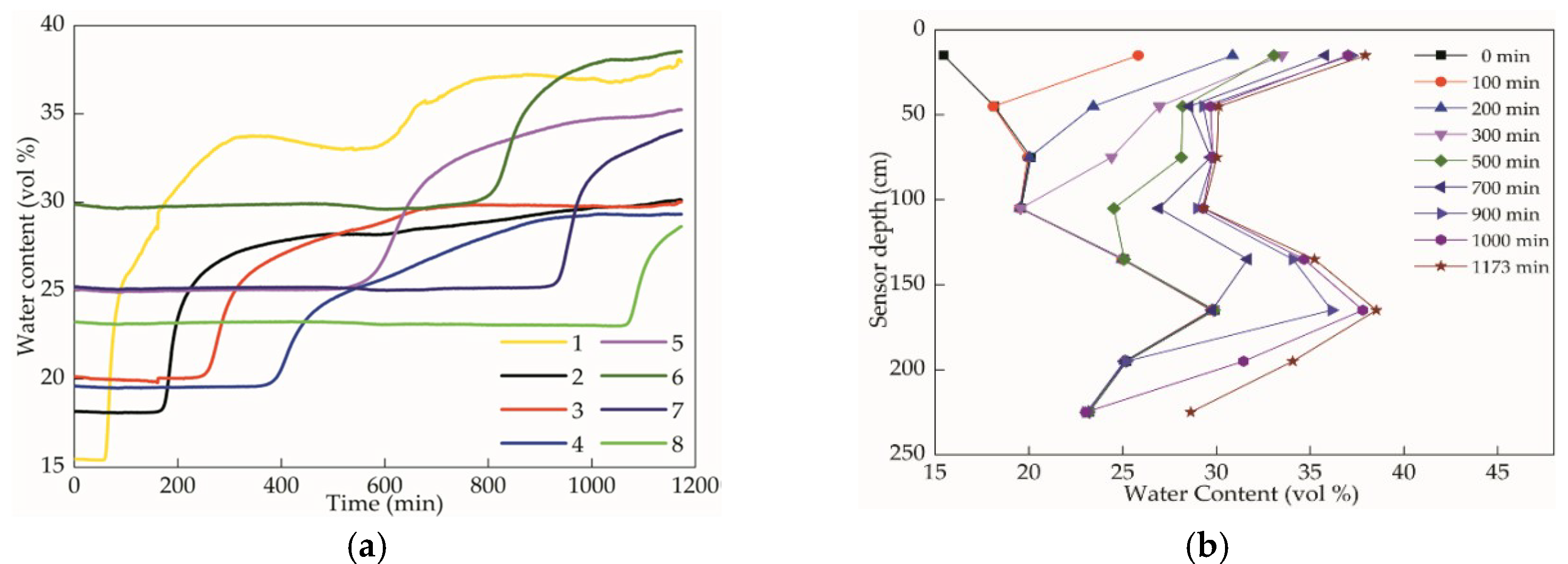
3.1. The Field Infiltration Experiment
3.2. Laboratory Soil Column Infiltration Experiment Results
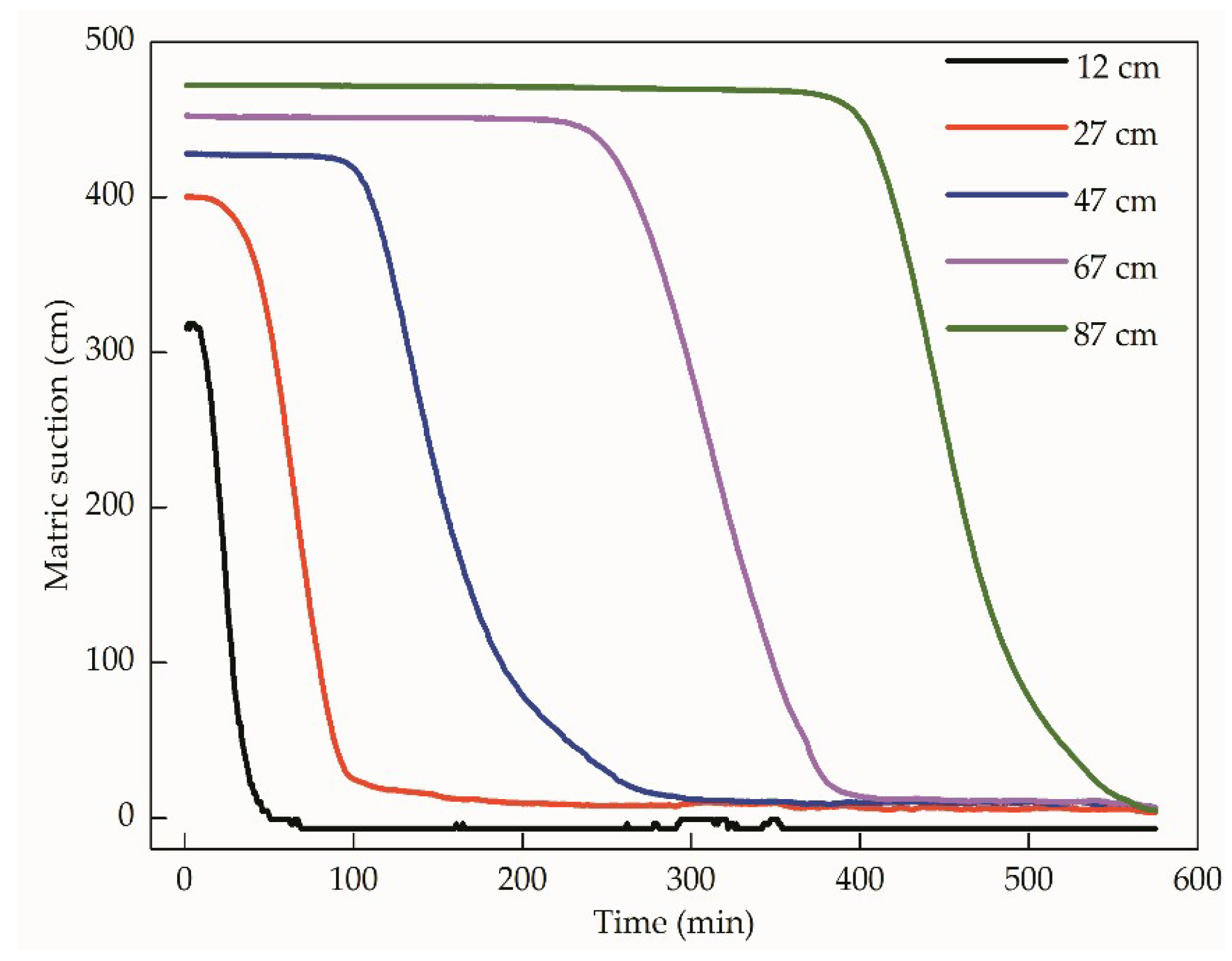
3.2.1. Variance of the Matric Suction during the Infiltration Process
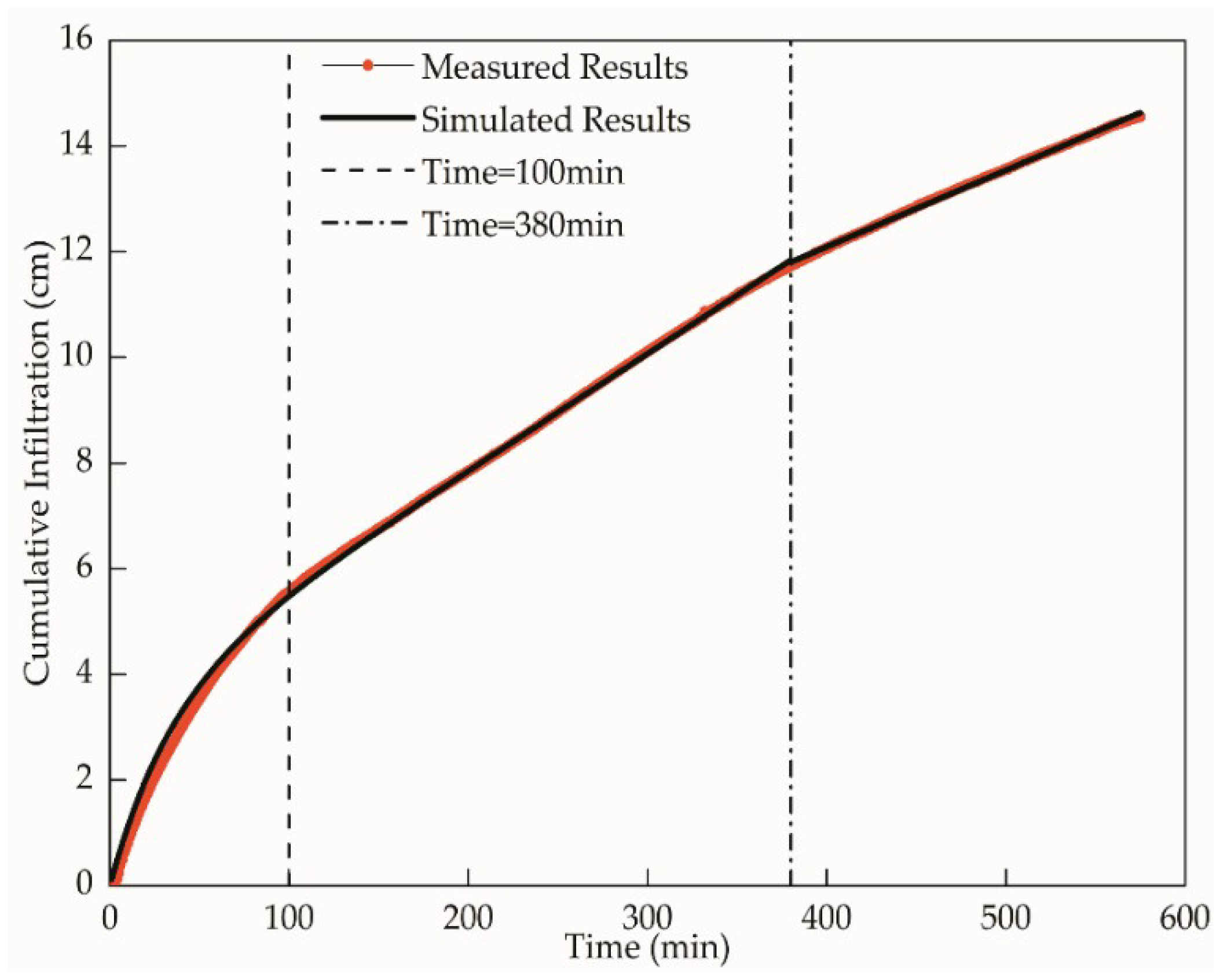
3.2.2. Infiltration Models
3.3. The Basic Physical and Hydraulic Properties
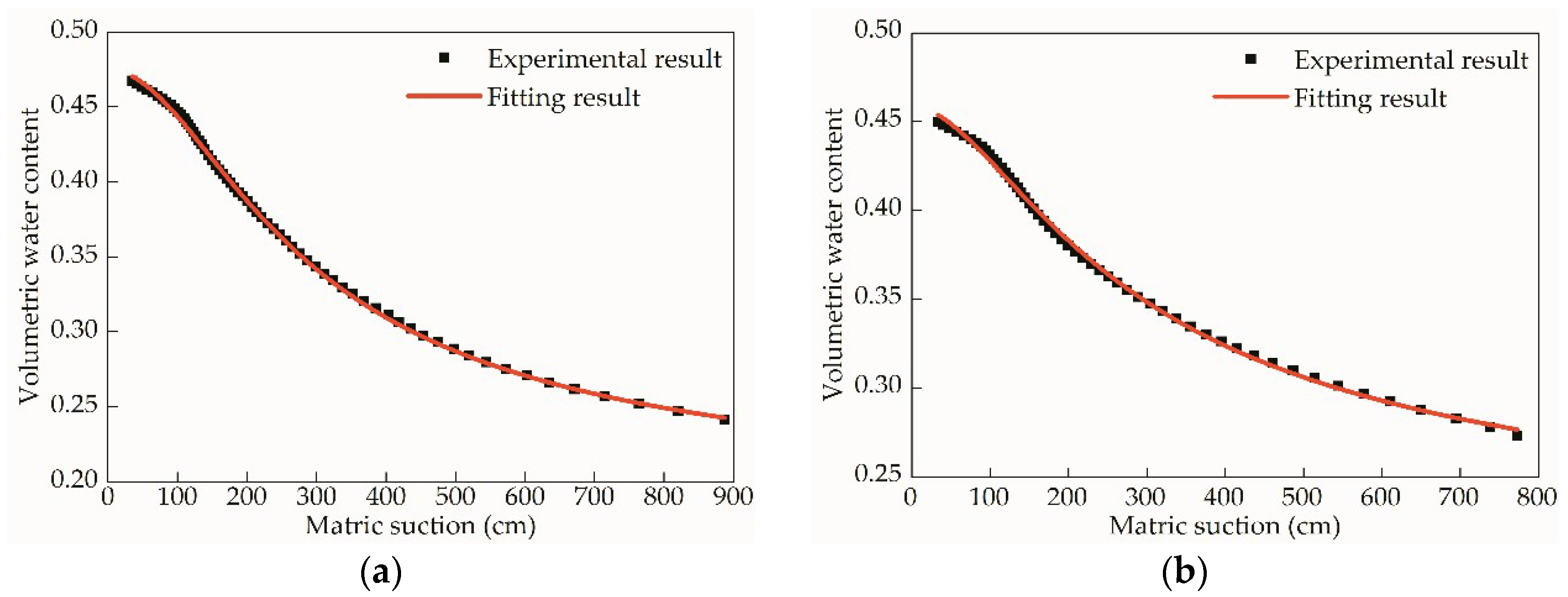
3.3.1. Laboratory SWCC Experiments
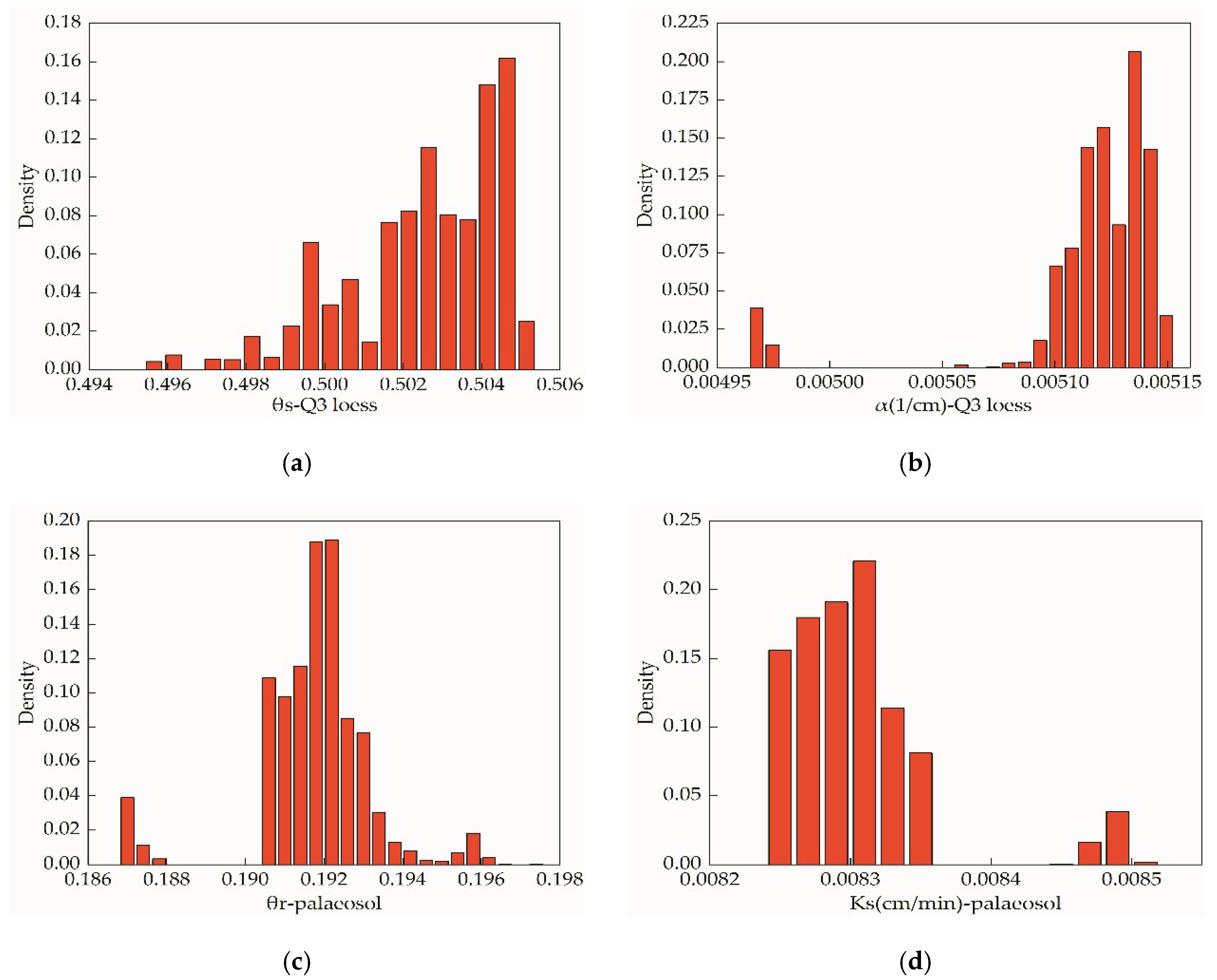
3.3.2. Inverse Simulation Results of the DREAM Algorithm
4. Conclusions
- According to the comparison of SWCC between loess and palaeosol, the water holding capacity of palaeosol is stronger than that of loess under the same matrix suction. Therefore, the water content of palaeosol is always higher than that of loess at the beginning and ending of the field test. The loess does not weaken the infiltration of the palaeosol. The reason for the water-resistance of the palaeosol is that its unsaturated hydraulic conductivity is lower than that of loess, which also leads to the appearance of a temporary water table at the interface between loess and palaeosol under certain infiltration conditions.
- In the laboratory infiltration test, before the wetting front reached the interface between loess and palaeosol, the relationship between the cumulative infiltration and time was nonlinear, which is consistent with that of homogeneous soil. However, after the wetting front reaches the interface, the relationship between the cumulative infiltration and time became linear. The superposition model based on the capacitance law can continuously simulate the nonlinear and linear relationships between the cumulative infiltration and time well.
- The water infiltration simulation experiments with two different scales illustrated that the process of water content change in the layered loess–palaeosol sequence can be divided into two stages: the first stage is the free infiltration stage of the loess under the constant water head; the second stage is the free infiltration stage of the palaeosol under the variable water head.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peng, J.B.; Wang, G.H.; Wang, Q.Y.; Zhang, F.Y. Shear wave velocity imaging of landslide debris deposited on an erodible bed and possible movement mechanism for a loess landslide in Jingyang, Xi’an, China. Landslides 2017, 14, 1503–1512. [Google Scholar] [CrossRef]
- Leng, Y.Q.; Peng, J.B.; Wang, Q.Y.; Meng, Z.J.; Huang, W.L. A fluidized landslide occurred in the Loess Plateau: A study on loess landslide in South Jingyang tableland. Eng. Geol. 2018, 236, 129–136. [Google Scholar] [CrossRef]
- Zhuang, J.Q.; Peng, J.B.; Wang, G.H.; Javed, I.; Wang, Y.; Li, W. Distribution and characteristics of landslide in Loess Plateau: A case study in Shaanxi province. Eng. Geol. 2018, 236, 89–96. [Google Scholar] [CrossRef]
- Xu, L.; Dai, F.C.; Tham, L.G.; Tu, X.B.; Min, H.; Zhou, Y.F.; Wu, C.X.; Xu, K. Field testing of irrigation effects on the stability of a cliff edge in loess, North-west China. Eng. Geol. 2011, 120, 10–17. [Google Scholar] [CrossRef]
- Xu, L.; Dai, F.C.; Tu, X.B.; Tham, L.G.; Zhou, Y.F.; Iqbal, J. Landslides in a loess platform, North-West China. Landslides 2014, 11, 993–1005. [Google Scholar] [CrossRef]
- Zhuang, J.Q.; Peng, J.B. A coupled slope cutting—A prolonged rainfall-induced loess landslide: A 17 October 2011 case study. Bull. Eng. Geol. Environ. 2014, 73, 997–1011. [Google Scholar] [CrossRef]
- Wang, H.F.; Wang, M.Y. Infiltration experiments in layered structures of upper porous and lower fractured media. J. Earth Sci. 2013, 24, 843–853. [Google Scholar] [CrossRef]
- Zhao, P.P.; Shao, M.A.; Melegy, A.A. Soil Water Distribution and Movement in Layered Soils of a Dam Farmland. Water Resour. Manag. 2010, 24, 3871–3883. [Google Scholar] [CrossRef]
- Samani, Z.; Cheraghi, A.; Willardson, L. Water Movement in Horizontal Layered Soils. J. Irrig. Drain. Eng. 1989, 115, 449–456. [Google Scholar] [CrossRef]
- Li, J.S.; Ji, H.Y.; Li, B.; Liu, Y.C. Wetting Patterns and Nitrate Distributions in Layered-Textural Soils under Drip Irrigation. Agric. Sci. China 2007, 6, 970–980. [Google Scholar] [CrossRef]
- Yang, H.; Rahardjo, H.; Leong, E.C. Behavior of Unsaturated Layered Soil Columns during Infiltration. J. Hydrol. Eng. 2006, 11, 329–337. [Google Scholar] [CrossRef]
- Wang, T.T.; Catherine, E.S.; Ma, J.B.; Zheng, J.Y.; Zhang, X.C. Applicability of five models to simulate water infiltration into soil with added biochar. J. Arid Land 2017, 9, 701–711. [Google Scholar] [CrossRef]
- Dashtaki, S.G.; Homaee, M.; Mahdian, M.H.; Kouchakzadeh, M. Site-Dependence Performance of Infiltration Models. Water Resour. Manag. 2009, 23, 2777–2790. [Google Scholar] [CrossRef]
- Chu, X.F.; Mariño, M.A. Determination of ponding condition and infiltration into layered soils under unsteady rainfall. J. Hydrol. 2005, 313, 195–207. [Google Scholar] [CrossRef]
- Sakellario-Makrantonaki, M. Water Drainage in Layered Soils. Laboratory Experiments and Numerical Simulation. Water Resour. Manag. 1997, 11, 437–444. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, S.Y.; Su, D.Y.; Gao, G.Y.; Huo, Z.L. Modeling water infiltration in a large layered soil column with a modified Green–Ampt model and HYDRUS-1D. Comput. Electron. Agric. 2010, 71, 40–47. [Google Scholar] [CrossRef]
- Corradini, C.; Morbidelli, R.; Flammini, A.; Govindaraju, R.S. A parameterized model for local infiltration in two-layered soils with a more permeable upper layer. J. Hydrol. 2011, 396, 221–231. [Google Scholar] [CrossRef]
- Mohammadzadeh-Habili, J.; Heidarpour, M. Application of the Green-Ampt model for infiltration into layered soils. J. Hydrol. 2015, 527, 824–832. [Google Scholar] [CrossRef]
- Al-Maktoumi, A.; Kacimov, A.; Al-Ismaily, S.; Al-Busaidi, H.; Al-Saqri, S. Infiltration into Two-Layered Soil: The Green–Ampt and Averyanov Models Revisited. Transp. Porous Media 2015, 109, 169–193. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, S.Y.; Zhan, H.B.; Liu, X.D.; Su, D.Y.; Kang, S.Z.; Song, X.F. Water Infiltration in Layered Soils with Air Entrapment: Modified Green-Ampt Model and Experimental Validation. J. Hydrol. Eng. 2011, 16, 628–638. [Google Scholar] [CrossRef]
- Zhao, J.B.; Long, T.W.; Wang, C.Y.; Zhang, Y. How the Quaternary climatic change affects present hydrogeological system on the Chinese Loess Plateau: A case study into vertical variation of permeability of the loess-palaeosol sequence. Catena 2012, 92, 179–185. [Google Scholar] [CrossRef]
- Zhao, J.B.; Ma, Y.D.; Cao, J.J.; Wei, J.P.; Shao, T.J. Effect of Quaternary climatic change on modern hydrological systems in the southern Chinese Loess Plateau. Environ. Earth Sci. 2015, 73, 1161–1167. [Google Scholar] [CrossRef]
- Ekblad, J.; Isacsson, U. Time-domain reflectometry measurements and soil-water characteristic curves of coarse granular materials used in road pavements. Can. Geotech. J. 2007, 44, 858–872. [Google Scholar] [CrossRef]
- Tarantino, A.; Ridley, A.M.; Toll, D.G. Field Measurement of Suction, Water Content, and Water Permeability. Geotech. Geol. Eng. 2008, 26, 751–782. [Google Scholar] [CrossRef]
- Godoy, V.A.; Zuquette, L.V.; Gómez-Hernández, J.J. Scale effect on hydraulic conductivity and solute transport: Small and large-scale laboratory experiments and field experiments. Eng. Geol. 2018, 243, 196–205. [Google Scholar] [CrossRef]
- Scharnagl, B.; Vrugt, J.A.; Vereecken, H.; Herbst, M. Inverse modelling of in situ soil water dynamics: Investigating the effect of different prior distributions of the soil hydraulic parameters. Hydrol. Earth Syst. Sci. 2011, 15, 3043–3059. [Google Scholar] [CrossRef]
- Li, B.L.; Liu, Y.; Nie, W.B.; Ma, X.Y. Inverse Modeling of Soil Hydraulic Parameters Based on a Hybrid of Vector-Evaluated Genetic Algorithm and Particle Swarm Optimization. Water 2018, 10, 84. [Google Scholar] [CrossRef]
- Sen, M.K.; Stoffa, P.L. Bayesian inference, Gibbs’ sampler and uncertainty estimation in geophysical inversion. Geophys. Prospect. 1996, 44, 313–350. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F.; Diks, C.G.H.; Robinson, B.A.; Hyman, J.M.; Higdon, D. Accelerating Markov Chain Monte Carlo Simulation by Differential Evolution with Self-Adaptive Randomized Subspace Sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar] [CrossRef]
- Qin, H.; Xie, X.Y.; Vrugt, J.A.; Zeng, K.; Hong, G. Underground structure defect detection and reconstruction using crosshole GPR and Bayesian waveform inversion. Autom. Constr. 2016, 68, 156–169. [Google Scholar] [CrossRef]
- Liu, W.P.; Luo, X.Y.; Huang, F.; Fu, M.F. Uncertainty of the Soil–Water Characteristic Curve and Its Effects on Slope Seepage and Stability Analysis under Conditions of Rainfall Using the Markov Chain Monte Carlo Method. Water 2017, 9, 758. [Google Scholar] [CrossRef]
- Vrugt, J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Model. Softw. 2016, 75, 273–316. [Google Scholar] [CrossRef]
- Zhang, J.P. Experimental Study on Infiltration Characteristics and Finger Flow in Layer Soils of the Loess Area. Ph.D. Thesis, Northwest Sci-Tech University of Agriculture and Forestry, Yangling, China, 2004. [Google Scholar]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–511. [Google Scholar] [CrossRef]






| Granular Group (Particle Size Range) | Content Ratio (%) | ||
|---|---|---|---|
| Q3 Loess Palaeosol | |||
| Sand (0.05–2 mm) | 3.91 | 8.95 | |
| Silt (0.005–0.05 mm) | Coarse silt (0.01–0.05 mm) | 67.88 | 56.57 |
| Fine silt (0.005–0.01 mm) | 1.76 | 2.78 | |
| Clay 0.005 mm) | 31.7 | ||
| Sensor Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| T = 0 h | 15 | 18 | 20 | 20 | 25 | 30 | 25 | 23 |
| T = 58.65 h | 38 | 31 | 30 | 29 | 35 | 39 | 34 | 29 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Dai, F.; Zhao, Z. Analysis of the Hydraulic Properties of Undisturbed Layered Loess in Northwest China. Water 2019, 11, 1379. https://doi.org/10.3390/w11071379
Guo Q, Dai F, Zhao Z. Analysis of the Hydraulic Properties of Undisturbed Layered Loess in Northwest China. Water. 2019; 11(7):1379. https://doi.org/10.3390/w11071379
Chicago/Turabian StyleGuo, Qinghua, Fuchu Dai, and Zhiqiang Zhao. 2019. "Analysis of the Hydraulic Properties of Undisturbed Layered Loess in Northwest China" Water 11, no. 7: 1379. https://doi.org/10.3390/w11071379
APA StyleGuo, Q., Dai, F., & Zhao, Z. (2019). Analysis of the Hydraulic Properties of Undisturbed Layered Loess in Northwest China. Water, 11(7), 1379. https://doi.org/10.3390/w11071379




