Assessment of System Responses in Intensively Irrigated Stream–Aquifer Systems Using SWAT-MODFLOW
Abstract
:1. Introduction
2. Model Construction and Composition
2.1. Overview of SWAT and MODFLOW
2.2. SWAT-MODFLOW Linkage
2.3. SWAT-MODFLOW Modifications
2.3.1. Irrigation Events
- HRUs and associated sub-basin assigned to each pumping well, with the pumping well designated by a row and column within the MODFLOW grid;
- Conveyance efficiency for each subbasin (percentage of pumped groundwater that is lost between the well and the field of application, representing loss from an earthen canal); and
- Runoff ratio (percentage of applied irrigation water that runs off the field).
2.3.2. Groundwater Evapotranspiration
3. SWAT-MODFLOW Application to Irrigated Stream–Aquifer System
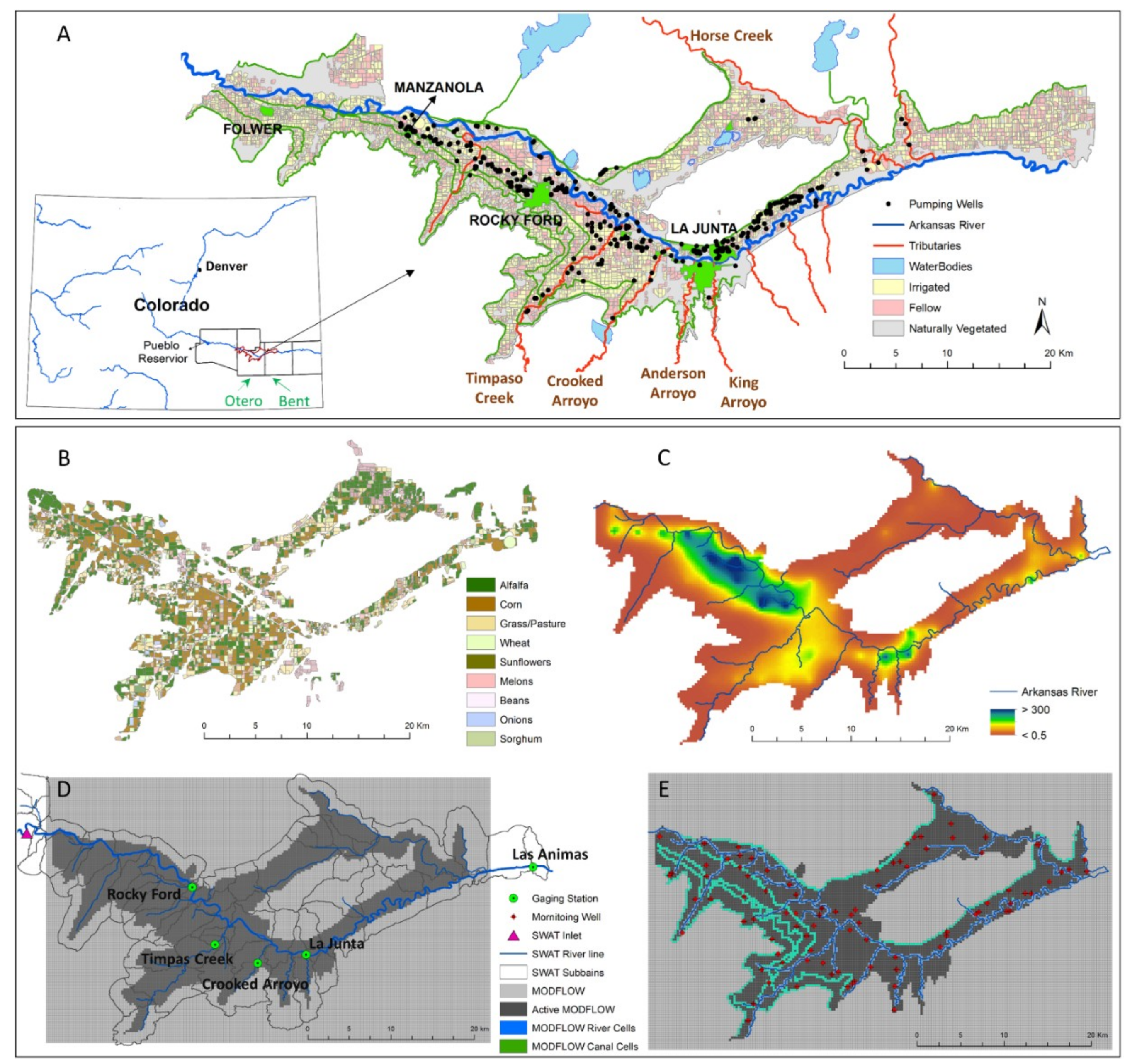
3.1. Study Region: Lower Arkansas River Valley, Colorado
3.2. Model Application
3.3. Model Calibration
3.4. Simulation of Irrigation Reduction Scenario
4. Results and Discussion
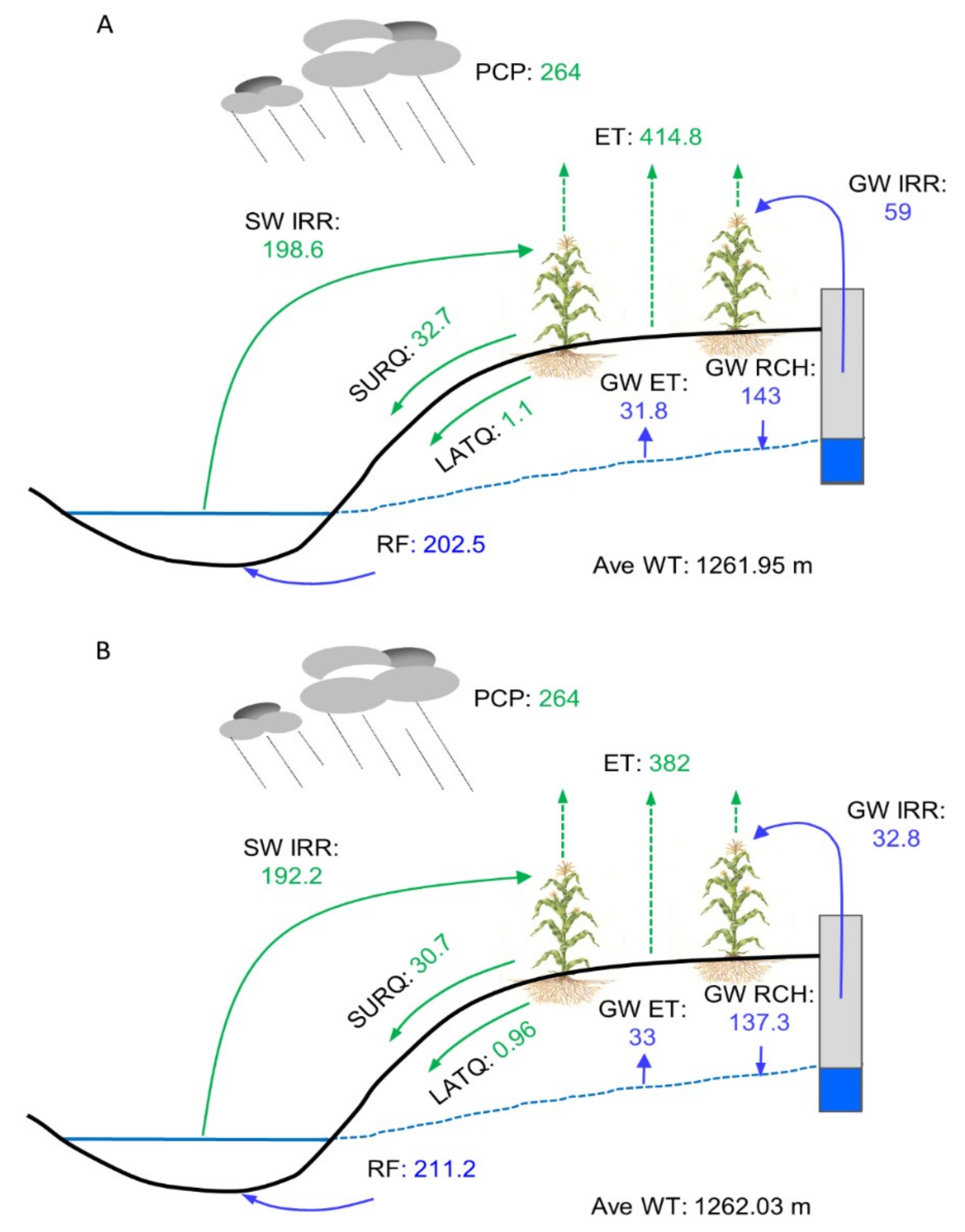
4.1. Water Balance
4.2. Streamflow
4.3. Groundwater Elevation
4.4. Surface Water–Groundwater Interactions
4.5. Groundwater ET
4.6. Crop Yield
4.7. Quantifying the Impacts of the Irrigation on System Responses
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lobell, D.B.; Lesch, S.M.; Corwin, D.L.; Ulmer, M.G.; Anderson, K.A.; Potts, D.J.; Doolittle, J.A.; Matos, M.R.; Baltes, M.J. Regional-scale Assessment of Soil Salinity in the Red River Valley Using Multi-year MODIS EVI and NDVI. J. Environ. Qual. 2010, 39, 35–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Törnqvist, R.; Jarsjö, J. Water Savings Through Improved Irrigation Techniques: Basin-Scale Quantification in Semi-Arid Environments. Water Resour. Manag. 2012, 26, 949–962. [Google Scholar] [CrossRef]
- Martin-Carrasco, F.; Garrote, L.; Iglesias, A.; Mediero, L. Diagnosing Causes of Water Scarcity in Complex Water Resources Systems and Identifying Risk Management Actions. Water Resour. Manag. 2013, 27, 1693–1705. [Google Scholar] [CrossRef]
- Robertson, A.D.; Zhang, Y.; Sherrod, L.A.; Rosenzweig, S.T.; Ma, L.; Ahuja, L.; Schipanski, M.E. Climate Change Impacts on Yields and Soil Carbon in Row Crop Dryland Agriculture. J. Environ. Qual. 2018, 47, 684–694. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Droogers, P.; Bastiaanssen, W. Irrigation performance using hydrological and remote sensing modeling. J. Irrig. Drain. Eng. 2002, 128, 11–18. [Google Scholar] [CrossRef]
- Cai, X.; McKinney, D.C.; Rosegrant, M.W. Sustainability analysis for irrigation water management in the Aral Sea region. Agric. Syst. 2003, 76, 1043–1066. [Google Scholar] [CrossRef] [Green Version]
- Niemann, J.D.; Lehman, B.M.; Gates, T.K.; Hallberg, N.U.; Elhaddad, A. Impact of Shallow Groundwater on Evapotranspiration Losses from Uncultivated Land in an Irrigated River Valley. J. Irrig. Drain. Eng. 2011, 137, 501–512. [Google Scholar] [CrossRef]
- Pokhrel, Y.N.; Koirala, S.; Yeh, P.J.-F.; Hanasaki, N.; Longuevergne, L.; Kanae, S.; Oki, T. Incorporation of groundwater pumping in a global Land Surface Model with the representation of human impacts. Water Resour. Res. 2015, 51, 78–96. [Google Scholar] [CrossRef]
- Aliyari, F.; Bailey, R.T.; Tasdighi, A.; Dozier, A.; Arabi, M.; Zeiler, K. Coupled SWAT-MODFLOW model for large-scale mixed agro-urban river basins. Environ. Model. Softw. 2019, 115, 200–210. [Google Scholar] [CrossRef]
- Pimentel, D.; Houser, J.; Preiss, E.; White, O.; Fang, H.; Mesnick, L.; Barsky, T.; Tariche, S.; Schreck, J.; Alpert, S. Water resources: Agriculture, the environment, and society. BioScience 1997, 47, 97–106. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Jolly, I.; Sophocleous, M.; Zhang, L. Global impacts of conversions from natural to agricultural ecosystems on water resources: Quantity versus quality. Water Resour. Res. 2007. [Google Scholar] [CrossRef]
- Gates, T.K.; Garcia, L.A.; Hemphill, R.A.; Morway, E.D.; Elhaddad, A. Irrigation Practices, Water Consumption, & Return Flows in Colorado’s Lower Arkansas River Valley: Field and Model Investigations. In Technical Report No. TR12-10; Colorado Agricultural Experiment Station: Fort Collins, CO, USA, 2012. [Google Scholar]
- Tanji, K.K.; Kielen, N.C. Agricultural Drainage Water Management in Arid and Semi-ARID areas; FAO: Rome, Italy, 2002. [Google Scholar]
- Burkhalter, J.P.; Gates, T.K. Agroecological Impacts from Salinization and Waterlogging in an Irrigated River Valley. J. Irrig. Drain. Eng. 2005, 131, 197–209. [Google Scholar] [CrossRef]
- Qureshi, A.S.; McCornick, P.G.; Sarwar, A.; Sharma, B.R. Challenges and Prospects of Sustainable Groundwater Management in the Indus Basin, Pakistan. Water Resour. Manag. 2010, 24, 1551–1569. [Google Scholar] [CrossRef]
- Borah, K.K.; Bera, M. Watershed-Scale Hydrologic and Nonpoint-Source Pollution Models: Review of Mathematical Bases. Trans. ASAE 2003, 46, 1553–1566. [Google Scholar] [CrossRef]
- Schoumans, O.F.; Silgram, M.; Walvoort, D.J.J.; Groenendijk, P.; Bouraoui, F.; Andersen, H.E.; Porto, A.L.; Reisser, H.; Gall, G.L.; Anthony, S.; et al. Evaluation of the difference of eight model applications to assess diffuse annual nutrient losses from agricultural land. J. Environ. Monit. 2009, 11, 540–553. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Francesconi, W.; Srinivasan, R.; Pérez-Miñana, E.; Willcock, S.P.; Quintero, M. Using the Soil and Water Assessment Tool (SWAT) to model ecosystem services: A systematic review. J. Hydrol. 2016, 535, 625–636. [Google Scholar] [CrossRef]
- Young, R.A.; Onstad, C.A.; Bosch, D.D.; Anderson, W.P. AGNPS: A nonpoint-source pollution model for evaluating agricultural watersheds. J. Soil Water Conserv. 1989, 44, 168–173. [Google Scholar]
- Bicknell, B.R.; Imhoff, J.C.; Kittle, J.L., Jr; Donigian, A.S., Jr; Johanson, R.C. Hydrologic Simulation Program-FORTRAN (HSPF): User’s Manual for version 11 1997. In Environmental Protection Agency Report No. EPA/600/R-97/080; US Environmental Protection Agency: Athens, Ga, USA, 1997. [Google Scholar]
- Charley, W.; Pabst, A.; Peters, J. The Hydrologic Modeling System (HEC-HMS): Design and Development Issues; Hydrologic Engineering Center: Davis, CA, USA, 1995. [Google Scholar]
- Woolhiser, D.A.; Smith, R.E.; Goodrich, D.C. KINEROS: A Kinematic Runoff and Erosion Model: Documentation and User Manual; US Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1990.
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Krysanova, V.; Wechsung, F.; Arnold, J.; Srinivasan, R.; Williams, J. SWIM (Soil and Water Integrated Model); Potsdam-Institut fuer Klimafolgenforschung (PIK): Potsdam, Germany, 2000; p. 239. [Google Scholar]
- Ogden, F.L.; Julien, P.Y.; Singh, V.; Frevert, D. CASC2D: A Two-Dimensional, Physically-Based, Hortonian Hydrologic Model; Water Resources Publications: Littleton, CO, USA, 2002. [Google Scholar]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Chiang, L.; Chaubey, I.; Gitau, M.W.; Arnold, J.G. Differentiating Impacts of Land Use Changes from Pasture Management in a CEAP Watershed Using the SWAT Model. Trans. ASABE 2010, 53, 1569–1584. [Google Scholar] [CrossRef]
- Ghebremichael, L.T.; Veith, T.L.; Watzin, M.C. Determination of Critical Source Areas for Phosphorus Loss: Lake Champlain Basin, Vermont. Trans. ASABE 2010, 53, 1595–1604. [Google Scholar] [CrossRef]
- Strehmel, A.; Schmalz, B.; Fohrer, N. Evaluation of Land Use, Land Management and Soil Conservation Strategies to Reduce Non-Point Source Pollution Loads in the Three Gorges Region, China. Environ. Manag. 2016, 58, 906–921. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.S.; Ahn, S.R.; Kim, S.J. Evaluation of executable best management practices in Haean highland agricultural catchment of South Korea using SWAT. Agric. Water Manag. 2017, 180, 224–234. [Google Scholar] [CrossRef]
- Jayakrishnan, R.; Srinivasan, R.; Santhi, C.; Arnold, J.G. Advances in the application of the SWAT model for water resources management. Hydrol. Process. 2005, 19, 749–762. [Google Scholar] [CrossRef]
- Ullrich, A.; Volk, M. Application of the Soil and Water Assessment Tool (SWAT) to predict the impact of alternative management practices on water quality and quantity. Agric. Water Manag. 2009, 96, 1207–1217. [Google Scholar] [CrossRef]
- Wang, R.; Bowling, L.C.; Cherkauer, K.A. Estimation of the effects of climate variability on crop yield in the Midwest USA. Agr. Forest Meteorol. 2016, 216, 141–156. [Google Scholar] [CrossRef] [Green Version]
- Ahmadzadeh, H.; Morid, S.; Delavar, M.; Srinivasan, R. Using the SWAT model to assess the impacts of changing irrigation from surface to pressurized systems on water productivity and water saving in the Zarrineh Rud catchment. Agric. Water Manag. 2016, 175, 15–28. [Google Scholar] [CrossRef]
- Fleckenstein, J.H.; Krause, S.; Hannah, D.M.; Boano, F. Groundwater-surface water interactions: New methods and models to improve understanding of processes and dynamics. Adv. Water Resour. 2010, 33, 1291–1295. [Google Scholar] [CrossRef]
- Spruill, C.A.; Workman, S.R.; Taraba, J.L. Simulation of daily and monthly stream discharge from small watersheds using the SWAT model. Trans. ASAE 2000, 43, 1431–1439. [Google Scholar] [CrossRef]
- Chu, T.W.; Shirmohammadi, A. Evaluation of the SWAT model’s hydrology component in the piedmont physiographic region of Maryland. Trans. ASAE 2004, 47, 1057. [Google Scholar] [CrossRef]
- Paniconi, C.; Marrocu, M.; Putti, M.; Verbunt, M. Newtonian nudging for a Richards equation-based distributed hydrological model. Adv. Water Resour. 2003, 26, 161–178. [Google Scholar] [CrossRef]
- Markstrom, S.L.; Niswonger, R.G.; Regan, R.S.; Prudic, D.E.; Barlow, P.M. GSFLOW-Coupled Ground-Water and Surface-Water FLOW Model Based on the Integration of the Precipitation-Runoff Modeling System (PRMS) and the Modular Ground-Water Flow Model (MODFLOW-2005); U.S. Geological Survey: Reston, VI, USA, 2008.
- Kollet, S.J.; Maxwell, R.M. Capturing the influence of groundwater dynamics on land surface processes using an integrated, distributed watershed model. Water Resour. Res. 2008. [Google Scholar] [CrossRef]
- Therrien, R.; McLaren, R.G.; Sudicky, E.A.; Panday, S.M. HydroGeoSphere: A Three-Dimensional Numerical Model Describing Fully-Integrated Subsurface and Surface Flow and Solute Transport; Groundwater Simulations Group, University of Waterloo: Waterloo, ON, Canada, 2010. [Google Scholar]
- Kolditz, O.; Bauer, S.; Bilke, L.; Böttcher, N.; Delfs, J.O.; Fischer, T.; Görke, U.J.; Kalbacher, T.; Kosakowski, G.; McDermott, C.I.; et al. OpenGeoSys: An open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ. Earth Sci. 2012, 67, 589–599. [Google Scholar] [CrossRef]
- Refsgaard, J.C. Parameterisation, calibration and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, Y.; Wu, B.; Tian, Y.; Han, F.; Zheng, C. Optimizing conjunctive use of surface water and groundwater for irrigation to address human-nature water conflicts: A surrogate modeling approach. Agric. Water Manag. 2016, 163, 380–392. [Google Scholar] [CrossRef]
- Larsen, M.A.D.; Rasmussen, S.H.; Drews, M.; Butts, M.B.; Christensen, J.H.; Refsgaard, J.C. Assessing the influence of groundwater and land surface scheme in the modelling of land surface–atmosphere feedbacks over the FIFE area in Kansas, USA. Environ. Earth Sci. 2016, 75, 130. [Google Scholar] [CrossRef]
- Ward, F.A.; Booker, J.F.; Michelsen, A.M. Integrated Economic, Hydrologic, and Institutional Analysis of Policy Responses to Mitigate Drought Impacts in Rio Grande Basin. J. Water Resour. Plan. Manag. 2006, 132, 488–502. [Google Scholar] [CrossRef] [Green Version]
- Scibek, J.; Allen, D.M.; Cannon, A.J.; Whitfield, P.H. Groundwater–surface water interaction under scenarios of climate change using a high-resolution transient groundwater model. J. Hydrol. 2007, 333, 165–181. [Google Scholar] [CrossRef]
- Ahrends, H.; Mast, M.; Rodgers, Ch.; Kunstmann, H. Coupled hydrological–economic modelling for optimised irrigated cultivation in a semi-arid catchment of West Africa. Environ. Model. Softw. 2008, 23, 385–395. [Google Scholar] [CrossRef]
- Shultz, C.D.; Bailey, R.T.; Gates, T.K.; Heesemann, B.E.; Morway, E.D. Simulating selenium and nitrogen fate and transport in coupled stream-aquifer systems of irrigated regions. J. Hydrol. 2018, 560, 512–529. [Google Scholar] [CrossRef]
- Wei, X.; Bailey, R.T.; Records, R.M.; Wible, T.C.; Arabi, M. Comprehensive simulation of nitrate transport in coupled surface-subsurface hydrologic systems using the linked SWAT-MODFLOW-RT3D model. Environ. Model. Softw. 2018. [Google Scholar] [CrossRef]
- Bauer, P.; Gumbricht, T.; Kinzelbach, W. A regional coupled surface water/groundwater model of the Okavango Delta, Botswana. Water Resour. Res. 2006. [Google Scholar] [CrossRef]
- Anibas, C.; Verbeiren, B.; Buis, K.; Chormański, J.; De Doncker, L.; Okruszko, T.; Meire, P.; Batelaan, O. A hierarchical approach on groundwater-surface water interaction in wetlands along the upper Biebrza River, Poland. Hydrol. Earth Syst. Sci. 2012, 16, 2329–2346. [Google Scholar] [CrossRef] [Green Version]
- Harbaugh, A.W. MODFLOW-2005, the US Geological Survey modular ground-water model: The ground-water flow process; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005.
- Morway, E.D.; Gates, T.K.; Niswonger, R.G. Appraising options to reduce shallow groundwater tables and enhance flow conditions over regional scales in an irrigated alluvial aquifer system. J. Hydrol. 2013, 495, 216–237. [Google Scholar] [CrossRef]
- Bailey, R.T.; Wible, T.C.; Arabi, M.; Records, R.M.; Ditty, J. Assessing regional-scale spatio-temporal patterns of groundwater–surface water interactions using a coupled SWAT-MODFLOW model. Hydrol. Process. 2016, 30, 4420–4433. [Google Scholar] [CrossRef]
- Geza, M.; McCray, J.E. Effects of soil data resolution on SWAT model stream flow and water quality predictions. J. Environ. Manag. 2008, 88, 393–406. [Google Scholar] [CrossRef]
- Srinivasan, R.; Zhang, X.; Arnold, J. SWAT ungauged: Hydrological budget and crop yield predictions in the Upper Mississippi River Basin. Trans. ASABE 2010, 53, 1533–1546. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Arnold, J.; Izaurralde, R.C.; Bosch, D. Simultaneous calibration of surface flow and baseflow simulations: A revisit of the SWAT model calibration framework. Hydrol. Process. 2011, 25, 2313–2320. [Google Scholar] [CrossRef]
- Garg, K.K.; Bharati, L.; Gaur, A.; George, B.; Acharya, S.; Jella, K.; Narasimhan, B. Spatial mapping of agricultural water productivity using the SWAT model in Upper Bhima Catchment, India. Irrig. Drain. 2012, 61, 60–79. [Google Scholar] [CrossRef]
- Baker, T.J.; Miller, S.N. Using the Soil and Water Assessment Tool (SWAT) to assess land use impact on water resources in an East African watershed. J. Hydrol. 2013, 486, 100–111. [Google Scholar] [CrossRef]
- Kundu, D.; Vervoort, R.W.; Ogtrop, F.F. The value of remotely sensed surface soil moisture for model calibration using SWAT. Hydrol. Process. 2017, 31, 2764–2780. [Google Scholar] [CrossRef]
- Niswonger, R.G.; Panday, S.; Ibaraki, M. MODFLOW-NWT, a Newton formulation for MODFLOW-2005. US Geol. Surv. Tech. Methods 2011, 6, 44. [Google Scholar]
- Sophocleous, M.; Perkins, S.P. Methodology and application of combined watershed and ground-water models in Kansas. J. Hydrol. 2000, 236, 185–201. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT–MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Guzman, J.A.; Moriasi, D.N.; Gowda, P.H.; Steiner, J.L.; Starks, P.J.; Arnold, J.G.; Srinivasan, R. A model integration framework for linking SWAT and MODFLOW. Environ. Model. Softw. 2015, 73, 103–116. [Google Scholar] [CrossRef]
- Wei, X.; Bailey, R.T.; Tasdighi, A. Using the SWAT Model in Intensively Managed Irrigated Watersheds: Model Modification and Application. J. Hydrol. Eng. 2018, 23, 04018044. [Google Scholar] [CrossRef]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. MODFLOW-2000, The U. S. Geological Survey Modular Ground-Water Model-User Guide to Modularization Concepts and the Ground-Water Flow Process; Open-File Report 00-92; United States Geological Survey: Reston, VI, USA, 2000.
- Dennehy, K.F.; Litke, D.W.; McMahon, P.B.; Heiny, J.S.; Toetz, T.M. Water Quality Assessment of the South Platte River basin, Colorado, Nebraska, and Wyoming–Analysis of Available Nutrients, Suspended Sediment and Pesticide Data, Water Years 1980–92. In Water-Resources Investigations Report 94-4095; United States Geological Survey: Denver, CO, USA, 1995. [Google Scholar]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Molina-Navarro, E.; Bailey, R.T.; Andersen, H.E.; Thodsen, H.; Nielsen, A.; Park, S.; Jensen, J.S.; Jensen, J.B.; Trolle, D. Comparison of abstraction scenarios simulated by SWAT and SWAT-MODFLOW. Hydrol. Sci. J. 2019, 64, 434–454. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional estimation of base flow and groundwater recharge in the Upper Mississippi river basin. J. Hydrol. 2000, 227, 21–40. [Google Scholar] [CrossRef]
- Sun, H.; Cornish, P.S. Estimating shallow groundwater recharge in the headwaters of the Liverpool Plains using SWAT. Hydrol. Process. 2005, 19, 795–807. [Google Scholar] [CrossRef]
- Gates, T.K.; Cox, J.T.; Morse, K.H. Uncertainty in mass-balance estimates of regional irrigation-induced return flows and pollutant loads to a river. J. Hydrol. Reg. Stud. 2018, 19, 193–210. [Google Scholar] [CrossRef]
- Dozier, A.Q.; Arabi, M.; Wostoupal, B.C.; Goemans, C.G.; Zhang, Y.; Paustian, K. Declining agricultural production in rapidly urbanizing semi-arid regions: Policy tradeoffs and sustainability indicators. Environ. Res. Lett. 2017, 12, 085005. [Google Scholar] [CrossRef]
- English, M. Deficit irrigation. I: Analytical framework. J. Irrig. Drain. Eng. 1990, 116, 399–412. [Google Scholar] [CrossRef]
- Zhang, Y.; Hansen, N.; Trout, T.; Nielsen, D.; Paustian, K. Modeling Deficit Irrigation of Maize with the DayCent Model. Agron. J. 2018, 110, 1754–1764. [Google Scholar] [CrossRef]















| Parameter | Definition | Calibrated Values |
|---|---|---|
| Parameters governing surface water response | ||
| CN2 | Soil Conservation Service (SCS) runoff curve number for moisture condition II | +25% |
| EPCO | Plant uptake compensation factor | 0.85 |
| CH_N2 | Manning’s n value for the main channel | 0.22 |
| CH_K2 | Effective hydraulic conductivity of channel (mm/hr) | 22.91 |
| OV_N | Manning’s n value for overland flow | 7.86 |
| SURLAG | Surface runoff lag coefficient | 3.28 |
| Parameters governing soil properties | ||
| SOL_Z | Depth from soil surface to bottom of layer (mm) | 2076 |
| SOL_K | Saturated hydraulic conductivity | −19% |
| SOL_AWC | Available water capacity | −10% |
| SOL_ZMX | Maximum rooting depth of soil profile | −5% |
| Parameters governing snow response | ||
| TIMP | Snow pack temperature lag factor | 0.61 |
| SFTMP | Snowfall temperature (°C) | −1.22 |
| SMTMP | Snow melt base temperature (°C) | −0.34 |
| SMFMX | Melt factor for snow on June 21 (mm/°C-day) | 2.12 |
| SMFMN | Melt factor for snow on December 21 (mm/°C-day) | 1.58 |
| Parameters governing groundwater response | ||
| COND | Riverbed hydraulic conductance (m2/s) | 0.00134–39.55 |
| Sy | Specific yield | 0.01–0.36 |
| Ss | Specific storage (1/m) | 1.69 × 10−5 |
| Gauging Stations | Statistical Comparison | Model Performance |
|---|---|---|
| Rocky Ford | NSE | 0.823 |
| R2 | 0.831 | |
| La Junta | NSE | 0.909 |
| R2 | 0.923 | |
| Las Animas | NSE | 0.902 |
| R2 | 0.942 | |
| Timpas Creek | NSE | 0.132 |
| R2 | 0.665 | |
| Crooked Arroyo | NSE | 0.117 |
| R2 | 0.443 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Bailey, R.T. Assessment of System Responses in Intensively Irrigated Stream–Aquifer Systems Using SWAT-MODFLOW. Water 2019, 11, 1576. https://doi.org/10.3390/w11081576
Wei X, Bailey RT. Assessment of System Responses in Intensively Irrigated Stream–Aquifer Systems Using SWAT-MODFLOW. Water. 2019; 11(8):1576. https://doi.org/10.3390/w11081576
Chicago/Turabian StyleWei, Xiaolu, and Ryan T. Bailey. 2019. "Assessment of System Responses in Intensively Irrigated Stream–Aquifer Systems Using SWAT-MODFLOW" Water 11, no. 8: 1576. https://doi.org/10.3390/w11081576
APA StyleWei, X., & Bailey, R. T. (2019). Assessment of System Responses in Intensively Irrigated Stream–Aquifer Systems Using SWAT-MODFLOW. Water, 11(8), 1576. https://doi.org/10.3390/w11081576





