Turbulent Flow Structures and Scour Hole Characteristics around Circular Bridge Piers over Non-Uniform Sand Bed Channels with Downward Seepage
Abstract
:1. Introduction
2. Experimental Set-Up and Procedure
2.1. Experimental Facility
2.2. Experimental Measurements
3. Results
3.1. Turbulence Characteristics
3.1.1. Turbulence Intensities
3.1.2. Skewness
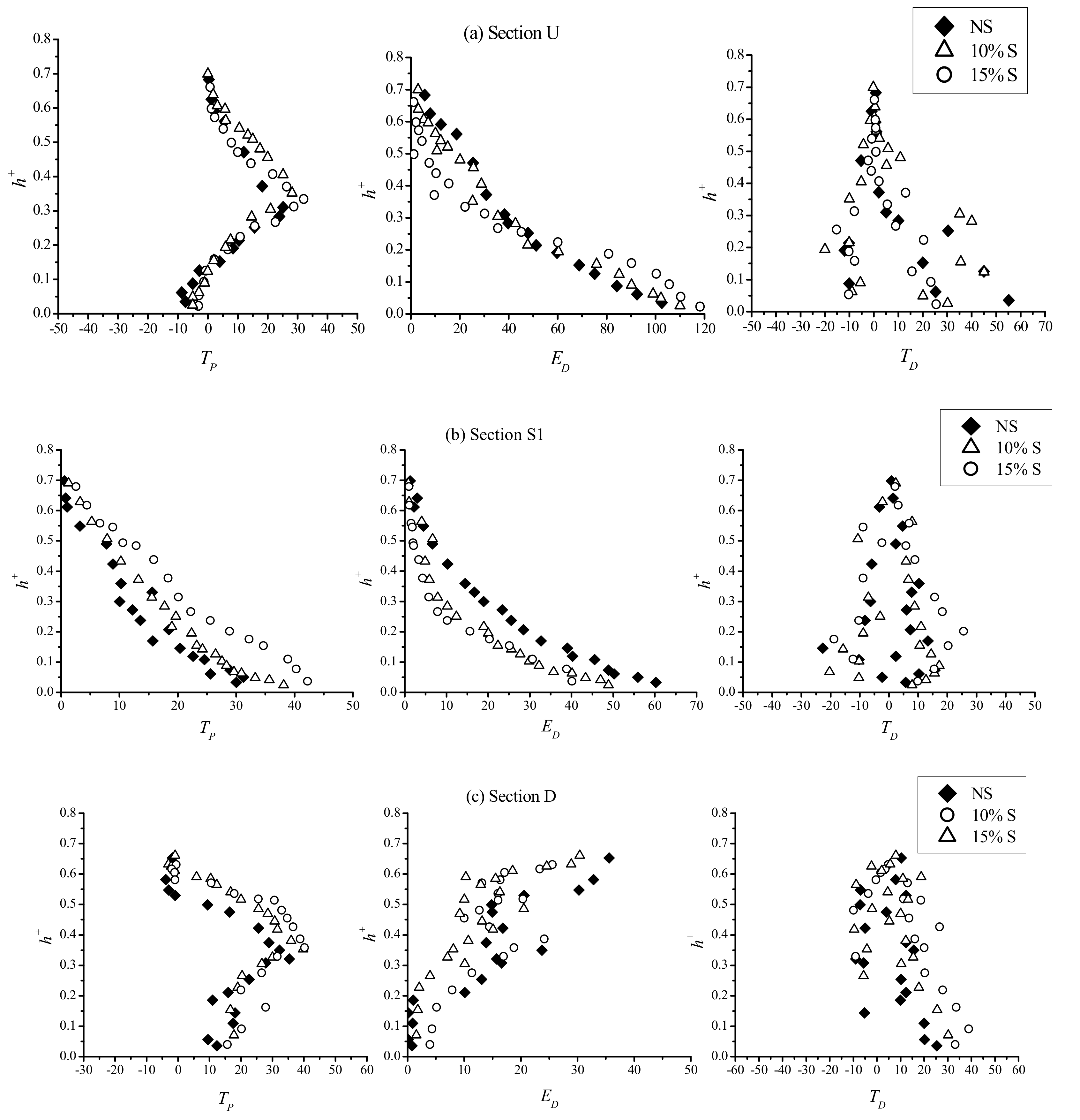
3.1.3. Turbulent Kinetic Energy Flux (TKE-Flux)
3.1.4. Turbulence Production, Dissipation, and Diffusion
3.2. Scour Hole Characteristics
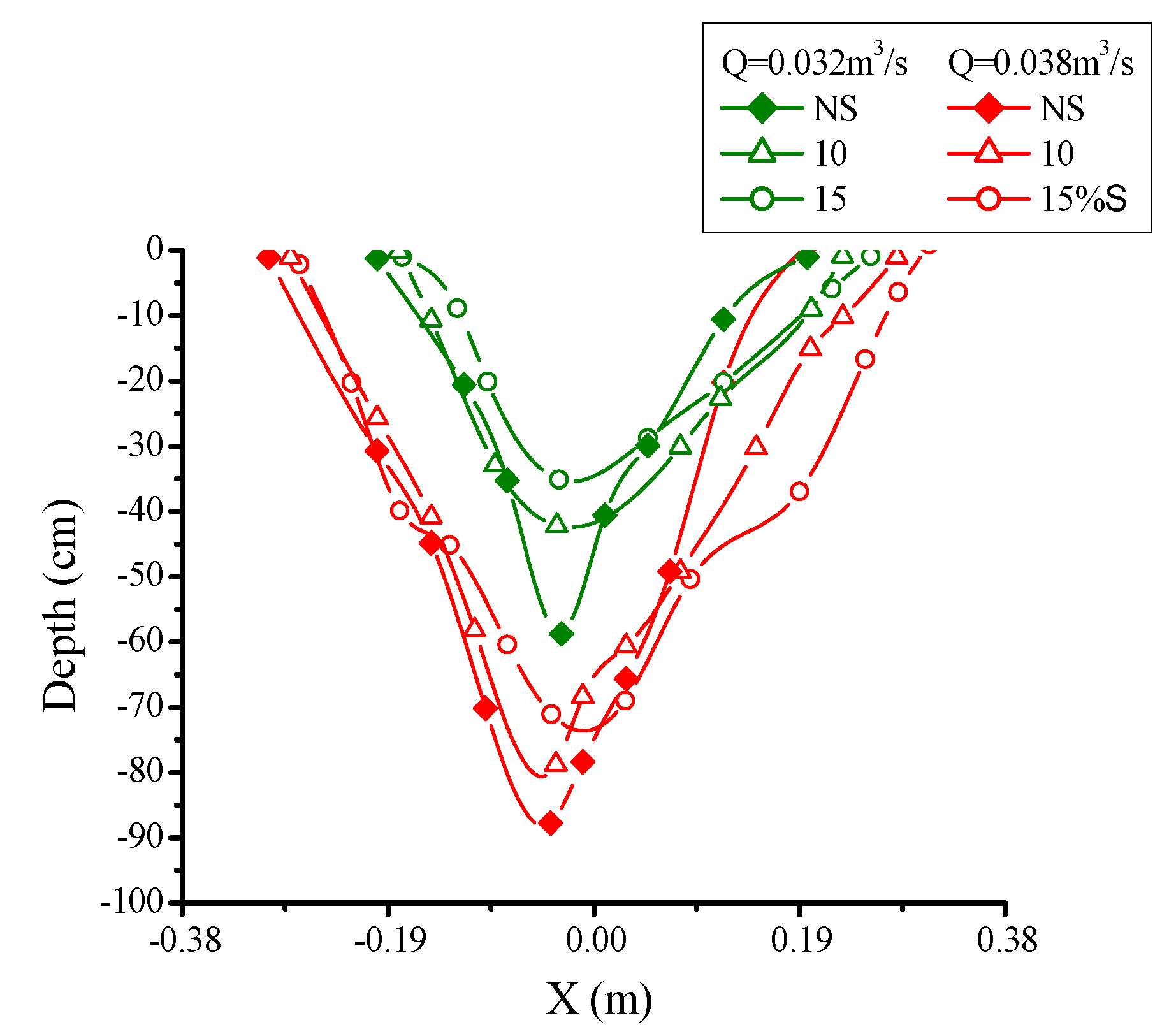
3.2.1. Geometry of Scour Hole
3.2.2. Dimensional Analysis
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chiew, Y.M. Local Scour at Bridge Piers. Ph.D. Dissertation, The University of Auckland, Auckland, NJ, USA, 1984. [Google Scholar]
- Melville, B.W. Local Scour at Bridge Sites. Ph.D. Dissertation, The University of Auckland, Auckland, NJ, USA, 1975. [Google Scholar]
- Ettema, R. Scour at Bridge Piers. Ph.D. Dissertation, The University of Auckland, Auckland, NJ, USA, 1980. [Google Scholar]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publication: Littleton, CO, USA, 2000. [Google Scholar]
- Richardson, E.V.; Davis, S.R. Evaluating Scour at Bridges, Hydraulic Engineering Circular No. 18 (hec-18). Publication No. FHWA NHI, 01-001. Available online: http://www.engr.colostate.edu/CIVE510/Manuals/HEC-18%204th%20Ed.(2001)%20-%20Evaluating%20Scour%20at%20Bridges.pdf (accessed on 27 July 2019).
- Istiarto, I. Flow Around a Cylinder in a Scoured Channel Bed. Ph.D. Thesis, Gadjah Mada University, Yogyakarta, Indonesia, 2001. [Google Scholar]
- Izadinia, E.; Heidarpour, M.; Schleiss, A.J. Investigation of turbulence flow and sediment entrainment around a bridge pier. Stoch. Environ. Res. Risk Assess. 2013, 27, 1303–1314. [Google Scholar] [CrossRef]
- Chavan, R.; Sharma, A.; Kumar, B. Effect of downward seepage on turbulent flow characteristics and bed morphology around bridge piers. J. Mar. Sci. Appl. 2017, 16, 60–72. [Google Scholar] [CrossRef]
- Breusers, H.N.C.; Nicollet, G.; Shen, H. Local Scour Around Cylindrical Piers. J. Hydraul. Res. 1977, 15, 211–252. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. Scour holes downstream of bed sills in low-gradient channels. J. Hydraul. Res. 2006, 44, 497–509. [Google Scholar] [CrossRef]
- Guan, D.; Melville, B.W.; Friedrich, H. Flow Patterns and Turbulence Structures in a Scour Hole Downstream of a Submerged Weir. J. Hydraul. Eng. 2014, 140, 68–76. [Google Scholar] [CrossRef]
- Raudkivi, A.J.; Ettema, R. Clear-Water Scour at Cylindrical Piers. J. Hydraul. Eng. 1983, 109, 338–350. [Google Scholar] [CrossRef]
- Chiew, Y.M.; Melville, B.W. Local scour around bridge piers. J. Hydraul. Res. 1987, 25, 15–26. [Google Scholar] [CrossRef]
- Chavan, R.; Kumar, B. Prediction of scour depth and dune morphology around circular bridge piers in seepage affected alluvial channels. Environ. Fluid Mech. 2018, 18, 923–945. [Google Scholar] [CrossRef]
- Richardson, J.R.; Abt, S.R.; Richardson, E.V. Inflow Seepage Influence on Straight Alluvial Channels. J. Hydraul. Eng. 1985, 111, 1133–1147. [Google Scholar] [CrossRef]
- Shukla, M.K.; Mishra, G.C. Canal discharge and seepage relationship. In Proceedings of the 6th National symposium on Hydro, Shillong, India, 6–7 March 1994; pp. 263–274. [Google Scholar]
- Tanji, K.K.; Kielen, N.C. Agricultural Drainage Water Management in Arid and Semi-Arid Areas; Food and Agriculture Organization: Rome, Italy, 2002. [Google Scholar]
- Kinzli, K.D.; Martinez, M.; Oad, R.; Prior, A.; Gensler, D. Using an ADCP to determine canal seepage loss in an irrigation district. Agric. Water Manag. 2010, 97, 801–810. [Google Scholar] [CrossRef]
- Martin, C.A.; Gates, T.K. Uncertainty of canal seepage losses estimated using flowing water balance with acoustic Doppler devices. J. Hydrol. 2014, 517, 746–761. [Google Scholar] [CrossRef]
- Lu, Y.; Chiew, Y.-M.; Cheng, N.-S. Review of seepage effects on turbulent open-channel flow and sediment entrainment. J. Hydraul. Res. 2008, 46, 476–488. [Google Scholar] [CrossRef]
- Rao, A.R.; Sreenivasulu, G.; Kumar, B. Geometry of sand-bed channels with seepage. Geomorphology 2011, 128, 171–177. [Google Scholar] [CrossRef]
- Cao, D.; Chiew, Y.M. Suction effects on sediment transport in closed-conduit flows. J. Hydraul. Eng. 2013, 140. [Google Scholar] [CrossRef]
- MacLean, A.G. Open channel velocity profiles over a zone of rapid infiltration. J. Hydraul. Res. 1991, 29, 15–27. [Google Scholar] [CrossRef]
- Chen, X.; Chiew, Y.M. Velocity Distribution of Turbulent Open-Channel Flow with Bed Suction. J. Hydraul. Eng. 2004, 130, 140–148. [Google Scholar] [CrossRef]
- Singh, A.; Al Faruque, M.A.; Balachandar, R. Vortices and large-scale structures in a rough open-channel flow subjected to bed suction and injection. J. Eng. Mech. 2011, 138, 491–501. [Google Scholar] [CrossRef]
- Devi, T.B.; Sharma, A.; Kumar, B. Turbulence Characteristics of Vegetated Channel with Downward Seepage. J. Fluids Eng. 2016, 138, 121102. [Google Scholar] [CrossRef]
- Marsh, N.A.; Western, A.W.; Grayson, R.B. Comparison of Methods for Predicting Incipient Motion for Sand Beds. J. Hydraul. Eng. 2004, 130, 616–621. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, S.; Ballio, F. Double-averaging turbulence characteristics in seeping rough-bed streams. J. Geophys. Res. Space Phys. 2011, 116, F03020. [Google Scholar] [CrossRef]
- Kumar, V.; Raju, K.G.R.; Vittal, N. Reduction of Local Scour around Bridge Piers Using Slots and Collars. J. Hydraul. Eng. 1999, 125, 1302–1305. [Google Scholar] [CrossRef]
- Goring, D.G.; Nikora, V.I. Despiking Acoustic Doppler Velocimeter Data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Chavan, R.; Kumar, B. Experimental investigation on flow and scour characteristics around tandem piers in sandy channel with downward seepage. J. Mar. Sci. Appl. 2017, 16, 313–322. [Google Scholar] [CrossRef]
- Bandyopadhyay, P.R.; Gad-El-Hak, M. Reynolds Number Effects in Wall-Bounded Turbulent Flows. Reynolds Number. Eff. Wall-Bounded Turbul. Flows 1994, 47, 307–365. [Google Scholar]
- Raupach, M.R. Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. J. Fluid Mech. 1981, 108, 363. [Google Scholar] [CrossRef]
- Krogstadt, P.Å.; Antonia, R. Surface roughness effects in turbulent boundary layers. Exp. Fluids 1999, 27, 450–460. [Google Scholar] [CrossRef]









| Expt. Run | Pier dia. D (mm) | Standard Deviation of River Sand σg | Flow Depth h (m) | Flow Rate Q (m3/s) | Reynolds Number (Re) | Froude Number (Fr) | Temp. (°C) | Seepage Percentage |
|---|---|---|---|---|---|---|---|---|
| 1 | 75 and 90 mm | 1.65 and 1.85 | 0.118 | 0.032 | 31,860 | 0.25 | 28 | 0 |
| 2 | 75 and 90 mm | 1.65 and 1.85 | 0.118 | 0.032 | 31,860 | 0.25 | 28 | 10 |
| 3 | 75 and 90 mm | 1.65 and 1.85 | 0.118 | 0.032 | 31,860 | 0.25 | 28 | 15 |
| 4 | 75 and 90 mm | 1.65 and 1.85 | 0.121 | 0.034 | 34,001 | 0.2579 | 28 | 0 |
| 5 | 75 and 90 mm | 1.65 and 1.85 | 0.121 | 0.034 | 34,001 | 0.2579 | 28 | 10 |
| 6 | 75 and 90 mm | 1.65 and 1.85 | 0.121 | 0.034 | 34,001 | 0.2579 | 28 | 15 |
| 7 | 75 and 90 mm | 1.65 and 1.85 | 0.123 | 0.036 | 36,039 | 0.2667 | 28 | 0 |
| 8 | 75 and 90 mm | 1.65 and 1.85 | 0.123 | 0.036 | 36,039 | 0.2667 | 28 | 10 |
| 9 | 75 and 90 mm | 1.65 and 1.85 | 0.123 | 0.036 | 36,039 | 0.2667 | 28 | 15 |
| 10 | 75 and 90 mm | 1.65 and 1.85 | 0.126 | 0.038 | 38,052 | 0.272 | 28 | 0 |
| 11 | 75 and 90 mm | 1.65 and 1.85 | 0.126 | 0.038 | 38,052 | 0.272 | 28 | 10 |
| 12 | 75 and 90 mm | 1.65 and 1.85 | 0.126 | 0.038 | 38,052 | 0.272 | 28 | 15 |
| 13 | 75 and 90 mm | 1.65 and 1.85 | 0.129 | 0.04 | 39,990 | 0.28 | 28 | 0 |
| 14 | 75 and 90 mm | 1.65 and 1.85 | 0.129 | 0.04 | 39,990 | 0.28 | 28 | 10 |
| 15 | 75 and 90 mm | 1.65 and 1.85 | 0.129 | 0.04 | 39,990 | 0.28 | 28 | 15 |
| Standard deviation | 2.22 × 10−3 | 9.9 × 10−4 | 4.2 × 10 −4 | 1.0 × 10−3 | 9.1 × 10−4 | 3.21 × 10−4 |
| Uncertainty % | 0.11 | 0.085 | 0.021 | 0.095 | 0.09 | 0.034 |
| Statistical Parameters | Standard Deviation | Standard Deviation about the Mean | Uncertainty % |
|---|---|---|---|
| 0.00095 | 0.01834 | 0.07264 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chavan, R.; Gualtieri, P.; Kumar, B. Turbulent Flow Structures and Scour Hole Characteristics around Circular Bridge Piers over Non-Uniform Sand Bed Channels with Downward Seepage. Water 2019, 11, 1580. https://doi.org/10.3390/w11081580
Chavan R, Gualtieri P, Kumar B. Turbulent Flow Structures and Scour Hole Characteristics around Circular Bridge Piers over Non-Uniform Sand Bed Channels with Downward Seepage. Water. 2019; 11(8):1580. https://doi.org/10.3390/w11081580
Chicago/Turabian StyleChavan, Rutuja, Paola Gualtieri, and Bimlesh Kumar. 2019. "Turbulent Flow Structures and Scour Hole Characteristics around Circular Bridge Piers over Non-Uniform Sand Bed Channels with Downward Seepage" Water 11, no. 8: 1580. https://doi.org/10.3390/w11081580
APA StyleChavan, R., Gualtieri, P., & Kumar, B. (2019). Turbulent Flow Structures and Scour Hole Characteristics around Circular Bridge Piers over Non-Uniform Sand Bed Channels with Downward Seepage. Water, 11(8), 1580. https://doi.org/10.3390/w11081580






