Sea Surface Circulation Structures in the Malta-Sicily Channel from Remote Sensing Data
Abstract
:1. Introduction
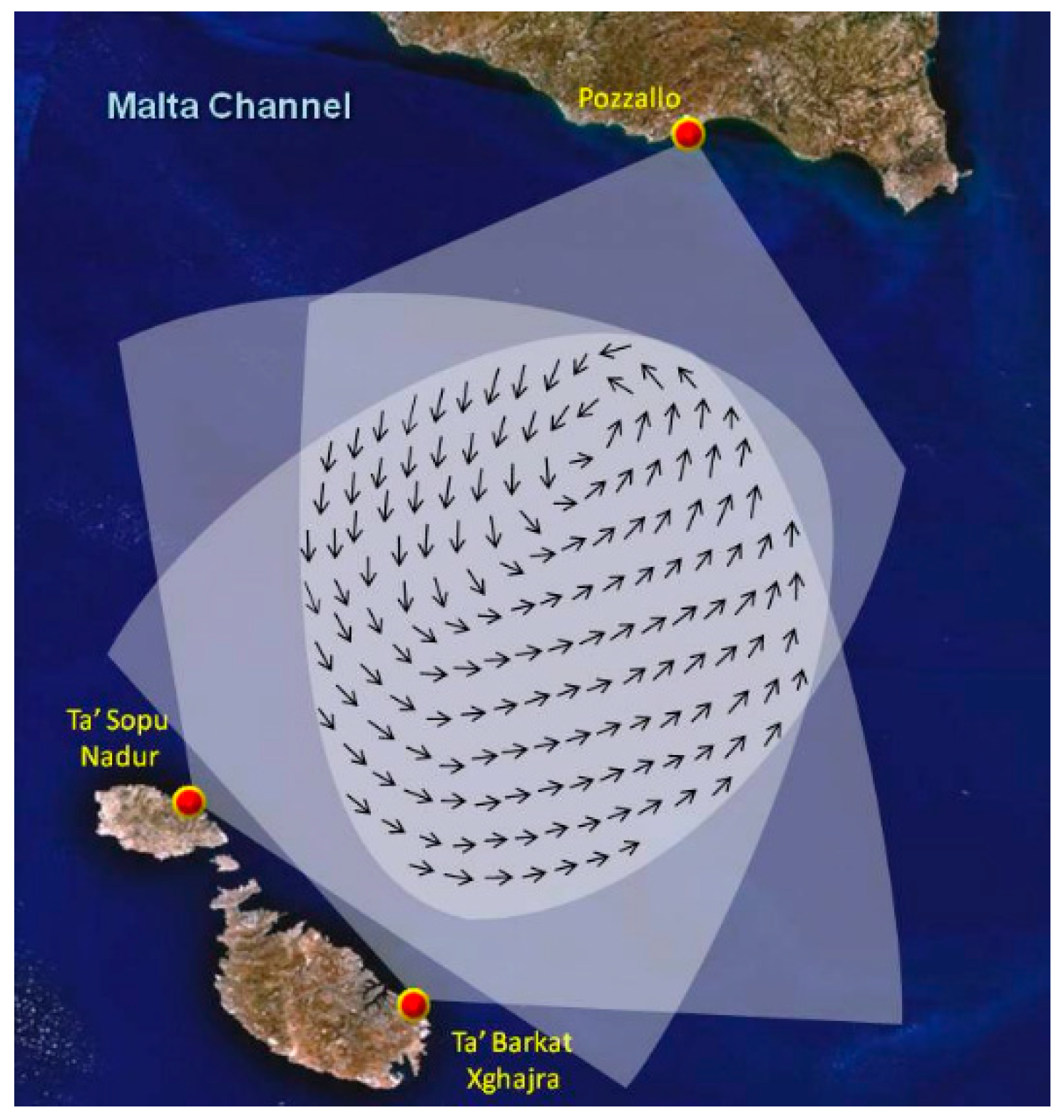
Study Area
2. Data and Methods
2.1. Remote Sensing Data
- HFR data from three CODAR SeaSondes stations installed in Ta’Sopu (Gozo, Malta), Ta’Barkat (Malta) and Pozzallo Harbor (Sicily, Italy) shown in Figure 2, provided surface current maps in the channel from the period August 2012 to January 2015. These data correspond to a setup of two HFR stations initially installed at Ta’Sopu and Ta’Barkat in August 2012. The third station was added in August 2013 in Pozzallo improving the spatial coverage of the channel [26]. The data are organized in time series of hourly velocity vectors with u (zonal, East-West) and v (meridional, North-South) components of the total velocity. The datasets were based on CALYPSO HFR, compiled and processed by Dr. Simone Cosoli from the University of Western Australia, Perth [27]. The CALYPSO system operating set-up and resolution (13.5 MHz frequency, angular resolution 5°, range resolution 1.6 km, for more details see Drago et al. [10]) provides radar measurements that are representative of the first meter of the ocean with grid sizes from 0.3 to 8.3 km2. The radars share the same transmit frequency using a GPS-synchronization module and operate with both the ideal and measured antenna beam patterns. Hourly sea surface current maps were derived on a Cartesian grid with 3 × 3 km2 horizontal resolution by least-squares fitting of the radial components of the ocean currents from two or more radar stations in areas of common overlap. Grid points were included in the analysis only if they satisfied a minimum data return of 50% using an interpolation technique described in Cosoli et al. [27]. Validation of this array has been carried out in different studies since the installation of the system making this dataset a reliable product [27,28,29].
- Ssalto/Duacs multi-mission L4 altimeter products in the period January 1993 to December 2015 containing daily multi-mission ADT on a 1/8° × 1/8° mercator projection grid, and distributed by the Copernicus Marine and Environment Monitoring Service (CMEMS) [4,5,31] were used to calculate SGV where,are the zonal and meridional geostrophic velocities, and ζ, denotes the dynamic topography provided by the altimeter.
- Monthly Level-3 binned SST [doi: 10.5067/AQUA/MODIS/L3M/SST/2014] and CHL [doi: 10.5067/AQUA/MODIS/L3B/CHL/2018] datasets with a spatial resolution of 4.6 km were downloaded from January to December 2013 from the OceanColor web portal (https://oceandata.sci.gsfc.nasa.gov/MODIS-Aqua/Binned/Monthly/) under the NASA aqua-MODIS (Moderate Resolution Imaging Spectroradiometer) satellite mission.
- A sub-grid ranging from 35.8–36.8° N to 13.8–15.4° E from the six-hourly gridded Cross-Calibrated Multi-Platform (CCMP) V2.0, Remote Sensing Systems (RSS), Santa Rosa, California, USA. Level-3 wind vector analyses product was downloaded from Remote Sensing Systems (RSS) for the period spanning August 2013 to January 2015 to analyze wind patterns in the channel [32]. The CCMP dataset combines cross-calibrated satellite microwave winds from scatterometers and radiometers with instrument observations using a variational analysis method to produce 1/4° gridded data [33]. Both radiometer and scatterometer data are validated against ocean moored buoys (in agreement within 0.8 m/s), where wind observations are referenced to a height of 10 m. For a complete description of the dataset see [32].
2.2. Complex Correlation and Veering Estimates
2.3. Kinematic Properties of an Eddy
3. Results and Discussion
3.1. Mean Surface Circulation, the Sicily Channel
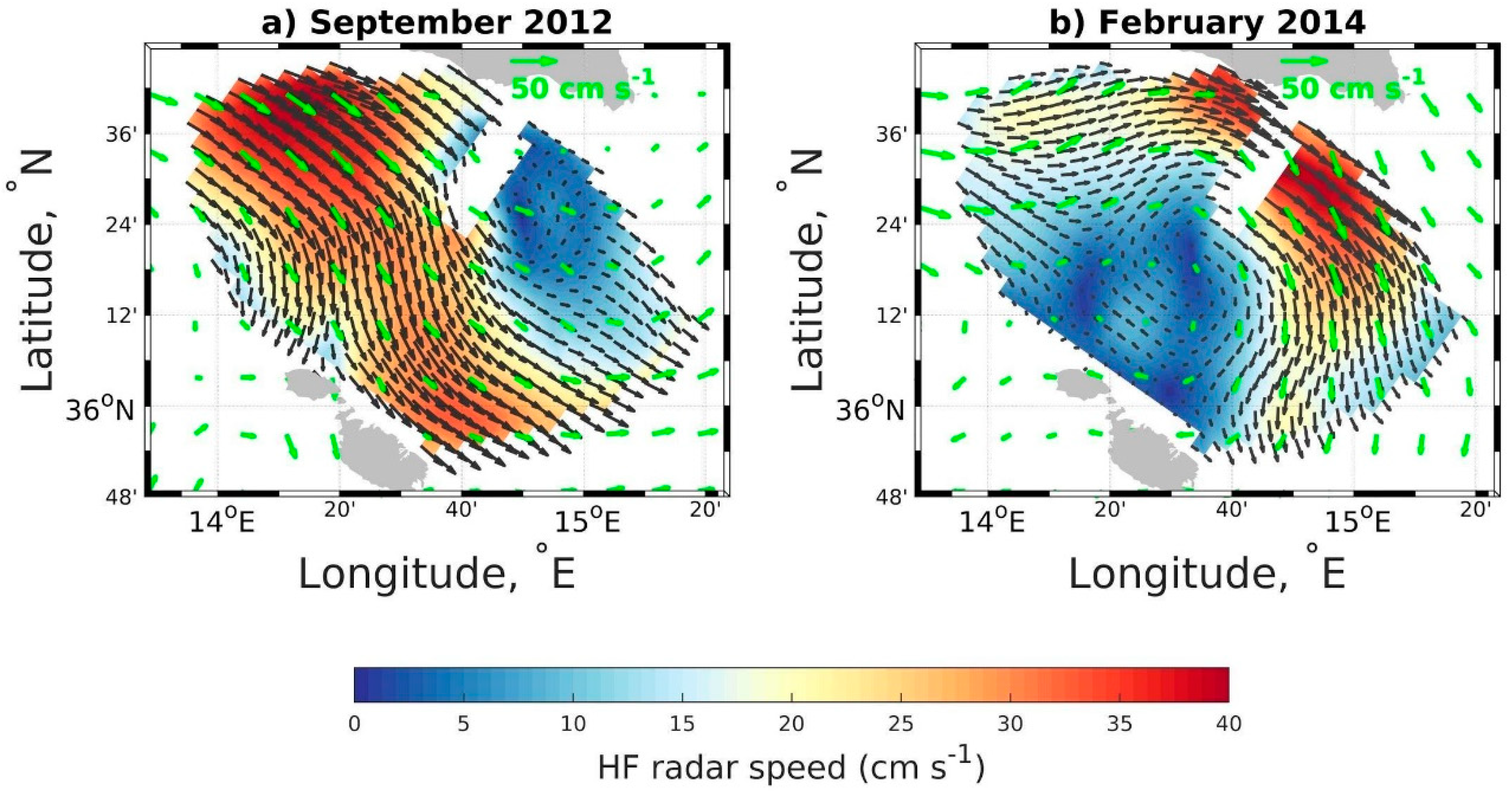
3.2. Short Time Scales in the Malta Sicily Channel
3.2.1. Comparison among Available Spatial Data
3.2.2. Complex Correlation
3.3. The Malta Sicily Gyre
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Currents | |
| AC | Atlantic Current |
| ATC | Atlantic Tunisian Current |
| AIS | Atlantic Ionian Stream |
| BAC | Bifurcation Atlantic/Algerian current |
| MIJ | Mid-Ionian Jet |
| Water Masses | |
| AW | Atlantic Water |
| Geographical Names | |
| AB | Adventure Bank |
| MP | Malta Plateau |
| GB | Gela Basin |
| MT | Malta Trough |
| La | Lampedusa |
| P | Pantelleria |
| Li | Linosa |
| PT | Pantelleria Trough |
| LT | Linosa Trough |
| S | Sicily |
| M | Maltese Islands |
| SC | Sicily Channel |
| Channel | Malta-Sicily Channel |
| SME | Sicily-Malta Escarpment |
| MB | Medina Bank |
| SS | Sicily Strait |
| TP | Tunisia Plateau |
| Gyres | |
| ABV | Adventure Bank Vortex (Cyclonic) |
| MRV | Mesina Rise Vortex (Cyclonic) |
| ISV | Ionian Shelf Break Vortex (Cyclonic) |
| MSG | Malta-Sicily Gyre (Anticyclonic) |
| MCC | Malta Channel Crest (Anticyclonic) |
| MG | Medina Gyre (Cyclonic) |
| NIG | North Ionian Gyre (Cyclonic/Anticyclonic) |
| PV | Pantelleria vortex (Anticyclonic) |
| Datasets | |
| CCMP | Cross-Calibrated Multi-Platform wind vector analysis |
| CMEMS | Copernicus Marine and Environment Monitoring Service |
| CODAR | Coastal ocean dynamics applications radar |
| HFR | High Frequency Radar |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| NASA | National Aeronautics and Space Administration |
| NOAA | The National Oceanic and Atmospheric Administration |
| NSF | National Science Foundation |
| RSS | Remote sensing systems (scientific company) |
| Physical Properties | |
| ADT | Absolute Dynamic Topography |
| CHL | Satellite Sea surface chlorophyll concentrations |
| EKE | Eddy Kinetic Energy |
| SGV | Surface Geostrophic Velocity |
| SST | Satellite Sea Surface Temperature |
References
- Robinson, A.R.; Leslie, W.G.; Theocharis, A.; Lascaratos, A. Encyclopedia of Ocean Sciences: Mediterranean Sea Circulation, 2nd ed.; Academic London: London, UK, 2001; Volume 3, pp. 1689–1705. [Google Scholar] [CrossRef]
- Malanotte-Rizzoli, P.M.; Robinson, A.R. Ocean Processes in Climate Dynamics: Global and Mediterranean Examples; Springer Science & Business Media: Berlin, Germany, 2012; Volume 419. [Google Scholar] [CrossRef]
- Jouini, M.; Béranger, K.; Arsouze, T.; Beuvier, J.; Thiria, S.; Crépon, M.; Taupier-Letage, I. The Sicily Channel surface circulation revisited using a neural clustering analysis of a high-resolution simulation. J. Geophys. Res. Oceans 2016, 121, 4545–4567. [Google Scholar] [CrossRef]
- Menna, M.; Reyes-Suarez, N.C.; Civitarese, G.; Gačić, M.; Poulain, P.-M.; Rubino, A. Decadal variations of circulation in the Central Mediterranean and its interactions with the mesoscale gyres. Deep Sea Res. Part II Top. Stud. Oceanogr. 2019. [Google Scholar] [CrossRef]
- Menna, M.; Poulain, P.-M.; Ciani, D.; Doglioli, A.; Notarstefano, G.; Gerin, R.; Rio, M.H.; Santoleri, R.; Gauci, A.; Drago, A. New insights of the Sicily Channel and southern Tyrrhenian Sea variability. Water 2019, 11, 1355. [Google Scholar] [CrossRef]
- Würtz, M.; Rovere, M. Atlas of the Mediterranean Seamounts and Seamount-Like Structures; IUCN: Grand, Switzerland, 2015. [Google Scholar]
- Ismail, S.B.; Schroeder, K.; Sammari, C.; Gasparini, G.P.; Borghini, M.; Aleya, L. Interannual variability of water mass properties in the Tunisia–Sicily Channel. J. Mar. Syst. 2014, 135, 14–28. [Google Scholar] [CrossRef]
- Lodolo, E.; Ben-Avraham, Z. A submerged monolith in the Sicilian Channel (central Mediterranean Sea): Evidence for Mesolithic human activity. J. Archaeol. Sci. Rep. 2015, 3, 398–407. [Google Scholar] [CrossRef]
- Drago, A.; Azzopardi, J.; Gauci, A.; Tarasova, R.; Ciraolo, G.; Capodici, F.; Gačić, M. Sea surface currents by HF radar in the Malta channel. Rapp. Comm. Int. Mer Medit. 2013, 40, 144. [Google Scholar]
- Drago, A.; Ciraolo, G.; Capodici, F.; Cosoli, S.; Gačić, M.; Poulain, P.-M.; Tarasova, R.; Azzopardi, J.; Gauci, A.; Maltese, A.; et al. CALYPSO—An operational network of HF radars for the Malta-Sicily Channel. In Proceedings of the 7th International Conference on EuroGOOS, Lisbon, Portugal, 28–30 October 2014; Volume 30, pp. 28–30. [Google Scholar]
- Smith, W.H.F.; Sandwell, D.T. Global seafloor topography from satellite altimetry and ship depth soundings. Science 1997, 277, 1957–1962. [Google Scholar] [CrossRef]
- Robinson, A.R.; Sellschopp, J.; Warn-Varnas, A.; Leslie, W.G.; Lozano, C.J.; Haley, P.J., Jr.; Anderson, L.A.; Lermusiaux, P.F.J. The Atlantic Ionian Stream. J. Mar. Syst. 1999, 20, 129–156. [Google Scholar] [CrossRef]
- Drago, A.; Sorgente, R.; Olita, A. Sea Temperature, Salinity and Total Velocity Climatological Fields for the South-Central Mediterranean Sea. MedSudMed Technical Documents Gcp/Rer/010/Ita/Msm-Td-14. 2010, 35. No. 14. Available online: http://www.faomedsudmed.org/html/doc/Publication_issue.asp?id=195 (accessed on 30 July 2019).
- Lermusiaux, P.F.J. Estimation and study of mesoscale variability in the Strait of Sicily. Dyn. Atmos. Oceans 1999, 29, 255–303. [Google Scholar] [CrossRef]
- Lermusiaux, P.F.J.; Robinson, A.R. Features of dominant mesoscale variability, circulation patterns and dynamics in the Strait of Sicily. Deep Sea Res. Part I Oceanogr. Res. Pap. 2001, 48, 1953–1997. [Google Scholar] [CrossRef]
- Béranger, K.; Mortier, L.; Gasparini, G.P.; Gervasio, L.; Astraldi, M.; Crépon, M. The dynamics of the Sicily Strait: A comprehensive study from observations and models. Deep Sea Res. Part II Top. Stud. Oceanogr. 2004, 51, 411–440. [Google Scholar] [CrossRef]
- Robinson, A.R.; Malanotte-Rizzoli, P.; Hecht, A.; Michelato, A.; Roether, W.; Theocharis, A.; Ünlüata, Ü; Pinardi, N.; Artegiani, A.; Bergamasco, A.; et al. General circulation of the Eastern Mediterranean. Earth-Sci. Rev. 1992, 32, 285–309. [Google Scholar] [CrossRef]
- Pinardi, N.; Zavatarelli, M.; Adani, M.; Coppini, G.; Fratianni, C.; Oddo, P.; Simoncelli, S.; Tonani, M.; Lyubartsev, V.; Dobricic, S.; et al. Mediterranean Sea large-scale low-frequency ocean variability and water mass formation rates from 1987 to 2007: A retrospective analysis. Prog. Oceanogr. 2015, 132, 318–332. [Google Scholar] [CrossRef]
- Gačić, M.; Borzelli, G.E.; Civitarese, G.; Cardin, V.; Yari, S. Can internal processes sustain reversals of the ocean upper circulation? The Ionian Sea example. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Gačić, M.; Civitarese, G.; Eusebi Borzelli, G.L.; Kovačević, V.; Poulain, P.M.; Theocharis, A.; Menna, M.; Catucci, A.; Zarokanellos, N. On the relationship between the decadal oscillations of the northern Ionian Sea and the salinity distributions in the eastern Mediterranean. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Gačić, M.; Schroeder, K.; Civitarese, G.; Cosoli, S.; Vetrano, A.; Eusebi Borzelli, G.L. Salinity in the Sicily Channel corroborates the role of the Adriatic–Ionian Bimodal Oscillating System (BiOS) in shaping the decadal variability of the Mediterranean overturning circulation. Ocean Sci. 2013, 9, 83–90. [Google Scholar] [CrossRef]
- Civitarese, G.; Gačić, M.; Lipizer, M.; Eusebi Borzelli, G.L. On the impact of the Bimodal Oscillating System (BiOS) on the biogeochemistry and biology of the Adriatic and Ionian Seas (Eastern Mediterranean). Biogeosciences 2010, 7, 3987–3997. [Google Scholar] [CrossRef] [Green Version]
- Bessières, L.; Rio, M.H.; Dufau, C.; Boone, C.; Pujol, M.I. Ocean state indicators from MyOcean altimeter products. Ocean Sci. 2013, 9. [Google Scholar] [CrossRef]
- Sammari, C.; Millot, C.; Taupier-Letage, I.; Stefani, A.; Brahim, M. Hydrological characteristics in the Tunisia–Sardinia–Sicily area during spring 1995. Deep Sea Res. Part I Oceanogr. Res. Pap. 1999, 46, 1671–1703. [Google Scholar] [CrossRef]
- Ciappa, A.C. Surface circulation patterns in the Sicily Channel and Ionian Sea as revealed by MODIS chlorophyll images from 2003 to 2007. Cont. Shelf Res. 2009, 29, 2099–2109. [Google Scholar] [CrossRef]
- Capodici, F.; Ciraolo, G.; Cosoli, S.; Maltese, A.; Mallandrino, G. The synergy of water quality and sea surface currents data in determining the spatio-temporal evolution of large-scale circulation features. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XVI; International Society for Optics and Photonics: Amsterdam, The Netherlands, 2014; Volume 9239, p. 923927. [Google Scholar] [CrossRef]
- Cosoli, S.; Drago, A.; Ciraolo, G.; Capodici, F. Tidal currents in the Malta–Sicily Channel from high-frequency radar observations. Cont. Shelf Res. 2015, 109, 10–23. [Google Scholar] [CrossRef]
- Gauci, A.; Drago, A.; Abela, J. Gap Filling of the CALYPSO HF Radar Sea Surface Current Data through Past Measurements and Satellite Wind Observations. Int. J. Navig. Obs. 2016. [Google Scholar] [CrossRef]
- Capodici, F.; Cosoli, S.; Ciraolo, G.; Nasello, C.; Maltese, A.; Poulain, P.M.; Drago, A.; Azzopardi, J.; Gauci, A. Validation of HF radar sea surface currents in the Malta-Sicily Channel. Remote Sens. Environ. 2019, 225, 65–76. [Google Scholar] [CrossRef]
- CALYPSO: Real-Time Viewing of Sea Surface Currents in the Malta Channel. Available online: http://www.mongoos.eu/-/calypso-real-time-viewing-of-sea-surface-currents-in-the-malta-channel (accessed on 4 July 2018).
- Rio, M.H.; Pascual, A.; Poulain, P.M.; Menna, M.; Barceló, B.; Tintoré, J. Computation of a new mean dynamic topography for the Mediterranean Sea from model outputs, altimeter measurements and oceanographic in situ data. Ocean Sci. 2014, 10, 731–744. [Google Scholar] [CrossRef] [Green Version]
- Wentz, F.J.; Scott, J.; Hoffman, R.N.; Leidner, S.M.; Atlas, R.; Ardizzone, J. Remote Sensing Systems Cross-Calibrated Multi-Platform (CCMP) 6-Hourly Ocean Vector Wind Analysis Product on 0.25 deg Grid, Version 2.0, [Aug 2013–Jan 2015]. Remote Sensing Systems: Santa Rosa, CA. Available online: www.remss.com/measurements/ccmp (accessed on 5 December 2017).
- Atlas, R.; Hoffman, R.N.; Ardizzone, J.; Leidner, S.M.; Jusem, J.C.; Smith, D.K.; Gombos, D. A cross-calibrated, multiplatform ocean surface wind velocity product for meteorological and oceanographic applications. Bull. Am. Meteorol. Soc. 2011, 92, 157–174. [Google Scholar] [CrossRef]
- Kundu, P.K. Ekman veering observed near the ocean bottom. J. Phys. Oceanogr. 1976, 6, 238–242. [Google Scholar] [CrossRef]
- Sanderson, B.G. Structure of an eddy measured with drifters. J. Geophys. Res. Oceans 1995, 100, 6761–6776. [Google Scholar] [CrossRef]
- Malanotte-Rizzoli, P.; Artale, V.; Borzelli-Eusebi, G.L.; Brenner, S.; Crise, A.; Gačić, M.; Kress, N.; Marullo, S.; Ribera d’Alcalà, M.; Sofianos, S.; et al. Physical forcing and physical/biochemical variability of the Mediterranean Sea: A review of unresolved issues and directions for future research. Ocean Sci. 2014, 10, 281–322. [Google Scholar] [CrossRef]
- Jebri, F.; Birol, F.; Zakardjian, B.; Bouffard, J.; Sammari, C. Exploiting coastal altimetry to improve the surface circulation scheme over the central Mediterranean Sea. J. Geophys. Res. Oceans 2016, 121, 4888–4909. [Google Scholar] [CrossRef] [Green Version]
- Jebri, F.; Zakardjian, B.; Birol, F.; Bouffard, J.; Jullion, L.; Sammari, C. Interannual variations of surface currents and transports in the Sicily channel derived from coastal altimetry. J. Geophys. Res. Oceans 2017, 122, 8330–8353. [Google Scholar] [CrossRef]
- Drago, A.; Sorgente, R.; Ribotti, A. A high resolution hydrodynamic 3-D model simulation of the Malta shelf area. Ann. Geophys. 2003, 21, 323–344. [Google Scholar] [CrossRef]
- Manzella, G.M.; Gasparini, G.P.; Astraldi, M. Water exchange between the eastern and western Mediterranean through the Strait of Sicily. Deep Sea Res. Part A Oceanogr. Res. Pap. 1988, 35, 1021–1035. [Google Scholar] [CrossRef]
- Pujol, M.I.; Larnicol, G. Mediterranean Sea eddy kinetic energy variability from 11 years of altimetric data. J. Mar. Syst. 2005, 58, 121–142. [Google Scholar] [CrossRef]
- Jordi, A.; Wang, D.P. Mean dynamic topography and eddy kinetic energy in the Mediterranean Sea: Comparison between altimetry and a 1/16 degree ocean circulation model. Ocean Model. 2009, 29, 137–146. [Google Scholar] [CrossRef]
- Paduan, J.D.; Washburn, L. High-frequency radar observations of ocean surface currents. Annu. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef]
- Paduan, J.D.; Graber, H.C. Introduction to high-frequency radar: Reality and myth. Oceanography 1997, 10, 36–39. [Google Scholar] [CrossRef]








| HFR | Altimetry | MODIS | MODIS | CCMP | |
|---|---|---|---|---|---|
| Variable | Sea surface velocities | ADT, geostrophic currents | SST | CHL-a | Wind stress |
| Frequency | Hourly | Daily | Monthly | Monthly | 6-Hourly |
| Spatial resolution | 1 km | 1/8° | 4.6 km | 4.6 km | 1/4° |
| Vertical integration | 1 m | surface | surface | surface | 10 m above sea level |
| Study period | 1 Aug 2012–31 Jan 2015 | 1 Jan 1993–31 Dec 2015 | Jan–Dec 2013 | Jan–Dec 2013 | 1 Aug 2013–31 Jan 2015 |
| Time Series | Correlation Coefficient | Phase Angle |
|---|---|---|
| Radar to Wind | p1 = 0.3848 | θ1 = 34.1950 |
| p2 = 0.3586 | θ2 = 38.9211 | |
| p3 = 0.3515 | θ3 = 40.1103 | |
| p4 = 0.3554 | θ4 = 23.1126 | |
| p5 = 0.3249 | θ5 = 44.4289 | |
| p6 = 0.2475 | θ6 = 53.4827 | |
| p7 = 0.2971 | θ7 = 33.9368 | |
| Residual to Wind | p1 = 0.4669 | θ1 = 37.9316 |
| p2 = 0.3749 | θ2 = 38.9211 | |
| p3 = 0.4030 | θ3 = 49.3575 | |
| p4 = 0.4424 | θ4 = 31.4394 | |
| p5 = 0.3145 | θ5 = 45.5068 | |
| p6 = 0.2920 | θ6 = 59.7371 | |
| p7 = 0.3202 | θ7 = 42.1535 | |
| Geostrophic to Wind | p1 = 0.0566 | θ1 = −101.4697 |
| p2 = 0.0230 | θ2 = −14.4575 | |
| p3 = 0.1082 | θ3 = −86.2521 | |
| p4 = 0.0876 | θ4 = −97.4430 | |
| p5 = 0.0511 | θ5 = −34.6377 | |
| p6 = 0.0961 | θ6 = −99.0749 | |
| p7 = 0.0712 | θ7 = −91.4430 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reyes Suarez, N.C.; Cook, M.S.; Gačić, M.; Paduan, J.D.; Drago, A.; Cardin, V. Sea Surface Circulation Structures in the Malta-Sicily Channel from Remote Sensing Data. Water 2019, 11, 1589. https://doi.org/10.3390/w11081589
Reyes Suarez NC, Cook MS, Gačić M, Paduan JD, Drago A, Cardin V. Sea Surface Circulation Structures in the Malta-Sicily Channel from Remote Sensing Data. Water. 2019; 11(8):1589. https://doi.org/10.3390/w11081589
Chicago/Turabian StyleReyes Suarez, Nydia C., Michael S. Cook, Miroslav Gačić, Jeffrey D. Paduan, Aldo Drago, and Vanessa Cardin. 2019. "Sea Surface Circulation Structures in the Malta-Sicily Channel from Remote Sensing Data" Water 11, no. 8: 1589. https://doi.org/10.3390/w11081589
APA StyleReyes Suarez, N. C., Cook, M. S., Gačić, M., Paduan, J. D., Drago, A., & Cardin, V. (2019). Sea Surface Circulation Structures in the Malta-Sicily Channel from Remote Sensing Data. Water, 11(8), 1589. https://doi.org/10.3390/w11081589






