Modelling of Flow Parameters through Subsurface Drainage Modules for Application in BIOECODS
Abstract
:1. Introduction
2. Theory and Governing Equations
3. Numerical Simulation Setup
3.1. Geometry Creation and Model Setup
3.2. Meshing and Sensitivity Analysis
3.3. Boundary Conditions and Solution Initialization
4. Design of the Validation Experiments in the Laboratory
4.1. Estimation of Manning’s Coefficient
4.2. Froude and Reynold’s Number (Fr, Re)
5. Results and Discussions
5.1. Numerical Model Validation
5.2. Free Flow without Module and Flow with Module
5.3. Effects of the Module on Mannng’s Roughness
5.4. Contour Plots of Velocity and Flow Pattern Visualization
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BIOECODS | Bio-Ecological Drainage System |
| REDAC | River Engineering and Urban Drainage Research Centre |
| DID | Department of Irrigation and Drainage |
| FWM | Flow With Module |
| FFWM | Free Flow Without model |
| CFD | Computational Fluid Dynamics |
| VOF | Volume Of Fluid |
| FAVOR | Fractional Area/Volume Obstacle Representation |
| RNG | Re-Normalisation Group |
| STL | Stereolithography |
| CGS | Centimetre–Gram–Second system |
| MB | Mesh Block |
| DS | Downstream |
| US | Upstream |
| DSV | Downstream Velocity |
| GFO | Gate Fully Opened |
| USM | Universiti Sains Malaysia |
| Num | Numerical |
| Exp | Experimental |
| Vel | Velocity |
| Nomenclature | |
| The following nomenclature are used in this manuscript: | |
| fluid volume function | |
| p | pressure |
| Body acceleration in x coordinate | |
| Body acceleration in y coordinate | |
| Body acceleration in z coordinate | |
| Energy dissipation rate | |
| k | Turbulence kinetic energy |
| t | Time (s) |
| Coordinate in the i axis | |
| Dynamic viscosity | |
| Turbulent dynamic viscosity | |
| Production of TKE | |
| v | Velocity (cm/s) |
| Viscous accelerations in the x direction | |
| Viscous accelerations in the y direction | |
| Viscous accelerations in the z direction | |
References
- Abdurrasheed, A.S.I.; Yusof, K.W.; Takaijudin, H.B.; Ghani, A.A.; Muhammad, M.M.; Sholagberu, A.T. Advances and Challenging Issues in Subsurface Drainage Module Technology and BIOECODS: A Review. In Proceedings of the International Conference on Civil, Offshore & Environmental Engineering (ICCOEE2018), Kuala Lumpur, Malaysia, 13–15 August 2018; Volume 203, p. 07005. [Google Scholar]
- Abdurrasheed, A.S.I.; Yusof, K.W.; Takaijudin, H.B.; Ab, A.; Iskandar, B.S. Effects of backwater on hydraulic performance evaluation of rainsmart modules in sustainable drainage systems. In Proceedings of the International Conference on Water Resources, Langkawi, Malaysia, 27–28 November 2018. [Google Scholar]
- Ainan, A.; Zakaria, N.A.; Ghani, A.A.; Abdullah, R.; Sidek, L.M.; Yusof, M.F.; Wong, L.P. Peak flow attenuation using ecological swale and dry pond. Adv. Hydro-Sci. Eng. 2003, 6, 1–9. [Google Scholar]
- Barber, M.E.; King, S.G.; Yonge, D.R.; Hathhorn, W.E. Ecology ditch: A best management practice for storm water runoff mitigation. J. Hydrol. Eng. 2003, 8, 111–122. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Mikkelsen, P.S. SUDS, LID, BMPs, WSUD and more—The evolution and application of terminology surrounding urban drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Hammond, M.J.; Chen, A.S.; Djordjević, S.; Butler, D.; Mark, O. Urban flood impact assessment: A state-of-the-art review. Urban Water J. 2015, 12, 14–29. [Google Scholar] [CrossRef]
- Zakaria, N.A.; Ab Ghani, A.; Abdullah, R.; Mohd. Sidek, L.; Ainan, A. Bio-ecological drainage system (BIOECODS) for water quantity and quality control. Int. J. River Basin Manag. 2003, 1, 237–251. [Google Scholar] [CrossRef]
- Benisi Ghadim, H.; Sai Hin, L.; Hooi Bu, C.; Jie Chin, R. Effectiveness of BIOECODS for peak flow attenuation: an appraisal using InfoWorks SD. Hydrol. Sci. J. 2017, 62, 421–430. [Google Scholar] [CrossRef]
- Muhammad, M.M.; Yusof, K.W.; Mustafa, M.R.; Ghani, A.A. Hydraulic assessment of grassed swale as bioengineered channel. In Engineering Challenges for Sustainable Future; ROUTLEDGE in Association with GSE Research: Kuala Lumpur, Malaysia, 2016; Volume 273, pp. 273–278. [Google Scholar]
- Ahmad, N.A.; Ghani, A.A.; Zakaria, N.A. Hydraulic Characteristic for Flow in Swales. 2011. Available online: http://redac.eng.usm.my/html/publish/2011_23.pdf (accessed on 25 July 2019).
- Lai, S.H.; Kee, L.C.; Zakaria, N.A.; Ghani, A.A.; Chang, C.K.; Leow, C.S. Flow Pattern and Hydraulic Characteristic for Subsurface Drainage Module. In Proceedings of the International Conference on Water Resources (ICWR 2009), Kedah, Malaysia, 26–27 May 2009. [Google Scholar]
- Muhammad, M.M.; Yusof, K.W.; Mustafa, M.R.U.; Zakaria, N.A.; Ghani, A.A. Artificial neural network application for predicting drag coefficient in flexible vegetated channels. J. Telecommun. Electron. Comput. Eng. (JTEC) 2018, 10, 99–102. [Google Scholar]
- Zakaria, N.A.; Takara, K.; Abdullah, R.; Sidek, L.M.; Ghani, A.A. Bio-Ecological Drainage Systems (Bioecods): An Integrated Approach for Urban Water Environmental Planning; International Islamic University Malaysia: Kuala Lumpur, Malaysia, 2004. [Google Scholar]
- Kee, L.C.; Zakaria, N.A.; Lau, T.L.; Chang, C.K.; Ghani, A.A. Determination of Manning’sn for Subsurface Modular Channel. 2011. Available online: http://redac.eng.usm.my/html/publish/2011_25.pdf (accessed on 25 July 2019).
- Muhammad, M.; Yusof, K.; Mustafa, M.; Zakaria, N.; Ghani, A.A. Hydraulic performance of sub-surface drainage module. In Proceedings of the IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017; pp. 6059–6066. [Google Scholar]
- Pradhan, A.; Khatua, K.K. Assessment of roughness coefficient for meandering compound channels. KSCE J. Civ. Eng. 2017, 22, 2010–2022. [Google Scholar] [CrossRef]
- Sánchez-Beltrán, H.; Rodríguez, C.M.; Triviño, J.B.; Iglesias-Rey, P.L.; Valderrama, J.S.; Martínez-Solano, F.J. Characterization of modular deposits for urban drainage networks using CFD techniques. Procedia Eng. 2017, 186, 84–92. [Google Scholar] [CrossRef]
- Faram, M.G.; Guymer, I.; Saul, A.J. Assessment of modular block stormwater storage systems. In Proceedings of the NOVATECH: 5th International Conference on Sustainable Techniques and Strategies in Urban Water Management, Lyon, France, 6–10 June 2004; pp. 235–242. [Google Scholar]
- Jarman, D.S.; Faram, M.G.; Butler, D.; Tabor, G.; Stovin, V.R.; Burt, D.; Throp, E. Computational Fluid Dynamics as a Tool for Urban Drainage System Analysis: A Review of Applications and Best Practice. 2008. Available online: http://hdl.handle.net/10036/4259 (accessed on 25 July 2019).
- Savage, B.M.; Crookston, B.M.; Paxson, G.S. Physical and numerical modeling of large headwater ratios for a 15 labyrinth spillway. J. Hydraul. Eng. 2016, 142, 04016046. [Google Scholar] [CrossRef]
- Choufu, L.; Abbasi, S.; Pourshahbaz, H.; Taghvaei, P.; Tfwala, S. Investigation of Flow, Erosion, and Sedimentation Pattern around Varied Groynes under Different Hydraulic and Geometric Conditions: A Numerical Study. Water 2019, 11, 235. [Google Scholar] [CrossRef]
- Lo, D.C.; Liou, J.S.; Chang, S. Hydrodynamic performances of air-water flows in gullies with and without swirl generation vanes for drainage systems of buildings. Water 2015, 7, 679–696. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sousa, J.P.M.; Moya, R.A.C.; Prohasky, D.; Vaz, C.E.V. Empirical analysis of three wind simulation tools to support urban planning in early stages of design. Blucher Des. Proc. 2015, 2, 363–370. [Google Scholar]
- Li, G.; Li, X.; Ning, J.; Deng, Y. Numerical Simulation and Engineering Application of a Dovetail-Shaped Bucket. Water 2019, 11, 242. [Google Scholar] [CrossRef]
- Jarman, D.S.; Faram, M.G.; Tabor, G.; Butler, D. A review of the opportunities presented through the application of Computational Fluid Dynamics (CFD) to water management challenges. In Proceedings of the Water Management Challenges in Global Change, CCWI2007 and SUWM2007 Conference, Leicester, UK, 3–5 September 2007. [Google Scholar]
- Bayon, A.; Valero, D.; García-Bartual, R.; López-Jiménez, P.A. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Kim, S.D.; Lee, H.J.; An, S.D. Improvement of hydraulic stability for spillway using CFD model. Int. J. Phys. Sci. 2010, 5, 774–780. [Google Scholar]
- Mustaffa, N.; Ahmad, N.A.; Razi, M.A.M. Variations of roughness coefficients with flow depth of grassed swale. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; p. 012082. [Google Scholar]
- Zahabi, H.; Torabi, M.; Alamatian, E.; Bahiraei, M.; Goodarzi, M. Effects of Geometry and Hydraulic Characteristics of Shallow Reservoirs on Sediment Entrapment. Water 2018, 10, 1725. [Google Scholar] [CrossRef]
- Choo, K.L. Determination of Flow Resistance in Modular Open Channel. Master’s Thesis, River Engineering and Urban Drainage Research Centre REDAC, Parit Buntar, Malaysia, 2011. [Google Scholar]
- Chen, Y.C.; Kao, S.P.; Lin, J.Y.; Yang, H.C. Retardance coefficient of vegetated channels estimated by the Froude number. Ecol. Eng. 2009, 35, 1027–1035. [Google Scholar] [CrossRef]


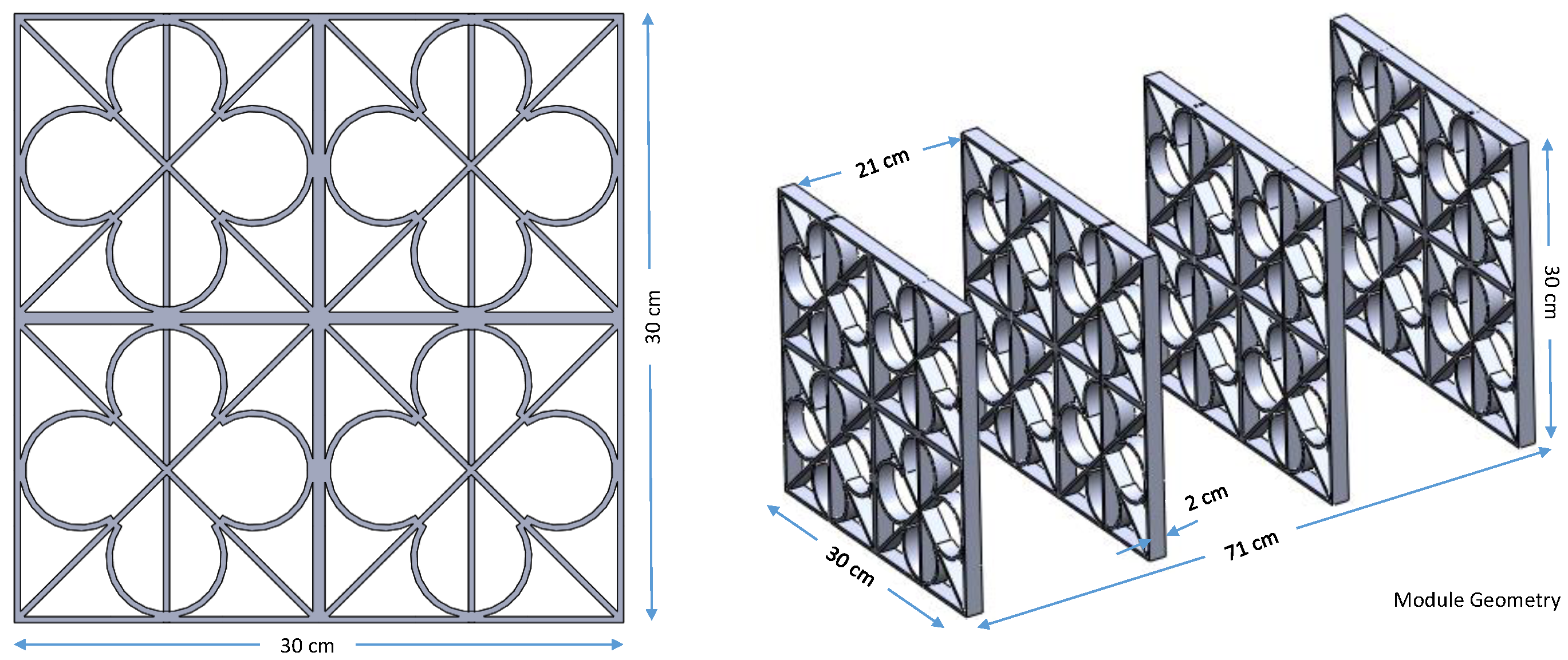









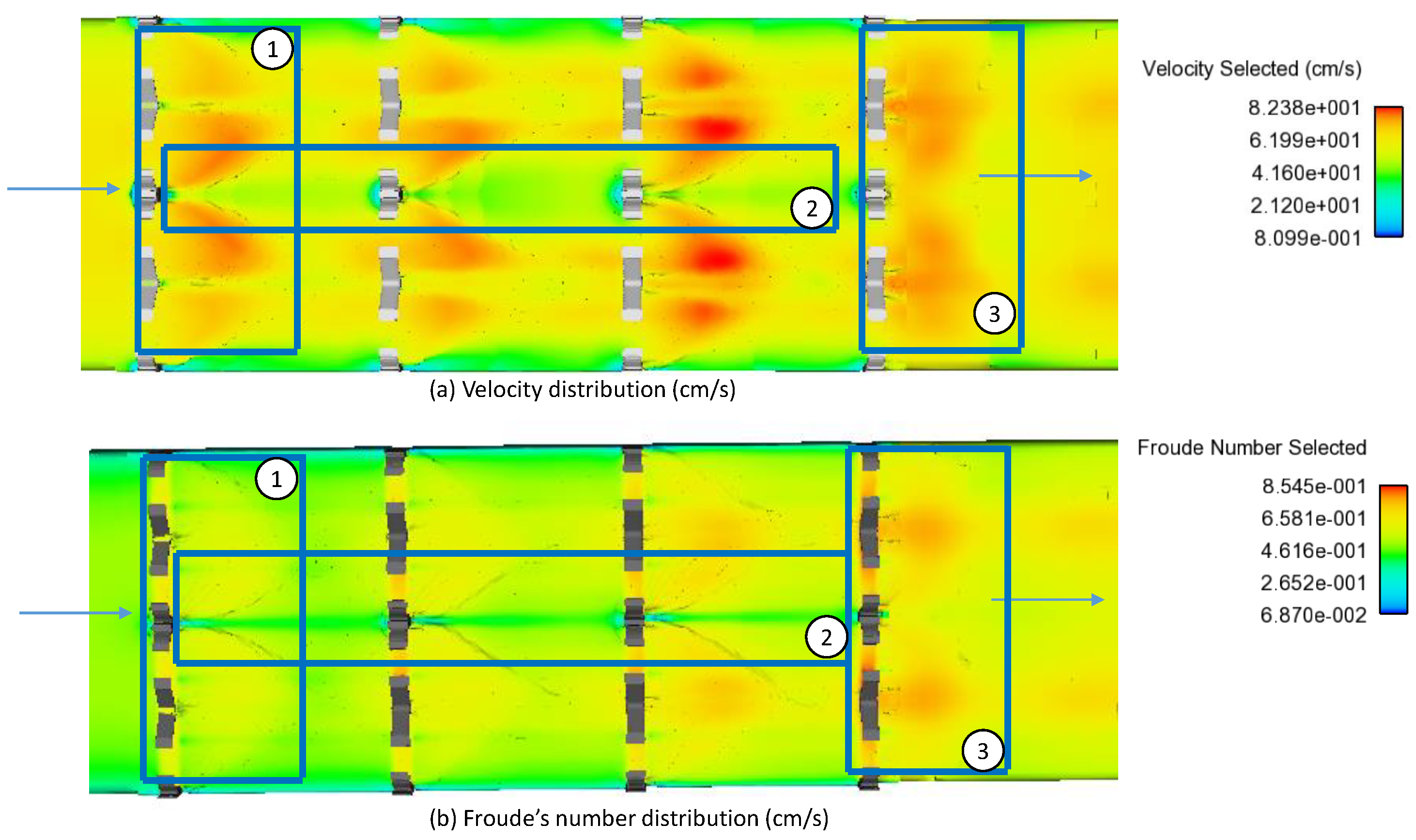
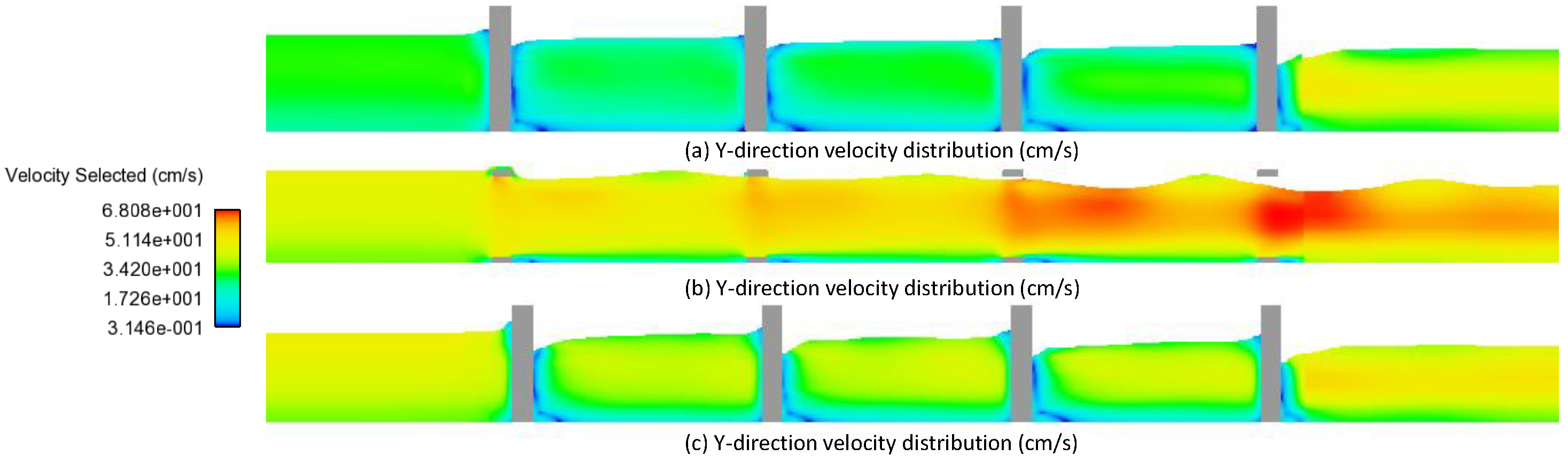

| Test Number | Mesh Size | Total Grid (Millions) | DSV (cm/s) |
|---|---|---|---|
| 1 | 0.26 | 1.78 | 45.30 |
| 2 | 0.21 | 3.41 | 46.50 |
| 3 | 0.17 | 6.41 | 48.60 |
| Flow Parameter | Working Conditions | ||||||
|---|---|---|---|---|---|---|---|
| FFWM | FWM | ||||||
| Exp. | Num. | % Error | Exp. | Num. | % Error | ||
| US | 51.6 | 50.40 | 2.38 | 42.00 | 43.50 | 3.45 | |
| Flow Velocity (cm/s) | DS | 52.5 | 53.18 | 1.28 | 44.50 | 46.50 | 4.30 |
| US | 7.6 | 7.71 | 1.43 | 7.65 | 7.75 | 1.29 | |
| Flow Depth (cm) | DS | 6.38 | 6.52 | 2.15 | 6.30 | 6.50 | 3.08 |
| Case | Flow Depth (cm) | Average Vel (cm/s) | Wetted Perimeter (cm) | Hydraulic Radius (cm) | Manning’s Roughness (s/cm1/3) | ||
|---|---|---|---|---|---|---|---|
| FFWM | Experimental | US | 7.60 | 51.60 | 45.20 | 5.04 | 0.06 |
| DS | 6.38 | 52.50 | 42.76 | 4.48 | 0.05 | ||
| Numerical | US | 7.71 | 50.40 | 45.42 | 5.09 | 0.06 | |
| DS | 6.52 | 53.18 | 43.14 | 4.54 | 0.05 | ||
| FWM | Experimental | US | 7.65 | 42.00 | 45.30 | 5.07 | 0.07 |
| DS | 6.30 | 44.50 | 42.60 | 4.44 | 0.06 | ||
| Numerical | US | 7.75 | 43.50 | 45.50 | 5.11 | 0.07 | |
| DS | 6.50 | 46.50 | 43.00 | 4.53 | 0.06 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sa’id Abdurrasheed, A.; Wan Yusof, K.; Hamid Hussein Alqadami, E.; Takaijudin, H.; Ab. Ghani, A.; Muhammad, M.M.; Sholagberu, A.T.; Zainalfikry, M.K.; Osman, M.; Shihab Patel, M. Modelling of Flow Parameters through Subsurface Drainage Modules for Application in BIOECODS. Water 2019, 11, 1823. https://doi.org/10.3390/w11091823
Sa’id Abdurrasheed A, Wan Yusof K, Hamid Hussein Alqadami E, Takaijudin H, Ab. Ghani A, Muhammad MM, Sholagberu AT, Zainalfikry MK, Osman M, Shihab Patel M. Modelling of Flow Parameters through Subsurface Drainage Modules for Application in BIOECODS. Water. 2019; 11(9):1823. https://doi.org/10.3390/w11091823
Chicago/Turabian StyleSa’id Abdurrasheed, Abdurrasheed, Khamaruzaman Wan Yusof, Ebrahim Hamid Hussein Alqadami, Husna Takaijudin, Aminuddin Ab. Ghani, Muhammad Mujahid Muhammad, Abdulkadir Taofeeq Sholagberu, Muhammad Kashfy Zainalfikry, Manal Osman, and Mohammed Shihab Patel. 2019. "Modelling of Flow Parameters through Subsurface Drainage Modules for Application in BIOECODS" Water 11, no. 9: 1823. https://doi.org/10.3390/w11091823
APA StyleSa’id Abdurrasheed, A., Wan Yusof, K., Hamid Hussein Alqadami, E., Takaijudin, H., Ab. Ghani, A., Muhammad, M. M., Sholagberu, A. T., Zainalfikry, M. K., Osman, M., & Shihab Patel, M. (2019). Modelling of Flow Parameters through Subsurface Drainage Modules for Application in BIOECODS. Water, 11(9), 1823. https://doi.org/10.3390/w11091823






