Impact of North Atlantic Oscillation on the Snowpack in Iberian Peninsula Mountains

Abstract

The North Atlantic Oscillation (NAO) is considered to be the main atmospheric factor explaining the winter climate and snow evolution over much of the Northern Hemisphere. However, the absence of long-term snow data in mountain regions has prevented full assessment of the impact of the NAO at the regional scales, where data are limited. In this study, we assessed the relationship between the NAO of the winter months (DJFM-NAO) and the snowpack of the Iberian Peninsula. We simulated temperature, precipitation, and snow data for the period 1979–2014 by dynamic downscaling of ERA-Interim reanalysis data, and correlated this with the DJFM-NAO for the five main mountain ranges of the Iberian Peninsula (Cantabrian Range, Central Range, Iberian Range, the Pyrenees, and the Sierra Nevada). The results confirmed that negative DJFM-NAO values generally occur during wet and mild conditions over most of the Iberian Peninsula. Due to the direction of the wet air masses, the NAO has a large influence on snow duration and the annual peak snow water equivalent (peak SWE) in most of the mountain ranges in the study, mostly on the slopes south of the main axis of the ranges. In contrast, the impact of NAO variability is limited on north-facing slopes. Negative (positive) DJFM-NAO values were associated with longer (shorter) duration and higher (lower) peak SWEs in all mountains analyzed in the study. We found marked variability in correlations of the DJFM-NAO with snow indices within each mountain range, even when only the south-facing slopes were considered. The correlations were stronger for higher elevations in the mountain ranges, but geographical longitude also explained the intra-range variability in the majority of the studied mountains.

1. Introduction

The North Atlantic Oscillation (NAO) is a mode of atmospheric circulation, and its index value is calculated as the difference in atmospheric pressure for the dipole centered on Iceland and the Azores Islands [1]. The NAO is considered to be the main pattern of climate variability in the Northern Hemisphere [2,3], especially during winter. Negative (positive) NAO phases generally are related to weak (strong) westerly winds to Europe, leading to positive (negative) anomalies of temperature and precipitation in Southern (Northern) Europe [4,5,6]. It is also clear that NAO anomalies are more related with the winter precipitation variability than with the interannual winter temperature fluctuations [7,8].

As NAO fluctuations are related with the winter temperature and precipitation over much of the Northern Hemisphere, it is unsurprising that many studies have reported that the NAO is a good indicator of the duration and depth of the snowpack. This is the case for Mediterranean mountains [7], the Pyrenees [9,10], the Alps [11,12,13], Nordland [14], Western Poland [15], Bulgaria [16], and the Russian Arctic [17]. At wider spatial scales, Henderson and Leathers [18] associated negative (positive) phases of the NAO with expansion (reduction) of the snow cover in Europe. Keylock [19], Jomelli et al. [20], and García et al. [21] also found significant relationships between NAO phases and the frequency of avalanches in Iceland, the French Alps, and the Pyrenees, respectively. The main value of understanding the relationship between snow and interannual fluctuations of the snowpack is that, despite the stochastic nature of the NAO, the statistic and dynamic seasonal forecasting of this phenomenon has been very promising, to the point of achieving useful levels of predictability [22,23,24]. Improving predictions of snowpack anomalies has a clear applied importance because of the direct impact of the snowpack on water availability, plant and animal phenology, and a wide range of economic activities in mountain and downstream areas [25,26]. In addition, a good understanding of the relationship between the NAO and the snowpack is necessary to accurately interpret the reported trends in the snowpack over recent decades, as a strong correlation has been observed between trends in the snowpack and the duration of dominant NAO anomalies [27].

Although studies have provided clear insights into how the NAO is related with the snowpack in many mountains and cold regions of Europe, at the local scale, many uncertainties about its effects remain. This is because mountain ranges present a topographical barrier to main wind flows, causing shadow effects in the main atmospheric circulation patterns [28,29]. In addition, elevation also affects the impact relationship of NAO with snow in mountain areas because of its greater relationship with precipitation relative to temperature. Thus, at high elevations, interannual variability of the snowpack is mainly driven by precipitation, so such areas are expected to exhibit a stronger response to the NAO than lower elevation sites, where temperature has a major role in snow variability [30]. López-Moreno and Vicente-Serrano [9] suggested that this phenomenon is the main explanation for the control of NAO on the snowpack in areas above 2000 m a.s.l. in the Spanish Pyrenees. The spatial variability in the relationship between the NAO and snow cover makes it difficult to assess NAO effects in many areas, because of the limited data on snowpacks, especially in mountain areas at the highest elevations.

The aim of this study is to extend knowledge of the NAO and snowpack relationship in the main mountainous regions of the Iberian Peninsula. This is one of the highest elevation regions of Europe, where the accumulation of snow is of major importance to water resource availability [31,32], and on which many economically important activities, including agriculture, forestry, and winter tourism, depend [33,34]. Because of the limited data on snowpacks in the Iberian Peninsula, we used a recently developed database on snow water equivalent (SWE) and snow depth (SD) for the main mountain areas of the Iberian Peninsula [35], to enable us to undertake the first detailed assessment of the relationship between the winter (December, January, February, and March) NAO (DJFM-NAO) on the interannual variability in the peak SWE and the duration of snow on the ground.

2. Study Area

The Iberian Peninsula is located at the southwest edge of Europe, between latitudes 36° N and 44° N. It is an area of contrasting climate, as a consequence of Atlantic and Mediterranean influences. The topography is characterized by two main plateaus surrounded by mountainous areas and comprises five main mountain ranges that have seasonal snow cover, including the Cantabrian Range, the Central Range, the Iberian Range, the Pyrenees, and the Sierra Nevada. The highest elevation (3478 m a.s.l.) is Mulhacén Peak in the Sierra Nevada, followed by Aneto Peak in the Pyrenees (3404 m a.s.l.). The other mountainranges exceed 2000 m a.s.l., reaching 2648 m a.s.l. (Torrecerredo Peak) in the Cantabrian Range, 2596 m a.s.l. (Almanzor Peak) in the Central Range, and 2314 m a.s.l. in the Iberian Range.

The spatial distribution of these mountain ranges (Figure 1), which extend within Spain from west to east at differing latitudes and distances to the sea, results in wide snowpack variability at similar elevations, even within the same mountain range [36].

3. Methods

3.1. NAO Index and Temperature and Precipitation Patterns

The NAO index, which is defined as the normalized sea surface pressure (SLP) difference between the Icelandic low pressure and the Azores high pressure regions [1], is a widely used indicator of the atmospheric situation over the North Atlantic. In this study the NAO index was calculated from the SLP difference between the positions 65° N 20° W (near Reykjavik, Iceland) and 35° N 5° W (near Gibraltar Straight), following the procedure and recommendations of Osborn et al. [37], Trigo et al. [38], and Fernández-González et al. [39], among others. The SLP data were downloaded from the NCAR SLP reanalysis dataset (https://climatedataguide.ucar.edu/climate-data/ncar-sea-level-pressure; last accessed 20 October 2019). The normalization was performed in relation to normal values for the study period 1979–2015.

The accumulated winter precipitation and the minimum and maximum averaged daily temperatures were linearly correlated with the DJFM-NAO index. The temperature and precipitation meteorological variables were obtained from the regional atmospheric simulation described below. In this study the winter period was considered to encompass the months December, January, February, and March.

3.2. Snowpack Database and Statistical Analysis

The SWE and SD database used in this study was developed using the weather research and forecast (WRF) model [40], forced using the ERA-Interim reanalysis [41,42]. The spatial resolution of the atmospheric simulations was ~10 km, and the simulations covered the period 1979–2014 [43]. The surface meteorological outputs of the simulations were subsequently projected to various elevation bands that differed by 100 m, using an array of psychrometric and radiative formulae and lapse rates [35]. The new meteorological data were used as forcing data for the physically based energy and mass balance snowpack factorial snow model (FSM) [44]. The final product was a semi-distributed daily SWE and SD database. Alonso-González et al. [35] validated the database, using in situ observations and remote sensing information, and were able to reproduce the spatial and temporal patterns of the snowpack over the entire Iberian Peninsula.

We computed the annual peak SWE and the annual snowpack duration for each elevation band from the snowpack database. These values were linearly correlated with the averaged DJFM-NAO, along with the Pearson’s R value. To identify different responses of the snowpack on the windward and leeward sides of each mountain range, we separated the correlation values for each mountain range along the principal longitudinal axis, which runs generally from west to east. The Wilcoxon–Mann–Whitney test [45] was used to identify statistical differences between the groupings of north- and south-facing slopes.

Following calculation of the Pearson’s R values between the DJFM-NAO and the snow indices, we correlated the value with the elevation and geographical longitude, to investigate the spatial patterns of DJFM-NAO influence on the snowpack within each mountain range.

Finally, to highlight the spatial patterns of the correlation between the DJFM-NAO and the snow indices, 500 random samples of 100 values of the Pearson’s R values were calculated. We performed partial correlations between snow indices and longitude (removing the effect of the elevation), and elevation (removing the effect of the longitude). This recursive resampling of the dataset was performed to avoid using excessively big samples, which can lead to overestimation of statistically significant correlations and has associated problems caused by spatial autocorrelation [46,47].

4. Results and Discussion

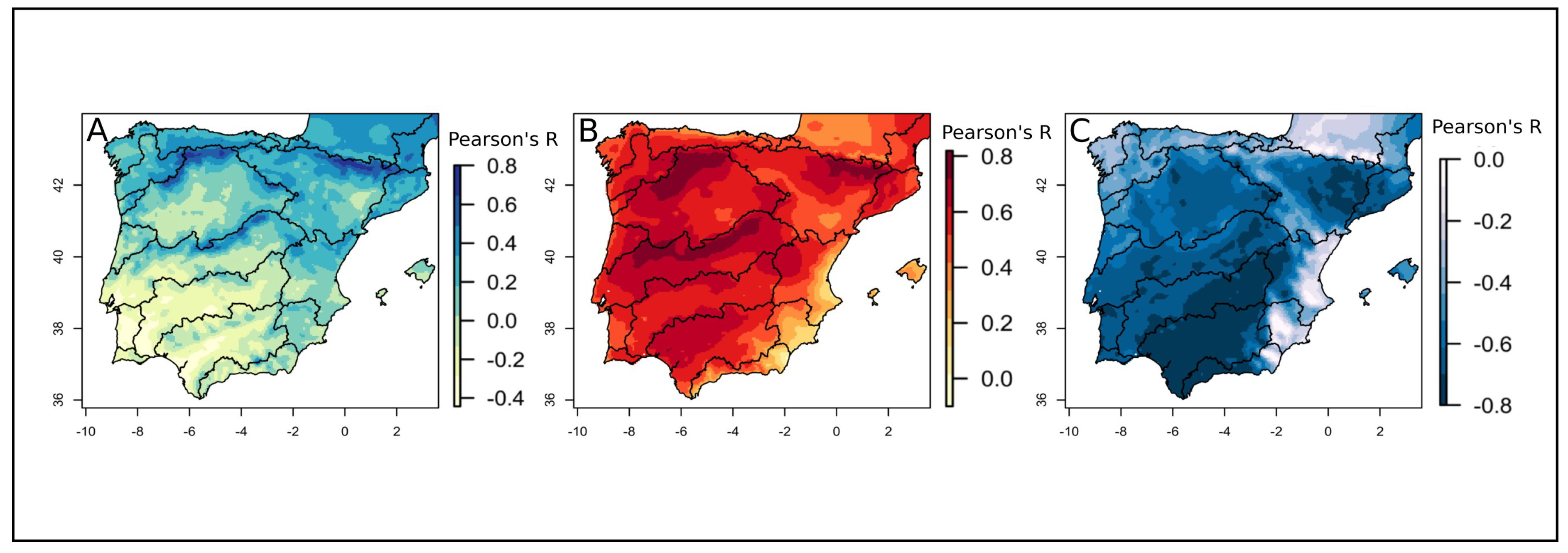
4.1. Relationship between the DJFM-NAO and Temperature and Precipitation

Except for small areas on the Mediterranean coast, most of the Iberian Peninsula showed positive correlations between the NAO and the maximum temperature (Figure 2), being consistent with previous studies in the Mediterranean mountain ranges [48]. A clear difference was evident between the north- and south-facing slopes along the main longitudinal axis of the mountain ranges, including in the Central Range (north approximately 0.5, south approximately 0.8) and Cantabrian Range (north approximately 0.4, south approximately 0.8). This result is consistent with previous studies based on meteorological observations [49], and can be explained by the Foehn effect on the northern slopes during negative NAO phases [50]. This phenomenon is very common in the Cantabrian and Pyrenean ranges during DJFM-NAO negative phases.

4.2. Relationship between the Winter NAO and Temperature and Precipitation

High elevation areas generally showed strong positive correlations, which we attribute to the fact that mountain climates are strongly related to the movement of air masses [51]. Thus, during positive NAO phases, the maximum air temperature on the slopes and summits increase, and during negative NAO phases, the lapse rates increase and the summits cool, although the existence of southern fluxes [28].

The correlations between the DJFM-NAO and minimum temperatures tended to be positive, but showed a progressive decrease towards the southwest and lower areas of the main hydrological basins. In the valley bottoms the correlations became negative, as reported by del Río et al. [52] for the Duero basin. This progressive change is because of the increased cloudiness during negative NAO phases in this Atlantic southwest area, related to the associated southern and western cyclonic flows. The cloudiness slows the nighttime reduction in the air temperature [53], but this effect does not penetrate fully inland to the north, making the signal less obvious.

The DJFM-NAO and temperature were generally positively correlated. During negative DJFM-NAO phases the occurrence of more frequent cyclonic circulations brings lower temperatures than during anticyclonic periods, but the most frequent wind directions during negative DJFM-NAO phases has a clear Atlantic influence, which generally brings mild temperatures during snowfall events. This causes a marked increase of the elevation where precipitation changes from liquid to solid phase compared to other synoptic situations over Iberia [28,54].

The correlation between monthly accumulated precipitation and the NAO index was negative for the entire Iberian Peninsula, as previously reported by other authors over central Portugal [38] or in the northwestern part of Spain [39], as well as in the main mountain ranges of the Iberian Peninsula [48] (Figure 2); although, for small Mediterranean and Cantabrian areas, the correlations were negligible [55,56]. Southwest areas showed the greatest negative correlations (values of approximately 0.8), which is consistent with the findings of Muñoz-Díaz and Rodrigo [57], where they found different areas of correlation of the precipitation with the NAO index over the Iberian Peninsula and, more specifically, Queralt et al. [58] about extreme precipitation events associated with DJFM-NAO phases.

There was differentiation between the highly correlated southern slopes and the less correlated northern slopes, as previously reported for the Spanish Pyrenees by Vada et al. [59] and Buisan et al. [60], and for the Alps by Stefanicki et al. [51]. This differentiation was especially evident for the mountain ranges located at higher elevations (i.e., the Cantabrian Range and the Pyrenees).

The differences between the southward and northward slopes of the mountain ranges were clear for the Pyrenees (north approximately 0.1; south approximately 0.7), the Cantabrian Range (north approximately 0.3; south approximately 0.6), and the Iberian Range (north approximately 0.2; south approximately 0.6). The differences were less marked for the Central Range (north approximately 0.4; south approximately 0.5), and for the Sierra Nevada were almost negligible. This effect is caused likely by the geographical position of Sierra Nevada and Central Range, and its limited potential to be an effective topographical barrier against the westerly and southwesterly wind directions associated to negative DJFM-NAO phases.

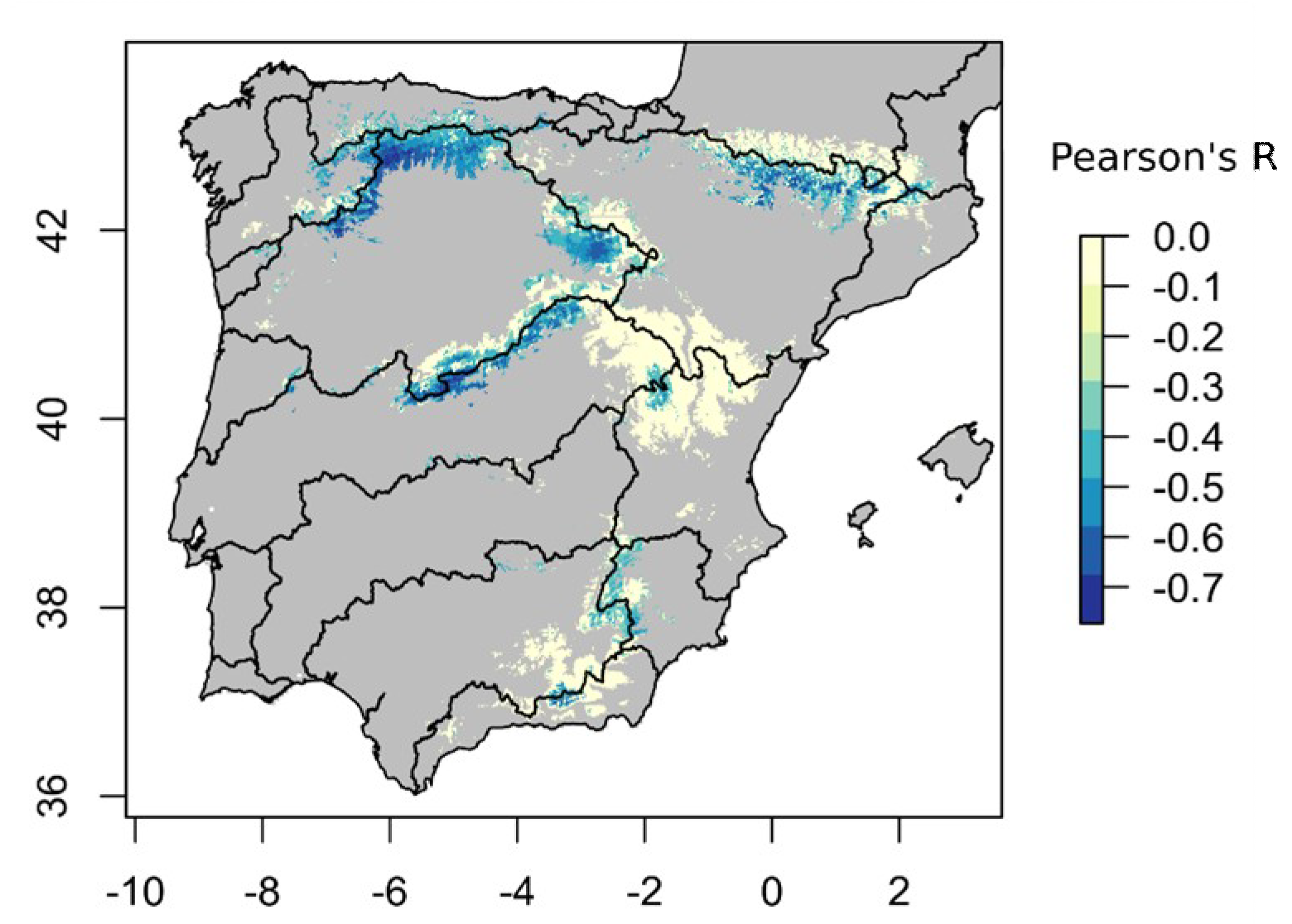
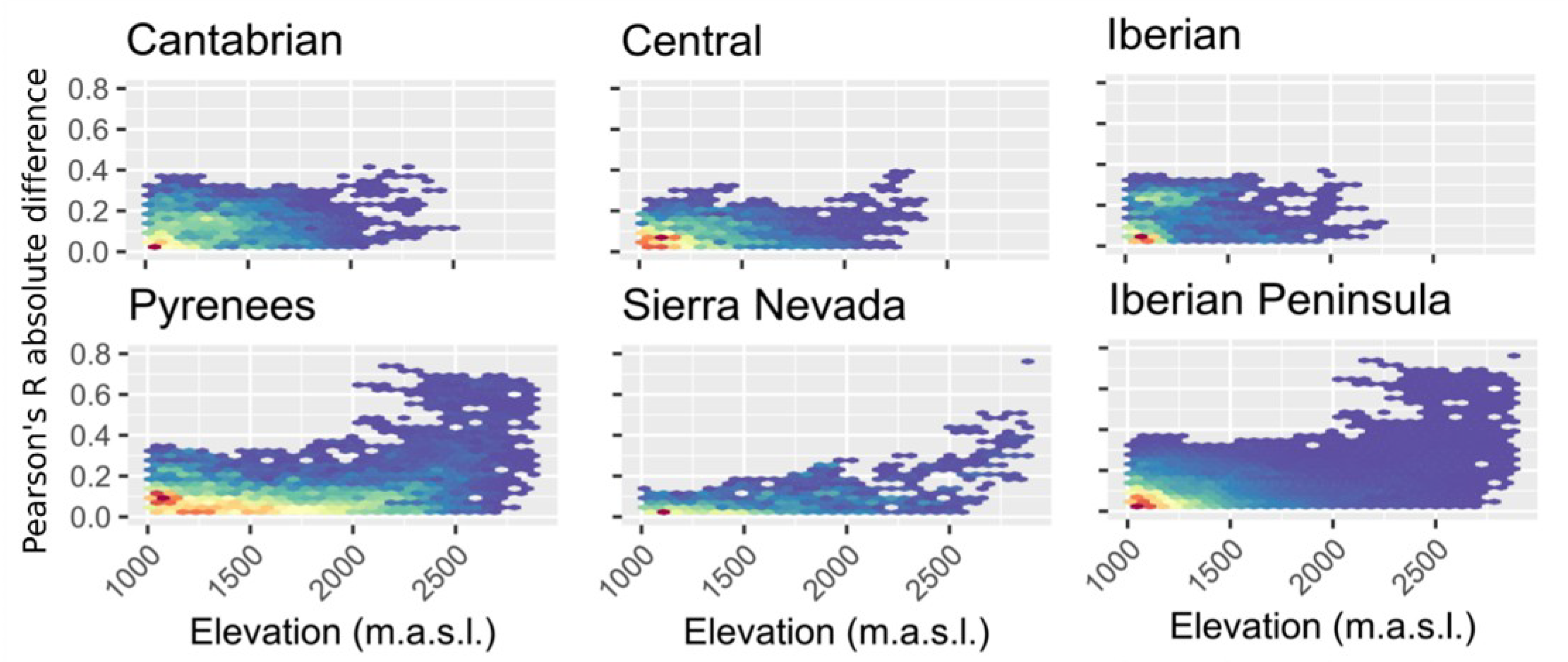
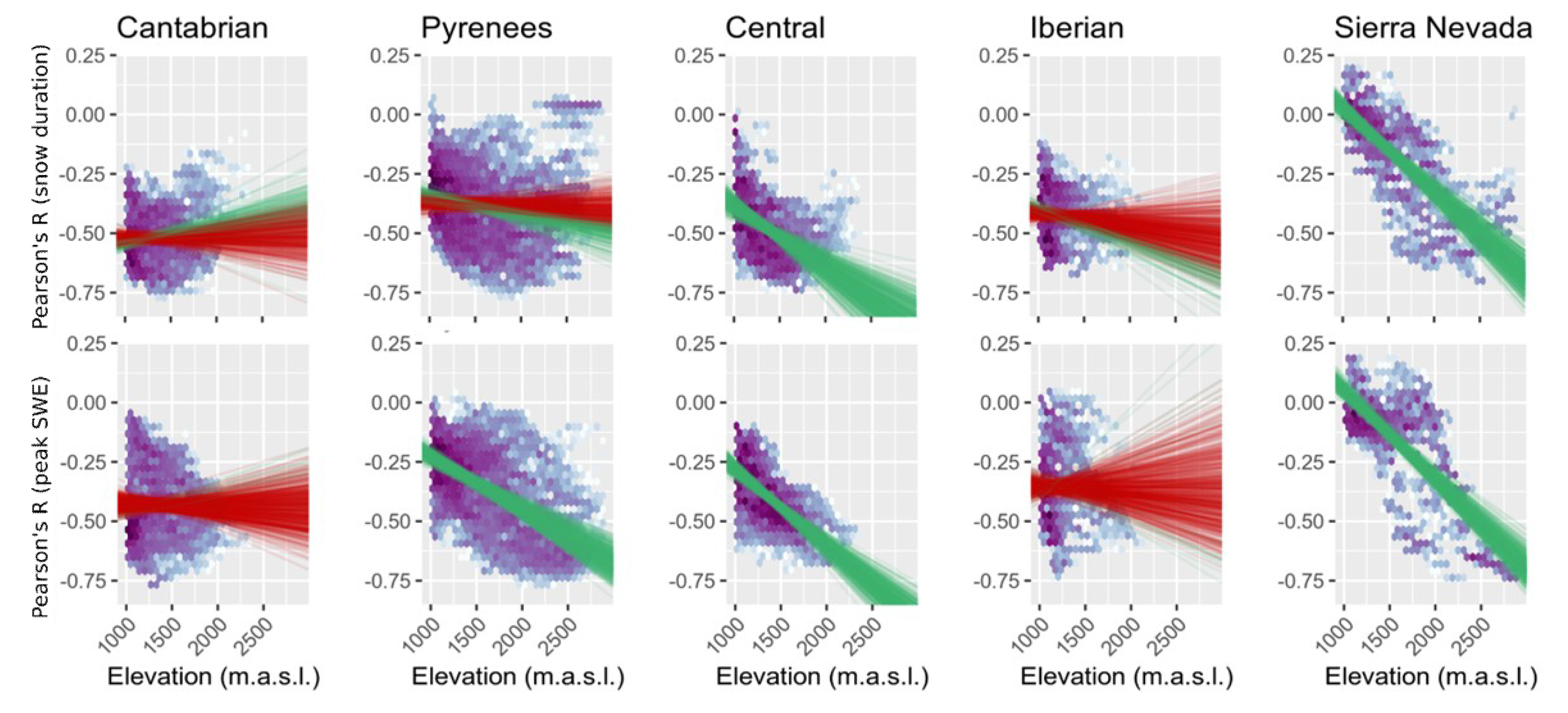
4.3. NAO Spatial Influence on Peak SWE and Snow Season Duration

Figure 3 shows that the DJFM-NAO has a clear correlation with the interannual variability of the snow duration on the southern slopes of the Pyrenees and the Cantabrian, Central, and Iberian ranges. The correlation of the DJFM-NAO with snow duration was high and statistically significant at the highest elevations of the Sierra Nevada, but with no statistically significant differences between the north- and south-facing slopes. However, the other mountain areas showed statistical significance (p-value < 0.05; Wilcoxon–Mann–Whitney test) between north- and south-facing slopes. This finding is consistent with the spatial patterns shown in Section 3.2, between the NAO and the interannual variability of winter temperature and precipitation.

The spatial patterns and magnitude of the correlations for peak SWE were very similar to those for snow duration (Supplementary Figure S1). However, there were differences between these snow variables. Figure 4 shows the absolute difference in the Pearson’s correlation coefficients of the DJFM-NAO with the snow duration and the peak SWE for each pixel for the south-facing slopes, where high correlation values were found (except for the Sierra Nevada, for which all pixels were considered). The greatest differences were found for the higher elevations in the Pyrenees and the Sierra Nevada, where the correlations for peak SWE were higher than those for snow duration. These two mountain ranges exhibit large areas above 2000 m a.s.l, in contrast with the other mountain ranges. We hypothesize that, at high elevations, the correlation of the DJFM-NAO with the temperature and precipitation leads to high levels of snow accumulation during the DJFM-NAO phases, as a consequence of the driving mechanism that controls the DJFM-NAO; however, this is not reflected in the duration of the snow cover. This is mainly because snow duration also depends on solid precipitation occurring during April and May, which is not related to the DJFM-NAO. In addition, the very late and rapid melting that occurs in these high elevation areas [61] is mostly due to the marked increase of the incoming solar radiation at the end of the snow season period.

Figure 4 shows that there was large spatial variability in the correlation coefficients between the DJFM-NAO and the snow indices within each of the analyzed mountain ranges. The influence of elevation on the distribution of the DJFM-NAO correlation values between snow duration and the peak SWE (on south-facing slopes, except in the Sierra Nevada, where both slopes were considered) is shown in Figure 5, and the comparable influence of geographical longitude is shown in Figure 6.

For the Cantabrian Range, most of the correlations of the DJFM-NAO with snow duration ranged from 0.25 to 0.75, and with peak SWE ranged from 0 to 0.75. This variability showed no relationship to elevation, but a clear link with longitude was evident, with an increase in correlation westward. For the Pyrenees, most correlations ranged from 0 to 0.75 for snow duration and peak SWE. While the response of snow duration to elevation was unclear, there was a strong negative relationship for peak SWE. The increase in the correlation of the DJFM-NAO on snow magnitude at high elevations has previously been reported by López-Moreno and Vicente-Serrano [9], where they found statistically significant correlations of the DJFM-NAO with snowpack observations above 1700 m a.s.l., being consistent with our results. These findings suggest that the frequent westerly and southwesterly air fluxes during negative DJFM-NAO years bring mild temperatures during snowfall events, which may cause rain precipitation at low and mid elevations, but heavy snowfalls over 1800–2000 m a.s.l. The absence of a vertical gradient on the relationship of the DJFM-NAO on snow duration is explained by the presence of snow cover and snowfalls until late spring (end of May to early June); these are also highly dependent on spring precipitation, which is unrelated to the DJFM-NAO. Figure 6 does not show statistically significant correlations with longitude but reveals a clear pattern for both indices, characterized by the highest correlations (values reaching 0.75) for the Central Pyrenees, and a decrease westward and eastward. This effect is likely a consequence of the small surface with elevation above 1800 m a.s.l. in the western part compared to the Central Pyrenees, causing low correlation between DJFM-NAO and snow indices (Figure 5). The also-low correlations at the easternmost part are explained because southwestern air fluxes, which are frequent during negative DJFM-NAO phases and generally affect only the Western and Central Pyrenees. Thus, DJFM-NAO are not clearly related with both temperature and precipitation in this sector (Figure 2). In the Central Range, the correlation with the DJFM-NAO ranged from 0 to 0.75 for snow duration and 0.1 to 0.6 for peak SWE. This variability showed a clear negative trend with elevation for both indices. There was no strong relationship with longitude for the correlations between the snow indices and the DJFM-NAO for the Central Range. For the Iberian Range, most of the correlations with the DJFM-NAO ranged from 0.1 to 0.6 for snow duration, and 0 to 0.75 for peak SWE. The reduced area at high elevations and their limited geographical extent made it difficult to distinguish clear spatial patterns in the relationship of the DJFM-NAO and the snow indices. The Sierra Nevada showed the largest variability in the correlation values for both indices, ranging from slightly positive values to 0.75. For both indices the impact of the DJFM-NAO was clearer at higher elevations and eastward in this southern mountain range.

This study shows that the relationship of the DJFM-NAO and the snowpack can be seen in long-term trends of snow cover over wide areas of the Iberian Peninsula. Thus, very different trends in snow accumulation have been found in the Pyrenees when different periods have been analyzed. López-Moreno [54] found a statistically significant decrease in snow accumulation in the central Spanish Pyrenees for the period 1950–1999, but Buisan et al. [60] found no significant trends for the period 1985–2014. Such disagreements were explained by strong decadal fluctuations in the snow data, which correlated with the DJFM-NAO. The marked spatial differences observed in the correlation between the DJFM-NAO and snow indices may explain the marked contrast in snow trends over very short distances, as has been observed in the Pyrenees [10,62]. The presence of areas showing strong correlations between the snowpack and the DJFM-NAO, independent of the study period (as demonstrated by Buisan et al. 2015 for the Pyrenees), provides the promise of improving the seasonal forecasting of snowpack based on short- and medium-term projections for the DJFM-NAO from climate models [63]. This could improve optimization of water management and benefit the skiing industry, both of which are highly affected by interannual fluctuations in snow accumulation and the duration of the snowpack.

5. Conclusions

The DJFM-NAO is related to the atmospheric circulation patterns over the Iberian Peninsula during the snow-accumulation period. The NAO is related to contrasts in precipitation and temperature over the Iberian Peninsula, and hence related to the snow-accumulation and melting processes.

The mountain ranges analyzed in this study are topographic barriers to the main westerly and southwesterly air fluxes related to the DJFM-NAO and explain their variable impacts on the snowpack. Thus, the snowpack on north-facing slopes along the main mountain range axes did not show statistically significant correlations in most of its surface, but there were significant correlations in south-facing slopes. The Sierra Nevada was the only mountain range where this north south difference was not observed. For all Iberian mountain areas, the statistically significant correlations between the DJFM-NAO and snow indices were negative, and, in some cases, R values exceeded 0.7. Marked spatial differences were found, even for those slopes where the DJFM-NAO generally affects the temporal evolution of the snow. In most of the mountain areas, the strength of the relationship between the DJFM-NAO and peak SWE increased with elevation. This also occurred for snow duration, except in the Pyrenees, where spring snowfall can have a strong influence on the snow duration at high elevations, and snowmelt occurs later and more rapidly. This explains why the snowpack duration and peak SWE are not always related, and explains the weaker correlations between the DJFM-NAO and snow duration compared with peak SWE.

In several mountain areas, we found spatial differences that were related to geographical longitude. This was evident for the Cantabrian Range and the Sierra Nevada, where the correlation values decreased from west to east. For the Pyrenees, the maximum correlations were found for the central valleys and decreased toward its western and eastern edges. The results of this study have clear implications for understanding the effect of the length of the study period on the detection of robust long-term trends in snow data, and also spatial differences in trend analyses over short distances.