The Groundwater Demand for Industrial Uses in Areas with Access to Drinking Publicly-Supplied Water: A Microdata Analysis

Abstract

This study examines, from an economic perspective, the factors influencing the decision of companies to use groundwater or not, in a context in which they have access to drinking publicly-supplied water and can also opt for self-supplying groundwater, and then estimates its groundwater demand. The Heckman two-stage model is applied, using microdata of a sample of 2579 manufacturing and service companies located in Zaragoza (Spain). The results of the first stage show that companies have economically rational behavior in the choice of their water supply sources: the probability to capture groundwater depends negatively on its cost and positively on the cost of publicly-supplied water. The results of the second stage indicate that the demand for self-supplied groundwater is normal, but inelastic (elasticity of −0.50), and that self-supplied and publicly-supplied water are substitutive inputs, where the cross-elasticity of the demand is much higher than the direct elasticity. These results warn of the undesirable consequences, on overall efficiency and environmental sustainability, of the lack of a volumetric fee that charges companies with the environmental and resource costs caused by the extraction of groundwater and emphasize the need for integrated management of all water resources.

1. Introduction

Water is an essential resource for socio-economic development, human life sustenance, and ecosystem preservation. Therefore, it is necessary to ensure the sustainability of water resources and their efficient and equitable allocation to enable an acceptable level of economic and social welfare. Nevertheless, population growth, urbanization, water pollution, and unsustainable development are all increasing pressure on water resources across the world, and that pressure is further exacerbated by climate change [1]. Pressure affects both surface water and groundwater.

There is general agreement on the importance of groundwater and the severity of the pressures it bears. Groundwater comprises a much larger freshwater volume than surface water and it is increasingly important for water security in many countries and regions, but many aquifers are subject to unsustainable abstraction levels and pollution [2,3]. The United Nations [4] reports that groundwater provides drinking water to at least 50% of the global population and accounts for 43% of all water used for irrigation, and that an estimated 20% of the world’s aquifers are overexploited.

The main causes of this overexploitation of aquifers are the abstraction for irrigation, drinking water, industrial and mining uses [1]. The relative importance of each of these uses varies significantly by country, depending on climate and the degree of economic development. The problem of overexploitation arises in fossil aquifers because of their lack of natural replenishment, and in aquifers with natural recharge when groundwater is withdrawn faster than its long-term replenishment. The main consequences are falling groundwater levels, increased pumping costs, land subsidence, reduced baseflows of rivers (desiccation of springs, streams, and wetlands), water quality degradation, saline intrusion, and rising sea levels [5,6,7].

The proposed solutions involve both an increase in water supply and its conservation: in the first case, through artificial recharge of aquifers and interventions to improve groundwater quality; in the second case, through the implementation of administrative controls and economic incentives to reduce abstractions [8]. Furthermore, given the close relationship between surface water and groundwater [9,10,11], the long-term sustainability of their use requires integrated management of all water resources, in line with the approach adopted in the Water Framework Directive [12] and the recommendations of the United Nations [1,2,3]. Unfortunately, the implementation of policies aimed at the sustainability of groundwater exploitation faces serious difficulties, as evidenced in its increasing deterioration. These problems can be mainly attributed to the invisibility of groundwater which limits the availability of information on the real situation of aquifers and also to its character as a common-pool resource in the sense of Hardin [13], which encourages users to overexploit [14].

Typically, groundwater use occurs in water-stressed regions, where aquifers are used as an additional source to surface water, but also occurs in regions without water scarcity and where the supply of water from other sources is sufficient and secure, as in urban settings in developed countries. In these urban areas, households and industries have access to the drinking water provided by the public water supply network, but they sometimes complement or replace that public supply with self-supply of groundwater when they use water for some purposes which do not require drinking water. The possibility of choosing between alternative water sources has relevant consequences for the management of aquifers and public drinking water supply services, since the measures adopted by policy makers regarding one of these sources will surely affect the other and vice versa.

Despite the key role of self-supply, this water source has been barely analyzed by the economic literature. This lack of empirical evidence is more pronounced in the case of industry (where we can only cite Ref. [15,16]) than in that of households (Ref. [17,18,19,20] among others), where there is a broader literature focused on developing countries in which the low reliability in public supply leads households to use other alternative sources (wells, rainwater tanks, public water fountains, water vended from tank trucks, bottled water). The studies regarding self-supplied water encountered problems regarding lack of information because microdata are rarely available to the public. As a consequence, researches face serious difficulties in knowing the quantity of intake water and the cost born by each user. In the case of groundwater, there is usually an absence of public meters for monitoring the water extracted by each user, and a lack of statistics on its unitary cost, which includes the costs of investment, extraction, and treatment.

The mainstream of literature that estimates water demand implicitly assumes that the source of supply is determined exogenously, both for analyzing publicly and self-supplied water. Focusing on self-supply for industrial activities, this was the case in a study by Reynaud [16] who estimated self-supplied water demand for 55 industrial and service companies located in France. However, a suitable approach should take into account that a considerable number of users can choose their water sources and how much to use from each one. The literature has usually addressed this issue by means of a two-stage process where in the first stage the user decides whether to use a given source (for example, self-supply), and in the second stage, decides on the volume of water to capture. This strategy is rather common when analyzing water recirculation [21,22,23] and self-supply in the domestic sphere (for example, [17,18,19,20]), but for industrial users, we can only refer to a study by Renzetti [15], who estimated self-supplied water demand in the US using a survey of more than 2000 manufacturing firms. This shows that more empirical evidence is needed on the choice and relationship between water supply sources and the estimation of groundwater demand in the industrial field, in order to establish adequate policies for an integrated water management.

The purpose of this study is to analyze the factors that influence decisions on the use of self-supplied groundwater by manufacturing and service companies in urban settings in which they can also choose to supply from the public drinking water network, and to estimate the groundwater demand for these activities. The study is based on a sample of 2579 companies located in Zaragoza (Spain), 44 of which use self-supplied water. We use the Heckman two-stage model, which allows us to obtain the marginal effect of the different factors on the probability of self-supply and on the volume of self-supplied groundwater. Our attention is focused on economic factors since, in the absence of technical impediments, it will be the expectation of benefit from water use that will induce companies to choose to pump water from the aquifer [24]. The analysis is oriented towards the design of public policies to promote sustainability and efficiency in the use of water resources.

After this introduction, Section 2 presents the case study. Section 3 describes our data. Section 4 introduces the model and the corresponding estimation techniques. The results are discussed in Section 5. Finally, Section 6 presents the main conclusions.

2. The Case Study

The municipality of Zaragoza has the fifth largest population in Spain. Its production structure is similar to the national average, characterized by the dominance of the service sector (84% of employment), followed by manufacturing (10%), construction (5%), and farming (1%), according to data for 2012 from the Aragonese Statistics Institute [25].

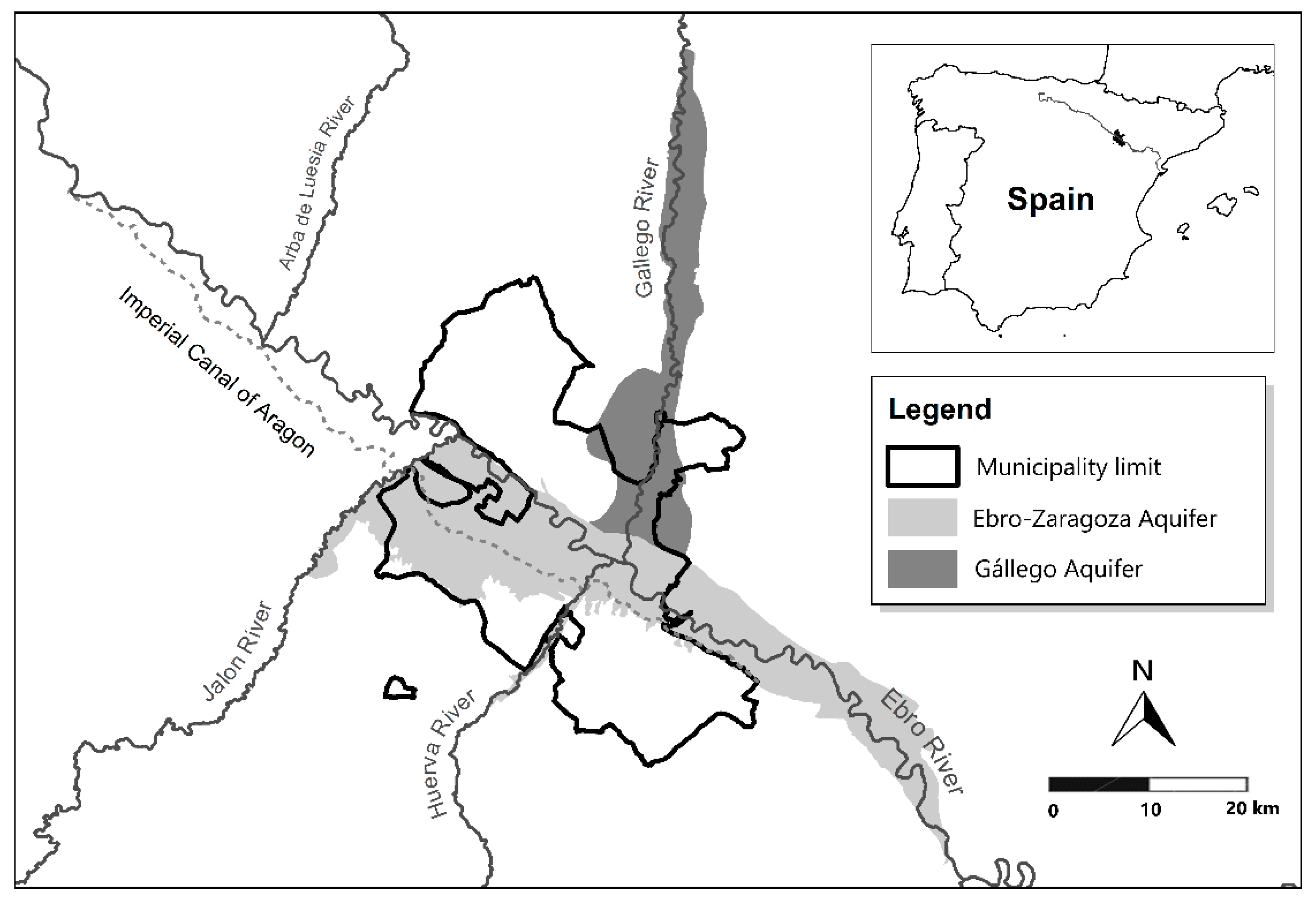
The municipality is located in the center of the Ebro River basin, at the mouths of two tributaries, the Gállego and the Huerva rivers. The management and administration of the different water masses in this basin are the responsibility of the Ebro Hydrographic Confederation (CHE), a public agency dependent on the Spanish government. The drinking water supply in the municipality has traditionally come from the Imperial Canal of Aragon, which runs alongside the Ebro, the source of its water, although since 2010 it has been supplemented with water channeled from the Pyrenees. The drinking water supply and wastewater services are the responsibility of the Zaragoza City Council. Both services are taxed by a binomial tariff system which combines a fixed and variable charge (volumetric charge). The fixed charge depends on the caliber of the meters which measure the water supplied to each user and the variable charge depends on the volume of water recorded in these meters and is obtained by applying an increasing block tariff.

There are two groundwater masses underlying the municipality of Zaragoza: The Ebro-Zaragoza alluvial aquifer and the river Gállego alluvial aquifer (see Figure 1). These two groundwater masses, known as the Zaragoza aquifer, provide the municipality with an abundant water source, easily accessed using wells only about twenty meters deep. The groundwater resources’ availability is also common in many other areas of Spain where aquifer systems cover two thirds of the surface area [26] and, on average, groundwater meets around 20% of the demand for water, but can represent up to 75% of total water use in the Mediterranean Basin [7].

The water extracted from the Zaragoza aquifer has a constant temperature and is turbidity-free, so it does not usually need any treatment before its use for certain industrial purposes. For current extraction levels, there are no overexploitation problems, so it is a source with almost guaranteed availability [27,28,29]. In the Ebro River basin, the use of this resource is subject to the concession of a license by the CHE (according to the 1985 Spanish Water Act [30]), who authorizes a maximum volume of water extraction based on the request of each user. In order to control this volume, users are obligated to install private meters for their monitoring [31]. However, the lack of public homologated meters, along with the difficulty of monitoring all existing wells in the river basin, imply that the CHE does not have official records on the real volume captured by all users, but only for some specific users or for some water bodies with serious problems of water availability, which is not the case of the Zaragoza aquifer. Therefore, water extraction control in practice is mostly based on occasional inspections to verify that users do not exceed the maximum volume authorized. The direct discharge of water into water bodies is also subject to an authorization and control process similar to that of water extractions [31] and faces similar problems in its practical application.

Unlike publicly-supplied water, the use of this resource is not subject to a supply tariff; it is subject only to a one-off administrative fee linked to the licensing procedure for groundwater extraction and designed to cover the costs of the procedure. On the contrary, users do must pay for the discharge of this resource. If the self-supplied water is discharged directly into the river channels or into the aquifer, a dumping fee [32] should be paid to the CHE based on the volume of water discharged authorized and the quality of the discharge (this fee is very low, 0.03005 €/m³, and can vary depending on the quality of the discharge). If it is discharged into the municipal sanitation network, the municipal wastewater tariff should be paid to the City Council (this tariff includes both the dumping fee plus the corresponding wastewater treatment costs). This means that the unit cost of self-supply born by users (including the license fee, the cost of groundwater extraction, well drilling, pumping equipment and pumping water, and the cost of discharge) is, in most cases, lower than the publicly-supplied water tariff.

This easy accessibility has led to strong pressures on these water bodies in terms of quality [27,28]. This implies that these aquifers are in risk of not achieving the good qualitative status of water bodies established in the Water Framework Directive as the 30.9% of Spanish groundwater masses [33]. The origin of these pressures depends on the uses of water. In the case of Zaragoza, 92% of groundwater extractions are intended for the industrial sector [29], which also represents an important source of pollutants. However, for the whole of Spain the main groundwater withdrawer is irrigated agriculture, which accounts for 75% of the extractions [7].

3. Data

We have a sample of 2579 companies located in Zaragoza over the aquifer. For each company we observed the following data in 2012: the volume of publicly-supplied water and its fixed and variable cost, obtained from data provided by the Zaragoza City Council; the volume of self-supplied groundwater, obtained by combining information from the City Council and the CHE; the fixed and variable cost of self-supply, calculated from data provided by the CHE; and the value of production and the sector of activity, from the database “Iberian Balance Sheet Analysis System” (SABI) (http://informa.es/en/financial-solutions/sabi).

The data on the volume of publicly-supplied water were obtained based on records of the water meters installed in each company by the municipal water service. The data on the volume of self-supplied groundwater, in the absence of public meters, were calculated by means of two complementary procedures: the first one, as a difference between the volume discharged into the municipal sanitation network and the volume captured from the municipal supply network, based on information from the meters installed by the municipal water service; the second one, as the volume authorized in the license to use groundwater, based on records from the CHE. With the data from the City Council, we monitored the companies discharging used self-supplied water into the municipal sanitation network, and with data from the CHE we monitored the companies that instead discharge it into river channels or into the aquifer itself. Using both types of information, it was possible to build a dataset of companies who obtained water through self-supply, since no company in our sample uses surface water for self-supply, according to the CHE (this is mainly due to the poor quality of this source of water and its reduced flow in many months of the year).

To calculate the cost of self-supplied groundwater, we first need information on the depth of the aquifer at the location of the company and on the flow rate of the self-supplied water. From the geographical coordinates for each company, taken from SABI, the Geological and Mining Institute of Spain (IGME), in collaboration with the CHE, provided us information on aquifer depth, based on IGME [34] and Moreno et al. [29].

Table 1. Main magnitudes relating to water consumption. Average per company for 2012.

	Aggregate	Manufacturing	Services
No. of companies with self-supply of groundwater	44	24	20
No. of companies without self-supply of groundwater	2535	242	2293
Percentage of companies with self-supply of groundwater (%)	1.71	9.02	0.86
For all Companies:
Production (1000 €)	1482.89	2999.25	1308.51
Quantity of publicly-supplied water (m3)	377.90	542.57	358.96
Quantity of self-supplied groundwater (m3)	336.89	1066.30	253.00
Total water consumed (m3)	714.78	1608.87	611.97
Percentage of self-supplied groundwater (%)	47.13	66.28	41.34
Quantity of self-supplied groundwater per € of production (L/€)	0.28	0.38	0.27
Quantity of publicly-supplied water per € of production (L/€)	0.80	0.30	0.86
Aquifer depth (m)	19.82	19.63	19.84
Companies with Self-Supply of Groundwater:
Production (1000 €)	12,127.22	11,808.07	12,510.21
Quantity of publicly-supplied water (m3)	4735.19	1619.9	8473.55
Quantity of self-supplied groundwater (m3)	19,746.27	11,818.12	29,260.05
Total water consumed (m3)	24,481.47	13,438.02	37,733.60
Percentage of self-supplied groundwater (%)	80.66	87.95	77.54
Quantity of self-supplied groundwater per € of production (L/€)	4.47	4.17	4.85
Quantity of publicly-supplied water per € of production (L/€)	0.71	0.18	1.35
Aquifer depth (m)	16.50	16.89	16.04
Companies without Self-Supply of Groundwater:
Production (1000 €)	1298.14	2125.66	1210.81
Quantity of publicly-supplied water (m3)	302.27	435.73	288.18
Quantity of publicly-supplied water per € of production (L/€)	0.80	0.31	0.85
Aquifer depth (m)	19.87	19.89	19.87

shows the average aquifer depth for our sample (19.82 m) of self-supplying companies located in areas where the aquifer has a lower depth (16.50 m) compared to companies who do not self-supply (19.87 m). The flow rate of each company’s self-supplied water was estimated based on their volume of self-supplied water, assuming that they pump 16 h a day, according to the standard of the Spanish Ministry of Agriculture, Food and the Environment [35] for water captured by industries.

The annual fixed cost of self-supplied groundwater (FCS) was calculated according to [35], as follows:

$$FCS=F+CC+CM+OMC$$

(1)

where $F$ is the one-off administrative fee that users must pay when processing the license to use groundwater, assumed to be valid for 20 years according to [36]; $CC$ is the cost of well construction (drilling, laying pipes, and finishing the well), supposing this to be amortized over 20 years; $CM$ is the cost of investment in machinery (pumping equipment), to be redeemed in 10 years; and $OMC$ is operating and maintenance costs (representing 2% of the investment cost).

We calculated the well construction costs based on the depth of the aquifer, while the cost of the pumping equipment was obtained according to its market price, depending on the power needed for the pumps. The power was obtained using the approximation of [37]:

$$P=\frac{h\times Q}{r\times 75}$$

(2)

where $P$ is the power (in metric horsepower); $h$ is the manometric height (in meters), which we make equal to the aquifer depth; $Q$ is the flow rate (in liters per second); $r$ is pump performance, considered to be 70% in all cases ($r=0.70$); and the constant 75 in the denominator enables us to go from kilogram-meters per second to metric horsepower.

The variable unit cost of self-supplied groundwater (VUCS) is the cost of the energy needed to capture a cubic meter of water, plus the cost of the municipal sanitation charge for companies which discharge self-supplied water into the municipal sanitation network, or the cost of the dumping fee paid to the CHE otherwise.

We calculated the energy cost per cubic meter of water extracted (UEC) according to [37], as follows:

$$UEC=0.002726\frac{h\times k}{r}$$

(3)

where h is the manometric height (in meters); k is the approximate price of energy (€/Kwh) for the average price of electricity in Spain [38]; r is pump performance (again, set at 70%); and the constant 0.002726 is energy consumption (Kwh) incurred by raising one m³ of water one meter.

For companies that only use publicly-supplied water, we need to know the fixed and variable unit cost of self-supplied water that they would face if they decided to capture water from the aquifer. So, for these companies, we calculated FCS and VUCS supposing that, if they decided to self-supply, they would capture the same percentage of self-supplied water as the average for companies that self-supply.

The annual fixed cost of publicly-supplied water (FCP) is obtained as the annual municipal fixed charge of the publicly-supplied water supply and sanitation bill. In turn, we calculated the variable unit cost of publicly-supplied water (VUCP) by dividing the municipal variable charge of the publicly-supplied water and sanitation bill by the intake volume.

As before, we need to estimate the fixed and variable unit costs of publicly-supplied water that companies would encounter by using self-supplied water, if they decided to use only the public water network. In these cases, we estimated the corresponding FCP and VUCP assuming that, if they decided to publicly-supply, they would capture the same volume in publicly-supplied water as they do in self-supply.

Finally, SABI contains information about the value of production (Y) and the sector of activity each company belongs to (manufacturing or services). Based on the last item, we generated the corresponding dummy variable (DM).

Table 1 offers additional detail in relation to companies that use self-supplied and publicly-supplied water. A total of 1.71% of companies in our sample capture water from the aquifer, but the self-supplied water used by these firms represents 47.13% of total water used by the industrial sector. In the manufacturing sector, the percentage of companies is 9.02% (representing 66.28% of total water volume), while in the services sector the percentage of companies is lower than 1% (representing 41.34% of water use). We also observed that companies using groundwater self-supply are larger than companies using only publicly-supplied water (the average output for these groups is 12,127,220 € vs. 1,298,140 €) and use a much higher total volume of water per euro of production (5.18 L/€ vs. 0.80 L/€).

For companies using self-supply, 80.66% of the water they consume is self-supplied. Again, this percentage is higher in manufacturing companies (87.95%) than in services (77.54%). However, the volume of self-supplied water per euro of production is slightly greater in companies in the services sector (4.85 L/€) than in manufacturing (4.17 L/€).

4. Empirical Application

Our approach is based on the assumption that companies choose their sources of water (publicly and/or self-supplied water) and the amount of each in order to minimize the cost of production. This point leads us to a two-stage model where, first, the company decides whether or not to self-supply with groundwater and, if it does, then it decides the volume of water extracted from the aquifer. Section 4.1 introduces the methodological background for our approach whereas Section 4.2 discusses the application to our case study.

4.1. Methodology: Heckman Two-Stage Model

There are several alternatives to proceed with two-stage models [39]. Among the existing alternatives, we prefer the classical Heckman approach [40] because of its greater flexibility, allowing different factors to intervene in each stage. Before going into the details, we shall introduce briefly the basis of this approach.

The aim in the first stage is to model the probability that a company decides to capture groundwater, through a probit equation for a binary decision variable, $h_i$, such as the following:

$$\begin{array}{c}{h}_i=1(y_i>0)if{h}_i^{*}>0\\ h_i=0(y_i=0)if{h}_i^{*}\le 0\end{array}\mathrm{with}{h}_i^{*}=x_{1i}^{\prime }{\beta }_1+{\epsilon }_{1i}i=1,2,\dots ,N$$

(4)

where $y_i$ is the volume of self-supplied groundwater and $h_i^{*}$ is a latent, unobserved variable representing the decision process ($N$ is the sample size); $x_{1i}$ is a vector of observed characteristics of the company. It is usual to assume normality for the error term of the equation, ${\epsilon }_{1i}$. This is the decision equation, which allows us to quantify the probability of self-supply:

$$P\left(h_i=1\right)=\mathsf{\Phi }\left(x_{1i}^{\prime }{\beta }_1\right)=1-\mathsf{\Phi }\left(-x_{1i}^{\prime }{\beta }_1\right)$$

(5)

The purpose of the second stage is to explain the volume of groundwater captured by each company, using a truncated regression model such as:

$$y_i=x_{2i}^{\prime }{\beta }_2+{\epsilon }_{2i}if{y}_i>0$$

(6)

This is the quantity equation. The error terms of both equations could be correlated, $corr({\epsilon }_{1i;}{\epsilon }_{2i})=\mathsf{\rho }\ne 0$, so that the least squares estimations of the first equation would be biased. The Heckman approach corrects for this source of inconsistency introducing the inverse of the so-called Mills ratio (IMR), or non-selection hazard in Equation (6):

$$y_i=x_{2i}^{\prime }{\beta }_2+\rho {\sigma }_{{\epsilon }_{1i}}IM{R}_i+{\eta }_i$$

(7)

where $IM{R}_i=\frac{\varphi \left(-x_{1i}^{\prime }{\beta }_1\right)}{1-\mathsf{\Phi }\left(-x_{1i}^{\prime }{\beta }_1\right)}$ with $\varphi$(.) and $\mathsf{\Phi }$(.) being the standard normal density and distribution functions estimated in the decision equation; $x_{2i}$ is a vector of observed characteristics of the company, possibly different from $x_{1i}$. The significance of the composed coefficient, $\mathsf{\gamma }=\rho {\sigma }_{{\epsilon }_{1i}}$, is crucial for the specification.

Once the two-stage model is estimated, it is possible to evaluate the marginal effects. The effect of a continuous z variable on the probability of self-supply is:

$$\frac{\partial P\left(h_i=1\right)}{\partial z}=\varphi \left(x_{1i}^{\prime }{\beta }_1\right)\frac{\partial \left(x_{1i}^{\prime }{\beta }_1\right)}{\partial z}$$

(8)

The effect on the conditional volume of self-supplied groundwater is:

$$\frac{\partial E\left(y_i|h_i=1\right)}{\partial z}=\frac{\partial \left(x_{2i}^{\prime }{\beta }_2\right)}{\partial z}-\mathsf{\gamma }\left(\frac{\varphi \left(-x_{1i}^{\prime }{\beta }_1\right)}{1-\Phi \left(-x_{1i}^{\prime }{\beta }_1\right)}\right)\left[\frac{\varphi \left(-x_{1i}^{\prime }{\beta }_1\right)}{1-\Phi \left(-x_{1i}^{\prime }{\beta }_1\right)}+x_{1i}^{\prime }{\beta }_1\right]\frac{\partial \left(x_{1i}^{\prime }{\beta }_1\right)}{\partial z}$$

(9)

Moreover, the effect of a discrete variable is the difference between the two states of the binary $h_i$ variable.

4.2. Application to the Case Study

From Table 1, presented in the previous section, we can observe that our case study fits well with the Heckman approach; in fact, it is a two-stage decision process where the factors intervening in the two instances can vary. For example, companies in the manufacturing sector seem to be more likely to self-supply but, once they have made the decision, other factors such as volume of activity seem to be more important.

Therefore, we can adapt the Heckman model described in Section 4.1. to our case study as follows. For the first stage we have:

$$\begin{array}{c}D{S}_i=1if{h}_i^{*}>0\\ D{S}_i=0if{h}_i^{*}\le 0\end{array}with{h}_i^{*}=x_{1i}^{\prime }{\beta }_1+{\epsilon }_{1i}i=1,2,\dots ,N$$

(10)

where:

$$x_{1i}^{\prime }{\beta }_1={\beta }_{1,FCS}lnFC{S}_i+{\beta }_{1,VUCS}lnVUC{S}_i+{\beta }_{1,FCP}lnFC{P}_i+{\beta }_{1,VUCP}lnVUC{P}_i+{\beta }_{1,DI}D{M}_i$$

(11)

$D{S}_i$ is a binary indicator of positive self-supplied groundwater. The set of $k_1$ first stage factors, $x_{1i},$ are the variables described in Section 3. Note that the variables in the right hand side of the equation have been log-transformed to be more consistent with the second stage of the procedure.

For the quantity equation of the second stage, we specify a double logarithmic model to prevent negative estimates (other functional forms were discarded based on misspecification tests), so that:

$$lnV{S}_i=x_{2i}^{\prime }{\beta }_2+{\epsilon }_{2i};{\epsilon }_{2i}~N\left(0,{\sigma }_2^2\right)$$

(12)

where:

$$x_{2i}^{’}{\beta }_1={\beta }_{2,1}+{\beta }_{2,VUCS}lnVUC{S}_i+{\beta }_{2,VUCP}lnVUC{P}_i+{\beta }_{2,Y}ln{Y}_i+{\beta }_{2,DI}D{M}_i$$

(13)

$V{S}_i$ is the quantity of pumped groundwater conditioned to $D{S}_i=1$, and $x_{2i}$ is a set of $k_2$ explicative factors ruling in the second stage (described in Section 3).

In the equation of the first stage, we include the fixed cost (investment cost) and the variable unit cost of self-supply groundwater; we expect that an increase in both variables will reduce the probability of self-supply. We also include the fixed cost and the variable unit cost of publicly-supplied water; we expect that an increase in both variables will increase the probability of self-supply. Finally, we include a sectoral dummy, for which we have not any a priori, since it would depend on the uses of water inputs in each sector. Nevertheless, data from Table 1 suggest that there is a higher percentage of self-suppling companies in the manufacturing sector (9.02%) than in the service sector (0.86%). It should be noticed that we have not included an output variable in the first stage equation. The reason is that the level of production of a company has been implicitly taken into account when including the costs of investment in the self-supply decision equation. This means that, given a certain fixed cost of self-supply, the company will decide whether this investment is profitable or not given its level of production, and therefore, whether to self-supply or not. So, the inclusion of the variable output in the equation of the first stage would have been redundant.

Regarding the quantity equation (second stage), we include the following: the variable unit cost of self-supply, for which a negative relationship with the quantity demanded of this water source is expected; the variable unit cost of publicly-supplied water, for which we did not adopt an a priori hypothesis because the sign of this relationship depends on technical factors and not just economic ones (an increase in this variable will increase the quantity of self-supply if both types of water are substitutes and reduce the quantity if they are complementary); the level of production, for which a positive relationship with the quantity demanded of this water source is expected; and a sectoral dummy. For the latter, we note again, there is not any a priori, although data from Table 1 show that service self-supplying companies seem to consume more groundwater (29,260.05 m³) than manufacturing companies (11,818.12 m³). We do not include in the quantity equation the fixed cost of publicly and self-supplied water. The reason is that, once the decision to self-supply is taken, and the necessary investment made, the fixed costs will not determine the amount of water that the company demands.

Table 2. Average values of the variables for the case study (2012).

	Description	First Stage		Second Stage
$\mathrm{DS}$	= 1 if the company self-supplies; 0 if not	0.017		−	−
$\mathrm{VS}$	Volume of self-supplied groundwater (m3)	−	−	19,746.27	(60,114.48)
$\mathrm{FCS}$	Fixed cost of self-supplied groundwater (€/year)	2425.88	(78,487.09)	−	−
$\mathrm{VUCS}$	Variable unit cost of self-supplied groundwater (€/m3)	0.68	(0.26)	0.85	(0.65)
$\mathrm{FCP}$	Fixed cost of publicly-supplied water (€/year)	207.14	(1048.75)	−	−
$\mathrm{VUCP}$	Variable unit cost of publicly-supplied water (€/m3)	1.38	(0.59)	2.95	(0.32)
$\mathrm{Y}$	Value of production (thousands of €/year)	−	−	12,127.22	(2,046,581)
$\mathrm{DM}$	= 1 if the company belongs to the manufacturing sector; 0 if not	0.10		0.55

Note: Standard deviation appears in parentheses.

presents some descriptive data of the main variables of our model; we distinguish between the first and second stage equations. We confirm that half of the companies capturing water from the aquifer belong to the manufacturing sector, while only 10% of the companies in the sample in fact belong to this sector.

The fixed cost of water captured from the aquifer (investment cost) is substantially higher (2425.88 €/year) than the fixed cost of publicly-supplied water (207.14 €/year). In addition, the variable unit cost of both sources of water is greater for self-supplying companies (0.85 €/m³ for self-supplied water and 2.95 €/m³ for publicly-supplied water) than for the average of the sample (0.68 €/m³ for self-supplied water and 1.38 €/m³ for publicly-supplied water).

Table 3. Heckman two-stage model. Results of the estimation.

	$\mathbf{First}\mathbf{Stage}\left(\mathit{D}\mathit{S}\right)$		$\mathbf{Sec}\mathbf{ond}\mathbf{Stage}\left(\mathit{l}\mathit{n}\mathit{V}\mathit{S}\right)$
$\mathrm{lnFCS}$	−0.6463	(0.00)	−
$\mathrm{lnFCP}$	0.1525	(0.02)	−
$\mathrm{lnVUCS}$	−0.3185	(0.00)	−0.5034	(0.00)
$\mathrm{lnVUCP}$	1.9068	(0.00)	5.6738	(0.00)
$\mathrm{DM}$	0.8462	(0.00)	−0.1026	(0.83)
$\mathrm{Y}$	−		0.3776	(0.00)
$\mathrm{Intercept}$	−		−6.1988	(0.05)
Wald test: 28.00 (0.000); $\widehat{\rho }$ = 0.6037116; LR test ($\widehat{\rho }$ = 0): 16.05 (0.0001)

Note: p-value in parentheses; Wald test refers to the ${\chi }^2\left(4\right)$ that all coefficients in the quantity equation are not significant. $\mathrm{LR}\mathrm{test}\left(\widehat{\rho }=0\right)$ is the likelihood ratio test that the coefficient $\widehat{\rho }$ is zero (the two equations are independent), distributed ${\chi }^2\left(1\right)$.

presents the results of the two-stage model estimation, obtained using Equations (10) and (11). The coefficient of the IMR, $\widehat{\mathsf{\rho }}$, is positive and significant, indicating the presence of the so-called sample selection bias. Therefore, if both equations (self-supply decision and self-supply volume) were estimated separately without entering the IMR, the estimation of the parameters of the model would be biased. This confirms the appropriateness of using the Heckman two-stage model.

5. Discussion of Results

The results obtained in the selection equation (first stage), shown in Table 3, confirm the expected signs of the explanatory variables. Thus, an increase in the cost of investment in self-supply (FCS) or the variable unit cost of captured groundwater (VUCS) reduces the probability of self-supplying water from the aquifer. This coincides with Renzetti [15] for the case of self-supplied water and is also consistent with the results obtained in the literature for the recirculation decision [21]. Moreover, an increase in the fixed cost of access to the public supply network (FCP) or its variable unit cost (VUCP) increases the probability of self-supplying groundwater, as a way of reducing the cost of water. Once again, this is in line with Renzetti [15] for the case of self-supplied water (although in his study these variables are not significant), and with the results obtained for water recirculation by Bruneau and Renzetti [21] and Féres et al. [23]. These results confirm that the companies have an economically rational behavior in this stage of selection of the water source. These results cannot be compared with those of the literature regarding households’ self-supply, because this literature focuses on developing countries with public water supply quality problems, where the decision about self-supply is dependent on the reliability of the public supply and household characteristics, but not on the costs of the different sources of water [17,18,19,20]. Also, as anticipated by descriptive data, companies in the manufacturing sector are more likely to capture water from the aquifer compared to companies in the services sector. This result may be related to the predominant uses of water in each sector. Thus, while manufacturing companies need large volumes of water for tasks which do not require high quality (cooling, washing, transporting raw materials, etc.), most service companies tend to use water only for sanitary or personal care purposes requiring drinking water. On this issue, as far as we know, the literature has not provided results to compare with ours.

The results regarding the quantity equation (second stage) show that an increase in the variable unit cost of self-supplied water (VUCS) reduces the quantity of groundwater demanded. Thus, as we expected, we obtained that the demand for groundwater is normal. Renzetti [15] and Reynaud [16] also obtained a negative sign for self-supplied water in industry for the coefficient of this variable, although it is hardly significant. However, this variable appears to be very relevant in the case of recirculated water, with a negative impact on the volume of processed water [21,22,41,42,43], the same as for household self-supply [17,18,19,20].

Moreover, an increase in the price of publicly-supplied water (VUCP) increases the volume of groundwater captured. Therefore, both water inputs behave as substitutes. This result differs from that obtained by Reynaud [16] according to which publicly-supplied and self-supplied water for manufacturing firms are complementary, although the elasticities obtained in this case are not significant. However, the result coincides with that usually obtained in literature focused on recirculated vs. intake water in the industry [22,23,41,42,43,44] or on the demand of different types of water by households (for example, [17,18,19]).

The use of self-supplied water is also positively influenced by the level of production, indicating that larger companies capture larger volumes of groundwater. This result is in line with Renzetti [15] and Reynaud [16] for the case of self-supplied water, and with the results obtained for water recirculation (for example, [24,25,41,42,44]). They also coincide with those obtained commonly in the literature focusing on industrial demand for publicly-supplied water (for example, [45,46,47]).

The coefficient of the dummy manufacturing variable is negative but not significant. Therefore, although manufacturing companies are more likely to capture water from the aquifer (as shown in the selection equation), once they have decided to self-supply, the sector of activity does not determine the volume of intake groundwater. In fact, most service companies only use publicly-supplied water, but those that decide to self-supply utilize groundwater for uses requiring large volumes, such as cooling or filling swimming pools.

Table 4. Marginal effects on the probability of self-supply and conditional effects of self-supplied groundwater.

	Effect on the Probability of Self-Supply Groundwater	Effect on the Conditional Volume of Self-Supplied Groundwater (Elasticities)
$\mathrm{lnFCS}$	−0.0121859	−
$\mathrm{lnFCP}$	0.0028746	−
$\mathrm{lnVUCS}$	−0.006004	−0.5033737
$\mathrm{lnVUCP}$	0.0359508	5.673772
$\mathrm{DM}$	0.0552805	−
$\mathrm{Y}$	−	0.377608

Note: The marginal effects of the sectoral dummy on the volume of self-supplied groundwater were not estimated, since the coefficient associated to this variable in the second stage of the model is not significant (see Table 3).

shows the marginal effects, obtained applying Equations (8) and (9), to the case study. The first column indicates that a 1% increase in FCS and VUCS reduces the probability of self-supply groundwater by −0.0122% and −0.0060%, respectively. In contrast, a 1% increase in FCP and VUCP increases the probability of self-supply by 0.0028% and 0.0359%, respectively. Also, the probability of self-supply is 0.0553% higher for manufacturing companies. Therefore, the most relevant effects occur through the sectoral dummy and the price of publicly-supplied water, being the magnitude of the latter effect in the middle range of values previously obtained in the literature for the probability of recirculated water, which ranges from 0.02 [23] to 0.05 [22]. For the other variables, there are no previous results in the literature for establishing a comparison.

The second column reports on the effect of the variables on the volume of self-supplied groundwater for those companies that have already decided to self-supply (conditional effect). It shows that a 1% increase in VUCS reduces the self-supplied volume by −0.5034%. Therefore, demand for groundwater is inelastic. This value of the direct price elasticity is similar to that obtained for the demand of non-publicly-supplied water by households [17,20]. In the industrial sphere, it is in the middle range of those of the literature for publicly-supplied water, which ranges from −0.1 to −1.1 [45], and for recirculated water, between −0.27 [22] and −1.83 [43].

In addition, a 1% increase in VUCP raises the self-supplied volume by 5.6738%. Therefore, the demand for groundwater is highly elastic with respect to the price of publicly-supplied water. This reflects that once a company has made the necessary investments to be able to self-supply, any increase in the publicly-supplied water tariff leads to intense substitution of publicly-supplied water by self-supplied groundwater. The value of this cross-price elasticity is far superior to that obtained by previous literature, both regarding the relationship between publicly and non-publicly-supplied water demand by households, where it ranges from 0.25 [20] to 1.37 [18], and when analyzing intake water vs. recirculation, with values between 0.14 [42] and 0.52 [43].

Finally, a 1% increase in the production level (Y) raises the self-supplied volume by 0.3776%. Therefore, the increase in production has a moderate impact on the demand for groundwater. The magnitude of this output elasticity is slightly smaller than that obtained by Reynaud [16] for manufacturing self-supply (0.58). It is also below the values obtained by other studies focusing on industrial publicly-supplied water, with values from 0.71 to 1.52 [45], and water recirculation, with values ranging from 0.38 [22] to 2.4 [42].

6. Conclusions

Based on a sample of 2579 manufacturing and service companies located in the city of Zaragoza (Spain), which have access to drinking water through the public-supply network and can opt for self-supply groundwater, we analyzed the determining factors in the decision whether or not to use groundwater and then analyzed the factors influencing the decision on the amount of groundwater used. For this purpose, we applied the Heckman two-stage model. The first stage examined the decision of whether or not to capture groundwater, whereas the second stage focused on the factors conditioning the volume of self-supplied groundwater.

The results obtained in the first stage indicate that the probability to use groundwater decreases when the fixed and variable cost of self-supply increase, whereas the probability increases when the fixed and variable cost of publicly-supplied water increase and when the firm belongs to the manufacturing sector. The results of the second stage show that the demand for self-supplied groundwater decreases when its variable cost increases and increases when the variable cost of publicly-supplied water or the output level increases. All the coefficients of the explanatory variables are significant, except the sectoral dummy in the second step, and their signs are consistent indicating that companies have economically rational behavior in the use of groundwater. Of particular relevance is the result indicating that groundwater self-supply is a substitute for public supply of drinking water.

The substitutability between both types of water is good news for productive efficiency, because companies can adapt the characteristics of the water collected to their needs, and thus avoid incurring unnecessary costs. From this perspective, all those policies favoring the possibility of choice between water sources are desirable. Urban planning and land management policies can contribute in this direction through the delimitation of industrial land facilitating, whenever possible, the location of companies on places where groundwater abstraction is feasible.

However, substitutability may not be good news for global efficiency and environmental sustainability. If the unit costs reflect the true social costs of the resource, both for publicly-supplied water and for groundwater self-supplied by companies, the possibility of substitution would have a positive effect on global efficiency and would not be detrimental to sustainability; but if part of those costs is not borne by companies (as usually happens when the extraction of groundwater contributes to the overexploitation of an aquifer or its contamination and when there is water shortage), the substitution of water from the public supply network by self-supplied groundwater can cause a loss of global efficiency and contribute to environmental unsustainability. In this regard, the solution lies, at least theoretically, in introducing a volumetric fee that taxes groundwater abstraction and discharge passing on the environmental and opportunity costs of the resource to users, in line with the cost recovery principle established in the European Water Framework Directive. However, the implementation of this fee faces significant difficulties, especially due to its information requirements and the opposition of those affected in the different sectors of activity. Thus, although some countries have volumetric fees for groundwater, they hardly comply with the aforementioned characteristics [48,49].

The marginal effects of the explanatory variables are very small in the first stage (effect on the probability of self-supply groundwater) but important in the second stage (effect on the volume of self-supplied water of the companies that self-supply).

The value (−0.50) of the direct price elasticity of groundwater demand (variation of the demand for groundwater when its variable unit cost (VUCS) varies) is in the middle range of those obtained in the literature for publicly-supplied water use in industry. Since this value is conditioned by the reduced magnitude of the VUCS, the adoption of a significant volumetric fee, by increasing the amount of VUCS, is expected to increase the elasticity and, therefore, the effectiveness of the groundwater pricing as an instrument for managing demand.

The high value (5.67) of the cross-price elasticity (variation of the demand for groundwater when the variable unit cost of publicly-supplied water (VUCP) varies) is above those obtained in the literature and shows the extraordinary easiness of substituting publicly-supplied water by self-supplied water once the users have made the necessary investments to make self-supply possible. This result alerts about the overestimation of water savings induced by the increase in the price of publicly-supplied water when users have access to several water sources. Under these conditions, if policy makers do not take into account the possibility of substitution of one type of water for another, they may overstate the effectiveness of publicly-supplied water pricing as an instrument to reduce pressure on the resource. Thus, in order to achieve the sustainability objective, the need to promote integrated water management must be emphasized, in line with the Water Framework Directive’s recommendation. To make progress on this matter, institutional mechanisms should be established to coordinate the different government agencies responsible for the different water masses and services associated with the water cycle, which in Spain belong to the three main government levels (city councils, autonomous communities, and the central government).

Given the limited evidence accumulated on the economic determinants of groundwater demand for industrial uses, more empirical studies are necessary. However, the results obtained in this research are in line with those obtained in other related fields, such as water recirculation in industry and water self-supply in households. The data on which this analysis is based are the best available, but they are not ideal because the lack of public meters in wells for control by water authorities forced us to estimate a proxy of groundwater use. Therefore, the systematic monitoring and control of groundwater extraction and discharge by the authorities are important conditions for improving research. In addition, in a possible future extension of this analysis, the inclusion of all alternative water inputs, such as recirculation, should be considered, although data constraints are significant.