Identification of Parameters of Evaporation Equations Using an Optimization Technique Based on Pan Evaporation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Study Area
2.3. Brief Description of Evaporation Equations
2.3.1. The Hamon Method
2.3.2. Penman Equation
2.3.3. Jensen–Haise Equation
2.3.4. Makkink (MK) Method
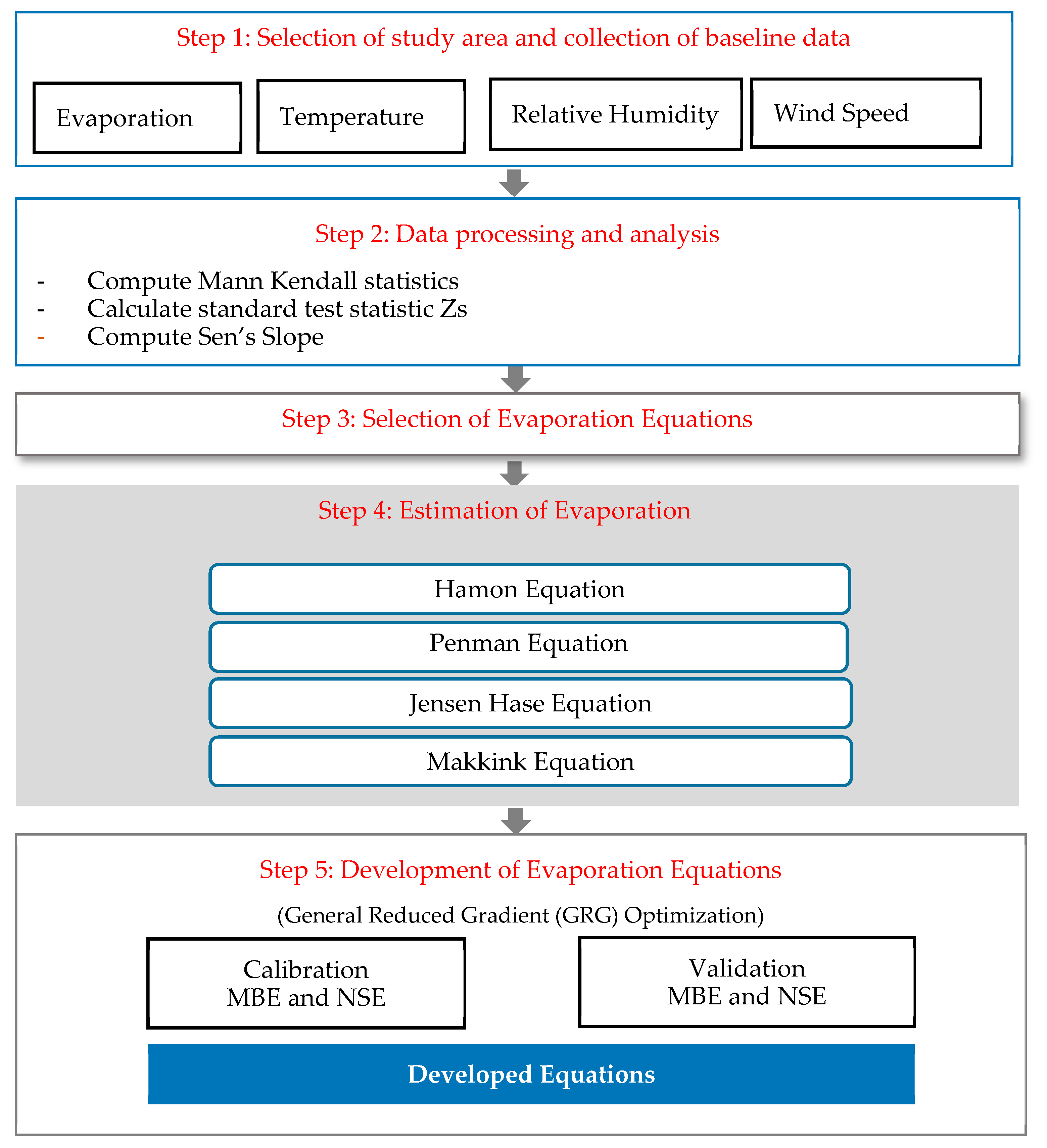
2.4. Development of Evaporation Equations Using Optimization
2.4.1. Mann–Kendall Test
2.4.2. Sen’s Slope Estimator Test
2.4.3. General Reduced Gradient (GRG) Method of Optimization
2.5. Performance Evaluation of Evaporation Equations
3. Results and Discussion
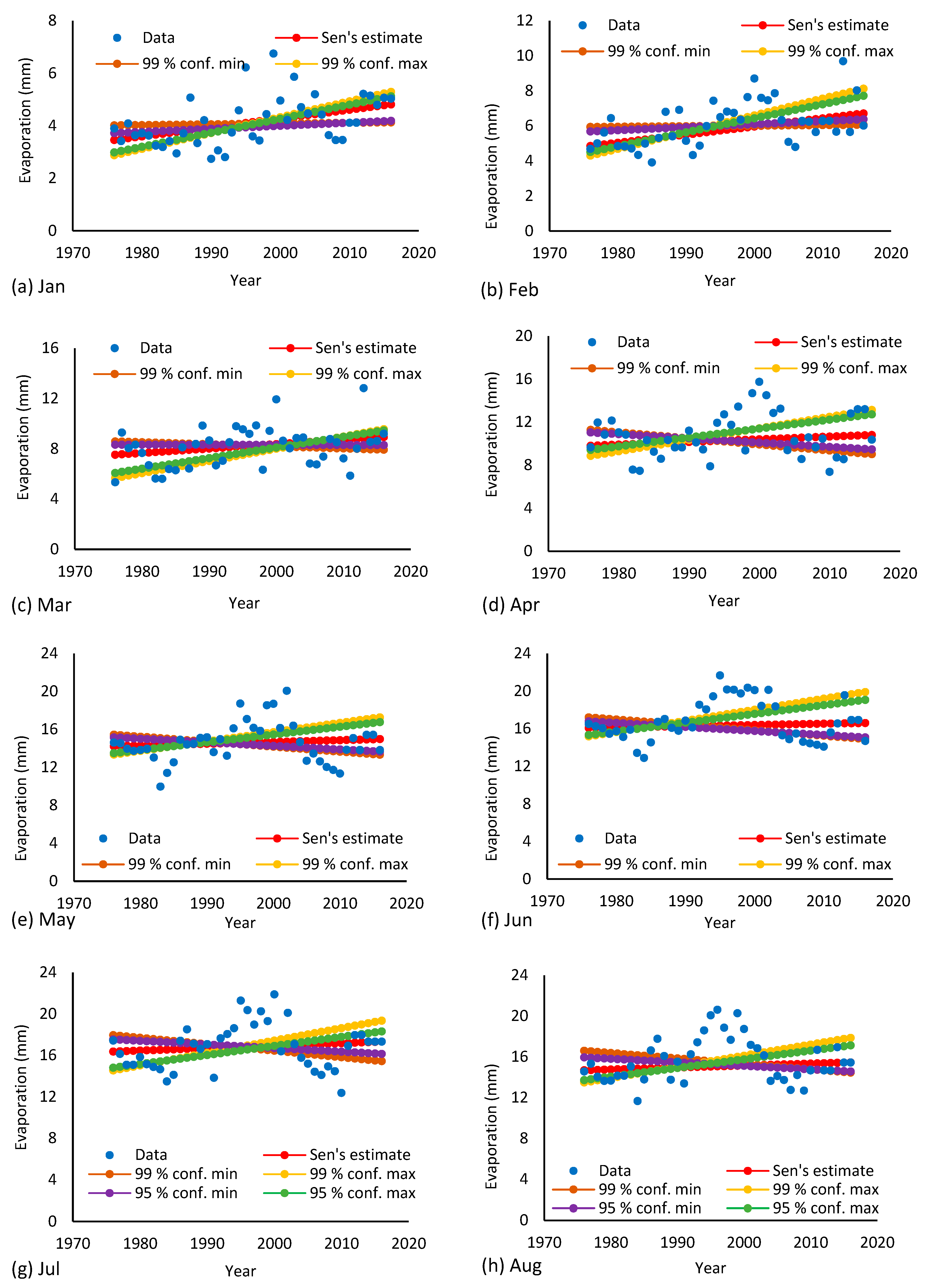
3.1. Data Analysis
3.2. Data Analysis Results
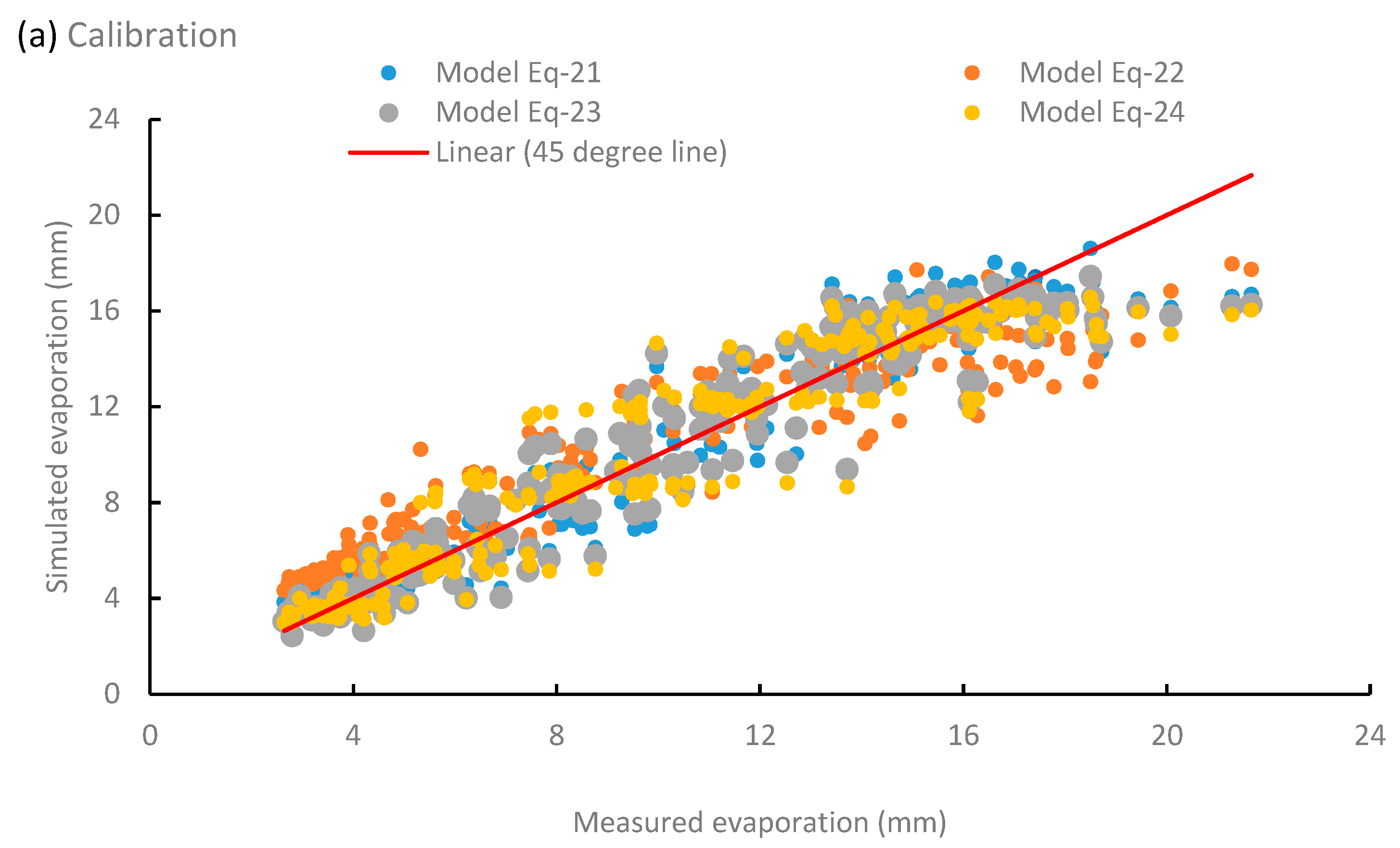
3.3. Comparison of Evaporation Simulated by Various Equations
3.4. Calibration and Validation of the Developed Equations
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tarawneh, Q.Y.; Chowdhury, S. Trends of Climate Change in Saudi Arabia: Implications on Water Resources. Climate 2018, 6, 8. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Roderick, M.L. Radiation, Surface Temperature and Evaporation Over Wet Surfaces. Q. J. R. Meteorol. Soc. 2019, 145, 1118–1129. [Google Scholar] [CrossRef]
- Stassen, C.; Dommenget, D.; Loveday, N. A Hydrological Cycle Model for the Globally Resolved Energy Balance (GREB) model v1.0. Geosci. Model Dev. 2019, 12, 425–440. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Ma, Y.; Ma, W.; Su, B.; Dong, X. Evaluation of Ten Methods for Estimating Evaporation in a Small High-Elevation Lake on the Tibetan Plateau. Appl. Clim. 2019, 136, 1033–1045. [Google Scholar] [CrossRef]
- Ahmadipour, A.; Shaibani, P.; Mostafavi, S.A. Assessment of Empirical Methods for Estimating Potential Evapotranspiration in Zabol Synoptic Station by REF-ET Model. Medbiotech J. 2019, 3, 1–4. [Google Scholar]
- Zolá, R.P.; Bengtsson, L.; Berndtsson, R.; Martí-Cardona, B.; Satgé, F.; Timouk, F.; Bonnet, M.P.; Mollericon, L.; Gamarra, C.; Pasapera, J. Modelling Lake Titicaca’s Daily and Monthly Evaporation. Hydrol. Earth Syst. Sci. 2019, 23, 657–668. [Google Scholar] [CrossRef] [Green Version]
- Al-Domany, M.; Touchart, L.; Bartout, P.; Choffel, Q. Direct Measurements and a New Mathematical Method to Estimate the Pond Evaporation of the French Midwest. Appl. Sci. Innov. Res. 2018, 2, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Duan, Z.; Bastiaanssen, W.G.M. Evaluation of Three Energy Balance-Based Evaporation Models for Estimating Monthly Evaporation for Five Lakes Using Derived Heat Storage Changes from a Hysteresis Model. Environ. Res. Lett. 2017, 12, 4005. [Google Scholar] [CrossRef] [Green Version]
- Scavo, F.B.; Tina, G.M.; Gagliano, A. Comparison of Evaporation Models for Free Water Basins Surfaces. In Proceedings of the 4th International Conference on Smart and Sustainable Technologies (SpliTech), Split, Croatia, 18–21 June 2019. [Google Scholar] [CrossRef]
- Said, M.A.; Hussein, M.M.A. Estimation of Evaporation from Lake Burullus (Egypt) Using Different Techniques. J. King Abdel Aziz Univ. Mar. Sci. 2013, 24, 55–67. [Google Scholar] [CrossRef]
- Crago, R.D.; Brutsaert, W.A. Comparison of Several Evaporation Equations. Water Resour. Res. 1992, 28, 951–954. [Google Scholar] [CrossRef]
- Hussein, M.M.A. Evaluation of Alexandria Eastern Harbor Evaporation Estimate Methods. Water Resour. Manag. 2015, 29, 3711. [Google Scholar] [CrossRef]
- Patel, J.A.; Majmundar, B.P. Development of Evaporation Estimation Methods for a Reservoir in Gujarat, India. Am. Water Works Assoc. 2016, 108, E489–E500. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, S.; Ma, D.; Liu, B.; Lin, H.; Li, S. Meteorological Factors Affecting Pan Evaporation in the Haihe River Basin, China. Water 2019, 11, 317. [Google Scholar] [CrossRef] [Green Version]
- Bhatt, R.; Hossain, A. Concept and Consequence of Evapotranspiration for Sustainable Crop Production in the Era of Climate Change. Adv. Evapotranspiration Methods Appl. 2019. [Google Scholar] [CrossRef] [Green Version]
- Meng, W.; Sun, X.; Ma, J.; Guo, X.; Zheng, L. Evaporation and Soil Surface Resistance of the Water Storage Pit Irrigation Trees in the Loess Plateau. Water 2019, 11, 648. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Kinefuchi, I.; Wilke, K.L.; Vaartstra, G.; Wang, E.N. A Unified Relationship for Evaporation Kinetics at Low Mach Numbers. Nat. Commun. 2019, 10, 2368. [Google Scholar] [CrossRef] [Green Version]
- Rayner, D.P. Wind Run Changes: The Dominant Factor Affecting Pan Evaporation Trends in Australia. J. Clim. 2007, 20, 3379–3394. [Google Scholar] [CrossRef]
- Cummings, N.W.; Richardson, B. Evaporation from Lakes. Phys. Rev. 1927, 30, 527. [Google Scholar] [CrossRef]
- Majidi, M.; Alizadeh, A.; Farid, A.; Vazifedoust, M. Estimating Evaporation from Lakes and Reservoirs under Limited Data Condition in a Semi-Arid Region. Water Resour. Manag. 2015, 29, 3711. [Google Scholar] [CrossRef]
- Andersen, M.E.; Jobson, H.E. Comparison of Techniques for Estimating Annual Lake Evaporation Using Climatological Data. Water Resour. Res. 1982, 18, 630–636. [Google Scholar] [CrossRef]
- Penman, H.L. Natural Evaporation from Open Water, Bare Soil, and Grass. Proc. R. Soc. 1948, 76, 372–383. [Google Scholar]
- Upadhyaya, A. Comparison of Different Methods to Estimate Mean Daily Evapotranspiration from Weekly Data at Patna, India. Irrig. Drain. Syst. Eng. 2006, 5, 1–7. [Google Scholar]
- Assouline, S.; Mahrer, Y. Evaporation from Lake Kinneret 1: Eddy Correlation System Measurements and Energy Budget Estimates. Water Resour. Res. 1993, 29, 901–910. [Google Scholar] [CrossRef]
- Collison, J.W. The Collison Floating Evaporation Pan: Design, Validation, and Comparison. 2019. Available online: https://digitalrepository.unm.edu/ce_etds/233 (accessed on 23 October 2019).
- Tanny, J.; Cohen, S.; Assouline, S.; Lange, F.; Grava, A.; Berger, D.; Teltch, B.; Parlange, M.B. Evaporation from a Small Water Reservoir: Direct Measurements and Estimates. J. Hydrol. 2008, 351, 218–229. [Google Scholar] [CrossRef] [Green Version]
- Chu, C.R.; Li, M.H.; Chang, Y.F.; Liu, T.C.; Chen, Y.Y. Wind-Induced Splash in Class a Evaporation Pan. J. Geophys. Res. 2012, 117, D11101. [Google Scholar] [CrossRef]
- Morton, F.I. Catchment Evaporation and Potential Evaporation Further Development of a Climatological Relationship. J. Hydrol. 1971, 12, 81–99. [Google Scholar] [CrossRef]
- Yao, H.; Creed, I.F. Determining Spatially Distributed Annual Water Balances for Un-Gauged Locations on Shikoku Island, Japan: A Comparison of Two Interpolators. Hydrol. Sci. J. 2005, 50, 245–263. [Google Scholar] [CrossRef]
- Winter, T.C.; Rosenberry, D.O.; Sturrock, A.M. Evaluation of 11 Equations for Determining Evaporation for a Small Lake in The North Central United States. Water Resour. Res. 1995, 31, 983–993. [Google Scholar] [CrossRef]
- Winter, T.; Buso, D.; Rosenberry, D.; Likens, G.; Sturrock, A., Jr.; Mau, D. Evaporation determined by the energy budget method for Mirror Lake, New Hampshire. Limnol. Oceanogr. 2003, 48, 995–1009. [Google Scholar] [CrossRef] [Green Version]
- Moazed, H.; Ghaemii, A.A.; Rafiee, M.R. Evaluation of Several Reference Evapotranspiration Methods: A Comparative Study of Greenhouse and Outdoor Conditions. Trans. Civ. Eng. 2014, 38, 421. [Google Scholar]
- Paparrizos, S.; Maris, F.; Matzarakis, A. Estimation and Comparison of Potential Evapotranspiration Based on Daily and Monthly Data from Sperchios Valley in Central Greece. Glob. Nest J. 2014, 16, 204–217. [Google Scholar]
- Anderson, R.J.; Smith, S.D. Evaporation Coefficient for the Sea Surface from Eddy Flux. J. Geophys. Res. 1981, 86, 449–456. [Google Scholar] [CrossRef]
- Djaman, K.; Balde, A.B.; Sow, A.; Muller, B.; Irmak, S.; N’Diaye, M.K.; Manneh, B.; Moukoumbi, Y.D.; Futakuchi, K.; Saito, K. Evaluation of Sixteen Reference Evapotranspiration Methods under Sahelian Conditions in the Senegal River Valley. J. Hydrol. Reg. Stud. 2015, 3, 139–159. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Lu, F.; Xiao, W.; Zhu, K.; Zhou, Y.; Xie, Z. Performance of Twelve Reference Evapotranspiration Estimation Methods to Penman-Monteith Method and the Potential Influences in Northeast China. Meteorol. Appl. 2019, 26, 83–96. [Google Scholar] [CrossRef] [Green Version]
- Hosseinzadeh, T.P.; Tabari, H.; Abghari, H. Pan Evaporation and Reference Evapotranspiration Trend Detection in Western Iran with Consideration of Data Persistence. Hydrol. Res. 2014, 45, 213–225. [Google Scholar] [CrossRef]
- Lee, T.; Najim, M.; Aminul, M. Estimating Evapotranspiration of Irrigated Rice at the West Coast of the Peninsular of Malaysia. J. Appl. Irrig. Sci. 2004, 39, 103–117. [Google Scholar]
- Muniandy, J.M.; Yusop, Z.; Askari, M. Evaluation of Reference Evapotranspiration Models and Determination of Crop Coefficient for Momordica Charantia and Capsicum Annuum. Agric. Water Manag. 2016, 169, 77–89. [Google Scholar] [CrossRef]
- Ali, M.H.; Lee, T.; Kwok, C.; Eloubaidy, A.F. Modelling Evaporation and Evapotranspiration under Temperature Change in Malaysia. Pertanika J. Sci. Technol. 2000, 8, 191–204. [Google Scholar]
- Ali, M.H.; Shui, L.T. Potential Evapotranspiration Model for Muda Irrigation Project, Malaysia. Water Resour. Manag. 2008, 23, 57. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Tukimat, N.N.A.; Harun, S.; Shahid, S. Comparison of Different Methods in Estimating Potential Evapotranspiration at Muda Irrigation Scheme of Malaysia. J. Agric. Rural Dev. Trop. Subtrop. 2012, 113, 77–85. [Google Scholar]
- Doorenbos, J.; Pruitt, W. Crop Water Requirements; FAO Irrigation and Drainage Paper 24; FAO Land and Water Development Division: Rome, Italy, 1977; pp. 1–144. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Hamon, W.R. Estimating Potential Evapotranspiration. J. Hydraul. Div. Proc. Am. Soc. Civ. Eng. 1963, 871, 107–120. [Google Scholar]
- Lang, D.; Zheng, Z.; Shi, J.; Liao, F.; Ma, X.; Wang, W.; Chen, X.; Zhang, M. A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China. Water 2017, 7, 734. [Google Scholar] [CrossRef] [Green Version]
- Doorenbus, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements, Irrigation and Drainage Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 1977. [Google Scholar]
- Alazrd, M.; Leduc, C.; Travi, Y.; Boulet, G.; Ben Salem, A. Estimating Evaporation in Semi-Arid Areas Facing Data Scarcity: Examples of the El Haouraeb Dam (Merguellil catchment, Central Tunisia). J. Hydrol. Reg. Stud. 2015, 3, 265–284. [Google Scholar] [CrossRef] [Green Version]
- Yao, H.; Terakawa, A.; Chen, S. Rice Water Use and Response to Potential Climate Changes: Calculation and Application to Jianghan, China. In Proceedings of the International Conference on Water Resources and Environment Research, Kyoto, Japan, 5–9 June 1996; Volume 2, pp. 611–618. [Google Scholar]
- Souch, C.; Wolfe, C.P.; Susan, C.; Grimmond, B. Wetland Evaporation and Energy Partitioning: Indiana Dunes National Lakeshore. J. Hydrol. 1996, 184, 189–208. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Simplified Version for the Penman Evaporation Equation Using Routine Weather Data. J. Hydrol. 2006, 331, 690–702. [Google Scholar] [CrossRef]
- Vardavas, I.M. Modeling the Seasonal Radiation of Net All-Wave Radiation Flux and Evaporation in a Tropical Wet-Dry Region. Ecol. Modell. 1987, 39, 247–268. [Google Scholar] [CrossRef]
- Vardvas, I.M.; Fountoulakis, A. Estimation of Lake Evaporation from Standard Meteorological Measurements: Application to Four Australian Lakes in Different Climatic Regions. Ecol. Modell. 1996, 84, 139–150. [Google Scholar] [CrossRef]
- Jensen, M.E.; Hake, H.R. Estimating Evapotranspiration from Solar Radiation. J. Irrig. Drain. Div. 1963, 96, 25–28. [Google Scholar]
- Nagai, A. Estimation of Pan Evaporation by Makkink Equation. J. Jpn. Soc. Hydrol. Water Resour. 1993, 6, 238–243. [Google Scholar] [CrossRef]
- Mann, H.B. Non-Parametric Tests against Trend. Econmetrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles, G., Ed.; Griffin: London, UK, 1975. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Test. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Rathnayake, U. Comparison of Statistical Methods to Graphical Methods in Rainfall Trend Analysis: Case Studies from Tropical Catchments. Adv. Meteorol. 2019. [Google Scholar] [CrossRef] [Green Version]
- Ali, R.O.; Abubaker, S.H. Trend Analysis Using Mann-Kendall, Sen’s Slope Estimator Test and Innovative Trend Analysis Method in River Basin, China: Review. Int. J. Eng. Technol. 2019, 8, 110–119. [Google Scholar]
- Totaro, V.; Gioia, A.; Iacobellis, V. Power of Parametric and Non-Parametric Tests for Trend Detection in Annual Maximum Series. Hydrol. Earth Syst. Sci. 2019, 2019, 8603586. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Yang, B.; Han, J.; Huang, Y. Robust Linear Programming and Its Application to Water and Environmental Decision-Making under Uncertainty. Sustainability 2019, 11, 33. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting Through Conceptual Models, Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Lu, J.; Sun, G.; McNulty, S.; Amatya, D.M.A. Comparison of Six Potential Evapotranspiration Methods for Regional Use in the Southeastern United States. J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Poyen, F.B.; Ghosh, A.K.; Kundu, P. Review on Different Evapotranspiration Empirical Equations. Int. J. Adv. Eng. Manag. Sci. 2016, 2, 17–24. [Google Scholar]
- Fernandes, L.C.; Paiva, C.M.; Filho, O.C.R. Evaluation of Six Empirical Evapotranspiration Equations—Case Study. Rev. Bras. Meteorol. 2012, 27, 272–280. [Google Scholar] [CrossRef] [Green Version]







| Reference | Data Required | Identified Parameters by Optimization | |||
|---|---|---|---|---|---|
| Temperature | Humidity | Wind | Radiation | ||
| Yang and Roderick 2019 [2] | √ | × | √ | √ | × |
| Stassen et al. 2019 [3] | √ | × | √ | × | × |
| Wang et al. 2019 [4] | √ | √ | √ | × | × |
| Ahmadipour et al. 2019 [5] | √ | √ | √ | × | × |
| Zolá et al. 2019 [6] | √ | × | √ | × | × |
| Al-Domany et al. 2018 [7] | √ | × | √ | × | × |
| Duan and Bastiaanssen 2017 [8] | √ | × | √ | √ | × |
| Said and Hussein 2013 [10] | √ | √ | × | × | × |
| Hussein 2015 [12] | √ | √ | √ | √ | × |
| Patel and Majmundar 2016 [13] | √ | × | × | √ | × |
| Majidi et al. 2015 [20] | √ | × | × | √ | × |
| Morton 1971 [28] | √ | √ | × | × | × |
| Yao and Creed 2005 [29] | √ | √ | × | × | × |
| Winter et al. 1995 & 2003 [30,31] | √ | √ | × | √ | × |
| Moazed et al. 2014 [32] | √ | √ | √ | √ | × |
| Paparrizos et al. 2014 [33] | √ | √ | √ | √ | × |
| Evaporation | Temperature | ||||||
|---|---|---|---|---|---|---|---|
| Month | Daily Maximum (mm) | Daily Minimum (mm) | Daily Average (mm) | Monthly (mm) | Average of Daily Maximum (°C) | Average of Daily Minimum (°C) | Daily Mean (°C) |
| Jan. | 8.15 | 2.06 | 4.21 | 129.06 | 19.92 | 6.45 | 13.18 |
| Feb. | 9.55 | 3.18 | 6.14 | 171.33 | 22.88 | 8.45 | 15.67 |
| Mar. | 12.49 | 3.78 | 8.13 | 250.82 | 27.16 | 12.45 | 19.81 |
| Apr. | 16.31 | 4.73 | 10.72 | 322.82 | 32.94 | 17.46 | 25.20 |
| May. | 19.56 | 8.18 | 14.60 | 451.45 | 39.10 | 22.90 | 31.00 |
| Jun. | 20.75 | 12.95 | 16.88 | 504.02 | 42.55 | 24.99 | 33.77 |
| Jul. | 20.72 | 12.90 | 16.87 | 520.10 | 43.53 | 25.36 | 34.45 |
| Aug. | 19.27 | 12.22 | 15.80 | 485.51 | 43.77 | 25.59 | 34.68 |
| Sep. | 17.91 | 9.94 | 13.91 | 412.40 | 41.47 | 22.90 | 32.19 |
| Oct. | 14.94 | 6.61 | 10.56 | 322.62 | 35.91 | 17.93 | 26.92 |
| Nov. | 11.68 | 3.08 | 6.48 | 190.70 | 27.15 | 12.50 | 19.83 |
| Dec. | 8.08 | 2.23 | 4.28 | 131.94 | 21.70 | 8.32 | 15.01 |
| Month | Jan. | Feb. | Mar. | Apr. | May. | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z values | 2.97 | 2.79 | 1.92 | 0.65 | 0.69 | 0.43 | 0.74 | 0.84 | 1.44 | 1.75 | 2.52 | 2.84 |
| Trend | Yes | Yes | No | No | No | No | No | No | No | No | Yes | Yes |
| Error | Hamon Method | Penman Method | Jensen–Haise Method | Makkink Method |
|---|---|---|---|---|
| Maximum Absolute Error (mm) | 5.66 | 6.66 | 5.76 | 6.48 |
| Minimum Absolute Error (mm) | −6.25 | −4.41 | −5.07 | −5.11 |
| Average Absolute Error (mm) | 1.75 | 1.80 | 1.75 | 1.84 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghumman, A.R.; Ghazaw, Y.M.; Alodah, A.; Rauf, A.u.; Shafiquzzaman, M.; Haider, H. Identification of Parameters of Evaporation Equations Using an Optimization Technique Based on Pan Evaporation. Water 2020, 12, 228. https://doi.org/10.3390/w12010228
Ghumman AR, Ghazaw YM, Alodah A, Rauf Au, Shafiquzzaman M, Haider H. Identification of Parameters of Evaporation Equations Using an Optimization Technique Based on Pan Evaporation. Water. 2020; 12(1):228. https://doi.org/10.3390/w12010228
Chicago/Turabian StyleGhumman, Abdul Razzaq, Yousry Mehmood Ghazaw, Abdullah Alodah, Ateeq ur Rauf, Md. Shafiquzzaman, and Husnain Haider. 2020. "Identification of Parameters of Evaporation Equations Using an Optimization Technique Based on Pan Evaporation" Water 12, no. 1: 228. https://doi.org/10.3390/w12010228
APA StyleGhumman, A. R., Ghazaw, Y. M., Alodah, A., Rauf, A. u., Shafiquzzaman, M., & Haider, H. (2020). Identification of Parameters of Evaporation Equations Using an Optimization Technique Based on Pan Evaporation. Water, 12(1), 228. https://doi.org/10.3390/w12010228







