Discharge Coefficients for Sluice Gates Set in Weirs at Different Upstream Wall Inclinations
Abstract
:1. Introduction
- two vertical vortices are found at the upstream sides of the sluice gate, interfering with the flow;
- a recirculation zone is present on the upper part of the flow upstream from the sluice gate, influencing the contraction of the effluent vein and consequently the discharge coefficient.
2. Materials and Methods
2.1. Dimensional Analysis
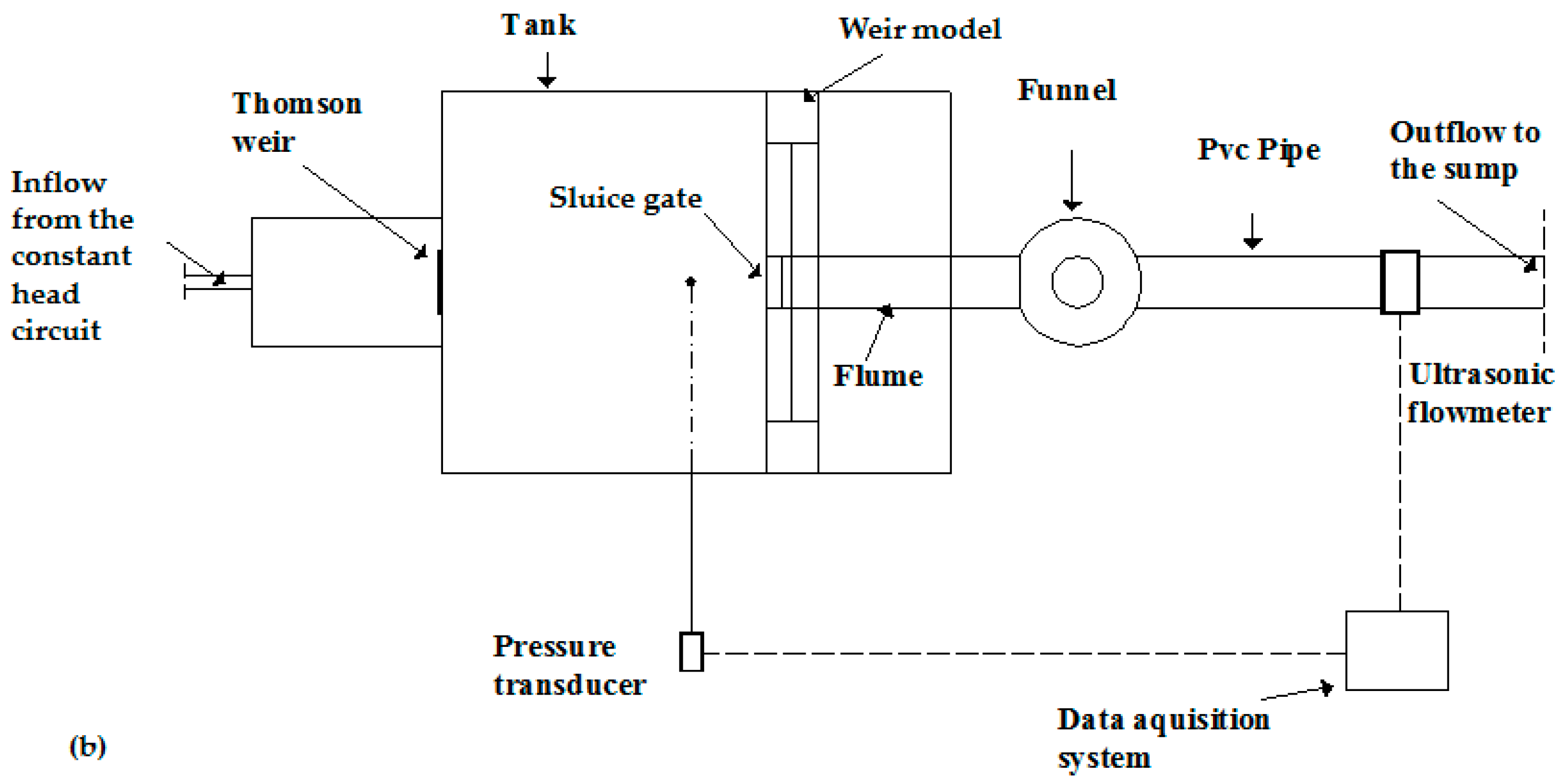
2.2. Experimental Set-Up and Tests
2.3. Numerical Simulations
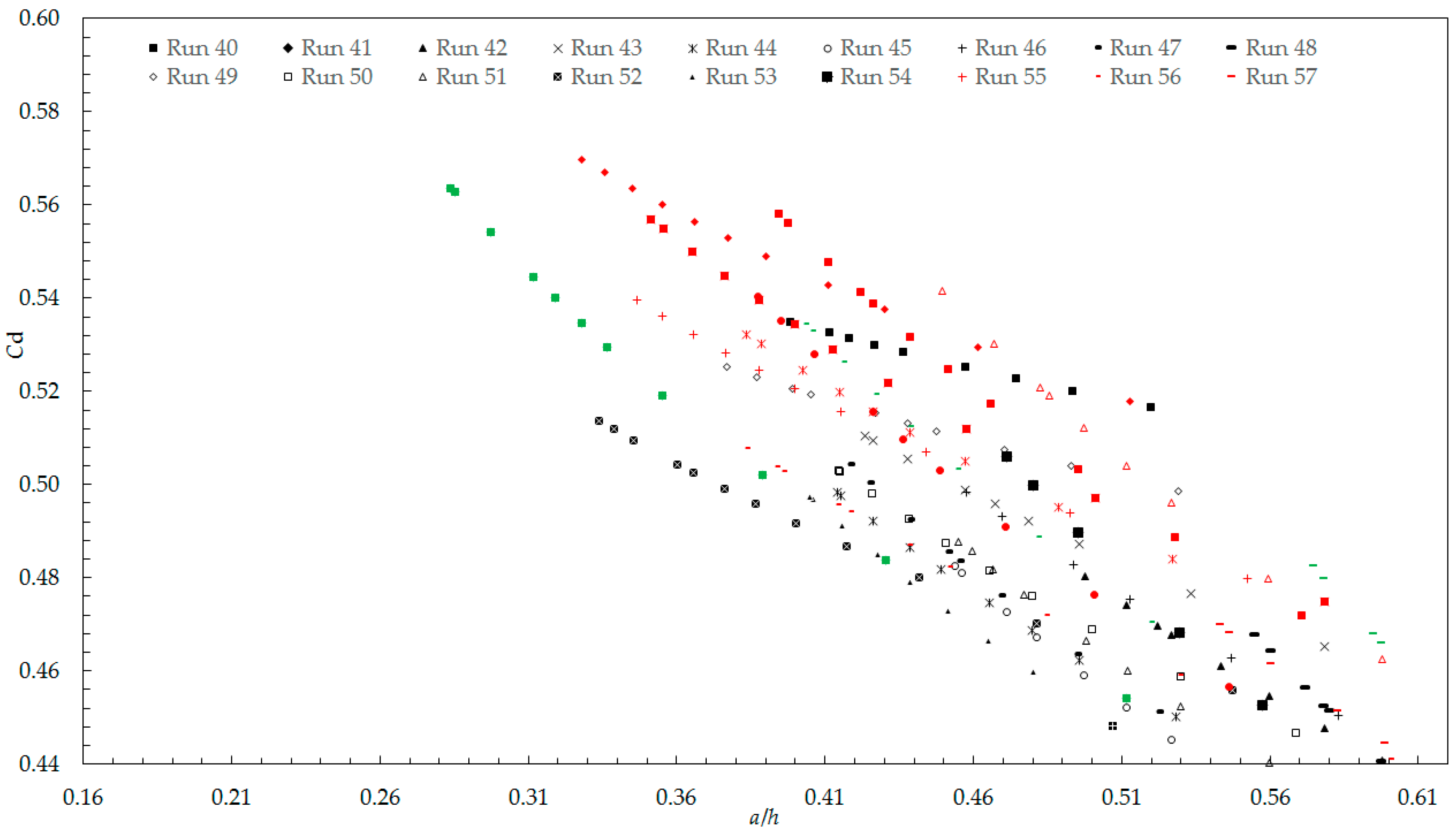
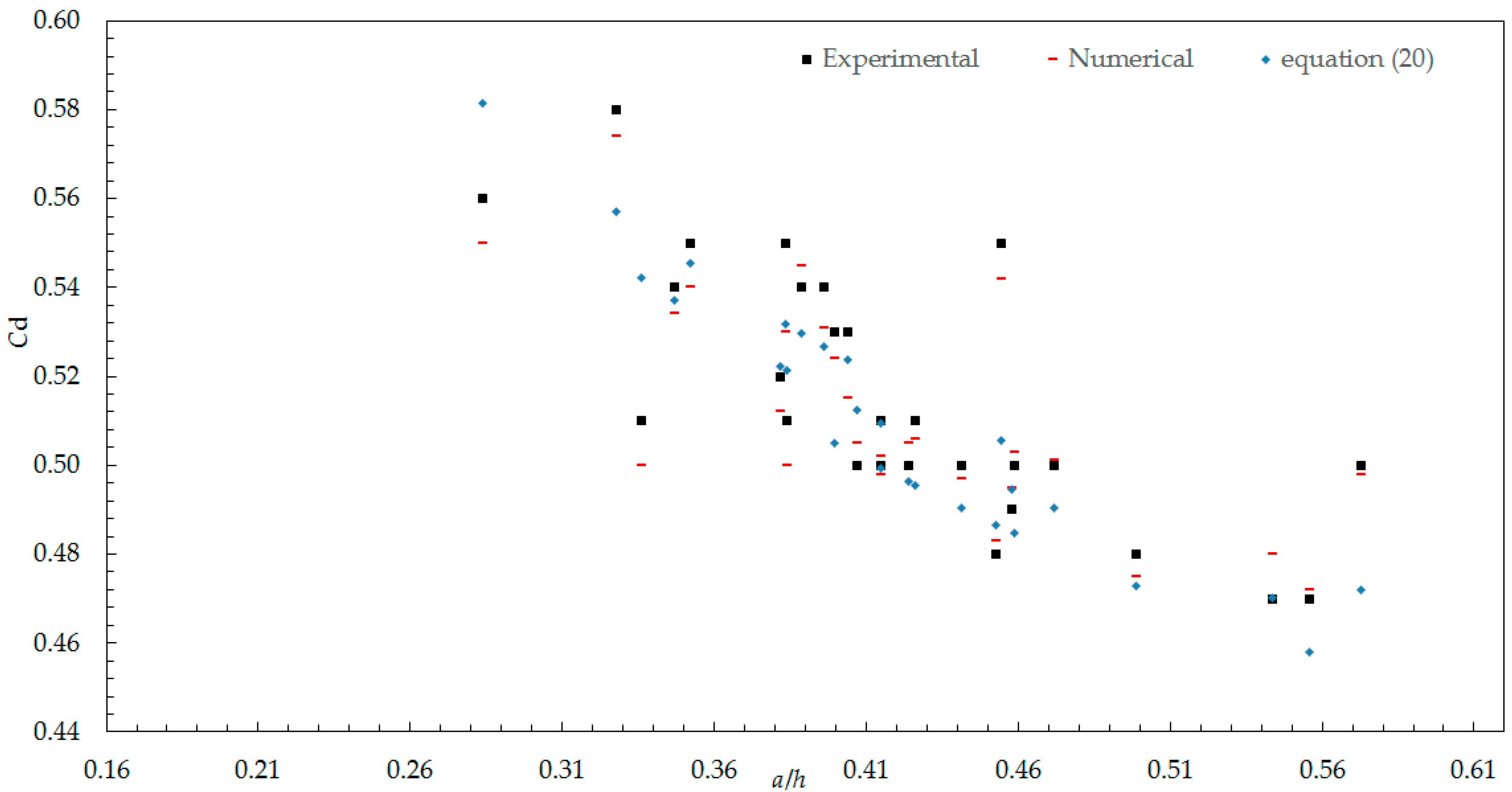
3. Results and Discussion
Experimental Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sinniger, R.; Hager, W.H. Constructions Hydrauliques. Ecoulements Stationnaires; Presses Polytechniques Romandes; Traité de Génie Civil de l’Ecole polytechniques fédérale de Lausanne: Lausanne, Switzerland, 1988; Volume 15. [Google Scholar]
- Montes, J.S. Irrotational flow and real fluid effects under planar sluice gates. J. Hydraul. Eng. 1997, 123, 219–232. [Google Scholar] [CrossRef]
- Gentilini, B. Efflusso dalle luci soggiacenti alle paratoie piane inclinate e a settore. L’Energia Elettrica 1941, 18, 361–380. [Google Scholar]
- Rajaratnam, N.; Subramanya, K. Flow equation for the sluice gate. J. Irrig. Drain. Eng. 1967, 93, 167–186. [Google Scholar]
- Roth, A.; Hager, W.H. Underflow of standard sluice gate. Exp. Fluids 1999, 27, 339–350. [Google Scholar] [CrossRef]
- Rajaratnam, N. Free flow immediately below sluice gates. J. Hydraul. Div. ASCE 1977, 103, 345–351. [Google Scholar]
- Kim, D.G. Contraction and discharge coefficient of free flow past a sluice gate. In Proceedings of the Korea Water Resources Association Conference; Korea Water Resources Association: Seoul, Korea, 2005; pp. 1281–1282. [Google Scholar]
- Kim, D.G. Numerical Analysis of Free Flow Past a Sluice Gate. KSCE J. Civ. Eng. 2007, 11, 127–132. [Google Scholar] [CrossRef]
- Akoz, M.S.; Kirkgoz, M.S.; Oner, A.A. Experimental and numerical modeling of a sluice gate flow. J. Hydraul. Res. 2009, 47, 167–176. [Google Scholar] [CrossRef]
- Oskuyi, N.; Salmasi, F. Vertical Sluice Gate Discharge Coefficient. J. Civ. Eng. Urban. 2012, 2, 108–114. [Google Scholar]
- Raju, R. Scale Effects in Analysis of Discharge Characteristics of Weir and Sluice Gates; Kobus: Esslingen am Neckar, Germany, 1984. [Google Scholar]
- Lauria, A. Efflusso da luce di fondo di una traversa per laminazione delle piene. Analisi Sperimentale e Modellazione Numerica 3D. Ph.D. Thesis, Università della Calabria, Rende, Italy, 2008. [Google Scholar]
- Calomino, F.; Lauria, A.; Miglio, A.; Palma, G. Discharge coefficients for sluice gates in weir. In Proceedings of the Congress-International Association for Hydraulic Research, Venice, Italy, 1–6 July 2007. [Google Scholar]
- Calomino, F.; Lauria, A.; Miglio, A.; Palma, G. Determinazione sperimentale dei coefficienti d’efflusso da paratoie con diversa inclinazione per casse d’espansione. In Proceedings of the 30° Corso di aggiornamento in Tecniche per la difesa dall’inquinamento, Guardia Piemontese Terme (CS), Cosenza, Italy, June 2009; pp. 261–290. [Google Scholar]
- Calomino, F.; Lauria, A. 3-D Underflow of a Sluice Gate at a Channel Inlet; Experimental Results and CFD Simulations. J. Civ. Eng. Urban. 2014, 4, 501–508. [Google Scholar]
- Aristodemo, F.; Lauria, A.; Tripepi, G.; Rivera-Velasquéz, M.F.; Fallico, C. Smoothing of Slug Tests for Laboratory Scale Aquifer Assessment—A Comparison among Different Porous Media. Water 2018, 11, 1569. [Google Scholar] [CrossRef] [Green Version]
- Calomino, F.; Alfonsi, G.; Gaudio, R.; D’Ippolito, A.; Lauria, A.; Tafarojnoruz, A.; Artese, S. Experimental and numerical study of free-surface flows in a corrugated pipe. Water 2018, 10, 638. [Google Scholar] [CrossRef] [Green Version]
- D’Ippolito, A.; Lauria, A.; Alfonsi, G.; Calomino, F. Investigation of flow resistance exerted by rigid emergent vegetation in open channel. Acta Geophys. 2019, 67, 971–986. [Google Scholar] [CrossRef]
- Lauria, A.; Alfonsi, G. Numerical investigation of ski jump hydraulics. J. Hydraul. Eng. ASCE 2020, in press. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Cañada, CA, USA, 1998. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- FLOW SCIENCE. FLOW-3D User Manual: Excellence in Flow Modeling, Software Version 9.1; Flow Science, Inc.: Santa Fe, NM, USA, 2004. [Google Scholar]
- Alfonsi, G.; Lauria, A.; Primavera, L. Recent reults from analysis of flow structures and energy modes induced by viscous wave around a surface-piercing cylinder. Math. Probl. Eng. 2017. [Google Scholar] [CrossRef] [Green Version]
- Alfonsi, G.; Lauria, A.; Primavera, L. On evaluation of wave forces and runups on cylindrical obstacles. J. Flow Visual. Image Process. 2013, 20, 269–291. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Alfonsi, G.; Lauria, A.; Primavera, L. Proper orthogonal flow modes in the viscous-fluid wave-diffraction case. J. Flow Visual. Image Process. 2013, 20, 227–241. [Google Scholar] [CrossRef]
- Alfonsi, G.; Lauria, A.; Primavera, L. The field of flow structures generated by a wave of viscous fluid around vertical circular cylinder piercing the free surface. Procedia Eng. 2015, 116, 103–110. [Google Scholar] [CrossRef] [Green Version]
- Alfonsi, G.; Lauria, A.; Primavera, L. A study of the vortical structures past the lower portion of the Ahmed car model. J. Flow Visual. Image Process. 2013, 19, 81–95. [Google Scholar] [CrossRef]
- Novak, P.; Moffat, A.I.B.; Nalluri, C.; Narayanan, R. Hydraulic Structures; E & FN Spon: London, UK, 1996. [Google Scholar]










| Run | θ (°) | a (mm) | b (mm) | h (mm) | Q (L/s) | b/a | a/h | Cd |
|---|---|---|---|---|---|---|---|---|
| 1 | 63.4 | 20 | 142 | 43.4 ÷ 116.4 | 1.58 ÷ 2.74 | 7.10 | 0.17 ÷ 0.46 | 0.60 ÷ 0.64 |
| 2 | 63.4 | 24 | 86 | 40.7 ÷ 109.1 | 1.02 ÷ 1.85 | 3.55 | 0.22 ÷ 0.60 | 0.55 ÷ 0.61 |
| 3 | 63.4 | 30 | 86 | 57.6 ÷ 140.9 | 1.45 ÷ 2.53 | 2.84 | 0.22 ÷ 0.53 | 0.52 ÷ 0.58 |
| 4 | 63.4 | 30 | 106 | 52.6 ÷ 130.4 | 1.62 ÷ 3.04 | 3.55 | 0.23 ÷ 0.57 | 0.50 ÷ 0.60 |
| 5 | 63.4 | 30 | 142 | 56.4 ÷ 151.4 | 2.43 ÷ 4.44 | 4.73 | 0.20 ÷ 0.53 | 0.54 ÷ 0.61 |
| 6 | 63.4 | 37 | 106 | 64.9 ÷ 121.8 | 2.15 ÷ 3.41 | 2.84 | 0.31 ÷ 0.58 | 0.48 ÷ 0.56 |
| 7 | 63.4 | 40 | 142 | 91.9 ÷ 131.4 | 4.08 ÷ 5.03 | 3.55 | 0.30 ÷ 0.44 | 0.54 ÷ 0.55 |
| 8 | 63.4 | 50 | 86 | 89.0 ÷ 105.0 | 2.73 ÷ 3.13 | 1.72 | 0.48 ÷ 0.56 | 0.48 ÷ 0.51 |
| 9 | 63.4 | 50 | 142 | 86.8 ÷ 128.8 | 4.33 ÷ 6.08 | 2.84 | 0.39 ÷ 0.58 | 0.47 ÷ 0.54 |
| 10 | 63.4 | 53 | 106 | 90.5 ÷ 123.6 | 3.45 ÷ 4.40 | 2.00 | 0.43 ÷ 0.59 | 0.46 ÷ 0.50 |
| 11 | 63.4 | 60 | 86 | 104.8 ÷ 136.9 | 3.45 ÷ 4.25 | 1.43 | 0.44 ÷ 0.57 | 0.47 ÷ 0.50 |
| 12 | 63.4 | 60 | 142 | 100.9 ÷ 144.5 | 5.65 ÷ 7.48 | 2.37 | 0.42 ÷ 0.59 | 0.47 ÷ 0.52 |
| 13 | 63.4 | 62 | 106 | 102.1 ÷ 142.6 | 4.15 ÷ 5.46 | 1.72 | 0.43 ÷ 0.61 | 0.45 ÷ 0.50 |
| 14 | 63.4 | 74 | 106 | 122.8 ÷ 145.9 | 5.55 ÷ 6.43 | 1.43 | 0.51 ÷ 0.60 | 0.46 ÷ 0.48 |
| 15 | 63.4 | 75 | 86 | 124.8 ÷ 140.5 | 4.52 ÷ 5.02 | 1.15 | 0.53 ÷ 0.60 | 0.45 ÷ 0.47 |
| Run | θ (°) | a (mm) | b (mm) | h (mm) | Q (L/s) | b/a | a/h | Cd |
|---|---|---|---|---|---|---|---|---|
| 16 | 63.4 | 50 | 142 | 86.8 ÷ 128.0 | 4.30 ÷ 6.10 | 2.84 | 0.58 ÷ 0.39 | 0.47 ÷ 0.54 |
| 17 | 63.4 | 60 | 142 | 100.9 ÷ 144.5 | 5.60 ÷ 7.50 | 2.37 | 0.59 ÷ 0.41 | 0.47 ÷ 0.52 |
| 18 | 63.4 | 50 | 86 | 89.0 ÷ 104.8 | 2.70 ÷ 3.50 | 1.72 | 0.56 ÷ 0.48 | 0.48 ÷ 0.51 |
| 19 | 63.4 | 60 | 86 | 104.8 ÷ 136.9 | 3.50 ÷ 4.30 | 1.43 | 0.57 ÷ 0.44 | 0.47 ÷ 0.50 |
| 20 | 63.4 | 75 | 86 | 124.8 ÷ 140.5 | 4.50 ÷ 5.00 | 1.15 | 0.60 ÷ 0.53 | 0.45 ÷ 0.47 |
| 21 | 63.4 | 53 | 106 | 90.5 ÷ 123.6 | 3.50 ÷ 4.40 | 2.00 | 0.59 ÷ 0.43 | 0.46 ÷ 0.50 |
| 22 | 63.4 | 62 | 106 | 102.1 ÷ 142.6 | 4.20 ÷ 5.50 | 1.72 | 0.60 ÷ 0.43 | 0.46 ÷ 0.50 |
| 23 | 63.4 | 74 | 106 | 122.8 ÷ 143.3 | 5.60 ÷ 6.40 | 1.43 | 0.60 ÷ 0.51 | 0.46 ÷ 0.48 |
| 24 | 90.0 | 50 | 86 | 73.5 ÷ 97.0 | 2.40 ÷ 3.20 | 1.72 | 0.68 ÷ 0.51 | 0.47 ÷ 0.53 |
| 25 | 90.0 | 60 | 86 | 98.2 ÷ 124.8 | 3.50 ÷ 4.30 | 1.43 | 0.61 ÷ 0.48 | 0.49 ÷ 0.53 |
| 26 | 90.0 | 75 | 86 | 109.7 ÷ 129.1 | 4.40 ÷ 5.10 | 1.15 | 0.68 ÷ 0.58 | 0.46 ÷ 0.50 |
| 27 | 90.0 | 53 | 106 | 91.1 ÷ 112.1 | 3.80 ÷ 4.40 | 2.00 | 0.58 ÷ 0.47 | 0.50 ÷ 0.53 |
| 28 | 90.0 | 62 | 106 | 103.9 ÷ 124.5 | 4.60 ÷ 5.40 | 1.71 | 0.60 ÷ 0.50 | 0.49 ÷ 0.52 |
| 29 | 90.0 | 74 | 106 | 108.4 ÷ 131.2 | 5.60 ÷ 6.30 | 1.43 | 0.68 ÷ 0.56 | 0.40 ÷ 0.50 |
| 30 | 90.0 | 50 | 142 | 101.5 ÷ 123.9 | 5.30 ÷ 6.40 | 2.84 | 0.49 ÷ 0.40 | 0.53 ÷ 0.57 |
| 31 | 90.0 | 60 | 142 | 109.6 ÷ 138.6 | 6.20 ÷ 7.60 | 2.37 | 0.55 ÷ 0.43 | 0.50 ÷ 0.54 |
| 32 | 56.3 | 50 | 142 | 78.8 ÷ 155.0 | 4.30 ÷ 6.60 | 2.84 | 0.63 ÷ 0.32 | 0.48 ÷ 0.53 |
| 33 | 56.3 | 60 | 142 | 90.0 ÷ 153.9 | 5.20 ÷ 7.60 | 2.37 | 0.67 ÷ 0.39 | 0.46 ÷ 0.52 |
| 34 | 56.3 | 53 | 106 | 81.4 ÷ 125.9 | 3.30 ÷ 4.50 | 2.00 | 0.65 ÷ 0.42 | 0.46 ÷ 0.51 |
| 35 | 56.3 | 62 | 106 | 93.9 ÷ 139.7 | 4.00 ÷ 5.50 | 1.71 | 0.66 ÷ 0.44 | 0.45 ÷ 0.50 |
| 36 | 56.3 | 74 | 106 | 104.6 ÷ 143.8 | 4.90 ÷ 6.50 | 1.43 | 0.71 ÷ 0.51 | 0.43 ÷ 0.49 |
| 37 | 56.3 | 50 | 86 | 72.0 ÷ 102.8 | 2.30 ÷ 3.20 | 1.72 | 0.69 ÷ 0.49 | 0.44 ÷ 0.52 |
| 38 | 56.3 | 60 | 86 | 88.4 ÷ 136.5 | 3.00 ÷ 4.30 | 1.43 | 0.68 ÷ 0.44 | 0.44 ÷ 0.51 |
| 39 | 56.3 | 75 | 86 | 100.8 ÷ 137.1 | 3.90 ÷ 5.00 | 1.15 | 0.74 ÷ 0.55 | 0.43 ÷ 0.47 |
| Run | θ (°) | a (mm) | b (mm) | h (mm) | Q (L/s) | b/a | a/h | Cd |
|---|---|---|---|---|---|---|---|---|
| 40 | 90 | 50 | 142 | 74.9 ÷ 176.1 | 3.30 ÷ 7.40 | 2.84 | 0.67 ÷ 0.28 | 0.39 ÷ 0.56 |
| 41 | 90 | 60 | 142 | 115.5 ÷ 148.6 | 6.10 ÷ 7.70 | 2.36 | 0.52 ÷ 0.40 | 0.47 ÷ 0.53 |
| 42 | 90 | 70 | 142 | 87.7 ÷ 122.2 | 4.80 ÷ 7.50 | 2.03 | 0.80 ÷ 0.57 | 0.37 ÷ 0.50 |
| 43 | 90 | 50 | 106 | 66.6 ÷ 142.0 | 2.70 ÷ 4.90 | 2.12 | 0.75 ÷ 0.35 | 0.44 ÷ 0.55 |
| 44 | 90 | 60 | 106 | 79.3 ÷ 156.4 | 3.00 ÷ 6.00 | 1.76 | 0.76 ÷ 0.38 | 0.38 ÷ 0.55 |
| 45 | 90 | 70 | 106 | 89.7 ÷ 180.1 | 3.50 ÷ 7.60 | 1.51 | 0.78 ÷ 0.39 | 0.35 ÷ 0.54 |
| 46 | 90 | 50 | 86 | 65.9 ÷ 152.5 | 2.40 ÷ 4.20 | 1.72 | 0.76 ÷ 0.33 | 0.49 ÷ 0.58 |
| 47 | 90 | 60 | 86 | 73.9 ÷ 151.5 | 2.60 ÷ 4.80 | 1.43 | 0.81 ÷ 0.40 | 0.41 ÷ 0.54 |
| 48 | 90 | 70 | 86 | 87.4 ÷ 154 | 3.10 ÷ 5.50 | 1.23 | 0.80 ÷ 0.45 | 0.40 ÷ 0.55 |
| 49 | 63.4 | 50 | 142 | 46.1 ÷ 144.06 | 3.30 ÷ 6.30 | 2.84 | 1.08 ÷ 0.35 | 0.48 ÷ 0.54 |
| 50 | 63.4 | 60 | 142 | 99.9 ÷ 156.3 | 5.00 ÷ 7.60 | 2.36 | 0.60 ÷ 0.38 | 0.42 ÷ 0.51 |
| 51 | 63.4 | 70 | 142 | 46.1 ÷ 128.8 | 4.20 ÷ 7.40 | 2.03 | 1.52 ÷ 0.54 | 0.45 ÷ 0.47 |
| 52 | 63.4 | 50 | 106 | 76.5 ÷ 148.7 | 2.80 ÷ 4.70 | 2.12 | 0.65 ÷ 0.34 | 0.43 ÷ 0.51 |
| 53 | 63.4 | 60 | 106 | 82.7 ÷ 147.5 | 3.10 ÷ 5.50 | 1.76 | 0.72 ÷ 0.41 | 0.38 ÷ 0.50 |
| 54 | 63.4 | 70 | 106 | 92.1 ÷ 148.4 | 3.50 ÷ 6.10 | 1.51 | 0.76 ÷ 0.47 | 0.36 ÷ 0.50 |
| 55 | 63.4 | 50 | 86 | 64.5 ÷ 131 | 2.30 ÷ 3.60 | 1.72 | 0.77 ÷ 0.38 | 0.48 ÷ 0.52 |
| 56 | 63.4 | 60 | 86 | 80.7 ÷ 144.6 | 2.60 ÷ 4.30 | 1.43 | 0.74 ÷ 0.41 | 0.39 ÷ 0.51 |
| 57 | 63.4 | 70 | 86 | 90.4 ÷ 152.8 | 3.00 ÷ 5.10 | 1.23 | 0.77 ÷ 0.46 | 0.37 ÷ 0.49 |
| 58 | 45 | 50 | 142 | 62.1 ÷ 109 | 3.00 ÷ 5.20 | 2.84 | 0.80 ÷ 0.46 | 0.38 ÷ 0.50 |
| 59 | 45 | 60 | 142 | 93.8 ÷ 141.5 | 4.70 ÷ 7.20 | 2.36 | 0.64 ÷ 0.42 | 0.41 ÷ 0.50 |
| 60 | 45 | 70 | 142 | 85.7 ÷ 125.9 | 4.30 ÷ 7.40 | 2.03 | 0.82 ÷ 0.56 | 0.33 ÷ 0.47 |
| 61 | 45 | 50 | 106 | 65.1 ÷ 117.3 | 2.50 ÷ 4.10 | 2.12 | 0.77 ÷ 0.43 | 0.42 ÷ 0.51 |
| 62 | 45 | 60 | 106 | 75.7 ÷ 144.62 | 2.90 ÷ 5.40 | 1.76 | 0.79 ÷ 0.41 | 0.38 ÷ 0.50 |
| 63 | 45 | 70 | 106 | 86.3 ÷ 154.6 | 3.40 ÷ 6.30 | 1.51 | 0.81 ÷ 0.45 | 0.35 ÷ 0.48 |
| 64 | 45 | 50 | 86 | 66.1 ÷ 125.1 | 2.50 ÷ 3.50 | 1.72 | 0.76 ÷ 0.40 | 0.50 ÷ 0.53 |
| 65 | 45 | 60 | 86 | 76.2 ÷ 136.0 | 2.50 ÷ 4.20 | 1.43 | 0.79 ÷ 0.44 | 0.40 ÷ 0.50 |
| 66 | 45 | 70 | 86 | 86.9 ÷ 140.3 | 2.90 ÷ 4.80 | 1.23 | 0.81 ÷ 0.50 | 0.37 ÷ 0.48 |
| Air Density | Water Density | Air Kinematic Viscosity | Water Kinematic Viscosity |
|---|---|---|---|
| 1.225 kg/m3 | 1000 kg/m3 | 1.48 × 10−5 m2/s | 1.0 × 10−6 m2/s |
| Nx | Ny | Nz | Δx_min (m) | Δy_min (m) | Δz_min (m) |
|---|---|---|---|---|---|
| 124 | 100 | 150 | 0.002 | 0.002 | 0.002 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lauria, A.; Calomino, F.; Alfonsi, G.; D’Ippolito, A. Discharge Coefficients for Sluice Gates Set in Weirs at Different Upstream Wall Inclinations. Water 2020, 12, 245. https://doi.org/10.3390/w12010245
Lauria A, Calomino F, Alfonsi G, D’Ippolito A. Discharge Coefficients for Sluice Gates Set in Weirs at Different Upstream Wall Inclinations. Water. 2020; 12(1):245. https://doi.org/10.3390/w12010245
Chicago/Turabian StyleLauria, Agostino, Francesco Calomino, Giancarlo Alfonsi, and Antonino D’Ippolito. 2020. "Discharge Coefficients for Sluice Gates Set in Weirs at Different Upstream Wall Inclinations" Water 12, no. 1: 245. https://doi.org/10.3390/w12010245
APA StyleLauria, A., Calomino, F., Alfonsi, G., & D’Ippolito, A. (2020). Discharge Coefficients for Sluice Gates Set in Weirs at Different Upstream Wall Inclinations. Water, 12(1), 245. https://doi.org/10.3390/w12010245






