Next Article in Journal
Inter-Regional Agricultural Virtual Water Flow in China Based on Volumetric and Impact-Oriented Multi-Regional Input-Output (MRIO) Approach
Next Article in Special Issue
A Modeling Comparison of Groundwater Potential Mapping in a Mountain Bedrock Aquifer: QUEST, GARP, and RF Models
Previous Article in Journal
Sediment Management at Run-of-River Reservoirs Using Numerical Modelling
Previous Article in Special Issue
Using OCO-2 Satellite Data for Investigating the Variability of Atmospheric CO2 Concentration in Relationship with Precipitation, Relative Humidity, and Vegetation over Oman
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 12
Issue 1
10.3390/w12010250
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Hydrological Modeling to Assess the Efficiency of Groundwater Replenishment through Natural Reservoirs in the Hungarian Drava River Floodplain

by
Ali Salem
1,2,*,
József Dezső
3,
Mustafa El-Rawy
2,4 and
Dénes Lóczy
3
1
Doctoral School of Earth Sciences, University of Pécs, Ifjúság útja 6, H-7624 Pécs, Hungary
2
Civil Engineering Department, Faculty of Engineering, Minia University, Minia 61111, Egypt
3
Institute of Geography and Earth Sciences, Faculty of Sciences, University of Pécs, Ifjúság útja 6, H-7624 Pécs, Hungary
4
Civil Engineering Department, College of Engineering, Shaqra University, Dawadmi, Ar Riyadh 11911, Saudi Arabia
*
Author to whom correspondence should be addressed.
Water 2020, 12(1), 250; https://doi.org/10.3390/w12010250
Submission received: 5 December 2019 / Revised: 6 January 2020 / Accepted: 13 January 2020 / Published: 16 January 2020
(This article belongs to the Special Issue Spatial Modelling in Water Resources Management)
Browse Figures
Versions Notes

Abstract

:
Growing drought hazard and water demand for agriculture, ecosystem conservation, and tourism in the Hungarian Drava river floodplain call for novel approaches to maintain wetland habitats and enhance agricultural productivity. Floodplain rehabilitation should be viewed as a complex landscape ecological issue which, beyond water management goals to relieve water deficit, ensures a high level of provision for a broad range of ecosystem services. This paper explores the hydrological feasibility of alternative water management, i.e., the restoration of natural reservoirs (abandoned paleochannels) to mitigate water shortage problems. To predict the efficiency of the project, an integrated surface water (Wetspass-M) and groundwater model (MODFLOW-NWT) was developed and calibrated with an eight-year data series. Different management scenarios for two natural reservoirs were simulated with filling rates ranging from 0.5 m3 s−1 to 1.5 m3 s−1. In both instances, a natural reservoir with a feeding rate of 1 m3 s−1 was found to be the best scenario. In this case 14 days of filling are required to reach the possible maximum reservoir stage of +2 m. The first meter rise increases the saturation of soil pores and the second creates an open surface water body. Two filling periods per year, each lasting for around 180 days, are required. The simulated water balance shows that reservoir–groundwater interactions are mainly governed by the inflow into and outflow from the reservoir. Such an integrated management scheme is applicable for floodplain rehabilitation in other regions with similar hydromorphological conditions and hazards, too.

1. Introduction

Water availability is of primary importance for landscape functions. Over the last centuries, half of European wetlands and more than 95% of riverine floodplains were converted to agricultural and urban lands [1]. The human intervention has fundamentally altered the water availability of floodplain landscapes [2]. River floodplains provide various ecosystem services [3,4], including groundwater replenishment, water purification, flood protection, biodiversity/habitat, sediment and nutrient retention, recreation and tourism, cultural values, buffering capacity of climate change, and various floodplain products (fish, wood, reed, game) [5]. Changes in the water regimes of rivers are predicted to be damaging to these ecosystems under extensive human pressure, resources exploitation, and pollution. Abandoned channels and oxbow lakes, the most common landforms of floodplains, are regarded particularly sensitive to such pressures [6,7].
In the Drava floodplain of SW Hungary drought and flood periods alternate rapidly, occasionally even within a single year [8]. With groundwater tables dropping by 1.5 to 2.5 m, the entrenchment of the river leads to intensified drought hazard and water stress in the floodplain [9,10,11]. Water shortages, particularly manifested in decreased river discharge and wetlands desiccation, are aggravated by the aridification trend induced by global climate change [12]. As a consequence, the ecological functioning of the natural systems and physical habitats are deteriorated. Moreover, water shortages have adverse effects on agricultural productivity, related socio-economic conditions, and the life quality of local population [13]. The optimal design of groundwater table in the floodplain is a complex task because of the conflicts between agriculture, forestry, flood control, and natural conservation demands [8]. To amend the situation, a large-scale landscape rehabilitation project, the Old Drava Programme, was launched in 2013 [14]. It is intended to solve interrelated problems of water governance, land management, and human employment.
In the Drava basin alternative water resources have to be explored. International examples show that the integrated (conjunctive) use of surface water and groundwater within a proper management system increases the efficiency of water utilization [15,16], provides sufficient irrigation water for agriculture [17,18,19], and improves the environmental conditions of irrigated lands [20]. Construction of recharge dams and controlling the rate of groundwater abstraction are considered common practices [21,22]. Managed Aquifer Recharge (MAR) using treated wastewater is a feasible option for non-conventional water resources in arid and semiarid regions [18,23,24,25,26,27,28,29].
The interaction between lakes (subsurface reservoir) and groundwater is the most important part of the lake water budget and it substantially affects lake water quality [30,31,32]. This interaction has been studied through different approaches. The exchange between reservoir/lake water and groundwater is controlled by the texture, stratification, and isotropy of sediments in the shoreline zone [33,34]. Lee [35], Winter et al. [36], and Ong and Zlotnik [37] used point measurement tools such as seepage meters, piezometers, dye tracing, and potentio-manometers to estimate the exchange of seepage from the lake to groundwater. The difficulty of such methods lies in the spatial and temporal integration of fluxes. Geochemical analyses and mass-balance methods quantify groundwater inflow, which determines isotope or solute concentration in the lake [38,39]. The latter methods are complex, as they need a conservative tracer unaffected by land use [40,41,42,43].
Isotope-balance approaches [44] using δ2H or δ18O measurements of water were used in several hydrological studies to assess groundwater inflow to lakes, with varying degrees of success [40,45,46,47,48]. Hydrological models are the most reliable tools for the assessment of lake water/groundwater interactions [49]. A Modular Three-Dimensional Finite-Difference Ground-Water Flow Model (MODFLOW) [50] is applied widely to assess this interaction from different approaches. Leblanc et al. [51] simulated the lake as a constant stage source or sink through river package. Another approach to simulate the water balance of lakes uses the General-Head Boundary (GHB) Package [52]. The main disadvantage of these approaches is that the lake stage is assumed to be constant during each stress period. Fenske et al. [53] used the Reservoir Package to simulate the lake. This approach requires previous knowledge of lakebed seepage to assess the lake stages [54]. Another approach that represents the lake volume with high hydraulic conductivity cells [55] is called the “high-K” technique. Yihdego and Becht [56] applied a 3D flow model with the high-K technique to simulate lake/groundwater interaction in Naivasha, Kenya. In this approach, however, it is difficult to simulate the connection between the lakes and streams [54]. Cheng and Anderson [57] developed the MODFLOW lake package (LAK1) to solve the mentioned problems. The main advantage of the lake package is that it allows the fluctuation of lake stage. Also, the exchange of volumetric water between the lake and the aquifer is determined [49]. The LAK2 package is capable of simulating more than one lake simultaneously. The simulation of solute transport is also provided in LAK. Kidmose et al. [58] validated the LAK3 package through measurements by seepage meter. The advantages and disadvantages of three approaches for simulating lake–groundwater interactions (namely, fixed lake stages, high-K nodes, and LAK3 package) were compared by Hunt [59]. Water balance is simulated more realistically in the latest update LAK7 package [49]. The experience gathered from the MODFLOW lake packages is utilized in the modeling of water balance for the reservoir planned in the Drava floodplain.
This paper evaluates the feasibility of water replenishment through natural reservoirs using a hydrological model (Wetspass-M) and a Newton-Raphson formulation for MODFLOW-2005 (MODFLOW-NWT) with ModelMuse as a graphical interface. The consequences of applying a natural reservoir in augmenting surface water storage are investigated under variable management scenarios of recharging or feeding the reservoir. The assessment of such reservoir/groundwater interactions according to different scenarios of reservoir recharge is a precondition to establishing a new water governance in the region, which can, in turn, be the basis of exploiting economic opportunities. Sustainable ecotourism and related development would ensure a safe livelihood for the local population.

2. Materials and Methods

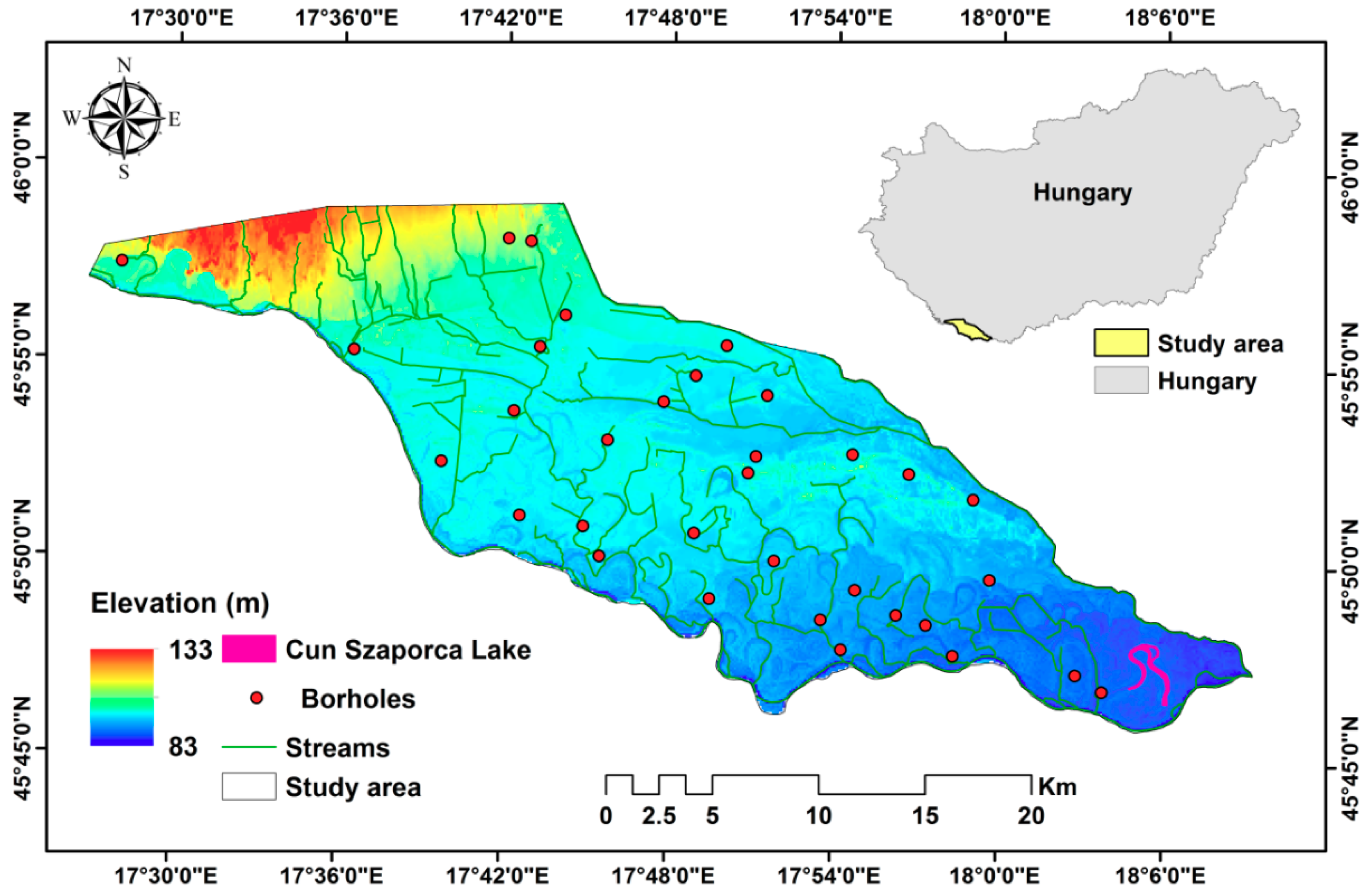
2.1. Study Area

The 15 km-wide Drava river floodplain is located on the national border between Hungary and Croatia. The Hungarian section of the floodplain is traditionally affected by floods prior to river regulation. Floods mostly take place during June–July due to an Atlantic influence and during October–November due to a Mediterranean influence. Drava river channelization began in 1750 and reduced the river length by 50% [60]. The floodplain has a total area of 500 km2. There are 13 tributary streams, 20 major side channels, hundreds of meander scars, and 18 oxbow lakes in the Hungarian section of the Drava River (Figure 1) [61]. The long-term average discharge of the Drava River was 595 m3 s−1 for the period 1896–2018 [62]. Maximum discharge of 0.1% probability is assumed to be 3070 m3 s−1 (reached during the flood of 1827), while 170 m3 s−1 and 900 m3 s−1 are accounted to baseflow and bankfull discharge, respectively [62]. As a possible source of water replenishment, the Fekete-víz stream is a tributary with an average discharge of Qav = 2–2.5 m3 s−1. The main features of the floodplain are oxbows, scroll bar systems, abandoned channels with natural levees, backswamps, and in the north, elongated blown sand of east to west strike [63]. The digital elevation model (DEM) of the study area was obtained from the South-Transdanubian Water Management Directorate, Pécs, at 10 m resolution. The Drava floodplain is apparently flat at 83–133 m elevation, with an average relative relief 2 m km−2 (Figure 1). Settlements were built on elevated terrain.

2.1.1. Meteorological Data

The meteorological data for the period 2010–2018 (time selected as this study period) were obtained from the South-Transdanubian Water Management Directorate, Pécs. The climate of the Drava Plain is moderately wet and warm in the west under Atlantic influence, and moderately dry and warm in the east under Mediterranean influence [64]. The long-term mean annual temperature is 10.8 °C in the east and 10.2 °C in the west. Absolute maximum and minimum temperatures are 35 °C and −17 °C, respectively. The number of cold days (mean daily temperature below −10 °C) is 10, while the number of hot days (mean temperature above 30 °C) is 21. The long-term average annual rainfall ranges from 383 mm y−1 to 1057 mm y−1, with a mean value of 682 mm y−1. The rainy season (summer and spring) has a share of 60% of the annual rainfall, while the remaining 40% falls in the drier season (winter and autumn) [65]. Daily evaporation from the lake surface was calculated using the Penman open-water equation [66] based on wind speed, hourly incoming solar radiation, air temperature, relative humidity, air temperature, and wind-speed. Evaporation from the lake is concentrated on the summer months and shows a large variation between 0.0 mm d−1 and 6.8 mm d−1, with a mean value of 1.85 mm d−1. Daily potential evapotranspiration (PET) was computed from meteorological data using the Food and Agriculture Organization of the United Nations (FAO) Penman–Monteith method [67] and varies from 0.0 mm to 46 mm, with an average of 19.8 mm. About 88% of the PET is attributed to summer and spring.

2.1.2. Soil Data

Altogether, 72 soil samples were taken from the floodplain for particle size analysis and the identification of textural classes (Figure 2a). Over around 50% of the floodplain soils are of sandy texture, in 12% clay, in 8% loam, while in over 30% of the area sandy loam and clay loam occur. Fluvisols formed under periodical water surplus and forest vegetation dominate the area. Soil thickness is highly variable, from a few centimeters to a meter, the top 0.5 m has more organic material. In addition to particle size distribution, soils were studied using GPR (ground penetrating radar) and satellite image analysis, in combination with the survey of landforms [68,69].
Figure 2b shows the vertical distribution and frequency of the different textural types and their thicknesses by a box diagram for the top 100 m. The CMu (clayey mud) layers mostly occurred at around 25–30 m depths (ranging from 20 to 40 m) and their average thickness was 5 m (2 to 8 m). All texture classes turned out in the top 20 m of the modeling space. These sediments were deposited in point bars, channels, and oxbows [69]. During the late Pleistocene–Holocene in the top 100 m fluvial coarse-sand–heavy clay series deposited in the basin (Figure 2b). Subsurface water flow and capillary rise are influenced by the above-mentioned landforms and deposits.

2.1.3. Land Use and Groundwater Depth

Land use data for the Drava floodplain in 2018 were obtained from the Coordination of Information on the Environment (CORINE) data base (https://land.copernicus.eu/pan-european/corine-land-cover/clc2018). Land use was composed of 13 classes, with a dominance of agriculture (45%), followed by deciduous forests (23.83%), whereas shrub areas, sealed surfaces, and water bodies took up 11%, 4%, and 1.1%, respectively (Figure 3a). For daily groundwater depth, 18 observation wells were used to depict the spatial distribution of groundwater level for the Drava floodplain (Figure 3b). The average depth to groundwater table during the period from 2000 to 2018 ranged from 91.3 m to 117.8 m, with an average of 99.3 m [70].

2.2. Groundwater Recharge and Evapotranspiration

The spatial distribution of groundwater recharge and evapotranspiration were estimated by the WetSpass-M model [71]. The WetSpass model has been applied to assess water balance components in different regions around the world [72,73,74,75,76,77]. The WetSpass model considers the spatial distribution of the soil, land use, slope, groundwater depth, and the meteorological data of every grid cell are divided into four fractions (vegetated, bare soil, open water surface). The seasonal water balance for each fraction is calculated as:
P = S + ET + R,
where P is precipitation, S is surface runoff, ET is evapotranspiration, and R is groundwater recharge. The actual evapotranspiration is calculated as a function of potential evapotranspiration and a vegetation coefficient [78]. R is determined as a residual part of the water balance. The simulated annual groundwater recharge of the Drava floodplain ranged from 0 mm y−1 to 360 mm y−1 as the lowest and highest values, with an average of 241 mm y−1 (Figure 4a). The estimated evapotranspiration varied from 211 mm y−1 to a maximum of 1394 mm y−1, with an average value of 310 mm y−1 (Figure 4b).

2.3. Numerical Groundwater Modeling

MODFLOW-NWT [79] with ModelMuse [80] as a graphical user interface was used to simulate groundwater flow. It was expressly developed to solve problems which are caused by nonlinearities of drying and rewetting of the unconfined groundwater flow, similar to that treated in this paper. This is in contrast with other versions of MODFLOW, which exclude dry cells from calculation. The LAK7 package was developed to simulate lake/groundwater interactions. The lake stage is determined based on the exchanges of volumetric water in and out of the lake and the overall water balance of the lake. The seepage between a lake and its groundwater system depends on lake stage, lakebed leakage in grid cell dimensions, the hydraulic conductivity of the lakebed material, the adjacent aquifer, and hydraulic heads in the groundwater system. The seepage is calculated by Darcy’s law [54], as follows:
q = K   ( h 1   −   h a ) / d ,
where q is the seepage rate (L T−1); K is the hydraulic conductivity (L T−1) of materials between the lake and the aquifer; h 1 is the stage of the lake (L); h a is the aquifer head (L); d is the distance (L) between the points at which h 1 and h a are measured; and the volumetric flux Q (L3 T−1) is established by the following equation:
Q = q A = (K (h1 − ha)/d) A = C (h1 − ha),
where c = KA/d is the conductance (L2 T−1) and K/d is the leakage (T−1).
Inputs to the groundwater system are groundwater recharge from precipitation, river seepage and lake seepage, lateral groundwater inflow from a part of the northern boundary, while output from the groundwater system includes groundwater seepage to rivers and lakes, lateral groundwater outflow from the southwestern boundary, and evaporation from groundwater.

2.3.1. Groundwater Flow Model Setup

According to evidence from geological boreholes, pumping tests and GPR surveys, the groundwater flow system consists of four layers. Since the sediments in the area range from coarse sand to clay, the four layers are highly heterogeneous in space. The model was discretized by a 100 m by 100 m grid and the model was refined for lake area with 30 m by 30 m, resulting in a domain of 361 rows and 742 columns, and four layers with a total number of 1,339,310 cells, 655,390 of which were active cells. The records of GPR, supplemented with auger holes, presented high heterogeneity in the hydraulic proprieties of the sediment depending on particle size (ranging from coarse sand to clay). The fall head method was applied to calculate the hydraulic conductivity for each borehole. According to the boreholes data, the first layer consisted of four K-zones of hydraulic conductivity (Figure 5), varying from 375 to 0.15 m d−1, while the second layer was characterized by three zones with a range of 375 and 75 m d−1. The third and fourth layers were described by two zones, with a range from between 375 and 75 m d−1 and 0.15 to 3 m d−1, respectively (Figure 5). Although all the hydraulic parameters were determined in the field, because of limited spatial representativeness and the influence of modeling scale in accordance with [81,82,83], they still had to be adjusted in the calibration process. Fortunately, the majority of the units had natural boundaries.
The southern boundary is represented by the Drava River and assigned as a river package. Based on data available from observation wells, the general direction of groundwater flow is from north to south. The Fekete-víz and Okor streams comprise the northern, eastern, and part of the western boundary and they are assigned by a river package (Figure 6a). All streams in the floodplain are assigned by a river package. The conductance of the riverbed was initially set to 5 m2 d−1, and then adjusted during the calibration process. MODFLOW General-Head Boundary (GHB) was assigned to the southwestern and part of the northern boundary to simulate lateral groundwater inflow and outflow of the system based on the time series of groundwater level from the available observation wells. Initially, the conductance of GHB was set to be 20 m2 d−1, based on geological boreholes and adjusted during the calibration process. Cún-Szaporca Lake was assigned in the model through the LAK7 package (Figure 6a). The lake simulation was performed using a separate additional inactive layer [54] with variable thickness. The top of inactive layer had a 1.0 m thickness outside the lake and the top equaled the maximum lake stage within the lake area. The bottom was equal to the bathymetrically defined lake bottom. Lakebed leakage was assigned from field measurements for the vertical hydraulic conductivity and the thickness of the lakebed. Lakebed leakage was set to 0.05 d−1.

2.3.2. Calibration and Sensitivity Analysis

A steady-state model was developed to represent an initial case for the transient model by applying long-term average parameters, i.e., mean precipitation, mean groundwater levels, mean PET, and mean groundwater recharge for the period from 1 January 2010 to 20 September 2018. The steady-state model was calibrated using average groundwater levels for 16 observation wells. Calibrated results showed a good agreement between observed and simulated groundwater heads, with R2 = 0.98. The mean error was −0.016 m, and the mean absolute error was 0.09 m. However, starting the transient model by steady-state model as an initial condition proved to be unsuccessful due to a large difference between the steady-state parameters and the measured daily values at the start-up of the transient model on 1 January 2010.
The first three hydrological years from which data were available, i.e., from 1 January 2010 until 31 December 2012, were used as a warm-up period, after which the model was run (calibrated) throughout the following six hydrological years from 1 January 2013 to 20 September 2018 with a daily time step. The calibrated results of the transient model against the time series of observation well heads and the stages of the Cún-Szaporca Lake are shown in Figure 7. The calibration process of groundwater head was carried out using 16 time series of daily groundwater levels from observation wells extending over 10 years. Calibrated results showed a good match between observed and simulated groundwater heads, with R2 = 0.98. The mean error was −0.08 m, and the root mean square error was 0.4 m (Figure 7a). Additionally, the calibration of lake stages showed a good agreement between simulated and observed stages with a correlation coefficient of 0.90, a mean error of −0.07 m, mean absolute error of 0.15 m, and root mean square error of 0.2 m (Figure 7b). The calibrated parameters of hydraulic conductivity, river conductance, general head conductance, and groundwater recharge are shown in Table 1.
The sensitivity analysis was achieved using computer code for universal sensitivity analysis, calibration, and uncertainty evaluation (UCODE-2005) [84] with the help of ModelMate [85]. It was studied for the groundwater recharge (RCH), hydraulic conductivity (HK), which was divided into five zones, evapotranspiration (EVT), river conductance (RIVC), and general head boundary (GHB) parameters. The parameters of the groundwater recharge (RCH), hydraulic conductivity (HKZ1), and evapotranspiration (EVT) had the highest composite scaled sensitivity values and were therefore the most sensitive parameters (Figure 7c).

3. Results and Discussion

3.1. Water Budget of the Groundwater Flow Model

The water balance at the end stress of the calibrated transient model is shown in Table 2. The inflow rate from GHB boundary to the aquifer represents 42.25% of the total inflow to the aquifer through 627,789.00 m3 d−1. Water seepage from streams and the Cún-Szaporca Lake represents 4.68% of the total inflow. Groundwater discharge from the aquifer to streams is 1,275,244.38 m3 d−1, which amounts to 85.82% of the total outflow from groundwater system as the area characterized by shallow groundwater table, while evapotranspiration represents 10% of total outflow.

3.2. Simulated Scenarios

The natural water reservoirs are the former oxbows, paleomeanders, and deeper-lying floodplain sections, which are under excess water effect. These areas may be suitable for the storage of surplus water provided by the adjacent watercourses. The model space covered two subareas: 1, the Korcsina oxbow system (Figure 6b); and 2, the Okor–Fekete-víz backswamps (Figure 6c). The exact location of the potential reservoir was selected from the analysis of the topography and hydraulic soil properties explored by auger samples. The selected subareas were simulated as natural reservoirs with filling and discharge conditions based on +2 m vertical water depth increasing theoretically with different stream discharges of 0.5, 0.75, 1, and 1.5 m3 s−1. (The excess water hazard on agricultural land excludes water level rise above +2 m.) Based on measurements of stream discharge, to obtain feeding with stream discharge larger than 1 m3 d−1, constructing a dam is required. Evaporation from the open water surface of the reservoir is a main challenge of the natural reservoir solution. The forested environs of the reservoir, however, reduce evaporation. This model is the first attempt to investigate whether water management through establishing a natural reservoir can be a major contribution to floodplain rehabilitation. Results of the management scenarios are discussed below.

3.2.1. Korcsina Subarea

The Korcsina paleochannel system is a potential water reservoir in the western central part of the floodplain. With streams feeding 0.5 m3 s−1, the total upfilling (+2 m relative water level from 98 to 100 m) in the Korcsina reservoir would take 55 days, with 2,376,000 m3 water demand. The discharge (seepage) period lasts 11 days from a level of 100 m to 98.75 m. By the end of the filling period, seepage from the reservoir to groundwater reaches 35,815 m3. Recharge from groundwater to the reservoir in the filling period from the water level stage of 98 to 99 m and over this level becomes zero (Figure 8a). For filling at a rate of 0.75 m3 s−1, the reservoir reaches the stage 100 m after 27 days with reservoir seepage of 38,900 m3, while the recharge from groundwater to the reservoir takes place in the first five days of the filling process at the level of 99 m (Figure 8b). In the filling with a discharge of 1 and 1.5 m3 s−1, 18 and 11 days are required to achieve +2 m relative water level rise in the reservoir (Figure 8c,d). For all scenarios with different discharge to the reservoir, the reservoir stage did not reach 98 m again because of the shallow groundwater table, which allows groundwater recharge larger than the seepage when reaching a level of 98.83 m (i.e., the inflow from groundwater to the reservoir, which is equal to the seepage from the reservoir at this stage) (Figure 8).

3.2.2. Simulation of the Water Storage Opportunities in the Okor–Fekete-víz Area

These randomly distributed and irregular-shaped paleochannels and backswamps are located at the confluence of the Okor and Fekete-víz streams. The main textural types in the west are medium to coarse sands, in the middle part fine sands, and in the southeastern part loamy sands (Figure 2a). The bed level of the Okor natural reservoir is at 95.95 m. Feeding is from the two mentioned streams. With streams feeding at a rate of 0.5 m3 s−1, the reservoir stage does not reach +2 m relative water level (from 95.95 to 97.95 m), but it reaches 97.7 m within 61 days (Figure 9a), while with a stream discharge of 0.75 m3 s−1 the reservoir stage is at 97.95 m after 22 days, with seepage of 49,733 m3 (Figure 9b). Regarding the scenario of stream feeding at 1 m3 s−1, 13 days are needed to reach the stage of 97.95 m, while the discharge (seepage) period lasts for 180 days (the reservoir dries out) (Figure 9c). With a stream discharge of 1.5 m3 s−1, the reservoir achieves the stage of 97.95 within one week (62,215 m3 seepage) (Figure 9d). There is no recharge from groundwater to the Okor reservoir at the stage of 97.35 m during the filling and discharge period.
The entrenchment and recent incision of the Drava River resulted in a dropping of groundwater tables by 2.5 m. For both reservoirs, and with a feeding discharge of 0.5 and 0.75 m3 s−1, the feeding stream capacity does not allow the recharge of the reservoirs in 60 days and 25 days, respectively, based on the observed discharge of the feeding stream. However, feeding the reservoir at a rate of 1.5 m3 s−1, a +2 m rise to be achieved in five days requires the construction of a dam on the feeding stream. Therefore, this scenario would not be economically feasible. Thus, the best scenario for both reservoirs is a feeding rate of 1.0 m3 s−1, as 18 and 13 days are needed for filling the Korcsina and Okor reservoirs, respectively, and water recharge to the reservoirs could be implemented by two filling periods per year, each providing water storage for six months. The drop of the water level in the reservoir after the filling period is attributed to the pressure differences between the reservoir water and the adjacent groundwater. The reservoir bed seepage analysis was a crucial step to understand the interactions between the reservoir and groundwater system. The seepage from the reservoir to the groundwater system, up to 25,000 m3 d−1, was dominant during stages higher than ~99 m, whereas the recharge from groundwater to the reservoir, up to 5000 m3 d−1, was dominant during stages below 99.00 m. Water levels in the reservoirs are primarily effected by the surrounding groundwater levels, regulated by the hyporheic flow of the streams. The first 1 m of filling increases the saturation of soil pores, which raises soil moisture content in the root zone and the second meter creates an open water body, which is useful to create wetland habitats in the floodplain.

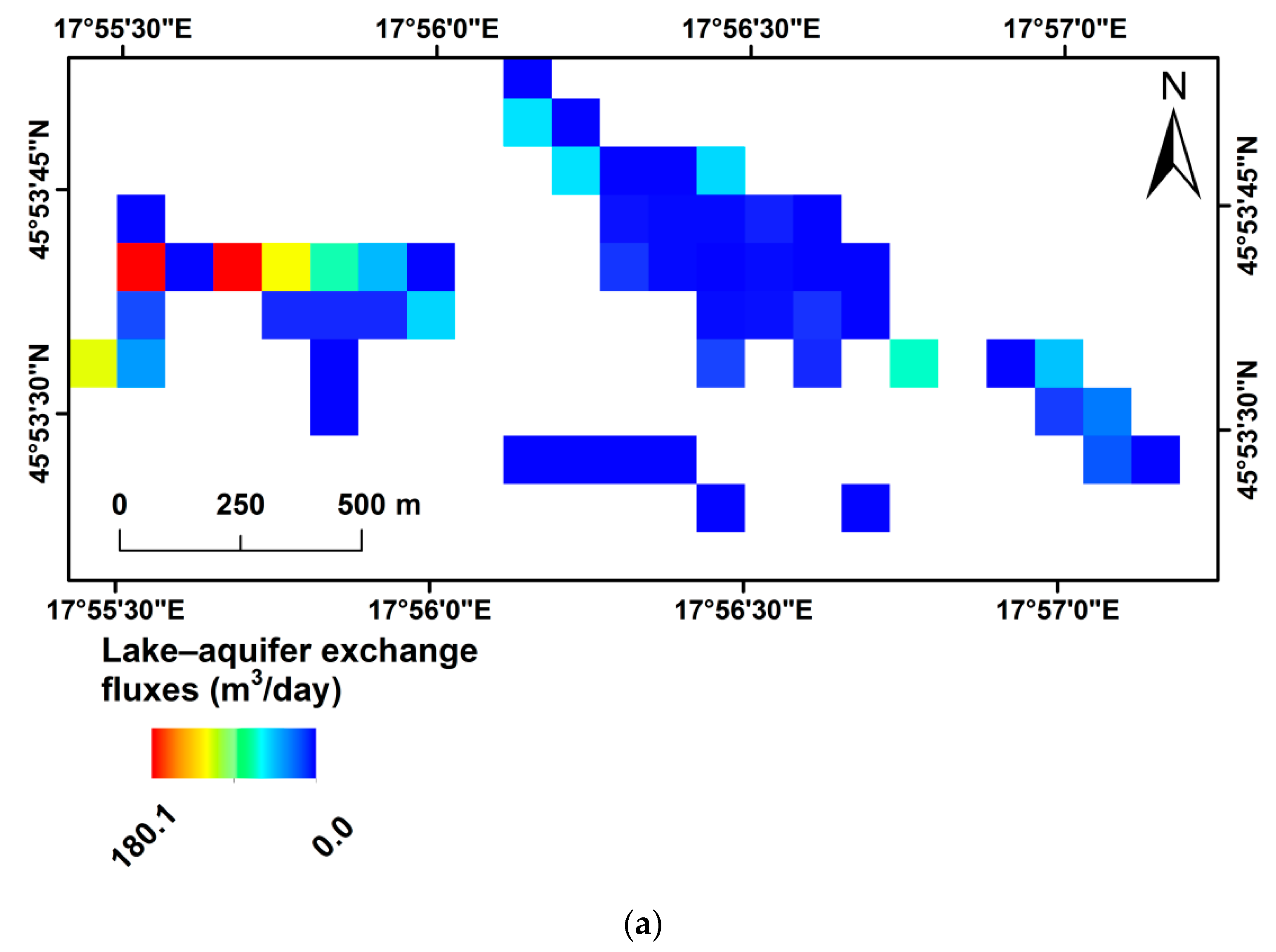
3.3. Spatio-Temporal Extent of Reservoir Impact

The assessment of the spatio-temporal impact of a lake (reservoir) on groundwater conditions is required to manage the groundwater systems adjacent to artificial lakes. The developed groundwater head of lakes Korcsina and Okor for a filling scenario with a discharge of 1 m3 s−1 at different filling and discharge periods were plotted against distances at a cross-section which passes through the lakes (Figure 6b,c) for the selected stress periods (Figure 10 and Figure 11). The influence of the lake on groundwater levels decreases with distance (Figure 10 and Figure 11). However, there are differences between the trends of the two sections due to the variance in hydrogeological and hydraulic conditions for the two locations. The results clearly indicate that after 10 and 20 days of filling the Korcsina reservoir, the average groundwater head increased by 1 m and 1.6 m, respectively, with respect to the base case along the cross section. For the Okor reservoir, the average groundwater head increased by 0.7 m and 1.3 m after filling periods of 10 days and 20 days, respectively, with respect to the base case, while the average groundwater table decreased by 0.9 m and 1.0 m after discharge periods of 70 days and 170 days, respectively, compared to the base case (Figure 11). As depicted in the gradual rise in groundwater table after successive filling (Figure 10 and Figure 11), the natural reservoirs improve aquifer storage and hence maintain the level of ecosystem services and increase agricultural productivity in the Drava basin.
Lake–aquifer exchange fluxes in the Korcsina and Okor reservoirs are shown in Figure 12 and Figure 13, identifying the losing and gaining zones of the planned reservoirs with the help of the cell-to-cell flux terms in the model output files. Exchange fluxes between the reservoirs and the groundwater system for different periods of filling and discharge were analyzed. The sign on the graph indicates the direction of fluxes between the reservoirs and the aquifer. A positive sign represents upward reservoir seepage gain and negative represents downward reservoir seepage loss. For the Korcsina reservoir with 20 days of filling (+2 m), the seepage from reservoir to groundwater system ranged from 0 to 245 m3 d−1 with an average value of 55 m3 d−1, with higher values in the northeast (Figure 12a). The average exchange between reservoir and aquifer was 1.4 m3 d−1 after 40 days of discharge period, the majority of which the reservoir has gained from the aquifer (Figure 12b).
Similar seepage patterns can be observed for the Okor reservoir (Figure 13a,b), with average values of seepage of 25.3 m3 d−1 and 0.7 m3 d−1 after 14 days of filling (+2 m) and 40 days of discharge (+1 m), respectively. The patterns of spatial seepage at various reservoir stages through filling and discharge periods are different, attributed to variations in reservoir-bed leakage and reservoir stages. The magnitude and direction of seepage between the reservoir and underlying groundwater system relies on the reservoir-bed leakage and the difference between reservoir stage and hydraulic head of an underlying aquifer. In the Drava Plain, of highly variable alluvial deposits and soil textural types, the modeling of reservoir/groundwater interchanges is central to the planning of rehabilitation measures.
The findings point out that several factors influence the interactions of reservoir with the groundwater system. The regulated recharge to the reservoir and the large spatio-temporal variability of interactions indicate that sophisticated and complex modeling methods are required to depict such a complex hydrological system. Therefore, the integration of a spatially-distributed water balance model (WetSpass-M), and a groundwater flow model (MODFLOW-NWT) to represent the volumetric exchanges between reservoir and groundwater was applied for case studies in the Drava floodplain.

4. Conclusions

The regulation works and incision of Drava River have changed the water regime and water budget of the floodplain, and, as a consequence, the water stress has increased and threatens the sustainable development of different sectors in the Drava basin. This study assessed the feasibility of the natural reservoir in augmenting the water resources of the floodplain through surface water storage and to mitigate water shortage problems caused by drought and human interventions using MODFLOW-NWT with ModelMuse as a graphical interface. The transient groundwater flow model was calibrated with a correlation coefficient of 0.96, a mean error of −0.016 m, and a mean absolute error of 0.4 m. A digital elevation model and hydraulic soil properties revealed by auger samples were used to identify possible allocations of a natural reservoir. The two selected subareas were selected as potential natural reservoir sites. Simulated reservoirs had filling and discharge conditions based on +2 m vertical water depth with different discharges from adjacent streams at 0.5, 0.75, 1, and 1.5 m3 s−1 rates. For both reservoirs, around 60 days and 25 days of stream feeding of 0.5 and 0.75 m3 s−1, respectively, are required to achieve the target water depth for the reservoir (+2 m), the optimal and economic scenario of filling the reservoirs is with a stream discharge of 1 m3 s−1 for 14 days, based on the capacity of the feeding stream. Feeding at a rate of 1.5 m3 s−1 would need around just six days, but this is not an economic scenario as it necessitates impoundment and dam construction. With feeding at 1 m3 s−1, filling would be repeated twice per year, as the reservoir lasts for 180 days. The effect of the reservoir on the groundwater table in the adjacent area depends on reservoir stage, leakage, and the distribution of the groundwater head using the reservoir results in raising the groundwater table by 0.8 m at the end of the filling period. Natural reservoirs can be regarded as an economically feasible management practice of water resources retention and can help protect ecological values, the restoration of wetlands, and enhance agriculture productivity on the Hungarian section of the Drava floodplain. Moreover, the findings of this research can be utilized in planning rehabilitation measures in lowlands with water shortage.

Author Contributions

Conceptualization, A.S.; Data curation, J.D.; Formal analysis, A.S. and M.E.-R.; Methodology, A.S. and M.E.-R.; Project administration, J.D. and D.L.; Software, A.S. and M.E.-R.; Supervision, J.D. and D.L.; Validation, A.S.; Visualization, M.E.-R.; Writing—original draft, A.S.; Writing—review and editing, J.D., M.E.-R. and D.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the project that supported by the European Union, and co-financed by the European Social Fund: Comprehensive Development for Implementing Smart Specialization Strategies at the University of Pécs (EFOP-3.6.1.-16-2016- 00004).

Acknowledgments

The present scientific contribution is dedicated to the 650th anniversary of the foundation of the University of Pécs, Hungary. The first author would like to thank the Egyptian Ministry of Higher Education (MoHE) and Tempus Public Foundation for providing him the Stipendium Hungaricum Scholarship. Also, the authors are grateful for financial support from the project that supported by the European Union, and co-financed by the European Social Fund: Comprehensive Development for Implementing Smart Specialization Strategies at the University of Pécs (EFOP-3.6.1.-16-2016- 00004), the Hungarian National Science Foundation (OTKA, contract no K 104552) and by FEKUTSTRAT (No. 20765-3/2018) “Innovation for a Sustainable, Healthy Life and Environment” grant and to the South-Transdanubian Water Management Directorate for providing access to the necessary data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gumiero, B.; Mant, J.; Hein, T.; Elso, J.; Boz, B. Linking the restoration of rivers and riparian zones/wetlands in Europe: Sharing knowledge through case studies. Ecol. Eng. 2013, 56, 36–50. [Google Scholar] [CrossRef]
  2. De Vries, A. (Ed.) Summary of Master Plans of Wetland Sub-Group Partners for Water Project; University of Debrecen, Centre for Environmental Management and Policy: Debrecen, Hungary, 2013; p. 76. [Google Scholar]
  3. Mori, K. Can market-based policies accomplish the optimal floodplain management? A gap between static and dynamic models. J. Environ. Manag. 2009, 90, 1191–1194. [Google Scholar] [CrossRef] [PubMed]
  4. Hopkins, K.G.; Noe, G.B.; Franco, F.; Pindilli, E.J.; Gordon, S.; Metes, M.J.; Claggett, P.R.; Gellis, A.C.; Hupp, C.R.; Hogan, D.M. A method to quantify and value floodplain sediment and nutrient retention ecosystem services. J. Environ. Manag. 2018, 220, 65–76. [Google Scholar] [CrossRef] [PubMed]
  5. WWF International. Assessment of the Restoration Potential along the Danube and Main Tributaries. In Working Paper for the Danube River Basin; World-Wide Fund for Nature: Vienna, Austria, 2010; p. 60. [Google Scholar]
  6. Anderson, J.; Arblaster, K.; Bartley, J.; Cooper, T.; Kettunen, M.; Kaphengst, T.; Leipprand, A.; Laaser, C.; Umpfenbach, K.; Kuusisto, E. Climate Change-Induced Water Stress and Its Impacts on Natural and Managed Ecosystems; European Parlament: Brussels, Belgium, 2008; p. 108. [Google Scholar]
  7. Hulisz, P.; Michalski, A.; Dąbrowski, M.; Kusza, G.; Łéczyński, L. Human-induced changes in the soil cover at the mouth of the Vistula River Cross-Cut (northern Poland). Soil Sci. Annu. 2015, 66, 67–74. [Google Scholar] [CrossRef] [Green Version]
  8. Lóczy, D.; Dezső, J.; Czigány, S.; Gyenizse, P.; Pirkhoffer, E. Amadé Halász Rehabilitation potential of the Drava river floodplain in Hungary. In Proceedings of the Water Resources and Wetlands, Tulcea, Romania, 11–13 September 2014; pp. 21–29. [Google Scholar]
  9. Lóczy, D.; Dezső, J.; Czigány, S.; Prokos, H.; Tóth, G. An environmental assessment of water replenishment to a floodplain lake. J. Environ. Manag. 2017, 202, 337–347. [Google Scholar] [CrossRef]
  10. Dezső, J.; Lóczy, D.; Salem, A.; Gábor, N. Floodplain connectivity. In The Drava River: Environmental Problems and Solutions; Springer Science + Media: Cham, Switzerland, 2019; pp. 215–230. [Google Scholar]
  11. Burián, A.; Horváth, G.; Márk, L. Channel Incision Along the Lower Drava. In The Drava River: Environmental Problems and Solutions; Springer Science + Media: Cham, Switzerland, 2019; pp. 139–157. [Google Scholar]
  12. Goler, R.A.; Frey, S.; Formayer, H.; Holzmann, H. Influence of Climate Change on River Discharge in Austria. Meteorol. Z. 2016, 25, 621–626. [Google Scholar] [CrossRef]
  13. Gálosi-Kovács, B.; Császár, Z.M.; Pap, N.; Remény, P.; Elekes, T. Social problems of the most disadvantaged southern transdanubian micro-regions in Hungary. Rom. Rev. Reg. Stud. 2011, 7, 41–50. [Google Scholar]
  14. AQUAPROFIT Ős-Dráva Program—Összefogással az Ormánság fellendítéséért. Vezetői összefoglaló (Old Drava Programme—Cooperation for the Progress of Ormánság: Executive summary); AQUAPROFIT: Budapest, Hungary, 2010; p. 29. [Google Scholar]
  15. Cheng, Y.; Lee, C.-H.; Tan, Y.-C.; Yeh, H.-F. An optimal water allocation for an irrigation district in Pingtung County, Taiwan. Irrig. Drain. 2009, 58, 287–306. [Google Scholar] [CrossRef]
  16. Salem, A.; Dezső, J.; El-Rawy, M.; Loczy, D. Water management and retention opportunities along the Hungarian section of the Drava River. In Proceedings of the 2nd Euro-Mediterranean Conference for Environmental Integration (EMCEI), Sousse, Tunisia, 10–13 October 2019. [Google Scholar]
  17. Singh, H.; Sinha, T.; Sankarasubramanian, A. Impacts of Near-Term Climate Change and Population Growth on Within-Year Reservoir Systems. J. Water Resour. Plann. Manag. 2015, 141, 04014078. [Google Scholar] [CrossRef] [Green Version]
  18. El-Rawy, M.; Zlotnik, V.A.; Al-Raggad, M.; Al-Maktoumi, A.; Kacimov, A.; Abdalla, O. Conjunctive use of groundwater and surface water resources with aquifer recharge by treated wastewater: Evaluation of management scenarios in the Zarqa River Basin, Jordan. Environ. Earth Sci. 2016, 75, 1146. [Google Scholar] [CrossRef]
  19. Seo, S.B.; Mahinthakumar, G.; Sankarasubramanian, A.; Kumar, M. Conjunctive Management of Surface Water and Groundwater Resources under Drought Conditions Using a Fully Coupled Hydrological Model. J. Water Resour. Plann. Manag. 2018, 144, 04018060. [Google Scholar] [CrossRef] [Green Version]
  20. Liu, L.; Cui, Y.; Luo, Y. Integrated Modeling of Conjunctive Water Use in a Canal-Well Irrigation District in the Lower Yellow River Basin, China. J. Irrig. Drain Eng. 2013, 139, 775–784. [Google Scholar] [CrossRef]
  21. Krešić, N. Groundwater Resources: Sustainability, Management, and Restoration; McGraw-Hill: New York, NY, USA, 2009; ISBN 978-0-07-149273-7. [Google Scholar]
  22. Healy, R.W.; Scanlon, B.R. Estimating Groundwater Recharge; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-511-78074-5. [Google Scholar]
  23. Asano, T.; Cotruvo, J.A. Groundwater recharge with reclaimed municipal wastewater: Health and regulatory considerations. Water Res. 2004, 38, 1941–1951. [Google Scholar] [CrossRef] [PubMed]
  24. Gale, I. Strategies for Managed Aquifer Recharge (MAR) in Semi-Arid Areas; UNESCO IHP: Paris, France, 2005; p. 33. [Google Scholar]
  25. Allam, M.N.; Allam, G.I. Water Resources in Egypt: Future Challeges and Opportunities. Water Int. 2007, 32, 205–218. [Google Scholar] [CrossRef]
  26. Khan, S.; Mushtaq, S.; Hanjra, M.A.; Schaeffer, J. Estimating potential costs and gains from an aquifer storage and recovery program in Australia. Agric. Water Manag. 2008, 95, 477–488. [Google Scholar] [CrossRef]
  27. Abiye, T.A.; Sulieman, H.; Ayalew, M. Use of treated wastewater for managed aquifer recharge in highly populated urban centers: A case study in Addis Ababa, Ethiopia. Environ. Geol. 2009, 58, 55–59. [Google Scholar] [CrossRef]
  28. Al-Maktoumi, A.; El-Rawy, M.; Zekri, S. Management options for a multipurpose coastal aquifer in Oman. Arab. J. Geosci. 2016, 9, 636. [Google Scholar] [CrossRef]
  29. El-Rawy, M.; Al-Maktoumi, A.; Zekri, S.; Abdalla, O.; Al-Abri, R. Hydrological and economic feasibility of mitigating a stressed coastal aquifer using managed aquifer recharge: A case study of Jamma aquifer, Oman. J. Arid Land 2019, 11, 148–159. [Google Scholar] [CrossRef] [Green Version]
  30. Schwartz, F.W.; Gallup, D.N. Some factors controlling the major ion chemistry of small lakes: Examples from the prairie parkland of Canada. Hydrobiologia 1978, 58, 65–81. [Google Scholar] [CrossRef]
  31. Stauffer, R.E. Effects of citrus agriculture on ridge lakes in Central Florida. Water Air Soil Pollut. 1991, 59, 125–144. [Google Scholar] [CrossRef]
  32. Nakayama, T.; Watanabe, M. Missing role of groundwater in water and nutrient cycles in the shallow eutrophic lake Kasumigaura, Japan. Hydrol. Process. 2008, 22, 1150–1172. [Google Scholar] [CrossRef]
  33. Sanford, W. Recharge and groundwater models: An overview. Hydrogeol. J. 2002, 10, 110–120. [Google Scholar] [CrossRef]
  34. Salem, A.; Dezső, J.; Lóczy, D.; El-Rawy, M.; Slowik, M. Modeling Surface Water-Groundwater Interaction in an Oxbow of the Drava Floodplain. In Proceedings of the 13th International Conference on Hydroinformatics HIC 2018, Palermo, Italy, 1–6 July 2018. [Google Scholar]
  35. Lee, D.R. A device for measuring seepage flux in lakes and estuaries1. Limnol. Oceanogr. 1977, 22, 140–147. [Google Scholar] [CrossRef]
  36. Winter, T.C.; LaBaugh, J.W.; Rosenberry, D.O. The design and use of a hydraulic potentiomanometer for direct measurement of differences in hydraulic head between groundwater and surface water. Limnol. Oceanogr. 1988, 33, 1209–1214. [Google Scholar] [CrossRef]
  37. Ong, J.B.; Zlotnik, V.A. Assessing Lakebed Hydraulic Conductivity and Seepage Flux by Potentiomanometer. Ground Water 2011, 49, 270–274. [Google Scholar] [CrossRef]
  38. Stauffer, R.E. Use of solute tracers released by weathering to estimate groundwater inflow to seepage lakes. Environ. Sci. Technol. 1985, 19, 405–411. [Google Scholar] [CrossRef]
  39. Sacks, L.A.; Swancar, A.; Lee, T.M. Estimating Ground-Water Exchange with Lakes Using Water-Budget and Chemical Mass-Balance Approaches for Ten Lakes in Ridge Areas of Polk and Highlands Counties, Florida; U.S. Geological Survey: Reston, VA, USA, 1998; p. 52.
  40. Krabbenhoft, D.P.; Bowser, C.J.; Anderson, M.P.; Valley, J.W. Estimating groundwater exchange with lakes: The stable isotope mass balance method. Water Resour. Res. 1990, 26, 2445–2453. [Google Scholar] [CrossRef]
  41. Brindha, K.; Neena Vaman, K.V.; Srinivasan, K.; Sathis Babu, M.; Elango, L. Identification of surface water-groundwater interaction by hydrogeochemical indicators and assessing its suitability for drinking and irrigational purposes in Chennai, Southern India. Appl. Water Sci. 2014, 4, 159–174. [Google Scholar] [CrossRef] [Green Version]
  42. Kanduč, T.; Grassa, F.; McIntosh, J.; Stibilj, V.; Ulrich-Supovec, M.; Supovec, I.; Jamnikar, S. A geochemical and stable isotope investigation of groundwater/surface-water interactions in the Velenje Basin, Slovenia. Hydrogeol. J. 2014, 22, 971–984. [Google Scholar] [CrossRef]
  43. Sacks, L.A.; Lee, T.M.; Swancar, A. The suitability of a simplified isotope-balance approach to quantify transient groundwater–lake interactions over a decade with climatic extremes. J. Hydrol. 2014, 519, 3042–3053. [Google Scholar] [CrossRef] [Green Version]
  44. Coplen, T.B. Guidelines and recommended terms for expression of stable-isotope-ratio and gas-ratio measurement results: Guidelines and recommended terms for expressing stable isotope results. Rapid Commun. Mass Spectrom. 2011, 25, 2538–2560. [Google Scholar] [CrossRef]
  45. Dinçer, T. The Use of Oxygen 18 and Deuterium Concentrations in the Water Balance of Lakes. Water Resour. Res. 1968, 4, 1289–1306. [Google Scholar] [CrossRef]
  46. Turner, J.V.; Allison, G.B.; Holmes, J.W. The water balance of a small lake using stable isotopes and tritium. J. Hydrol. 1984, 70, 199–220. [Google Scholar] [CrossRef]
  47. LaBaugh, J.W.; Winter, T.C.; Rosenberry, D.O.; Schuster, P.F.; Reddy, M.M.; Aiken, G.R. Hydrological and chemical estimates of the water balance of a closed-basin lake in north central Minnesota. Water Resour. Res. 1997, 33, 2799–2812. [Google Scholar] [CrossRef]
  48. Sacks, L.A. Estimating Ground-Water Inflow to Lakes in Central Florida Using the Isotope Mass-Balance Approach; Water-Resources Investigations Report 2002-4192; U.S. Dept. of the Interior, U.S. Geological Survey: Reston, VA, USA, 2002.
  49. El-Zehairy, A.A.; Lubczynski, M.W.; Gurwin, J. Interactions of artificial lakes with groundwater applying an integrated MODFLOW solution. Hydrogeol. J. 2018, 26, 109–132. [Google Scholar] [CrossRef]
  50. McDonald, M.G.; Harbaugh, A.W. A Modular Three-Dimensional Finite-Difference Ground-Water Flow Model; Book 6, Chapter A1; U.S. Geological Survey, Techniques of Water-Resources Investigations: Reston, VA, USA, 1988; p. 586.
  51. Leblanc, M.; Favreau, G.; Tweed, S.; Leduc, C.; Razack, M.; Mofor, L. Remote sensing for groundwater modelling in large semiarid areas: Lake Chad Basin, Africa. Hydrogeol. J. 2007, 15, 97–100. [Google Scholar] [CrossRef]
  52. Mylopoulos, N.; Mylopoulos, Y.; Tolikas, D.; Veranis, N. Groundwater modeling and management in a complex lake-aquifer system. Water Resour Manag. 2007, 21, 469–494. [Google Scholar] [CrossRef]
  53. Fenske, J.P.; Leake, S.A.; Prudic, D.E. Documentation of A Computer Program (RES1) to Simulate Leakage from Reservoirs Using the Modular Finite-Difference Ground-Water Flow Model (MODFLOW); U.S. Geological Survey: Reston, VA, USA, 1996; p. 51.
  54. Merritt, M.L.; Konikow, L.F. Documentation of A Computer Program to Simulate Lake-Aquifer Interaction Using the MODFLOW Ground Water Flow Model and the MOC3D Solute-Transport Model; Water-Resources Investigations Report 2000-4167; U.S. Dept. of the Interior, U.S. Geological Survey: Reston, VA, USA, 2000; p. 146.
  55. Lee, T.M. Hydrogeologic Controls on the Groundwater Interactions with an Acidic Lake in Karst Terrain, Lake Barco, Florida. Water Resour. Res. 1996, 32, 831–844. [Google Scholar] [CrossRef]
  56. Yihdego, Y.; Becht, R. Simulation of lake–aquifer interaction at Lake Naivasha, Kenya using a three-dimensional flow model with the high conductivity technique and a DEM with bathymetry. J. Hydrol. 2013, 503, 111–122. [Google Scholar] [CrossRef]
  57. Cheng, X.; Anderson, M.P. Numerical Simulation of Ground-Water Interaction with Lakes Allowing for Fluctuating Lake Levels. Groundwater 1993, 31, 929–933. [Google Scholar] [CrossRef]
  58. Kidmose, J.; Engesgaard, P.; Nilsson, B.; Laier, T.; Looms, M.C. Spatial Distribution of Seepage at a Flow-Through Lake: Lake Hampen, Western Denmark. Vadose Zone J. 2011, 10, 110. [Google Scholar] [CrossRef]
  59. Hunt, R. Ground Water-Lake Interaction Modeling Using the LAK3 Package for MODFLOW 2000. Ground Water 2003, 41, 114–118. [Google Scholar] [CrossRef]
  60. Buchberger, P. A Dráva-völgy árvédelmének története (History of flood control in the Drava Valley). Vízügyi Közlemények 1975, 75, 103–113. [Google Scholar]
  61. Pálfai, I. Magyarország Holtágai (Oxbows in Hungary); Hungarian Ministry of Transport and Water Management: Budapest, Hungary, 2001; p. 231.
  62. VKKI Vízgyűjtő-gazdálkodási terv. Dráva részvízgyűjtő (Water Basin Management Plan: Drava Partial Water Basin); Central Directorate for Water Management and Environmental Protection: Budapest, Hungary, 2010. [Google Scholar]
  63. Lóczy, D. Geological and Geomorphological Setting. In The Drava River: Environmental Problems and Solutions; Springer Science + Media: Cham, Switzerland, 2018; pp. 5–21. [Google Scholar]
  64. Lóczy, D.; Dezső, J.; Gyenizse, P.; Czigány, S.; Tóth, G. Oxbow Lakes: Hydromorphology. In The Drava River: Environmental Problems and Solutions; Springer Science + Media: Cham, Switzerland, 2019; pp. 177–198. [Google Scholar]
  65. Salem, A.; Dezső, J.; El-Rawy, M.; Lóczy, D. Statistical analysis of precipitation trend for Drava flood plain region in Hungary. In Proceedings of the GSRD International Conference, 579th International Conferences on Engineering and Natural Science (ICENS), Istanbul, Turkey, 21 March 2019; pp. 43–47. [Google Scholar]
  66. Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. A 1948, 193, 120–145. [Google Scholar]
  67. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Allen, R.G.; Food and Agriculture Organization of the United Nations (Eds.) FAO Irrigation and Drainage Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; ISBN 978-92-5-104219-9. [Google Scholar]
  68. Dezső, J.; Salem, A.; Lóczy, D.; Slowik, M.; Dávid, P. Randomly layered fluvial sediments influenced groundwater-surface water interaction. In Proceedings of the 17th International Multidisciplinary Scientific GeoConference SGEM 2017, Vienna, Austria, 27 June–6 July 2017; Volume 17, pp. 331–338. [Google Scholar]
  69. Słowik, M.; Dezső, J.; Marciniak, A.; Tóth, G.; Kovács, J. Evolution of river planforms downstream of dams: Effect of dam construction or earlier human-induced changes?: Evolution of river planforms downstream of dams. Earth Surf. Process. Landf. 2018, 43, 2045–2063. [Google Scholar] [CrossRef]
  70. Salem, A.; Dezső, J.; El-Rawy, M.; loczy, D.; Halmai, Á. Estimation of groundwater recharge distribution using Gis based WetSpass model in the Cun-Szaporca oxbow, Hungary. In Proceedings of the 19th International Multidisciplinary Scientific GeoConference SGEM 2019, Albena, Bulgaria, 28 June–7 July 2019; Volume 19, pp. 169–176. [Google Scholar]
  71. Abdollahi, K.; Bashir, I.; Verbeiren, B.; Harouna, M.R.; Van Griensven, A.; Huysmans, M.; Batelaan, O. A distributed monthly water balance model: Formulation and application on Black Volta Basin. Environ. Earth Sci. 2017, 76, 198. [Google Scholar] [CrossRef]
  72. Batelaan, O.; Smedt, F.D. WetSpass: A flexible, GIS based, distributed recharge methodology for regional groundwater modelling. In Impact of Human Activity on Groundwater Dynamics; Gehrels, H., Peters, J., Leibundgut, C., Eds.; International Association of Hydrological Sciences: Wallingford, UK, 2001; pp. 11–17. [Google Scholar]
  73. Abu-Saleem, A.; Al-Zubi, Y.; Rimawi, O.; Al-Zubi, J.; Alouran, N. Estimation of Water Balance Components in the Hasa Basin with GIS based WetSpass Model. J. Agron. 2010, 9, 119–125. [Google Scholar] [CrossRef] [Green Version]
  74. Gebreyohannes, T.; De Smedt, F.; Walraevens, K.; Gebresilassie, S.; Hussien, A.; Hagos, M.; Amare, K.; Deckers, J.; Gebrehiwot, K. Application of a spatially distributed water balance model for assessing surface water and groundwater resources in the Geba basin, Tigray, Ethiopia. J. Hydrol. 2013, 499, 110–123. [Google Scholar] [CrossRef]
  75. Armanuos, A.M.; Negm, A.; Yoshimura, C.; Valeriano, O.C.S. Application of WetSpass model to estimate groundwater recharge variability in the Nile Delta aquifer. Arab. J. Geosci. 2016, 9, 553. [Google Scholar] [CrossRef]
  76. Zhang, Y.; Liu, S.; Cheng, F.; Shen, Z. WetSpass-Based Study of the Effects of Urbanization on the Water Balance Components at Regional and Quadrat Scales in Beijing, China. Water 2017, 10, 5. [Google Scholar] [CrossRef] [Green Version]
  77. Salem, A.; Dezső, J.; El-Rawy, M. Assessment of Groundwater Recharge, Evaporation, and Runoff in the Drava Basin in Hungary with the WetSpass Model. Hydrology 2019, 6, 23. [Google Scholar] [CrossRef] [Green Version]
  78. Batelaan, O.; De Smedt, F. GIS-based recharge estimation by coupling surface–subsurface water balances. J. Hydrol. 2007, 337, 337–355. [Google Scholar] [CrossRef]
  79. Niswonger, R.G.; Panday, S.; Ibaraki, M. MODFLOW-NWT, A Newton Formulation for MODFLOW-2005; U.S. Geological Survey: Reston, VA, USA, 2011.
  80. Winston, R.B. ModelMuse-A Graphical User Interface for MODFLOW-2005 and PHAST: US Geological Survey Techniques And Methods 6-A29; U.S. Geological Survey: Reston, VA, USA, 2009.
  81. Guimerà, J.; Vives, L.; Carrera, J. A discussion of scale effects on hydraulic conductivity at a granitic site (El Berrocal, Spain). Geophys. Res. Lett. 1995, 22, 1449–1452. [Google Scholar] [CrossRef]
  82. Zhang, Y.; Gable, C.W.; Person, M. Equivalent hydraulic conductivity of an experimental stratigraphy: Implications for basin-scale flow simulations: Equivalent conductivity of experimental stratigraphy. Water Resour. Res. 2006, 4, W05404. [Google Scholar] [CrossRef] [Green Version]
  83. Zhang, Y.; Person, M.; Gable, C.W. Representative hydraulic conductivity of hydrogeologic units: Insights from an experimental stratigraphy. J. Hydrol. 2007, 339, 65–78. [Google Scholar] [CrossRef]
  84. Poeter, E.E.; Hill, M.C.; Banta, E.R.; Mehl, S.; Christensen, S. UCODE_2005 and Six Other Computer Codes for Universal Sensitivity Analysis, Calibration, and Uncertainty Evaluation; U.S. Geological Survey: Reston, VA, USA, 2006; p. 283.
  85. Banta, E.R. ModelMate—A Graphical User Interface for Model Analysis; U.S. Geological Survey: Reston, VA, USA, 2011; p. 26.
Water 12 00250 g001 550
Figure 1. Location of the Drava River floodplain, SW Hungary, with water-courses, existing (Cún-Szaporca) lake, and topography.
Figure 1. Location of the Drava River floodplain, SW Hungary, with water-courses, existing (Cún-Szaporca) lake, and topography.
Water 12 00250 g001
Water 12 00250 g002 550
Figure 2. (a) Spatial distribution of soil textures in the Drava floodplain, (b) vertical distribution of sediment textures in the top 100 m. ClMu: clayey mud; FiS: fine sand; COMedSa: coarse to medium sand.
Figure 2. (a) Spatial distribution of soil textures in the Drava floodplain, (b) vertical distribution of sediment textures in the top 100 m. ClMu: clayey mud; FiS: fine sand; COMedSa: coarse to medium sand.
Water 12 00250 g002
Water 12 00250 g003 550
Figure 3. (a) Land use classes of the Drava floodplain, (b) contour line of the average depth to groundwater level.
Figure 3. (a) Land use classes of the Drava floodplain, (b) contour line of the average depth to groundwater level.
Water 12 00250 g003
Water 12 00250 g004 550
Figure 4. Spatial distribution of simulated mean water balance components: (a) Groundwater recharge; (b) actual evapotranspiration.
Figure 4. Spatial distribution of simulated mean water balance components: (a) Groundwater recharge; (b) actual evapotranspiration.
Water 12 00250 g004
Water 12 00250 g005 550
Figure 5. Hydraulic conductivity zones for (a) layer 1; (b) layer 2; (c) layer 3; (d) layer 4.
Figure 5. Hydraulic conductivity zones for (a) layer 1; (b) layer 2; (c) layer 3; (d) layer 4.
Water 12 00250 g005
Water 12 00250 g006 550
Figure 6. (a) Boundary conditions, observation wells, and planned reservoirs; (b) Korcsina reservoir; (c) Okor reservoir.
Figure 6. (a) Boundary conditions, observation wells, and planned reservoirs; (b) Korcsina reservoir; (c) Okor reservoir.
Water 12 00250 g006
Water 12 00250 g007 550
Figure 7. Model calibration. (a) Scatter plot for simulated versus observed groundwater piezometric heads; (b) simulated and observed daily variability of lake stages; (c) composite scaled sensitivities calculated with the parameter values.
Figure 7. Model calibration. (a) Scatter plot for simulated versus observed groundwater piezometric heads; (b) simulated and observed daily variability of lake stages; (c) composite scaled sensitivities calculated with the parameter values.
Water 12 00250 g007
Water 12 00250 g008 550
Figure 8. Daily variability of Lake Korcsina stage, groundwater seepage into the lake (GW-Inflow), seepage from the lake into groundwater (GW-Outflow), and net lake seepage (LAKnet) during the simulation period of one year. Note that the fluxes are referenced to the temporally variable lake with different feeding discharge from the stream. (a) Feeding at Q = 0.5 m3 s−1, (b) Q = 0.75 m3 s−1, (c) Q = 1.0 m3 s−1, (d) Q = 1.5 m3 s−1.
Figure 8. Daily variability of Lake Korcsina stage, groundwater seepage into the lake (GW-Inflow), seepage from the lake into groundwater (GW-Outflow), and net lake seepage (LAKnet) during the simulation period of one year. Note that the fluxes are referenced to the temporally variable lake with different feeding discharge from the stream. (a) Feeding at Q = 0.5 m3 s−1, (b) Q = 0.75 m3 s−1, (c) Q = 1.0 m3 s−1, (d) Q = 1.5 m3 s−1.
Water 12 00250 g008
Water 12 00250 g009 550
Figure 9. Daily variability of Okor lake stage, groundwater seepage into the lake (GW-Inflow), seepage from the lake into groundwater (GW-Outflow), and net lake seepage (LLKnet) during simulation period of one year. Note that the fluxes are referenced to the temporally variable lake with different feeding discharges. (a) Feeding by Q = 0.5 m3 s−1, (b) Q = 0.75 m3 s−1, (c) Q = 1.0 m3 s−1 and (d) Q = 1.5 m3 s−1.
Figure 9. Daily variability of Okor lake stage, groundwater seepage into the lake (GW-Inflow), seepage from the lake into groundwater (GW-Outflow), and net lake seepage (LLKnet) during simulation period of one year. Note that the fluxes are referenced to the temporally variable lake with different feeding discharges. (a) Feeding by Q = 0.5 m3 s−1, (b) Q = 0.75 m3 s−1, (c) Q = 1.0 m3 s−1 and (d) Q = 1.5 m3 s−1.
Water 12 00250 g009
Water 12 00250 g010 550
Figure 10. Simulated groundwater levels at a line crossing the Lake Korcsina at 10 and 20 days of filling and at 70 and 170 days of discharge period with respect to the base case.
Figure 10. Simulated groundwater levels at a line crossing the Lake Korcsina at 10 and 20 days of filling and at 70 and 170 days of discharge period with respect to the base case.
Water 12 00250 g010
Water 12 00250 g011 550
Figure 11. Simulated groundwater levels at a line crossing Lake Okor at 10 and 20 days of the filling period and at 70 and 170 days of the discharge period with respect to the base case.
Figure 11. Simulated groundwater levels at a line crossing Lake Okor at 10 and 20 days of the filling period and at 70 and 170 days of the discharge period with respect to the base case.
Water 12 00250 g011
Water 12 00250 g012a 550Water 12 00250 g012b 550
Figure 12. Lake–aquifer exchange fluxes for the Korcsina reservoir: (a) at the end of filling period of 14 days (+2 m reservoir stage), (b) for 40 days of discharge period (+1 m) (positive represents upward reservoir seepage gain and negative represents downward reservoir seepage loss).
Figure 12. Lake–aquifer exchange fluxes for the Korcsina reservoir: (a) at the end of filling period of 14 days (+2 m reservoir stage), (b) for 40 days of discharge period (+1 m) (positive represents upward reservoir seepage gain and negative represents downward reservoir seepage loss).
Water 12 00250 g012aWater 12 00250 g012b
Water 12 00250 g013a 550Water 12 00250 g013b 550
Figure 13. Lake–aquifer exchange fluxes of the Okor reservoir: (a) at the end of filling period of 10 days (+2 m reservoir stage), (b) for 40 days of the discharge period (+1 m) (positive represents upward reservoir seepage gain and negative represents downward reservoir seepage loss).
Figure 13. Lake–aquifer exchange fluxes of the Okor reservoir: (a) at the end of filling period of 10 days (+2 m reservoir stage), (b) for 40 days of the discharge period (+1 m) (positive represents upward reservoir seepage gain and negative represents downward reservoir seepage loss).
Water 12 00250 g013aWater 12 00250 g013b
Table
Table 1. Calibrated parameters for the calibrated model. R represents the spatial distribution map of average groundwater recharge.
Table 1. Calibrated parameters for the calibrated model. R represents the spatial distribution map of average groundwater recharge.
ParameterValueUnitDescription
HKZ1360m d−1Hydraulic conductivity of zone 1
HKZ225m d−1Hydraulic conductivity of zone 2
HKZ30.10m d−1Hydraulic conductivity of zone 3
HKZ45m d−1Hydraulic conductivity of zone 4
HKZ560m d−1Hydraulic conductivity of zone 5
RIVC1300m2 d−1River conductance of streams 1
RIVC25m2 d−1River conductance of streams 2
GHB40m2 d−1Conductance of general head boundary
RCH0.95Rmm d−1Groundwater recharge
Table
Table 2. Water balance at the end stress of the calibrated transient model.
Table 2. Water balance at the end stress of the calibrated transient model.
InputOutputInput−Output
(m3 day−1)%(m3 day−1)%(m3 day−1)
Recharge546,40336.84570.0545,946
Evapotranspiration00.0149,99210.1−149,992
GHB boundary627,78942.310,9490.7616,840
River62,7664.21,275,24485.8−1,212,478
Lake68680.549670.31901
Storage242,05516.344,2653.0197,783
Total1,485,881100.01,485,874100.00

Share and Cite

MDPI and ACS Style

Salem, A.; Dezső, J.; El-Rawy, M.; Lóczy, D. Hydrological Modeling to Assess the Efficiency of Groundwater Replenishment through Natural Reservoirs in the Hungarian Drava River Floodplain. Water 2020, 12, 250. https://doi.org/10.3390/w12010250

AMA Style

Salem A, Dezső J, El-Rawy M, Lóczy D. Hydrological Modeling to Assess the Efficiency of Groundwater Replenishment through Natural Reservoirs in the Hungarian Drava River Floodplain. Water. 2020; 12(1):250. https://doi.org/10.3390/w12010250

Chicago/Turabian Style

Salem, Ali, József Dezső, Mustafa El-Rawy, and Dénes Lóczy. 2020. "Hydrological Modeling to Assess the Efficiency of Groundwater Replenishment through Natural Reservoirs in the Hungarian Drava River Floodplain" Water 12, no. 1: 250. https://doi.org/10.3390/w12010250

APA Style

Salem, A., Dezső, J., El-Rawy, M., & Lóczy, D. (2020). Hydrological Modeling to Assess the Efficiency of Groundwater Replenishment through Natural Reservoirs in the Hungarian Drava River Floodplain. Water, 12(1), 250. https://doi.org/10.3390/w12010250

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop