Discussion on the Characteristics of Seismic Signals Due to Riverbank Landslides from Laboratory Tests
Abstract
:1. Introduction
2. Methodology
2.1. Test Configuration
2.2. Analysis Method of Seismic Signal
2.3. Self-Potential Data Measurement and Analysis Method
3. Results and Discussion
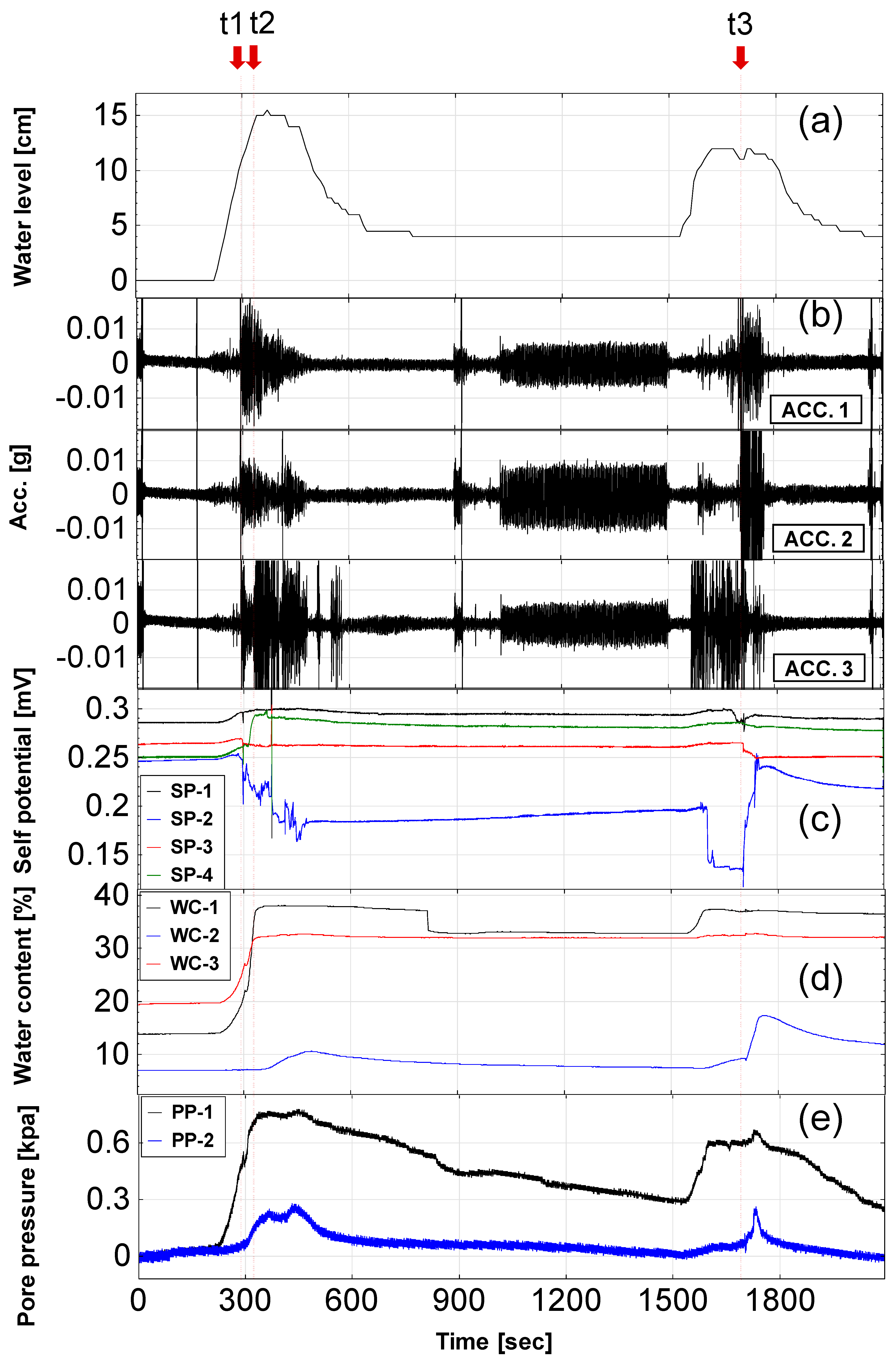
3.1. The Original Measured Signal
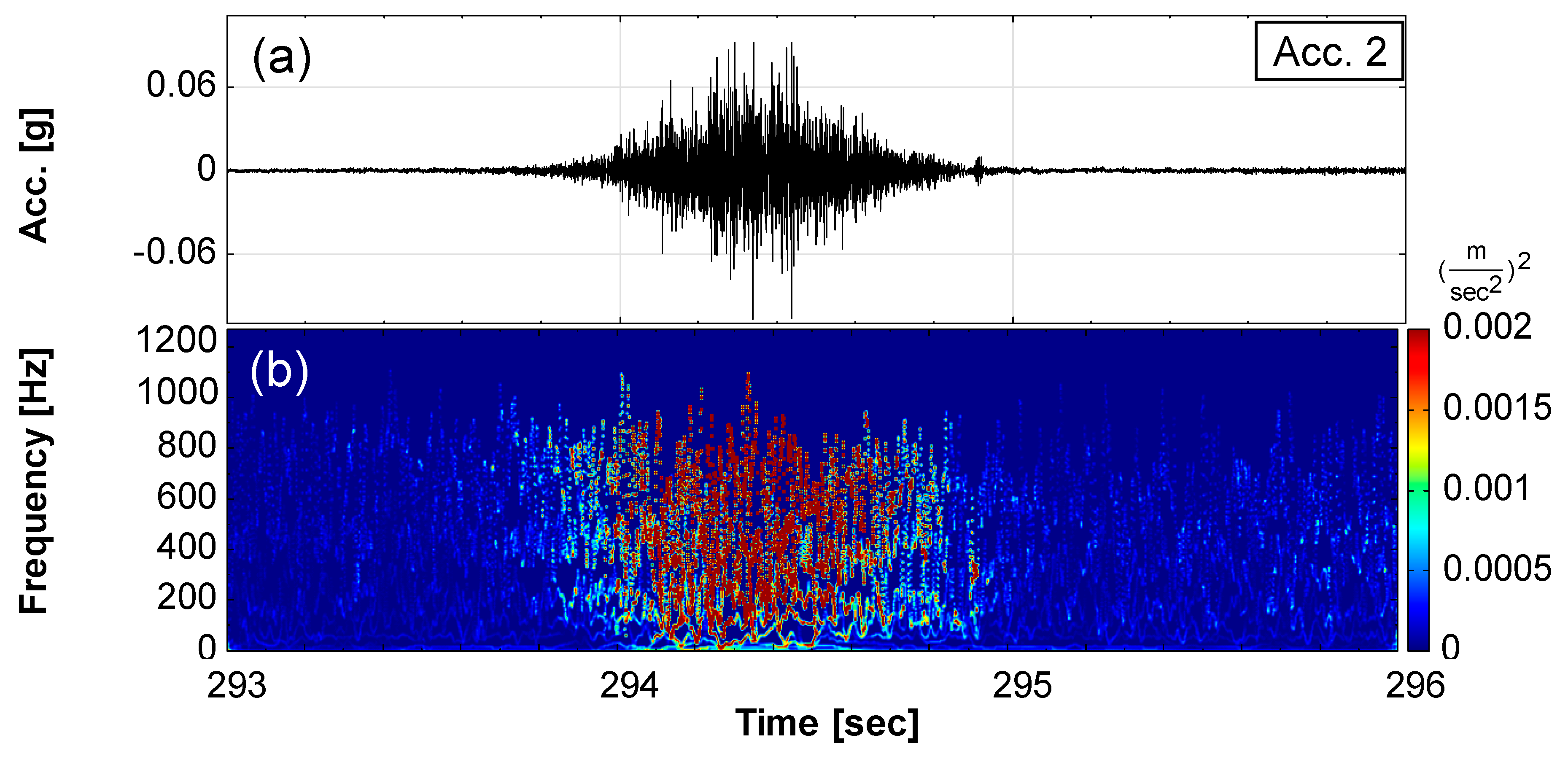
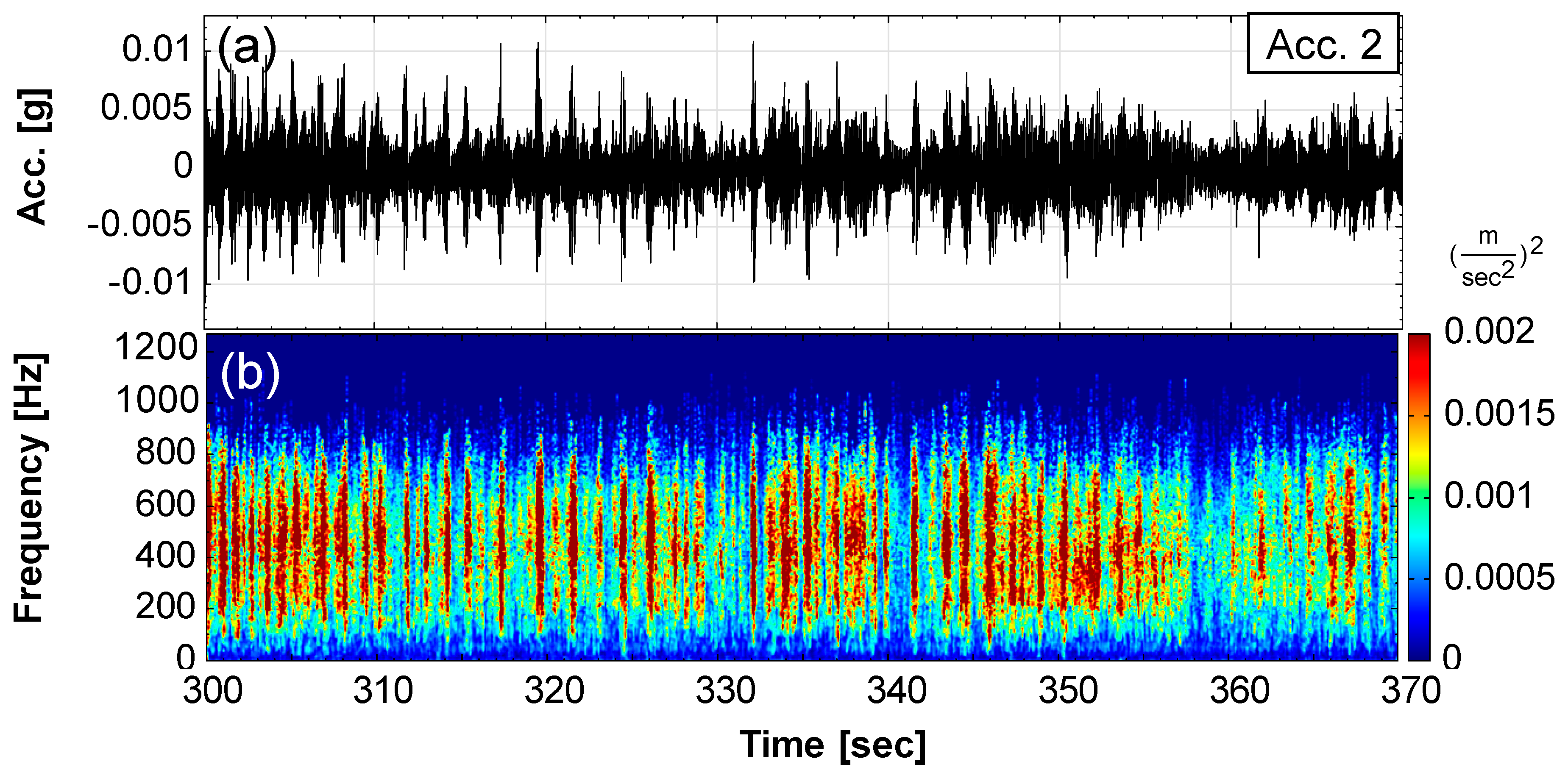
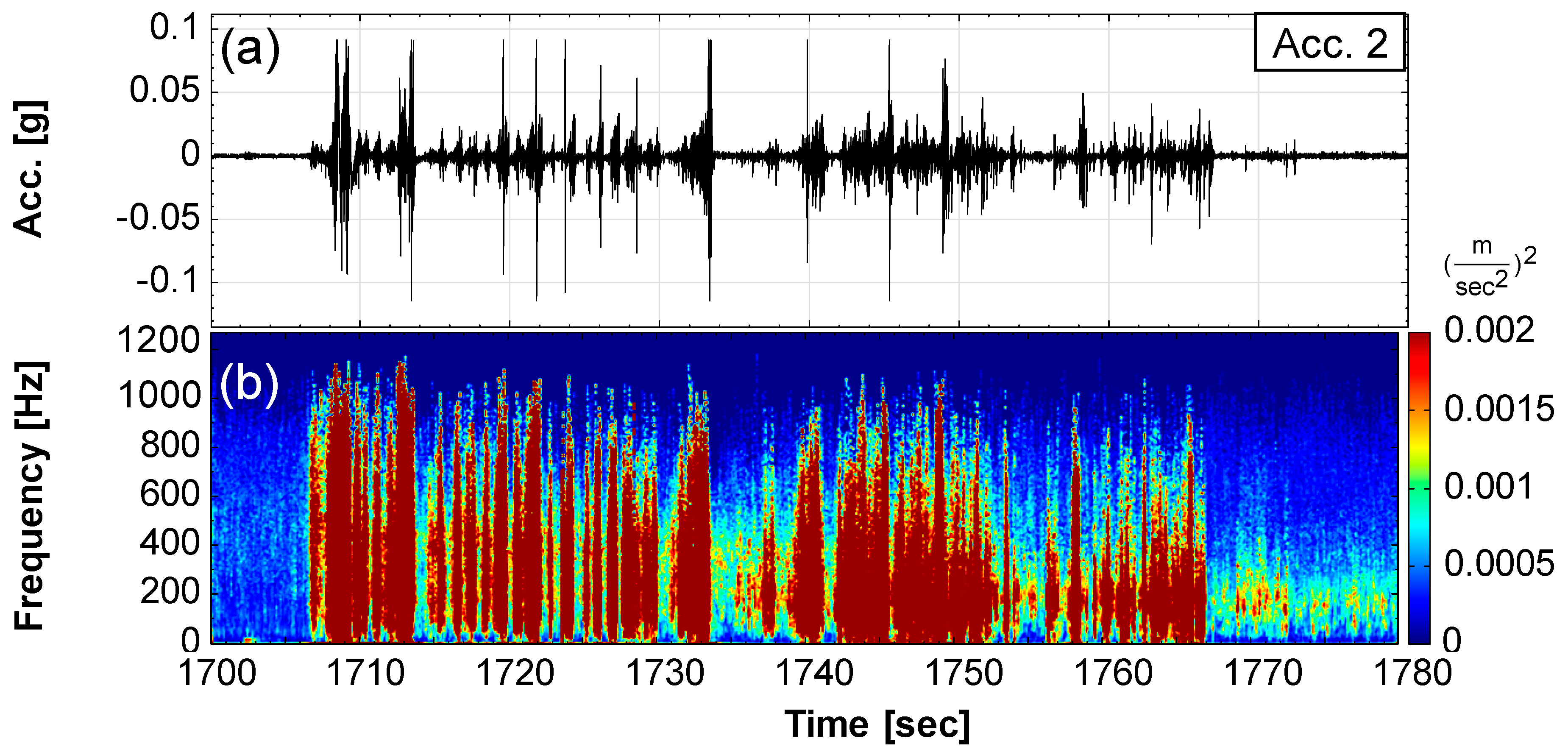
3.2. Seismic Signal Characteristics of Three Types of Landslides: Single, Intermittent, and Successive
3.3. Correspondence between Variation of Self-Potential, Water Content, and Seismic Signals
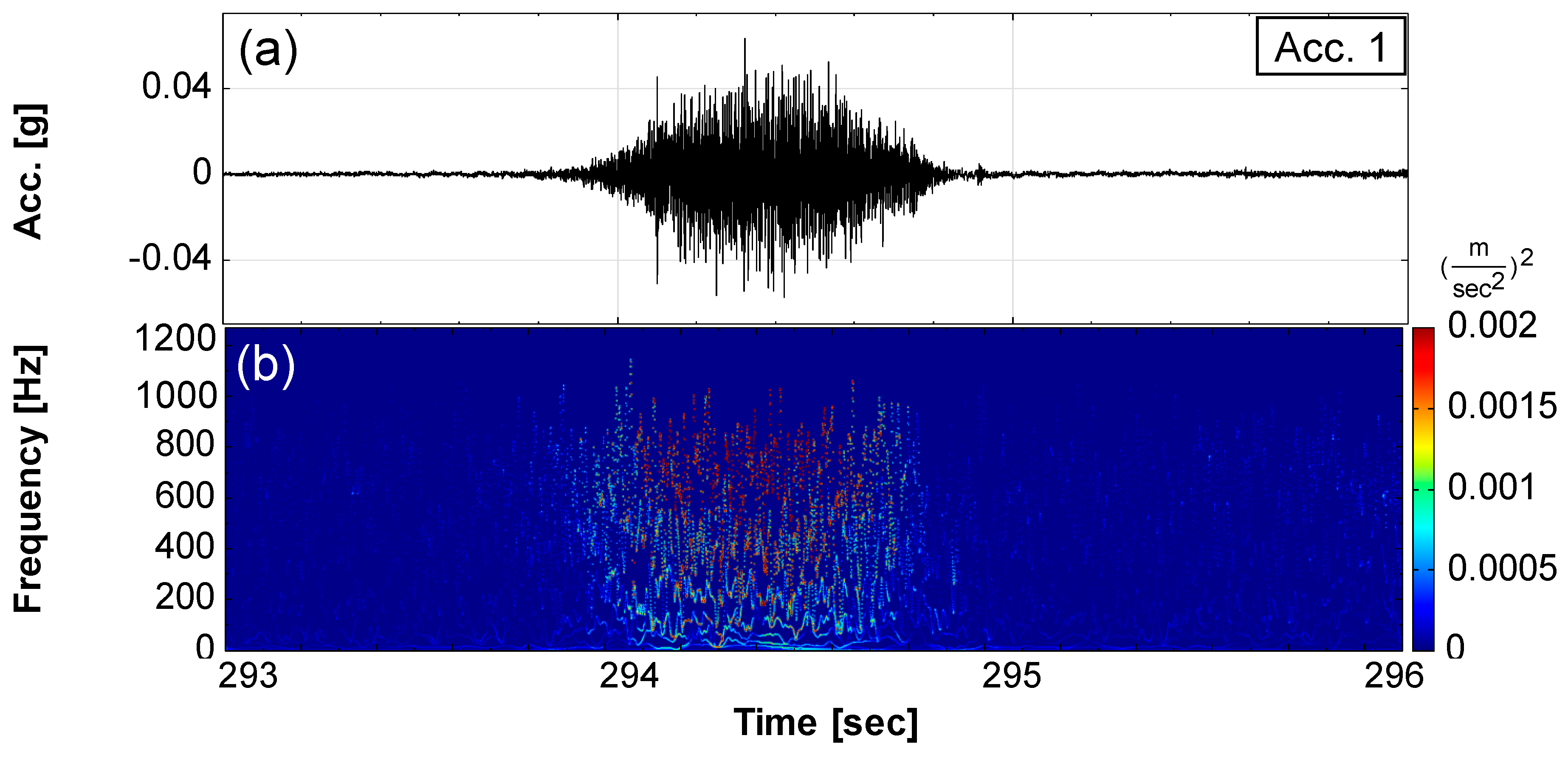
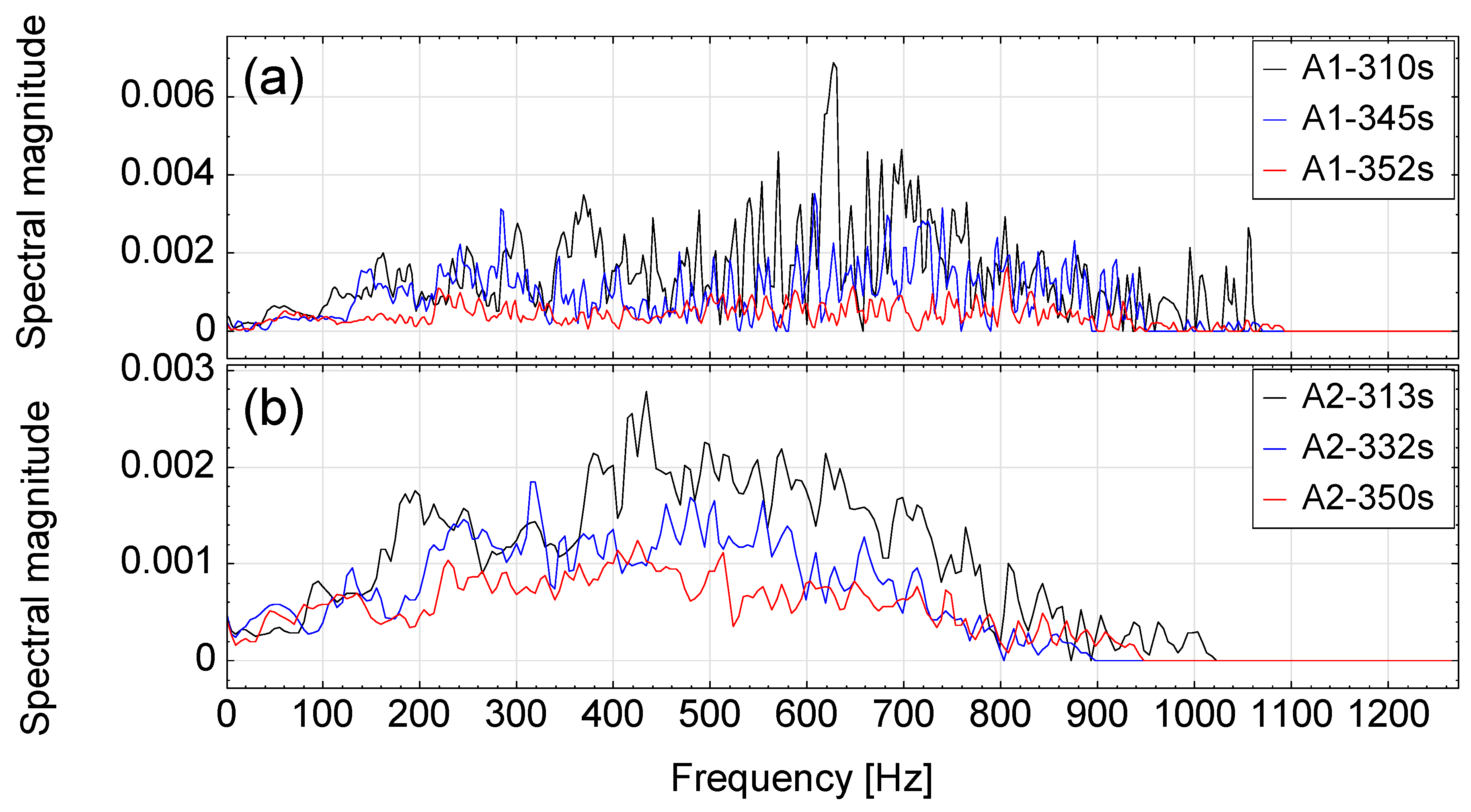
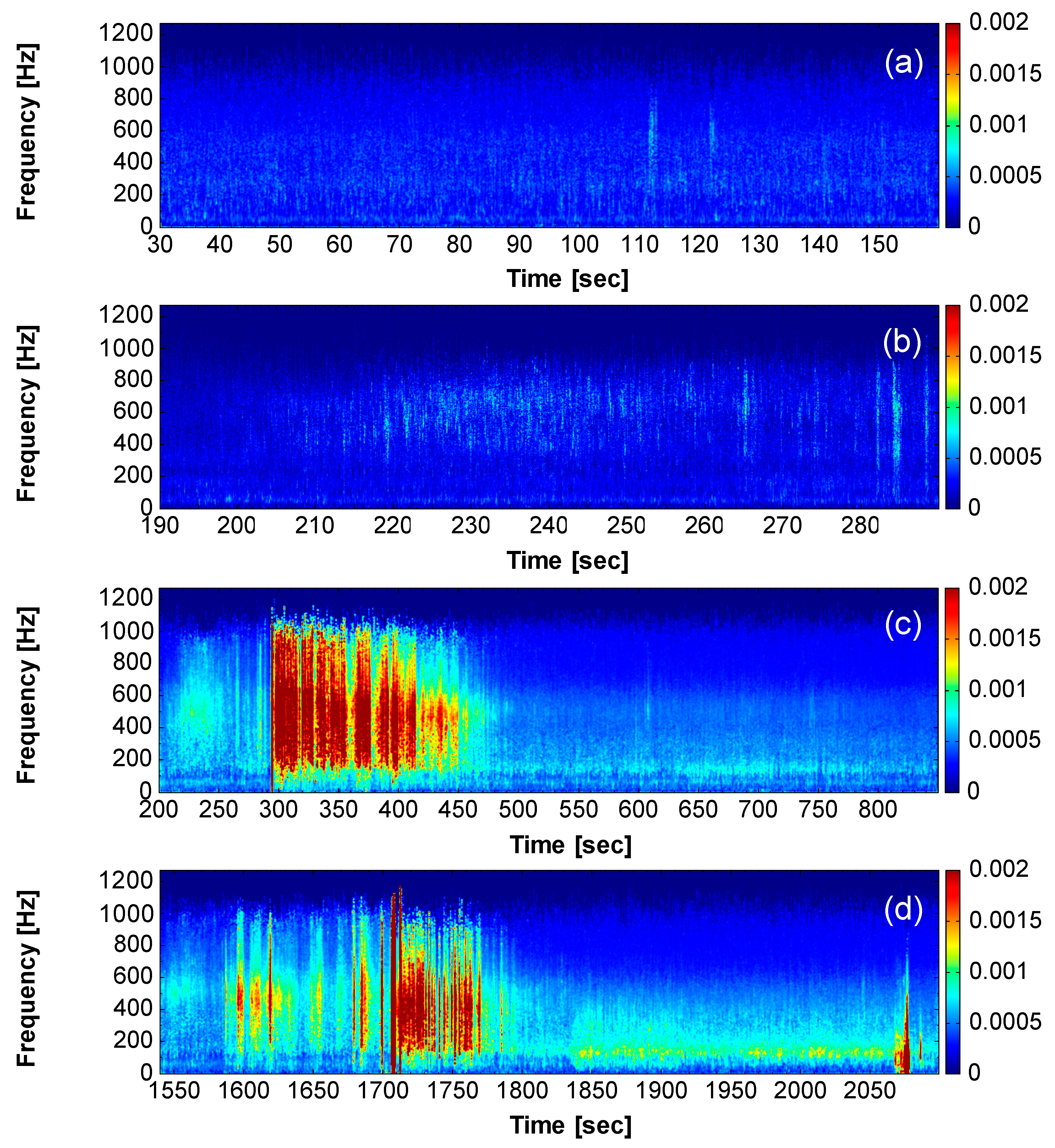
3.4. Comparison of Seismic Signal Spectrograms
3.5. Effect of Water Depth
3.6. Results of Water Content and Pore Water Pressure
4. Conclusions
- [1]
- Three types of riverbank slope landslides during erosion were identified: (a) single landslide: soil sliding down on one failure surface once; (b) intermittent landslide: soil gradually sliding down along the same sliding surface intermittently; and (c) successive landslide: different soils continuously sliding down from different sliding surfaces. The characteristics and processes of these three types of landslides corresponded to their seismic signals and spectrograms. The seismic signals can be used to clearly indicate the timing of landslide occurance.
- [2]
- The occurrence intervals of the intermittent landslides in this study were approximately 1–2 s in the test. Seismic signals can be monitored by means of accelerometers and velocimeters on an actual slope for landslide events. The monitored signals are helpful for identifying landslide events and have the potential to provide early landslide warnings.
- [3]
- High-frequency seismic energy attenuates faster than low-frequency seismic energy.
- [4]
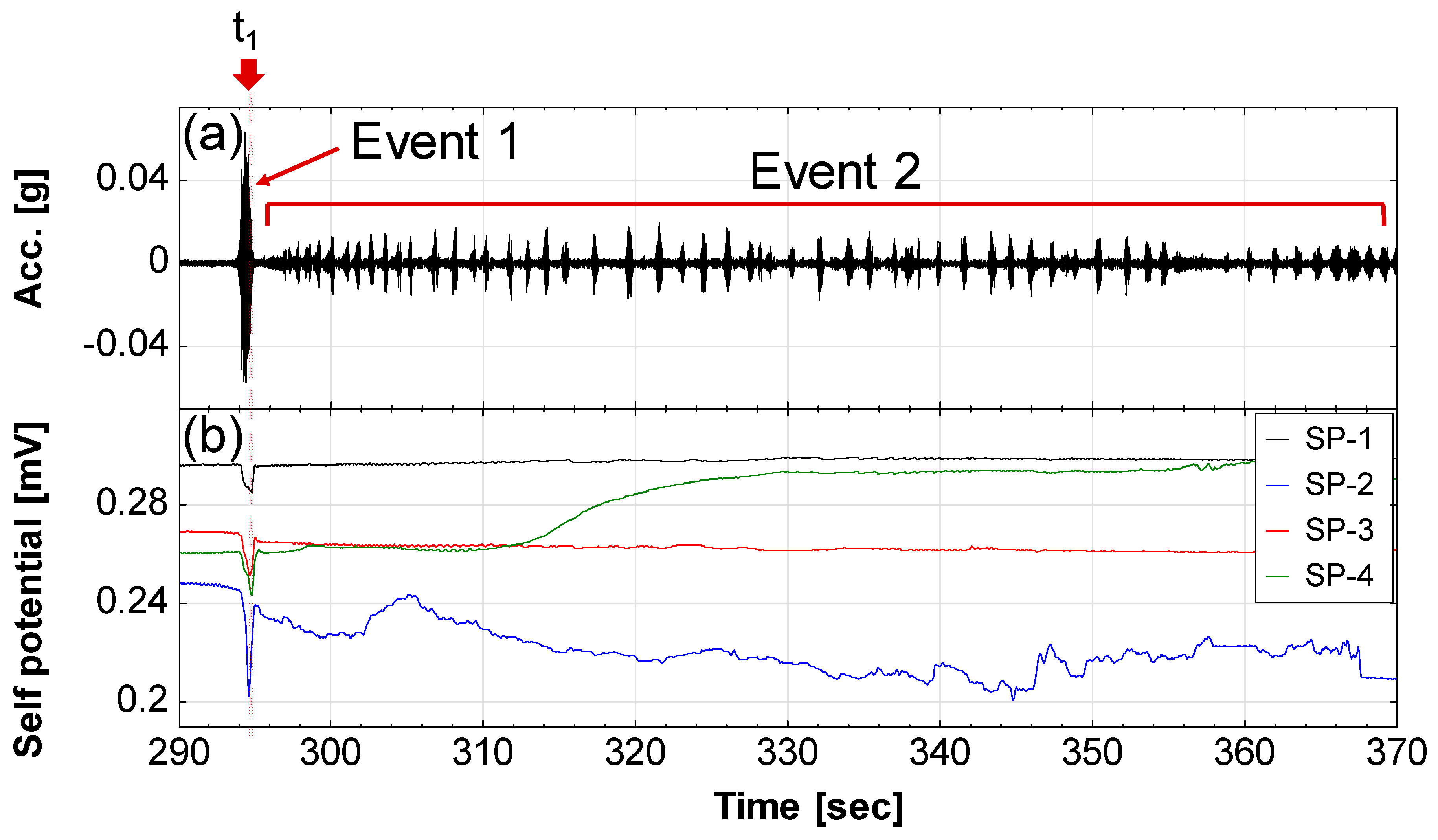
- Self-potential can be used to indicate the timing of landslide events and the time when the water level contacts the electrode. Based on changes in self-potential, it was noted that self-potential rose gradually as the water level rose to make contact with the nonpolarized electrode. The self-potential dropped instantly and jumped back again when a landslide occurred near the electrode. The self-potential decreased continuously when the electrode slid down with the soil.
- [5]
- In the case of higher water level (15 cm) flow, the riverbank slope exhibited a greater landslide range with more soils. However, in the case of a lower water level (10 cm), the landslide range was smaller because of a lower erosion capacity.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rosser, N.J.; Petley, D.N.; Lim, M.; Dunning, S.A.; Allison, R.J. Terrestrial laser scanning for monitoring the process of hard rock coastal cliff erosion. Q. J. Eng. Geol. Hydrogeol. 2005, 38, 363–375. [Google Scholar] [CrossRef]
- Kociuba, W.; Kubisz, W.; Zagórski, P. Use of terrestrial laser scanning (TLS) for monitoring and modelling of geomorphic processes and phenomena at a small and medium spatial scale in Polar environment (Scott River—Spitsbergen). Geomorphology 2014, 212, 84–96. [Google Scholar] [CrossRef]
- Longoni, L.; Papini, M.; Brambilla, D.; Barazzetti, L.; Roncoroni, F.; Scaioni, M.; Ivanov, V.I. Monitoring riverbank erosion in mountain catchments using terrestrial laser scanning. Remote Sens. 2016, 8, 241. [Google Scholar] [CrossRef] [Green Version]
- Orense, R.P.; Shimoma, S.; Maeda, K.; Towhata, I. Instrumented model slope failure due to water seepage. J. Nat. Disaster Sci. 2004, 26, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Lourenço, S.D.; Sassa, K.; Fukuoka, H. Failure process and hydrologic response of a two layer physical model: Implications for rainfall-induced landslides. Geomorphology 2006, 73, 115–130. [Google Scholar] [CrossRef]
- Terajima, T.; Miyahira, E.I.; Miyajima, H.; Ochiai, H.; Hattori, K. How hydrological factors initiate instability in a model sandy slope. Hydrol. Process. 2014, 28, 5711–5724. [Google Scholar] [CrossRef] [Green Version]
- Arosio, D.; Hojat, A.; Ivanov, V.I.; Loke, M.H.; Longoni, L.; Papini, M.; Tresoldi, G.; Zanzi, L. A laboratory experience to assess the 3D effects on 2D ERT monitoring of river levees. In Proceedings of the 24th European Meeting of Environmental and Engineering Geophysics, Porto, Portugal, 9–12 September 2018. [Google Scholar]
- Tresoldi, G.; Arosio, D.; Hojat, A.; Longoni, L.; Papini, M.; Zanzi, L. Long-term hydrogeophysical monitoring of the internal conditions of river levees. Eng. Geol. 2019, 259, 105139. [Google Scholar] [CrossRef]
- Rinaldi, M.; Casagli, N.; Dapporto, S.; Gargini, A. Monitoring and modelling of pore water pressure changes and riverbank stability during flow events. Earth Surf. Process. Landf. 2004, 29, 237–254. [Google Scholar] [CrossRef]
- Revil, A.; Hermitte, D.; Voltz, M.; Moussa, R.; Lacas, J.G.; Bourrié, G.; Trolard, F. Self-potential signals associated with variations of the hydraulic head during an infiltration experiment. Geophys. Res. Lett. 2002, 29, 10–11. [Google Scholar] [CrossRef]
- Hattori, K.; Kohno, H.; Tojo, Y.; Terajima, T.; Ochiai, H. Early warning of landslides based on landslide indoor experiments. In Ch. 20.8 of Landslides—Disaster Risk Reduction Monitoring; Sassa, K., Canuti, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 363–366. ISBN 978-3-540-69970-5. [Google Scholar]
- Shinbrot, T.; Kim, N.H.; Thyagu, N.N. Electrostatic precursors to granular slip events. Proc. Natl. Acad. Sci. USA 2012, 109, 10806–10810. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hong, J.L. Monitoring of the Infiltration Process of Shallow Soil Layer by Using Self-Potential Method. Master’s Thesis, National Central University, Taoyuan City, Taiwan, 2014; 77p. (In Chinese). [Google Scholar]
- Lin, C.W. Assessment of Saturation Triggered Slope Failure by Using Self-Potential Measurements and FLAC3D Numerical Model. Master’s Thesis, National Central University, Taoyuan City, Taiwan, 2016; 88p. (In Chinese). [Google Scholar]
- Senfaute, G.; Duperret, A.; Lawrence, J.A. Micro-seismic precursory cracks prior to rock-fall on coastal chalk cliffs: A case study at Mesnil-Val, Normandie, NW France. Nat. Hazards Earth Syst. Sci. 2009, 9, 1625–1641. [Google Scholar] [CrossRef]
- Suwa, H.; Mizuno, T.; Ishii, T. Prediction of a landslide and analysis of slide motion with reference to the 2004 Ohto slide in Nara, Japan. Geomorphology 2010, 124, 157–163. [Google Scholar] [CrossRef]
- Dammeier, F.; Moore, J.R.; Haslinger, F.; Loew, S. Characterization of alpine rockslides using statistical analysis of seismic signals. J. Geophys. Res. Earth Surf. 2011, 116, F04024. [Google Scholar] [CrossRef]
- Hibert, C.; Ekström, G.; Stark, C.P. Dynamics of the Bingham Canyon Mine landslides from seismic signal analysis. Geophys. Res. Lett. 2014, 41, 4535–4541. [Google Scholar] [CrossRef]
- Provost, F.; Malet, J.P.; Hibert, C.; Helmstetter, A.; Radiguet, M.; Amitrano, D.; Langet, N.; Larose, E.; Abancó, C.; Hürlimann, M.; et al. Towards a standard typology of endogenous landslide seismic sources. Earth Surf. Dyn. 2018, 6, 1059–1088. [Google Scholar] [CrossRef] [Green Version]
- Feng, Z.Y. The seismic signatures of the surge wave from the 2009 Xiaolin landslide-dam breach in Taiwan. Hydrol. Process. 2012, 26, 1342–1351. [Google Scholar] [CrossRef]
- Chao, W.A.; Wu, Y.M.; Zhao, L.; Tsai, V.C.; Chen, C.H. Seismologically determined bedload flux during the typhoon season. Sci. Rep. 2015, 5, 8261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- AnCAD, Inc. Visual Signal Reference Guide, Version1.5. Available online: http://www.ancad.com.tw/ (accessed on 24 August 2019). (In Chinese).
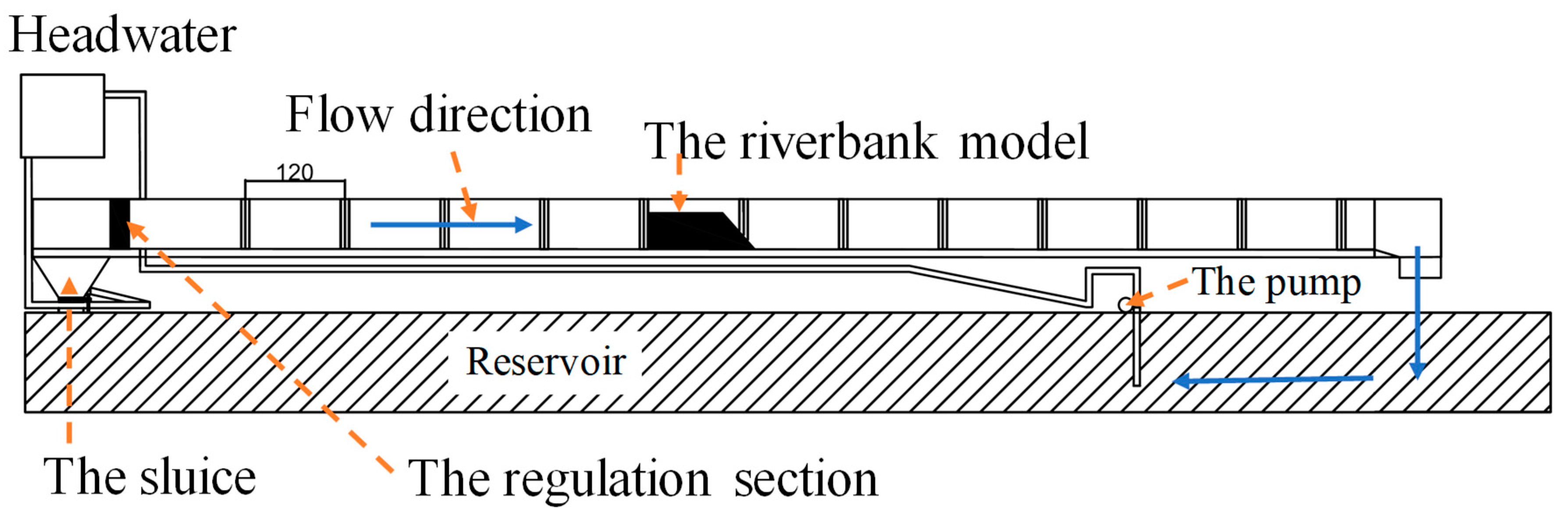

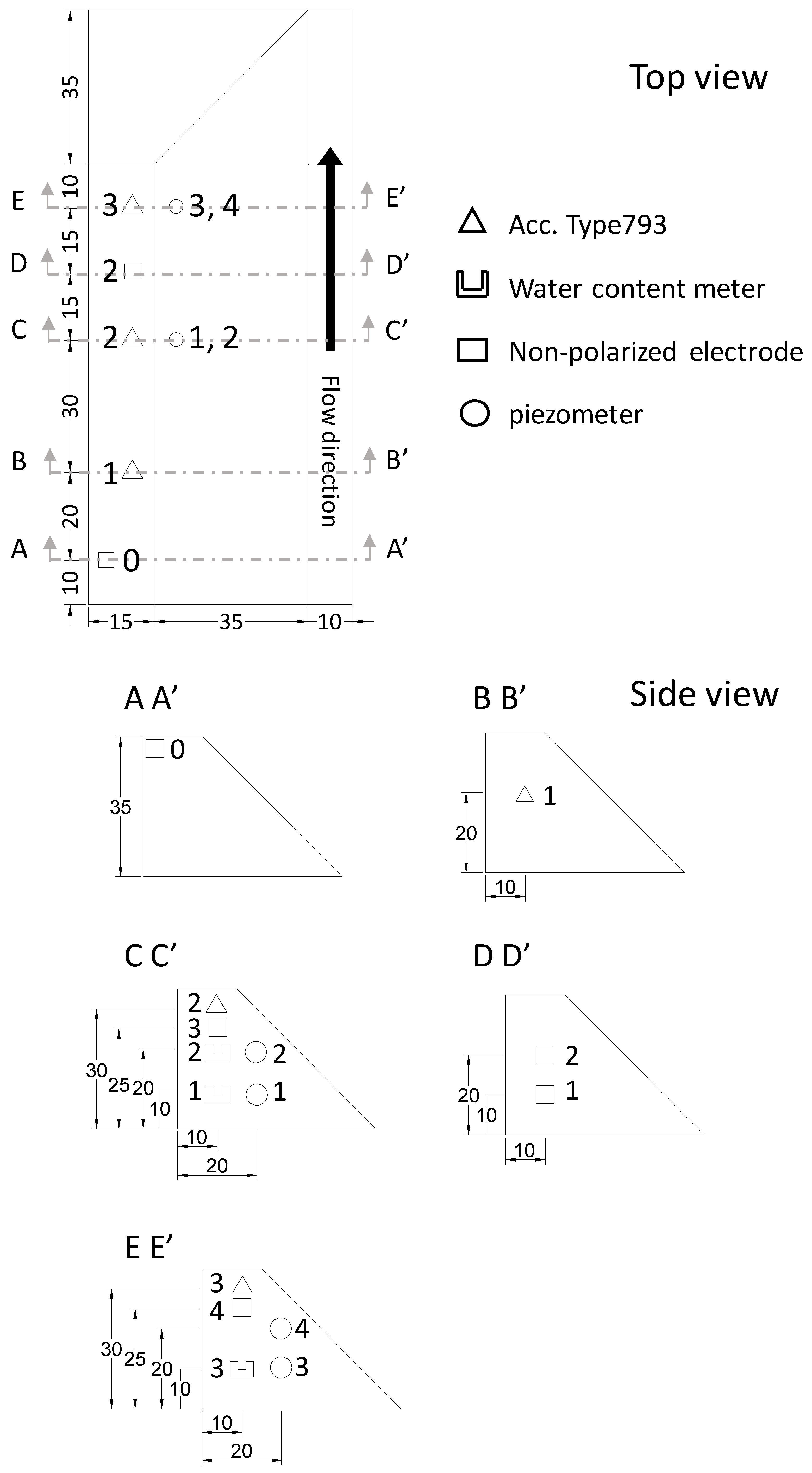






| Sloping of the Riverbank (°) | Height of the Riverbank (cm) | Length of the Riverbank Top (cm) | Length of the Riverbank Bottom (cm) | Maximum Water Level (cm) |
|---|---|---|---|---|
| 45 | 45 | 100 | 135 | 15 |
| Time (s) | Event | Variation of the Signals |
|---|---|---|
| 0–180 | Baground; the sluice was closed. | Background noise |
| 181–292 | The sluice was opened; start of measurement. | Seismic signals, self-potential, water content, and pore pressure were gradually increased. |
| 293–295 | T1, 293–295 s: a single slide (Event 1, see Supplementary Materials) occurred. | Seismic signals significantly increased; self-potential of SP-1 and SP-3 decreased first and then increased. |
| 297–370 | T2, 297–370 s: an intermittent slide (Event 2) occurred. | Seismic signals significantly increased; self-potential of SP-4 increased obviously due to the electrode exposed in the air. |
| 1030–1500 | The sluice was closed, and the flow pump was opened again to fill the headwater tank. | The noise of the flow pump appeared; water content and pore pressure decreased. |
| 1530 | The sluice was opened again. | - |
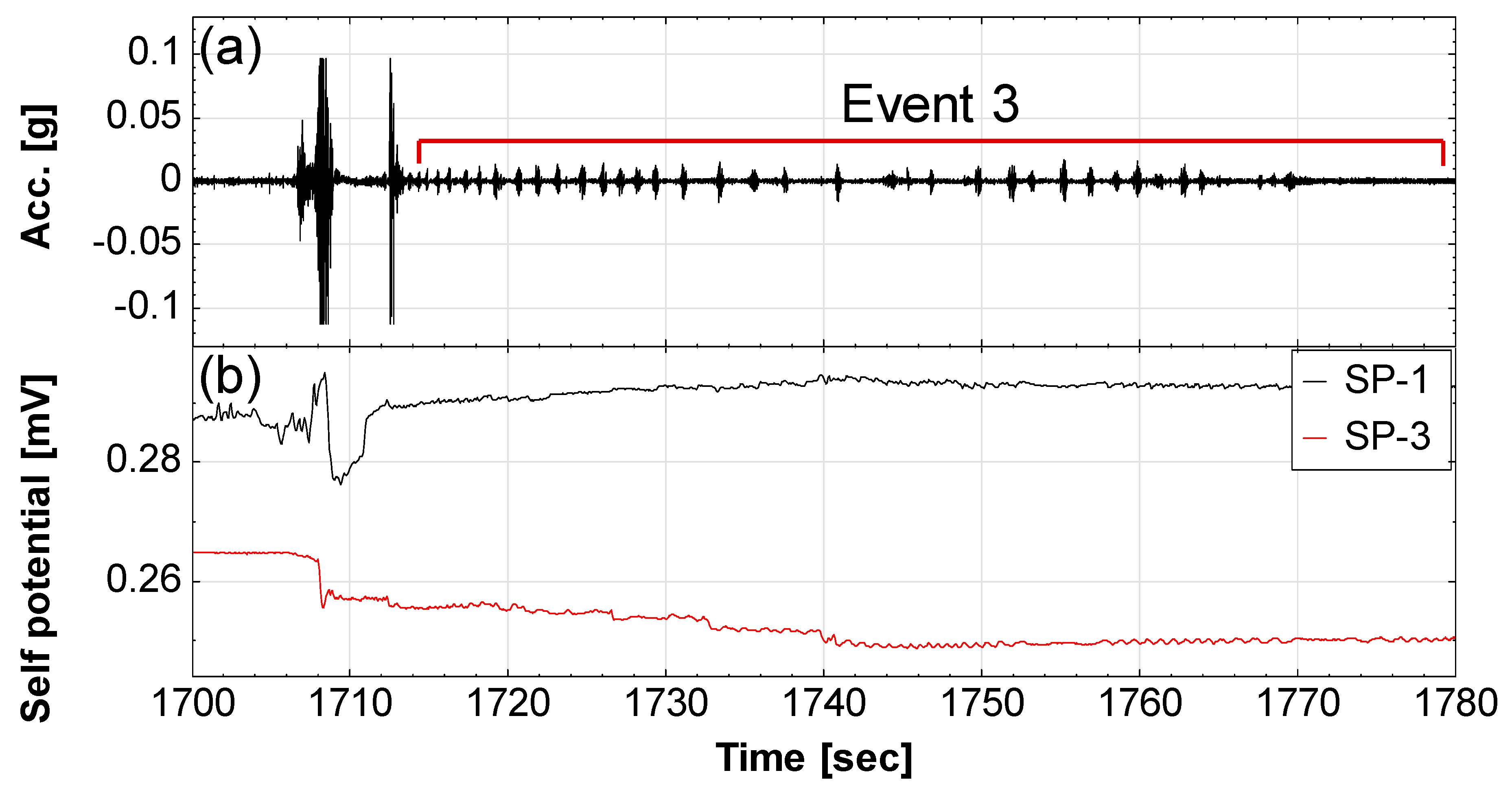
| 1705–1770 | T3, 1705 s: a single slide occurred; 1713–1770s: a sucessive slide (Event 3) occurred. | Seismic signals significantly increased; self-potential of SP-1 and Sp-3 decreased; water content meter (WC-2) was exposed and the readings were abnormal; pore pressure of PP-2 suddenly decreased. |
| 2095 | End of measurement. |
| Channel | Accelerometer A1 | Accelerometer A2 | ||
|---|---|---|---|---|
| Average Frequency (Hz) | Power (%) | Average Frequency (Hz) | Power (%) | |
| IMF 1 | 840 | 79.8 | 812 | 71.6 |
| IMF 2 | 418 | 14.6 | 416 | 18.9 |
| IMF 3 | 211 | 3.6 | 210 | 7.1 |
| IMF 4 | 102 | 1.1 | 111 | 1.6 |
| IMF 5 | 53.2 | 0.3 | 58.2 | 0.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.-Y.; Hsu, C.-M.; Chen, S.-H. Discussion on the Characteristics of Seismic Signals Due to Riverbank Landslides from Laboratory Tests. Water 2020, 12, 83. https://doi.org/10.3390/w12010083
Feng Z-Y, Hsu C-M, Chen S-H. Discussion on the Characteristics of Seismic Signals Due to Riverbank Landslides from Laboratory Tests. Water. 2020; 12(1):83. https://doi.org/10.3390/w12010083
Chicago/Turabian StyleFeng, Zheng-Yi, Chia-Ming Hsu, and Shi-Hao Chen. 2020. "Discussion on the Characteristics of Seismic Signals Due to Riverbank Landslides from Laboratory Tests" Water 12, no. 1: 83. https://doi.org/10.3390/w12010083
APA StyleFeng, Z.-Y., Hsu, C.-M., & Chen, S.-H. (2020). Discussion on the Characteristics of Seismic Signals Due to Riverbank Landslides from Laboratory Tests. Water, 12(1), 83. https://doi.org/10.3390/w12010083






