Assessing Po River Deltaic Vulnerability Using Earth Observation and a Bayesian Belief Network Model
Abstract
:1. Introduction
2. Materials and Methods
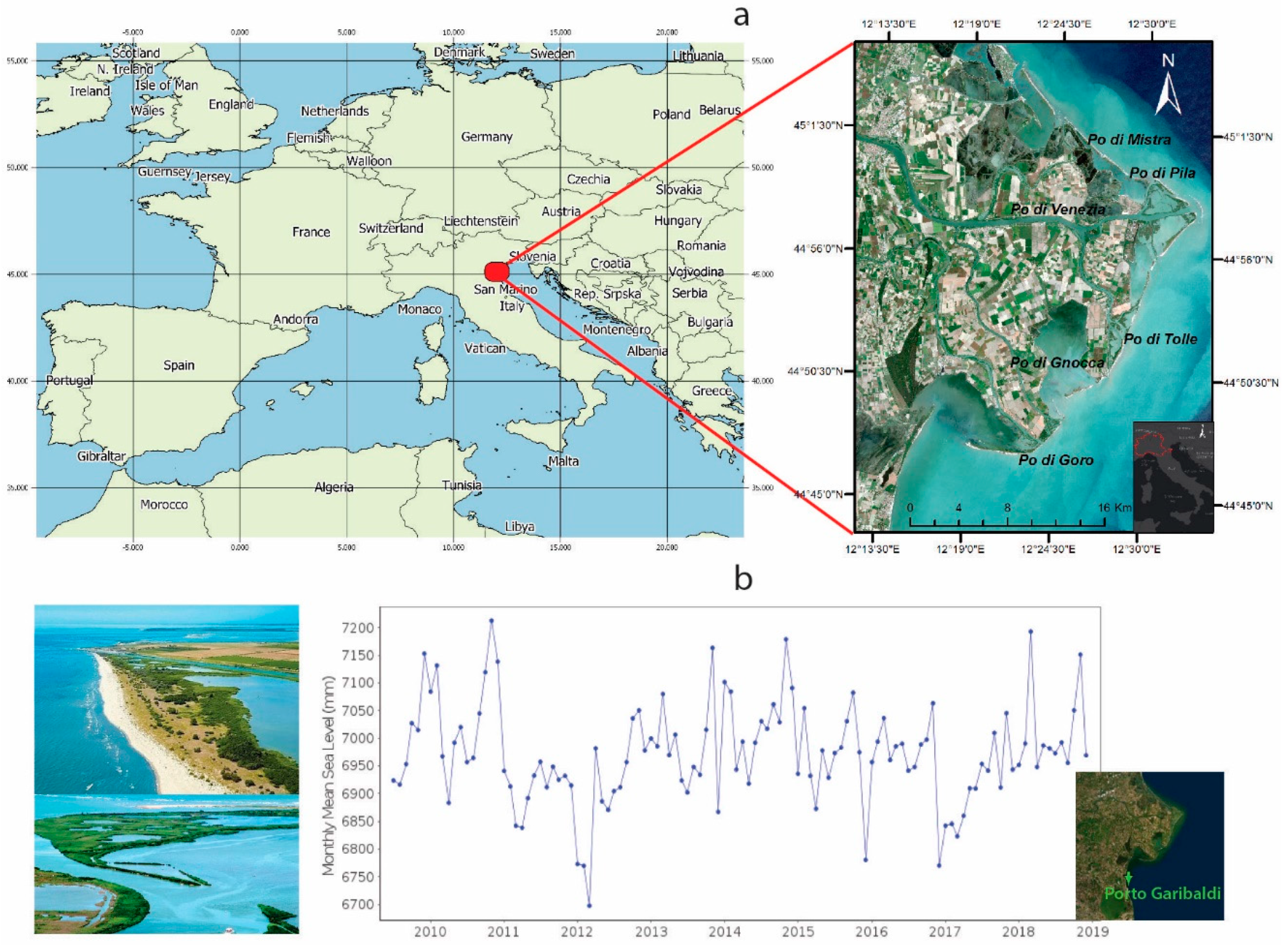
2.1. Study Area: Po Delta
2.2. Vulnerability Assessment
2.3. Data Input
2.4. BBN Model Design
- Phase 1. The categorization phase involved an extensive literature review and expert consultations on the key variables and their relationships. The discretization was based on defining the number of intervals for each input variable by choosing thresholds computed using exploratory geo-statistics according to one of the three following criteria: (i) equidistant intervals, where each interval has the same width; (ii) quantiles or percentile, where each interval tends to have the same number of elements; and (iii) expertise or literature-review-based intervals, where the user defines the upper and lower limits of each interval. Accordingly, the states of a variable have been defined by translating parameter intervals in corresponding categorical (e.g., very low, low, moderate, high) or Boolean (i.e., yes/no) values (Figure 4). Based on the discrete quantities, a score from 1 to 4 contributing in increasing the final probable vulnerability has been assigned.
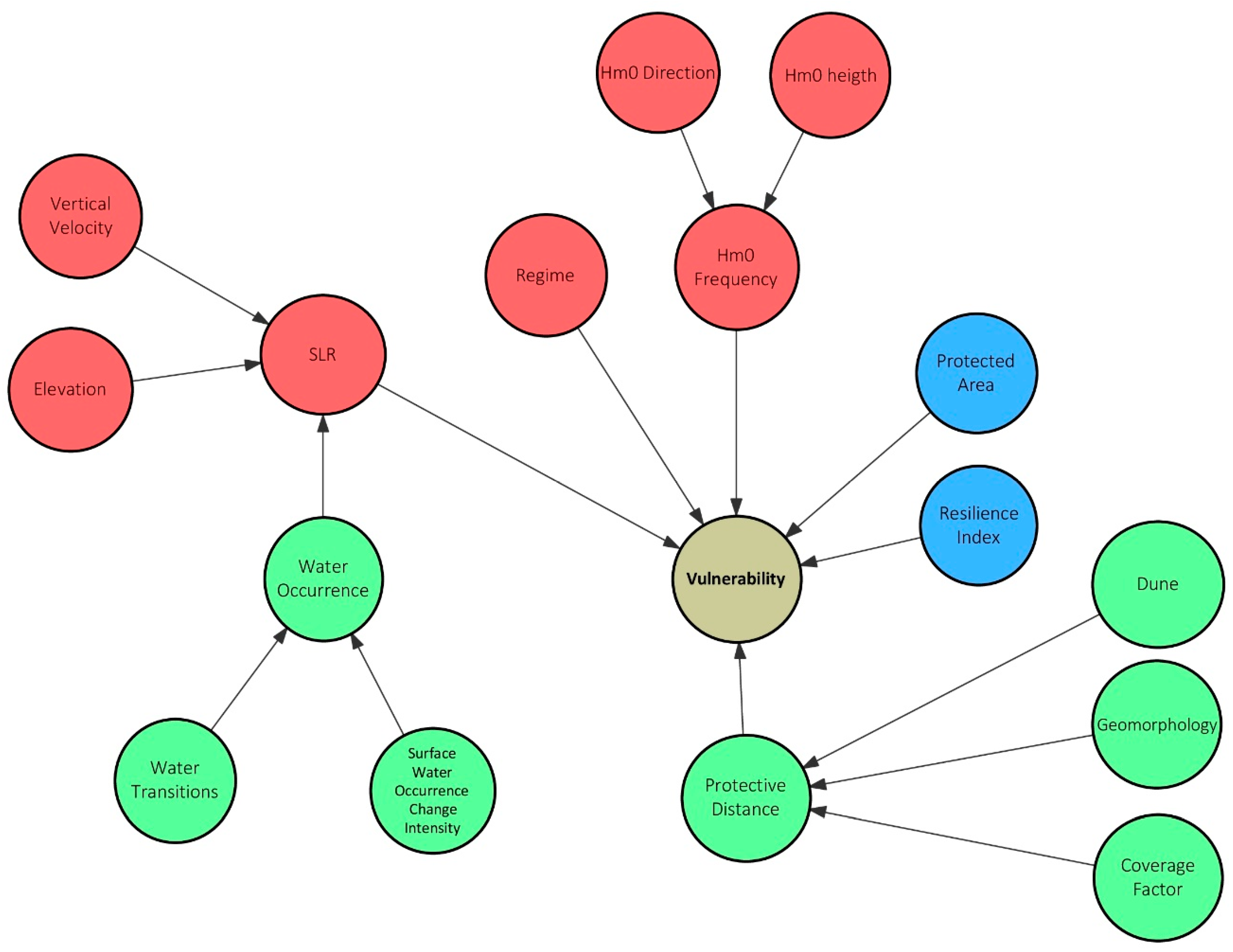
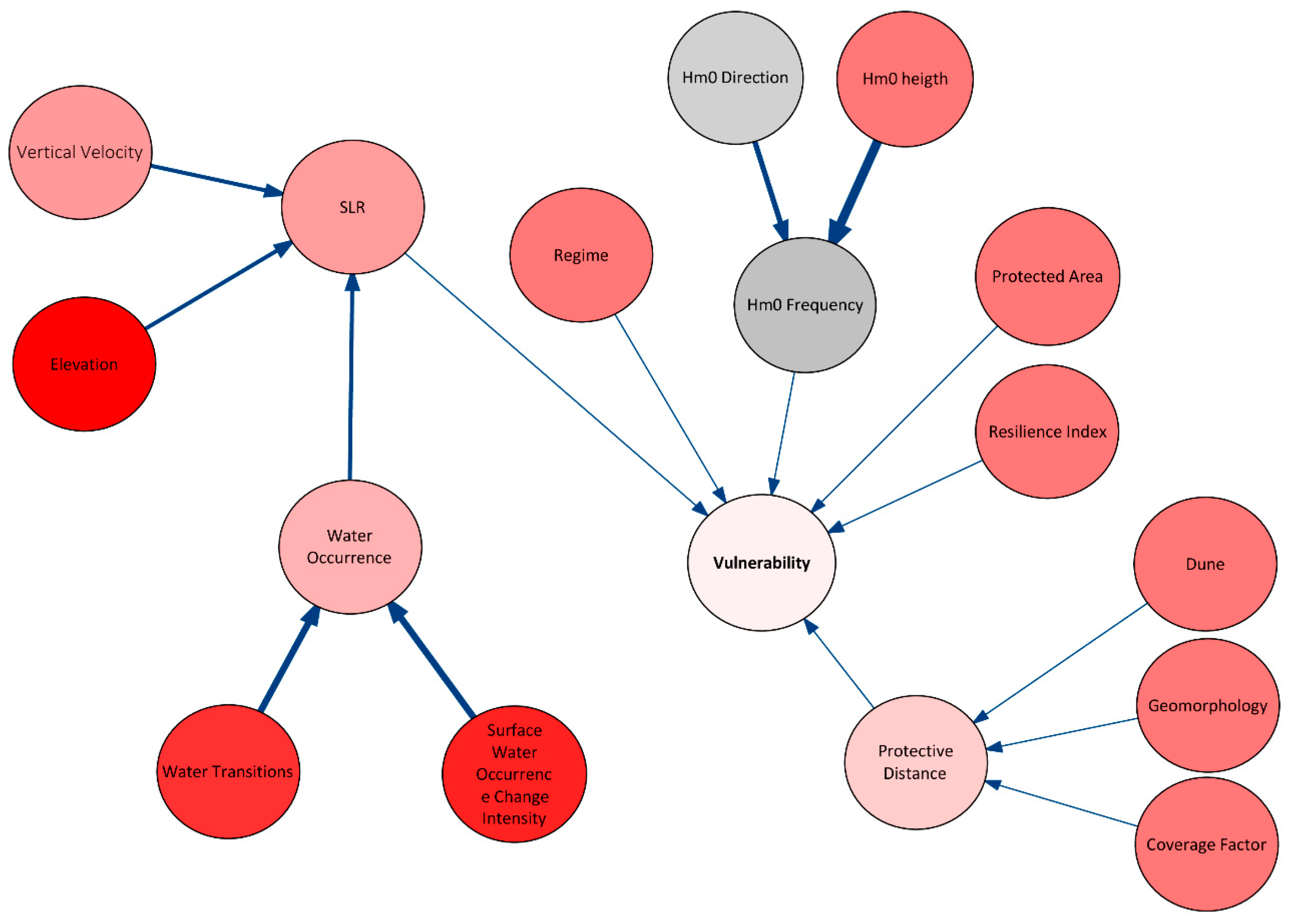
- Phase 2. A generic conceptual model (Figure 5) was used to develop an integrated network able to represent the relationships between input variables and the interconnection with source–pathway–receptor–consequence (SPRC) model applied to the vulnerability assessment. BBN is a directed acyclic graph (DAG) where the selected variables are represented by nodes and the arrows indicate the direct cause–effect relationships between the nodes [91] (Figure 5). The network is solved when nodes have been updated using Bayes’ Rule Equation (3):where P(A) is the prior distribution of parameter A; P(A|B) is the posterior distribution, the probability of A given new data B; and P(B|A) the likelihood function, the probability of B given existing data A. Our hypothesis is that the functional relationship can be learned from available data set and cast in terms of a probabilistic estimate in the form Equation (4):
- Phase 3. To construct the BBN, the GeNie Academic Version 2.4 software package (BayesFusion, LCC, Pittsburgh, PA, US) was chosen. Classes corresponding to assigned score categories as described above resolve each parent or child node. The connection of each node in the BBN is determined by the conditional probability table (CPT) and probability table (PT), where the degree of belief (probability) that a variable will be in a particular state given the state of the parent variable [93] is defined.
- Phase 4. The entries in the CPTs and PTs can be discovered using a range and combination of methods, including directly observed data and probabilistic or empirical equations, results from model simulations and elicitation from expert knowledge. Some of the parameter learning functions are also based on expectation maximization (EM) algorithm (i.e., it requires only the model structure to be known beforehand and iteratively calculates maximum likelihood estimates for the parameters given the data and the model structure [38]) available in GeNie [94], implemented to provide prior probability for root nodes, while target node conditional probabilities is reported as a specific matrix representing the frequency of vulnerability scores associated with each input variables from one to four per cell. Vulnerability is selected as target node, the output variable that directly represents the phenomenon [92] (Figure 5). The prior probability is provided for regime, vertical velocity, dune, protective distance, coverage factor, global water surface dynamic, protected natural areas, and resilience index.
- Phase 5. Accordingly, the output of running the network contains the posterior probability distribution of the vulnerability node implementing extracted and reclassified values from resampling a GIS-based data set at 100 × 100 m resolution.
2.5. Vulnerability Assessment
2.6. Sensitive Analysis
3. Results
3.1. Data Input Discretization
3.2. BBN Model
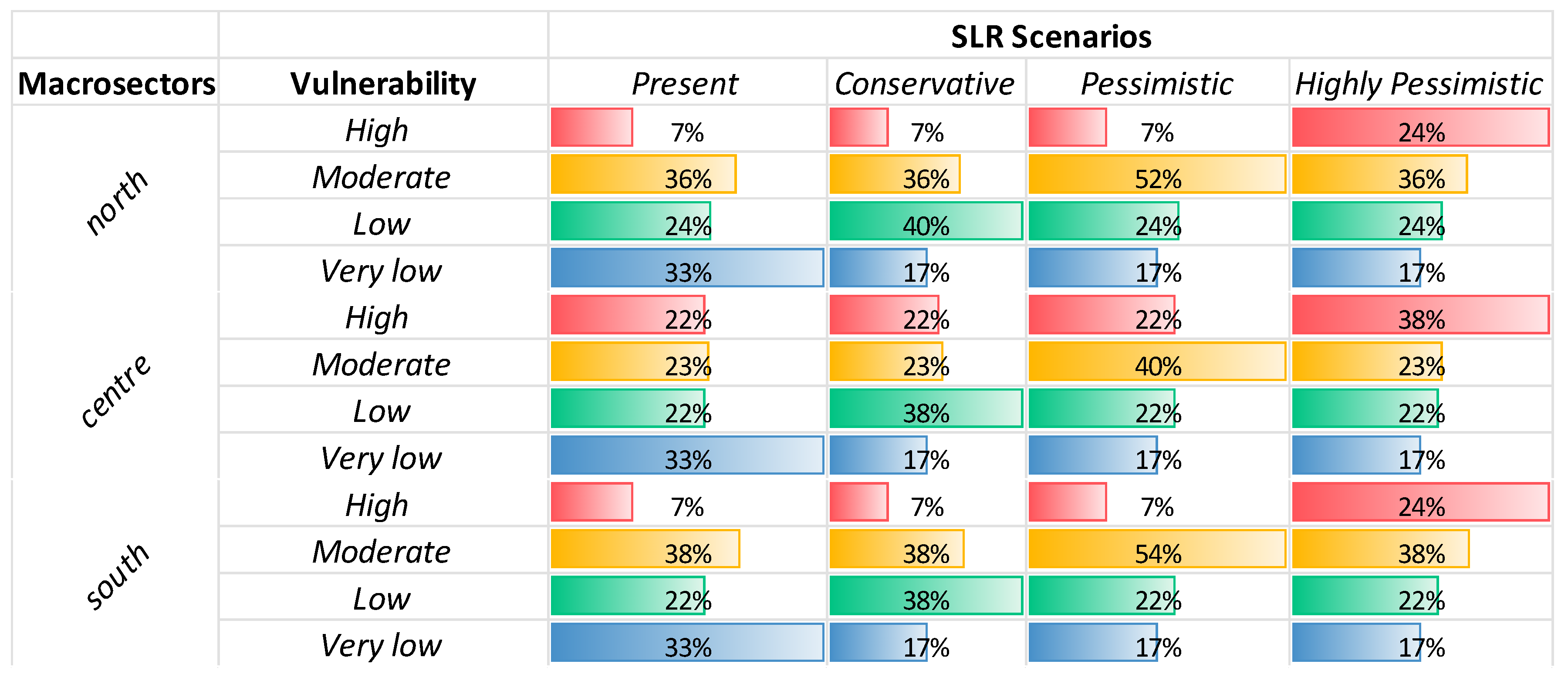
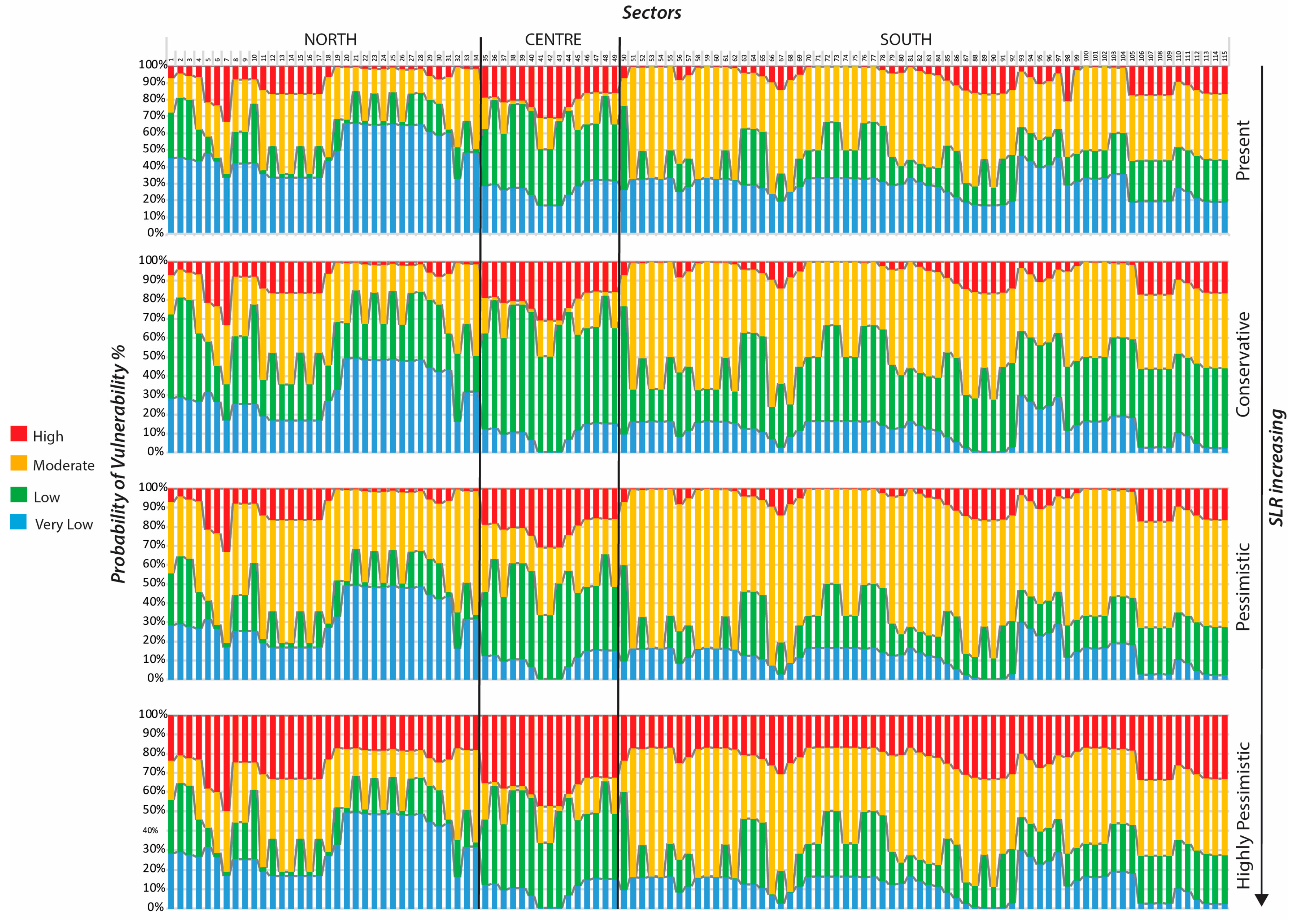
3.3. Testing Scenarios
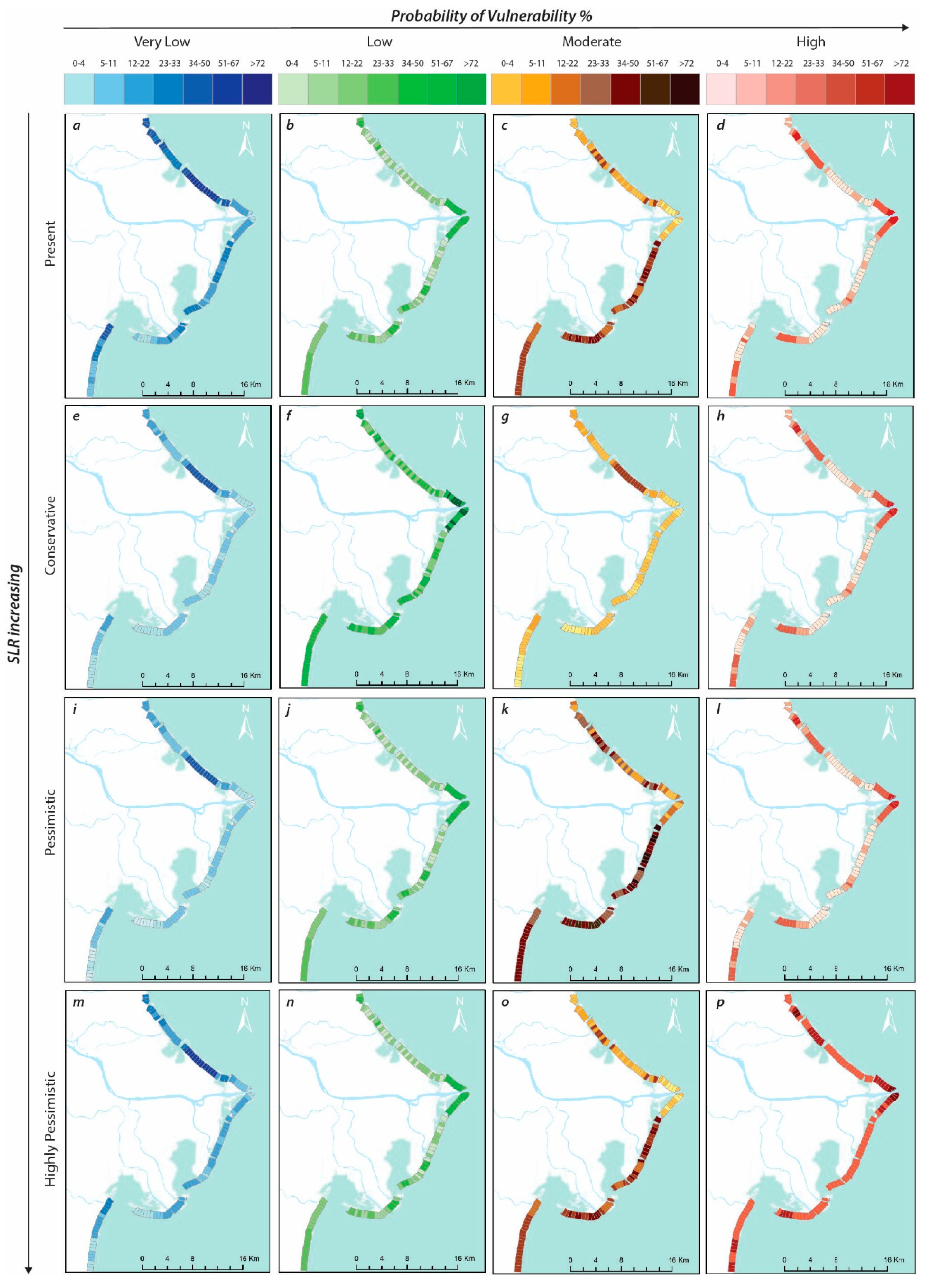
3.4. Identification of Hotspot Areas
3.5. Sensitivity Analysis
4. Discussion
4.1. Data Input Relevance
4.2. BBN Model Development
4.3. Vulnerability Assessment and Key Findings
4.4. Management Implications
5. Conclusions
- EO satellite data keeps proving its high potential for monitoring the Earth, easing spatial and temporal analysis in very complex and dynamic areas.
- The implementation of EO data into the BBN model provides a statistical framework performing inference on a very large amount of different data that describes what is known about the physical, ecological, and social parameters of the system and, perhaps more importantly, what is known about the causal relationships between them.
- The BBN approach, based on the definition of conditional probabilities, associated to the use of a GIS tool, provided the trend of distributions of vulnerability along the shore, which is especially useful for management and planning purposes.
- The overall assessment reveals that almost the 35% of the Po Delta is highly vulnerable to the highly pessimistic SLR scenario. The high heterogeneity of vulnerability to SLR reflects the combined results of the selected variables: 29% of the northern cells, 100% of the central cells, and 23% of the southern cells fall into vulnerability target classes that range from 0.34% to >72% of probability to being highly vulnerable. Our findings highlight potential changes in the sediment budget considering the major vulnerability of the central ebb that is the gate between the river sediment supply and the costal sediment transport.
- The outcomes highlight the strength of influence of each variable on the target and their evident dependence and interconnection. Wave climate mostly depending on events frequency, land subsidence, and changes in land cover, which are the more sensitive variables playing a key role in vulnerability to SLR.
- The study mainly highlights the need (i) to update and expand coastal data sets, specifically concerning local scale environmental and human-induced processes, and (ii) to include both bio-geophysical and socio-economic aspects within delta analysis of the distribution and change in risk components, identifying vulnerable areas and communities, and where changes in hot spots may occur in the future. This can inform other analyses, such as the design of surveys and data collection, as well as identify policy needs and indicate where adaptation actions are likely to be required.
- The findings of this study are also valuable for the further performance of a gap analysis between the available tools and operational user needs. Emerged results provide a contribution in term of completeness of the information for a clearer overview of the expected vulnerability pattern and key variables. These insights could be useful to assess and verify the compliance and the capability of existing products to the user and stakeholder needs and to define a suitable strategy that could fulfil those needs.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ericson, J.P.; Vorosmarty, C.; Dingman, S.L.; Ward, L.G.; Meybeck, M. Effective sea-level rise and deltas: Causes of change and human dimension implications. Glob. Planet. Chang. 2006, 50, 63–82. [Google Scholar] [CrossRef]
- Field, C.B.; Barros, V.R.; Dokken, D.J.; Mach, K.J.; Mastrandrea, M.D. Climate change 2014-impacts, adaptation and vulnerability: Part A: Global and sectoral aspects by intergovernmental panel on climate change. Impacts Adapt. Vulnerability 2014, 315–356. [Google Scholar] [CrossRef] [Green Version]
- Ricaurte, L.F.; Olaya-Rodríguez, M.H.; Cepeda-Valencia, J.; Lara, D.; Arroyave-Suárez, J.; Finlayson, C.M.; Palomo, I. Future impacts of drivers of change on wetland ecosystem services in Colombia. Glob. Environ. Chang. 2017, 44, 158–169. [Google Scholar] [CrossRef]
- Besset, M.; Anthony, E.J.; Sabatier, F. River delta shoreline reworking and erosion in the Mediterranean and Black Seas: The potential roles of fluvial sediment starvation and other factors. Elem. Sci. Anth. 2017, 5, 54. [Google Scholar] [CrossRef] [Green Version]
- Wong, P.P.; Losada, I.J.; Gattuso, J.-P.; Hinkel, J.; Khattabi, A.; McInnes, K.L.; Saito, Y.; Sallenger, A. Coastal systems and low-lying areas. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Proceedings of the Part A: Global and Sectoral Aspects, Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 361–409. [Google Scholar]
- Szabo, S.; Brondizio, E.; Renaud, F.G.; Hetrick, S.; Nicholls, R.J.; Matthews, Z.; Tessler, Z.; Tejedor, A.; Sebesvari, Z.; Foufoula-Georgiou, E.; et al. Population dynamics, delta vulnerability and environmental change: Comparison of the Mekong, Ganges–Brahmaputra and Amazon delta regions. Sustain. Sci. 2016, 11, 539–554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coleman, J.M.; Huh, O.K.; Braud Jr, D.H.; Roberts, H.H. Gulf. Coast. Assoc. Geol. Soc. 2006, 55, 102–131. [Google Scholar]
- Coleman, J.M.; Huh, O.K.; Braud, D. Wetland loss in world deltas. J. Coast. Res. 2008, 1, 1–14. [Google Scholar] [CrossRef]
- Torresan, S.; Gallina, V.; Gualdi, S.; Bellafiore, D.; Umgiesser, G.; Carniel, S.; Sclavo, M.; Benetazzo, A.; Giubilato, E.; Critto, A. Assessment of climate change impacts in the north Adriatic coastal area. Part I: A multi-model chain for the definition of climate change hazard scenarios. Water 2019, 11, 1157. [Google Scholar] [CrossRef] [Green Version]
- Overeem, I.; Syvitski, J.P.M. Dynamics and vulnerability of delta systems. In LOICZ Reports Studies; GKSS Res. Center: Geesthacht, Germany, 2009; p. 54. [Google Scholar]
- Woodroffe, C.D.; Nicholls, R.J.; Saito, Y.; Chen, Z.; Goodbred, S.L. Landscape Variability and the Response of Asian Megadeltas to Environmental Change BT-Global Change and Integrated Coastal Management: The Asia-Pacific Region; Harvey, N., Ed.; Springer: Dordrecht, The Netherland, 2006; pp. 277–314. ISBN 978-1-4020-3628-6. [Google Scholar]
- Plant, N.; Thieler, E.R.; Passeri, D.L. Coupling centennial-scale shoreline change to sea-level rise and coastal morphology in the Gulf of Mexico using a Bayesian network. Earth’s Futur. 2016, 4, 143–158. [Google Scholar] [CrossRef] [Green Version]
- Gallina, V.; Torresan, S.; Zabeo, A.; Rizzi, J.; Carniel, S.; Sclavo, M.; Pizzol, L.; Marcomini, A.; Critto, A. Assessment of climate change impacts in the north Adriatic coastal area. Part II: Consequences for coastal erosion impacts at the regional scale. Water 2019, 11, 1300. [Google Scholar] [CrossRef] [Green Version]
- Sallenger, A.H. Storm impact scale for barrier islands. J. Coast. Res. 2000, 16, 890–895. [Google Scholar]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Sanuy, M.; Jiménez, J.; Plant, N. A Bayesian Network methodology for coastal hazard assessments on a regional scale: The BN-CRAF. Coast. Eng. 2020, 157, 103627. [Google Scholar] [CrossRef]
- Taramelli, A.; Manzo, C.; Valentini, E.; Cornacchia, L. Coastal subsidence: Causes, mapping, and monitoring. In Natural Hazards: Earthquakes, Volcanoes, and Landslides; Ramesh Singh, D.B., Ed.; CRC Press: Boca Raton, FL, USA, 2018; pp. 253–290. ISBN 9781138054431. [Google Scholar]
- Martinez, M.L.; Taramelli, A.; Silva, R. Resistance and resilience: Facing the multidimensional challenges in coastal areas. J. Coast. Res. 2017, 77, 1–6. [Google Scholar] [CrossRef]
- Wolff, C.; Vafeidis, A.T.; Muis, S.; Lincke, D.; Satta, A.; Lionello, P.; Jiménez, J.; Conte, D.; Hinkel, J. A Mediterranean coastal database for assessing the impacts of sea-level rise and associated hazards. Sci. Data 2018, 5, 180044. [Google Scholar] [CrossRef] [Green Version]
- Dadson, S.; Ashpole, I.; Harris, P.P.; Davies, H.N.; Clark, D.B.; Blyth, E.; Taylor, C.M. Wetland inundation dynamics in a model of land surface climate: Evaluation in the Niger inland delta region. J. Geophys. Res. Space Phys. 2010, 115, 115. [Google Scholar] [CrossRef] [Green Version]
- Passalacqua, P.; Lanzoni, S.; Paola, C.; Rinaldo, A. Geomorphic signatures of deltaic processes and vegetation: The Ganges-Brahmaputra-Jamuna case study. J. Geophys. Res. Earth Surf. 2013, 118, 1838–1849. [Google Scholar] [CrossRef]
- Passalacqua, P. The Delta Connectome: A network-based framework for studying connectivity in river deltas. Geomorphology 2017, 277, 50–62. [Google Scholar] [CrossRef] [Green Version]
- Kuenzer, C.; Heimhuber, V.; Huth, J.; Dech, S. Remote sensing for the quantification of land surface dynamics in large river delta regions—A review. Remote Sens. 2019, 11, 1985. [Google Scholar] [CrossRef] [Green Version]
- Huth, J.; Kuenzer, C. The potential of innovative earth observation approaches to assess ecologic dynamics in wetlands and their water sheds. In Proceedings of the Advanced International Forum on Ecological Security of Poyang Lake, Nanchang, China, 27–30 August 2016. [Google Scholar]
- Taramelli, A.; Valentini, E.; Cornacchia, L.; Monbaliu, J.; Sabbe, K. Indications of dynamic effects on scaling relationships between channel sinuosity and vegetation patch size across a salt marsh platform. J. Geophys. Res. Earth Surf. 2018, 123, 2714–2731. [Google Scholar] [CrossRef]
- Torresan, S.; Critto, A.; Valle, M.D.; Harvey, N.; Marcomini, A. Assessing coastal vulnerability to climate change: Comparing segmentation at global and regional scales. Sustain. Sci. 2008, 3, 45–65. [Google Scholar] [CrossRef]
- Taramelli, A.; Valentini, E.; Nguyen Xuan, A.; Filipponi, F.; Casarotti, C.; Morelli, A. Deltaic margins vulnerability: The role of landscape patches in flood regulation and climate adaptation. In Proceedings of the NH33B-1921 American Geophysical Union (AGU) Fall Meeting 2016, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- McLeod, E.; Hinkel, J.; Vafeidis, A.T.; Nicholls, R.J.; Harvey, N.; Salm, R. Sea-level rise vulnerability in the countries of the Coral Triangle. Sustain. Sci. 2010, 5, 207–222. [Google Scholar] [CrossRef]
- Gutierrez, B.T.; Plant, N.; Thieler, E.R. A Bayesian network to predict coastal vulnerability to sea level rise. J. Geophys. Res. Space Phys. 2011, 116, 1–15. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, S.; Cooper, A. A multi-scale coastal vulnerability index: A tool for coastal managers? Environ. Hazards 2010, 9, 233–248. [Google Scholar] [CrossRef]
- Aucelli, P.P.C.; Di Paola, G.; Rizzo, A.; Rosskopf, C.M. Present day and future scenarios of coastal erosion and flooding processes along the Italian Adriatic coast: The case of Molise region. Environ. Earth Sci. 2018, 77, 371. [Google Scholar] [CrossRef]
- Zhu, Z.-T.; Cai, F.; Chen, S.; Gu, D.; Feng, A.-P.; Cao, C.; Qi, H.-S.; Lei, G. Coastal vulnerability to erosion using a multi-criteria index: A case study of the Xiamen Coast. Sustainability 2018, 11, 93. [Google Scholar] [CrossRef] [Green Version]
- Da Lio, C.; Tosi, L. Vulnerability to relative sea-level rise in the Po river delta (Italy). Estuar. Coast. Shelf Sci. 2019, 228, 106379. [Google Scholar] [CrossRef]
- Hamid, A.I.A.; Din, A.H.M.; Yusof, N.; Abdullah, N.M.; Omar, A.H.; Khanan, M.F.A. Coastal vulnerability index development: A review. ISPRS-Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2019, 229–235. [Google Scholar] [CrossRef] [Green Version]
- Eurosion. Living with Coastal Erosion in Europe: Sediment and Space for Sustainability. Part III-Methodology for Assessing Regional Indicators. Available online: http://www.eurosion.org/database/geomorphology.html (accessed on 22 April 2020).
- Richards, J.; Nicholls, R. Impacts of Climate Change in Coastal Systems in Europe. PESETA-Coastal Systems Study. Available online: http://www.eurosfaire.prd.fr/7pc/doc/1266936165_peseta_costal_system_jrc55390.pdf (accessed on 22 April 2020).
- Taramelli, A.; Valentini, E.; Cornacchia, L.; Bozzeda, F. A hybrid power law approach for spatial and temporal pattern analysis of salt marsh evolution. J. Coast. Res. 2017, 77, 62–72. [Google Scholar] [CrossRef] [Green Version]
- Uusitalo, L. Advantages and challenges of Bayesian networks in environmental modelling. Ecol. Model. 2007, 203, 312–318. [Google Scholar] [CrossRef]
- Hart, B.; Pollino, C. Bayesian Modelling for Risk-Based Environmental Water Allocation. 2009. Available online: https://www.waterboards.ca.gov/waterrights/water_issues/programs/bay_delta/deltaflow/docs/exhibits/swrcb/swrcb_hart2009.pdf (accessed on 30 April 2020).
- Yates, M.L.; Le Cozannet, G. Brief communication. Evaluating European coastal evolution using Bayesian networks. Nat. Hazards Earth Syst. Sci. 2012, 12, 1173–1177. [Google Scholar] [CrossRef]
- Sperotto, A.; Torresan, S.; Gallina, V.; Coppola, E.; Critto, A.; Marcomini, A. A multi-disciplinary approach to evaluate pluvial floods risk under changing climate: The case study of the municipality of Venice (Italy). Sci. Total. Environ. 2016, 562, 1031–1043. [Google Scholar] [CrossRef] [PubMed]
- Cencini, C. Processes and Human Activities in the Evolution of the Po Delta. Italy. J. Coast. Res. 1998, 14-3, 774–793. [Google Scholar]
- Beuzen, T.; Splinter, K.D.; Turner, I.L.; Harley, M.D.; Marshall, L. Predicting storm erosion on sandy coastlines using a Bayesian network. Australasian Coasts Ports 2017, 102–108. [Google Scholar]
- Hapke, C.J.; Plant, N.G. Predicting coastal cliff erosion using a Bayesian probabilistic model. Mar. Geol. 2010, 278, 140–149. [Google Scholar] [CrossRef] [Green Version]
- Plant, N.G.; Holland, K.T. Prediction and assimilation of surf-zone processes using a Bayesian network. Coast. Eng. 2011, 58, 119–130. [Google Scholar] [CrossRef]
- Plant, N.; Stockdon, H. Probabilistic prediction of barrier-island response to hurricanes. J. Geophys. Res. Space Phys. 2012, 117, 117. [Google Scholar] [CrossRef]
- Wilson, C. Geomorphology and landscape evolution model for the natural and human-impacted regions of the Ganges-Brahmaputra. In Proceedings of the American Geophysical Union, Fall Meeting, San Francisco, CA, USA, 9–13 December 2013. [Google Scholar]
- Palmsten, M.L.; Splinter, K.D.; Plant, N.G.; Stockdon, H.F. Probabilistic estimation of dune retreat on the Gold Coast, Australia. Shore Beach 2014, 82, 35–43. [Google Scholar]
- Poelhekke, L.; Jäger, W.S.; Van Dongeren, A.; Plomaritis, T.A.; McCall, R.; Ferreira, Ó.; Van Dongeren, A. Predicting coastal hazards for sandy coasts with a Bayesian network. Coast. Eng. 2016, 118, 21–34. [Google Scholar] [CrossRef]
- Van Verseveld, H.; Van Dongeren, A.; Plant, N.; Jäger, W.; Heijer, C.D. Modelling multi-hazard hurricane damages on an urbanized coast with a Bayesian network approach. Coast. Eng. 2015, 103, 1–14. [Google Scholar] [CrossRef]
- Hapke, C.J.; Plant, N.G.; Henderson, R.E.; Schwab, W.C.; Nelson, T.R. Decoupling processes and scales of shoreline morphodynamics. Mar. Geol. 2016, 381, 42–53. [Google Scholar] [CrossRef] [Green Version]
- Hall, S.J. The continental shelf benthic ecosystem: Current status, agents for change and future prospects. Environ. Conserv. 2002, 29, 350–374. [Google Scholar] [CrossRef]
- Filipponi, F.; Valentini, E.; Liberti, L.; Zucca, F.; Taramelli, A. Generation of gridded Ocean Color products from MERIS: An efficient processing chain. In Proceedings of the IEEE Gold Remote Sensing Conference, Berlin, Germany, 5–6 June 2014. [Google Scholar]
- Taramelli, A.; Valentini, E.; Cornacchia, L. Remote sensing solutions to monitor biotic and abiotic dynamics in coastal ecosystems. In Coast. Zones; Elsevier BV: Amsterdam, The Netherlands, 2015; pp. 125–138. [Google Scholar]
- Gutierrez, B.T.; Plant, N.G.; Thieler, E.R.; Turecek, A. Using a Bayesian network to predict barrier island geomorphologic characteristics. J. Geophys. Res. Earth Surf. 2015, 120, 2452–2475. [Google Scholar] [CrossRef] [Green Version]
- IPCC Summary for Policymakers. In Climate Change 2013—The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Intergovernmental Panel on Climate Change (Ed.) Cambridge University Press: Cambridge, UK, 2014; pp. 1–30. ISBN 9781107057999. [Google Scholar]
- Torresan, S.; Critto, A.; Rizzi, J.; Marcomini, A. Assessment of coastal vulnerability to climate change hazards at the regional scale: The case study of the North Adriatic Sea. Nat. Hazards Earth Syst. Sci. 2012, 12, 2347–2368. [Google Scholar] [CrossRef]
- Aucelli, P.; De Pippo, T.; Iannantuono, E.; Rosskopf, C. Caratterizzazione morfologico-dinamica e meteomarina della costa molisana nel settore compreso tra la foce del torrente Sinarca e Campomarino Lido (Italia meridionale). Stud. Costieri 2007, 13, 75–92. [Google Scholar]
- Tosi, L.; Da Lio, C.; Strozzi, T.; Teatini, P. Combining L-and X-band SAR interferometry to assess ground displacements in heterogeneous coastal environments: The Po river delta and Venice Lagoon, Italy. Remote Sens. 2016, 8, 308. [Google Scholar] [CrossRef] [Green Version]
- Teatini, P.; Tosi, L.; Strozzi, T. Quantitative evidence that compaction of Holocene sediments drives the present land subsidence of the Po Delta, Italy. J. Geophys. Res. Space Phys. 2011, 116, 1–10. [Google Scholar] [CrossRef]
- Travers, A.; Elrick-Barr, C.; Kay, R. Background Paper: Climate Change in Coastal Zones of the Mediterranean; Split, Priority Actions Programme; Coastal Zone Management Pty Ltd.: Claremont, Australia, 2010. [Google Scholar]
- Cozzi, S.; Giani, M. River water and nutrient discharges in the Northern Adriatic Sea: Current importance and long term changes. Cont. Shelf Res. 2011, 31, 1881–1893. [Google Scholar] [CrossRef]
- Simeoni, U.; Corbau, C. A review of the Delta Po evolution (Italy) related to climatic changes and human impacts. Geomorphology 2009, 107, 64–71. [Google Scholar] [CrossRef]
- Corbau, C.; Zambello, E.; Rodella, I.; Utizi, K.; Nardin, W.; Simeoni, U. Quantifying the impacts of the human activities on the evolution of Po delta territory during the last 120 years. J. Environ. Manag. 2019, 232, 702–712. [Google Scholar] [CrossRef]
- Ninfo, A.; Ciavola, P.; Billi, P. The Po Delta is restarting progradation: Geomorphological evolution based on a 47-years Earth observation dataset. Sci. Rep. 2018, 8, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Corbau, C.; Simeoni, U.; Zoccarato, C.; Mantovani, G.; Teatini, P. Coupling land use evolution and subsidence in the Po Delta, Italy: Revising the past occurrence and prospecting the future management challenges. Sci. Total. Environ. 2019, 654, 1196–1208. [Google Scholar] [CrossRef] [PubMed]
- Taramelli, A.; Di Matteo, L.; Ciavola, P.; Guadagnano, F.; Tolomei, C. Temporal evolution of patterns and processes related to subsidence of the coastal area surrounding the Bevano River mouth (Northern Adriatic)-Italy. Ocean. Coast. Manag. 2015, 108, 74–88. [Google Scholar] [CrossRef]
- Holgate, S.J.; Matthews, A.; Woodworth, P.L.; Rickards, L.J.; Tamisiea, M.E.; Bradshaw, E.; Foden, P.R.; Gordon, K.M.; Jevrejeva, S.; Pugh, J. New data systems and products at the permanent service for mean sea level. J. Coast. Res. 2012, 29, 493–504. [Google Scholar] [CrossRef]
- Permanent Service for Mean Sea Level (PSMSL). Tide Gauge Data. Available online: http://www.psmsl.org/data/obtaining/ (accessed on 27 April 2020).
- Brochier, F.; Ramieri, E. Climate change impacts on the Mediterranean coastal zones. SSRN Electron. J. 2001. [Google Scholar] [CrossRef] [Green Version]
- Umgiesser, G.; Anderson, J.; Artale, V.; Breil, M.; Gualdi, S.; Lionello, P.; Marinova, N.; Orlic, M.; Pirazzoli, P.; Rahmstorf, S.; et al. From global to regional: Local sea level rise scenarios-Focus on the Mediterranean Sea and the Adriatic Sea. In Proceedings of the Workshop Organized by UNESCO Venice Office and ISMAR-CNR, Venice, Italy, 22–23 November 2010. [Google Scholar]
- Tsimplis, M.N.; Shaw, A. Seasonal sea level extremes in the Mediterranean Sea and at the Atlantic European coasts. Nat. Hazards Earth Syst. Sci. 2010, 10, 1457–1475. [Google Scholar] [CrossRef]
- Carbognin, L.; Teatini, P.; Tosi, L. The impact of relative sea level rise on the Northern Adriatic Sea coast, Italy. Manag. Nat. Res. Sustain. Dev. Ecol. Hazards II 2009, 127, 137–148. [Google Scholar] [CrossRef] [Green Version]
- Antonioli, F.; Anzidei, M.; Amorosi, A.; Presti, V.L.; Mastronuzzi, G.; Deiana, G.; De Falco, G.; Fontana, A.; Fontolan, G.; Lisco, S.; et al. Sea-level rise and potential drowning of the Italian coastal plains: Flooding risk scenarios for 2100. Quat. Sci. Rev. 2017, 158, 29–43. [Google Scholar] [CrossRef] [Green Version]
- Füssel, H.-M.; Klein, R.J.T. Climate change vulnerability assessments: An evolution of conceptual thinking. Clim. Chang. 2006, 75, 301–329. [Google Scholar] [CrossRef]
- Liquete, C.; Zulian, G.; Delgado, I.; Stips, A.; Maes, J. Assessment of coastal protection as an ecosystem service in Europe. Ecol. Indic. 2013, 30, 205–217. [Google Scholar] [CrossRef] [Green Version]
- Lisi, I.; Bruschi, A.; Gizzo, M.; Archina, M.; Barbano, A.; Corsini, S. Le unità fisiografiche e le profondità di chiusura della costa italiana. L’Acqua 2010, 2, 35–52. [Google Scholar]
- Fleming, G. Learning to live with rivers-the ICE’s report to government. Proc. Inst. Civ. Eng. Civ. Eng. 2002, 150, 15–21. [Google Scholar] [CrossRef]
- Mar, B.W.; Morais, B.G. Frat-A basic framework for systems engineering. INCOSE Int. Symp. 2002, 12, 1–7. [Google Scholar] [CrossRef]
- Small, C. The Landsat ETM+ spectral mixing space. Remote. Sens. Environ. 2004, 93, 1–17. [Google Scholar] [CrossRef]
- Filipponi, F.; Valentini, E.; Xuan, A.N.; Guerra, C.A.; Wolf, F.; Andrzejak, M.; Taramelli, A. Global MODIS fraction of green vegetation cover for monitoring abrupt and gradual vegetation changes. Remote Sens. 2018, 10, 653. [Google Scholar] [CrossRef] [Green Version]
- Filipponi, F.; Taramelli, A.; Zucca, F.; Valentini, E.; El Serafy, G.Y. Ten-years sediment dynamics in Northern Adriatic sea investigated through optical remote sensing observations. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 25–31 July 2015; pp. 2265–2268. [Google Scholar] [CrossRef]
- Taramelli, A.; Valentini, E.; Cornacchia, L.; Mandrone, S.; Monbaliu, J.; Hoggart, S.; Thompson, R.C.; Zanuttigh, B. Modeling uncertainty in estuarine system by means of combined approach of optical and radar remote sensing. Coast. Eng. 2014, 87, 77–96. [Google Scholar] [CrossRef]
- Mathiesen, M.; Goda, Y.; Hawkes, P.J.; Mansard, E.; Martín, M.J.; Peltier, E.; Thompson, E.F.; Van Vledder, G. Recommended practice for extreme wave analysis. J. Hydraul. Res. 1994, 32, 803–814. [Google Scholar] [CrossRef]
- Armaroli, C.; Ciavola, P.; Masina, M.; Perini, L. Run-up computation behind emerged breakwaters for marine storm risk assessment. J. Coast. Res. SI 2009, 56, 1612–1616. [Google Scholar]
- Duo, E.; Sanuy, M.; Jiménez, J.A.; Ciavola, P. How good are symmetric triangular synthetic storms to represent real events for coastal hazard modelling. Coast. Eng. 2020, 159, 103728. [Google Scholar] [CrossRef]
- Berkes, F.; Colding, J.; Folke, C. Navigating social-ecological systems: Building resilience for complexity and change. Ecol. Soc. 2003, 9, 393. [Google Scholar]
- Morelli, A. Measuring Community Resilience to Disasters through Stakeholders’ Frames and Practices: Towards a Resilience Informed Interactive Governance. Ph.D. Thesis, University School for Advance Studies Pavia, Pavia, Italy, 2017. [Google Scholar]
- Tarquini, S.; Vinci, S.; Favalli, M.; Doumaz, F.; Fornaciai, A.; Nannipieri, L. Release of a 10-m-resolution DEM for the Italian territory: Comparison with global-coverage DEMs and anaglyph-mode exploration via the web. Comput. Geosci. 2012, 38, 168–170. [Google Scholar] [CrossRef] [Green Version]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nat. Cell Biol. 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Kyburg, H.E.; Pearl, J. Probabilistic reasoning in intelligent systems: Networks of plausible inference. J. Philos. 1991, 88, 434. [Google Scholar] [CrossRef]
- Norton, J.; Logic, L. Incorporating dynamics and feedback into Bayesian modelling of natural resource system. In Landscape Logic Technical Report No. 7; Landscape Logic: Hobart, Tasmania, Australia, February 2010. [Google Scholar]
- Chen, S.H.; Pollino, C. Good practice in Bayesian network modelling. Environ. Model. Softw. 2012, 37, 134–145. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B Stat. Methodol. 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Marcot, B.G. Metrics for evaluating performance and uncertainty of Bayesian network models. Ecol. Model. 2012, 230, 50–62. [Google Scholar] [CrossRef]
- Gaag, L.C.; Kjaerulff, U. Making sensitivity analysis computationally efficient. In 16th Conference on Uncertainty in Artificial Intelligence; Boutilier, G., Goldszmidt, M., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 2000; pp. 317–325. [Google Scholar]



| Variables (and Periods) | Description | Data Type | Processing Method and Data Source |
|---|---|---|---|
| Elevation (2007) | The elevation of the area is partially below mean sea level (msl) due to subsidence induced by hydraulic engineering works, extraction of gas-bearing water, and reduction of sediment supply and embanking. | EO-derived raster, continuous, terrestrial, 10-m-cell grid, digital elevation model (DEM). | DEM obtained from the achievement of the DIGITALIA project of Istituto Nazionale di Geofisica e Vulcanologia, INGV [89] Data source: http://www.pi.ingv.it/banche-dati/ |
| Vertical velocity * (2003–2010) | The average vertical velocity represents a driver factor in terms of changes in rates of subsidence as well as it is a measure of the uncertainty in the erosion and flooding processes estimation. | EO-derived raster, continuous, terrestrial, 100-m-cell grid. | SBAS SARscape version 5.0.001 and ENVI version 5.0 (service pack 3). Data source: ESA Cat1 Envisat data access. |
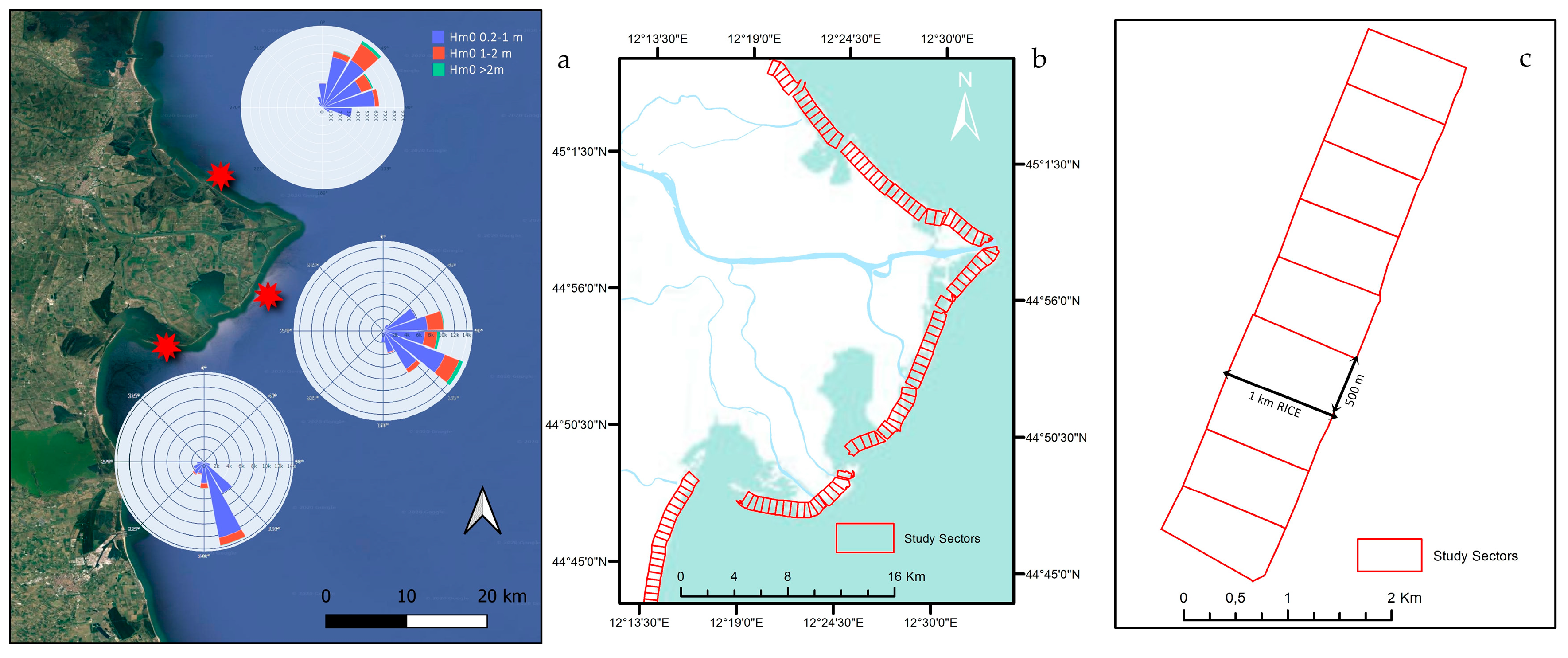
| Waves (2007–2017) | Significant wave height and frequency are considered as proxy driver of coastal erosion summarizing the wave energy and wave impact. Three dominant wave directions were used considering the coastline shape and orientation of the study area: north (0–60°), center (60–120°) and south (120–180°). | Waves model derived points, discrete, aquatic, H0 = height, energy-based derived from significant wave height; and H0f = frequency, number of events related to the wave height. | Wave model transformed, with offshore wave rider buoy data (lat: 44.729168 lon: 12.833333), into nearshore equivalent significant wave height, direction and frequency. Data source: CMEMS. |
| Regime * (2010) | The regimes represent different levels of impact, depending on waves and coastal morphology, with thresholds indicating where processes and magnitudes of impacts change. | Calculated value using DEM and waves model derived points, discrete, terrestrial, topography transect based. | Runup parameterization Equation (1) applied to 115 topographic transects. Data source: elevation and waves. |
| Sea Level Rise (SLR) (2000–2100) | Future SLR scenarios, in this study, are classified as conservative, pessimistic and highly pessimistic scenario within 100 years. | Discrete, aquatic, added to the waves model derived points. | Added to height, energy-based derived from significant wave height of + 0.52 m and 0.74 m. Data source: [56]. |
| Dune (2018) | Dunes and wetlands have a buffering capacity to reduce the adverse impacts of climate change in terms of natural barriers and responding capacity to SLR and erosion. | Vectorial polygons classified as dune and wetlands presence or absence, discrete, terrestrial. | Cover type classified as dune from regional Corine Land Cover (CLC) 2018 level 4 [30]. Data source: CLMS. |
| Coverage Factor * (2018) | The coverage factor stands for vegetation presence and abundance assuming that the susceptibility to erosion decrease with vegetation coverage due to higher wave energy dissipation. | Raster of the coastal buffer vegetation fractional abundance, continuous, terrestrial, 20-m-cell grid. | Sentinel 2 MSI satellite data processed with LSMA. Data source: https://scihub.copernicus.eu/ |
| Protective Distance * (1991–2019) | The mean value of the maximum sediment spatial variations in the last 30 years is considered as the potential protective distance acting as a defense buffer against erosion processes. It is related to the dune presence and to the deltaic small-scale coastline changes. | Raster of the alongshore averaged values of the coastline sediment variation in the last 30 years, continuous, terrestrial, 30-m-cell grid. | Landsat (19912015) and Sentinel (2015–2019) satellite data processed with LSMA and EOF techniques. Data sources: https://earthexplorer.usgs.gov/; https://scihub.copernicus.eu/. |
| Geomorphology (1990–2005) | The geomorphology classifies the geomorphological and sedimentological elements of the shore in six major types: rocky, beaches, muddy, estuaries, harbors, and artificial coast. | Vectorial shore classified as geomorpho-sedimentological types, discrete, terrestrial-intertidal. | Based on the European coastline at scale 1:100,000 and CORINE Coastal Erosion version 1 updated after 1990. Data source: http://www.eurosion.org/database/geomorphology.html. |
| Global Surface Water Dynamic (GSVD) (1984–2015) | The GSVD represents where and when open water was present in 32 years. The transitions map represents the changes in water classes like no water, seasonal, permanent. The Occurrence Change map shows where surface water occurrence increased, decreased or remained constant. | Raster, continuous, aquatic, 30-m-cell grid divided in two 15-year time span. | The spatial and temporal variability of global surface water presence and its long-term changes (i.e., 32 years) calculated on 3 million Landsat images [90]. Data source: https://global-surface-water.appspot.com/. |
| Protected natural area (2010) | The network of core natural habitat types represents the natural capital of the area and corresponds to high exposure levels. | Vectorial polygons classified as protection designation, discrete, terrestrial. | It is the Natura 2000 network based on the Habitat and Birds Directives reporting and designation. Data source: CLMS. |
| Resilience Index (2017) | The resilience index is referred to the adaptive capacity of the Po Delta social subsystem and it involves socio-economic factors that affect community resilience at municipality scale. | Vectorial points at municipality scale, classified as degree of resilience, discrete, terrestrial. | Metrics obtained from stakeholders’ interviews, to score infrastructure and environment resilience’s subcomponents. Data source: [88]. |
| Scenarios | Sea Level Rise (IPCC, 2014) |
|---|---|
| Present | 0.00 m |
| Conservative | 0.52 m |
| Pessimistic | 0.74 m |
| Highly Pessimistic | 0.98 m |
| Input Variables | Discretization Method and Main Distribution Results | Interval | Score | State | |
|---|---|---|---|---|---|
| Elevation | Expert decision/literature review Elevation above sea level represent the 38% of emerged areas, mostly concentrated in the northern macro-sector. The central and southern macro-sectors emerged areas are mostly below sea level reaching elevation values of −3 m above sea level in some specific sectors. | >1 m | 1 | Very Low | |
| 0 m–−1 m | 2 | Low | |||
| −1 m–0 m | 3 | Moderate | |||
| −3 mm/year–−1 m | 4 | High | |||
| Vertical velocity | Expert decision/literature review Vertical velocity reaches the maximum value values in the area of Porto Tolle, Po di Goro (average rates of ~9–10 mm/year), despite the null values observed in the inland area | >−1 mm/year | 1 | Very Low | |
| −2.5 mm/year–−1 mm/year | 2 | Low | |||
| −4.1 mm/year–−2.5 mm/year | 3 | Moderate | |||
| <−4.1 mm/year | 4 | High | |||
| Waves | H0 Height | Expert decision H0 raging between 0.2 and 1 m represents the 87% of the occurred events, while the 12% of the events was classified between 1–2 m and the 1% as greater than 2 m. | 0.2 m–1 m | 2 | Low |
| 1 m–2 m | 3 | Moderate | |||
| >2 m | 4 | High | |||
| H0 Frequency | Percentile The 53% and 15% of the events occurred in the central and southern macro-sectors respectively, while 2017 the 32% of the events occurred in the northern macro-sector. | 571 events–6771 events | 1 | Low | |
| 6771 events–12,970 events | 2 | Moderate | |||
| >12,970 events | 3 | High | |||
| Regime | Equal intervals/literature review In the northern macro-sector 9.7 km2 could be characterized by the “collision” regime, whilst 6.4 km2 could be characterized by the “overwash” regime. In the central part of the delta “collision” regime is more probable north of Po di Pila mouth, while the “overwash” regime is expected in the sector adjacent and south of Po di Pila mouth. In the southern part of the study area ‘collision’ regime is more probable, while along the coastline located close to Po di Tolle mouth, the occurrence of the “overwash” regime is expected. | −1–−0.5 | 1 | Very | |
| −0.5–0 | 2 | Low | |||
| 0–0.5 | 3 | Moderate | |||
| 0.5–1 | 4 | High | |||
| Sea Level Rise | Expert decision/literature review Three SLR future scenarios have been classified in: present scenario, conservative scenario, pessimistic scenario and highly pessimistic scenario. | 0.13 m | 1 | Present | |
| 0.52 m | 2 | Conservative | |||
| 0.74 m | 3 | Pessimistic | |||
| 0.98 m | 4 | Highly Pessimistic | |||
| Dune | Expert decision Dune coverage an area of 5.2 km2 of which 2.3 km2 in the northern macro-sector, 0.7 km2 in the central macro-sector and the other 2.2 km2 in the southern macro-sector. | Presence | 1 | Yes | |
| Absence | 4 | No | |||
| Coverage Factor | Percentile The cover map based on the per-pixel vegetation abundance obtained with the LSMA, the average value of the vegetation abundance (AVA) in % of the pixels that each polygon contains has been calculated, obtaining 45% as the maximum AVA. The final cover map differs between vegetated and non-vegetated emerged areas, depending on the AVA being higher or lower than the 50th percentile. Mapped vegetated areas are mostly distributed close to Po di Mistra, Po di Pila, and Po di Tolle and south of Po di Goro. | >16.65% | 1 | Yes | |
| ≤16.65% | 4 | No | |||
| Protective Distance | Equal intervals The potential protective distance acting as a defense buffer against erosion processes obtained using the EOF approach, divided in four classes, from less than 40 m up to 1500 m. The highest values are found along the coastline, between Po di Mistra and Po di Pila mouths, and in the southern part, close to Lido di Volano. | >1500 m | 1 | Very Low | |
| 1500 m–230 m | 2 | Low | |||
| 230 m–40 m | 3 | Moderate | |||
| <40 m | 4 | High | |||
| Geomorphology | Expert Decision 21.8 km of the coastline were classified as developed beaches of which 4.6 km located in the northern macro-sector, whilst 38.4 km are classified as non-cohesive sediments of which 13.6 km located in the northern, 18.2 km located in the southern. The central macro-sector is completely characterized by non-cohesive sediments. | Soft non-cohesive sediments | 2 | Low | |
| Developed beaches (<1 km long) | 4 | High | |||
| Global Surface Water Dynamic | Water Transition | Expert Decision In the central macro-sector in correspondence of Po di Pila mouth, a loss of permanent water is observed as a consequence of conversion of permanent water into land. Rather, in the southern macro-sector close to the Po di Gnocca mouth land converted into seasonal water, while in correspondence of the sandy spit (the Scanno in Sacca di Goro) located south of Po di Goro mouth a loss of permanent water occurred. | 0–110% | 1 | Very Low |
| 111–142% | 2 | Low | |||
| 143–177% | 3 | Moderate | |||
| 178–200% | 4 | High | |||
| Surface Water Occurrence Change Intensity | Expert Decision Surface water occurrence changes are mainly distributed along the coastline higher intensity of surface water occurrence change, where the surface water occurrence decreased across the 32 years period, located in the central macro-sector in correspondence of Po di Pila mouth. In the southern macro-sector, water occurrence increased more intensely close to the Po di Gnocca mouth and decrease in correspondence of the sandy spit (The Scanno in Sacca di Goro) located south of Po di Goro mouth. | -Permanent water surfaces, no change -Conversion of permanent water into land -Conversion of a seasonal water into land | 1 | Very Low | |
| -Seasonal water surfaces, no change -Land replaced by permanent or seasonal water that subsequently disappears | 2 | Low | |||
| -Conversion of land or permanent water into seasonal water | 3 | Moderate | |||
| -Conversion of land or seasonal water into permanent water | 4 | High | |||
| Protected natural area | Expert decision The 57% of the study area is classified as “protected” according to Natura2000. In the northern macro-sector, 8.2 km2 of a total 19.1 km2 are classified as protected areas. In the central macro-sector 4.3 km2 are protected areas on 8.1 km2. In the southern macro-sector, protected areas cover 24.6 km2 of a total of 37 km2. | Absence | 1 | No | |
| Presence | 4 | Yes | |||
| Resilience Index | Percentile The average, maximum and minimum values obtained are 4.2, 5.1 recorded in Rosolina, and 3.2 recorded in Goro, respectively. Higher values mean greater resilience resulting in lower vulnerability. In the Rosolina municipality, higher values of infrastructure and social resilience subcomponents (equal to 1) led to a higher index value. | >4.3 | 1 | Very Low | |
| 3.5–4.3 | 2 | Low | |||
| 3.2–3.5 | 3 | Moderate | |||
| <3–2 | 4 | High | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taramelli, A.; Valentini, E.; Righini, M.; Filipponi, F.; Geraldini, S.; Nguyen Xuan, A. Assessing Po River Deltaic Vulnerability Using Earth Observation and a Bayesian Belief Network Model. Water 2020, 12, 2830. https://doi.org/10.3390/w12102830
Taramelli A, Valentini E, Righini M, Filipponi F, Geraldini S, Nguyen Xuan A. Assessing Po River Deltaic Vulnerability Using Earth Observation and a Bayesian Belief Network Model. Water. 2020; 12(10):2830. https://doi.org/10.3390/w12102830
Chicago/Turabian StyleTaramelli, Andrea, Emiliana Valentini, Margherita Righini, Federico Filipponi, Serena Geraldini, and Alessandra Nguyen Xuan. 2020. "Assessing Po River Deltaic Vulnerability Using Earth Observation and a Bayesian Belief Network Model" Water 12, no. 10: 2830. https://doi.org/10.3390/w12102830
APA StyleTaramelli, A., Valentini, E., Righini, M., Filipponi, F., Geraldini, S., & Nguyen Xuan, A. (2020). Assessing Po River Deltaic Vulnerability Using Earth Observation and a Bayesian Belief Network Model. Water, 12(10), 2830. https://doi.org/10.3390/w12102830






