Investigating Groundwater Discharge into a Major River under Low Flow Conditions Based on a Radon Mass Balance Supported by Tritium Data

Abstract

The potentially detrimental impact of groundwater discharge into rivers on the ecosystem services provided by the river makes the localization of groundwater discharge areas as well as the quantification of the associated mass fluxes an issue of major interest. However, localizing groundwater discharge zones and evaluating their impact are challenging tasks because of (i) the limited number of suitable tracers and (ii) the high spatio-temporal variability of groundwater/river water interaction in general. In this study, we applied the ubiquitous naturally occurring radioactive noble gas radon (²²²Rn) as an aqueous tracer to localize and quantify groundwater discharge along a 60 km reach of the upper German part of the major river Elbe under drought conditions. All radon data processing was executed with the numerical implicit finite element model FINIFLUX, a radon mass balance-based approach, which has been developed specifically to quantify the groundwater flux into rivers. The model results were compared to the tritium (³H) distribution pattern in the studied river reach. The results of the study proved the applicability of both (i) the methodical approach (i.e., radon as tracer) and (ii) the application of FINIFLUX to drought conditions (with river discharge rates as low as 82 m³/s vs. a long time mean of 300 m³/s). Applying the model, the recorded dataset allowed differentiating between groundwater baseflow, on the one hand, and interflow and surface water runoff distributions to the river, on the other. Furthermore, the model results allowed assessing the location and the intensity of groundwater discharge into the river under low flow conditions. It was also shown that analysing discrete river water samples taken from distinct points in a major stream might lead to slightly incorrect results because of an incomplete mixing of river water and locally discharging groundwater. An integrating sampling approach (as applied for radon) is preferable here.

1. Introduction

Rivers provide ecosystem services, such as hydrological regulation or sediment and nutrient retention. Furthermore, they provide habitats for a wide range of freshwater species. Finally, yet importantly, rivers represent a major resource for drinking water abstraction and are popular for recreational activities. All these services are highly dependent on the river water quality, which is, in turn, directly linked to the quality of the water sources feeding the river, including the groundwater component. For instance, groundwater borne nutrient (C, N, P) input into rivers increases the risk of eutrophication in the river’s estuaries [1,2]. Particularly during drought conditions, the groundwater component becomes a water (and potentially pollutant and nutrient) source of key importance as other sources (such as interflow, surface runoff and small tributaries) cease to flow. Hence, localizing areas of groundwater discharge into a major river as well as quantifying the associated mass fluxes is of primary interest.

Despite this importance, groundwater discharge into rivers is often neglected in river status assessment and water resource allocation. A reason for this is the limited number of (easily detectable) indicators that meet the demands of tracing highly diffuse groundwater/river water interaction processes. Another challenge is the high spatio-temporal variability of groundwater discharge into rivers. A river reach that is subject to groundwater discharge (i.e., a “gaining” river section) can change into a river reach that is dominated by river water infiltration into the aquifer (i.e., a “loosing” river section) due to an inverting hydraulic gradient between groundwater and river. Such switch may occur on the long term with the change of the seasons or on the short term because of an extreme event (i.e., a flood wave) or a (temporary) physical obstacle in the riverbed (e.g., [3]).Sophocleous (2002) [4] discussed a range of mechanisms that govern groundwater/surface water exchange. Kalbus et al. (2006) [5] discussed methodical approaches for related investigations.

Groundwater/river water interactions can generally be assessed based on the hydraulic gradient between river and connected groundwater bodies. However, the related numerical flow modelling requires high quality input data describing the hydraulic properties of the aquifer and the hyporheic zone. In many cases such quality data are scarce, and model calculations need to rely on vague assumptions concerning small-scale but still influential variations of the aquifer conditions, thereby increasing the uncertainty of the modelling results substantially.

In contrast to “indirect” modelling that is solely based on hydrogeological data, “direct” discharge measurement by means of seepage meters results in more reliable data [6]. However, a general drawback of this approach is that the gained data give only point-scale information (<1 m²). Since groundwater discharge is likely to be highly heterogeneous in space and time and is in most cases a diffusive flux, the derived conclusions are often not representative for longer river reaches.

Numerical groundwater flow modelling that is based on discrete tracer data represents an alternative that combines the advantages of integrative hydrological modelling and point-scale discharge measurements. A range of environmental tracers (i.e., naturally occurring substances that show a significant concentration gradient between hydraulically connected groundwater and river water) have proven suitable to parameterize hydrological models with the aim to disentangle surface water and groundwater components. Applicable tracers include the stable isotopes of water (e.g., [7,8,9,10,11,12,13]) as well as naturally occurring radioisotopes. Examples for the latter are 35-sulphur, 3-hydrogen (tritium), 222-radon, and the radium 224/223 ratio (e.g., [14,15,16,17,18,19]). Major ions and trace elements are also frequently applied as tracers (e.g., [20,21,22]). However, the resulting data are usually associated with large uncertainties due a limited concentration contrast between the groundwater and surface water and heterogeneity in the aquifer system. In any case, the use of tracer data has a high potential to yield integrated information allowing the assessment of extended river reaches. Still, the related tracer data processing requires tailor-made model applications that account for both, tracer specific properties and site-specific aquifer conditions.

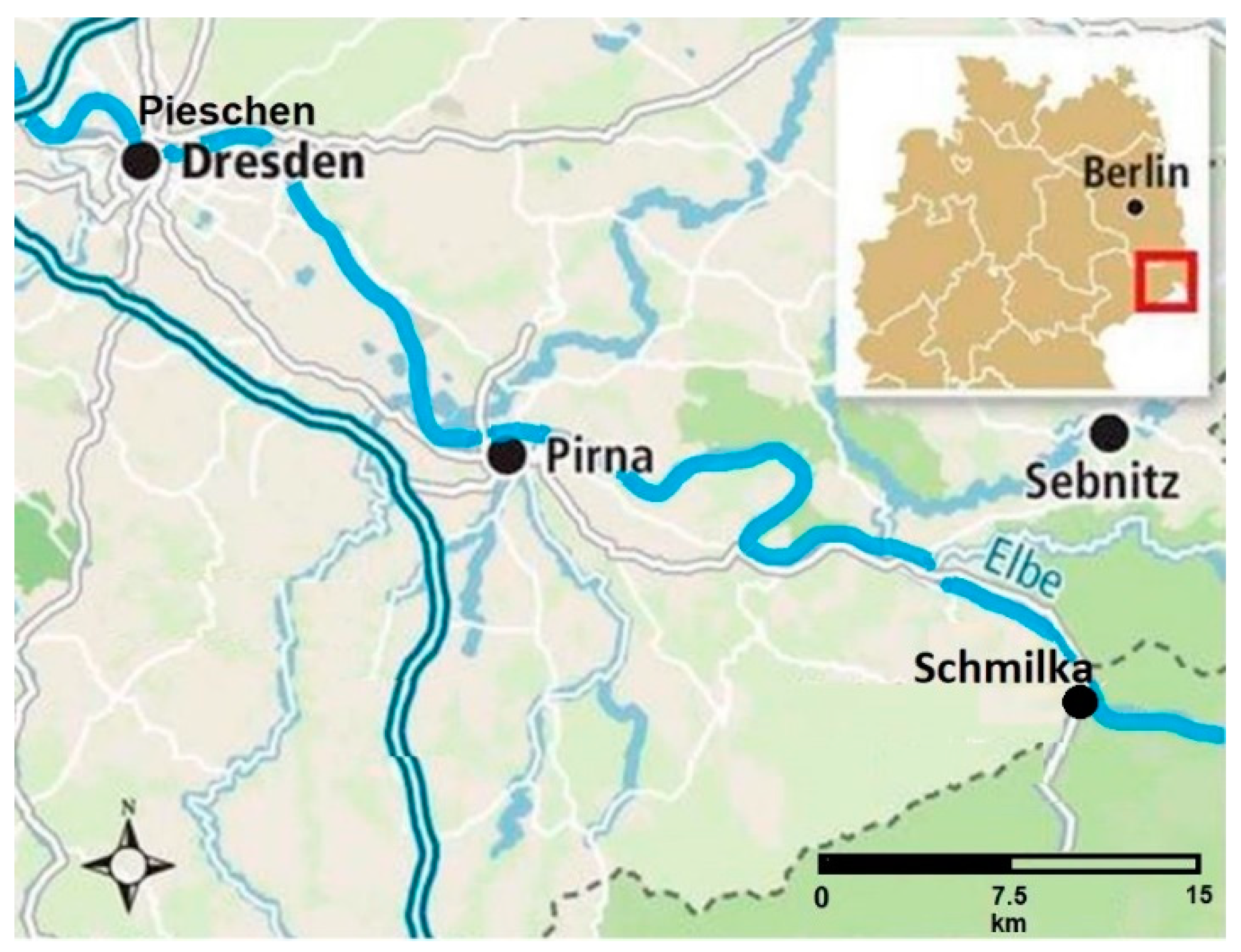
In our study, we applied the ubiquitously occurring radioactive noble gas radon (²²²Rn; half-life 3.8 days) as aqueous tracer for localizing and quantifying groundwater discharge into a 60 km reach of a major river, the River Elbe between the Czech/German border at Schmilka (upstream) and Pieschen (downstream) (Figure 1). Radon data processing was executed with the numerical implicit finite element model FINIFLUX, a tailor-made model approach that is based on a mass balance equation for in-stream radon allowing investigations of groundwater/river water interaction at the river reach scale ([23,24,25]). The radon-based model results were compared against the (completely independent) tritium distribution pattern in the investigated 60 km river reach, which was recorded simultaneously to the radon survey.

2. Materials and Methods

2.1. Onsite Activities

The study site was a 60 km reach of the River Elbe between Schmilka and Pieschen (a district of the City of Dresden; Figure 1). The radon distribution pattern in the river water along this profile was mapped twice during two independent two-day sampling campaigns. Hydrologically, both sampling campaigns reflected the extreme low flow and drought conditions that were prevalent in Germany during the late summer of 2018 (first campaign 13–14 August; second campaign 11–12 September). Despite the generally dry conditions, short but heavy rainfall upstream of the study area triggered a flood wave that was rolling down the river exactly during the second campaign increasing the river discharge at starting point of the profile from ~87 m³/s to ~145 m³/s over about 12 hours. This is in contrast to the long-time average discharge at this station, which is about 315 m³/s, which highlights the drought conditions at the time of sampling.

During both campaigns, river water was sampled from a vessel (rubber boat), cruising down the river slightly faster than the river velocity (in order to keep the vessel manoeuvrable). While cruising, radon was detected directly on-board by means of a mobile detection setup (cf. Section 2.5.4). During the first campaign, additional discrete river water samples (every 2 km) were taken for tritium analysis. The samples were analysed at the Federal Institute of Hydrology (BfG) (cf. Section 2.4). To define groundwater endmembers for both radon and tritium, samples (four and three, respectively) were taken during an individual field campaign from springs (cf. Section 2.5.5).

2.2. Study Area and Meteorological Situation during the Time of Investigation

In August 2018 (first sampling campaign), the River Elbe reached its lowest water level since the beginning of gauge measurements ([26]). The river discharge recorded prior to the first campaign at the upstream station (Schmilka) was 87 m³/s. The related long-time average is 301 m³/s, i.e., nearly four times the measured discharge. Despite the fact that drought conditions were prevailing during both campaigns, the above-mentioned flood wave during the second campaign resulted in distinctively different results of the two campaigns.

The investigated 60 km reach of the river runs in its main part though Cretaceous sand-, clay- and siltstones, and bioturbate marls [27]. These rock formations are exposed in a picturesque valley in the upper 30 km section of the investigated river reach. At the same time, they form a complex fractured aquifer system with a low to moderate hydraulic permeability. The total thickness of the aquifer rock deposits is about 300 m. The drainage of the aquifer follows fault zones, which are generally directed towards the River Elbe (Ad-Hoc-AG Hydrogeologie, 2016). The uranium and radium bearing minerals in the sandstone matrix, which are the source of the radon that is used as a tracer in our study, originate from the Markersbach granite pluton, located in the easternmost Erzgebirge (Ore Mountains).

In particular, the widespread sandstone domains of the aquifer system yield relatively high radon concentrations in the groundwater, which is advantageous for the applied radon tracer approach. While radon concentrations in groundwater in middle and northern Germany range generally below 10 Bq/l, the concentrations that are found in the study area can be as high as 90 Bq/l (own measurements). These elevated ²²²Rn concentrations in the groundwater are due to enhanced ²²⁶Ra concentrations of the sandstone mineral matrix.

2.3. Radon (²²²Rn) as Tracer

²²²Rn (3.8-day half-life) is constantly produced in any aquifer matrix by radioactive decay of ²²⁶Ra. In contrast to its resulting ubiquitous presence in groundwater, it shows very low concentrations in surface waters due to the lack of radium there. Main reason for the radium absence in rivers and lakes is the sorption of ²²⁶Ra²⁺ ions onto iron/manganese oxides and clay minerals in the mineral matrices of aquifers and sediments. On average, the radon concentration in groundwater is about three to five orders of magnitude higher than in surface waters (for this reason all radon in groundwater concentrations in this paper are given as [Bq/l] and all radon in river water concentrations as [Bq/m³]). Hence, locally enhanced ²²²Rn concentrations in a river indicate local groundwater discharge. However, only discharging groundwater with residence times of several weeks in the aquifer (i.e., baseflow), yields radon signals in the river water that are strong enough to allow statistically reliable data evaluation. Generally, five ²²²Rn half-lives (i.e., 20 days) are required to reach complete decay equilibrium between ²²⁶Ra present in the aquifer matrix and ²²²Rn in the freshly recharged groundwater. Consequently, the discharge of very young groundwater (i.e., interflow with residence times of hours or a few days) would not result in any significant radon signal in the river.

Once in the river water, the radon is lost rapidly due to degassing to the atmosphere and, to a minor degree, due to radioactive decay. That allows using (i) radon distribution patterns in a river to localize preferential groundwater discharge zones and (ii) radon mass balances for the quantification of groundwater discharge rates (and the associated matter fluxes). The latter requires all radon sources and sinks to be accounted for quantitatively. The radon approach discussed in this paper requires sound information on both the radon distribution pattern in the river course (cf. Section 2.5.4) and the radon endmember in the hydraulically connected groundwater (cf. Section 2.5.5).

2.4. Tritium (³H) as Tracer

In natural systems, the tritium concentration in river water is determined by the tritium concentration of the local precipitation and the tritium concentration of the groundwater that is discharging into the river. In Europe, the annual average tritium concentration in precipitation is around 1 Bq/l ([28] Schmidt el al., 2019) with slightly higher values in spring and slightly lower values in autumn and winter. Tritium concentrations in groundwater range between ~0 Bq/l (groundwater with ages > 100 years) and ~1 Bq/l (young newly recharged groundwater).

However, anthropogenic activities may significantly increase the tritium concentration in a river. A potential major tritium source is any nuclear power plant that is located at a river and that releases process water enriched in tritium into the river. Since such tritium inputs are well-defined point sources, the downstream decrease of the tritium concentration in the river can be used as indicator for the dilution impact of inflowing natural water from (i) tributary streams, (ii) direct surface water runoff, (iii) direct rainfall, and (iv) discharging groundwater. With a half-life of 12.32 years radioactive decay of tritium is of little relevance over the time scales of surface water flow through a catchment.

A nuclear power plant is located in Temelin (Czech Republic), on the banks of River Vltava, which is an upstream tributary of the River Elbe. At Temelin tritium release prior to the first sampling campaign caused significantly elevated tritium concentration in the River Elbe at the upstream end of the investigated 60 km profile (Schmilka) (cf. Section 3.7). As result of the prevailing drought conditions, tributary stream discharge, direct surface water runoff and rainfall were insignificant within the study area during the two sampling campaigns. Consequently, declining tritium concentrations in the river water could be assigned to groundwater discharge (low in ³H) and hence be used as a Supplementary Data to validate the radon-based results.

Samples for tritium analysis were distilled, and tritium was electrolytically enriched 15-fold. The tritium concentration was measured by low background liquid scintillation counting (Quantulus GCT 6220) with a detection limit of about 0.08 Bq/l. In spite of sound sampling, sample preparation and measurement, it shall be pointed out that the resulting tritium data could only be interpreted semi-quantitatively due to its rather high statistical uncertainty. Consequently, the tritium data were solely used for evaluating the plausibility of the radon-based model results.

2.5. The FINIFLUX Model

2.5.1. The Model Approach

The FINIFLUX model [29] allows calculating the groundwater discharge into a defined river reach on the catchment scale based on radon data. For the model calculation, the river reach is divided into sub-reaches. The total number of sub-reaches depends on their individual lengths and thus (i) on the cruise velocity of the vessel that is used for radon sampling [m/min] and (ii) the length of the radon detectors’ counting cycle [min] that is required for attaining statistically reliable results (cf. Section 2.5.4).

The FINIFLUX model uses a steady state mass balance approach for in-stream radon within each of the sub-reaches. The model approach is based on a Petrov–Galerkin Finite Element scheme as given in Equation (1), where x [m] is the length of the investigated sub-reach, w [m] is its mean width, and d [m] its mean depth. Q_s [m³/d] is the river discharge within the sub-reach; c and c_gw [Bq/m³] are the ²²²Rn concentrations in the river water and the groundwater endmember, respectively, both representative for the sub-reach. The parameter k [d⁻¹] represents the ²²²Rn degassing coefficient, and λ_Rn [d⁻¹] the first order decay constant for ²²²Rn. The parameters α₁ and α₂ quantify hyporheic exchange. They depend on the physical characteristics of the hyporheic zone and its residence time distribution, i.e., hyporheic depth and mean water residence time. The related details on the definition of α₁ and α₂ are discussed in [30] and [31]. Q_r [m³/d] is the surface water inflow from tributaries within the sub-reach, R_L [m] the mean width of the tributaries where they enter the stream and c_trib [Bq/m³] the mean ²²²Rn activity in the tributaries. I [m³/m × d] is the rate of groundwater discharge within this sub-reach, i.e., the parameter of interest.

$$Q_s\frac{dc}{dx}=I\left(c_{gw}-c\right)-kwdc-dwc{\lambda }_{Rn}+{\alpha }_1-{\alpha }_{2}c+\frac{Q_r}{R_L}\left(c_{trib}-c\right)$$

(1)

The mass-balance equation is fitted to the onsite detected radon data by varying (i) the groundwater discharge as well as both (ii) hyporheic depth and (iii) hyporheic mean residence time. This fitting process is done using the BeoPEST code [32]. Due to the prevailing drought conditions during the sampling campaigns, no relevant contributions from tributaries along the investigated 60 km section of River Elbe were observed, and the three parameters Q_r, R_L and c_trib could be neglected in our calculations.

The following sections discuss the input data that is required by the FINIFLUX model. The dataset, which is required for each sub-reach (all average values that are representative for the sub-reach), includes (i) length, depth and width of the sub-reach [m]; (ii) river discharge rate [m³/s]; (iii) radon concentration in river water [Bq/m³]; (iv) radon endmember concentration in the hydraulically connected groundwater [Bq/m³] and (v) the radon degassing coefficient (d⁻¹).

2.5.2. FINIFLUX Data Collection (i): Lengths, Depth and Width of the Sub-reaches

In order to keep the vessel manoeuvrable during the two sampling campaigns, the vessel was cruising with a speed slightly above the flow velocity of the river (ca. 6.8 and 6.6 km/h, respectively). The counting cycle of the mobile radon monitor was set to 15 min during the first campaign and 10 min during the second campaign. That resulted in lengths of the sub-reaches of ca. 1.7 km and 1.1 km, respectively, and in total numbers of sub-reaches of 32 and 52, respectively. All river depth and width data were provided by the Federal Institute of Hydrology (BfG) with a 500 m resolution.

2.5.3. FINIFLUX Data Collection (ii): River Discharge

All river discharge data were interpolated from river discharge time series recorded at the two endpoints of the investigated 60 km river profile, i.e., Schmilka (upstream) and Pieschen (downstream), respectively. (This discharge time series were recorded by the Federal Waterways and Shipping Administration (WSV) and provided by the BfG.) The two datasets were provided by the BfG with a 15 min resolution. Each interpolated value reflects the distinct point of the cruising sampling vessel. Representative interpolation was achieved by averaging the endpoint values of the two end-point datasets weighted based on the actual time and position of the vessel.

2.5.4. FINIFLUX Data Collection (iii): Radon Concentration in the River Water

The radon concentration in the river water was measured directly on the cruising vessel by means of two mobile Rn-in-air monitors RAD7 (Durridge, USA), which were operated in parallel. The radon monitors were attached to a permanent water pump stream (water flow rate 2 L/min), which was connected to a radon extraction unit (MiniModule^®, Membrana GmbH, Germany; [33]). Within the extraction unit, radon equilibrates between water pump stream and a closed air loop as a consequence of temperature dependent radon partitioning between water and air [34]. A key advantage of measuring radon continuously while cruising is that the resulting radon values reflect the average radon concentration in the river water integrative over the complete investigated sub-reach. Hence, any locally occurring incomplete mixing between flowing river water and (potentially) locally discharging groundwater is balanced out. (As it will be shown later for the tritium sampling, river water samples that are taken at discrete locations may not be fully representative for the river water at the sampling position due to locally incomplete mixing between river water and groundwater.)

2.5.5. FINIFLUX Data Collection (iv): Radon Groundwater Endmember

In general, the radon endmember of any groundwater body is difficult to determine due to the general heterogeneity of most aquifer rock materials. This is also the case for the River Elbe study site. In order to guarantee a high statistical reliability of the radon endmember, we collected and processed data from three different and independent sources.

The first source is an existing but unpublished radon dataset collected and made available by the WISMUT GmbH, an industrial project partner that is involved in local groundwater management [35]. The data source provided radon concentrations representative for the groundwater in the upper 30 km section of the investigated river profile. All groundwater samples had been collected from wells that tap aquifer domains, which are assumed to be hydraulically connected to the River Elbe.

The second way to determine the radon groundwater endmember was to calculate the pore water radon concentration in the river sediment based on measured ²²⁶Ra concentrations in the sediment matrix. As in the aquifer, ²²²Rn is permanently produced in the river sediment by ²²⁶Ra decay. Since the river sediment is dominated by the local aquifer host rock, the radon concentration in the sediment pore water can be used as proxy for the radon concentration in the groundwater. For this purpose, 15 sediment samples were taken from the bank of the investigated river profile. Six of the samples were taken on a profile crossing the river at the upstream end of the investigated river section (Schmilka). Another nine samples were taken along the river course equidistantly every 5 km.

Radium concentrations were measured by γ-spectroscopy using an ORTEC-Gamma-X HPGe coaxial low-energy n-type detector with an active volume of 39 cm³ and a 0.5 mm beryllium window. Detector and measuring geometry (applying cylindrical radon-tight capsules of 113 cm³) were calibrated using the certified IAEA reference material RGU-1. The radium concentration was determined based on the distinct gamma emission energies of the short-lived radon progeny ²¹⁴Pb (295.2 and 351.9 keV) and ²¹⁴Bi (609.3 and 1120.3 keV) with a mean standard deviation of 5%. For ensuring decay equilibrium between radium and the short-lived radon progeny, all samples were stored before measurement for 27 days (i.e., seven ²²²Rn half-lives) in the radon-tight capsules that were placed on the detector for measurement afterwards.

As a third option, the radon groundwater endmember was determined by own measurements at four springs located close to the river within the upper 30 km section of the investigated river profile. For immediate on-site radon analysis, the water samples were transferred into a stripping unit by means of a peristaltic pump with a low pump rate thus avoiding turbulence and minimizing degassing during sampling. The executed water sampling and on-site radon measurement process has been described in detail by [36]. To allow a high statistical reliability of the data, a stripping unit was chosen that allowed stripping a rather large water volume of two litres.

2.5.6. FINIFLUX Data Collection (v): Radon Loss by Degassing

Radon degassing is the major loss term in the river radon mass-balance. Generally, degassing is predominately driven by turbulence in the stream water [37]. Still, there are a number of different methods for quantifying the loss of gasses (such as radon) to the atmosphere from a stream or any other surface water body. The methods include (i) injections of tracer gases such as propane or SF₆ ([24,38,39]), (ii) evaluating the gas concentration in losing river reaches [39] and, nowadays most commonly, (iii) using empirical equations that correlate the physical properties of the river and the flow regime to the gas loss [23,25,40]. All these methods result in a degassing coefficient, k (d⁻¹), that is used to quantify the gas (i.e., radon) loss from the water body.

Given the length scale and the river discharge rate of the investigated River Elbe reach, we have chosen to use the third of the given options to quantify degassing, i.e., an empirical equation.

Empirical equations were initially developed to quantify re-aeration of streams ([41,42]) affected by organic matter from waste treatment plants. Given the importance of these processes, there have been more than 30 different equations developed since the 1950s (e.g., [43,44]). We have chosen to use the equation published by [41] scaled to SI units (Equation (2)). In previous work, we have found that this equation predicts radon degassing well in mid to large rivers such as River Elbe (although not so well in small headwater streams; cf. in this issue: Schubert et al. “Investigating river water/groundwater interaction along a rivulet section by ²²²Rn mass balancing”).

$$k=9.301\times {10}^{-3}\left(\frac{v^{0.5}}{D^{1.5}}\right)$$

(2)

In Equation (2), D is the river depth [m] and v is the flow velocity [m/d].

3. Results and Discussion

3.1. River Depth and Width

Both river depth and width show, apart from a few single-point anomalies of the width (small harbours or natural embayment), only one significant irregularity over the investigated 60 km river reach: at around km 33.5 the river becomes shallow and wide over a distance of about 3 km (Figure 2 and Figure 3). This results locally in (i) a larger river water/aquifer interface, i.e., a (potentially) increased groundwater discharge rate, (ii) a larger water surface to volume ratio, i.e., an increased radon degassing rate, and (iii) a reduced intensity of mixing between (potentially) locally discharging groundwater and river water.

3.2. River Discharge

While the first radon survey allowed an uncomplicated discharge interpolation between the two end-point stations Schmilka (upstream) and Pieschen (downstream) (Figure 4), interpolation was more involved for the second cruise. The complication was due to the abovementioned flood wave, which rolled down the river exactly at the time of the two-day survey (Figure 5). The situation resulted in river discharge values valid for a downstream positions of the cruising vessel that were lower than values valid for an upstream position of the vessel passed earlier on. That relation complicated defining the boundary conditions of the modelling since it violates the model assumption of steady-state flow continuation (dQ / dt = 0).

3.3. Radon Profiles in River Water

The first radon survey was executed under extreme low flow conditions. The results show generally a steady decrease of the radon concentration in the river water [Bq/m³] over the complete 60 km profile starting in Schmilka with 1400 Bq/m³ and ending in Pieschen with 900 Bq/m³ (R = 0.81; cf. Figure 7). The associated radon mass flux [kBq/s] shows a comparable picture, starting in Schmilka with 120 kBq/s and dropping to 77 kBq/s in Pieschen (Figure 8). These values correspond for both parameters to a relative decrease to 65% of the initial value over the 60 km profile.

The observed steady decrease in the radon mass flux indicates that the radon loss by degassing to the atmosphere is not compensated by the discharge of groundwater (i.e., baseflow) into the river. Two reasons can be assumed for this: (i) limited baseflow discharge due to a low-pressure gradient between groundwater and river water as a result of the prevailing drought conditions and (ii) increased radon degassing due to the generally shallow river water level resulting in a large surface to volume ratio of the water body. Because of the flow velocity of the river, radioactive decay is only of limited relevance as a radon sink. A pocket of river water would cover the complete 60 km distance of the profile in about 12 hours resulting in a maximum decay of 10%.

The second radon survey executed four weeks later was also carried out under drought conditions. However, as mentioned above, the two-day sampling campaign was accompanied by a flood wave rolling down the river; the sampling vessel was literally riding on this wave during the campaign (Figure 6). While the river discharge was around 85 m³/s during the first campaign, it reached about 145 m³/s during the second campaign, i.e., it was about 70% higher (cf. Figure 4 and Figure 5). The wave was triggered by intense rain events upstream of the study area in the days prior to the survey.

Due to these exceptional conditions during the second campaign, the plots for radon concentration as well as radon mass flux reveal significantly different pictures for the two surveys (Figure 7 and Figure 8). During the second survey, the mean radon concentration of the river water was only about 50% of the mean concentration detected during the first campaign. This can be explained with radon dilution in the river water by surface water runoff and discharge of very young groundwater low in radon (interflow) upstream of the study area due to the previous intense rains there (resulting in “the wave”). Besides dilution, the temporarily higher river water level of the wave (and the resulting higher hydrostatic pressure on the riverbed) hindered groundwater discharge into the river both upstream of the study area and within the study area during the campaign.

Another obvious difference between the results of the first and the second survey is that during the second survey the radon concentration is not decreasing steadily over the 60 km profile but initially rising (starting at a very low level) until the end of the mountainous section of the profile (at km 30). Only after this, it starts decreasing with about the same rate as during the first campaign. The initial radon concentration during the second campaign (about 500 Bq/m³) is very low in comparison to the first campaign (about 1350 Bq/m³). At such a low concentration, minor baseflow discharge is already sufficient for causing the observed concentration rise. Due to minor rains in the mountainous section of the study region, three days before the second survey (in total 30 mm), minor but steady baseflow discharge into the river was likely in particular in the mountainous section of the study area (despite the overall drought conditions). In the second part of the 60 km profile, the catchment becomes rather flat. Due to the resulting lower groundwater/river water pressure gradient, baseflow discharge was only very limited in this flat section, and radon loss by degassing dominated the river radon budget resulting in the observed steady concentration decrease.

Although the plots of radon concentration and radon mass flux of the second campaign show the same shape, it has to be kept in mind that (in contrast to concentration) dilution due to “the wave” does not affect the mass flux rate. The much lower mass flux rate at the beginning of the profile indicates therefore a decreased baseflow discharge already upstream of the study area, probably due to the temporary elevated river water level and the related increased hydrostatic pressure on the riverbed. The increase of the radon mass flux rate within the mountainous section of the investigated river reach (i.e., the upstream 30 km of the profile), indicates baseflow discharge into the river at a rate that is more than compensating the radon loss by degassing. From its peak at around km 30, the mass flux rate decreases with the same rate as during the first survey because baseflow discharge does not balance the loss by degassing anymore.

3.4. Radon Groundwater Endmember

3.4.1. ²²²Rn Endmember Assessment Based on Existing Data

The existing unpublished dataset provided by the WISMUT GmbH included 25 individual groundwater radon concentrations all representative for the catchment of the upstream 30 km of the investigated river section (i.e., the mountainous part). However, only six of the samples had been collected from wells that were both located sufficiently close to the river and taping the hydraulically connected aquifer. In addition to these six values, four more wells located in further distance to the river were included in our study because they are also fed by the aquifer of relevance. The resulting dataset (n = 10) revealed radon groundwater concentrations ranging between 10 and 45 Bq/l with an average of 27 ± 13 Bq/l. This value can be assumed to reflect the groundwater endmember representative for the upstream 30 km section of the investigated River Elbe reach.

3.4.2. ²²²Rn Endmember Assessment Based on ²²⁶Ra in the River Sediment

The detected mean ²²⁶Ra activity of the 15 sediment samples was 23 Bq/kg. With a measured sediment dry density of 1900 kg/m³, an assumed emanation coefficient of 0.25 [45] and a measured sediment porosity of 0.4 this radium activity yields theoretically a mean radon pore water concentration of about 28 kBq/m³. While an uncertainty of about 5% is valid for the three parameters ²²⁶Ra activity, dry density and pore space, the emanation coefficient is only an assumption with an uncertainty of ca. 20%. Hence, the mean ²²⁶Ra activity in the sediment samples yields a mean ²²²Rn concentration in the pore water of 28 ± 3 Bq/l.

This value comes close to the radon endmember that was assumed based on the existing data set (Section 3.4.1). It needs to be kept in mind though, that (apart from the most downstream sample taken at km 45) the ²²⁶Ra activities of the sediment decrease slightly in flow direction of the river. They start upstream with about 29 Bq/l and end downstream with about 22 Bq/l (Figure 9), thus yielding theoretically radon concentrations in the pore water of 34 and 26 Bq/l, respectively. Furthermore, the data of the cross section show that ²²⁶Ra is not homogeneously distributed in the sediment across the river (Figure 10). Hence, even though all sediment samples displayed in Figure 9 were taken from the northeast bank of the river, the uncertainty of the radon endmember that is based on ²²⁶Ra in river sediment data might be higher than the calculated one given above.

3.4.3. Spring Water Measurements

Four natural springs, all fed by the aquifer that is hydraulically connected with the river, were sampled and analysed for radon immediately on-site. All four springs were located in the mountainous section of the investigated River Elbe profile. The radon concentrations ranged between 15 and 50 Bq/l with an average of 34 ± 11 Bq/l. This value confirms the radon groundwater endmembers assumed based on the WISMUT data set (Section 3.4.1) and on ²²⁶Ra in the river sediment (Section 3.4.2).

3.4.4. Radon Groundwater Endmember Definition

In conclusion, it can be stated that all three approaches for radon groundwater endmember determination resulted in comparable values (

Table 1. Groundwater radon activities from various sources.

Data Source	Upstream Section (Upstream 30 km) 222Rn [Bq/l]	Downstream Section (Downstream 30 km) 222Rn [Bq/l]
WISMUT data	27 ± 13	n.a.
226Ra in sediment	34 ± 04	26 ± 3
springs	34 ± 11	n.a.

). While the WISMUT dataset and the spring samples resulted in values representative for the mountainous 30 km upstream section of the investigated river reach, the ²²⁶Ra based values cover the whole 60 km profile. Hence, the ²²⁶Ra based values were used for FINIFLUX modelling.

3.5. Radon Mass-Balance Used by FINIFLUX

The calculated degassing coefficient during the first campaign ranged between 3.1 and 4.0 d⁻¹ with an average of 3.5 d⁻¹. Implementing the k-values into the mass-balance showed that over the complete investigated 60 km river reach radon loss to the atmosphere ranged from −1 × 10⁴ Bq/s to −7 × 10⁴ Bq/s and was the largest sink term. The highest degassing loss along the profile occurred at its start where the relatively high flow velocity and the shallower depth contributed to high turbulence, which enhanced degassing.

During the second campaign, the average k-value was 3.0 d^-1 with maximum and minimum values of 3.7 d⁻¹ and 2.3 d⁻¹, respectively. The related radon loss due to degassing averaged −2.3 × 10³ Bq/s ranging from −1.3 × 10³ Bq/s to −3.4 × 10³ Bq/s. The lower degassing during the second campaign can mainly be attributed to the lower radon concentration present in the river. In contrast to degassing, the loss to radioactive decay was low with around −150 Bq/s.

The groundwater (baseflow) discharge was the dominant radon source to the river during both campaigns (up to 1.6 × 10⁴ Bq/s). However, hyporheic water exchange was also calculated to be a noteworthy radon source, with a relatively constant flux of around 5 × 10³ Bq/s during the first and up to 10⁴ Bq/s during the second campaign. In particular, in the low groundwater discharge sub-reaches, this hyporheic term was at least as important as the groundwater flux for the radon balance, with a more important role when the flood wave passed through the catchment (second campaign). The large hyporheic flux can be attributed to the large width and low depth of the river during drought conditions favouring exchange with the riverbed.

All data that contribute to the overall radon mass-balances for both the first and the second sampling campaign (i.e., radon sinks: decay, degassing, hyporheic exchange loss; radon sources: groundwater discharge, hyporheic exchange gain) are individually displayed in Figure 11A,B.

3.6. Groundwater Discharge Localization and Quantification Using FINIFLUX

The FINIFLUX model solves the 1D radon mass-balance, accounting for all sources and sinks along each sub-reach of the river (Figure 11). The model was fit to the measured radon data by varying the groundwater discharge as well as the hyporheic parameters. Figure 12A,B shows that during both measurement campaigns, the model could reproduce the measured radon data, with a correlation coefficient between measured and modelled data being above 0.9.

During the first measurement campaign the model calculated a total of 2.9 m³/s groundwater discharged to the River Elbe over the 60 km (Figure 12C). The upstream sections contributed more groundwater to the river than the downstream sections (~60%) with the contribution decreasing downstream of km 25, i.e., downstream of the mountainous section. Groundwater discharge was most intense and concentrated in the upper sub-reaches at km 6 and km 20. These areas can be considered preferential groundwater discharge zones. In the downstream, sub-reaches discharge occurred preferentially (but in a reduced magnitude) at km 35 and km 50. In total, the groundwater discharge to the River Elbe over the complete 60 km section contributed about 3.5% of the total flow recorded in Pieschen during the first campaign.

Despite the dynamic boundary conditions that made the use of the FINIFLUX model difficult during the second campaign, the model was also able to fit the measured radon data well. The calculated groundwater discharge rates were highly reduced compared to the first campaign, with only 1 m³/s discharging to the river over 60 km (Figure 12D). This is consistent with the lower radon activities. While there are few clear trends in the groundwater discharge data, it seems that the upper sub-reaches are again contributing more baseflow groundwater (~60%) than the lower sub-reaches. Other than right at the beginning of the investigated river section, there were no clear areas of preferential groundwater discharge during the second campaign. As discussed above, the lower fluxes during the second campaign were likely due to the flood wave reversing, or at least reducing, the hydraulic gradient towards the river. This is likely to have been extenuated by the generally low groundwater levels in the aquifer before the event as a result of the drought.

3.7. Tritium Data

Tritium in rivers can have both natural and anthropogenic sources. Current tritium concentrations in rainfall range from 0.5–1.5 Bq/l. Tritium that is found in the River Elbe is predominantly released into the River Vltava from the nuclear power plant in Temelin (Czech Republic), located 25 km NW of České Budějovice. The River Vltava discharges about 200 km downstream of the nuclear power plant into the River Elbe. About 100 km downstream of this conjunction River Elbe reaches the German/Czech border, i.e., the upstream end of the investigated river section (Schmilka).

The tritium concentration in the river water at that upstream point during the first campaign was found to be around 8 Bq/l. Over the following 60 km, the tritium concentration in the river water decreased notably (Figure 13). Since decay, rainfall and discharge of tributaries can be ruled out as reason for the concentration decrease, the decrease can be attributed solely to dilution by the discharge of tritium-free baseflow groundwater into the river. The three groundwater samples that were taken from springs located in the vicinity of the river (but still in a distance that allows excluding any river water influence) revealed tritium activities between 0.9 and 1.1 Bq/l with an average of 1.0 Bq/l.

However, an accurate discharge quantification based on the tritium data alone is difficult. As illustrated in Figure 13, the tritium concentration in the river water samples fluctuates significantly. We explain this fluctuation with a locally incomplete mixing of flowing river water (high in tritium) and locally discharging groundwater (practically tritium-free) within the river water column. In contrast to radon, which was detected from a continuously running water pump stream resulting in integrative values each valid for a whole sub-reach, tritium was measured in discrete 1-litre samples. The effect of incomplete mixing becomes particularly obvious around profile km 33.5 where a notable local drop in the tritium concentration was observed, indicating an unrepresentative high share of tritium-free groundwater in the sample. Besides a locally increased groundwater discharge rate, which is likely in this area because of the increased river water/groundwater interface, this local anomaly can be explained with a significantly poorer mixing of river water and groundwater due to the locally wider and shallower riverbed (cf. Section 3.1). The sample, which was taken close to the riverbank, is hence likely to contain an unrepresentatively high share of groundwater.

Despite these uncertainties, the tritium dataset can still be used as a conservative estimate of groundwater discharge into the river. Using data averaged for the start and end points of the investigated 60 km river section, the tritium concentration drops from around 8.0 ± 0.28 Bq/l to 7.7 ± 0.25 Bq/l, i.e., by 3.8 ± 0.2%. This decrease corresponds theoretically to a 3.9% dilution of the river water with tritium free water. If we assume a tritium concentration of the discharging groundwater of 1.0 Bq/l (as found in the tree sampled springs), the decrease corresponds theoretically to a 4.5% dilution of the river water.

This result comes close to the 3.5% cumulative groundwater discharge resulting from the FINIFLUX model (cf. Section 3.6) and does hence support the results of the radon-based modelling. Still, it has to be kept in mind that the statistical uncertainty of the tritium-based assumption is high because the recorded tritium profile is affected by partly incomplete mixing of river water and groundwater in the stream. It can be stated though, that the tritium results of our survey, besides being consistent with the radon data, are reasonable. The BfG runs a monitoring station at km 58 of the investigated River Elbe profile. At the station, tritium is measured as a monthly pooled sample since the late 1990s. In the period 2018–2019, the monthly tritium concentrations varied between 3.5 ± 0.26 and 12.3 ± 0.85 Bq/l, i.e., in a range that covers our data set. The variation in the monthly tritium level over this two-years-period is due to the fact that the Temelin nuclear power plant releases process water not continuously but in pulses. Unfortunately, no value is available for August 2018 (i.e., for the first sampling campaign) due to the low river water level. However, in September 2018, a value of 6.7 ± 0.48Bq/l was recorded, which comes close to the 8 Bq/l that we detected as input value for the August campaign.

4. Conclusions

Two field campaigns were carried out along a 60 km section of the River Elbe that is characterized by a mountainous and a non-mountainous part. Both surveys took place under hydrological drought conditions reflected by an exceptional low flow situation of the river. The fieldwork and the subsequent data evaluation aimed at (i) localizing groundwater discharge zones into the River Elbe and (ii) quantifying the volume of discharging groundwater (baseflow). The results of the study confirmed:

(1)

The suitability of radon (²²²Rn) as environmental tracer for the evaluation of river water/groundwater (i.e., baseflow) interaction;

(2)

The necessity of a sound groundwater endmember determination for radon;

(3)

The suitability of the FINIFLUX model for groundwater discharge localization and quantification under extreme drought conditions in major streams based on radon data;

(4)

The general applicability of tritium (³H) as supplementary tracer for the evaluation of radon-based results;

(5)

The strong influence of the local geography (geographic gradients, river depth and width) and the prevailing hydrologic conditions (local recharge, river level, drought situation) on location and intensity of groundwater discharge into rivers; and

(6)

The high spatial and temporal variability of groundwater discharge into a major river on the catchment scale.

(7)

That (as revealed by the radon mass-balance modelling) despite groundwater being generally considered a diffusive flux, there are certain river reaches that preferentially receive groundwater discharge. This is likely to be caused by landscape topographic controls such as an increase in the catchment slope that also increases the hydrological gradient towards the river. This can be seen in the case of the investigated river reach in the upper regions of the river.