On the Use of a Real-Time Control Approach for Urban Stormwater Management
Abstract
1. Introduction
1.1. Background
1.2. Real-Time Control Approach
1.3. Aims of the Study
2. Materials and Methods
2.1. Case Study
2.2. Data Analysis
2.3. The Distributed Real-Time Control Approach
2.4. Modeling Scenarios
2.5. Hydrological Performance Indicators
- (1)
- Flood Volume Reduction (FVRn–m) was expressed as the percentage difference between the total Flood Volume (FV) of n and m scenarios:
- (2)
- Hours Flooded Reduction (HFRn–m) was determined as the percentage difference between the Hours Flooded (HF) of n and m scenarios:
- (3)
- The percentage of nodes flooding (NFn) was calculated concerning the total number of nodes (NNtot):
- (4)
- The percentage of conduit surcharge (CSn) was evaluated concerning the total number of conduits (NCtot):
3. Results and Discussion
3.1. Rainfall Events
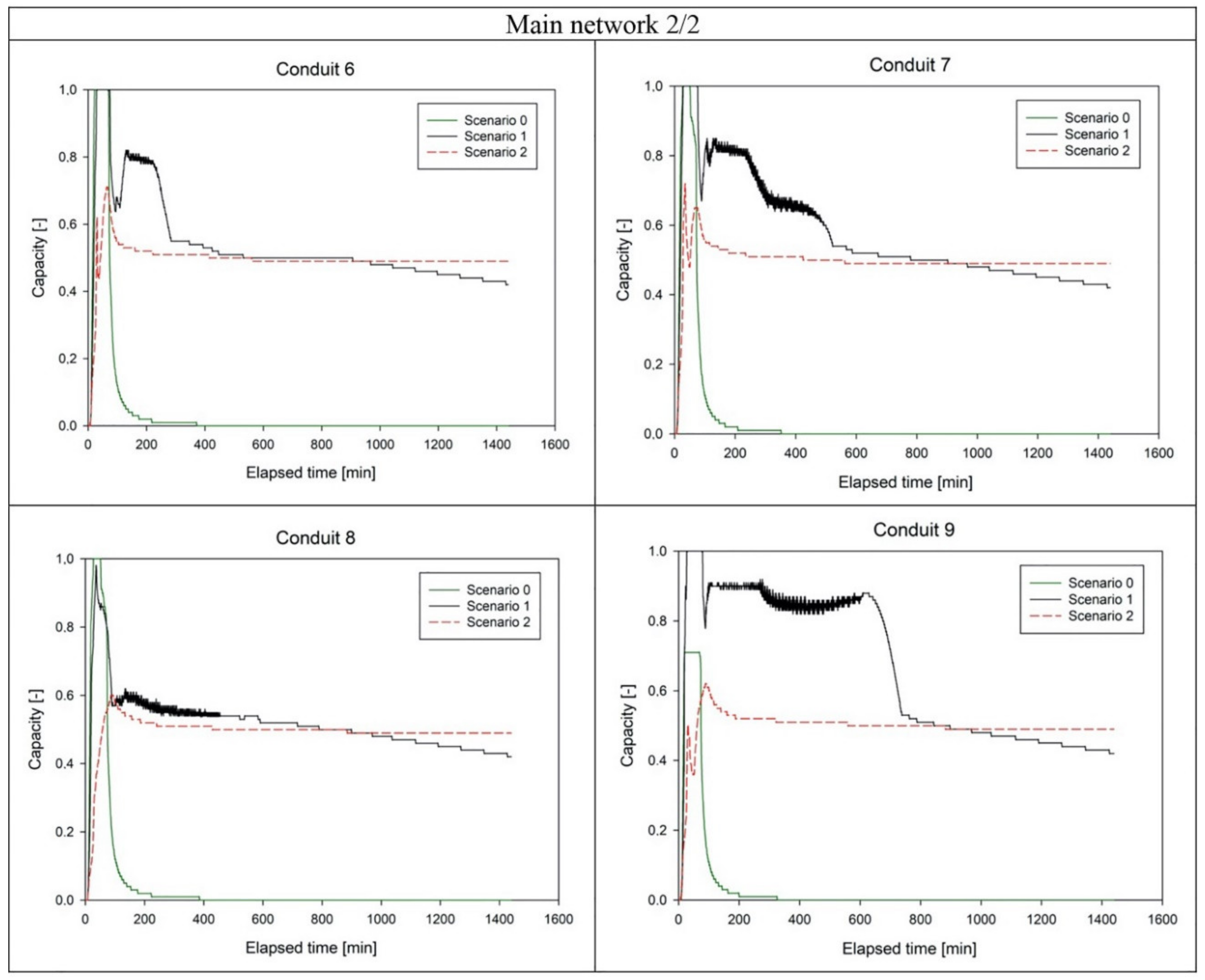
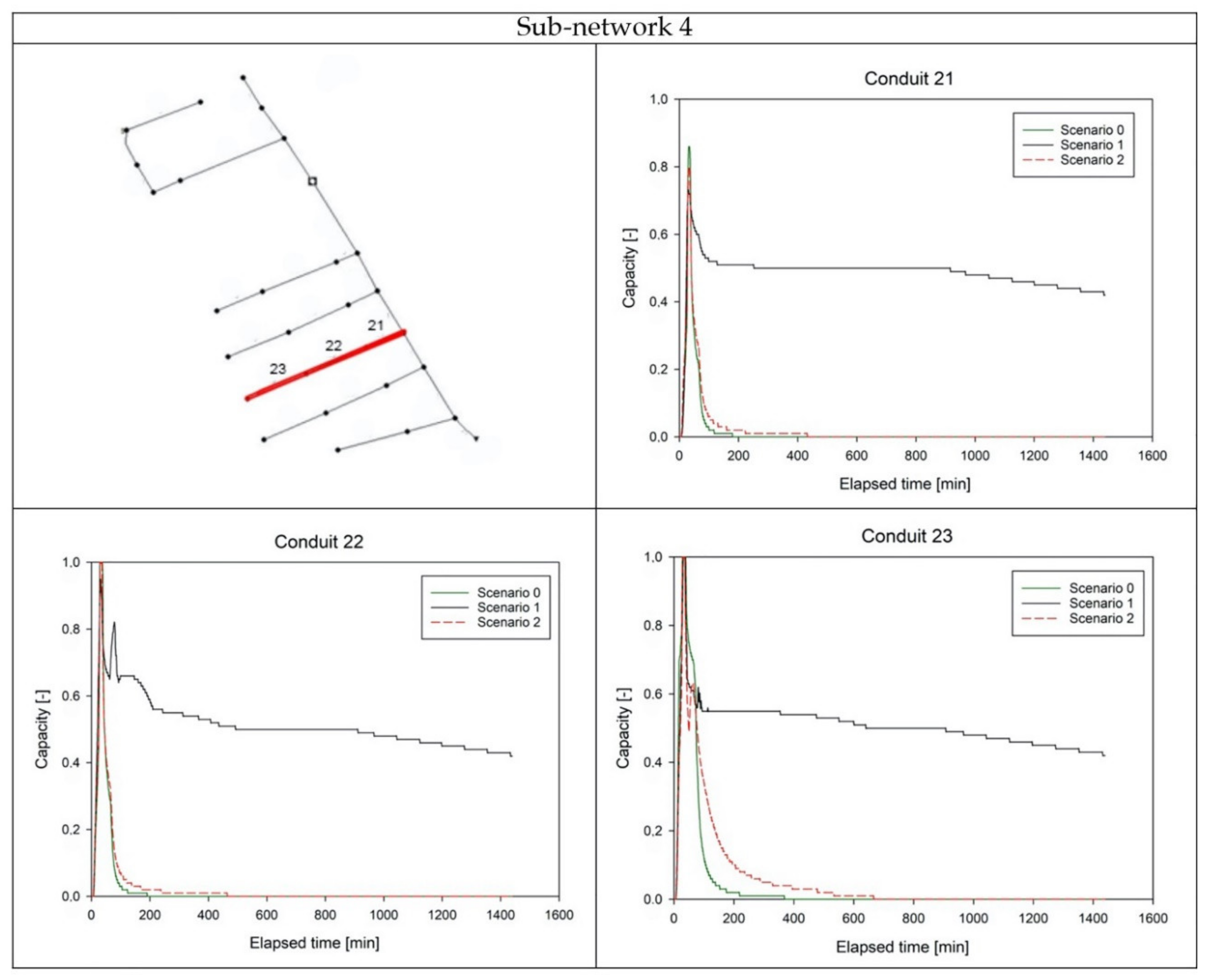
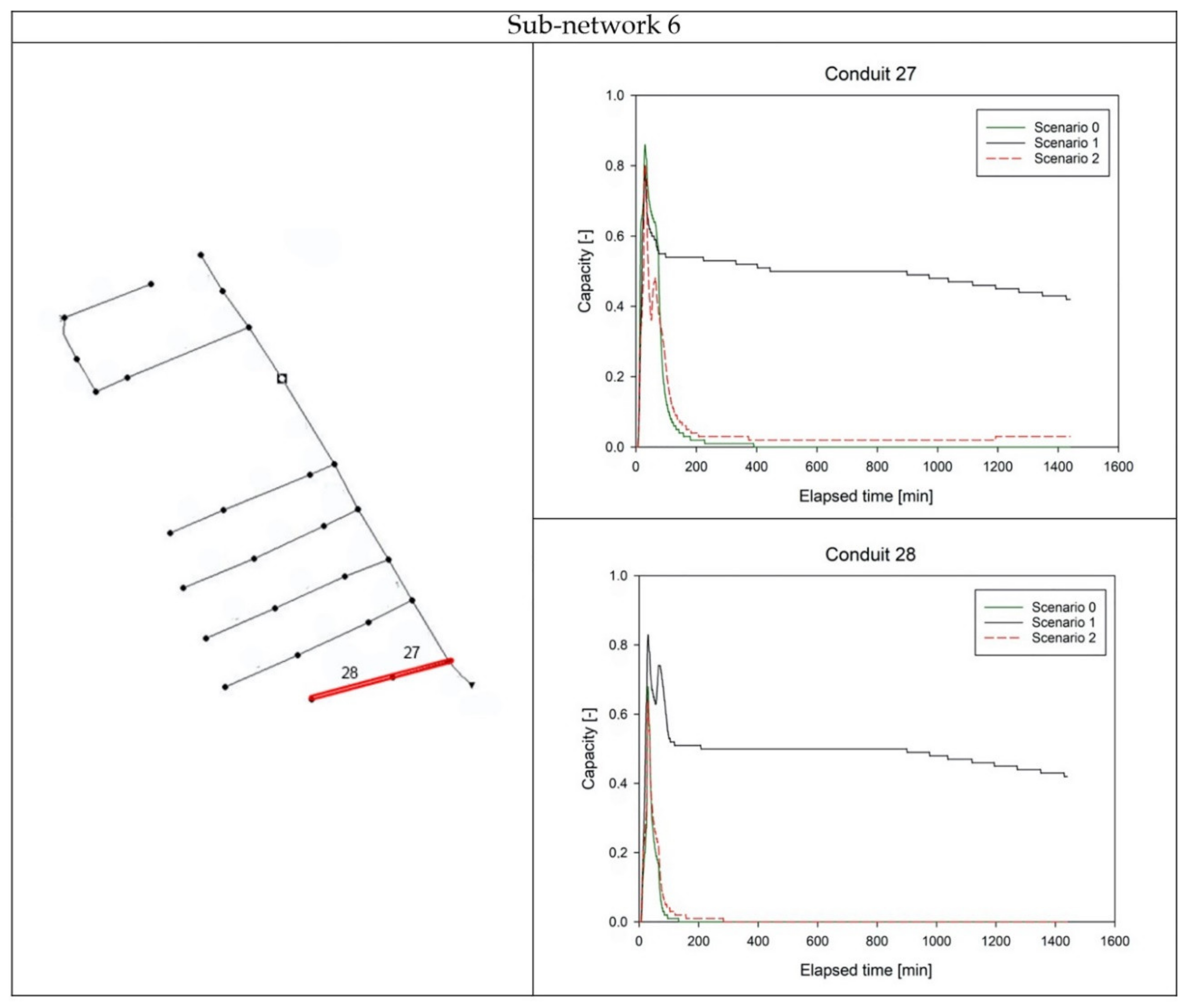
3.2. DRTC Approach Efficiency
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A





References
- United States Environmental Protection Agengy (US EPA). Real Time Control of Urban Drainage Networks; US EPA: Washington, DC, USA, 2006. [Google Scholar]
- Kaźmierczak, A.; Cavan, G. Surface water flooding risk to urban communities: Analysis of vulnerability, hazard and exposure. Landsc. Urban Plan. 2011, 103, 185–197. [Google Scholar] [CrossRef]
- Aronica, G.T.; Palla, A.; Lanza, G.L. Drenaggio delle acque meteoriche e rischio di allagamento in area urbana. In Focus su AcQuE E AmbIEntE uRbAno. Qualità Dell’ambiente Urbano IX Rapporto; ISPRA—Istituto Superiore per la Protezione e la Ricerca Ambientale: Roma, Italy, 2013; pp. 189–195. ISBN 9788844806224. [Google Scholar]
- Piro, P.; Carbone, M. A modelling approach to assessing variations of total suspended solids (tss) mass fluxes during storm events. Hydrol. Process. 2014, 28, 2419–2426. [Google Scholar] [CrossRef]
- Pirouz, B.; Palermo, S.A.; Turco, M.; Piro, P. New Mathematical Optimization Approaches for LID Systems. In NUMTA 2019: Numerical Computations: Theory and Algorithm; Lecture Notes in Computer Science, Volume 11973; Sergeyev, Y., Kvasov, D., Eds.; Spinger: Cham, Switzerland, 2020; pp. 583–595. [Google Scholar] [CrossRef]
- Tebaldi, C.; Hayhoe, K.; Arblaster, J.M.; Meehl, G.A. Going to the Extremes. Clim. Chang. 2006, 79, 185–211. [Google Scholar] [CrossRef]
- Jacobson, C.R. Identification and quantification of the hydrological impacts of imperviousness in urban catchments: A review. J. Environ. Manag. 2011, 92, 1438–1448. [Google Scholar] [CrossRef]
- Palermo, S.A.; Talarico, V.C.; Pirouz, B. Optimizing Rainwater Harvesting Systems for Non-potable Water Uses and Surface Runoff Mitigation. In NUMTA 2019: Numerical Computations: Theory and Algorithm; Lecture Notes in Computer Science, Volume 11973; Sergeyev, Y., Kvasov, D., Eds.; Springer: Cham, Switzerland, 2020; pp. 570–582. [Google Scholar] [CrossRef]
- Pichs Madruga, R.; Seyboth, K.; Eickemeier, P.; Matschoss, P.; Hansen, G.; Kadner, S.; Schlömer, S.; Zwickel, T.; Von Stechow, C. Renewable Energy Sources and Climate Change Mitigation Special Report of the Intergovernmental Panel on Climate Change; Sokona, O.E.Y., Ed.; Cambridge University Press: Cambridge, UK, 2012; ISBN 9781107607101. [Google Scholar]
- Füssel, H.-M.; Jol, A.; Kurnik, B.; Hemming, D. Climate Change, Impacts and Vulnerability in Europe 2012: An Indicator-Based Report; European Environment Agency: Copenhagen, Denmark, 2012; ISBN 9789292133467. [Google Scholar] [CrossRef]
- Starzec, M.; Dziopak, J.; Słyś, D.; Pochwat, K.; Kordana, S. Dimensioning of Required Volumes of Interconnected Detention Tanks Taking into Account the Direction and Speed of Rain Movement. Water 2018, 10, 1826. [Google Scholar] [CrossRef]
- Kordana, S. The identification of key factors determining the sustainability of stormwater systems. E3S Web Conf. 2018, 45, 00033. [Google Scholar] [CrossRef]
- Piro, P.; Turco, M.; Palermo, S.A.; Principato, F.; Brunetti, G. A Comprehensive Approach to Stormwater Management Problems in the Next Generation Drainage Networks. In Internet of Things for Smart Urban Ecosystems; Springer: Cham, Switzerland, 2019; pp. 275–304. [Google Scholar] [CrossRef]
- Pumo, D.; Arnone, E.; Francipane, A.; Caracciolo, D.; Noto, L.V. Potential implications of climate change and urbanization on watershed hydrology. J. Hydrol. 2017, 554, 80–99. [Google Scholar] [CrossRef]
- Berz, G.; Kron, W.; Loster, T.; Rauch, E.; Schimetschek, J.; Schmieder, J.; Siebert, A.; Smolka, A.; Wirtz, A. World map of natural hazards—A global view of the distribution and intensity of significant exposures. Nat. Hazards 2001, 23, 443–465. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Wetherald, R.T.; Dunne, K.A.; Delworth, T.L. Increasing risk of great floods in a changing climate. Nature 2002, 415, 514–517. [Google Scholar] [CrossRef]
- Semadeni-Davies, A.; Hernebring, C.; Svensson, G.; Gustafsson, L.G. The impacts of climate change and urbanisation on drainage in Helsingborg, Sweden: Combined sewer system. J. Hydrol. 2008, 350, 100–113. [Google Scholar] [CrossRef]
- United Nations, Department of Economic and Social Affairs. World Urbanization Prospects The 2018 Revision; United Nations: New York, NY, USA, 2018. [Google Scholar]
- Turco, M.; Brunetti, G.; Palermo, S.A.; Capano, G.; Grossi, G.; Maiolo, M.; Piro, P. On the environmental benefits of a permeable pavement: metals potential removal efficiency and Life Cycle Assessment. Urban Water J. 2020, 1–9. [Google Scholar] [CrossRef]
- Oberascher, M.; Zischg, J.; Palermo, S.A.; Kinzel, C.; Rauch, W.; Sitzenfrei, R. Smart Rain Barrels: Advanced LID Management Through Measurement and Control. In UDM 2018: New Trends in Urban Drainage Modelling; Green Energy and Technology; Mannina, G., Ed.; Springer: Cham, Switzerland, 2019; pp. 777–782. [Google Scholar] [CrossRef]
- Oberascher, M.; Zischg, J.; Kastlunger, U.; Schöpf, M.; Kinzel, C.; Zingerle, C.; Rauch, W.; Sitzenfrei, R. Advanced Rainwater Harvesting through Smart Rain Barrels. In Proceedings of the World Environmental and Water Resources Congress 2019, Pittsburgh, PA, USA, 19–23 May 2019; American Society of Civil Engineers: Reston, VA, USA, 2019; pp. 75–82. [Google Scholar]
- Sadler, J.M.; Goodall, J.L.; Behl, M.; Bowes, B.D.; Morsy, M.M. Exploring real-time control of stormwater systems for mitigating flood risk due to sea level rise. J. Hydrol. 2020, 583, 124571. [Google Scholar] [CrossRef]
- Marchioni, M.; Becciu, G. Experimental results on permeable pavements in Urban areas: A synthetic review. Int. J. Sustain. Dev. Plan. 2015, 10, 806–817. [Google Scholar] [CrossRef]
- Piro, P.; Carbone, M.; Morimanno, F.; Palermo, S.A. Simple flowmeter device for LID systems: From laboratory procedure to full-scale implementation. Flow Meas. Instrum. 2019. [Google Scholar] [CrossRef]
- Weyand, M. Real-time control in combined sewer systems in Germany—Some case studies. Urban Water 2002, 4, 347–354. [Google Scholar] [CrossRef]
- Butler, D.; Schütze, M. Integrating simulation models with a view to optimal control of urban wastewater systems. Environ. Model. Softw. 2005, 20, 415–426. [Google Scholar] [CrossRef]
- Martin, C.; Ruperd, Y.; Legret, M. Urban stormwater drainage management: The development of a multicriteria decision aid approach for best management practices. Eur. J. Oper. Res. 2007, 181, 338–349. [Google Scholar] [CrossRef]
- Turco, M. Modelling the Hydraulic Behaviour of Permeable Pavements through a Reservoir Element Model. In Proceedings of the International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management; SGEM: Sofia, Bulgaria, 2018. [Google Scholar] [CrossRef]
- Carbone, M.; Turco, M.; Nigro, G.; Piro, P. Modeling of hydraulic behaviour of green roof in catchment scale. In Proceedings of the International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management; SGEM: Albena, Bulgaria, 2014. [Google Scholar] [CrossRef]
- Maiolo, M.; Pirouz, B.; Bruno, R.; Palermo, S.A.; Arcuri, N.; Piro, P. The Role of the Extensive Green Roofs on Decreasing Building Energy Consumption in the Mediterranean Climate. Sustainability 2020, 12, 359. [Google Scholar] [CrossRef]
- Brunetti, G.; Papagrigoriou, I.-A.; Stumpp, C. Disentangling model complexity in green roof hydrological analysis: A Bayesian perspective. Water Res. 2020, 182, 115973. [Google Scholar] [CrossRef]
- Pirouz, B.; Arcuri, N.; Pirouz, B.; Palermo, S.A.; Turco, M.; Maiolo, M. Development of an Assessment Method for Evaluation of Sustainable Factories. Sustainability 2020, 12, 1841. [Google Scholar] [CrossRef]
- Bevilacqua, P.; Mazzeo, D.; Arcuri, N. Thermal inertia assessment of an experimental extensive green roof in summer conditions. Build. Environ. 2018, 131, 264–276. [Google Scholar] [CrossRef]
- Schütze, M.; Campisano, A.; Colas, H.; Vanrolleghem, P.; Schilling, W. Real-Time Control of Urban Water Systems. In Proceedings of the International Conference on Pumps, Electromechanical Devices and Systems Applied to Urban Water Management PEDS, Lencia, Spain, 22–25 April 2003. [Google Scholar]
- Schütze, M.; Campisano, A.; Colas, H.; Schilling, W.; Vanrolleghem, P.A. Real time control of urban wastewater systems—Where do we stand today? J. Hydrol. 2004, 299, 335–348. [Google Scholar] [CrossRef]
- Bach, P.M.; Rauch, W.; Mikkelsen, P.S.; McCarthy, D.T.; Deletic, A. A critical review of integrated urban water modelling—Urban drainage and beyond. Environ. Model. Softw. 2014, 54, 88–107. [Google Scholar] [CrossRef]
- Beeneken, T.; Erbe, V.; Messmer, A.; Reder, C.; Rohlfing, R.; Scheer, M.; Schuetze, M.; Schumacher, B.; Weilandt, M.; Weyand, M. Real time control (RTC) of urban drainage systems—A discussion of the additional efforts compared to conventionally operated systems. Urban Water J. 2013, 10, 293–299. [Google Scholar] [CrossRef]
- Dirckx, G.; Schütze, M.; Kroll, S.; Thoeye, C.; De Gueldre, G.; Van De Steene, B. RTC versus static solutions to mitigate CSO’s impact. In Proceedings of the 12nd International Conference on Urban Drainage, Porto Alegre, Brazil, 10–15 September 2011. [Google Scholar]
- Fradet, O.; Pleau, M.; Marcoux, C. Reducing CSOs and giving the river back to the public: Innovative combined sewer overflow control and riverbanks restoration of the St Charles River in Quebec City. Water Sci. Technol. 2011, 63, 331–338. [Google Scholar] [CrossRef]
- Rauch, W.; Bertrand-Krajewski, J.-L.; Krebs, P.; Mark, O.; Schilling, W.; Schütze, M.; Vanrolleghem, P.A. Deterministic modelling of integrated urban drainage systems. Water Sci. Technol. 2002, 45, 81–94. [Google Scholar] [CrossRef]
- Vezzaro, L.; Grum, M. A generalised Dynamic Overflow Risk Assessment (DORA) for Real Time Control of urban drainage systems. J. Hydrol. 2014, 515, 292–303. [Google Scholar] [CrossRef]
- Thorndahl, S. Radar Based Flow and Water Level Forecasting in Sewer Systems: A danisk case study. In Urbanrain09: 8th International Workshop on Precipitation in Urban Areas: St. Moritz, Switzerland; Eidgenössische Technische Hochschule Zürich, Laboratorium für Lebensmittel-Verfahrenstechnik: Zürich, Switzerland, 2009; ISBN 9783909386277. [Google Scholar]
- Campisano, A.; Cabot Ple, J.; Muschalla, D.; Pleau, M.; Vanrolleghem, P.A. Potential and limitations of modern equipment for real time control of urban wastewater systems. Urban Water J. 2013, 10, 300–311. [Google Scholar] [CrossRef]
- Schilling, W.; Andersson, B.; Nyberg, U.; Aspegren, H.; Rauch, W.; Harremoës, P. Real time control of wastewater systems. J. Hydraul. Res. 1996, 34, 785–797. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model, Quality Assurance Report: Dynamic Wave Flow Routing; US Environmental Protection Agency, Office of Research and Development, National Risk Management Research Laboratory: Cincinnati, OH, USA, 2006. [Google Scholar]
- Erbe, V.; Schütze, M.; Haas, U. Application of A Guideline Document for Sewer System Real Time Control; Novatech: Lyon, France, 2007. [Google Scholar]
- Pleau, M.; Colas, H.; Lavallee, P.; Pelletier, G.; Bonin, R. Global optimal real-time control of the Quebec urban drainage system. Environ. Model. Softw. 2005, 20, 401–413. [Google Scholar] [CrossRef]
- Darsono, S.; Labadie, J.W. Neural-optimal control algorithm for real-time regulation of in-line storage in combined sewer systems. Environ. Model. Softw. 2007, 22, 1349–1361. [Google Scholar] [CrossRef]
- Garofalo, G.; Giordano, A.; Piro, P.; Spezzano, G.; Vinci, A. A distributed real-time approach for mitigating CSO and flooding in urban drainage systems. J. Netw. Comput. Appl. 2017, 78, 30–42. [Google Scholar] [CrossRef]
- Kändler, N.; Annus, I.; Vassiljev, A.; Puust, R. Real time controlled sustainable urban drainage systems in dense urban areas. J. Water Supply Res. Technol. 2020, 69, 238–247. [Google Scholar] [CrossRef]
- Aulinas, M.; Nieves, J.C.; Cortés, U.; Poch, M. Supporting decision making in urban wastewater systems using a knowledge-based approach. Environ. Model. Softw. 2011, 26, 562–572. [Google Scholar] [CrossRef]
- Klepiszewski, K.; Schmitt, T.G. Comparison of conventional rule based flow control with control processes based on fuzzy logic in a combined sewer system. Water Sci. Technol. 2002, 46, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Shishegar, S.; Duchesne, S.; Pelletier, G. An integrated optimization and rule-based approach for predictive real time control of urban stormwater management systems. J. Hydrol. 2019, 577, 124000. [Google Scholar] [CrossRef]
- Regneri, M.; Klepiszewski, K.; Seiffert, S.; Vanrolleghem, P.A.; Ostrowski, M. Transport Sewer Model Calibration by Experimental Generation of Discrete Discharges from Individual CSO Structures. In Proceedings of the 6th International Congress on Environmental Modelling and Software, Leipzig, Germany, 1–5 July 2012. [Google Scholar]
- Tang, W.; Wang, Z.; Feng, Q.; Wang, M. Application of fuzzy expert control to APMP Pulping Wastewater treatment process of aerobic. In Proceedings of the 2010 IEEE International Conference on Mechatronics and Automation, Xi’an, China, 4–7 August 2010; pp. 339–344. [Google Scholar]
- Seggelke, K.; Löwe, R.; Beeneken, T.; Fuchs, L. Implementation of an integrated real-time control system of sewer system and waste water treatment plant in the city of Wilhelmshaven. Urban Water J. 2013, 10, 330–341. [Google Scholar] [CrossRef]
- Chiang, Y.M.; Chang, L.C.; Tsai, M.J.; Wang, Y.F.; Chang, F.J. Auto-control of pumping operations in sewerage systems by rule-based fuzzy neural networks. Hydrol. Earth Syst. Sci. 2011, 15, 185–196. [Google Scholar] [CrossRef]
- Tagherouit, W.B.; Bennis, S.; Bengassem, J. A Fuzzy Expert System for Prioritizing Rehabilitation of Sewer Networks. Comput. Civ. Infrastruct. Eng. 2011, 26, 146–152. [Google Scholar] [CrossRef]
- Fuchs, L.; Beeneken, T.; Spönemann, P.; Scheffer, C. Model based real-time control of sewer system using fuzzy-logic. Water Sci. Technol. 1997, 36, 343–347. [Google Scholar] [CrossRef]
- Mounce, S.R.; Shepherd, W.; Ostojin, S.; Abdel-Aal, M.; Schellart, A.N.A.; Shucksmith, J.D.; Tait, S.J. Optimisation of a fuzzy logic-based local real-time control system for mitigation of sewer flooding using genetic algorithms. J. Hydroinf. 2020. [Google Scholar] [CrossRef]
- Lemos, J.M.; Pinto, L.F. Distributed Linear-Quadratic Control of Serially Chained Systems: Application to a Water Delivery Canal [Applications of Control]. IEEE Control Syst. Mag. 2012, 32, 26–38. [Google Scholar] [CrossRef]
- Muschalla, D. Optimization of integrated urban wastewater systems using multi-objective evolution strategies. Urban Water J. 2008, 5, 59–67. [Google Scholar] [CrossRef]
- Cho, J.H.; Seok Sung, K.; Ryong Ha, S. A river water quality management model for optimising regional wastewater treatment using a genetic algorithm. J. Environ. Manag. 2004, 73, 229–242. [Google Scholar] [CrossRef]
- Fu, G.; Butler, D.; Khu, S.-T. Multiple objective optimal control of integrated urban wastewater systems. Environ. Model. Softw. 2008, 23, 225–234. [Google Scholar] [CrossRef]
- Barreto, W.; Vojinovic, Z.; Price, R.; Solomatine, D. Multiobjective Evolutionary Approach to Rehabilitation of Urban Drainage Systems. J. Water Resour. Plan. Manag. 2010, 136, 547–554. [Google Scholar] [CrossRef]
- Ngamalieu-Nengoue, U.A.; Iglesias-Rey, P.L.; Martínez-Solano, F.J. Urban Drainage Networks Rehabilitation Using Multi-Objective Model and Search Space Reduction Methodology. Infrastructures 2019, 4, 35. [Google Scholar] [CrossRef]
- Ocampo-Martinez, C. Model Predictive Control of Wastewater Systems; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Toro, R.; Ocampo-Martínez, C.; Logist, F.; Van Impe, J.; Puig, V. Tuning of predictive controllers for drinking water networked systems. IFAC Proc. Vol. 2011, 44, 14507–14512. [Google Scholar] [CrossRef]
- Xu, M.; van Overloop, P.J.; van de Giesen, N.C. On the study of control effectiveness and computational efficiency of reduced Saint-Venant model in model predictive control of open channel flow. Adv. Water Resour. 2011, 34, 282–290. [Google Scholar] [CrossRef]
- Zamora, C.; Giraldo, J.M.; Leirens, S. Model predictive control of water transportation networks. In Proceedings of the 2010 IEEE ANDESCON, Bogota, Colombia, 15–17 September 2010. [Google Scholar]
- Ocampo-Martinez, C.; Ingimundarson, A.; Bemporad, A.; Puig, V. Suboptimal Hybrid Model Predictive Control: Application to Sewer Networks. IFAC Proc. Vol. 2008, 41, 10021–10026. [Google Scholar] [CrossRef]
- Van Heeringen, K.-J.; Gooijer, J.; Schwanenberg, D. Practical application of drainage system control by using MPC in Noorderzijlvest. In Proceedings of the EGU General Assembly, Vienna, Austria, 7–12 April 2013; Volume 15. [Google Scholar]
- Ocampo-Martinez, C.; Puig, V.; Grosso, J.M.; Montes-de-Oca, S. Multi-layer Decentralized MPC of Large-scale Networked Systems. Intell. Syst. Control Autom. Sci. Eng. 2014, 69, 495–515. [Google Scholar] [CrossRef]
- Leirens, S.; Zamora, C.; Negenborn, R.R.; De Schutter, B. Coordination in urban water supply networks using distributed model predictive control. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 3957–3962. [Google Scholar]
- Negenborn, R.R.; van Overloop, P.J.; Keviczky, T.; De Schutter, B. Distributed model predictive control of irrigation canals. Netw. Heterog. Media 2009, 4, 359–380. [Google Scholar] [CrossRef]
- Lihui, C.; Yugeng, X.; Dewei, L. Aggregation-based model predictive control of open channel networks. In Proceedings of the 29th Chinese Control Conference, Beijing, China, 29–31 July 2010. [Google Scholar]
- Malaterre, P.O.; Rodellar, J. Multivariable predictive control of irrigation canals. Design and evaluation on a 2-pool model. In Proceedings of the International Workshop on Regulation of Irrigation Canals: State of the Art of Research and Applications, Marrakesh, Morroco, 22–24 April 1997. [Google Scholar]
- Puig, V.; Cembrano, G.; Romera, J.; Quevedo, J.; Aznar, B.; Ramón, G.; Cabot, J. Predictive optimal control of sewer networks using CORAL tool: application to Riera Blanca catchment in Barcelona. Water Sci. Technol. 2009, 60, 869–878. [Google Scholar] [CrossRef] [PubMed]
- Ramirez-Llanos, E.; Quijano, N. A population dynamics approach for the water distribution problem. Int. J. Control 2010, 83, 1947–1964. [Google Scholar] [CrossRef]
- Barreiro-Gomez, J.; Obando, G.; Riano-Briceno, G.; Quijano, N.; Ocampo-Martinez, C. Decentralized Control for Urban Drainage Systems via population dynamics: Bogotá case study. In Proceedings of the 2015 European Control Conference, Linz, Austria, 15–17 July 2015; pp. 2426–2431. [Google Scholar]
- Messmer, A.; Schütze, M.; Ogurek, M. A Demonstration Software Tool For Real Time Control Of Urban Drainage Systems. In Proceedings of the 11th International Conference on Urban Drainage, Edinburgh, UK, 31 August–5 September 2008. [Google Scholar]
- Riaño-Briceño, G.; Barreiro-Gomez, J.; Ramirez-Jaime, A.; Quijano, N.; Ocampo-Martinez, C. MatSWMM—An open-source toolbox for designing real-time control of urban drainage systems. Environ. Model. Softw. 2016, 83, 143–154. [Google Scholar] [CrossRef]
- Li, J.; Burian, S.; Oroza, C. Exploring the potential for simulating system-level controlled smart stormwater system. In Proceedings of the World Environmental and Water Resources Congress 2019: Water Wastewater, and Stormwater; Urban Water Resources; and Municipal Water Infrastructure, Pittsburgh, PA, USA, 19–23 May 2019; pp. 46–56. [Google Scholar]
- Yuan, J.M.; Tilford, K.A.; Jiang, H.Y.; Cluckie, I.D. Real-time urban drainage system modelling using weather radar rainfall data. Phys. Chem. Earth Part B 1999, 24, 915–919. [Google Scholar] [CrossRef]
- Duchesne, S.; Mailhot, A.; Dequidt, E.; Villeneuve, J.-P. Mathematical modeling of sewers under surcharge for real time control of combined sewer overflows. Urban Water 2001, 3, 241–252. [Google Scholar] [CrossRef]
- Giordano, A.; Spezzano, G.; Vinci, A.; Garofalo, G.; Piro, P. A cyber-physical system for distributed real-time control of urban drainage networks in smart cities. In IDCS 2014: Internet and Distributed Computing Systems; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Palermo, S.A.; Talarico, V.C.; Turco, M. On the LID systems effectiveness for urban stormwater management: case study in Southern Italy. IOP Conf. Ser. 2020, 410, 012012. [Google Scholar] [CrossRef]
- García-Marín, A.P.; Ayuso-Muñoz, J.L.; Jiménez-Hornero, F.J.; Estévez, J. Selecting the best IDF model by using the multifractal approach. Hydrol. Process. 2013, 27, 433–443. [Google Scholar] [CrossRef]
- Afrin, S.; Islam, M.M.; Rahman, M.M. Development of IDF Curve for Dhaka City Based on Scaling Theory under Future Precipitation Variability Due to Climate Change. Int. J. Environ. Sci. Dev. 2015. [Google Scholar] [CrossRef]
- Ewea, H.A.; Elfeki, A.M.; Al-Amri, N.S. Development of intensity–duration–frequency curves for the Kingdom of Saudi Arabia. Geomatics, Nat. Hazards Risk 2017, 8, 570–584. [Google Scholar] [CrossRef]
- De Paola, F.; Giugni, M.; Topa, M.E.; Bucchignani, E. Intensity-Duration-Frequency (IDF) rainfall curves, for data series and climate projection in African cities. SpringerPlus 2014. [Google Scholar] [CrossRef] [PubMed]
- Arpacal. 2020. Available online: http://www.cfd.calabria.it/index.php/dati-stazioni/dati-storici (accessed on 12 June 2020).
- Keifer, C.; Chu, H.H. Synthetic Storm Pattern for Drainage Design. J. Hydraul. Div. 1957, 83, 1–25. [Google Scholar]
- Voyde, E.; Fassman, E.; Simcock, R. Hydrology of an extensive living roof under sub-tropical climate conditions in Auckland, New Zealand. J. Hydrol. 2010, 394, 384–395. [Google Scholar] [CrossRef]
- Stovin, V.; Vesuviano, G.; Kasmin, H. The hydrological performance of a green roof test bed under UK climatic conditions. J. Hydrol. 2012, 414, 148–161. [Google Scholar] [CrossRef]
- Palermo, S.A.; Turco, M.; Principato, F.; Piro, P. Hydrological effectiveness of an extensive green roof in Mediterranean climate. Water 2019, 11, 1378. [Google Scholar] [CrossRef]
- Bonabeau, E.; Dorigo, M.; Theraulaz, G. Swarm Intelligence: From Natural to Artificial Systems; Oxford University Press: Oxford, UK, 1999; Volume 4, ISBN 0195131592. [Google Scholar]
- Jelasity, M.; Montresor, A.; Babaoglu, O. Gossip-based aggregation in large dynamic networks. ACM Trans. Comput. Syst. 2005, 23, 219–252. [Google Scholar] [CrossRef]
- Cronshey, R. Urban Hydrology for Small Watersheds; US Department of Agriculture: Washington, DC, USA, 1986. [Google Scholar]





| No. | Date | PD | D | Max i | Mean i | |
|---|---|---|---|---|---|---|
| (day/month/year) | (hour:minute) | (mm) | (h) | (mm/h) | (mm/h) | |
| 1 | 04/05/2019 | 08:00 | 31.4 | 6.58 | 24 | 4.8 |
| 2 | 06/05/2019 | 06:00 | 4.8 | 1.58 | 9.6 | 3.0 |
| 3 | 12/05/2019 | 05:00 | 2.8 | 0.92 | 4.8 | 3.0 |
| 4 | 13/05/2019 | 00:00 | 16.2 | 1.5 | 43.2 | 10.8 |
| 5 | 15/05/2019 | 23:00 | 8.8 | 2.0 | 21.6 | 4.4 |
| 6 | 28/05/2019 | 02:00 | 9.4 | 2.5 | 21.6 | 3.8 |
| 7 | 01/06/2019 | 01:00 | 7.2 | 2.0 | 7.2 | 3.6 |
| 8 | 16/07/2019 | 01:00 | 31.0 | 2.08 | 57.6 | 14.9 |
| 9 | 02/09/2019 | 18:00 | 13.2 | 0.83 | 50.4 | 15.9 |
| 10 | 08/09/2019 | 11:00 | 21.6 | 1.25 | 45.6 | 17.3 |
| 11 | 19/09/2019 | 13:00 | 7.8 | 1.08 | 33.6 | 7.2 |
| 12 | 24/09/2019 | 02:00 | 4.0 | 0.5 | 4.8 | 8.0 |
| 13 | 26/09/2019 | 14:00 | 14.6 | 1.66 | 52.8 | 8.8 |
| 14 | 03/10/2019 | 04:00 | 10 | 1.92 | 16.8 | 5.2 |
| 15 | 05/10/2019 | 13:00 | 17.4 | 3.42 | 16.8 | 5.1 |
| 16 | 07/10/2019 | 06:00 | 40.6 | 3.75 | 76.8 | 10.8 |
| 17 | 16/10/2019 | 08:00 | 4.2 | 0.33 | 28.8 | 12.7 |
| 18 | 31/10/2019 | 19:00 | 4.2 | 1.25 | 4.8 | 3.4 |
| 19 | 04/11/2019 | 01:00 | 11.4 | 2.42 | 24.0 | 4.7 |
| 20 | 06/11/2019 | 13:00 | 33.2 | 6.58 | 21.6 | 5.0 |
| 21 | 09/11/2019 | 07:00 | 32.2 | 5.17 | 31.2 | 6.2 |
| 22 | 11/11/2019 | 19:00 | 17.00 | 4.08 | 26.4 | 4.2 |
| 23 | 13/11/2019 | 00:00 | 21.0 | 3.42 | 31.2 | 6.1 |
| 24 | 17/11/2019 | 07:00 | 34.0 | 4.17 | 43.2 | 8.2 |
| 25 | 19/11/2019 | 18:00 | 24.6 | 4.75 | 19.2 | 5.2 |
| 26 | 24/11/2019 | 07:00 | 74.6 | 12.25 | 33.6 | 6.1 |
| 27 | 28/11/2019 | 05:00 | 16.2 | 2.17 | 38.4 | 7.5 |
| 28 | 06/12/2019 | 04:00 | 3.4 | 1.25 | 4.8 | 2.7 |
| 29 | 07/12/2019 | 01:00 | 7.4 | 0.75 | 21.6 | 9.9 |
| 30 | 09/12/2019 | 12:00 | 18.4 | 3.67 | 9.6 | 5.0 |
| 31 | 12/12/2019 | 02:00 | 42.2 | 8.83 | 36.0 | 4.8 |
| 32 | 20/12/2019 | 03:00 | 3.2 | 0.92 | 7.2 | 3.5 |
| 33 | 21/12/2019 | 08:00 | 12.2 | 3.33 | 7.2 | 3.7 |
| 34 | 22/12/2019 | 00:00 | 12.4 | 3.08 | 12 | 4.0 |
| 35 | 25/12/2019 | 02:00 | 5.2 | 1.42 | 7.2 | 3.7 |
| 36 | 18/01/2020 | 10:00 | 11.0 | 24.0 | 16.8 | 0.5 |
| 37 | 29/01/2020 | 20:00 | 3.4 | 1.0 | 16.8 | 3.4 |
| 38 | 02/02/2020 | 03:00 | 2.8 | 1.08 | 4.8 | 2.6 |
| 39 | 05/02/2020 | 02:00 | 2.4 | 0.58 | 12.0 | 4.1 |
| 40 | 10/02/2020 | 07:00 | 4.2 | 1.67 | 4.8 | 2.5 |
| 41 | 14/02/2020 | 12:00 | 5.8 | 1.08 | 12.0 | 5.4 |
| 42 | 20/02/2020 | 00:00 | 4.8 | 0.75 | 19.2 | 6.4 |
| 43 | 28/02/2020 | 02:00 | 7.0 | 1.83 | 14.4 | 3.8 |
| 44 | 03/03/2020 | 02:00 | 21.0 | 5.67 | 21.6 | 3.7 |
| 45 | 04/03/2020 | 20:00 | 3.6 | 0.5 | 9.6 | 7.2 |
| 46 | 07/03/2020 | 11:00 | 16.6 | 4.33 | 9.6 | 3.8 |
| 47 | 22/03/2020 | 10:00 | 4.0 | 1.5 | 4.8 | 2.7 |
| 48 | 25/03/2020 | 04:00 | 105.2 | 24.5 | 19.2 | 4.3 |
| 49 | 01/04/2020 | 04:00 | 8.0 | 1.33 | 12.0 | 6.0 |
| 50 | 03/04/2020 | 06:00 | 6.2 | 2.25 | 4.8 | 2.8 |
| 51 | 20/04/2020 | 02:00 | 15.6 | 5.33 | 7.2 | 2.9 |
| 52 | 21/04/2020 | 22:00 | 47.6 | 9.08 | 36.0 | 5.2 |
| 53 | 19/05/2020 | 15:00 | 4.2 | 1.58 | 4.8 | 2.7 |
| 54 | 20/05/2020 | 11:00 | 32.2 | 3.58 | 31.2 | 9.0 |
| Maximum | 105.2 | 24.5 | 76.8 | 17.3 | ||
| Minimum | 2.4 | 0.33 | 4.8 | 0.5 | ||
| Mean | 17.1 | 3.6 | 21.4 | 5.8 | ||
| Sum | 923.4 | 195.05 | ||||
| No. | Date | PD | D | Max i | Mean i |
|---|---|---|---|---|---|
| (day/month/year) | (mm) | (h) | (mm/h) | (mm/h) | |
| 1 | 13/05/2019 | 16.2 | 1.5 | 43.2 | 10.8 |
| 2 | 16/07/2019 | 31 | 2.08 | 57.6 | 14.9 |
| 3 | 08/09/2019 | 21.6 | 1.25 | 45.6 | 17.3 |
| 4 | 07/10/2019 | 40.6 | 3.75 | 76.8 | 10.8 |
| 5 | 17/11/2019 | 34 | 4.17 | 43.2 | 8.2 |
| 6 | 24/11/2019 | 74.6 | 12.25 | 33.6 | 6.1 |
| 7 | 20/05/2020 | 32.2 | 3.58 | 31.2 | 9 |
| RP = 5 Years | RP = 10 Years | RP = 20 Years | |||||||
|---|---|---|---|---|---|---|---|---|---|
| S0 | S1 | S2 | S0 | S1 | S2 | S0 | S1 | S2 | |
| NF (-) | 12 | 6 | 5 | 12 | 8 | 7 | 12 | 8 | 7 |
| HF (h) | 3.87 | 1.07 | 0.49 | 4.43 | 1.63 | 0.96 | 4.89 | 2.09 | 1.13 |
| CS (-) | 19 | 8 | 7 | 19 | 10 | 9 | 19 | 12 | 9 |
| FV (106 L) | 0.88 | 0.19 | 0.04 | 1.08 | 0.33 | 0.09 | 1.28 | 0.49 | 0.14 |
| RP | FVR (%) | ||
|---|---|---|---|
| FVR0–1 | FVR0–2 | FVR1–2 | |
| 5 years | 78.41 | 95.45 | 78.95 |
| 10 years | 69.44 | 91.67 | 72.73 |
| 20 years | 61.72 | 89.06 | 71.43 |
| RP | HFR (%) | ||
|---|---|---|---|
| HFR0–1 | HFR0–2 | HFR1–2 | |
| 5 years | 72.35 | 87.34 | 54.21 |
| 10 years | 63.21 | 78.33 | 41.1 |
| 20 years | 57.26 | 76.89 | 45.93 |
| RP | NF (%) | ||
|---|---|---|---|
| NF 0 | NF 1 | NF 2 | |
| 5 years | 41.38 | 20.69 | 17.24 |
| 10 years | 41.38 | 27.59 | 24.14 |
| 20 years | 41.38 | 27.59 | 24.14 |
| RP | CS (%) | ||
|---|---|---|---|
| CS 0 | CS 1 | CS 2 | |
| 5 years | 67.86 | 28.57 | 25.00 |
| 10 years | 67.86 | 35.71 | 32.14 |
| 20 years | 67.86 | 42.86 | 32.14 |
| No. | NF (-) | HF (-) | FV (106 L) | CS (-) | ||||
|---|---|---|---|---|---|---|---|---|
| S0 | S2 | S0 | S2 | S0 | S2 | S0 | S2 | |
| 1 | 5 | 0 | 1.55 | 0.00 | 0.14 | 0.00 | 14 | 1 |
| 2 | 8 | 1 | 5.62 | 0.01 | 0.96 | 0.00 | 15 | 5 |
| 3 | 6 | 0 | 3.85 | 0.00 | 0.35 | 0.00 | 14 | 1 |
| 4 | 4 | 0 | 1.55 | 0.00 | 0.10 | 0.00 | 14 | 1 |
| 5 | 6 | 0 | 4.22 | 0.00 | 0.40 | 0.00 | 14 | 1 |
| 6 | 4 | 0 | 1.56 | 0.00 | 0.2 | 0.00 | 14 | 1 |
| 7 | 6 | 0 | 2.94 | 0.00 | 0.26 | 0.00 | 14 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maiolo, M.; Palermo, S.A.; Brusco, A.C.; Pirouz, B.; Turco, M.; Vinci, A.; Spezzano, G.; Piro, P. On the Use of a Real-Time Control Approach for Urban Stormwater Management. Water 2020, 12, 2842. https://doi.org/10.3390/w12102842
Maiolo M, Palermo SA, Brusco AC, Pirouz B, Turco M, Vinci A, Spezzano G, Piro P. On the Use of a Real-Time Control Approach for Urban Stormwater Management. Water. 2020; 12(10):2842. https://doi.org/10.3390/w12102842
Chicago/Turabian StyleMaiolo, Mario, Stefania Anna Palermo, Anna Chiara Brusco, Behrouz Pirouz, Michele Turco, Andrea Vinci, Giandomenico Spezzano, and Patrizia Piro. 2020. "On the Use of a Real-Time Control Approach for Urban Stormwater Management" Water 12, no. 10: 2842. https://doi.org/10.3390/w12102842
APA StyleMaiolo, M., Palermo, S. A., Brusco, A. C., Pirouz, B., Turco, M., Vinci, A., Spezzano, G., & Piro, P. (2020). On the Use of a Real-Time Control Approach for Urban Stormwater Management. Water, 12(10), 2842. https://doi.org/10.3390/w12102842











