Analysis of the Uncertainty in Estimates of Manning’s Roughness Coefficient and Bed Slope Using GLUE and DREAM
Abstract
1. Introduction
2. Materials and Methods
2.1. Calibration
2.1.1. GLUE
2.1.2. DREAM
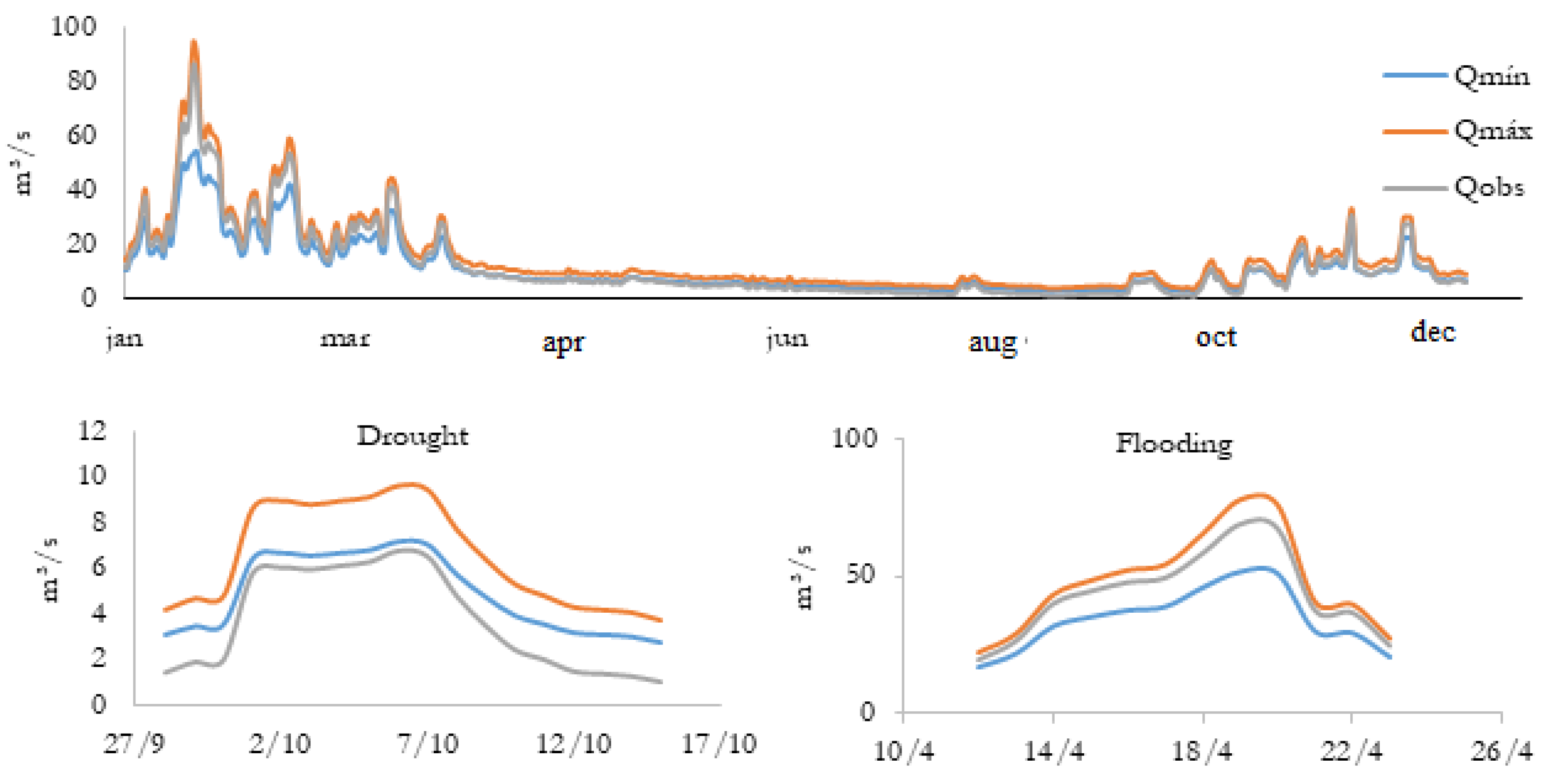
2.2. Validation and Uncertainty Quantification
3. Results and Discussion
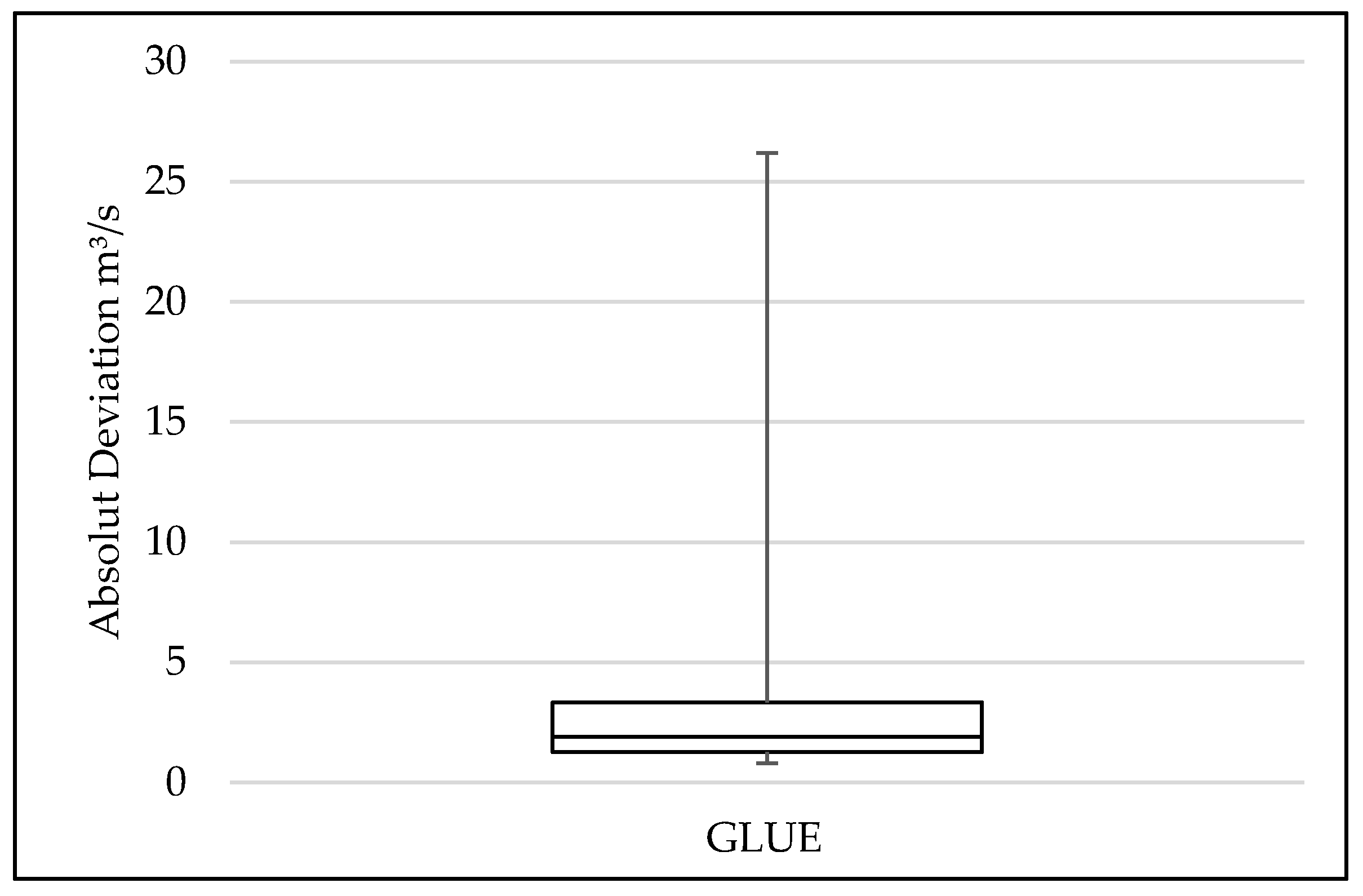
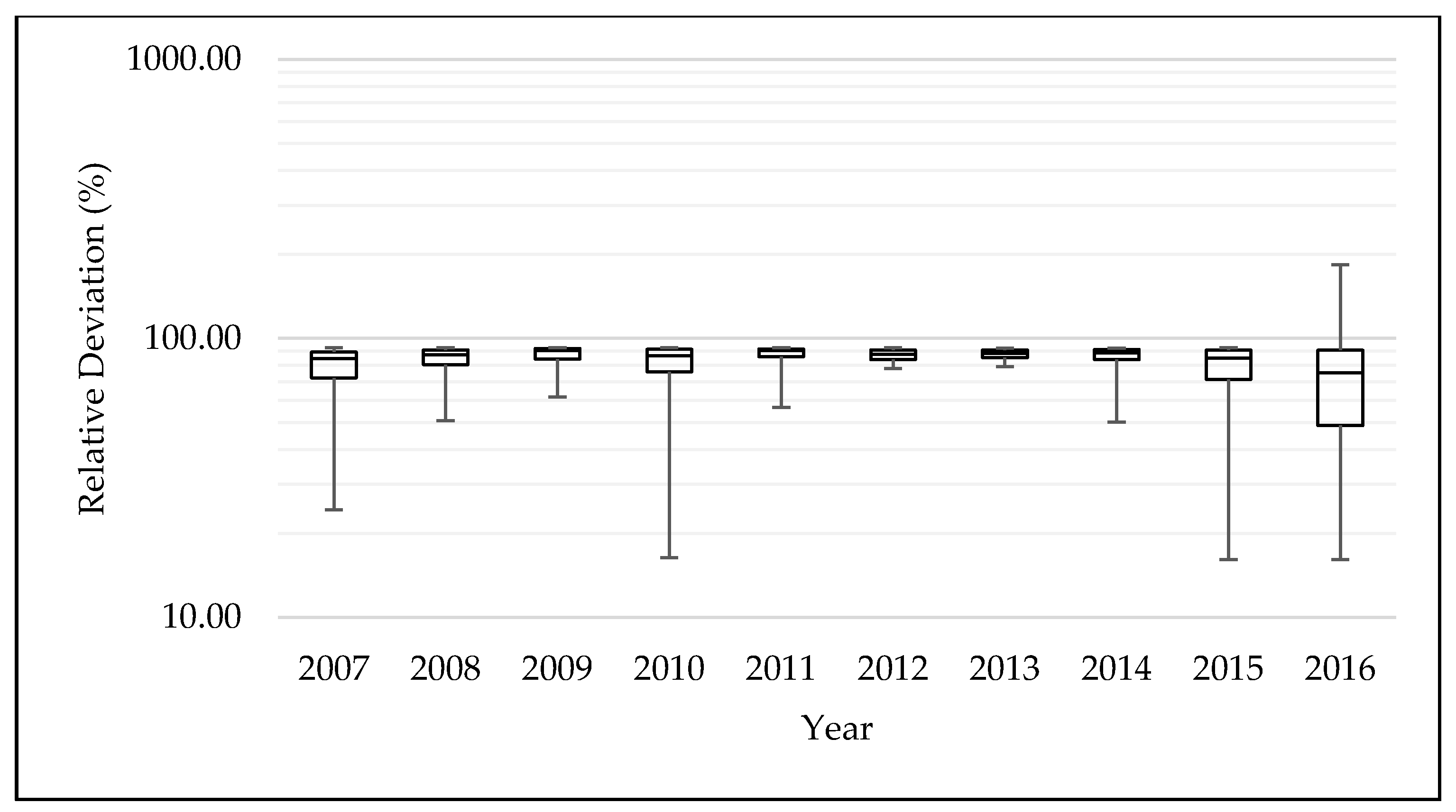
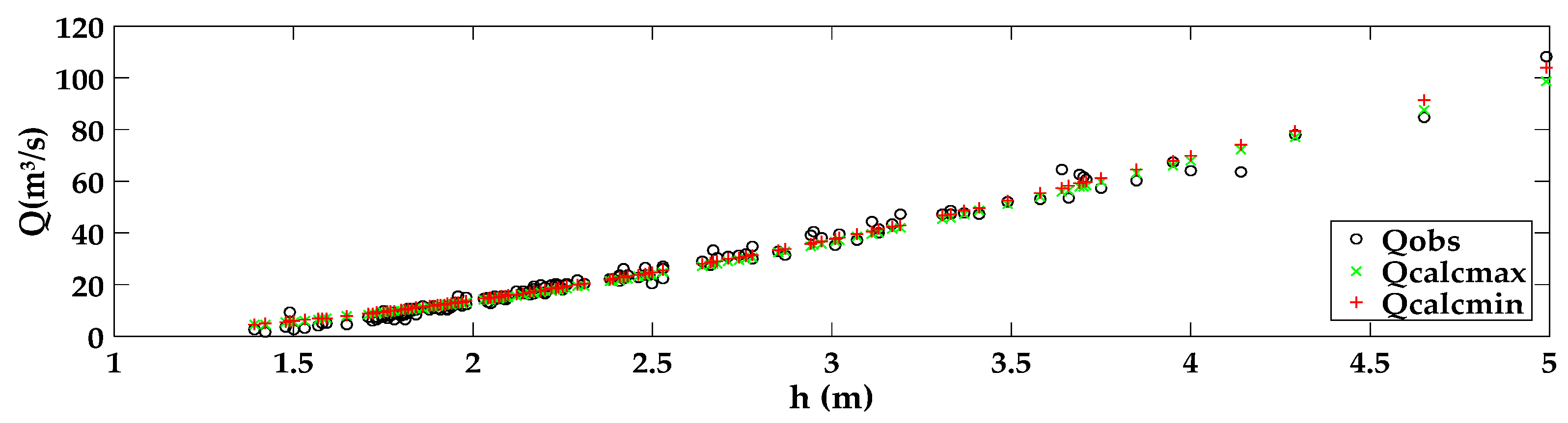
3.1. GLUE
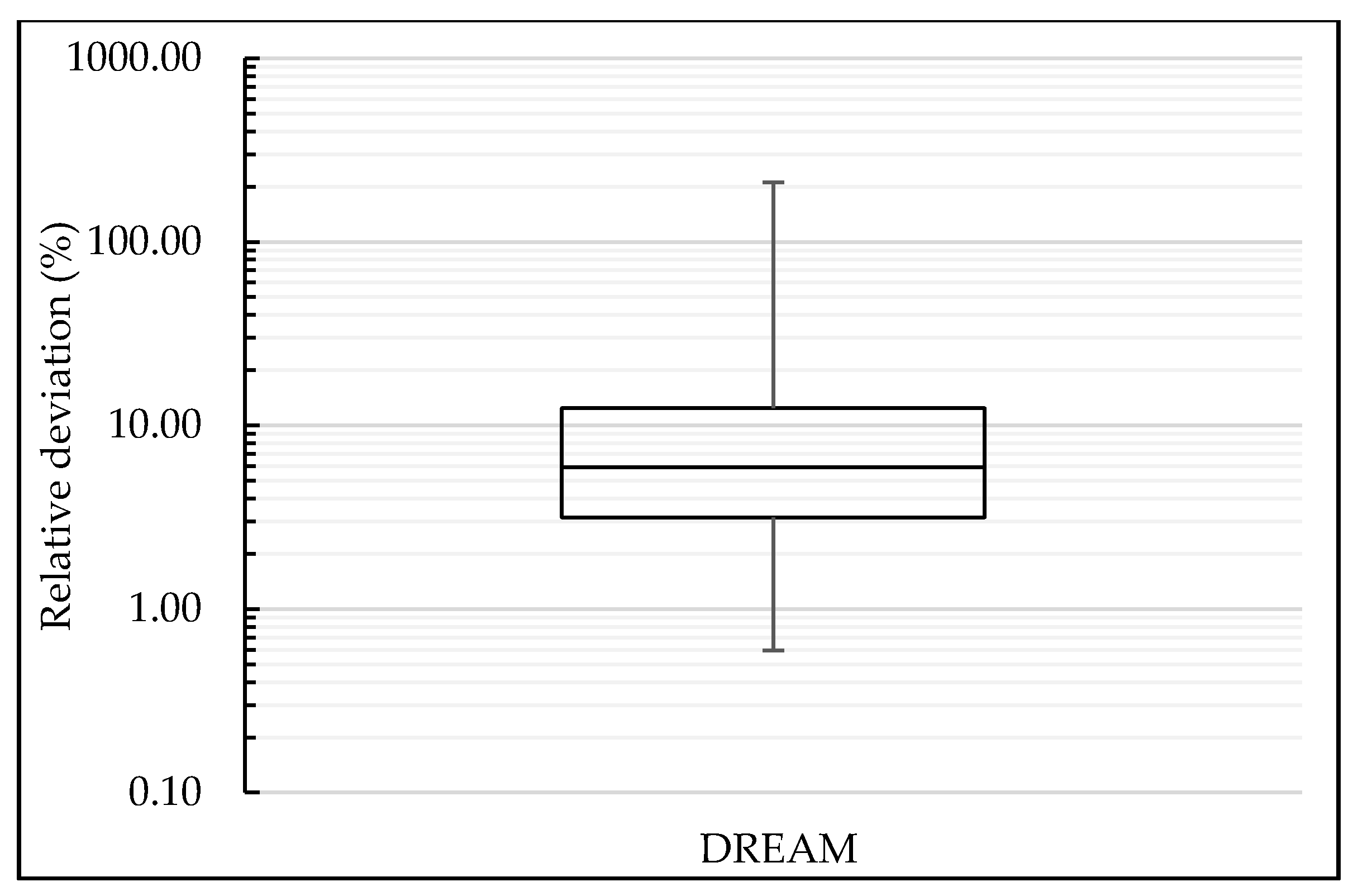
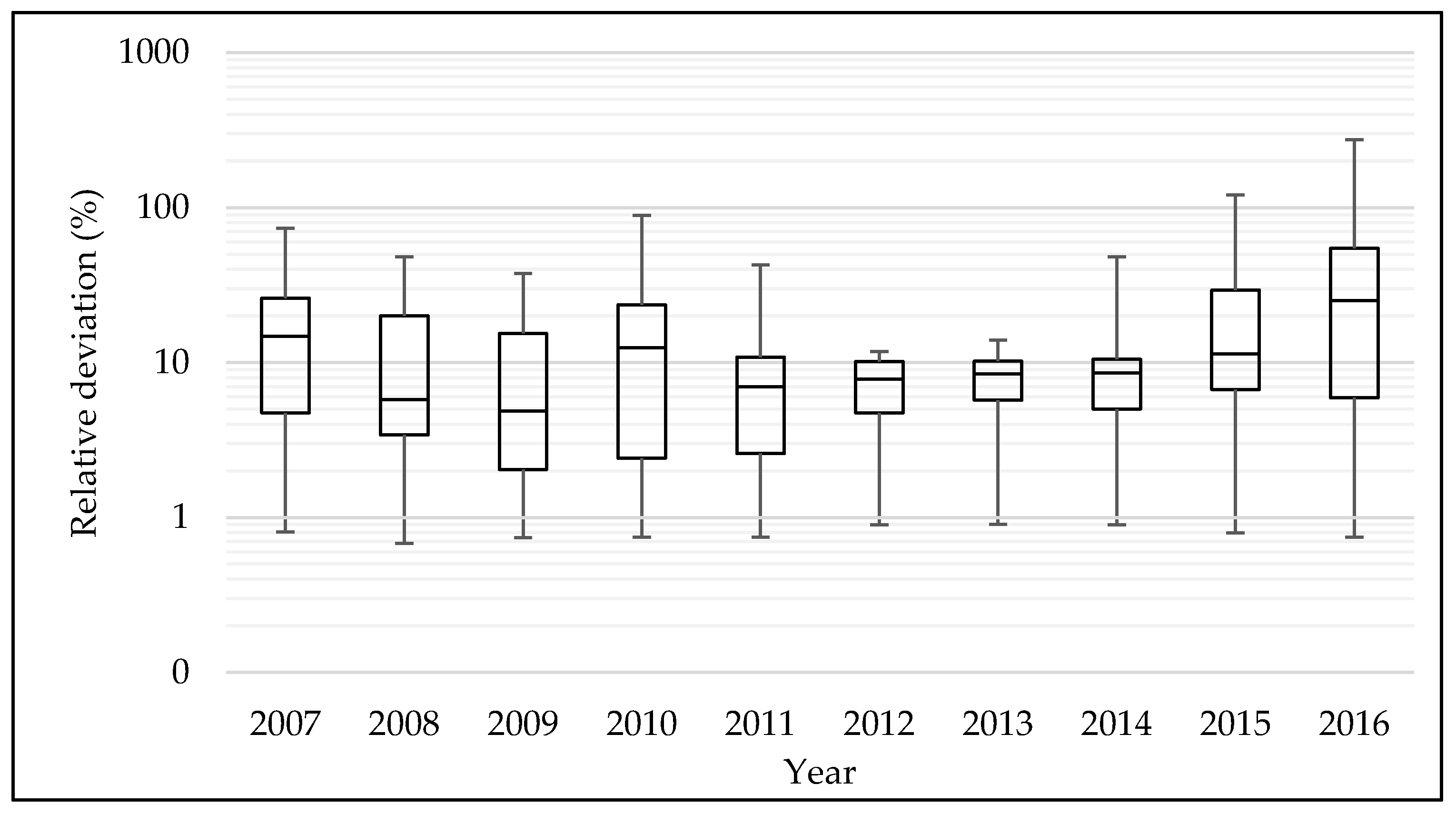
3.2. DREAM
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Oliveira, F.A.; Pereira, T.S.R.; Soares, A.K.; Formiga, K.T.M. Uso de modelo hidrodinâmico para determinação da vazão a partir de medições de nível. Rev. Bras. Recur. Hídricos 2016, 21, 707–718. [Google Scholar] [CrossRef][Green Version]
- Aricò, C.; Nasello, C.; Tucciarelli, T. Using unsteady-state water level data to estimate channel roughness and discharge hydrograph. Adv. Water Resour. 2009, 32, 1223–1240. [Google Scholar] [CrossRef]
- Perumal, M.; Moramarco, T.; Sahoo, B.; Barbetta, S. A methodology for discharge estimation and rating curve development at ungauged river sites. Water Resour. Res. 2007, 43, 02412. [Google Scholar] [CrossRef]
- Perumal, M.; Moramarco, T.; Sahoo, B.; Barbetta, S. On the practical applicability of the VPMS routing method for rating curve development at ungauged river sites. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Perumal, M. Hydrodynamic derivation of a variable parameter Muskingum method: 2. Verification. Hydrol. Sci. J. 1994, 39, 443–458. [Google Scholar] [CrossRef]
- Perumal, M.; Price, R.K. A fully mass conservative variable parameter McCarthy–Muskingum method: Theory and verification. J. Hydrol. 2013, 502, 89–102. [Google Scholar] [CrossRef]
- Perumal, M.; Sahoo, B.; Moramarco, T.; Barbetta, S. Multilinear Muskingum Method for Stage-Hydrograph Routing in Compound Channels. J. Hydrol. Eng. 2009, 14, 663–670. [Google Scholar] [CrossRef]
- Aricò, C.; Corato, G.; Tucciarelli, T.; Ben Meftah, M.; Petrillo, A.F.; Mossa, M. Discharge estimation in open channels by means of water level hydrograph analysis. J. Hydraul. Res. 2010, 48, 612–619. [Google Scholar] [CrossRef]
- Barbetta, S.; Brocca, L.; Melone, F.; Moramarco, T.; Singh, V.P. Addressing the Uncertainty Assessment for Real-Time Stage Forecasting. World Environ. Water Resour. Congr. 2011, 4791–4800. [Google Scholar] [CrossRef]
- Choo, T.H.; Chae, S.K.; Yoon, H.C.; Choo, Y.M. Discharge prediction using hydraulic characteristics of mean velocity equation. Environ. Earth Sci. 2014, 71, 675–683. [Google Scholar] [CrossRef]
- Choo, T.H.; Hong, S.H.; Yoon, H.C.; Yun, G.S.; Chae, S.K. The estimation of discharge in unsteady flow conditions, showing a characteristic loop form. Environ. Earth Sci. 2015, 73, 4451–4460. [Google Scholar] [CrossRef]
- Choo, T.H.; Yoon, H.C.; Lee, S.J. An estimation of discharge using mean velocity derived through Chiu’s velocity equation. Environ. Earth Sci. 2013, 69, 247–256. [Google Scholar] [CrossRef]
- Beven, K.J.; Binley, A.M. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F. DREAM(D): An adaptive Markov Chain Monte Carlo simulation algorithm to solve discrete, noncontinuous, and combinatorial posterior parameter estimation problems. Hydrol. Earth Syst. Sci. 2011, 15, 3701–3713. [Google Scholar] [CrossRef]
- Vrugt, J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Model. Softw. 2016, 75, 273–316. [Google Scholar] [CrossRef]
- PEREIRA, T.S.R. Modelagem e Monitoramento Hidrológico Das Bacias Hidrográficas Dos Córregos Botafogo e Cascavel, Goiânia—Go. Master’s Thesis, Universidade Federal de Goias, Goiania, Brazil, 2015. [Google Scholar]
- SIEG. Sistema de Informações Geográficas do Estado de Goiás. Secretaria de Estado de Gestão e Planejamento—SEGPLAN 2017. Available online: http://www.sieg.go.gov.br/siegdownloads/ (accessed on 1 November 2019).
- Portal HidroWeb. Agência Nacional de Água. Available online: https://www.snirh.gov.br/hidroweb/publico/apresentacao.jsf (accessed on 30 October 2018).
- Arcement, G.J.; Schneider, V.R. Guide for selecting Manning’s roughness coefficients for natural channels and flood plains. U.S. Geol. Surv. Water-Supply Pap. 1989, 2339, 38. [Google Scholar] [CrossRef]
- CHOW, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959; 680p. [Google Scholar]
- Pan, F.; Wang, C.; Xi, X. Constructing river stage-discharge rating curves using remotely sensed river cross-sectional inundation areas and river bathymetry. J. Hydrol. 2016, 540, 670–687. [Google Scholar] [CrossRef]
- Bravo, J.M.; Piccilli, D.G.A.; Collischonn, W.; Tassi, R.; Meller, A.; Tucci, C.E.M. Avaliação visual e numérica da calibração do modelo hidrológico IPH II com fins educacionais. In XVII Simpósio Brasileiro de Recursos Hídricos; ABRH: São Paulo, Brazil, 2007; pp. 1–20. [Google Scholar]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; Series in Water Resources Environmental Engineering; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Montanari, A. Uncertainty of Hydrological Predictions. In Treatise on Water Science; PETER, W., Ed.; Elsevier: Oxford, UK, 2011; pp. 459–478. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Gelman, A.G.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Seibt, A.C. Modelagem Hidrológica da Bacia Hidrográfica do Córrego Botafogo—Goiânia, GO. Dissertação (Mestrado). Programa de Pós-Graduação em Engenharia do Meio Ambiente. Master’s Thesis, Universidade Federal de Goiás, Goiânia, Brazil, 2013. [Google Scholar]
- Cu Thi, P.; Ball, J.E.; Dao, N.H. Uncertainty Estimation Using the Glue and Bayesian Approaches in Flood Estimation: A case Study—Ba River, Vietnam. Water 2018, 10, 1641. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Montanari, A. Uncertainty in river discharge observations: A quantitative analysis. Hydrol. Earth Syst. Sci. 2009, 13, 39–61. [Google Scholar] [CrossRef]


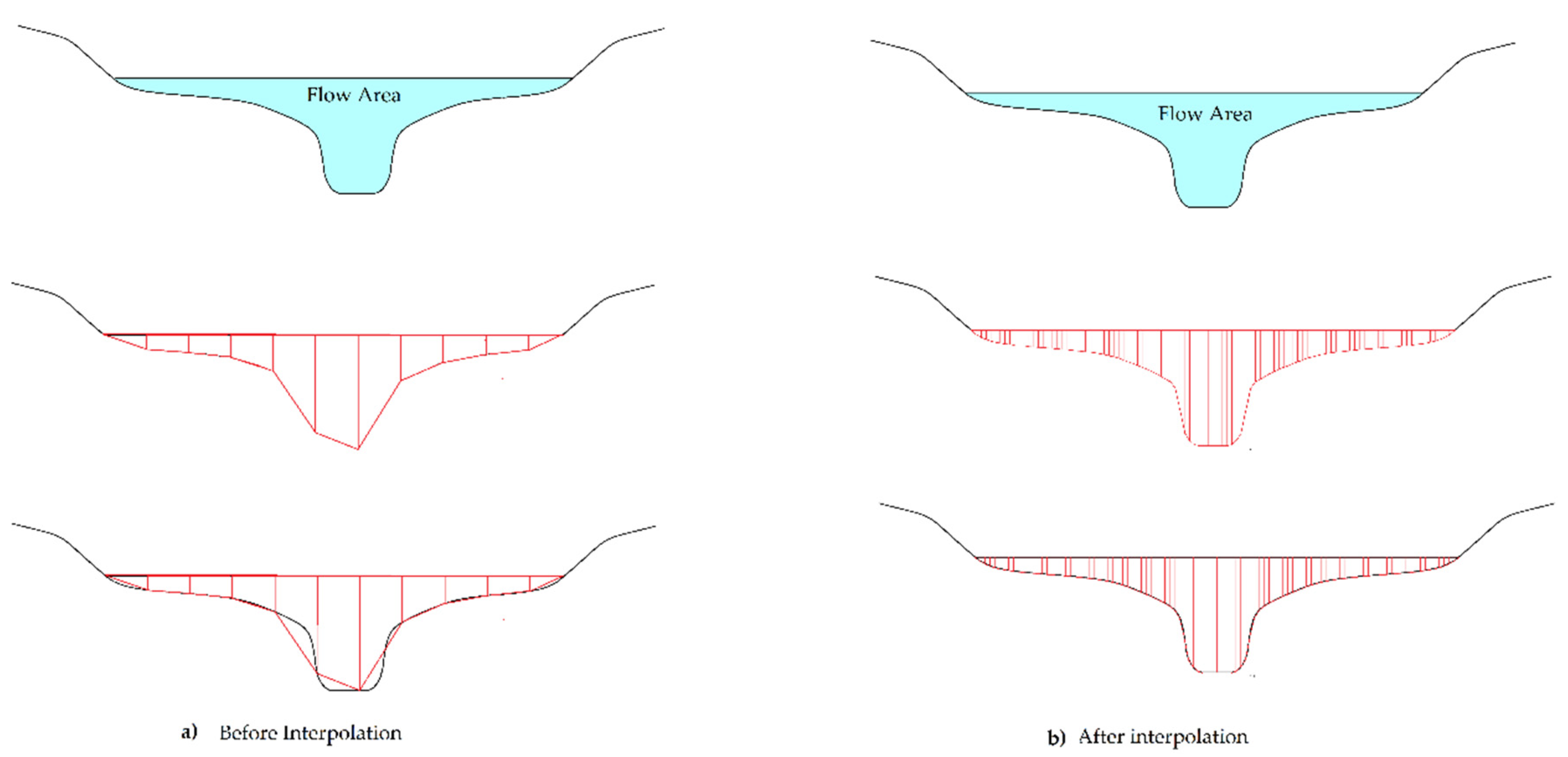






| Case 1: stage = h1 | 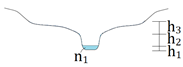 | |
| Case 2: stage = h1 + h2 | 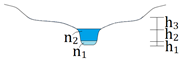 | |
| Case 3: stage = h1 + h2 + h3 | 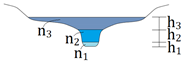 |
| NS | Sets (eNS > 0.90) | Computing Time (s) |
|---|---|---|
| 100 | 0 | 11 |
| 1000 | 2 | 89 |
| 10,000 | 38 | 917 |
| 100,000 | 1564 | 15340 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reis, G.d.C.d.; Pereira, T.S.R.; Faria, G.S.; Formiga, K.T.M. Analysis of the Uncertainty in Estimates of Manning’s Roughness Coefficient and Bed Slope Using GLUE and DREAM. Water 2020, 12, 3270. https://doi.org/10.3390/w12113270
Reis GdCd, Pereira TSR, Faria GS, Formiga KTM. Analysis of the Uncertainty in Estimates of Manning’s Roughness Coefficient and Bed Slope Using GLUE and DREAM. Water. 2020; 12(11):3270. https://doi.org/10.3390/w12113270
Chicago/Turabian StyleReis, Guilherme da Cruz dos, Tatiane Souza Rodrigues Pereira, Geovanne Silva Faria, and Klebber Teodomiro Martins Formiga. 2020. "Analysis of the Uncertainty in Estimates of Manning’s Roughness Coefficient and Bed Slope Using GLUE and DREAM" Water 12, no. 11: 3270. https://doi.org/10.3390/w12113270
APA StyleReis, G. d. C. d., Pereira, T. S. R., Faria, G. S., & Formiga, K. T. M. (2020). Analysis of the Uncertainty in Estimates of Manning’s Roughness Coefficient and Bed Slope Using GLUE and DREAM. Water, 12(11), 3270. https://doi.org/10.3390/w12113270





