The Impacts of Arable Land per Farmer on Water Markets in China
Abstract
:1. Introduction
2. The Debate on the Impact of ALPF on Water Market Performance
3. Data and Methods
3.1. Two-Sector Water Rights Trading Model
3.2. Data and Simulation
4. Results
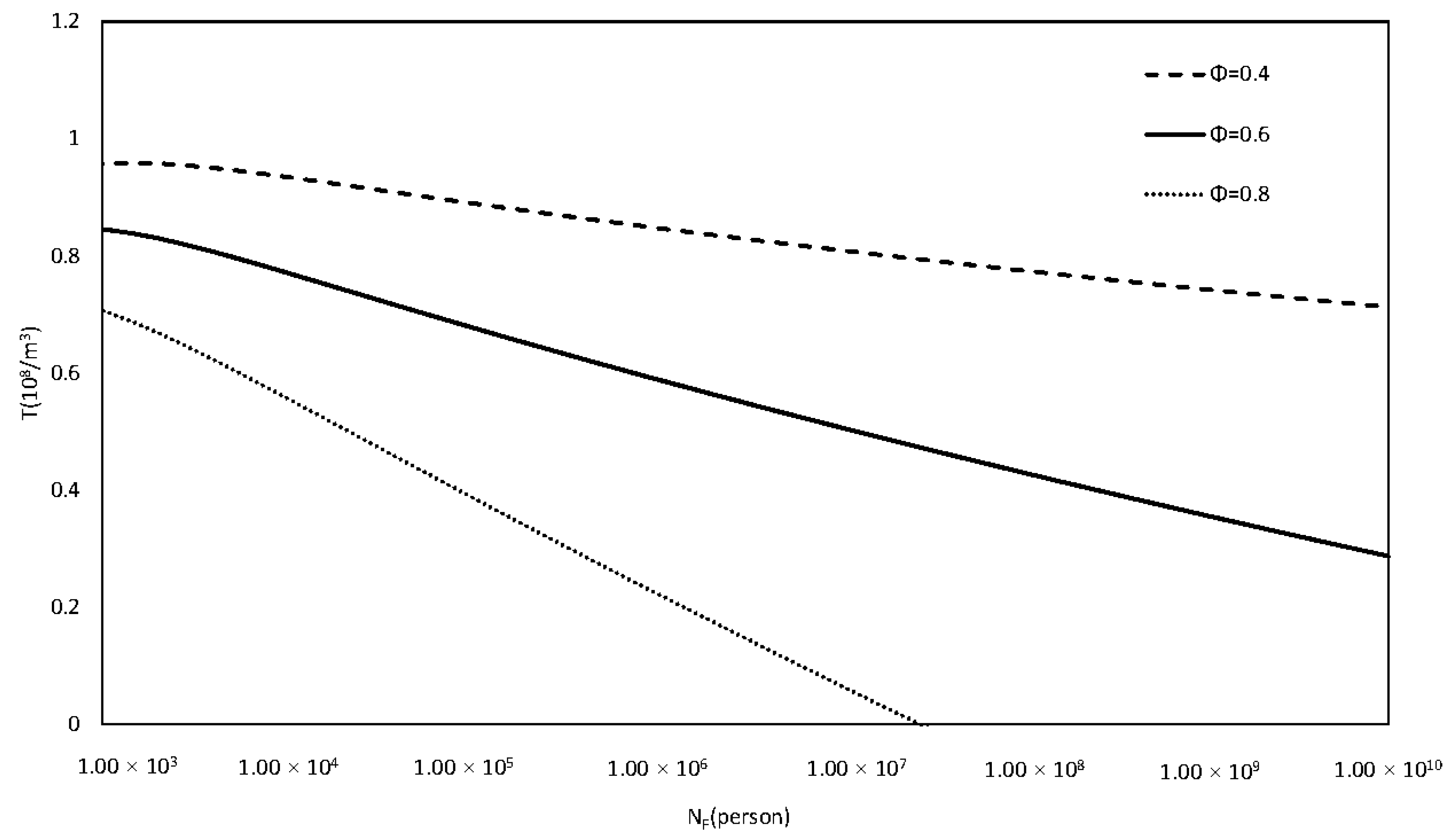
4.1. Transaction Volume and Trading Volume
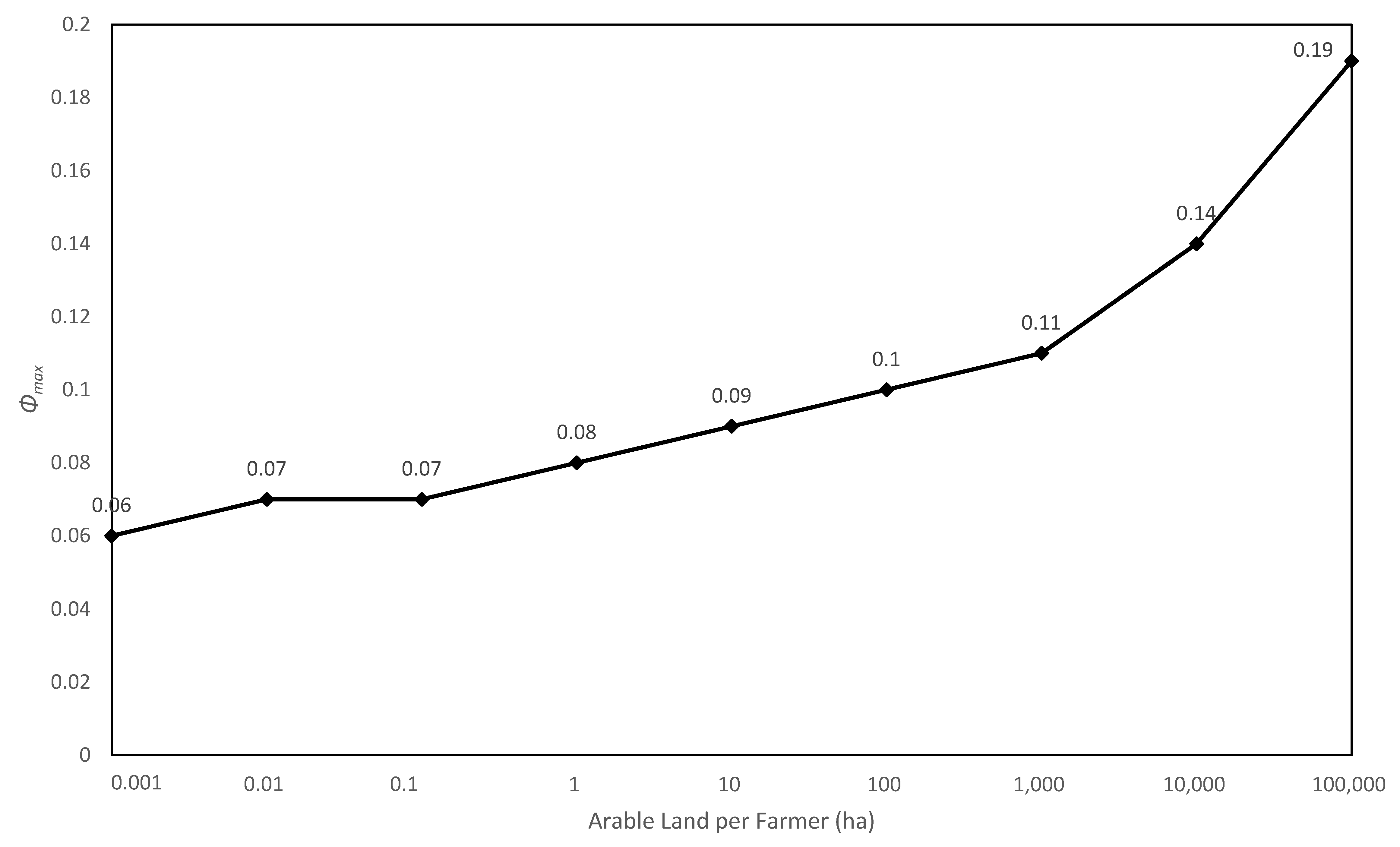
4.2. Maximum Acceptable Transaction Cost
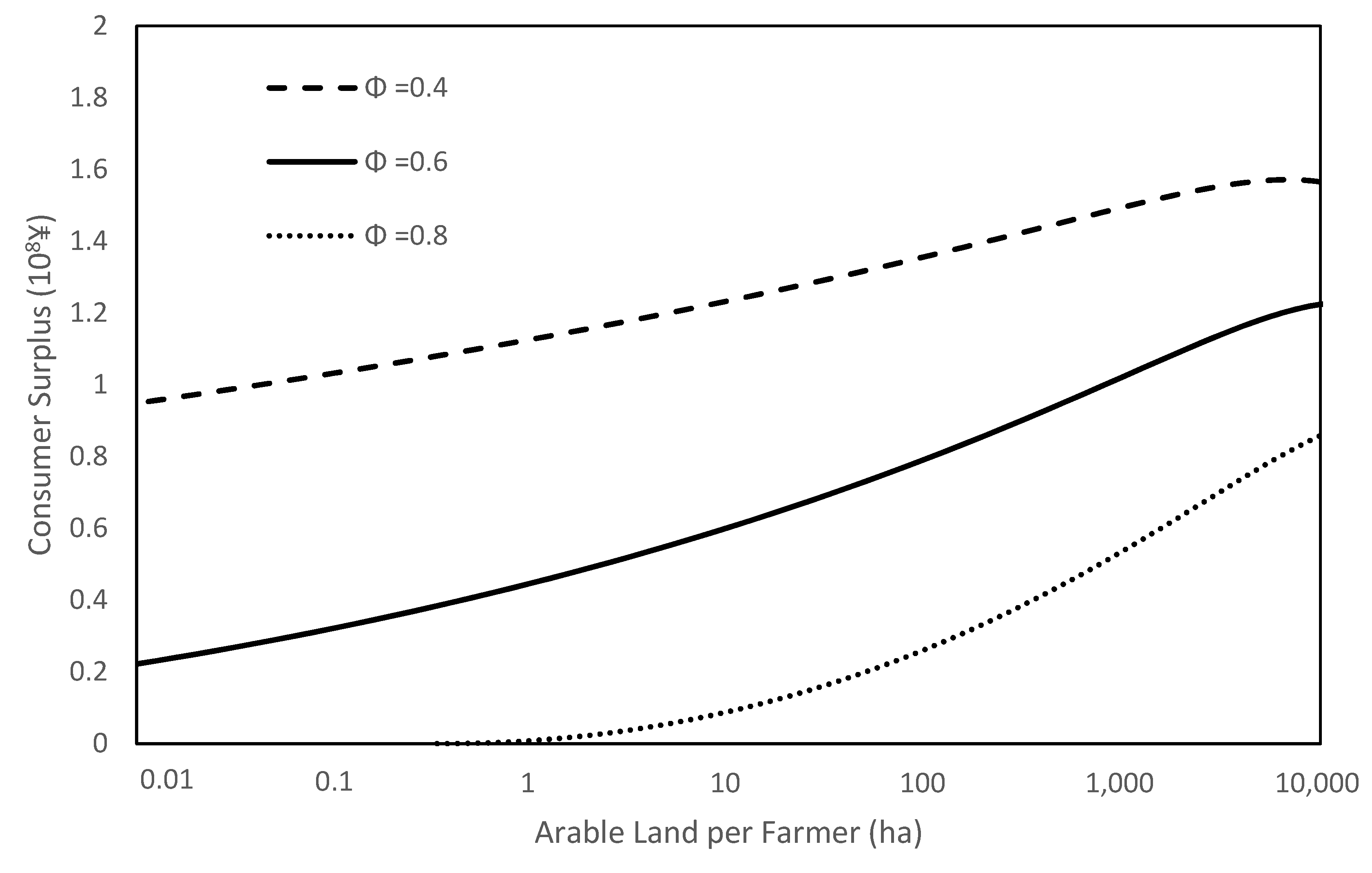
4.3. Social Welfare and Economic Efficiency
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- McDonald, R.I.; Weber, K.; Padowski, J.C.; Flörke, M.; Schneider, C.; Green, P.A.; Gleeson, T.; Eckman, S.; Lehner, B.; Balk, D.; et al. Water on an urban planet: Urbanization and the reach of urban water infrastructure. Glob. Environ. Chang. 2014, 27, 96–105. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Huang, Y.; Zhao, Y.; Li, H.; He, F.; Zhai, J.; Zhu, Y.; Wang, Q.; Jiang, S. Research on Optimal Water Allocation Based on Water Rights Trade under the Principle of Water Demand Management: A Case Study in Bayannur City, China. Water 2018, 10, 863. [Google Scholar] [CrossRef] [Green Version]
- Mekonnen, M.M.; Hoekstra, A.Y. Four billion people facing severe water scarcity. Sci. Adv. 2016, 2, e1500323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Chang, F.X.; Chen, J. Summary of researches on water rights and initial water rights allocation. J. Yangtze River Sci. Res. Inst. 2011, 28, 1–9. [Google Scholar]
- Jiang, J.Y. Economic analysis of the third-party effect of water rights trade. Water Resour. Dev. Res. 2012, 11, 48–51. [Google Scholar]
- Wheeler, S.A.; Loch, A.; Crase, L.; Young, M.; Grafton, R.Q. Developing a water market readiness assessment framework. J. Hydrol. 2017, 552, 807–820. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, S.; Loch, A.; Zuo, A.; Bjornlund, H. Reviewing the adoption and impact of water markets in the Murray–Darling Basin, Australia. J. Hydrol. 2014, 518, 28–41. [Google Scholar] [CrossRef]
- Wang, Y. How to use “two-hands force” in water management. China Water Resour. 2014, 10, 4–6. [Google Scholar]
- Watkins, K. Human Development Report 2006-Beyond Scarcity: Power, Poverty and the Global Water Crisis; United Nations Development Programme: New York, NY, USA, 2006. [Google Scholar]
- Anderson, T.L. Continental Water Marketing; Pacific Research Institute for Public Policy: San Francisco, CA, USA, 1994. [Google Scholar]
- Bekchanov, M.; Bhaduri, A.; Ringler, C. Potential gains from water rights trading in the Aral Sea Basin. Agric. Water Manag. 2015, 152, 41–56. [Google Scholar] [CrossRef]
- Young, M.D. Water Rights: An Ecological. Economics Perspective; Australian Agricultural and Resource Economics Society: Vermont, Victoria, Australia, 1997. [Google Scholar]
- Hearne, R.R. Institutional and organizational arrangements for water markets in Chile. In Markets for Water; Easter, K.W., Rosegrant, M.W., Dinar, A., Eds.; Springer: Boston, MA, USA, 1998; pp. 141–157. [Google Scholar]
- Simpson, L. Are” Water Markets” a Viable Option? Financ. Dev. 1994, 31, 30. [Google Scholar]
- Marino, M.; Kemper, K.E. Institutional Frameworks in Successful Water Markets: Brazil, Spain, and Colorado, USA; The World Bank: Washington, DC, USA, 1999. [Google Scholar]
- Khan, S.; Dassanayake, D.; Mushtaq, S.; Hanjra, M.A. Predicting water allocations and trading prices to assist water markets. Irrig. Drain. 2009, 59, 388–403. [Google Scholar] [CrossRef]
- Meinzen-Dick, R.S. Groundwater markets in Pakistan: Institutional development and productivity impacts. In Markets for Water; Easter, K.W., Rosegrant, M.W., Dinar, A., Eds.; Springer: Boston, MA, USA, 1998; pp. 207–222. [Google Scholar]
- Shah, T. Groundwater Markets and Irrigation Development; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Archibald, S.O.; Renwick, M.E. Expected transaction costs and incentives for water market development. Nat. Resour. Manag. Policy 1998, 15, 95–117. [Google Scholar]
- Bauer, C.J. Against the Current: Privatization, Water Markets, and the State in Chile; Springer: New York, NY, USA, 1998. [Google Scholar]
- Lee, T.R.; Jouravlev, A. Prices, Property and Markets in Water Allocation; Naciones Unidas Comisión Económica para América Latina y el Caribe: Santiago de Chile, Chile, 1998. [Google Scholar]
- Wang, Y. A simulation of water markets with transaction costs. Agric. Water Manag. 2012, 103, 54–61. [Google Scholar] [CrossRef]
- Liu, Y.M.; Luo, B.L. Effects of Tradeable Water Rights on Farmers′ Irrigation Water use Behaviour. Math. Pract. Theory 2014, 44, 7–14. [Google Scholar]
- Habakkuk, H.J. American and British Technology in the 19th Century; Cambridge University Press: Cambridge, UK, 1962. [Google Scholar]
- Nordhaus, W.D. Productivity Growth and the New Economy. Brookings Pap. Econ. Act. 2002, 2002, 211–265. [Google Scholar] [CrossRef] [Green Version]
- Rigby, D.; Alcon, F.; Burton, M. Supply uncertainty and the economic value of irrigation water. Eur. Rev. Agric. Econ. 2010, 37, 97–117. [Google Scholar] [CrossRef]
- Bjornlund, H.; McKay, J. Do Permanent Water Markets Facilitate Farm Adjustment and Structural Change Within Irrigation Communities? Rural Soc. 1999, 9, 555–572. [Google Scholar] [CrossRef]
- Amsalu, A.; De Graaff, J. Determinants of adoption and continued use of stone terraces for soil and water conservation in an Ethiopian highland watershed. Ecol. Econ. 2007, 61, 294–302. [Google Scholar] [CrossRef]
- Anley, Y.; Bogale, A.; Haile-Gabriel, A. Adoption decision and use intensity of soil and water conservation measures by smallholder subsistence farmers in Dedo district, Western Ethiopia. Land Degrad. Dev. 2007, 18, 289–302. [Google Scholar] [CrossRef]
- Bekele, W.; Drake, L. Soil and water conservation decision behavior of subsistence farmers in the Eastern Highlands of Ethiopia: A case study of the Hunde-Lafto area. Ecol. Econ. 2003, 46, 437–451. [Google Scholar] [CrossRef]
- Saleth, R.M. Water Markets in India: Extent and Impact. In Water Markets for the 21st Century; Easter, K.W., Huang, Q., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 239–261. [Google Scholar]
- Vaux, H.J., Jr.; Howitt, R.E. Managing water scarcity: An evaluation of interregional transfers. Water Resour. Res. 1984, 20, 785–792. [Google Scholar] [CrossRef]
- Becker, N. Value of moving from central planning to a market system: Lessons from the Israeli water sector. Agric. Econ. 1995, 12, 11–21. [Google Scholar] [CrossRef]
- Garrido, A. A mathematical programming model applied to the study of water markets within the Spanish agricultural sector. Ann. Oper. Res. 2000, 94, 105–123. [Google Scholar] [CrossRef]
- Garrick, D.; Whitten, S.M.; Coggan, A. Understanding the evolution and performance of water markets and allocation policy: A transaction costs analysis framework. Ecol. Econ. 2013, 88, 195–205. [Google Scholar] [CrossRef]
- Manuel, A.; Jos, A.G.; Mez-Lim, N.M. Local Water Markets for Irrigation in South Spain: A Multi-criteria Approach. Aust. J. Agric. Resour. Econ. 2002, 46, 21–43. [Google Scholar]
- Ge, M.; Wu, F.-P.; You, M. Initial Provincial Water Rights Dynamic Projection Pursuit Allocation Based on the Most Stringent Water Resources Management: A Case Study of Taihu Basin, China. Water 2017, 9, 35. [Google Scholar] [CrossRef] [Green Version]
- Bai, B. Research on the countermeasures of sustainable use and development for water resource in China. Future Dev. 1997, 10, 10–13. [Google Scholar]
- Heaney, A.; Hafi, A.; Beare, S.; Wang, J.X. Water reallocation in northern China: Towards more formal markets for water. In Agricultural Water Management in China; Willett, I.R., Gao, Z., Eds.; Australian Center for International Agricultural Research: Canberra, Australia, 2006. [Google Scholar]
- Li, H.; Hu, J.L. Influencing factors of water right transfer in Yellow River basin based on two-sector mode. J. Econ. Water Resour. 2011, 29, 27–34. [Google Scholar]
- Bolognesi, T.; Nahrath, S.; Cleveland, C.J. Environmental governance dynamics: Some micro foundations of macro failures. Ecol. Econ. 2020, 170, 106555. [Google Scholar] [CrossRef]
- Hearne, R.R.; Easter, K.W. The economic and financial gains from water markets in Chile. Agric. Econ. 1997, 15, 187–199. [Google Scholar] [CrossRef]
- Montero, J.-P. Marketable pollution permits with uncertainty and transaction costs. Resour. Energy Econ. 1998, 20, 27–50. [Google Scholar] [CrossRef]
- Stavins, R.N. Transaction Costs and Tradeable Permits. J. Environ. Econ. Manag. 1995, 29, 133–148. [Google Scholar] [CrossRef]
- Ostrom, E. Understanding Institutional Diversity; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Weisstein, E.W. Cubic Formula. Available online: https://mathworld.wolfram.com (accessed on 17 July 2017).
- China Water Web. Industrial Water Price. Available online: http://www.h2o-china.comn (accessed on 10 July 2017).
- Inner Mongolia Autonomous Region Government. Standard of Water Resources Fees. Available online: http://www.wulanchabu.gov.cn/information/wlcbzfw7011/msg948735058492.html (accessed on 17 July 2017).
- Water Conservancy Department of Inner Mongolia Autonomous Region Government. Inner Mongolia Water Resources Bulletin 2004. Available online: http://slt.nmg.gov.cn/xxgk/jcms_files/jcms1/web2/site/col/col56/index.html (accessed on 17 July 2017).
- Water Conservancy Department of Inner Mongolia Autonomous Region Government. Inner Mongolia Water Resources Bulletin 2014. Available online: http://slt.nmg.gov.cn/xxgk/jcms_files/jcms1/web2/site/col/col56/index.html (accessed on 17 July 2017).
- Wu, J. Analysis of Water Market Institution under the Social-Ecological System. Master′s Thesis, Tsinghua University, Beijing, China, 2015. [Google Scholar]
- Wang, H.; Lall, S. Valuing water for Chinese industries: A marginal productivity analysis. Appl. Econ. 2010, 34, 759–765. [Google Scholar] [CrossRef]
- Xi, Q. Study on Evaluation and Technical Efficiency of Industrial Water Saving Projects. Ph.D. Thesis, Tianjin University, Tianjin, China, 2011. [Google Scholar]
- Xu, M. [Raw Database] The Impacts of Arable Land Per Farmer on Water Markets in China. 2020. Available online: https://zenodo.org/record/4285502#.X82o5rMRWUm (accessed on 6 December 2020).
- Cason, T.N.; Gangadharan, L. Transactions Costs in Tradable Permit Markets: An Experimental Study of Pollution Market Designs. J. Regul. Econ. 2003, 23, 145–165. [Google Scholar] [CrossRef]
- Pender, J.L.; Kerr, J.M. Determinants of farmers′ indigenous soil and water conservation investments in semi-arid India. Agric. Econ. 1998, 19, 113–125. [Google Scholar]
- Jara-Rojas, R.; Bravo-Ureta, B.E.; Diaz, J.M.C. Adoption of water conservation practices: A socioeconomic analysis of small-scale farmers in Central Chile. Agric. Syst. 2012, 110, 54–62. [Google Scholar] [CrossRef]
- Huang, S.X. Research on the California Water Rights System. Master′s Thesis, Xiamen University, Xiamen, China, 2014. [Google Scholar]
- Dwyer, G.; Loke, P.; Appels, D.; Stone, S.F.; Peterson, D.C. Integrating Rural and Urban Water Markets in South East Australia: Preliminary Analysis. Productivity Commission OECD Conference Paper. 2005. Available online: https://ssrn.com/abstract=883562 (accessed on 6 December 2020). [CrossRef] [Green Version]
- Gorton, M.; Sauer, J.; Peshevski, M.; Bosev, D.; Shekerinov, D.; Quarrie, S.A. Water Communities in the Republic of Macedonia: An Empirical Analysis of Membership Satisfaction and Payment Behavior. World Dev. 2009, 37, 1951–1963. [Google Scholar] [CrossRef]
- Meinzen-Dick, R. Beyond panaceas in water institutions. Proc. Natl. Acad. Sci. USA 2007, 104, 15200–15205. [Google Scholar] [CrossRef] [Green Version]
- Ostrom, E. Governing the Commons: The Evolution of Institutions for Collective Action; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Wang, Y.; Wan, T.; Biswas, A.K. Structuring water rights in China: A hierarchical framework. Int. J. Water Resour. Dev. 2017, 34, 418–433. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S. Breaking the dilemma of agricultural water fee collection in China. Hydrol. Res. 2014, 16, 773–784. [Google Scholar] [CrossRef]





| Authors | Model Principles | Research Area | Transaction Form | Results |
|---|---|---|---|---|
| Vaux, Howitt [32] | The utility function of participants; Maximize social welfare | California, USA | Agriculture to industry | Transaction volume is 4130 × 106 m3 in 2020; $219 million market revenue in 2020 |
| Becker [33] | Maximize farmers’ utility; Consider transaction cost; | Israel | Region to region; agricultural water rights | $28 million market revenue per year, and proves transaction costs significantly reduces total social benefits |
| Garrido [34] | Maximization of farmers’ revenue | Four irrigated areas in southern Spain | Farmer to farmer; Region to region | Transaction can happen when transaction costs are very low, or when 30 to 60 percent of transaction costs are borne by watershed institutions. |
| Manuel [36] | The utility function of farmers is constructed, with small and medium-sized farmers as buyers and large farmers as sellers (small farmers are 5–10 ha; Large farmers over 20 ha) | Four irrigated areas in southern Spain | Farmer to farmer | It is concluded that small and medium-sized farmers are more likely to benefit from water rights market by exploring the impact of water rights market on farmers’ income, but transaction costs are not taken into account in the model. |
| Heaney et al. [39] | The production function of agricultural products is constructed to calculate the individual income of farmers under water rights market conditions | Eight provinces in the Yellow River Basin of China | Region to region; agricultural water rights | $150 million market revenue a year, and increases crop yields by 1.8 percent, without considering transaction costs. |
| Li & Hu [40] | A cost-benefit model of water rights market in agricultural and industrial sector | General | Agriculture to industry | Qualitatively analyzes the effects of initial water rights, transaction price and cost, water saving cost, and water resource production efficiency of enterprise on water market |
| Wang [22] | A cost minimization model for achieving policy objectives | Eight provinces in the Yellow River Basin of China | Agriculture to industry | The simulation results show that transaction costs have a significant impact on transaction volume and transaction price, and transaction costs have a more significant impact on farmers. |
| Liu & Luo [23] | Under the water quota management, the objective function of farmers’ water use decision is constructed, and the marginal cost and marginal benefit curves are used to solve equations. | China | Farmer to farmer | Discusses the effects of water price and transaction cost on the water rights market and emphasizes that the transaction cost of water rights will discourage farmers to participate in the market. |
| Agriculture | Parameter Value | Industry | Parameter Value |
|---|---|---|---|
| YF (108 Yuan) | 1627.85 | YE (108 Yuan) | 9119.79 |
| UF (108 m3) | 152.82 | UE (108 m3) | 10.38 |
| QF (108 m3) | 137.54 | QE (108 m3) | 19.73 |
| Elasticity | 0.2 | Elasticity | 0.06 |
| PF (yuan/m3) | 0.05 | PE (yuan/m3) | 4.36 |
| a | 3.915 | c | 1.0496 |
| b | 0.033 | d | 3.5913 |
| NF (Persons) | 1000 | 10,000 | 105 | 106 | 107 | 108 | 109 |
| ALPF (ha) | 10,000 | 1000 | 100 | 10 | 1 | 0.1 | 0.01 |
| Author | Research Area | Effect of Arable Land on Water Management |
|---|---|---|
| Amsalu & De Graaff [28] | Ethiopia | The larger the arable land is, the more positive the farmers will be to the government’s water resources policies. |
| Anley et al. [29] | Western Ethiopia | The larger the arable land is, the more active the farmers are in the practice of saving water and protecting the land. |
| Bekele & Drake [30] | Ethiopia | Farmers with larger farms have formed their own water and soil conservation committees. |
| Pender & Kerr [56] | Shirapur, India | The larger the farmland is, the more the farmers will invest in saving water |
| Jara-Rojas et al. [57] | Chile | Water price policy is an effective way to incentivize the farmers to save water. The government can provide subsidies or education to cover the water bills of the disadvantaged groups. |
| Saleth [31] | India | Due to inadequate resource endowments per farmer, informal water rights markets exist only in some parts of India. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, M.; Zhu, T. The Impacts of Arable Land per Farmer on Water Markets in China. Water 2020, 12, 3433. https://doi.org/10.3390/w12123433
Wang Y, Xu M, Zhu T. The Impacts of Arable Land per Farmer on Water Markets in China. Water. 2020; 12(12):3433. https://doi.org/10.3390/w12123433
Chicago/Turabian StyleWang, Yahua, Maosen Xu, and Tingju Zhu. 2020. "The Impacts of Arable Land per Farmer on Water Markets in China" Water 12, no. 12: 3433. https://doi.org/10.3390/w12123433
APA StyleWang, Y., Xu, M., & Zhu, T. (2020). The Impacts of Arable Land per Farmer on Water Markets in China. Water, 12(12), 3433. https://doi.org/10.3390/w12123433






