What is the Trade-Off between Snowpack Stratification and Simulated Snow Water Equivalent in a Physically-Based Snow Model?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Watersheds
2.2. Meteorological Data
2.3. Snow Data
2.4. Model Description: MASiN Snow Model
2.5. Methodology
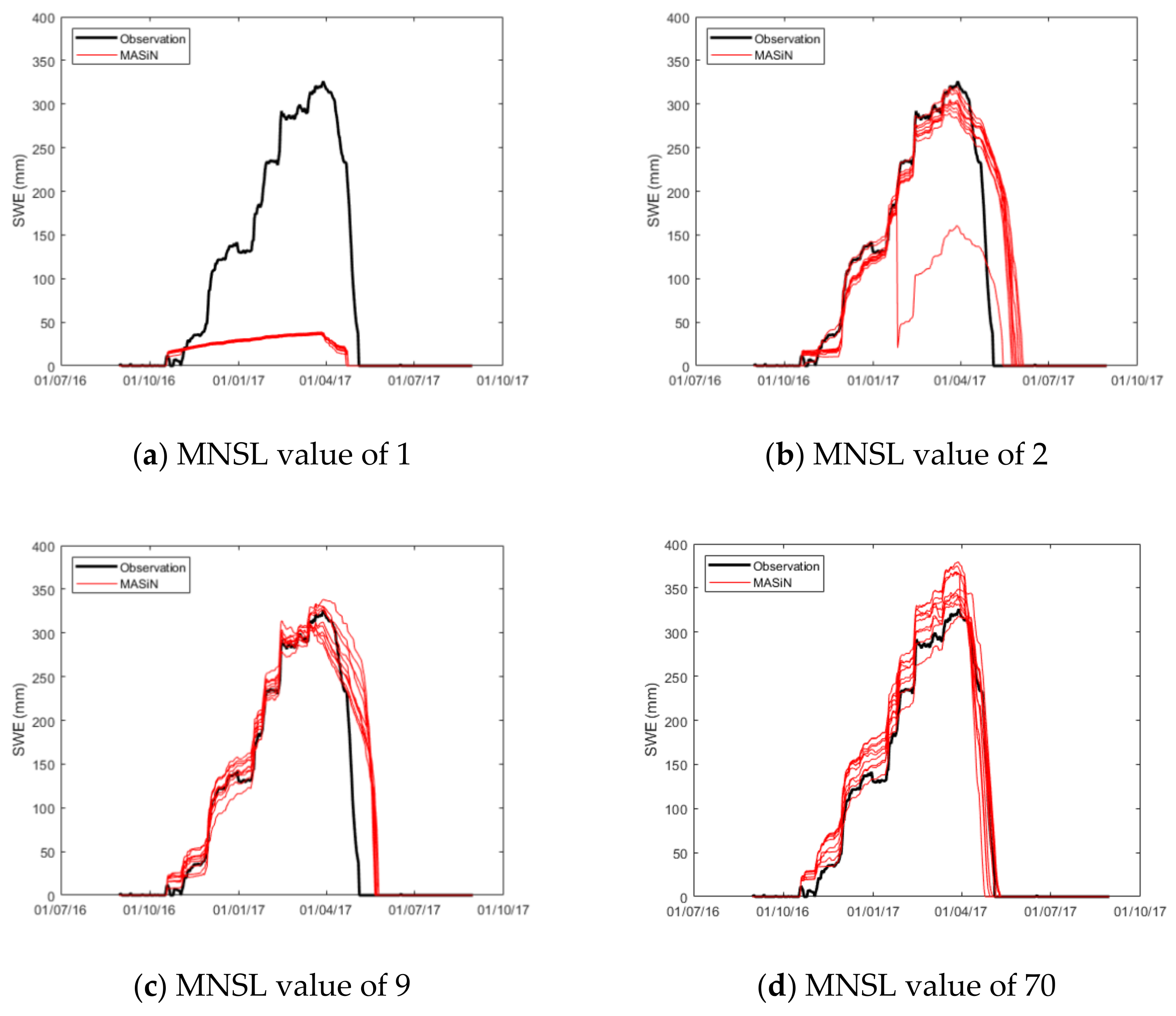
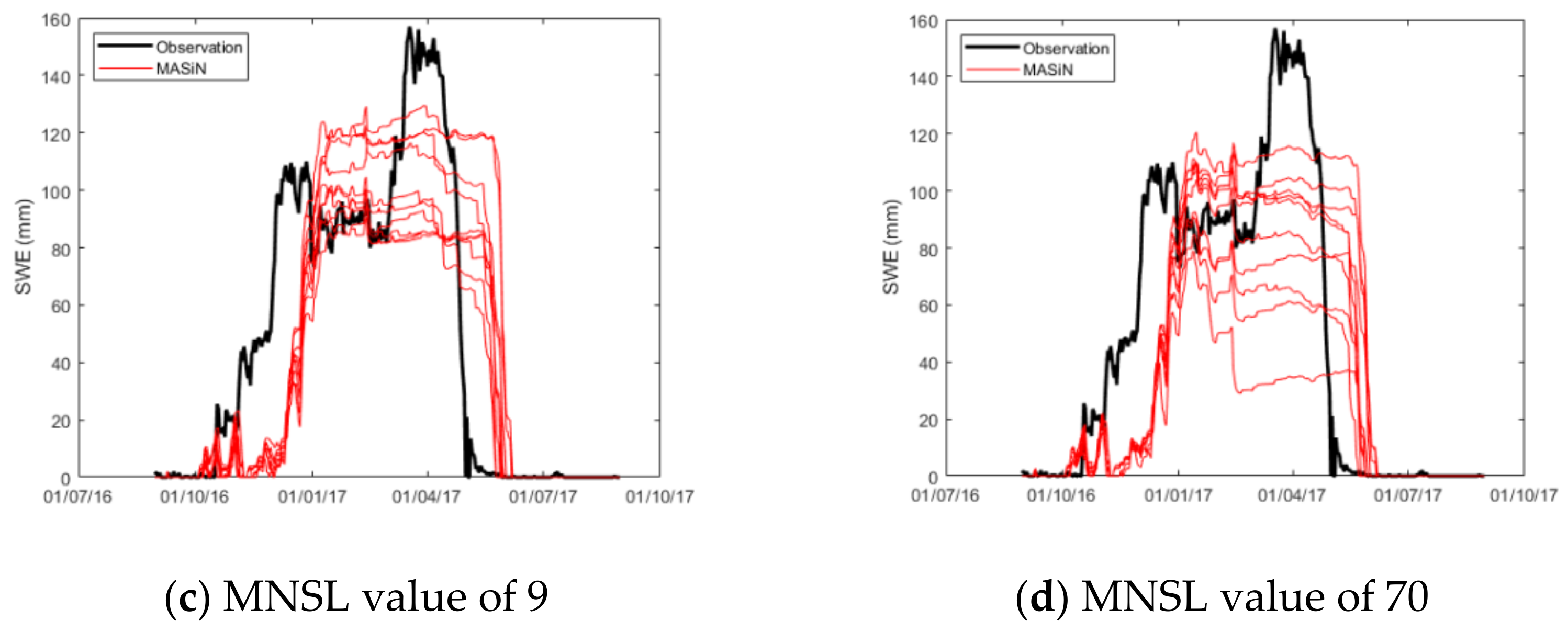
2.5.1. Sensitivity Analysis: Impact of the Number of Snow Layers
2.5.2. Calibration
3. Results
3.1. Snow-Water Equivalent (SWE) Modeling
3.2. Influence of the Maximum Number of Snow Layer on the Calibrated Parameters
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karl, T.R.; Groisman, P.Y.; Knight, R.W.; Heim, R.R., Jr. Recent Variations of Snow Cover and Snowfall in North America and Their Relation to Precipitation and Temperature Variations. J. Clim. 1993, 6, 1327. [Google Scholar] [CrossRef] [Green Version]
- Groisman, P.Y.; Easterling, D.R. Variability and Trends of Total Precipitation and Snowfall over the United States and Canada. J. Clim. 1994, 7, 184. [Google Scholar] [CrossRef] [Green Version]
- Iwata, Y.; Hayashi, M.; Suzuki, S.; Hirota, T.; Hasegawa, S. Effects of snow cover on soil freezing, water movement, and snowmelt infiltration: A paired plot experiment. Water Resour. Res. 2010, 46, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Cochand, F.; Therrien, R.; Lemieux, J.M. Integrated Hydrological Modeling of Climate Change Impacts in a Snow-Influenced Catchment. Groundwater 2019, 57, 3–20. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, K.; Kubota, J.; Ohata, T.; Vuglinsky, V. Influence of snow ablation and frozen ground on spring runoff generation in the Mogot Experimental Watershed, southern mountainous taiga of eastern Siberia. Nord. Hydrol. 2006, 37, 21–29. [Google Scholar] [CrossRef]
- Zdanowicz, C.; Karlsson, P.; Beckholmen, I.; Roach, P.; Poulain, A.; Yumvihoze, E.; Martma, T.; Ryjkov, A.; Dastoor, A. Snowmelt, glacial and atmospheric sources of mercury to a subarctic mountain lake catchment, Yukon, Canada. Geochim. Cosmochim. Acta 2018, 238, 374–393. [Google Scholar] [CrossRef]
- Brun, E.; Martin, E.; Simon, V.; Gendre, C.; Coleou, C. An energy and mass model of snow cover suitable for operational avalanche forecasting. J. Glaciol. 1989, 35, 333–342. [Google Scholar] [CrossRef] [Green Version]
- Brun, E.; David, P.; Sudul, M.; Brunot, G. A numerical model to simulate snow-cover stratigraphy for operational avalanche forecasting. J. Glaciol. 1992, 38, 13–22. [Google Scholar] [CrossRef] [Green Version]
- Valery, A. Modélisation Precipitations—Débit sous Influence Nivale. Elaboration d’un Module Neige et Évaluation sur 380 Bassins Versants. Ph.D. Thesis, Institut des Sciences et Industries du Vivant et de l’Environnement AgroParisTech, Paris, France, February 2010. [Google Scholar]
- Kokkonen, T.; Koivusalo, H.; Jakeman, A.; Norton, J. Construction of a Degree–day Snow Model in the Light of the Ten Iterative Steps in Model Development. In Proceedings of the iEMSs Third Biennial Meeting: “Summit on Environmental Modeling and Software”, Burlington, VT, USA, 9–13 July 2006. 12 p. [Google Scholar]
- Marks, D.; Domingo, J.; Susong, D.; Link, T.; Garen, D. A spatially distributed energy balance snowmelt model for application in mountain basins. Hydrol. Process. 1999, 13, 1935–1959. [Google Scholar] [CrossRef]
- Bartelt, P.; Lehning, M. A physical SNOWPACK model for the Swiss avalanche warning Part I: Numerical model. Cold Reg. Sci. Technol. 2002, 35, 123–145. [Google Scholar] [CrossRef]
- Musselman, K.N.; Pomeroy, J.W.; Essery, R.L.H.; Leroux, N. Impact of windflow calculations on simulations of alpine snow accumulation, redistribution and ablation. Hydrol. Process. 2015, 29, 3983–3999. [Google Scholar] [CrossRef]
- Turcotte, R.; Fortin, L.-G.; Fortin, V.; Fortin, J.-P.; Villeneuve, J.-P. Operational analysis of the spatial distribution and the temporal evolution of the snowpack water equivalent in southern Québec, Canada. Nord. Hydrol. 2007, 38, 211. [Google Scholar] [CrossRef]
- Anderson, E.A. National Weather Service River Forecast System—Snow Accumulation and Ablation Model; NOAA Technical Memorandum NWS HYDRO-17; US Department of Commerce: Washington, DC, USA, 1973.
- Domine, F.; Barrere, M.; Sarrazin, D. Seasonal evolution of the effective thermal conductivity of the snow and thesoil in high Arctic herb tundra at Bylot Island, Canada. Cryosphere 2016, 10, 2573–2588. [Google Scholar] [CrossRef] [Green Version]
- Domine, F.; Picard, G.; Morin, S.; Barrere, M.; Madore, J.-B.; Langlois, A. Major Issues in Simulating Some Arctic Snowpack Properties Using Current Detailed Snow Physics Models: Consequences for the Thermal Regime and Water Budget of Permafrost. J. Adv. Model. Earth Syst. 2019, 11, 34–44. [Google Scholar] [CrossRef]
- Essery, R.; Morin, S.; Lejeune, Y.; Ménard, C.B. A comparison of 1701 snow models using observations from an alpine site. Adv. Water Resour. 2013, 55, 131–148. [Google Scholar] [CrossRef] [Green Version]
- Magnusson, J.; Wever, N.; Essery, R.; Helbig, N.; Winstral, A.; Jonas, T. Evaluating snow models with varying process representations for hydrological applications. Water Resour. Res. 2015, 51, 2707–2723. [Google Scholar] [CrossRef] [Green Version]
- He, M.; Hogue, T.S.; Franz, K.J.; Margulis, S.A.; Vrugt, J.A. Characterizing parameter sensitivity and uncertainty for a snow model across hydroclimatic regimes. Adv. Water Resour. 2011, 34, 114–127. [Google Scholar] [CrossRef] [Green Version]
- Houle, E.S.; Livneh, B.; Kasprzyk, J.R. Exploring snow model parameter sensitivity using Sobol’ variance decomposition. Environ. Model. Softw. 2017, 89, 144–158. [Google Scholar] [CrossRef] [Green Version]
- Engel, M.; Notarnicola, C.; Endrizzi, S.; Bertoldi, G. Snow model sensitivity analysis to understand spatial and temporal snow dynamics in a high-elevation catchment. Hydrol. Process. 2017, 31, 4151–4168. [Google Scholar] [CrossRef]
- Arduini, G.; Balsamo, G.; Dutra, E.; Day, J.J.; Sandu, I.; Boussetta, S.; Haiden, T. Impact of a Multi-Layer Snow Scheme on Near-Surface Weather Forecasts. J. Adv. Model. Earth Syst. 2019, 11, 4687–4710. [Google Scholar] [CrossRef]
- Mas, A.; Baraer, M.; Arsenault, R.; Poulin, A.; Préfontaine, J. Targeting high robustness in snowpack modeling for Nordic hydrological applications in limited data conditions. J. Hydrol. 2018, 564, 1008–1021. [Google Scholar] [CrossRef]
- Fortin, J.-P.; Turcotte, R.; Massicotte, S.; Moussa, R.; Fitzbac, J.; Villeneuve, J.-P. Distributed Watershed Model Comptatible with Remote Sensing and GIS Data. I: Description of Model. J. Hydrol. Eng. 2001, 6, 91–99. [Google Scholar] [CrossRef]
- Turcotte, R.; Rousseau, A.N.; Fortin, J.-P.; Villeneuve, J.-P. A process-oriented, multiple-objective calibration strategy accounting for model structure. Water Sci. Appl. 2003, 6, 153–163. [Google Scholar] [CrossRef]
- Arndt, S.; Paul, S. Variability of Winter Snow Properties on Different Spatial Scales in the Weddell Sea. J. Geophys. Res. Ocean. 2018, 123, 8862–8876. [Google Scholar] [CrossRef] [Green Version]
- Monti, F.; Cagnati, A.; Valt, M.; Schweizer, J. A new method for visualizing snow stability profiles. Cold Reg. Sci. Technol. 2012, 78, 64–72. [Google Scholar] [CrossRef]
- Armstrong, R.L. An analysis of compressive strain in adjacent temperature- gradient and equi-temperature layers in a natural snow cover. J. Glaciol. 1980, 26, 283–289. [Google Scholar] [CrossRef] [Green Version]
- Tolson, B.A.; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007, 43, 1–16. [Google Scholar] [CrossRef]
- Heierli, J. Solitary fracture waves in metastable snow stratifications. J. Geophys. Res. 2005, 110, F02008. [Google Scholar] [CrossRef] [Green Version]
- Government of Canada. Environment and Climate Change Canada. Available online: https://climate.weather.gc.ca/climate_normals/results_1981_2010_e.html?stnID=6047&autofwd=1 (accessed on 24 April 2020).
- Government of Canada. Environment and Climate Change Canada. Available online: https://climate.weather.gc.ca/climate_normals/results_1981_2010_e.html?stnID=1617&autofwd=1 (accessed on 24 April 2020).
- Oreiller, M.; Nadeau, D.F.; Minville, M.; Rousseau, A.N. Modeling snow water equivalent and spring runoff in a boreal watershed, James Bay, Canada. Hydrol. Process. 2014, 28, 5991–6005. [Google Scholar] [CrossRef]
- Choquette, Y.; Lavigne, P.; Nadeau, M.; Ducharme, P.; Martin, J.P.; Houdayer, A.; Rogoza, J. GMON, a new sensor for snow water equivalent via gamma monitoring. In Proceedings of the Whistler 2008 International Snow Science Workshop, Whistler, BC, Canada, 21–27 September 2008; pp. 802–807. [Google Scholar]
- Arsenault, R.; Brissette, F.; Martel, J.-L. The hazards of split-sample validation in hydrological model calibration. J. Hydrol. 2018, 566, 346–362. [Google Scholar] [CrossRef]
- Lee, R. Evaluation of Solar Beam Irradiation as a Climatic Parameter of Mountain Watersheds. Hydrol. Pap. 2 1963, 2, 60. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modeling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]







| Station Name | Station Code | Temporal Period | Temporal Resolution | Station Type | Basin |
|---|---|---|---|---|---|
| Necopastic | Meteo_Neco | 2006–2011 | Daily & hourly | Auto | Necopastic |
| Lower Fantail | Meteo_LF | 2014–2017 | Daily & hourly | Auto | Upper Yukon |
| Lower Llewellyn | Meteo_LL | 2014–2017 | Daily & hourly | Auto | Upper Yukon |
| Wheaton | Meteo_W | 2014–2017 | Daily & hourly | Auto | Upper Yukon |
| Station Name | Station Code | Temporal Period | Temporal Resolution | Station Type | Watershed |
|---|---|---|---|---|---|
| Necopastic | GMON Neco | 2006–2011 | 6 h | Auto | Necopastic |
| Lower Fantail | GMON LF | 2014–2017 | 6 h | Auto | Upper Yukon |
| Lower Llewellyn | GMON LL | 2014–2017 | 6 h | Auto | Upper Yukon |
| Wheaton | GMON W | 2014–2017 | 6 h | Auto | Upper Yukon |
| Main Processes | Sub Processes | MASiN Parameters |
|---|---|---|
| Shortwave radiation | Extraterrestrial irradiation | N/A |
| Effect of cloud and vegetation | (Minimum radiation coefficient) (Maximum radiation coefficient) (Minimum Leaf Area Index) (Maximum Leaf Area Index) | |
| Separation of direct and diffuse radiations | (Minimum ratio of direct shortwave radiation to total shortwave radiation) (Maximum ratio of direct shortwave radiation to total shortwave radiation) | |
| Net shortwave radiation | (Minimum albedo for direct radiation) (Minimum albedo for diffuse radiation) | |
| Energy balances | Shortwave radiation | (Absorption coefficient for direct radiation) (Absorption coefficient for diffuse radiation) |
| Longwave radiation | N/A | |
| Turbulent heat fluxes | (Reduction coefficient of the turbulent transfer) (Snow cover surface roughness) | |
| Liquid water input | N/A | |
| Conduction fluxes | (Ground heat flux) | |
| Mass balances | Liquid water content update | (Maximum retention capacity of the snow layer) |
| New snow layer | (Fresh snow minimum density) (Atmospheric temperature threshold associated to the fresh snow minimum density) | |
| Snowmelt | N/A | |
| Settling | Settling | (Snow layer density triggering the metamorphism phenomenon of the snow layer) (Settlement coefficient) |
| Layer management | Layer management | N/A |
| Data Type | Parameter | Units | Temporal Resolution |
|---|---|---|---|
| Input | Precipitation | mm | Daily/Hourly |
| Air Temperature | °C | Hourly | |
| Relative Humidity | Hourly | ||
| Wind Speed | m·s−1 | Hourly | |
| Output | Snow Layer Depth | mm | Hourly |
| Snow Layer SWE | mm | Hourly | |
| Snow Layer Temperature | °C | Hourly | |
| Snow Layer Density | kg·m−3 | Hourly | |
| Water Outflow | mm | Hourly | |
| Evapotranspiration | mm | Hourly |
| Parameter | Description | Units | Lower Bound | Upper Bound |
|---|---|---|---|---|
| Snow layer density triggering the metamorphism phenomenon of the snow layer | kg·m−3 | 150 | 350 | |
| Fresh snow minimum density | kg·m−3 | 3 | 200 | |
| Atmospheric temperature threshold associated to the fresh snow minimum density | °C | −20 | 0 | |
| Maximum retention capacity of the snow layer | % | 0 | 20 | |
| Settlement coefficient | h−1 | 0 | 0.05 | |
| Ground heat flux | w·m−2 | 0 | 20 | |
| Snow cover surface roughness | m | 0 | 0.01 | |
| Reduction coefficient of the turbulent trade | 0 | 10 | ||
| Minimum radiation coefficient | 0 | 1 | ||
| Maximum radiation coefficient | 0 | 1 | ||
| Minimum albedo for direct radiation | 0.35 | 0.35 | ||
| Minimum albedo for diffuse radiation | 0.45 | 0.45 | ||
| Absorption coefficient for direct radiation | cm−1 | 0.4 | 0.4 | |
| Absorption coefficient for diffuse radiation | cm−1 | 4 | 4 | |
| Minimum ratio of direct shortwave radiation to total shortwave radiation | 0.35 | 0.35 | ||
| Maximum ratio of direct shortwave radiation to total shortwave radiation | 0.85 | 0.85 | ||
| Minimum Leaf Area Index | m2leaf·m−2area | 0 | 0 | |
| Maximum Leaf Area Index | m2leaf·m−2area | 0 | 0 |
| Variable | Lower Fantail | Lower Llewellyn | Wheaton | Necopastic | Global |
|---|---|---|---|---|---|
| 0.148 | 0.055 | 0.112 | 0.071 | 0.096 | |
| (0.03) | (0.4) | (0.1) | (0.3) | (0.005) | |
| −0.479 | −0.270 | −0.383 | −0.329 | −0.356 | |
| (2 × 10−13) | (8 × 10−5) | (1 × 10−8) | (1 × 10−6) | (2 × 10−26) | |
| −0.078 | 0.008 | 0.202 | −0.255 | −0.029 | |
| (0.3) | (0.9) | (0.003) | (2 × 10−4) | (0.4) | |
| 0.110 | 0.092 | 0.119 | 0.178 | 0.123 | |
| (0.1) | (0.2) | (0.1) | (0.01) | (3 × 10−4) | |
| 0.212 | 0.129 | 0.517 | 0.230 | 0.220 | |
| (0.002) | (0.06) | (9 × 10−16) | (8 × 10−4) | (1 × 10−10) | |
| −0.268 | −0.221 | 0.089 | −0.202 | −0.131 | |
| (8 × 10−5) | (0.001) | (0.2) | (0.003) | (1 × 10−4) | |
| 0.037 | 0.078 | 0.132 | −0.091 | 0.037 | |
| (0.6) | (0.3) | (0.06) | (0.2) | (0.3) | |
| 0.273 | −0.027 | 0.185 | 0.256 | 0.169 | |
| (6 × 10−5) | (0.7) | (0.007) | (2 × 10−4) | (8 × 10−7) | |
| −0.015 | −0.076 | 0.031 | 0.029 | −0.003 | |
| (0.8) | (0.3) | (0.7) | (0.7) | (0.9) | |
| −0.262 | −0.350 | −0.229 | −0.299 | −0.238 | |
| (1 × 10−4) | (2 × 10−7) | (8 × 10−4) | (1 × 10−5) | (2 × 10−12) | |
| 0.121 | −0.020 | 0.136 | 0.112 | 0.078 | |
| (0.08) | (0.8) | (0.05) | (0.1) | (0.02) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Augas, J.; Abbasnezhadi, K.; Rousseau, A.N.; Baraer, M. What is the Trade-Off between Snowpack Stratification and Simulated Snow Water Equivalent in a Physically-Based Snow Model? Water 2020, 12, 3449. https://doi.org/10.3390/w12123449
Augas J, Abbasnezhadi K, Rousseau AN, Baraer M. What is the Trade-Off between Snowpack Stratification and Simulated Snow Water Equivalent in a Physically-Based Snow Model? Water. 2020; 12(12):3449. https://doi.org/10.3390/w12123449
Chicago/Turabian StyleAugas, Julien, Kian Abbasnezhadi, Alain N. Rousseau, and Michel Baraer. 2020. "What is the Trade-Off between Snowpack Stratification and Simulated Snow Water Equivalent in a Physically-Based Snow Model?" Water 12, no. 12: 3449. https://doi.org/10.3390/w12123449







