Fragmentation in Seagrass Canopies Can Alter Hydrodynamics and Sediment Deposition Rates
Abstract
1. Introduction
2. Materials and Methods
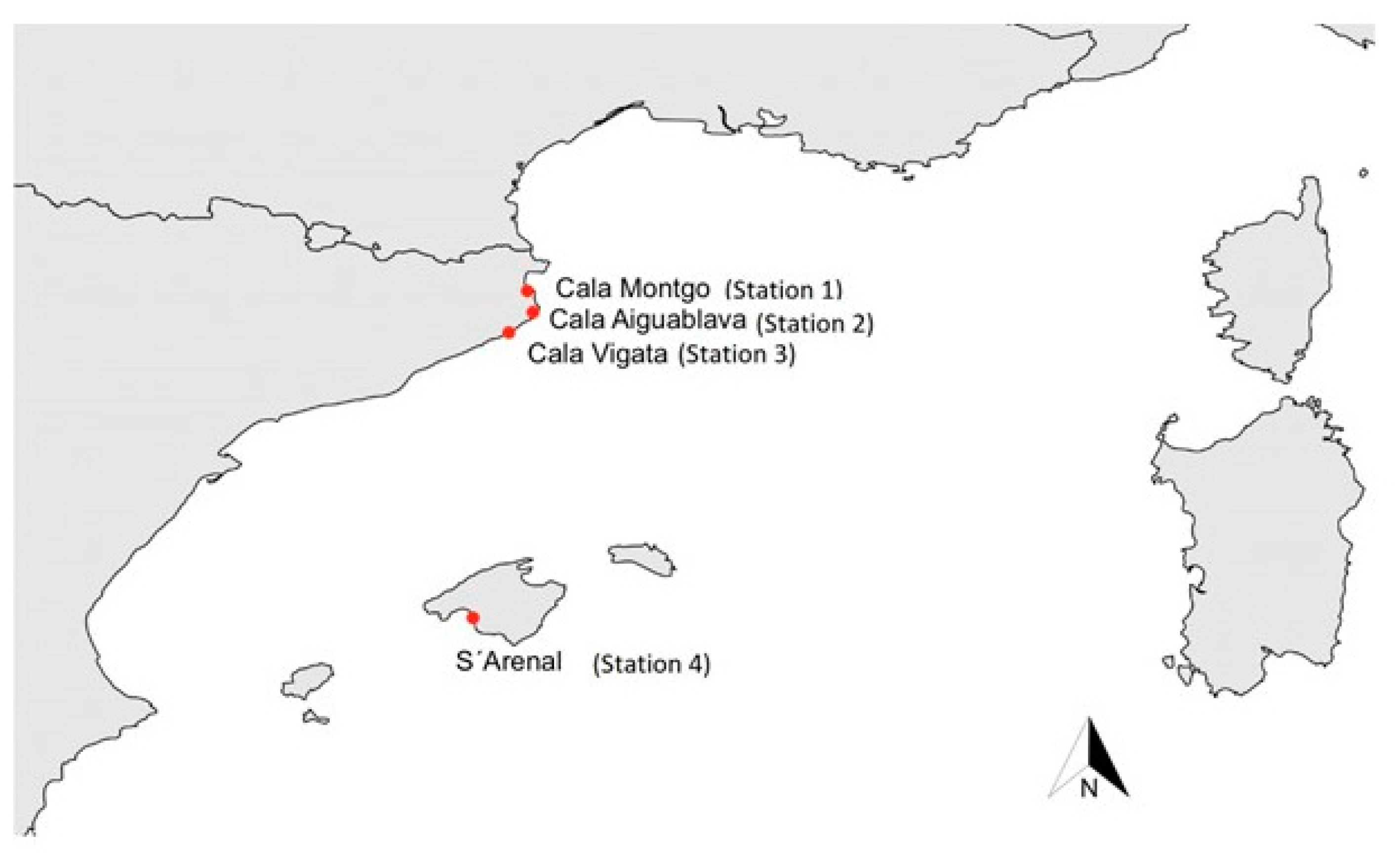
2.1. Description of the Sites
2.2. Fragmentation Level of the Meadows
2.3. Method of Analysis of ADV Data
2.4. Analysis of the Sediment
2.5. Statistical Analysis
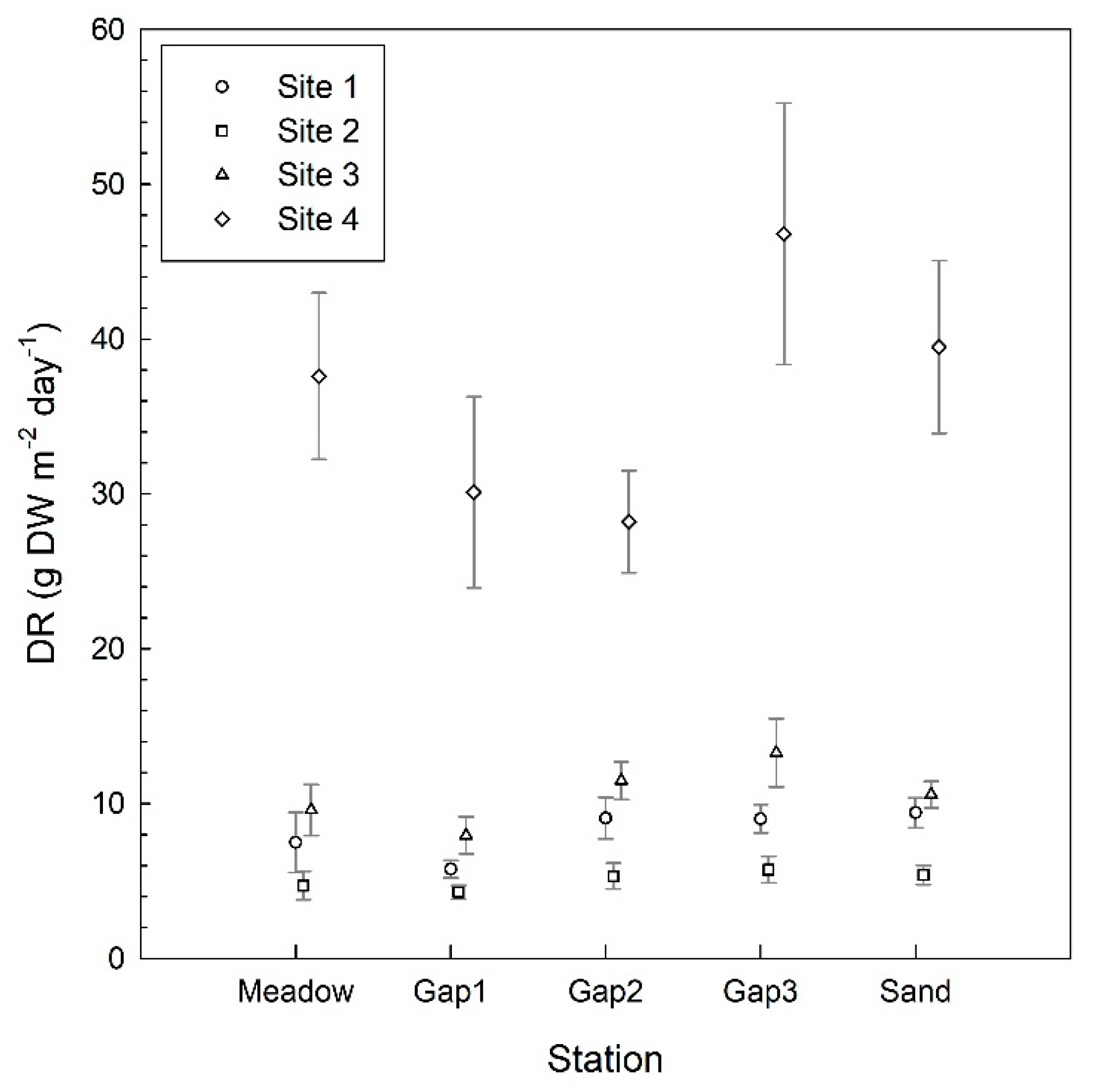
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hemming, M.A.; Duarte, C.M. Seagrass Ecology; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Short, F.; Wyllie-Echeverria, S. Natural and human-induced disturbance of seagrasses. Environ. Conserv. 1996, 23, 17–27. [Google Scholar] [CrossRef]
- de la Torre-Castro, M.; Rönnbäck, P. Links between humans and seagrasses—An example from tropical East Africa. Ocean Coast. Manag. 2004, 47, 361–387. [Google Scholar] [CrossRef]
- Jackson, E.L.; Rees, E.; Wilding, C.; Attrill, M.J. Use of a seagrass residency index to apportion commercial fishery landing values and recreation fisheries expenditure to seagrass habitat service. Conserv. Biol. 2015, 29, 899–909. [Google Scholar] [CrossRef] [PubMed]
- Whitfield, A.K. The role of seagrass meadows, mangrove forests, salt marshes and reed beds as nursery areas and food sources for fishes in estuaries. Rev. Fish Biol. Fish. 2017, 27, 75–110. [Google Scholar] [CrossRef]
- Costanza, R.; De Groot, R.; Sutton, P.; van der Ploeg, S.; Anderson, S.J.; Kubiszewski, J.; Farber, S.; Turner, R.K. Changes in the global value of ecosystem services. Glob. Environ. Chang. 2014, 26, 152–158. [Google Scholar] [CrossRef]
- Kennedy, H.; Beggins, J.; Duarte, C.M.; Fourqurean, J.W.; Holmer, M.; Marbà, N.; Middelburg, J.J. Seagrass sediments as a global carbon sink: Isotopic constraints. Glob. Biogeochem. Cycles 2010, 24, 1–8. [Google Scholar] [CrossRef]
- Duarte, C.M.; Kennedy, H.; Marbà, N.; Hendriks, I. Ocean & Coastal Management Assessing the capacity of seagrass meadows for carbon burial: Current limitations and future strategies. Ocean Coast. Manag. 2013, 83, 32–38. [Google Scholar] [CrossRef]
- Pergent-Martini, P.C.; Ge, C.F.B.; Ruitton, S.; Thibaut, T.; Verlaque, M. The necromass of the Posidonia oceanica seagrass meadow: Fate, role, ecosystem services and vulnerability. Hydrobiologia 2016, 781, 25–42. [Google Scholar] [CrossRef]
- Ondiviela, B.; Losada, I.J.; Lara, J.L.; Maza, M.; Galván, C.; Bouma, T.J.; van Belzen, J. The role of seagrasses in coastal protection in a changing climate. Coast. Eng. 2014, 87, 158–168. [Google Scholar] [CrossRef]
- Kantamaneni, K.; Du, X.; Aher, S.; Singh, R.M. Building blocks: A quantitative approach for evaluating coastal vulnerability. Water 2017, 9, 905. [Google Scholar] [CrossRef]
- Pantusa, D.; D’Alessandro, F.; Riefolo, L.; Principato, F.; Tomasicchio, G.R. Application of a coastal vulnerability index. A case study along the Apulian coastline, Italy. Water 2018, 10, 1218. [Google Scholar] [CrossRef]
- Halpern, B.S.; McLeod, K.L.; Rosenberg, A.; Crowder, L.B. Managing for cumulative impacts in ecosystem-based management through ocean zoning. Ocean Coast. Manag. 2008, 51, 203–211. [Google Scholar] [CrossRef]
- Trevathan-Tackett, S.M.; Sullivan, B.K.; Robinson, K.; Lilje, O.; Macreadie, P.I.; Gleason, F.H. Pathogenic Labyrinthula associated with Australian seagrasses: Considerations for seagrass wasting disease in the southern hemisphere. Microbiol. Res. 2018, 206, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Piazzi, L.; Balestri, E.; Cinelli, F. Grazing of inflorescences of the seagrass Posidonia oceanica (L.) Delile. Bot. Mar. 2000, 43, 581–584. [Google Scholar] [CrossRef]
- Tyllianakis, E.; Callaway, A.; Vanstaen, K.; Luisetti, T. The value of information: Releasing the economic benefits of mapping seagrass meadows in the British Virgin Islands. Sci. Total Environ. 2019, 650, 2107–2116. [Google Scholar] [CrossRef] [PubMed]
- Infantes, E.; Terrados, J.; Orfila, A.; Cañellas, B.; Álvarez-Ellacuria, A. Wave energy and the upper depth limit distribution of Posidonia oceanica. Bot. Mar. 2009, 52, 419–427. [Google Scholar] [CrossRef]
- Do, V.T.; de Montaudin, X.; Blanchet, H.; Lavesque, N. Seagrass burial by dredged sediments: Benthic community alteration, secondary production loss, biotic index reaction and recovery possibility. Mar. Pollut. Bull. 2012, 64, 2340–2350. [Google Scholar] [CrossRef]
- Holon, F.; Boissery, P.; Guilbert, A.; Freschet, E.; Deter, J. The impacts of 85 years of coastal development on shallow seagrass beds (Posidonia oceanica L. (Delile)) in South Eastern France: A slow but steady loss without recovery. Estuar. Coast. Shelf Sci. 2015, 165, 204–212. [Google Scholar] [CrossRef]
- Fernandes, M.B.; Benger, S.; Stuart-Williams, H.; Gaylard, S.; Bryars, S. Coastal nitrogen plumes and their relationship with seagrass distribution. Estuar. Coast. Shelf Sci. 2015, 167, 390–403. [Google Scholar] [CrossRef]
- Short, F.T.; Neckles, H.A. The effects of global climate change on seagrasses. Aquat. Bot. 1999, 63, 169–196. [Google Scholar] [CrossRef]
- Marbà, N.; Duarte, C.M. Mediterranean warming triggers seagrass (Posidonia oceanica) shoot mortality. Glob. Chang. Biol. 2010, 16, 2366–2375. [Google Scholar] [CrossRef]
- Waycott, M.; Duarte, C.M.; Carruthers, T.J.B.; Orth, R.J.; Dennison, W.C.; Olyarnik, S.; Calladine, A.; Fourqurean, J.W.; Heck, K.L., Jr.; Hughes, A.R.; et al. Accelerating loss of seagrasses across the globe threatens coastal ecosystems. Proc. Natl. Acad. Sci. USA 2009, 1. [Google Scholar] [CrossRef] [PubMed]
- Orth, R.J.; Carruthers, T.J.B.; Dennison, W.C.; Duarte, C.M.; Fourqurean, J.W.; Heck, K.L.; Hughes, A.R.; Kendrick, G.A.; Kenworthy, W.J.; Olyarnik, S.; et al. A global crisis for seagrass ecosystems. Bioscience 2006, 56, 987–996. [Google Scholar] [CrossRef]
- Montefalcone, M.; Vacchi, M.; Archetti, R.; Ardizzone, G.; Astruch, P.; Bianchi, C.N.; Calvo, S.; Criscoli, A.; Fernández-Torquemada, Y.; Luzzu, F.; et al. Geospatial modelling and map analysis allowed measuring regression of the upper limit of Posidonia oceanica seagrass meadows under human pressure. Estuar. Coast. Shelf Sci. 2019, 217, 148–157. [Google Scholar] [CrossRef]
- Macreadie, P.I.; Hindell, J.S.; Jenkins, G.P.; Connolly, R.M.; Keough, M.J. Fish responses to experimental fragmentation of seagrass habitat. Conserv. Biol. 2009, 23, 644–652. [Google Scholar] [CrossRef]
- Marbà, N.; Duarte, C.M. Rhizome elongation and seagrass clonal growth. Mar. Ecol. Prog. Ser. 1998, 174, 269–280. [Google Scholar] [CrossRef]
- Marbà, N.; Duarte, C.M.; Cebrián, J.; Gallegos, M.E.; Olesen, B.; Sand-Jensen, K. Growth and population dynamics of Posidonia oceanica on the Spanish Mediterranean coast: Elucidating seagrass decline. Mar. Ecol. Prog. Ser. 1996, 137, 203–213. [Google Scholar] [CrossRef]
- Ruiz-Reynés, D.; Gomila, D.; Sintes, T.; Hernández-García, E.; Marbà, N.; Duarte, C.M. Fairy circle landscapes under the sea. Sci. Adv. 2017, 3, e1603262. [Google Scholar] [CrossRef]
- Livernois, M.C.; Grabowski, J.; Poray, A.K.; Gouhier, T.C.; Hughes, A.R.; O’Brien, K.; Yeager, L.A.; Fodrie, F.J. Effects of habitat fragmentation on Zostera marina seed distribution. Aquat. Bot. 2017, 142, 1–9. [Google Scholar] [CrossRef]
- Shinomiya, Y.; Chiva, S.; Kanamori, M.; Hashizume, S.; Yoshino, K.; Goshima, S. Importance of patch size variation for the population persistence of a decapod crustacean in seagrass beds. Mar. Ecol. Prog. Ser. 2017, 570, 157–171. [Google Scholar] [CrossRef]
- Ricart, A.M.; Dalmau, A.; Pérez, M.; Romero, J. Effects of landscape configuration on the exchange of materials in seagrass ecosystems. Mar. Ecol. Prog. Ser. 2015, 532, 89–100. [Google Scholar] [CrossRef]
- Granata, T.C.; Serra, T.; Colomer, J.; Casamitjana, X.; Duarte, C.M.; Gacia, E. Flow and particle distributions in a nearshore seagrass meadow before and after a storm. Mar. Ecol. Prog. Ser. 2001, 218, 95–106. [Google Scholar] [CrossRef]
- Colomer, J.; Soler, M.; Serra, T.; Casamitjana, X.; Oldham, C. Impact of anthropogenically created canopy gaps on wave attenuation in a Posidonia oceanica meadow. Mar. Ecol. Prog. Ser. 2017, 569, 103–116. [Google Scholar] [CrossRef]
- Pujol, D.; Serra, T.; Colomer, J.; Casamitjana, X. Flow structure in canopy models dominated by progressive waves. J. Hydrol. 2013, 486, 281–292. [Google Scholar] [CrossRef]
- Ros, À.; Colomer, J.; Serra, T.; Pujol, D.; Soler, M.; Casamitjana, X. Experimental observations on sediment resuspension within submerged model canopies under oscillatory flow. Cont. Shelf Res. 2014, 91, 220–231. [Google Scholar] [CrossRef]
- Gacia, E.; Duarte, C.M. Sediment retention by a Mediterranean Posidonia oceanica meadow: The balance between deposition and resuspension. Estuar. Coast. Shelf Sci. 2001, 52, 505–514. [Google Scholar] [CrossRef]
- Gacia, E.; Granata, T.C.; Duarte, C.M. An approach to measurement of particle flux and sediment retention within seagrass (Posidonia oceanica) meadows. Aquat. Bot. 1999, 65, 255–268. [Google Scholar] [CrossRef]
- Terrados, J.; Duarte, C.M. Experimental evidence of reduced particle resuspension within a seagrass (Posidonia oceanica L.) meadow. J. Exp. Mar. Biol. Ecol. 2000, 243, 45–53. [Google Scholar] [CrossRef]
- Gacia, E.; Duarte, C.M.; Middelburg, J.J. Carbon and nutrient deposition in a Mediterranean seagrass (Posidonia oceanica) meadow. Limnol. Oceanogr. 2002, 47, 23–32. [Google Scholar] [CrossRef]
- Duarte, C.M.; Middelburg, J.J.; Caraco, N. Major role of marine vegetation on the oceanic carbon cycle. Biogeosciences 2005, 2, 1–8. [Google Scholar] [CrossRef]
- Duarte, C.M.; Losada, I.J.; Hendriks, I.; Mazarrasa, I.; Marbá, N. The role of coastal plant communities for climate change mitigation and adaptation. Nat. Clim. Chang. 2013, 3, 961–968. [Google Scholar] [CrossRef]
- Ricart, A.M.; Perez, M.; Romero, J. Landscape configuration modulates carbon storage in seagrass sediments. Estuar. Coast. Shelf Sci. 2017, 185, 69–76. [Google Scholar] [CrossRef]
- El Allaoui, N.; Serra, T.; Soler, M.; Colomer, J.; Pujol, D.; Oldham, C. Modified hydrodynamics in canopies with longitudinal gaps exposed to oscillatory flows. J. Hydrol. 2015, 531, 840–849. [Google Scholar] [CrossRef]
- El Allaoui, N.; Serra, T.; Colomer, J.; Soler, M.; Casamitjana, X.; Oldham, C. Interactions between fragmented seagrass canopies and the local hydrodynamics. PLoS ONE 2016, 11, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Folkard, A.M. Hydrodynamics of model Posidonia oceanica patches in shallow water. Limnol. Oceanogr. 2005, 50, 1592–1600. [Google Scholar] [CrossRef]
- Elibol, A.; Garcia, R.; Gracias, N.R. A new global alignment approach for underwater optical mapping. Ocean Eng. 2011, 38, 1207–1219. [Google Scholar] [CrossRef]
- Gleason, A.C.R.; Lirman, D.; Williams, D.E.; Gracias, N.R.; Gintert, B.; Madjidi, H.; Reid, R.P.; Boynton, G.C.; Negahdaripour, S.; Miller, M.; et al. Documenting hurricane impacts on coral reefs using two dimensional video-mosaic technology. Mar. Ecol. 2007, 28, 254–258. [Google Scholar] [CrossRef]
- Lirman, D.; Gracias, N.R.; Gintert, B.E.; Gleason, A.C.R.; Deangelo, G.; Dick, M.; Martinez, E.; Reid, R.P. Damage and recovery assessment of vessel grounding injuries on coral reef habitats by use of georeferenced landscape video mosaics. Limnol. Oceanogr. Methods 2010, 8, 88–97. [Google Scholar] [CrossRef]
- Luhar, M.; Coutu, S.; Infantes, E.; Fox, S.; Nepf, H.M. Wave-induced velocities inside a model seagrass bed. J. Geophys. Res. 2010, 115, C12005. [Google Scholar] [CrossRef]
- Pujol, D.; Casamitjana, X.; Serra, T.; Colomer, J. Canopy-scale turbulence under oscillatory flow. Cont. Shelf Res. 2013, 66, 9–18. [Google Scholar] [CrossRef]
- Rice, E.D.; Baird, R.B.; Eaton, A.D. (Eds.) Standard Methods for the Examination of Water and Wastewater; American Public Health Association, American Waterworks Association, Water Environment Association: Washington, DC, USA, 2017. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. Biometry; W.H. Freeman and Co.: New York, NY, USA, 1995. [Google Scholar]
- Donnell, M.J.O. Reduction of wave forces within bare patches in mussel beds. Mar. Technol. Soc. J. 2014, 362, 157–167. [Google Scholar] [CrossRef]
- Lara, M.; Peralta, G.; Alonso, J.J.; Morris, E.P.; González-Ortiz, V.; Rueda-Márquez, J.J.; Pérez-Lloréns, J.L. Effects of intertidal seagrass habitat fragmentation on turbulent diffusion and retention time of solutes. Mar. Pollut. Bull. 2012, 64, 2471–2479. [Google Scholar] [CrossRef] [PubMed]
- Dennison, W.C. Effects of light on seagrass photosynthesis, growth and depth distribution. Aquat. Bot. 1987, 27, 15–26. [Google Scholar] [CrossRef]
- Marbà, N.; Duarte, C.M.; Holmer, M.; Martínez, R.; Basterretxea, G.; Orfila, A.; Jordi, A.; Tintoré, J. Effectiveness of protection of seagrass (Posidonia oceanica) populations in Cabrera National Park (Spain). Environ. Conserv. 2002, 29, 509–518. [Google Scholar] [CrossRef]
- Hendriks, I.E.; Sintes, T.; Bouma, T.J.; Duarte, C.M. Experimental assessment and modeling evaluation of the effects of the seagrass Posidonia oceanica on flow and particle trapping. Mar. Ecol. Prog. Ser. 2008, 356, 163–173. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Chen, Y.; Wang, H. Analytical expression for predicting the reduced settling velocity of small particles in turbulence. Environ. Fluid Mech. 2020, 20, 905–922. [Google Scholar] [CrossRef]
- González-Ortiz, V.; Egea, L.G.; Jiménez-Ramos, R.; Moreno-Marín, F.; Pérez-Llorens, J.L.; Bouma, T.J.; Brun, F.G. Interactions between seagrass complexity, hydrodynamic flow and biomixing after food availability for associated filter-feeder organisms. PLoS ONE 2014, 9, e104949. [Google Scholar] [CrossRef]




| Site | n (Shoots m−2) | T (s) | Abare sand (m2) | Atotal (m2) | Fragmentation (%) | Uw (cm s−1) | TKE (cm2 s−2) | Wavelength (m) |
|---|---|---|---|---|---|---|---|---|
| 1 | 259 | 2.56 | 359.9 | 2622.2 | 13.7 | 0.90 | 2.55 | 10.25 |
| 2 | 422 | 2.67 | 1423.6 | 2247.4 | 63.3 | 0.98 | 2.19 | 11.38 |
| 3 | 387 | 3.17 | 537.6 | 2442.9 | 22.5 | 1.20 | 1.68 | 15.61 |
| 4 | 400 | 3.64 | 389.2 | 2162 | 18.0 | 1.08 | 4.03 | 24.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serra, T.; Gracias, N.; Hendriks, I.E. Fragmentation in Seagrass Canopies Can Alter Hydrodynamics and Sediment Deposition Rates. Water 2020, 12, 3473. https://doi.org/10.3390/w12123473
Serra T, Gracias N, Hendriks IE. Fragmentation in Seagrass Canopies Can Alter Hydrodynamics and Sediment Deposition Rates. Water. 2020; 12(12):3473. https://doi.org/10.3390/w12123473
Chicago/Turabian StyleSerra, Teresa, Nuno Gracias, and Iris E. Hendriks. 2020. "Fragmentation in Seagrass Canopies Can Alter Hydrodynamics and Sediment Deposition Rates" Water 12, no. 12: 3473. https://doi.org/10.3390/w12123473
APA StyleSerra, T., Gracias, N., & Hendriks, I. E. (2020). Fragmentation in Seagrass Canopies Can Alter Hydrodynamics and Sediment Deposition Rates. Water, 12(12), 3473. https://doi.org/10.3390/w12123473






