An Application of Correlation and Spectral Analysis in Hydrological Study of Neighboring Karst Springs
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Available Data
2.3. Methods
- no effect—input time series x is an antecedent cause of output time series y and there is no relationship between series z and y,
- explanation effect (control effect)—control series z is an antecedent cause of output series y and there is no relationship between series x and y,
- partial explanation effect—input series x is an antecedent cause of output series y, but control series z is also either antecedent or intervening cause,
- suppression effect—control series z has a positive effect through one path and a negative effect through another path, or when control series z is weakly correlated with one of the original series.
3. Results
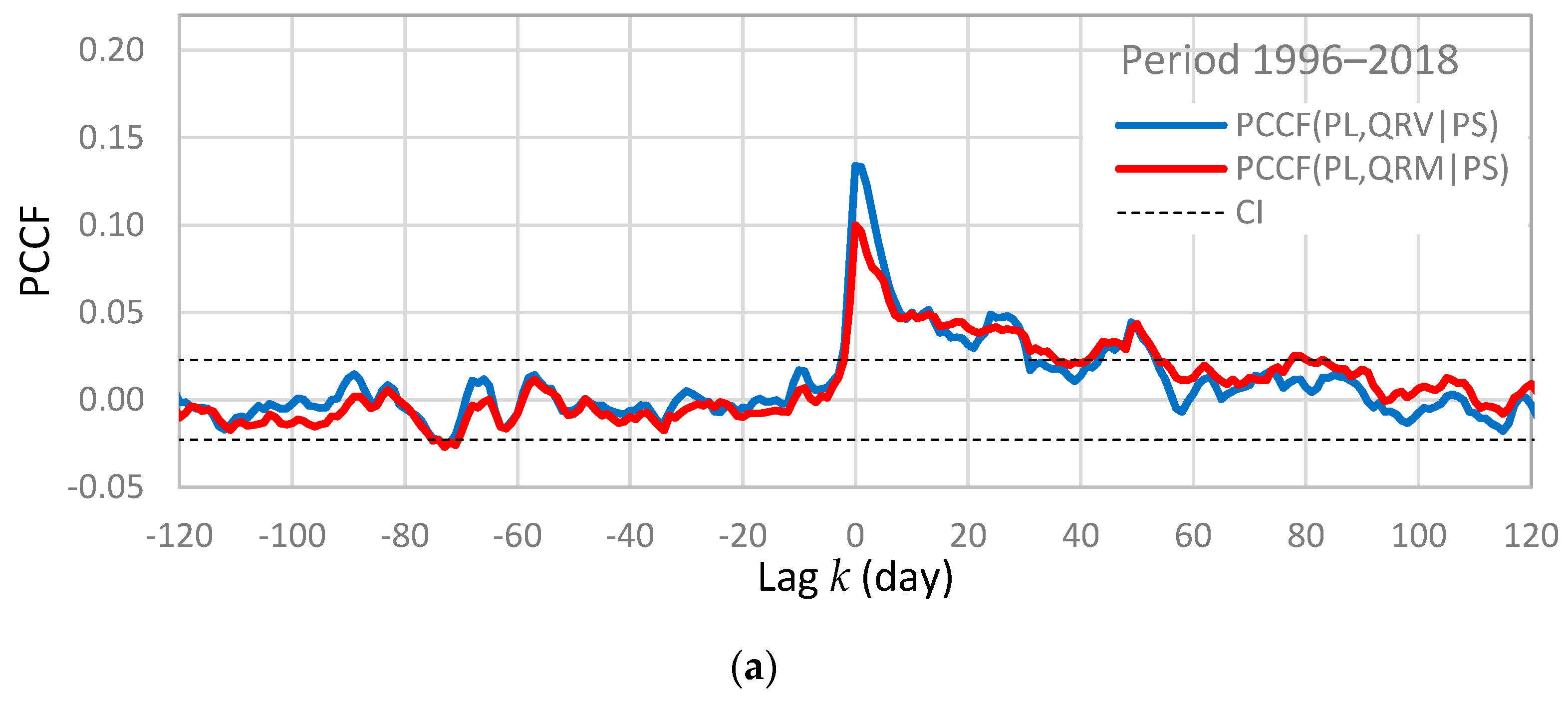
- The seasonal periodicity observed in rainfall (Figure 5a) is manifested in all functions, especially at negative lags where statistically significant values exist. This periodicity is more evident for the discharge from Rumin Mali (CCF(PS,QRM) and CCF(PL,QRM) in Figure 6) than for the Rumin Veliki (CCF(PS,QRV) and CCF(PL,QRV) in Figure 6). This result is in accordance with the results of spectral analyses, where the spectral density function for the Rumin Mali in Figure 4a obtained for the period 1996–2018 has larger values at frequency 0.00274 1/day than the spectral density function for the Rumin Veliki in Figure 4b for the same period.
- Differences between CCF(PS,QRM) and CCF(PL,QRM) and between CCF(PS,QRV) and CCF(PL,QRV) are small, which shows that the rainfall from MS Sinj and MS Livno produce similar cross-correlation functions. The same result is obtained also for RG Bitelić Donji for the period 1999–2008, which means that the entire catchment probably has a similar variation of daily rainfall, considering a long period.
- The time delay is the same for all functions. It amounts 1 day, so the pressure pulse is quickly transferred towards both springs after rainfall.
- CCF(PS,QRV) and CCF(PL,QRV) have larger values at lags below 10 days than CCF(PS,QRM) and CCF(PL,QRM), which means that the discharge from Rumin Veliki is better correlated with rainfall during the period of quick flow. On the other hand, the discharge from Rumin Mali is better correlated with rainfall during the period of baseflow. The spring Rumin Mali also has evidently longer duration of response. Specifically, CCF(PS,QRM) and CCF(PL,QRM) become statistically insignificant at legs above approximately 135 days, whereas CCF(PS,QRV) and CCF(PL,QRV) become insignificant at legs above 92 days. These results show that a difference in the degree of karstification between the aquifers of two springs exist.
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Milanović, P. Karst Hydrogeology; Water Resources Publication: Littleton, CO, USA, 1981. [Google Scholar]
- Bonacci, O. Karst Hydrology: With Special Reference to the Dinaric Karst; Springer: Berlin, Germany, 1987. [Google Scholar]
- White, W.B. Karst hydrology: Recent developments and open questions. Eng. Geol. 2002, 65, 85–105. [Google Scholar] [CrossRef]
- Ford, D.; Williams, P. Karst Hydrogeology and Geomorphology; Wiley: Chichester, UK, 2007. [Google Scholar]
- Atkinson, T.C. Diffuse flow and conduit flow in limestone terrain in the Mendip Hills, Somerset (Great Britain). J. Hydrol. 1977, 35, 93–110. [Google Scholar] [CrossRef]
- Vesper, D.J.; Loop, C.M.; White, W.B. Contaminant transport in karst aquifers. Theor. Appl. Karstology 2001, 13, 63–73. [Google Scholar]
- Kresic, N.; Stevanović, Z. Groundwater Hydrology of Springs: Engineering, Theory, Management, and Sustainability; Elsevier Butterworth-Heinemann: Burlington, MA, USA, 2010. [Google Scholar]
- Stevanović, Z. Major springs of southeastern Europe and their utilization. In Groundwater Hydrology of Springs: Engineering, Theory, Management, and Sustainability; Krešić, N., Stevanović, Z., Eds.; Elsevier: Oxford, UK, 2010; pp. 391–412. [Google Scholar]
- Goldscheider, N.; Drew, D. Methods in Karst Hydrogeology; Taylor & Francis Group: Leiden, The Netherlands, 2007. [Google Scholar]
- Komatina, M. Hydrogeologic features of Dinaric karst. In Hydrogeology of the Dinaric Karst; Mijatović, B., Ed.; Geozavod: Belgrade, Serbia, 1983; pp. 45–58. [Google Scholar]
- Worthington, S.R. Karst Hydrogeology of the Canadian Rocky Mountains; McMaster University: Hamilton, ON, Canada, 1991. [Google Scholar]
- Shumway, R.D.; Stoffer, D.S. Time Series Analysis and Its Applications; Springer: New York, NY, USA, 2000. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis, Forecasting and Control; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chatfield, C. The Analyses of Time Series: An Introduction, 6th ed.; Chapman & Hall: Boca Raton, FL, USA, 2004. [Google Scholar]
- Mangin, A. Pour une meilleure connaissance des systmes hydrologiques partir des analyses correlatoire et spectrale [For a better knowledge of hydrological systems by means of correlation and spectrum analyses]. J. Hydrol. 1984, 67, 25–43. [Google Scholar] [CrossRef]
- Padilla, A.; Pulido-Bosch, A. Study of hydrographs of karstic aquifers by means of correlation and cross-spectral analysis. J. Hydrol. 1995, 168, 73–89. [Google Scholar] [CrossRef]
- Larocque, M.; Mangin, A.; Razack, M.; Banton, O. Contribution of correlation and spectral analyses to the regional study of a large karst aquifer (Charente, France). J. Hydrol. 1998, 205, 217–231. [Google Scholar]
- Angelini, P. Correlation and spectral analysis of two hydrogeological systems in Central Italy. Hydrol. Sci. J. 1997, 42, 425–438. [Google Scholar] [CrossRef]
- Labat, D.; Ababou, R.; Mangin, A. Rainfall-runoff relationsfor karstic springs. Part I: Convolution and spectral analyses. J. Hydrol. 2000, 238, 123–148. [Google Scholar] [CrossRef]
- Mathevet, T.; Lepiller, M.; Mangin, A. Application of time-series analyses to the hydrological functioning of an Alpine karstic system: The case of Bange-L’Eau-Morte. Hydrol. Earth Syst. Sci. 2004, 8, 1051–1064. [Google Scholar] [CrossRef]
- Rahnemaei, M.; Zare, M.; Nematollahi, A.R.; Sedghi, H. Application of spectral analysis of daily water level and spring discharge hydrographs data for comparing physical characteristics of karstic aquifers. J. Hydrol. 2005, 311, 106–116. [Google Scholar] [CrossRef]
- Panagopoulos, G.; Lambrakis, N. The contribution of time series analysis to the study of the hydrodynamic characteristics of the karst systems: Application on two typical karst aquifers of Greece (Trifilia, Almyros Crete). J. Hydrol. 2006, 329, 368–376. [Google Scholar] [CrossRef]
- Jemcov, I.; Petrič, M. Measured precipitation vs. effective infiltration and their influence on the assessment of karst systems based on results of the time series analysis. J. Hydrol. 2009, 379, 304–314. [Google Scholar] [CrossRef]
- Bouchaou, L.; Mangin, A.; Chauve, P. Turbidity mechanism of water from a karstic spring: Example of the Ain Asserdoune spring (Beni Mellal Atlas, Morocco). J. Hydrol. 2002, 265, 34–42. [Google Scholar] [CrossRef]
- Massei, N.; Dupont, J.P.; Mahler, B.J.; Laignel, B.; Fournier, M.; Valdes, D.; Ogier, S. Investigating transport properties and turbidity dynamics of a karst aquifer using correlation, spectral, and wavelet analyses. J. Hydrol. 2006, 329, 244–257. [Google Scholar] [CrossRef]
- Bailly-Comte, V.; Jourde, H.; Roesch, A.; Pistre, S.; Batiot-Guilhe, C. Time series analyses for Karst/River interactions assessment: Case of the Coulazou river (southern France). J. Hydrol. 2008, 349, 98–114. [Google Scholar] [CrossRef]
- Tam, V.T.; De Smedt, F.; Batelaan, O.; Dassargues, A. Characterization of a cavern conduit system in Vietnam by time series correlation, cross-spectrum and wavelet analyses. Hydrol. Sci. J. 2004, 49, 879–900. [Google Scholar] [CrossRef]
- Gill, L.W.; Naughton, O.; Johnston, P.M.; Basu, B.; Ghosh, B. Characterization of hydrogeological connections in a lowland karst network using time series analysis of water levels in ephemeral groundwater-fed lakes (turloughs). J. Hydrol. 2013, 499, 289–302. [Google Scholar] [CrossRef]
- Herman, E.K.; Toran, L.; White, W.B. Quantifying the place of karst aquifers in the groundwater to surface water continuum: A time series analysis study of storm behaviour in Pennsylvania water resources. J. Hydrol. 2009, 376, 307–317. [Google Scholar] [CrossRef]
- Bailly-Comte, V.; Martin, J.B.; Screaton, E.J. Time variant cross correlation to assess residence time of water and implication for hydraulics of a sink-rise karst system. Water Resour. Res. 2011, 47, 1–16. [Google Scholar] [CrossRef]
- Bailly-Comte, V.; Martin, J.B.; Jourde, H.; Screaton, E.J.; Pistre, S.; Langston, A. Water exchange and pressure transfer between conduits and matrix and their influence on hydrodynamics of two karst aquifers with sinking streams. J. Hydrol. 2010, 386, 55–66. [Google Scholar] [CrossRef]
- Delbart, C.; Valdes, D.; Barbecot, F.; Tognelli, A.; Richon, P.; Couchoux, L. Temporal variability of karst aquifer response time established by the sliding-windows cross-correlation method. J. Hydrol. 2014, 511, 580–588. [Google Scholar] [CrossRef]
- Mayaud, C.; Wagner, T.; Benischke, R.; Birk, S. Single event time series analysis in a binary karst catchment evaluated using a groundwater model (Lurbach System, Austria). J. Hydrol. 2014, 511, 628–639. [Google Scholar] [CrossRef] [PubMed]
- Pinault, J.; Plagnes, V.; Aquilana, L.; Bakalowicz, M. Inverse modeling of the hydrological and the hydrochemical behavior of hydrosystems: Characterization of karst system functioning. Water Resour. Res. 2001, 37, 2191–2204. [Google Scholar]
- Fu, T.; Chen, H.; Wang, K. Structure and water storage capacity of a small karst aquifer based on stream discharge in southwest China. J. Hydrol. 2016, 534, 50–62. [Google Scholar] [CrossRef]
- Delbart, C.; Valdés, D.; Barbecot, F.; Tognelli, A.; Couchoux, L. Spatial organization of the impulse response in a karst aquifer. J. Hydrol. 2016, 537, 19–26. [Google Scholar] [CrossRef]
- Jemcov, I. Impact assessment of grout curtain on the hydraulic behavior in karst, based on time a series analysis. Environ. Earth Sci. 2019, 78, 1–17. [Google Scholar] [CrossRef]
- Paiva, I.; Cunha, L. Characterization of the hydrodynamic functioning of the Degracias-Sicó Karst Aquifer, Portugal. Hydrogeol. J. 2020, 28, 2613–2629. [Google Scholar] [CrossRef]
- Tamburini, A.; Menichetti, M. Groundwater Circulation in Fractured and Karstic Aquifers of the Umbria-Marche Apennine. Water 2020, 12, 1039. [Google Scholar]
- Jukić, D.; Denić-Jukić, V. Partial spectral analysis of hydrological time series. J. Hydrol. 2011, 400, 223–233. [Google Scholar] [CrossRef]
- Jukić, D.; Denić-Jukić, V. Investigating relationships between rainfall and karst-spring discharge by higher-order partial correlation functions. J. Hydrol. 2015, 530, 24–36. [Google Scholar] [CrossRef]
- Jukić, D.; Denić-Jukić, V. A theoretical basis for application of partial correlation functions in hydrological system analysis with reference to karst. In Proceedings of the 17th International Multidisciplinary Scientific GeoConference SGEM 2017, Vienna, Austria, 27–29 November 2017; pp. 11–18. [Google Scholar]
- Denić-Jukić, V.; Kadić, A.; Jukić, D. Higher-order partial cross-correlation function as a tool for investigating hydrological relations in karst. In Proceedings of the 17th International Multidisciplinary Scientific GeoConference SGEM 2017, Vienna, Austria, 27–29 November 2017; pp. 187–194. [Google Scholar]
- Kadić, A.; Denić-Jukić, V.; Jukić, D. Revealing hydrological relations of adjacent karst springs by partial correlation analysis. Hydrol. Res. 2018, 49, 616–633. [Google Scholar] [CrossRef]
- Kadić, A.; Denić-Jukić, V.; Jukić, D. Analiza meteoroloških i hidroloških odnosa u kršu primjenom kros-korelacijske funkcije višeg reda. Hrvat. Vode 2019, 109, 201–210. [Google Scholar]
- Magdalenić, A. Hidrogeologija sliva Cetine. Krš Jugosl. 1971, 7, 89–169. [Google Scholar]
- Slišković, I. Vode u Kršu Slivova Neretve i Cetine; HGI: Zagreb, Croatia, 2014. [Google Scholar]
- Bonacci, O.; Roje-Bonacci, T. The influence of hydroelectrical development on the flow regime of the karstic river Cetina. Hydrol. Process. 2003, 17, 1–15. [Google Scholar] [CrossRef]
- Bonacci, O. Hidrološka analiza krškog izvora Rumin Veliki. Hrvat. Vode 2015, 93, 201–210. [Google Scholar]
- Bonacci, O.; Buzjak, N.; Roje-Bonacci, T. Changes in hydrological regime caused by human intervention in karst: A case of the Rumin Springs. Hydrol. Sci. J. 2016, 61, 2387–2398. [Google Scholar] [CrossRef]
- Jukić, D.; Slatina, I.; Denić-Jukić, V. Effects of hydropower reservoirs on hydrology of two adjacent karst springs. In Proceedings of the 18th International Multidisciplinary Scientific GeoConference SGEM2018, Vienna, Austria, 3–6 December 2018; pp. 267–274. [Google Scholar]
- Pavlek, K.; Faivre, S. Geomorphological changes of the Cetina River channels since the end of the nineteenth century, natural vs anthropogenic impacts (the Dinarides, Croatia). Environ. Earth Sci. 2020, 79, 1–16. [Google Scholar] [CrossRef]
- Filipčić, A. Climatic regionalization of Croatia according to W. Köppen for the standard period 1961–1990 in relation to the period 1931–1960. Acta Geogr. Croat. 1998, 34, 1–15. [Google Scholar]
- Pandžić, K.; Cesarec, K.; Grgić, B. An analysis of the relationship between precipitation and discharge fields over a karstic river basin. Int. J. Climatol. 1997, 17, 891–901. [Google Scholar]
- Pandžić, K. and Trninić, D. Principal component analysis of the annual regime of hydrological and meteorological fields in a river basin. Int. J. Climatol. 1991, 11, 909–922. [Google Scholar] [CrossRef]
- Pandzić, K.; Trninić, D. Principal component analysis of a river basin discharge and precipitation anomaly fields associated with the global circulation. J. Hydrol. 1992, 132, 343–360. [Google Scholar] [CrossRef]
- Stevanović, Z.; Kukurić, N.; Pekaš, Ž.; Jolović, B.; Pambuku, A.; Radojević, D. Dinaric Karst Aquifer—One of the world’s largest transboundary systems and an ideal location for applying innovative and integrated water management. In Karst without Boundaries; Stevanović, Z., Krešić, N., Kukurić, N., Eds.; CRC Press: London, UK, 2016; pp. 3–25. [Google Scholar]
- Stevanović, Z.; Ristić-Vakanjac, V.; Milanović, S.; Vasić, H.; Petrović, B.; Čokorilo-Ilić, M. Karstification depth and storability as main factors of karst aquifer regimes: Some examples from southern Alpine branches (SE Europe and Middle East). Environ. Earth Sci. 2015, 74, 227–240. [Google Scholar] [CrossRef]








| 1950–1972 | 1996–2018 | 1999–2008 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Rumin Mali | Rumin Veliki | Livno | Sinj | Rumin Mali | Rumin Veliki | Bitelić Donji | |||||
| QRM (m3/s) | QRV (m3/s) | PL (mm) | TL (°C) | RHL (%) | PS (mm) | TS (°C) | RHS (%) | QRM (m3/s) | QRV (m3/s) | PB (mm) | |
| Min. | 0 | 0.26 | 0 | −15.6 | 15 | 0 | −7.2 | 22 | 0 | 0.04 | 0 |
| Mean | 2.74 | 19.2 | 3.21 | 10.2 | 74 | 3.18 | 13.1 | 69 | 1.61 | 6.91 | 3.47 |
| Max. | 16.5 | 106 | 125.1 | 29.1 | 100 | 153.4 | 30.4 | 100 | 9.38 | 87.6 | 187.7 |
| S. D. | 3.09 | 20.1 | 8.06 | 12.1 | 8.03 | 8.53 | 19.7 | 7.63 | 2.19 | 12.0 | 9.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denić-Jukić, V.; Lozić, A.; Jukić, D. An Application of Correlation and Spectral Analysis in Hydrological Study of Neighboring Karst Springs. Water 2020, 12, 3570. https://doi.org/10.3390/w12123570
Denić-Jukić V, Lozić A, Jukić D. An Application of Correlation and Spectral Analysis in Hydrological Study of Neighboring Karst Springs. Water. 2020; 12(12):3570. https://doi.org/10.3390/w12123570
Chicago/Turabian StyleDenić-Jukić, Vesna, Ana Lozić, and Damir Jukić. 2020. "An Application of Correlation and Spectral Analysis in Hydrological Study of Neighboring Karst Springs" Water 12, no. 12: 3570. https://doi.org/10.3390/w12123570
APA StyleDenić-Jukić, V., Lozić, A., & Jukić, D. (2020). An Application of Correlation and Spectral Analysis in Hydrological Study of Neighboring Karst Springs. Water, 12(12), 3570. https://doi.org/10.3390/w12123570






