Bayesian Model Weighting: The Many Faces of Model Averaging

Abstract

Model averaging makes it possible to use multiple models for one modelling task, like predicting a certain quantity of interest. Several Bayesian approaches exist that all yield a weighted average of predictive distributions. However, often, they are not properly applied which can lead to false conclusions. In this study, we focus on Bayesian Model Selection (BMS) and Averaging (BMA), Pseudo-BMS/BMA and Bayesian Stacking. We want to foster their proper use by, first, clarifying their theoretical background and, second, contrasting their behaviours in an applied groundwater modelling task. We show that only Bayesian Stacking has the goal of model averaging for improved predictions by model combination. The other approaches pursue the quest of finding a single best model as the ultimate goal, and use model averaging only as a preliminary stage to prevent rash model choice. Improved predictions are thereby not guaranteed. In accordance with so-called $\mathcal{M}$-settings that clarify the alleged relations between models and truth, we elicit which method is most promising.

1. Introduction

Models are used to investigate a single phenomenon or a whole system. Different models that are based on different concepts allow for looking at the physical truth from different angles, or to use contrasting approaches to prediction. Therefore, employing multiple models instead of only one has the potential for increasing system understanding and enhancing predictive power. However, each model has its own uncertainties, often classified as input, parameter, output uncertainties [1,2], or by other categories. Furthermore, when using multiple models, there is uncertainty in choosing between them. This is sometimes called conceptual uncertainty ([3] and references therein).

Having a set of alternative models that share the same objective, e.g., predicting a specific quantity of interest (QoI), it often remains unclear how to optimally operate them as an ensemble. Attempts to solve this issue have yielded a plethora of what we suggest to call multi-model frameworks (MMF): methods that quantify conceptual uncertainty between models, rate them accordingly and allow us to operate them as weighted ensemble.

Typical examples for such model rating methods are information criteria like the Akaike IC (AIC [4,5]) or the Bayesian IC (BIC [6]). Their results can be transferred into model weights that resemble the relative conceptual uncertainty between the models in the set. Based on these weights, a single model can be selected or a weighted ensemble can be obtained from the set. A popular BIC-type weighting method is Bayesian model averaging (BMA [7,8,9]).

Bayesian statistics offer uniform and coherent principles for quantifying uncertainty [10]. From a Bayesian perspective, uncertainty means lack of knowledge, and corresponding probability distributions—or probability density functions (PDFs)—express degree of belief in the available knowledge [11]. In light of evidence like observed data, this knowledge changes and Bayesian distributions are updated from so-called priors to posteriors.

Model averaging under the Bayesian paradigm means averaging of probability distributions implied by the models. Honouring conceptual uncertainty, Bayesian multi-model frameworks (BMMFs) like BMA use model weights to average predictive distributions of multiple models to cover modelling uncertainty more broadly. Several other BMMFs for model averaging exist, but the meaning and purpose of model weights between them deviate tremendously (see [12]). This complicates their use and often leads to misinterpretations.

We intend to clarify the reasons thereof and show how to ensure appropriate use of BMMFs. We focus on five popular methods: Bayesian model selection (BMS) and Bayesian model averaging (BMA), so-called Pseudo-BMS and Pseudo-BMA, and Bayesian Stacking (BS; e.g., [13]), which recently attracted increased attention ([14] and references therein).

In order to highlight similarities and differences between the BMMFs in model weighting, we use a modelling task and corresponding models that were already employed successfully in Bayesian multi-model inference by Schöniger et al. [15]. We present consecutive work to Schöniger et al. [15] that focused on model weighting via BMS and BMA as methods of choice for selecting the appropriate level of model complexity in applied modelling. Schöniger et al. [15] demonstrated the suitability of BMS and BMA to accomplish this quest but also elicited limitations. We add Pseudo-BMS, Pseudo-BMA and Bayesian Stacking in order to contrast them to BMS and BMA. Additionally, we show under what circumstances and goals which of these methods is the most promising approach for model selection or averaging.

The remainder of this article is structured as follows: First, we present the theoretical underpinnings for all chosen methods, specifically putting the assumption into perspective of whether the allegedly true model, i.e., the data-generating process $M_{\mathrm{true}}$, is part of the set of models under consideration $\mathit{M}$. Second, we revisit the work of Schöniger et al. [15] as a basis for our comparison of BMMFs. Third, we analyse and contrast the evolution of model weights from all frameworks over growing data size in an applied modelling task. Thereby, we elicit differences and discuss proper use and caveats of each BMMF. It is our goal to foster broader application of the investigated methods. Hence, fourth and finally, we summarize key findings and conclude general rules for their employment.

2. Bayesian Multi-Model Frameworks

The Bayesian average of multiple models is a convex linear combination ($w_m\ge 0$ and ${\sum }_{m=1}^{N_M}{w}_m=1$) of the model-wise posterior predictive distributions (see [8,15]):

$$p\left(\mathit{y}\right|\mathit{D})=\sum _{m=1}^{N_M}p\left(\mathit{y}\right|\mathit{D},M_m)w\left(M_m\right|\mathit{D})$$

(1)

with the individual posterior predictive distribution $p\left(\mathit{y}\right|\mathit{D},M_m)$ of model $M_m$ for the quantity of interest $\mathit{y}$ given data $\mathit{D}$ and corresponding posterior model weight $w\left(M_m\right|\mathit{D})$. $\mathit{D}$ are measured observations, i.e., $N_s$ sampled instances of the QoI. All models are members of a finite set: $M_m\in \mathit{M}$.

Note that the averaging does not occur on the level of model outputs themselves, but on their corresponding distributions. If actual model outputs were averaged, they would receive an own probability distribution that would differ from the above convex combination (see, e.g., [12]).

2.1. BMS/BMA

The two popular methods Bayesian Model Selection and Bayesian Model Averaging (BMS/BMA [7,8,9]) are different stages of the same BMMF—a fact often ignored as already pointed out by Minka [16]. Selection or averaging simply refer to different levels of confidence, usually depending on the informativeness of the available data $\mathit{D}$. Until sufficient data are available for a reliable selection, weighted model averaging prevents a rash exclusion of alternatives. Given the currently available data $\mathit{D}$, the model weight $w_{\mathrm{BME}}$ of model $M_m$ is given by

$$\begin{array}{c}\hfill w_{\mathrm{BME}}\left(M_m\right|\mathit{D})=p\left(M_m\right|\mathbf{D})=\frac{p\left(\mathbf{D}\right|M_m)p\left(M_m\right)}{{\sum }_{k=1}^{N_M}p\left(\mathbf{D}\right|M_k)p\left(M_k\right)}.\end{array}$$

(2)

Only in BMS/BMA can model weights also be interpreted as model probabilities: $p\left(M_m\right|\mathbf{D})$ and $p\left(M_m\right)$ are the posterior and prior model probabilities, respectively, that $M_m$ is the true model $M_{\mathrm{true}}$ that generated $\mathbf{D}$. The updating is based on the marginal likelihood a.k.a. Bayesian Model Evidence (BME), i.e., the prior predictive density for data $\mathit{D}$:

$$\begin{array}{c}\hfill p\left(\mathit{D}\right|M_m)=\int p\left(\mathit{D}\right|{\mathsf{\Theta }}_m,M_m)p\left({\mathsf{\Theta }}_m\right|M_m)\mathrm{d}{\mathsf{\Theta }}_m.\end{array}$$

(3)

In the large-sample-limit of data, the weight of the allegedly true model is supposed to converge to 1, turning the weighted average of models (BMA) into a selection of the single best one (BMS)—“weights in BMA only reflect a statistical inability to distinguish the hypothesis based on limited data” [16]. Ultimately, BMS seeks to identify $M_{\mathrm{true}}$ based on its prior predictive density for $\mathit{D}$. The ability of a selection procedure to converge to the true model (e.g., [17]) is called “consistency”.

The consistency property results in a natural tendency towards simpler over more complex models of BMS/BMA (e.g., [2]). Following the principle of parsimony (see [18]), the best-rated model should always only be as complex as necessary and as simple as possible—just as the truth itself (see Section 2.5).

Since the evaluation of the marginal likelihood according to Equation (3) in BMS/BMA is typically a computationally challenging task, methods for its approximation are used. Among others, the most popular ones are the Kashyap (KIC) and the already mentioned Bayesian (BIC) information criteria [19].

2.2. Pseudo-BMS/BMA

The classic way of estimating accuracy and precision of model predictions for yet unseen data is via cross-validation (CV; e.g., [20]): Available observations $\mathit{D}$ are split up into a part to train/calibrate the model and a remaining part for testing/validating the model afterwards. There are many variants of CV, a very popular but computationally expensive one is leave-one-out (LOO) CV: Over $N_s$ iterations, one data point after another is held-out as testing data $D_o$, and the model is trained on the remaining data ${\mathit{D}}_{⌀}$. The model is then rated on the average performance over all iterations.

Pseudo-BMS and Pseudo-BMA refer to the Bayesian version of CV [21,22]—implying different stages of data availability, just as with BMS and BMA in Section 2.1. Model weights are based on the so-called expected logarithmic predictive density $elp{d}_{LOO,m}$ [23], gained from LOO-CV:

$$\begin{array}{c}\hfill w_{\mathrm{LOO}}\left(M_m\right|\mathit{D})=\frac{\exp \left(elp{d}_{LOO,m}\right)}{{\sum }_{k=1}^{N_M}\exp \left(elp{d}_{LOO,k}\right)}.\end{array}$$

(4)

Following the principle of LOO-CV, the $elp{d}_{LOO,m}$ is the sum of the point-wise posterior predictive densities $p\left(D_o\right|{\mathit{D}}_{⌀},M_m)$ over all held-out data points. This implies the assumption that all data points are independent and identically distributed (i.i.d.), which is a frequent point of criticism (see, e.g., invited and contributed Discussion in [14]). Thereby, $p\left(D_o\right|{\mathit{D}}_{⌀},M_m)$ is a marginalized likelihood, but, opposed to BMS/BMA, integrated over the posterior and not the prior parameter distribution:

$$elp{d}_{LOO,m}=\sum _{o=1}^{N_s}p\left(D_o\right|{\mathit{D}}_{⌀},M_m)=\sum _{o=1}^{N_s}\int p\left(D_o\right|\mathsf{\Theta })p\left(\mathsf{\Theta }\right|{\mathit{D}}_{⌀},M_m)\mathrm{d}\mathsf{\Theta }.$$

(5)

In the large-sample-limit, the highest weight for one model does not imply that it is also the true model. Pseudo-BMS/BMA is one of so-called non-consistent (see, e.g., [24]) model selection methods that lack the ability to converge to the true model since they implicitly assume that $M_{\mathrm{true}}$ is not part of $\mathit{M}$. They yield a rating of the best probabilistic accuracy-precision trade-off currently supported by the available data in approximating the true model. They do not test for model truth as BMS/BMA, but for posterior predictive skill.

This results in a natural tendency towards more complex models over simpler model approaches because it is assumed that more complex models with more functional features can approximate and predict the data-generating process more closely. Therefore, if a model in Pseudo-BMS/BMA receives highest model weight, this means two things: First, the winning model currently offers the best available trade-off between all model alternatives, and, second, another model with even more or new features could be added to the set. Potentially, this model of higher complexity is then able to approximate the data even better and strike a better trade-off between accuracy and precision. Pseudo-BMS/BMA implicitly expects that, as soon as more (informative) data are available, more and more complex models can be supported.

The famous AIC is an estimator for the expected logarithmic predictive density and hence the model weights in Equation (4) are also often called Akaike weights [25]. Based on different assumptions, further approximations exist, e.g., the Deviance (DIC) or Watanabe–Akaike (WAIC) information criteria [19].

2.3. Bayesian Stacking

Opposed to BMS/BMA and Pseudo-BMS/BMA that both ultimately seek to select a single best model over growing data, Bayesian Stacking offers an alternative for averaging model predictive distributions as combination. Originally, stacking is an approach for averaging point estimators from deterministic models ([14] and references therein). Le and Clarke [26] provide a Bayesian generalization for averaging probabilistic models.

Model weights in Bayesian Stacking are also evaluated based on point-wise posterior predictive densities per model $p\left(D_o\right|{\mathit{D}}_{⌀},M_m)$. However, opposed to Pseudo-BMA/BMS, they are not based on individual model’s point-wise posterior predictive densities. In Bayesian Stacking, they are the result of a weight optimization to maximize the common point-wise posterior predictive density from all models in $\mathit{M}$ as defined by (see [14]):

$${\widehat{\mathit{w}}}_{\mathrm{stack}}=arg\underset{\mathit{w}}{max}\frac{1}{N_s}\sum _{o=1}^{N_s}\ln \sum _{m=1}^{N_M}{w}_{m}p\left(D_o\right|{\mathit{D}}_{⌀},M_m).$$

(6)

Similar to Pseudo-BMS/BMA, Bayesian Stacking does not assume that one of the models in $\mathit{M}$ is $M_{\mathrm{true}}$. Hence, Bayesian Stacking seeks to optimize weights such that the common (rather than an individual) posterior predictive distribution yields the best probabilistic accuracy-precision trade-off. At the limit of growing data size, stable weights reflect constant model shares in the ensemble. Thus, the goal of Bayesian Stacking is to use the entire model set for best-possible linear combination in prediction. The optimized weights from Equation (6) can be seen as a maximum predictive likelihood parameter choice of the mixed model implied by Equation (1).

2.4. Bayesian Bootstrap

The model weights gained in both Pseudo-BMS/BMA and Bayesian Stacking use the held-out data points as proxies for the future data distribution [14]. Furthermore, the model weights in Bayesian Stacking are the result of an optimization and are potentially unstable. Hence, it is questionable whether the available data are a sufficient proxy also for future data and whether the obtained weights are trustworthy.

An approach to counteract data scarcity and instability is so-called bootstrapping [27]. It accounts for the uncertainty in definiteness of data $\mathit{D}$ [28]: Using re-sampling, the uncertainty of insufficient sampling from a distribution of interest [29] becomes quantifiable. In particular, Bayesian Bootstrapping uses a Dirichlet distribution to generate a non-parametric approximation of the posterior distribution of each sample [28].

Here, the distribution of interest is the data distribution coming from the data-generating process. Therefore, we look at the predictions of all models for each $D_o$ by defining the logarithmic LOO predictive density as ${\zeta }_{o,m}=\ln p\left(D_o\right|{\mathit{D}}_{⌀},M_m)$. Over b bootstrapping replications with $b=1:N_{BB}$, posterior probabilities ${\mathit{\alpha }}_{1:N_s,b}$ for $\mathit{\zeta }$ are drawn from (see [14]):

$${\mathit{\alpha }}_{1:N_s,b}\sim Dirichlet\left(\mathbf{1}\right).$$

(7)

For each b, marginalization over ${\mathit{\alpha }}_{1:N_s,b}$ yields the desired statistical moment [28], here the mean [14]:

$${\overline{\zeta }}_{b,m}=\sum _{o=1}^{N_s}{\alpha }_{o,b}{\zeta }_{o,m}.$$

(8)

Then, the expected bootstrapped model weights $w_m^{\mathrm{BB}}$ are

$$w_m^{\mathrm{BB}}=\frac{1}{N_{\mathrm{BB}}}\sum _{b=1}^{N_{\mathrm{BB}}}\frac{\exp \left(N_s{\overline{\zeta }}_{b,m}\right)}{{\sum }_{m=1}^{N_M}\exp \left(N_s{\overline{\zeta }}_{b,m}\right)}.$$

(9)

By applying the Bayesian Bootstrap, extreme model weights like 0 or 1 are typically counteracted and model weights are stabilized [14]. Bayesian Bootstrapping is inexpensive in terms of additional computational cost because required quantities have already been generated for evaluating the BMMFs in Section 2.2 and Section 2.3 and only need to be processed in one more step [30].

2.5. $\mathcal{M}$-Settings

The above methods react sensitively to the minute differences in how $M_{\mathrm{true}}$ (termed “true model”, “truth”, “data-generating process”, etc.) relates to the members of the model set $\mathit{M}$. For any modelling task at hand, these interrelations can be distinguished and interpreted by distinct $\mathcal{M}$-settings adopted from Bernardo and Smith [31]: $\mathcal{M}$-closed, $\mathcal{M}$-complete, and $\mathcal{M}$-open. In addition, we specify a so-called Quasi-$\mathcal{M}$-closed setting for applied modelling. The $\mathcal{M}$-settings are depicted schematically in Figure 1, and corresponding properties are summarized in

Table 1. Qualitative summary of the four $\mathcal{M}$-settings: $\mathcal{M}$-closed, Quasi-$\mathcal{M}$-closed, $\mathcal{M}$-complete and $\mathcal{M}$-open with respect to the true model.

Model (PDF)…	M-Closed	Quasi-M-Closed	M-Complete	M-Open
…can be conceptualized	fully	fully	fully	incompletely
…can be written down	fully	nearly	incompletely	impossibly
…matches actual true model (PDF)	fully	nearly	maybe closely	by chance

.

In a so-called $\mathcal{M}$-closed setting, one of the models in $\mathit{M}$ is in fact the data-generating true model $M_{\mathrm{true}}$. Identifying $M_{\mathrm{true}}$ is often referred to as consistent model selection [24,32]. Therefore, $\mathcal{M}$-closed is the only setting where model weights can actually express how likely it is for a particular model to be $M_{\mathrm{true}}$. Among the presented BMMFs, only BMS/BMA supports this: Each model weight represents the probability of the particular model to be the true model that generated the observed data.

While the requirement of model weights to sum up to one in all convex linear combination methods can simply be seen as an unbiasedness constraint, in BMS/BMA, it resembles the axiom that the probability of all elements in an event space $\mathsf{\Omega }$ must sum up to one $P\left(\mathsf{\Omega }\right)=1$. Therefore, the enumeration to one hard-codes the assumption that $\mathit{M}$ contains $M_{\mathrm{true}}$, so that $P\left(\mathit{M}\right)=1$, and that the models are mutually exclusive possibilities.

In real world applications, it is unlikely that one model in the set is in fact the true model. Therefore, for application purposes, we suggest to relax the strict definition of the $\mathcal{M}$-closed setting to a Quasi-$\mathcal{M}$-closed setting [12]: For example, mechanistic models might be developed to represent the true system up to the current state of physical knowledge, and modellers might be interested in isolating the one model with a prior predictive distribution being nearly identical to the true data distribution. We consider this a quasi-true model. Terming such a scenario a Quasi-$\mathcal{M}$-closed setting allows us to apply BMS/BMA while acknowledging the unavailability of $\mathcal{M}$-closed settings in applied sciences [30]—yet with the restriction that model weights do not resemble probabilities.

In both other settings, $\mathcal{M}$-complete and $\mathcal{M}$-open, the true model is not a member of model set $\mathit{M}$. In $\mathcal{M}$-complete, it is still hypothetically possible to conceptualize the true model because it has finite complexity. Thus, one could write it down in some (incomplete) fashion and at least come close to $M_{\mathrm{true}}$. $\mathcal{M}$-open is even more critical about the data-generating process. It can only be incompletely conceptualized and writing it down as a true model is impossible [14], e.g., because it would be of infinite complexity. In both settings, model weights do not represent probabilities of being true because $M_{\mathrm{true}}\notin \mathit{M}$ and therefore $P\left(\mathit{M}\right)<1$, so that $\mathit{M}\ne \mathsf{\Omega }$ and a probabilistic interpretation would violate the axiom $P\left(\mathsf{\Omega }\right)=1$.

In $\mathcal{M}$-complete and $\mathcal{M}$-open, BMMFs rather quantify the relative abilities of the calibrated ensemble members to approximate or imitate the truth. Hence, model rating is based on posterior (rather than prior) predictive densities. Modellers have two options: They can select a single best (but still wrong) model via Pseudo-BMS/BMA if operating only one model for predictions is desired. This could be the case if, e.g., model run times prohibit multiple model use or the one best model shall successively be enlarged with additional features [23]—or, if multiple models shall be employed together, e.g., to obtain a better coverage of predictive uncertainty, Bayesian Stacking might be more promising. The combination of model distributions also cannot match the unknown truth but minimizes the risk of missing it by dropping model alternatives.

3. Modelling Task

As an application case for illustrating the above discussions, we take the modelling task from Schöniger et al. [15] that is typical in hydrosystem modelling: Finding the best model for the spatial distribution of hydraulic conductivity K to parameterize an aquifer. In the following, we provide an overview of the study which investigated the suitability of BMS/BMA to accomplish this task. For more details and further information, we refer to Schöniger et al. [15].

3.1. System and Models Revisited

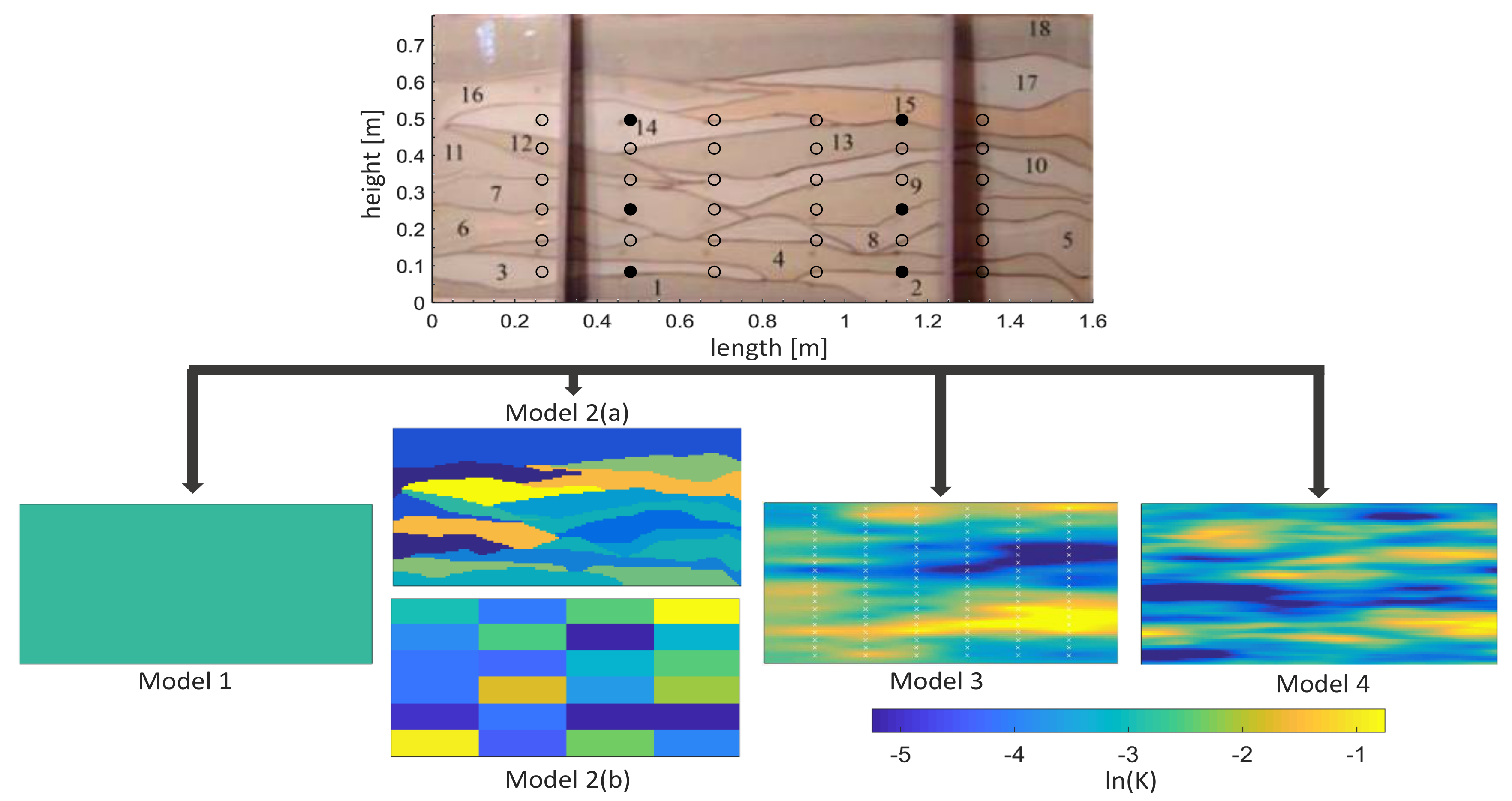
The modelled system was a synthetic laboratory-scale heterogeneous aquifer in a glass tank of 193.0 cm length, 82.6 cm height, and 10.2 cm depth that contained 18 different sand layers created by cyclic deposition of sediments [33]. The sandbox aquifer and the derived models are shown in Figure 2.

All models for this system are physics-based two-dimensional finite element models for fully saturated Darcy-flow. The models span a window of 160 cm length and 78 cm height as defined by Schöniger et al. [15] as relevant domain. A spatial resolution of 1 cm in each direction yielded 12,480 elements. Hydraulic conductivity was assigned cell-wise according to common parameterization approaches of increasing complexity [15]:

• a homogeneous model with a single effective parameter ($N_p=1$),
• a zonated model

  (a)

  with an informed zonation model based on the visible spatial distribution of sand layers ($N_p=19$),

  (b)

  with an uninformed zonation model that consists of unrealistic regular zones ($N_p=24$),

• a deterministic geostatistical model by Kriging based on stochastically parametrized pilot points for ln(K) ($N_p=120$),
• a stochastic geostatistical model generated from Fast Fourier Transform-based logarithmic multi-Gaussian random fields ($N_p$ = 12,480).

Besides the plain number of parameters $N_p$ that serves as measure for so-called parametric complexity, Schöniger et al. [15] presented alternative metrics based on factor analysis for measuring model complexity. All measures confirmed the increasing order of complexity from models 1 to 4, although the relative differences from one model to the next more complex one varied between the metrics.

3.2. Data and Numerical Simulation

In the original experiment conducted by Illman et al. [33], a regular grid of ports with 1.3 cm diameter granted access to the aquifer for measuring the hydraulic head during pumping tests. Over a number of sequential steady-state pumping tests (from which Schöniger et al. [15] selected six), one alternating port served as pumping port and 35 others were used to observe hydraulic drawdown, yielding a total of 210 data points in six batches each of 35 observations. The standard deviation of measurement error was 2 cm.

For rating the alternative parameterization models within the BMS/BMA framework, it was assessed how successful each model is in reproducing the measured data. Therefore, pumping tests were simulated with each model approach for the same ports as in the experiment. Model-specific parameters were drawn from the respective prior parameter distribution. These were based on physical hydraulic properties of the synthetic aquifer that were measured during the installation of ports [33]. Predictions from each statistical parameter sample were then obtained by plain forward model runs.

For Bayesian inference, an uncorrelated Gaussian likelihood function that represents the measurement error was used. Each model-specific marginalized likelihood (BME) was obtained by Monte Carlo integration over the entire prior parameter distribution. In accordance with rising model complexity, $2.0·{10}^5$ samples for the homogeneous model and $1.0·{10}^7$ samples for the other four approaches were drawn to assure convergence.

3.3. Former Results

Schöniger et al. [15] investigated the ability and limitations of BMS/BMA to identify the allegedly true data-generating process under a growing amount of available observations. We want to highlight the two major findings:

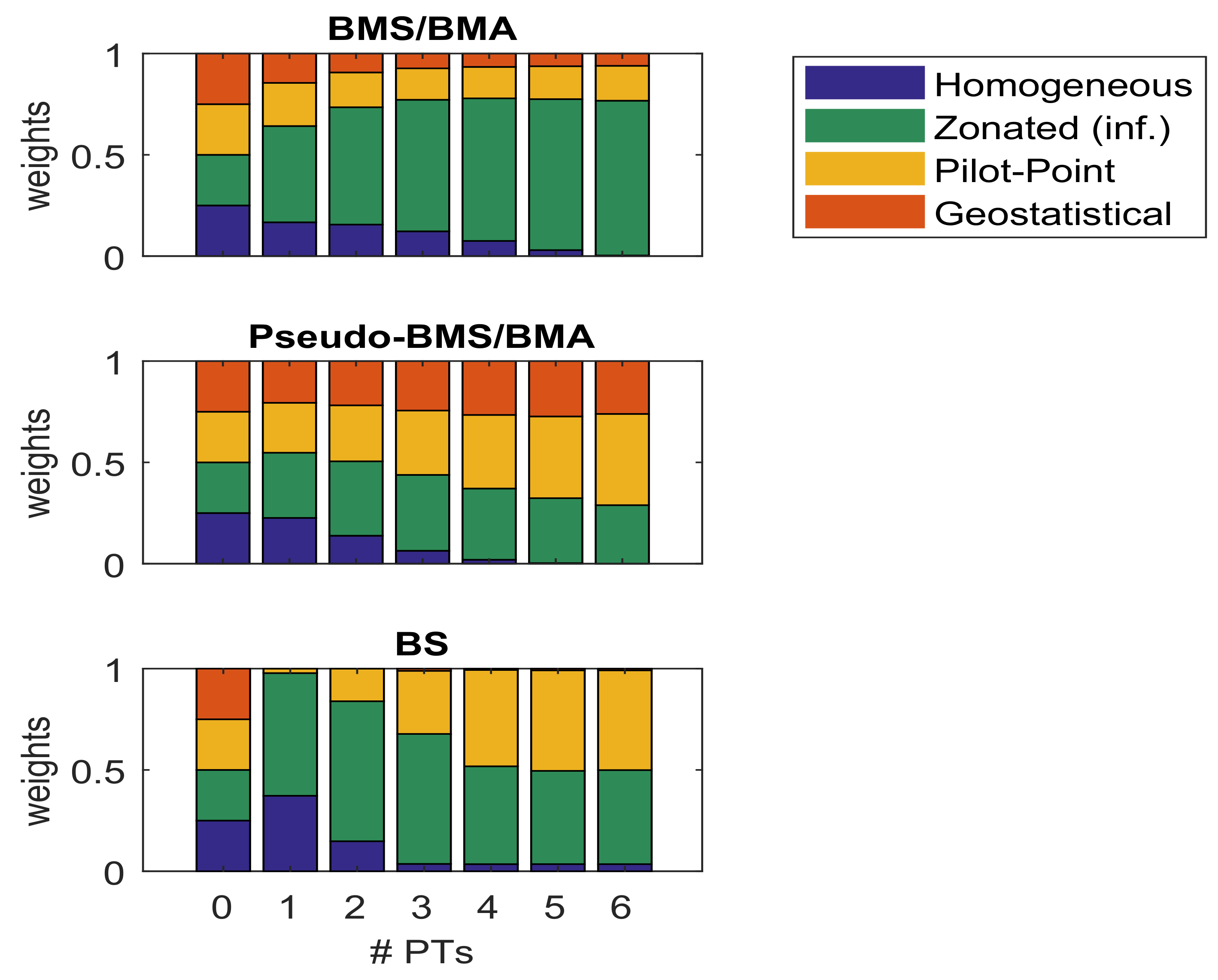
First, the evolution of model weights was analysed for two deviating model ensembles: One contained a visually close physical representation of the modelled system (informed zonated model 2a) and the other one an apparently wrong representation (uninformed zonated model 2b). For the first ensemble, BMS/BMA showed a clear convergence toward the (informed) zonated model. However, the uninformed zonated model was not prefered in the second ensemble, despite having a much lower model complexity than the geostatistical model alternatives.

Second, a model justifiability analysis based on a model confusion matrix was introduced. Using model (prior) predictions from all models in the first ensemble as synthetic observations, it was evaluated, first, how well BMS/BMA recognizes the data-generating model or another one as true model and, second, what the maximal model weights are that can be expected when only a limited subset of data are available. Given the limited amount of data (max. 210 observations), it was shown that, except for the simplest homogeneous model, none of the other models achieved a model weight of one even if actually being the data-generating model.

3.4. Study Extension

As extension to the investigation of Schöniger et al. [15], we shift focus on contrasting the model weight evolution of alternative BMMFs by

• explicitly arranging the model ensembles and data in $\mathcal{M}$-settings according to Section 2.5 and
• applying Pseudo-BMS/BMA and Bayesian Stacking in addition to BMS/BMA within the arranged $\mathcal{M}$-settings to contrast the respective evolution of model weights.

We use the same data and also work with the numerical samples from each model’s prior parameter distribution to obtain marginal likelihoods. Exploiting the i.i.d. assumption for $\mathit{D}$ and Bayes’ theorem, we then obtain the point-wise posterior predictive densities $p\left(D_o\right|{\mathit{D}}_{⌀})$ via:

$$\begin{array}{cc}\hfill p\left(D_o\right|{\mathit{D}}_{⌀})& =\int p\left(D_o\right|\mathsf{\Theta })p\left(\mathsf{\Theta }\right|{\mathit{D}}_{⌀})\mathrm{d}\mathsf{\Theta }\hfill \\ \hfill & =\int p\left(D_o\right|\mathsf{\Theta })\frac{p\left({\mathit{D}}_{⌀}\right|\mathsf{\Theta })p\left(\mathsf{\Theta }\right)}{p\left({\mathit{D}}_{⌀}\right)}\mathrm{d}\mathsf{\Theta }\hfill \\ \hfill & \stackrel{\mathrm{iid}}{=}\frac{1}{p\left({\mathit{D}}_{⌀}\right)}\int p(D_o,{\mathit{D}}_{⌀}|\mathsf{\Theta })p\left(\mathsf{\Theta }\right)\mathrm{d}\mathsf{\Theta }=\frac{p\left(\mathit{D}\right)}{p\left({\mathit{D}}_{⌀}\right)}.\hfill \end{array}$$

(10)

3.5. $\mathcal{M}$-Settings in Practise

The models and data are arranged in an $\mathcal{M}$-closed, an Quasi-$\mathcal{M}$-closed, and an $\mathcal{M}$-complete setting as depicted in Figure 3. An $\mathcal{M}$-open setting is not considered because it is possible to fully conceptualize the controlled laboratory experiment by Illman et al. [33]. For the considered $\mathcal{M}$-settings, it is either the observed or the synthetically generated data that represents the data-generating process (DGP).

The $\mathcal{M}$-closed setting consists of the homogeneous (1), the informed zonated (2a), the pilot-point (3) and the stochastic geostatistical (4) models. The DGP is represented by the synthetic observations generated with the informed zonated model (2a) as presumably closest physical representation of the true system. Exchanging the synthetic data by actual observations and leaving the ensemble the same turns the setting into our proposed Quasi-$\mathcal{M}$-closed case: unlike in typical field-scale experiments, the informed zonated model is a very accurate representation of the laboratory sandbox aquifer. However, it does not fully resolve the true system perfectly, e.g., the fringes between the different sand layers will be a mixture of sand grains that is not represented in the model. The difference between these two settings will indicate the strength of deviations one obtains when mistreating the assumption $M_{\mathrm{true}}\in \mathit{M}$ in real applications.

Finally, exchanging the informed zonated (2a) by the uninformed zonated (2b) model displays the $\mathcal{M}$-complete setting: it is only possible to incompletely conceptualize the true system with its zones, parameters, boundary conditions, etc. Hence, none of the ensemble members is an accurate representation of the true system. $\mathcal{M}$-complete refers to the rather typical situation in applied modelling that, even if we include everything we know about the observed system, we cannot fully resolve it but only approximate it, e.g., by matching statistical moments of its properties (as with models 3 and 4).

As synthetic data in the $\mathcal{M}$-closed setting, we use model predictions from the justifiability analysis in Schöniger et al. [15] for comparability. The model weights presented in Section 4 are averages over 100 realizations. Since one of the ensemble members is in fact $M_{\mathrm{true}}$ (model 2a) and single model selection is a reasonable objective, we purposely focus only on the two BMMFs for model selection. Only in the Quasi-$\mathcal{M}$-closed and $\mathcal{M}$-complete settings, the actual observations are used, Bayesian Stacking is included and Bayesian Bootstrapping is applied to compensate for the limited amount of data as proxy for the true data distribution.

4. Results and Discussion

4.1. $\mathcal{M}$-Closed

In the $\mathcal{M}$-closed setting, BMS/BMA and Pseudo-BMS/BMA yield similar results and favor the model 2a as can be seen in Figure 4. This is not surprise since both the prior and posterior predictive distribution of this model, which is also the data-generating true model, achieve highest predictive density for the (synthetic) data.

Only BMS/BMA also supports interpreting the model weights as probabilities “of being the true model”, which is correct in this artificial setup. Due to the limited amount of data (210 observation points), the maximum model weight is 75%, and an identification with probability one is not yet possible. This confirms the results of the justifiability analysis in Schöniger et al. [15]. Although favoring the informed zonated model too, Pseudo-BMS/BMA considers it only as the best approximation to an unknown truth. Model weights in Pseudo-BMS/BMA do not resemble model probabilities to be the true model and, despite knowing that $M_{\mathrm{true}}\in \mathit{M}$, a corresponding conclusion is not supported.

Primarily, the evolution of model weights in Figure 4 illustrates the inherent tendencies of the two philosophies behind the BMMFs: Besides the winning model 2a, BMS/BMA prefers the simpler model 1 over the more complex models through the entire ranking. To the potential price of restricted predictive power, BMA/BMA enforces parsimony. Contrarily, Pseudo-BMS/BMA shows higher model weights for models 3 and 4, which shows its tendency toward more complex models with higher predictive power in awaiting growing support for higher complexity with growing availability of data.

4.1.1. Quasi-$\mathcal{M}$-Closed Setting

In the Quasi-$\mathcal{M}$-closed setting, none of the ensemble members is the true model, but one (model 2a) is a very close resemblance. The three BMMF also yield three distinctly different results of model weighting, honouring their respective objective as shown in Figure 5.

Just like in the $\mathcal{M}$-closed setting, BMS/BMA ranks the informed zonated model 2a as best. Its consistency property and the concomitant tendency to simpler models promotes the selection of the quasi-true model 2a. However, in contrast to the $\mathcal{M}$-closed setting, comparably high weights are granted to the more complex models 3 and 4. This demonstrates how easily BMS/BMA might struggle in a model selection task with real data and incomplete representations of the true model—even if, by visual inspection, one model appears as a close resemblance of the true system.

In contrast, Pseudo-BMS/BMA favors the pilot-point model as a model with highest predictive power. Generally, more complex models are preferred: The most simple model 1 quickly diminishes in weight over growing data size. The most complex model 4 constantly receives significant weight. Unlike in the $\mathcal{M}$-closed setting, weighting by Pseudo-BMS/BMA differs completely from BMS/BMA, in particular for model 2a as quasi-true detailed physical representation of the true system. BMS/BMA succeeds to identify it as such, but fails to find the best predictive model. With Pseudo-BMS/BMA, it is vice versa.

Bayesian Stacking converges to stable model weights over growing data size. The nearly equal distribution of weights for model 2a and 3 can be interpreted from a physical perspective regarding the shortcomings of both parameterization approaches: Neighboring zones in the informed zonated model have too stark contrasts in conductivity between one another and neglect the fringes. Contrarily, pilot-point-based Kriging generates fields that are too smooth. Therefore, it is physically plausible that reality is somewhere in-between. Some fractions of the data set can be explained by one or the other model, and this is being reflected as shares in the model weights.

4.1.2. $\mathcal{M}$-Complete Setting

In the $\mathcal{M}$-complete setting, none of the ensemble members is the true model, and all models are incomplete representations. Figure 6 depicts the deviating model weightings.

As opposed to the other settings, BMS/BMA does not show a clear preference for one model over the same amount of data. Similar to the other settings, the model weights of the simplest model depict a declining trend. However, even the most complex model remains with significant weight on average. Over the considered range of data, rating on prior predictive densities remains indecisive between the uninformed zonated (2b) and pilot-point (3) model.

Pseudo-BMS/BMA yields model weights based on the posterior predictive density and therefore shows the strongest preference for the two most complex models between all $\mathcal{M}$-settings. Clearly, both of them benefit from their flexibility by parameter inference. However, due to the many parameters of model 4 that let the model struggle with non-identifiability and remaining predictive uncertainty after inference, the pilot-point model achieves the highest posterior predictive density and promises highest predictive power.

In this scenario, BMS/BMA fails in two ways: Neither does it provide a clear favorite as allegedly true model, nor does it point towards the one model with highest predictive power. This exemplifies why BMS/BMA often triggers false conclusions in applied modelling. Predictive models like Pseudo-BMS/BMA achieve their goal to find the level of model complexity that is supported by the currently available data.

Bayesian Stacking depicts negligible weight for the geostatistical and very small weight to the uninformed zonated model. Due to its high parametric complexity, predictions from model 4 only achieve low predictive density. The high posterior predictive density is mostly based on the pilot-point model 3. For small data sets, the homogeneous model also has a significant contribution, but it quickly declines afterwards. Overall, Bayesian Stacking succeeds with its goal to provide a stable weighted ensemble to cover predictive uncertainty.

5. Summary and Conclusions

BMS/BMA and Pseudo-BMS/BMA are selection frameworks that rate models on their prior and posterior predictive density, respectively. Thereby, BMS/BMA shows a “play-it-safe” tendency to prefer simpler models and Pseudo-BMS/BMA tends toward models of growing complexity. BMS/BMA-based model choice might trigger using a sub-optimal model for further predictions because it measures performance of uncalibrated models that only contain prior knowledge. Contrarily, while Pseudo-BMS/BMA rates calibrated models for high predictive power, it lacks the consistency property to ultimately identify a (quasi-)true model in the set (if such a true model actually existed and was part of the model set).

Averaging in either of the two BMMFs is only a compromise to prevent rash model selection and therefore implies a trade-off: Explanatory or predictive power of the allegedly best model might be “diluted” by alternative models. In return, conceptual uncertainty is accounted for and predictive uncertainty is covered more broadly over multiple model alternatives until it ultimately diminishes at the large-data limit.

In Bayesian Stacking, model averaging rather than selection is the actual goal. No model is supposed to be employed alone but the whole weighted ensemble. The common posterior predictive density is maximized by optimal model weights. Since the true model is assumed not to be in the ensemble, the predictive distribution of every member has only a partial overlap with the true model. Bayesian Stacking reflects this conceptual uncertainty by stable model weights and provides a linear combination of model posterior predictive distributions accordingly.

In an obvious $\mathcal{M}$-closed setting, BMS/BMA is the method of choice due to its consistency property. However, usually, the $\mathcal{M}$-setting is unknown and the choice of a certain BMMF is not straight-forward. Hence, as general rules for employing the three analysed BMMFs, we suggest to use:

• BMS if model selection shall have an implicit tendency to a preferably simple (parsimonious) model.
• Pseudo-BMS if model selection shall tend towards the model of maximal complexity that is still supported by the given data.
• BMA or Pseudo-BMA, respectively, if model averaging shall guard against rash selection of only one model until evidence clearly supports it.
• Bayesian Stacking if averaging of distributions for broad coverage of predictive uncertainty is the goal and the whole weighted ensemble shall be used for predictions rather than only a single best model.

However, note that:

• BMS/BMA is not supposed to select the model with best posterior (calibrated) predictive performance because the model rating is based on each model’s (uncalibrated) prior predictive performance.
• Pseudo-BMS/BMA will select the model with best (calibrated) posterior predictive performance given the currently available data, but at the price of potential overfitting and lack of the consistency property.
• Bayesian Stacking will yield a convex linear combination of model outputs’ posterior predictive distributions and not a combination of model outputs themselves. The latter obtained an own distribution that would be different from the former.

Typically, a modelling attempt is an iterative process. It might be challenging to develop a plausible first model for the task at hand. However, once it exists, there are usually various ideas about it being expanded, reduced or varied. This holds for both mechanistic models that are usually employed for process-understanding and system representation, or data-driven models that mimic the process of interest without knowledge of causality but extra-ordinary flexibility—and it also holds for the nuances of model types in-between these two extremes. Example applications of the three investigated BMMFs might therefore be:

• BMS/BMA for eliciting which processes are relevant and need to be represented, refined, etc. in a mechanistic model.
• Pseudo-BMS/BMA for restricting the amount of model parts and parameters in a data-driven model to the level that can still be constrained by the current data.
• Bayesian Stacking for combining models of the above two or other model types in order to benefit from complementary strengths.

We believe that Bayesian methods for model ensembles are still used much too often below their full potential. We advise to include the inherent goals of each used BMMF and the assumed $\mathcal{M}$-setting of the modelling task at hand into the analysis. Then, the interpretation of model weights becomes more insightful and reliable, and consecutive model averaging might honor conceptual uncertainty in the intended way. Thereby, model-based process understanding and predictive power can be strengthened.