Selection of CMIP5 GCM Ensemble for the Projection of Spatio-Temporal Changes in Precipitation and Temperature over the Niger Delta, Nigeria
Abstract
1. Introduction
2. Materials and Methods
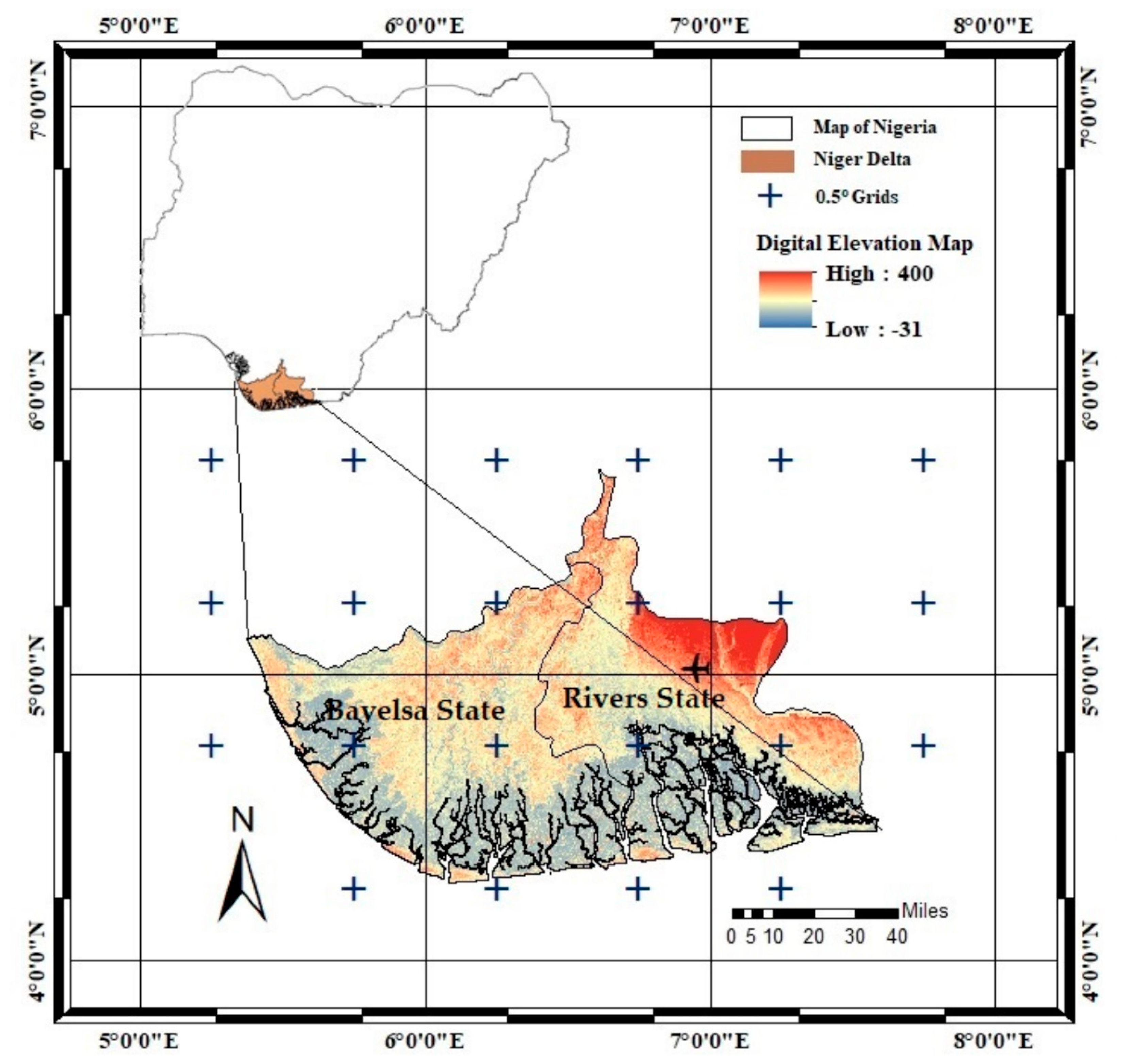
2.1. Description of the Study Area
2.2. Data and Sources
2.2.1. Gridded Dataset
2.2.2. Coupled Model Inter-comparison Project Phase 5 (CMIP5) GCM Datasets
3. Methodology
- Extracting and re-gridding of the selected 26 GCM datasets and CRU gridded datasets to a spatial resolution of 0.5° × 0.5° was carried out.
- SU was then applied to evaluate and assess the association between the 26 GCMs and the CRU gridded observations (prcp, Tmax, and Tmin) at each of the 22 grid points of 0.5° × 0.5° resolution covering the study area (Figure 1), over the reference period 1980–2005.
- The GCMs were then ranked based on the computed SU weight obtained at each grid points using the SU weighting technique, where a higher rank was given to GCMs with more weight in most of the grid points. A separate list of rank is prepared for each climatic variable (prcp, Tmax, and Tmin) and each gridded dataset (Table 2).
- The overall GCM ranks were then derived (Equation (4)) considering all their ranks and the weights obtained at all 22 grids over the entire study area.
- The final ranks of all three datasets were determined based on the frequency of occurrence of each GCM to combine the overall ranks in order to obtain a single rank for each GCM valid for the entire study.
- For simplicity, the easiest and the most common method of bias correction was carried out for correction of the biases in the best-selected future GCM ensemble against the CRU gridded observations. The additive correction method was used for temperature bias correction while the multiplicative correction method was used to correct the biases in prcp for GCM simulations under the two RCP scenarios for the period 2010–2099.
- The ensemble of the best four performing GCMs was then used for the prediction of spatial, temporal, and seasonal changes in rainfall for three future periods (2010–2039, 2040–2069, and 2070–2099) against the historical period (1980–2005).
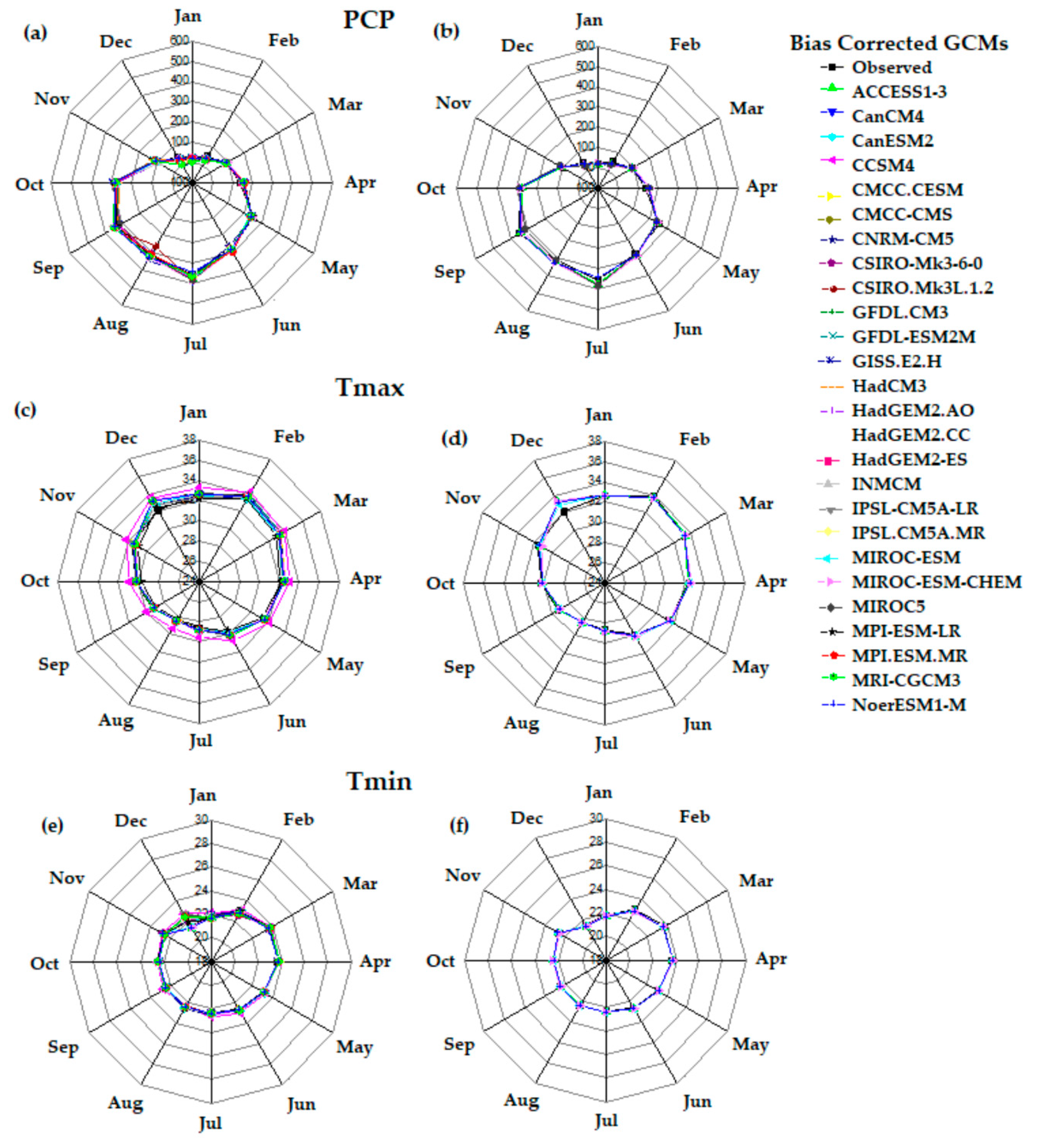
3.1. Model Selection Using Symmetrical Uncertainty
3.2. Ranking of GCMs Using the Weighting Method
3.3. Bias Correction
3.4. Performance Assessment
4. Results and Discussion
4.1. Ranking of the GCMs
4.2. Spatial Distribution of Top-Ranked GCMs
4.3. Selection of GCM Ensemble
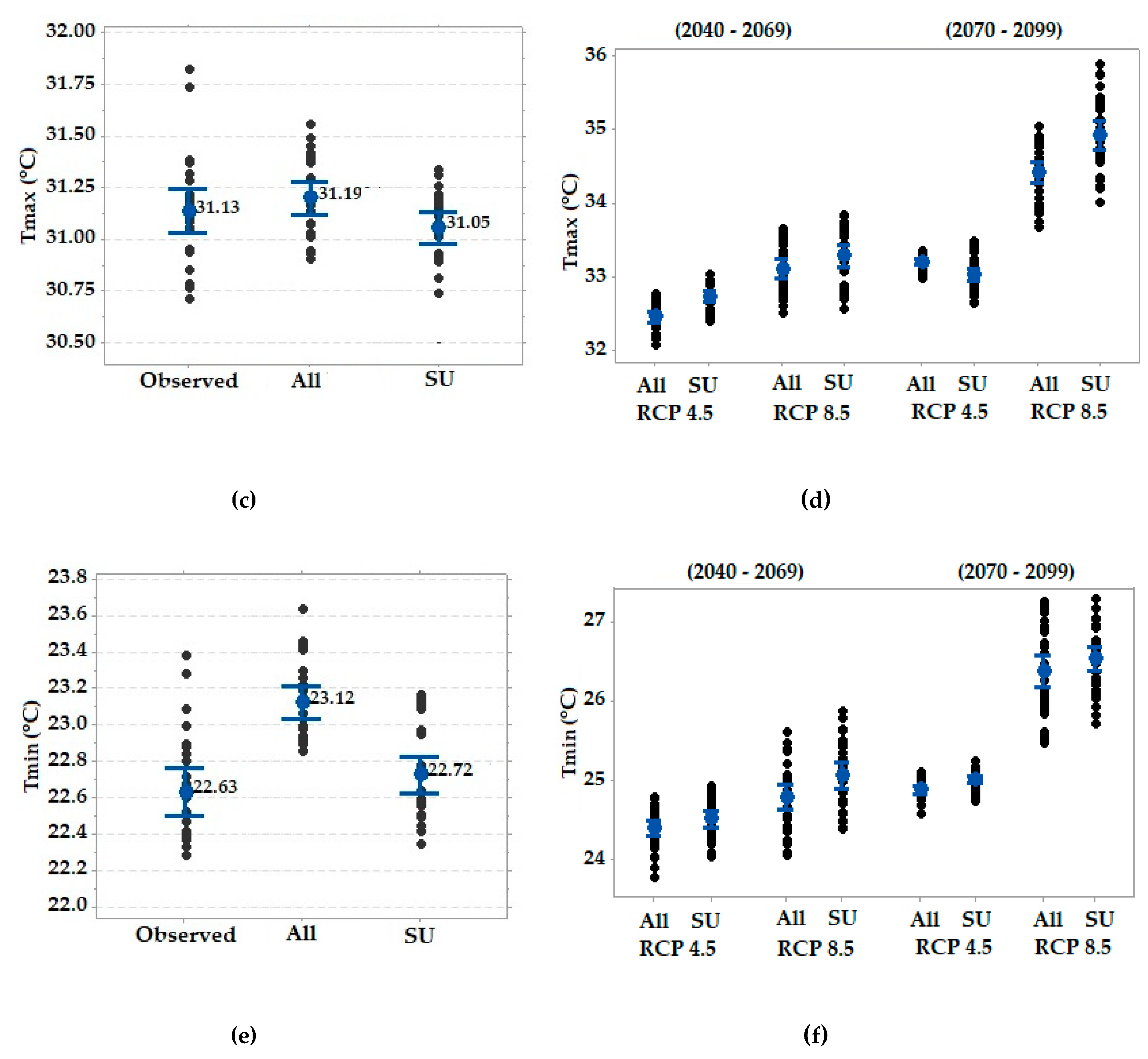
4.4. Ensemble Model Validation
4.5. Spatial Changes in Mean Annual Prcp, Tmax, and Tmin
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IPCC. Climate Change 2007: Impacts: Adaptation and Vulnerability: Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel. 2007. Available online: https://doi.org/10.1256/004316502320517344 (accessed on 12 April 2019).
- Northrop, P.J. A Simple, Coherent Framework for Partitioning Uncertainty in Climate Predictions. J. Clim. 2013, 26, 4375–4376. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Wang, X.; Nawaz, N.; Najeebullah, K. Evaluation of Gridded Precipitation Datasets over Arid Regions of Pakistan. Water 2019, 11. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very High Resolution Interpolated Climate Surfaces for Global Land Areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Khan, N.; Shahid, S.; Ahmed, K.; Ismail, T.; Nawaz, N.; Son, M. Performance Assessment of General Circulation Model in Simulating Daily Precipitation and Temperature Using Multiple Gridded Datasets. Water 2018, 10. [Google Scholar] [CrossRef]
- IPCC. Climate Change the IPCC Scientific Assessment. IPCC 1990, 414. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Ahmed, K.; Wang, X.J. Selection of Climate Models for Projection of Spatiotemporal Changes in Temperature of Iraq with Uncertainties. Atmos. Res. 2018, 213, 509–522. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of Downscaling Method in Quantifying the Impact of Climate Change on Hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Foley, A.M. Uncertainty in Regional Climate Modelling: A Review. Prog. Phys. Geogr. 2010, 34, 647–670. [Google Scholar] [CrossRef]
- Lutz, A.F.; ter Maat, H.W.; Biemans, H.; Shrestha, A.B.; Wester, P.; Immerzeel, W.W. Selecting Representative Climate Models for Climate Change Impact Studies: An Advanced Envelope-Based Selection Approach. Int. J. Climatol. 2016, 36, 3988–4005. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Sachindra, D.A.; Nawaz, N.; Chung, E.S. Fidelity Assessment of General Circulation Model Simulated Precipitation and Temperature over Pakistan Using a Feature Selection Method. J. Hydrol. 2019, 573, 281–298. [Google Scholar] [CrossRef]
- Lin, C.Y.; Tung, C.P. Procedure for Selecting GCM Datasets for Climate Risk Assessment. Terr. Atmos. Ocean. Sci. 2017, 28, 43–55. [Google Scholar] [CrossRef]
- Knutti, R.; Masson, D.; Gettelman, A. Climate Model Genealogy: Generation CMIP5 and How We Got There. Geophys. Res. Lett. 2013, 40, 1194–1199. [Google Scholar] [CrossRef]
- McSweeney, C.F.; Jones, R.G.; Lee, R.W.; Rowell, D.P. Selecting CMIP5 GCMs for Downscaling over Multiple Regions. Clim. Dyn. 2015, 44, 3237–3260. [Google Scholar] [CrossRef]
- Abramowitz, G.; Herger, N.; Gutmann, E.; Hammerling, D.; Knutti, R.; Leduc, M.; Lorenz, R.; Pincus, R.; Schmidt, G.A. ESD Reviews: Model Dependence in Multi-Model Climate Ensembles: Weighting, Sub-Selection and out-of-Sample Testing. Earth Syst. Dyn. 2019, 10, 91–105. [Google Scholar] [CrossRef]
- Srinivasa Raju, K.; Nagesh Kumar, D. Ranking General Circulation Models for India Using TOPSIS. J. Water Clim. Chang. 2015, 6, 288–299. [Google Scholar] [CrossRef]
- Warszawski, L.; Frieler, K.; Huber, V.; Piontek, F.; Serdeczny, O.; Schewe, J. The Inter-Sectoral Impact Model Intercomparison Project (ISI–MIP): Project Framework. Proc. Natl. Acad. Sci. 2014, 111, 3228–3232. [Google Scholar] [CrossRef]
- Shiru, M.S.; Shahid, S.; Chung, E.-S.; Alias, N.; Scherer, L. A MCDM-Based Framework for Selection of General Circulation Models and Projection of Spatio-Temporal Rainfall Changes: A Case Study of Nigeria. Atmos. Res. 2019, 225, 1–16. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A Survey on Feature Selection Methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Talavera, L. An Evaluation of Filter and Wrapper Methods for Feature Selection in Categorical Clustering. In International Symposium on Intelligent Data Analysis; Springer: Berlin, Germany, 2005; pp. 440–451. [Google Scholar]
- Barfus, K.; Bernhofer, C. Assessment of GCM Capabilities to Simulate Tropospheric Stability on the Arabian Peninsula. Int. J. Climatol. 2015, 35, 1682–1696. [Google Scholar] [CrossRef]
- Pierce, D.W.; Barnett, T.P.; Santer, B.D.; Gleckler, P.J. Selecting Global Climate Models for Regional Climate Change Studies. Proc. Natl. Acad. Sci. 2009, 106, 8441–8446. [Google Scholar] [CrossRef]
- Ruan, Y.; Liu, Z.; Wang, R.; Yao, Z. Assessing the Performance of CMIP5 GCMs for Projection of Future Temperature Change over the Lower Mekong Basin. Atmosphere (Basel). 2019, 10, 93. [Google Scholar] [CrossRef]
- Dudek, G. Tournament Searching Method to Feature Selection Problem. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 2010, 6114 LNAI, 437–444. [Google Scholar]
- Hammami, D.; Lee, T.S.; Ouarda, T.B.M.J.; Le, J. Predictor Selection for Downscaling GCM Data with LASSO. J. Geophys. Res. Atmos. 2012, 117, 1–11. [Google Scholar] [CrossRef]
- Sutha, K.; Tamilselvi, J. A Review of Feature Selection Algorithms for Data Mining Techniques. Int. J. Comput. Sci. Eng. 2015, 7, 63–67. [Google Scholar]
- Perkins, S.E.; Pitman, A.J.; Holbrook, N.J.; McAneney, J. Evaluation of the AR4 Climate Models’ Simulated Daily Maximum Temperature, Minimum Temperature, and Precipitation over Australia Using Probability Density Functions. J. Clim. 2007, 20, 4356–4376. [Google Scholar] [CrossRef]
- Jiang, X.; Waliser, D.E.; Xavier, P.K.; Petch, J.; Klingaman, N.P.; Woolnough, S.J.; Guan, B.; Bellon, G.; Crueger, T.; DeMott, C.; et al. Vertical Structure and Physical Processes of the Madden-Julian Oscillation: Exploring Key Model Physics in Climate Simulations. J. Geophys. Res. Atmos. 2015, 120, 4718–4748. [Google Scholar] [CrossRef]
- Min, S.-K.; Hense, A. A Bayesian Assessment of Climate Change Using Multimodel Ensembles. Part II: Regional and Seasonal Mean Surface Temperatures. J. Clim. 2007, 20, 2769–2790. [Google Scholar] [CrossRef]
- Shukla, J.; DelSole, T.; Fennessy, M.; Kinter, J.; Paolino, D. Climate Model Fidelity and Projections of Climate Change. Geophys. Res. Lett. 2006, 33, 3–6. [Google Scholar] [CrossRef]
- Reichler, T.; Kim, J. How Well Do Coupled Models Simulate Today’s Climate? Bull. Am. Meteorol. Soc. 2008, 89, 303–311. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. 2001, 5, 365–395. Available online: https://culturemath.ens.fr/sites/default/files/p3-shannon.pdf (accessed on 31 January 2020).
- Ma, C.-W.; Ma, Y.-G. Shannon Information Entropy in Heavy-Ion Collisions. Prog. Part. Nucl. Phys. 2018, 99, 120–158. [Google Scholar] [CrossRef]
- Singh, B.; Kushwaha, N.; Vyas, O.P. A Feature Subset Selection Technique for High Dimensional Data Using Symmetric Uncertainty. J. Data Anal. Inf. Process. 2014, 95–105. [Google Scholar] [CrossRef]
- Matemilola, S.; Adedeji, O.H.; Elegbede, I.; Kies, F. Mainstreaming Climate Change into the EIA Process in Nigeria: Perspectives from Projects in the Niger Delta Region. Climate 2019, 7. [Google Scholar] [CrossRef]
- Amadi, A.N. Impact of Gas-Flaring on the Quality of Rain Water, Groundwater and Surface Water in Parts of Eastern Niger Delta, Nigeria. J. Geosci. Geomatics 2014, 2, 114–119. [Google Scholar]
- Adejuwon, J.O. Rainfall Seasonality in the Niger Delta Belt, Nigeria. J. Geogr. Reg. Plan. 2012, 5, 51–60. [Google Scholar]
- Amadi, A.N.; Olasehinde, P.I.; Nwankwoala, H.O. Hydrogeochemistry and Statistical Analysis of Benin Formation in Eastern Niger Delta, Nigeria. Int. Res. J. Pure Appl. Chem. 2014, 4, 327–338. [Google Scholar] [CrossRef]
- Ituen, E.U.; Alonge, A.F. Niger Delta Region of Nigeria, Climate Change and the Way Forward. In Proceedings of the Bioenergy Engineering, Bellevue, DC, USA, 11–14 October 2009. [Google Scholar]
- Prince, C.; Mmom, P.C.M. Vulnerability and Resilience of Niger Delta Coastal Communities to Flooding. IOSR J. Humanit. Soc. Sci. 2013, 10, 27–33. [Google Scholar] [CrossRef]
- Amangabara, G.; Obenade, M. Flood Vulnerability Assessment of Niger Delta States Relative to 2012 Flood Disaster in Nigeria. Am. J. Environ. Prot. 2015, 3, 76–83. [Google Scholar]
- Ologunorisa, T.E.; Tersoo, T. The Changing Rainfall Pattern and Its Implication for Flood Frequency in Makurdi, Northern Nigeria. J. Appl. Sci. Environ. Manag. 2006, 10, 97–102. [Google Scholar] [CrossRef]
- Ologunorisa, T.E.; Adeyemo, A. Public Perception of Flood Hazard in the Niger Delta, Nigeria. Environmentalist 2005, 25, 39–45. [Google Scholar] [CrossRef]
- Tawari-fufeyin, P.; Paul, M.; Godleads, A.O. Some Aspects of a Historic Flooding in Nigeria and Its Effects on Some Niger-Delta Communities. Am. J. Water Resour. 2015, 3, 7–16. [Google Scholar]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated High-Resolution Grids of Monthly Climatic Observations - the CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Jones, P.D.; Harris, I.C. Climatic Research Unit (CRU) Time-Series Datasets of Variations in Climate with Variations in Other Phenomena. NCAS British Atmospheric Data Centre, 2008. Available online: http://catalogue.ceda.ac.uk/uuid/3f8944800cc48e1cbc29a5ee12d8542d (accessed on 13 June 2019).
- Ashraf Vaghefi, S.; Abbaspour, N.; Kamali, B.; Abbaspour, K.C. A Toolkit for Climate Change Analysis and Pattern Recognition for Extreme Weather Conditions–Case Study: California-Baja California Peninsula. Environ. Model. Softw. 2017, 96, 181–198. [Google Scholar] [CrossRef]
- Hassan, I.; Kalin, R.M.; White, C.J.; Aladejana, J.A. Evaluation of Daily Gridded Meteorological Datasets over the Niger Delta Region of Nigeria and Implication to Water Resources Management. Clim. Sci. SCRIP 2020. Available online: https://www.scirp.org/journal/paperinformation.aspx?paperid=97271 (accessed on 24 December 2019).
- Hempel, S.; Frieler, K.; Warszawski, L.; Schewe, J.; Piontek, F. A Trend-Preserving Bias Correction—The ISI-MIP Approach. Earth Syst. Dyn. 2013, 4, 219–236. [Google Scholar] [CrossRef]
- Wang, L.; Ranasinghe, R.; Maskey, S.; van Gelder, P.H.A.J.M.; Vrijling, J.K. Comparison of Empirical Statistical Methods for Downscaling Daily Climate Projections from CMIP5 GCMs: A Case Study of the Huai River Basin, China. Int. J. Climatol. 2016, 36, 145–164. [Google Scholar] [CrossRef]
- Piao, M.; Piao, Y.; Lee, J.Y. Symmetrical Uncertainty-Based Feature Subset Generation and Ensemble Learning for Electricity Customer Classification. Symmetry (Basel). 2019, 11, 498. [Google Scholar] [CrossRef]
- Adami, C. Information Theory in Molecular Biology. Phys. Life Rev. 2004, 1, 3–22. [Google Scholar] [CrossRef]
- Shreem, S.S.; Abdullah, S.; Nazri, M.Z.A. Hybrid Feature Selection Algorithm Using Symmetrical Uncertainty and a Harmony Search Algorithm. Int. J. Syst. Sci. 2016, 47, 1312–1329. [Google Scholar] [CrossRef]
- Roszkowska, E. Rank Ordering Criteria Weighting Methods-a Comparative Overview 2 5. Optimum. Stud. Ekon. 2013, 5, 65. [Google Scholar] [CrossRef]
- Balinski, M.; Laraki, R. Majority Judgment vs. Majority Rule; Springer: Berlin Heidelberg, 2019; Available online: https://doi.org/10.1007/s00355-019-01200-x (accessed on 28 October 2019).
- Mehrotra, R.; Sharma, A. Correcting for Systematic Biases in Multiple Raw GCM Variables across a Range of Timescales. J. Hydrol. 2015, 520, 214–223. [Google Scholar] [CrossRef]
- Beyer, R.; Krapp, M.; Manica, A. A Systematic Comparison of Bias Correction Methods for Paleoclimate Simulations. Clim. Past Discuss. 2019, 1–23. [Google Scholar] [CrossRef]
- Xu, Y. Hydrology and Climate Forecasting R Package for Data Analysis and Visualization. 2018. Available online: https://cran.r-project.org/web/packages/hyfo/vignettes/hyfo.pdf (accessed on 30 April 2019).
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar]
- Motovilov, Y.G.; Gottschalk, L.; Engeland, K.; Rodhe, A. Validation of a Distributed Hydrological Model against Spatial Observations. Agric. For. Meteorol. 1999, 99. [Google Scholar] [CrossRef]
- Srinivasa Raju, K.; Sonali, P.; Nagesh Kumar, D. Ranking of CMIP5-Based Global Climate Models for India Using Compromise Programming. Theor. Appl. Climatol. 2017, 128, 563–574. [Google Scholar] [CrossRef]
- Krinner, G.; Germany, F.; Shongwe, M.; Africa, S.; France, S.B.; Uk, B.B.B.B.; Germany, V.B.; Uk, O.B.; France, C.B.; Uk, R.C.; et al. Long-Term Climate Change: Projections, Commitments and Irreversibility. In Climate Change 2013-The Physical Science Basis: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2013; pp. 1029–1136. [Google Scholar]
- Expósito, F.J.; González, A.; Pérez, J.C.; Díaz, J.P.; Taima, D. High-Resolution Future Projections of Temperature and Precipitation in the Canary Islands. J. Clim. 2015, 28, 7846–7856. [Google Scholar] [CrossRef]
- Rangwala, I.; Miller, J.R. Climate Change in Mountains: A Review of Elevation-Dependent Warming and Its Possible Causes. Clim. Change 2012, 114, 527–547. [Google Scholar] [CrossRef]
- Martín, J.L.; Bethencourt, J.; Cuevas-Agulló, E. Assessment of Global Warming on the Island of Tenerife, Canary Islands (Spain). Trends in Minimum, Maximum and Mean Temperatures since 1944. Clim. Change 2012, 114, 343–355. [Google Scholar] [CrossRef]
- Agumagu, O.; Todd, M. Modelling the Climatic Variability in the Niger Delta Region: Influence of Climate Change on Hydrology. Earth Sci. Clim. Chang. 2015, 6. [Google Scholar] [CrossRef]
- Obroma Agumagu, O.A. Projected Changes in the Physical Climate of the Niger Delta Region of Nigeria. SciFed J. Glob. Warm. 2018. Available online: https://pdfs.semanticscholar.org/c5e7/17ebcd21acd09109553f3c11804f94ece611.pdf?_ga=2.9422967.312418545.1579023164-1793679239.1552909823 (accessed on 1 May 2019).
- Ike, P.C.; Emaziye, P.O. An Assessment of the Trend and Projected Future Values of Climatic Variables in Niger Delta Region, Nigeria. 2012, 4, 165–170. Available online: https://www.researchgate.net/profile/Pius_Ike/publication/268202347_An_Assessment_of_the_Trend_and_Projected_Future_Values_of_Climatic_Variables_in_Niger_Delta_Region_Nigeria/links/5b008a9ba6fdccf9e4f56f9a/An-Assessment-of-the-Trend-and-Projected-Future-Values-of-Climatic-Variables-in-Niger-Delta-Region-Nigeria.pdf (accessed on 12 April 2019).





| GCM No | GCM Name | Institute | Resolution |
|---|---|---|---|
| 1 | ACCESS1.3 | Commonwealth Scientific and Industrial Research Organization–Bureau of Meteorology, Australia | 1.9 × 1.2 |
| 2 | CanCM4 | Canadian Center for Climate Modelling and Analysis, Canada | 2.8 × 2.8 |
| 3 | CanESM2 | ||
| 4 | CCSM4 | National Centre for Atmospheric Research, USA | 0.94 × 1.25 |
| 5 | CMCC.CESM | Centro Euro-Mediterraneo sui Cambiamenti Climatici, Italy | 0.7 × 0.7 |
| 6 | CMCC.CMS | 1.9 × 1.9 | |
| 7 | CNRM.CM5 | Centre National de Recherches Météorologiques, Centre, France | 1.4 × 1.4 |
| 8 | CSIRO.Mk3.6.0 | Commonwealth Scientific and Industrial Research Organization, Australia | 1.9 × 1.9 |
| 9 | CSIRO.Mk3L.1.2 | ||
| 10 | GFDL.CM3 | Geophysical Fluid Dynamics Laboratory, USA | 2.5 × 2.0 |
| 11 | GFDL.ESM2M | ||
| 12 | GISS.E2.H | NASA/GISS (Goddard Institute for Space Studies), USA | 2.5 × 2.0 |
| 13 | HadCM3 | Met Office Hadley Centre, UK | 1.9 × 1.2 |
| 14 | HadGEM2.AO | ||
| 15 | HadGEM2.CC | ||
| 16 | HadGEM2.ES | ||
| 17 | INMCM4 | Institute of Numerical Mathematics, Russia | 2.0 × 1.5 |
| 18 | IPSL.CM45A.LR | Institut Pierre Simon Laplace, France | 2.5 × 1.3 |
| 19 | IPSL.CM5A.MR | 3.7 × 1.9 | |
| 20 | MIROC.ESM | The University of Tokyo, National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology, Japan | 2.8 × 2.8 |
| 21 | MIROC.ESM.CHM | ||
| 22 | MIROC5 | 1.4 × 1.4 | |
| 23 | MPI.ESM.LR | Max Planck Institute for Meteorology, Germany | 1.9 × 1.9 |
| 24 | MPI.ESM.MR | ||
| 25 | MRI.CGCM3 | Meteorological Research Institute, Japan | 1.1 × 1.1 |
| 26 | Noer.ESM1.M | Meteorological Institute, Norway | 2.5 × 1.9 |
| Ranks | GCMs | Prcp | Tmax | Tmin | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SU | NSE | R2 | SU | NSE | R2 | SU | NSE | R2 | ||
| 1 | ACCESS1-3 | 0.28 | 0.58 | 0.81 | 0.15 | 0.67 | 0.84 | 0.09 | 0.86 | 0.55 |
| 2 | MIROC-ESM | 0.14 | 0.63 | 0.84 | 0.10 | 0.87 | 0.44 | 0.12 | 0.62 | 0.49 |
| 3 | MIROC-ESM-CHM | 0.15 | 0.69 | 0.56 | 0.11 | 0.86 | 0.86 | 0.02 | 0.50 | 0.58 |
| 4 | Noer-ESM1-M | 0.13 | 0.57 | 0.82 | 0.14 | 0.82 | 0.89 | 0.05 | 0.38 | 0.48 |
| 5 | MIROC5 | 0.08 | 0.62 | 0.82 | 0.15 | 5.36 | 0.88 | 0.06 | 1.88 | 0.45 |
| 6 | HadGEM2-ES | 0.19 | 0.59 | 0.81 | 0.03 | 0.88 | 0.91 | 0.02 | 0.54 | 0.53 |
| 7 | CanCM4 | 0.07 | 0.49 | 0.74 | 0.08 | 0.91 | 0.91 | 0.01 | 0.65 | 0.48 |
| 8 | MRI-CGCM3 | 0.06 | 0.55 | 0.78 | 0.11 | 0.70 | 0.87 | 0.03 | 0.48 | 0.51 |
| 9 | MPI-ESM-MR | 0.06 | 0.35 | 0.78 | 0.05 | 0.75 | 0.87 | 0.02 | 0.49 | 0.51 |
| 10 | CMCC-CMS | 0.08 | 0.55 | 0.78 | 0.11 | 0.63 | 0.79 | 0.04 | 0.31 | 0.45 |
| 11 | CNRM-CM5 | 0.10 | 0.44 | 0.73 | 0.07 | 0.64 | 0.81 | 0.01 | 0.28 | 0.51 |
| 12 | CanESM2 | 0.10 | 0.52 | 0.77 | 0.12 | 2.18 | 0.67 | 0.01 | 6.48 | 0.25 |
| 13 | IPSL-CM45A-LR | 0.15 | 0.63 | 0.85 | 0.03 | 0.81 | 0.91 | 0 | 0.42 | 0.57 |
| 14 | HadGEM2-CC | 0.21 | 0.58 | 0.82 | 0 | 0.90 | 0.90 | 0 | 0.63 | 0.45 |
| 15 | HadCM3 | 0.09 | 0.58 | 0.80 | 0 | 0.91 | 0.91 | 0 | 0.67 | 0.51 |
| 16 | CMCC-CESM | 0.08 | 0.61 | 0.81 | 0.00 | 0.89 | 0.89 | 0 | 0.65 | 0.48 |
| 17 | IPSL-CM5A-MR | 0.11 | 0.47 | 0.74 | 0 | 0.84 | 0.85 | 0 | 0.64 | 0.46 |
| 18 | GFDL-ESM2M | 0.11 | 0.49 | 0.74 | 0.04 | 0.79 | 0.85 | 0 | 0.40 | 0.55 |
| 19 | CSIRO-Mk3L-1-2 | 0.05 | 0.31 | 0.60 | 0 | 0.89 | 0.89 | 0 | 0.68 | 0.53 |
| 20 | HadGEM2-AO | 0.03 | 0.62 | 0.83 | 0 | 0.84 | 0.81 | 0 | 0.49 | 0.29 |
| 21 | GISS-E2-H | 0.14 | 0.32 | 0.62 | 0 | 0.74 | 0.76 | 0 | 0.56 | 0.37 |
| 22 | MPI-ESM-LR | 0.06 | 0.55 | 0.80 | 0 | 0.00 | 0.87 | 0 | 0.63 | 0.56 |
| 23 | CSIRO-Mk3-6-0 | 0.13 | 0.44 | 0.71 | 0.02 | 0.15 | 0.83 | 0 | 0.06 | 0.57 |
| 24 | INMCM4 | 0.05 | 0.42 | 0.68 | 0 | 0.60 | 0.69 | 0 | 0.54 | 0.42 |
| 25 | CCSM4 | 0.09 | 0.51 | 0.76 | 0 | 0.70 | 0.66 | 0 | 0.44 | 0.46 |
| 26 | GFDL-CM3 | 0.21 | 0.35 | 0.42 | 0 | 0.62 | 0.15 | 0 | 0.37 | 0.20 |
| Mean Annual | Observed | GCM Ensemble | ||
|---|---|---|---|---|
| All | SU | |||
| Prcp (mm) | Sum | 2227.95 | 2166.91 | 2255.49 |
| Mean | 6.19 | 5.94 | 6.23 | |
| RMSE | - | 2.42 | 2.62 | |
| NSE | - | 0.58 | 0.62 | |
| R2 | - | 0.86 | 0.83 | |
| Tmax (°C) | Mean | 31.13 | 31.20 | 31.06 |
| RMSE | - | 0.68 | 0.71 | |
| NSE | - | 1.00 | 1.00 | |
| R2 | - | 0.92 | 0.92 | |
| Tmin (°C) | Mean | 22.63 | 23.12 | 22.72 |
| RMSE | - | 0.88 | 1.17 | |
| NSE | - | 1.00 | 1.00 | |
| R2 | - | 0.64 | 0.62 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, I.; Kalin, R.M.; White, C.J.; Aladejana, J.A. Selection of CMIP5 GCM Ensemble for the Projection of Spatio-Temporal Changes in Precipitation and Temperature over the Niger Delta, Nigeria. Water 2020, 12, 385. https://doi.org/10.3390/w12020385
Hassan I, Kalin RM, White CJ, Aladejana JA. Selection of CMIP5 GCM Ensemble for the Projection of Spatio-Temporal Changes in Precipitation and Temperature over the Niger Delta, Nigeria. Water. 2020; 12(2):385. https://doi.org/10.3390/w12020385
Chicago/Turabian StyleHassan, Ibrahim, Robert M. Kalin, Christopher J. White, and Jamiu A. Aladejana. 2020. "Selection of CMIP5 GCM Ensemble for the Projection of Spatio-Temporal Changes in Precipitation and Temperature over the Niger Delta, Nigeria" Water 12, no. 2: 385. https://doi.org/10.3390/w12020385
APA StyleHassan, I., Kalin, R. M., White, C. J., & Aladejana, J. A. (2020). Selection of CMIP5 GCM Ensemble for the Projection of Spatio-Temporal Changes in Precipitation and Temperature over the Niger Delta, Nigeria. Water, 12(2), 385. https://doi.org/10.3390/w12020385






