Uncertainty Analysis of a 1D River Hydraulic Model with Adaptive Calibration
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Implementation and Setup
2.1.1. Study Area
2.1.2. Hydraulic Model of the Chaudière River
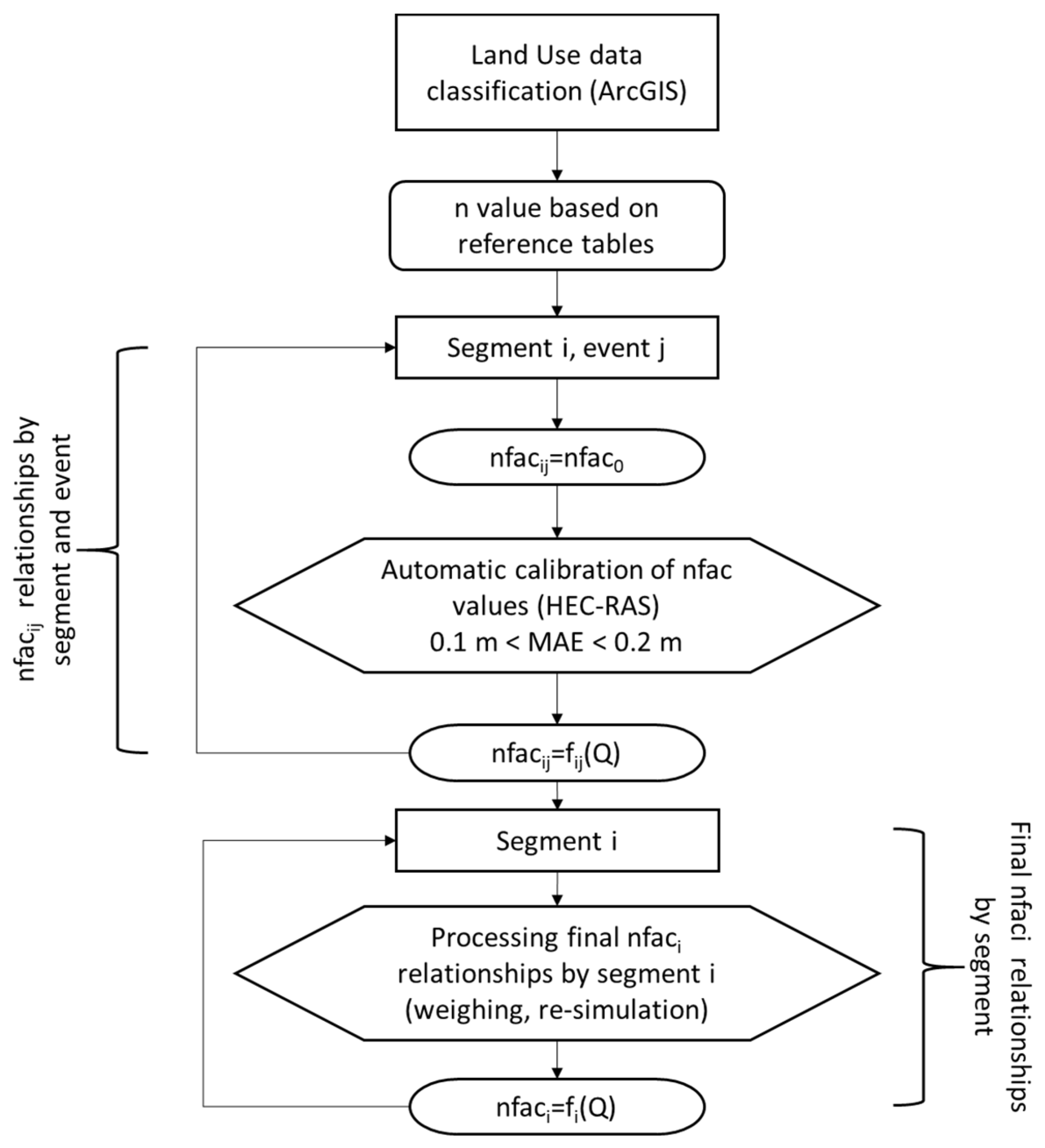
2.1.3. Calibration
2.2. Uncertainty Analysis
2.2.1. Accounted Sources of Uncertainty
Observed and Measured Data Uncertainty
Lateral Inflows
Roughness Parameters
2.2.2. Uncertainty Analysis Setup
2.2.3. Reliability Analysis
3. Results
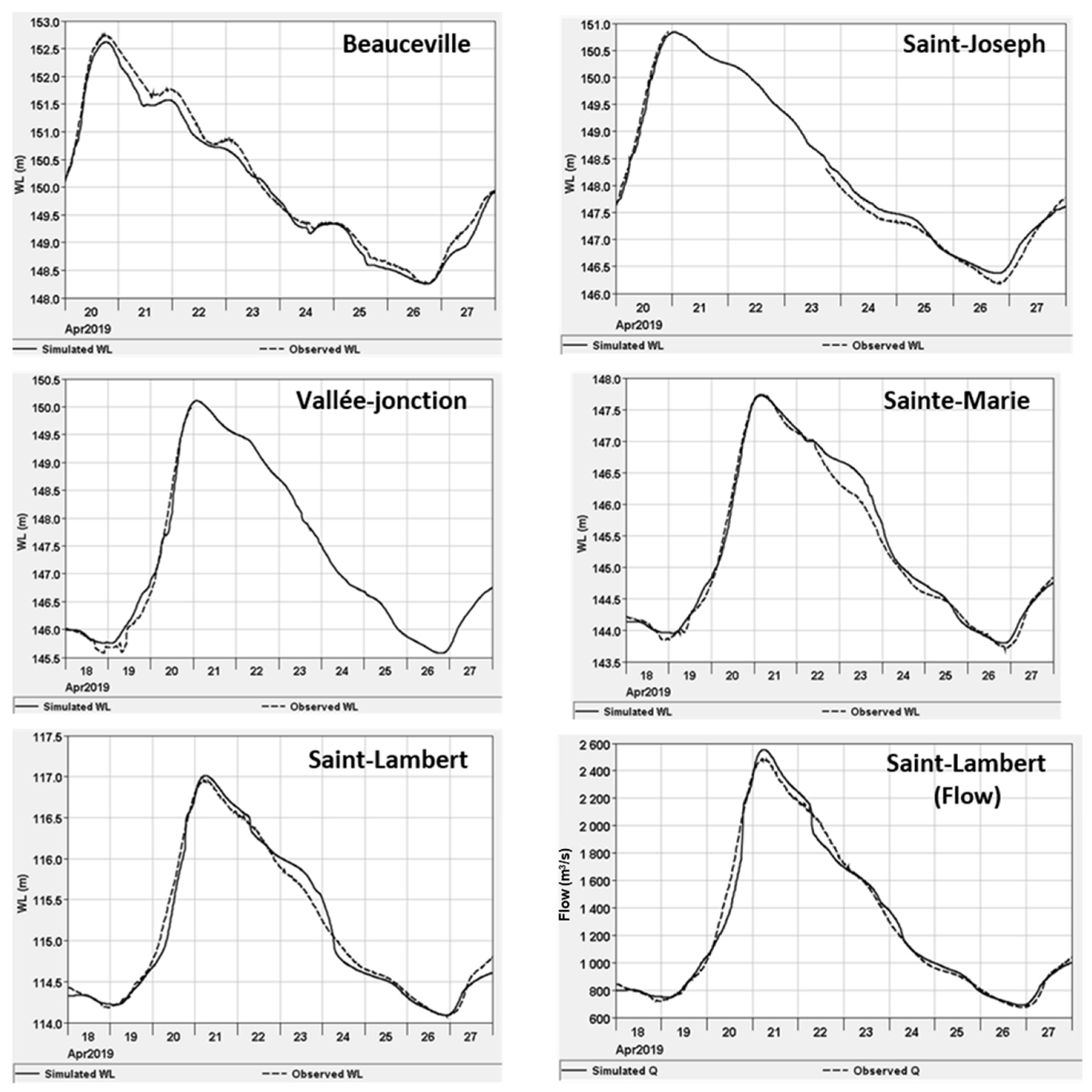
3.1. Model Calibration and Validation
3.1.1. Adaptive Flow-Based Calibration Results
3.1.2. Validation Results
3.2. Uncertainty Analysis
3.2.1. Quantification of the Uncertainty
3.2.2. Reliability Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Water Level Series for Adaptive Flow-Based Calibration vs. Constant Manning Calibration vs. Observation—Validation Event V2

Appendix B. Simulated Water Level (WL) Ensembles vs. Observation at Each Station for Validation Event V2

References
- Neal, J.; Schumann, G.; Bates, P.; Buytaert, W.; Matgen, P.; Pappenberger, F. A data assimilation approach to discharge estimation from space. Hydrol. Process. 2009, 3649, 3641–3649. [Google Scholar] [CrossRef]
- Giustarini, L.; Matgen, P.; Hostache, R.; Montanari, M.; Plaza, D.; Pauwels, V.R.N.; De Lannoy, G.J.M.; De Keyser, R.; Pfister, L.; Hoffmann, L.; et al. Assimilating SAR-derived water level data into a hydraulic model: A case study. Hydrol. Earth Syst. Sci. 2011, 15, 2349–2365. [Google Scholar] [CrossRef]
- Giustarini, L.; Matgen, P.; Hostache, R.; Dostert, J. From SAR-derived flood mapping to water level data assimilation into hydraulic models. Remote Sens. Agric. Ecosyst. Hydrol. XIV 2012, 8531, 85310U. [Google Scholar]
- Andreadis, K.M.; Schumann, G.J.P. Estimating the impact of satellite observations on the predictability of large-scale hydraulic models. Adv. Water Resour. 2014, 73, 44–54. [Google Scholar] [CrossRef]
- Grimaldi, S.; Li, Y.; Pauwels, R.N.; Walker, J.P. Remote sensing-derived water extent and level to constrain hydraulic flood forecasting models: opportunities and challenges. Surv. Geophys. 2016, 37, 977–1034. [Google Scholar] [CrossRef]
- Matte, P.; Secretan, Y.; Morin, J. Hydrodynamic modeling of the St. Lawrence fluvial estuary I: model setup, calibration, and validation. J. Waterw. Port Coast. Ocean Eng. 2017, 143, 1–15. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.; Frodsham, K.; Romanowicz, R.; Matgen, P. Grasping the unavoidable subjectivity in calibration of flood inundation models: A vulnerability weighted approach. J. Hydrol. 2007, 333, 275–287. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Schumann, G.; Bates, P.D.; Freer, J.E.; Beven, K.J. Flood-plain mapping: a critical discussion of deterministic and probabilistic approaches. Hydrol. Sci. J. 2010, 55, 364–376. [Google Scholar] [CrossRef]
- Barthélémy, S.; Ricci, S.; Rochoux, M.C.; Le Pape, E.; Thual, O. Ensemble-based data assimilation for operational flood forecasting—On the merits of state estimation for 1D hydrodynamic forecasting through the example of the “Adour Maritime” river. J. Hydrol. 2017, 552, 210–224. [Google Scholar] [CrossRef]
- Bates, P.D.; Pappenberger, F.; Romanowicz, R.J. Uncertainty in flood inundation modelling. In Applied Uncertainty Analysis for Flood Risk Management; World Scientific: Singapore, 2014; pp. 232–269. ISBN 9781848162716. [Google Scholar]
- Romanowicz, R.; Beven, K. Estimation of flood inundation probabilities as conditioned on event inundation maps. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Troy, T.J.; Wood, E.F.; Sheffield, J. An efficient calibration method for continental-scale land surface modeling. Water Resour. Res. 2008, 44, 1–13. [Google Scholar] [CrossRef]
- Acuña, G.J.; Ávila, H.; Canales, F.A. River Model Calibration Based on Design of Experiments Theory. A Case Study: Meta River, Colombia. Water 2019, 11, 382. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Fang, H.; Lai, R.; Zhang, Y.; Huang, L.; Liu, X. A real-time probabilistic channel flood-forecasting model based on the Bayesian particle filter approach. Environ. Model. Softw. 2017, 88, 151–167. [Google Scholar] [CrossRef]
- Tung, Y. Uncertainty and Reliability Analysis in Water Resources Engineering. J. Contemp. Water Res. Educ. 2011, 103, 4. [Google Scholar]
- Kalyanapu, A.J.; Judi, D.R.; McPherson, T.N.; Burian, S.J. Monte Carlo-based flood modelling framework for estimating probability weighted flood risk. J. Flood Risk Manag. 2012, 5, 37–48. [Google Scholar] [CrossRef]
- Huang, Y.; Qin, X. Uncertainty analysis for flood inundation modelling with a random floodplain roughness. Environ. Syst. Res. 2014, 3, 9. [Google Scholar] [CrossRef]
- Goeury, C.; David, T.; Ata, R.; Boyaval, S.; Audouin, Y.; Goutal, N.; Popelin, A.-L.; Couplet, M.; Baudin, M.; Barate, R. Uncertainty quantification on a real case with TELEMAC-2D. In Proceedings of the XXII TELEMAC-MASCARET Technical User Conference, Warrington, UK, 15–16 October 2015; pp. 44–51. [Google Scholar]
- Altarejos-Garcia, L.; Martinez-Chenoll, M.L.; Escuder-Bueno, I.; Serrano-Lombillo, A. Assessing the impact of uncertainty on flood risk estimates with reliability analysis using 1-D and 2-D hydraulic models. Hydrol. Earth Syst. Sci. 2012, 16, 1895–1914. [Google Scholar] [CrossRef]
- Franceschini, S.; Marani, M.; Tsai, C.; Zambon, F. A perturbance moment point estimate method for uncertainty analysis of the hydrologic response. Adv. Water Resour. 2012, 40, 46–53. [Google Scholar] [CrossRef]
- Jung, Y.; Merwade, V.; Asce, M. Uncertainty quantification in flood inundation mapping using generalized likelihood uncertainty estimate and sensitivity analysis. J. Hydrol. Eng. 2012, 17, 507–520. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences (International Geophysics); Academic Press: Cambridge, MA, USA, 2011; ISBN 978-0123850225. [Google Scholar]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Lemieux, C. Monte Carlo and Quasi-Monte Carlo Sampling; Springer: New York, NY, USA, 2009; ISBN 9780387781648. [Google Scholar]
- Cea, L.; French, J.R. Bathymetric error estimation for the calibration and validation of estuarine hydrodynamic models. Estuar. Coast. Shelf Sci. 2012, 100, 124–132. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Neelz, S.; Pender, G. Benchmarking 2D hydraulic models for urban flooding. Proc. Inst. Civ. Eng. Water Manag. 2008, 161, 13–30. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Enhancing river model set-up for 2-D dynamic flood modelling. Environ. Model. Softw. 2015, 67, 89–107. [Google Scholar] [CrossRef]
- Brunner, G. HEC-RAS River Analysis System, Hydraulic Reference Manual, Version 5.0; US Army Corps of Engineers, Hydrologic Engineer Center (HEC): Davis, CA, USA, 2016. [Google Scholar]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Anctil, F.; Ramos, M.-H. Verification Metrics for Hydrological Ensemble Forecasts. In Handbook of Hydrometeorological Ensemble Forecasting; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–30. ISBN 9783642404573. [Google Scholar]
- Domeneghetti, A.; Castellarin, A.; Brath, A. Assessing rating-curve uncertainty and its effects on hydraulic model calibration. Hydrol. Earth Syst. Sci. 2012, 16, 1191–1202. [Google Scholar] [CrossRef]
- Pelletier, M. Uncertainties in the single determination of river discharge: A literature review. Can. J. Civ. Eng. 1988, 15, 834–850. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Montanari, A. Uncertainty in river discharge observations: A quantitative analysis. Hydrol. Earth Syst. Sci. 2009, 13, 913–921. [Google Scholar] [CrossRef]
- Lerat, J.; Perrin, C.; Andréassian, V.; Loumagne, C.; Ribstein, P. Towards robust methods to couple lumped rainfall-runoff models and hydraulic models: A sensitivity analysis on the Illinois River. J. Hydrol. 2012, 418–419, 123–135. [Google Scholar] [CrossRef]
- Baringhaus, L.; Franz, C. On a new multivariate two-sample test. J. Multivar. Anal. 2004, 88, 190–206. [Google Scholar] [CrossRef]
- Székely, G.J.; Rizzo, M.L. A new test for multivariate normality. J. Multivar. Anal. 2005, 93, 58–80. [Google Scholar] [CrossRef]
- Fortin, V.; Abaza, M.; Anctil, F.; Turcotte, R. Why should ensemble spread match the RMSE of the ensemble mean? J. Hydrometeorol. 2014, 15, 1708–1713. [Google Scholar] [CrossRef]
- Thiboult, A.; Anctil, F.; Boucher, M.A. Accounting for three sources of uncertainty in ensemble hydrological forecasting. Hydrol. Earth Syst. Sci. 2016, 20, 1809–1825. [Google Scholar] [CrossRef]












| Process | Event | Start Date | End Date | Outflow | |
|---|---|---|---|---|---|
| Min (m3/s) | Max (m3/s) | ||||
| Calibration | Event C1 | 14 May 2016 | 22 May 2016 | 50 | 270 |
| Event C2 | 14 August 2016 | 16 August 2016 | 20 | 616 | |
| Event C3 | 17 August 2016 | 21 August 2016 | 75 | 950 | |
| Event C4 | 19 April 2019 | 27 April 2019 | 675 | 2488 | |
| Validation | Event V1 | 21 October 2016 | 26 October 2016 | 40 | 1085 |
| Event V2 | 22 April 2018 | 7 May 2018 | 400 | 1910 | |
| Station (Boundary Condition, BC) | Area (km2/(% Total Area)) |
|---|---|
| Sartigan Dam (upstream BC) | 3074 (52.8%) |
| Famine (tributary BC) | 696 (12%) |
| Intermediate catchments (lateral inflows) | 2050 (35.2%) |
| St-Lambert (downstream BC) | 5820 (100%) |
| Source of Uncertainty | Mean | Standard Deviation | Method | Members |
|---|---|---|---|---|
| Inflow | Observation | +/−10% Mean | Latin Hypercube Sampling following a Gaussian pdf | 50 |
| Roughness | Calibrated nfac = f(Q) | 50 | ||
| Lateral Inflows (LI) | Estimated LI from Outflow minus Inflow | 4 delays proposed to catch the hydrograph allure and peak at the outlet. The same uncertainty as Inflow is applied with +/−10% of estimated LI. | 4 | |
| Parameters set | 10,000 | |||
| Stations | Performance | Calibration | Validation | ||||
|---|---|---|---|---|---|---|---|
| Event C1 | Event C2 | Event C3 | Event C4 | Event V1 | Event V2 | ||
| Beauceville | ME (m) | 0.18 | −0.01 | −0.02 | −0.12 | −0.06 | −0.05 |
| MAE (m) | 0.18 | 0.17 | 0.17 | 0.14 | 0.16 | 0.12 | |
| RMSE (m) | 0.20 | 0.19 | 0.22 | 0.16 | 0.20 | 0.15 | |
| St-Joseph | ME (m) | - | - | −0.12 | 0.07 | 0.08 | 0.27 |
| MAE (m) | - | - | 0.22 | 0.12 | 0.13 | 0.27 | |
| RMSE (m) | - | - | 0.25 | 0.14 | 0.18 | 0.30 | |
| Vallée-jonction | ME (m) | - | 0.03 | −0.10 | 0.06 | 0.05 | 0.18 |
| MAE (m) | - | 0.11 | 0.20 | 0.13 | 0.15 | 0.21 | |
| RMSE (m) | - | 0.12 | 0.27 | 0.18 | 0.20 | 0.25 | |
| Sainte-Marie | ME (m) | −0.02 | 0.01 | −0.02 | 0.07 | 0.04 | 0.13 |
| MAE (m) | 0.05 | 0.15 | 0.11 | 0.11 | 0.11 | 0.15 | |
| RMSE (m) | 0.07 | 0.18 | 0.18 | 0.15 | 0.15 | 0.21 | |
| Saint-Lambert (WL) | ME (m) | - | - | 0.04 | −0.01 | 0.03 | 0.00 |
| MAE (m) | - | - | 0.15 | 0.08 | 0.15 | 0.11 | |
| RMSE (m) | - | - | 0.17 | 0.11 | 0.16 | 0.15 | |
| Saint-Lambert (Q) | ME (m3/s) | - | - | 3.0 | −0.3 | 2.7 | −0.8 |
| MAE (m3/s) | - | - | 43.3 | 41.4 | 34.1 | 65.5 | |
| RMSE (m3/s) | - | - | 66.3 | 63.3 | 41.6 | 86.2 | |
| Stations | Checkpoint | Depth | Flow | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| µ (m) | σ (m) | Cv (%) | Sk | Ku | µ (m3/s) | σ (m3/s) | Cv (%) | Sk | Ku | ||
| Beauceville | Peak 1 | 5.74 | 0.19 | 3.25 | −0.27 | 2.77 | 1090.0 | 54.6 | 5.01 | 0.03 | 2.87 |
| Peak 2 | 5.82 | 0.19 | 3.34 | −0.07 | 3.03 | 1128.0 | 59.9 | 5.31 | 0.30 | 3.18 | |
| Peak 3 | 4.72 | 0.24 | 4.99 | −0.31 | 2.78 | 734.3 | 37.4 | 5.09 | −0.29 | 2.59 | |
| St-Joseph | Peak 1 | 8.94 | 0.32 | 3.60 | −0.50 | 2.66 | 1466.7 | 65.9 | 4.49 | 0.20 | 3.76 |
| Peak 2 | 9.07 | 0.31 | 3.46 | −0.55 | 2.87 | 1535.4 | 89.7 | 5.84 | 0.95 | 4.12 | |
| Peak 3 | 7.11 | 0.20 | 2.76 | 0.23 | 3.08 | 913.2 | 49.9 | 5.46 | −0.11 | 2.34 | |
| Vallée-jonction | Peak 1 | 10.57 | 0.29 | 2.70 | −0.27 | 2.88 | 1577.6 | 68.4 | 4.34 | 0.57 | 3.23 |
| Peak 2 | 10.67 | 0.29 | 2.75 | −0.21 | 2.72 | 1622.3 | 97.7 | 6.02 | 1.16 | 4.43 | |
| Peak 3 | 8.66 | 0.21 | 2.42 | 0.05 | 2.99 | 976.8 | 45.7 | 4.67 | 0.15 | 2.88 | |
| Sainte-Marie | Peak 1 | 7.32 | 0.16 | 2.23 | 0.00 | 3.16 | 1639.4 | 73.9 | 4.51 | 0.60 | 2.97 |
| Peak 2 | 7.34 | 0.18 | 2.43 | 0.08 | 2.89 | 1676.2 | 107.1 | 6.39 | 1.24 | 4.72 | |
| Peak 3 | 5.54 | 0.17 | 3.05 | 0.01 | 2.86 | 1007.5 | 47.0 | 4.66 | 0.23 | 2.78 | |
| Saint-Lambert | Peak 1 | 4.60 | 0.15 | 3.36 | 0.28 | 2.96 | 1754.8 | 88.5 | 5.05 | 0.73 | 3.36 |
| Peak 2 | 4.61 | 0.19 | 4.04 | 0.79 | 3.65 | 1762.7 | 129.3 | 7.33 | 1.53 | 5.11 | |
| Peak 3 | 3.22 | 0.10 | 3.10 | 0.11 | 2.67 | 1063.8 | 51.3 | 4.82 | 0.11 | 2.57 | |
| Station | Spread (m) | RMSE (m) | % RMSE |
|---|---|---|---|
| Beauceville | 0.17 | 0.14 | 123% |
| St-Joseph | 0.22 | 0.29 | 76% |
| Vallé-Jonction | 0.23 | 0.27 | 83% |
| Ste-Marie | 0.19 | 0.20 | 91% |
| St-Lambert | 0.13 | 0.15 | 87% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bessar, M.A.; Matte, P.; Anctil, F. Uncertainty Analysis of a 1D River Hydraulic Model with Adaptive Calibration. Water 2020, 12, 561. https://doi.org/10.3390/w12020561
Bessar MA, Matte P, Anctil F. Uncertainty Analysis of a 1D River Hydraulic Model with Adaptive Calibration. Water. 2020; 12(2):561. https://doi.org/10.3390/w12020561
Chicago/Turabian StyleBessar, Mohammed Amine, Pascal Matte, and François Anctil. 2020. "Uncertainty Analysis of a 1D River Hydraulic Model with Adaptive Calibration" Water 12, no. 2: 561. https://doi.org/10.3390/w12020561
APA StyleBessar, M. A., Matte, P., & Anctil, F. (2020). Uncertainty Analysis of a 1D River Hydraulic Model with Adaptive Calibration. Water, 12(2), 561. https://doi.org/10.3390/w12020561





