When Green Infrastructure Turns Grey: Plant Water Stress as a Consequence of Overdesign in a Tree Trench System

Abstract

Green infrastructure (GI) systems are often overdesigned. This may be a byproduct of static sizing (e.g., accounting for a design storm’s runoff volume but not exfiltration rates) or may be deliberate (e.g., buffering against performance loss through time). In tree trenches and other GI systems that require stormwater to accumulate in an infiltration bed before it contacts the planting medium, overdesign could reduce plant water availability significantly. This study investigated the hydrological dynamics and water relations of an overdesigned tree trench system and identified factors contributing to, compounding, and mitigating the risk of plant stress. Water in the infiltration bed reached soil pits only once in three years, with that event occurring during a hydrant release. Moreover, minimal water was retained in soil pits during the event due to the hydraulic properties of the soil media. Through a growing season, one of the two tree types frequently experienced water stress, while the other did so only rarely. These contrasting responses can likely be attributed to roots being largely confined to the soil pits vs. reaching a deeper water source, respectively. Results of this study demonstrate that, in systems where soil pits are embedded in infiltration beds, overdesign can raise the storm size required for water to reach the soil media, reducing plant water availability between storms, and ultimately inducing physiological stress.

1. Introduction

The use of green infrastructure (GI) to control non-point pollution associated with stormwater has been written into law by municipalities around the world [1,2,3]. Such laws protect surface water bodies in and adjacent to urban areas from contaminants transported by stormwater as well as those released during combined sewer overflow events [4]. By reducing the volume of stormwater entering combined sewer systems, GI lowers pollutant loading, runoff velocity, and peak flow rates [5]. Although GI systems need not be vegetated, plants and soils can contribute substantially to volume reduction, in particular by enhancing rates of evapotranspiration (ET), interception, and infiltration [6,7,8,9]. Evapotranspiration is arguably the most effective of these processes with respect to volume reduction; studies using weighing lysimeters have found that 50% of incident precipitation can be removed by ET [10,11,12,13,14,15]. Moreover, vegetated GI systems provide additional ecosystem services such as improving air quality and cooling the local environment, thereby promoting human health [16].

Many GI systems are overdesigned (i.e., built larger than required), which can be done for a variety of reasons. It can be deliberate, principally to ensure that not only is a design goal achieved but that there is a margin for performance degradation, e.g., due to sedimentation or increasing storm sizes in the future. It can also be unintended, such as when a system is sized to meet a static guideline (e.g., a design storm volume) without accounting for the rate of exfiltration. Nonetheless, overdesign is generally considered benign to stormwater control performance and is often favored [17]. However, there is some evidence that overdesign can have negative implications for plant water availability in systems designed to use stormwater as the primary water source for vegetation [18]. For plants that have limited access to alternative water sources between storms, overdesign may increase the frequency, intensity, and duration of plant water stress events, ultimately reducing their transpiration rates and diminishing the associated benefits.

Any implications of overdesign for GI hydrology and plant water stress are likely to be influenced by plants’ biological characteristics. For example, woody plants in overdesigned systems may experience water shortages more rapidly after storms compared to herbaceous species, given their greater canopy-scale transpiration rates [19]. However, there may also be considerable differences among species within a given functional type. For example, variation in the size, architecture, or morphology of root systems is known to influence transpiration responses to varying soil moisture regimes and water access [20,21], suggesting that these factors may affect water relations in overdesigned GI systems.

A number of physiological measurements can provide insight into plant water relations, including stress responses, though they have been used infrequently to evaluate GI systems. Transpiration (i.e., the efflux of water from a leaf or canopy) can be measured or estimated using a variety of methods, though many cannot differentiate plant transpiration from soil evaporation; the combined efflux of water from plant and soil surfaces (i.e., that of ET) is therefore commonly-used as well. Moreover, while transpiration plays a large role in the water balance of GI systems, it is influenced by atmospheric conditions and is therefore only loosely indicative of plant water stress. In contrast, stomatal conductance (g_s) describes the component of water release influenced by plants themselves; g_s can be considered transpiration normalized to the evaporative demand of the atmosphere (specifically the vapor pressure difference between the leaf and the air [22]). Values below approximately 150 mmol m⁻² s⁻¹ under well-lit conditions are often indicative of water stress in temperate woody species, though this varies significantly [23]. Perhaps the most reliable measure of water stress is the potential of water in plant tissue (i.e., the tension it is under), with measurements made on leaves when they are at their daily minimum near mid-day (Ψ_md) being the most commonly used. Values below −1.5 MPa typically indicate a stressed state in species that are intolerant of drought or saline soils [22].

A series of investigations were carried out to probe the dynamics of a tree trench suspected to have been overdesigned. Tree trenches are a type of GI in which one or more tree/soil pits are embedded in a gravel-filled catchment. As the catchment fills with stormwater, it is intended to enter the soil pits from below, potentially subjecting these systems to hydrological limitation if overdesigned. This study had four objectives, each of which was addressed through a distinct investigation:

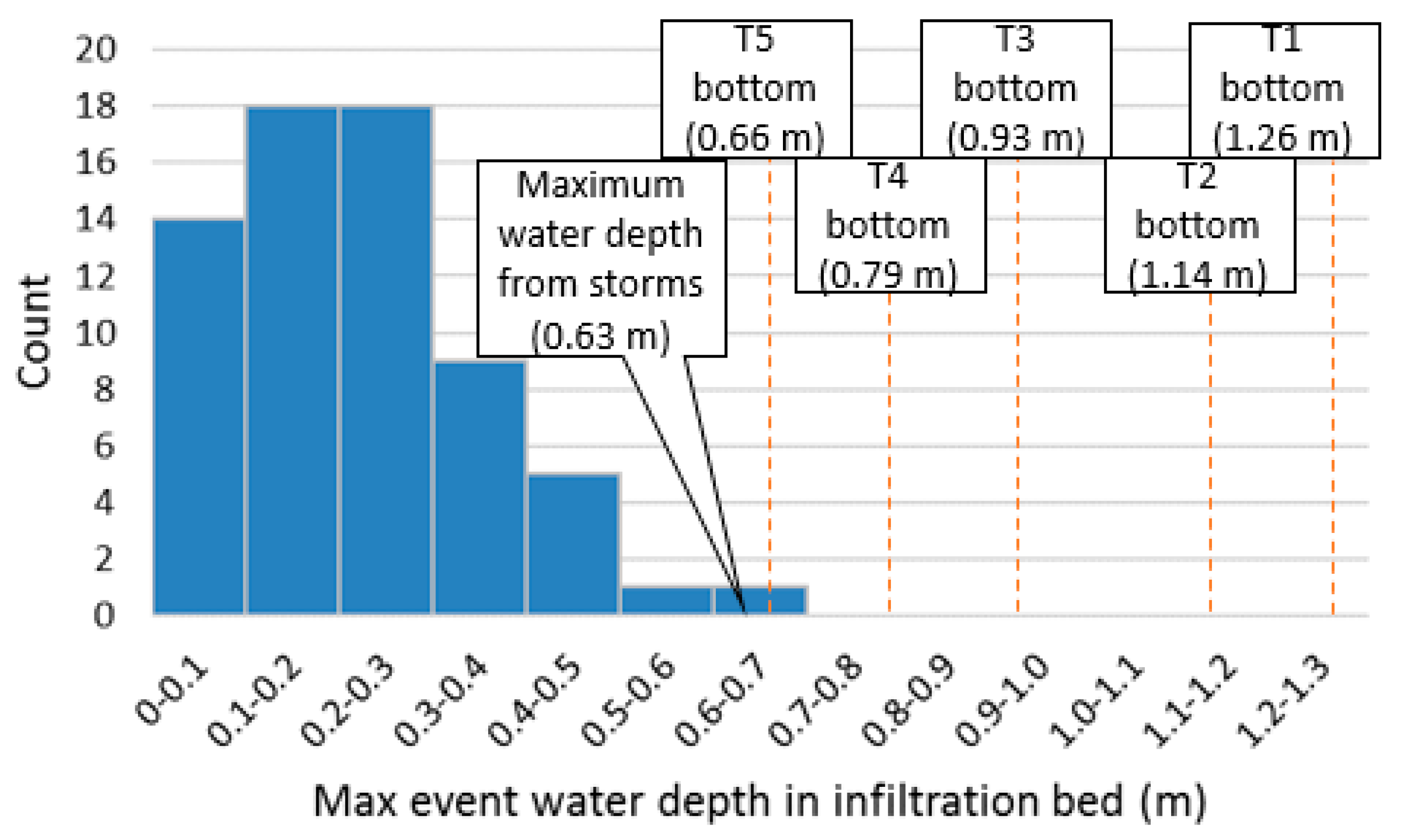
• Confirm with hydrological data that the tree trench was overdesigned. This was done by determining the frequency at which stormwater in the trench intercepted soil pits.
• Characterize the response of tree water relations to varying soil moisture conditions and determine how this response differed between species. This was done by evaluating how leaf water potential and stomatal conductance changed for two species in response to variation in soil moisture conditions throughout a growing season.
• Determine how soil moisture levels and tree water use respond to an extremely large storm event (i.e., the best-case scenario with respect to stormwater delivery to soil pits if the system is overdesigned). To achieve this, a simulated runoff test was conducted in the focal system simultaneous with repeated measurements of stomatal conductance.
• Evaluate how the composition of media in the soil pits influences the soil moisture response to wetting by the infiltration bed. This was done using a 2D unsaturated zone hydrologic model of a soil pit that was parameterized with empirical measurements of the soil’s hydraulic properties and the time series of water inputs and water levels in the infiltration bed during the simulated runoff test.

2. Materials and Methods

2.1. Site Description

This study focused on a GI tree trench located in northwest Philadelphia, USA, at 40.070° N, 75.175° W. The tree trench was constructed in 2013 and is composed of a gravel-filled infiltration bed installed beneath a sidewalk. Five trees and their associated soil pits (numbered T1 to T5) were embedded in the gravel bed (Figure 1). The soil pits contained an engineered sandy soil (87.6% sand, 8.2% silt, 4.2% clay) surrounded with geotextile. The trees in T1, T3, and T5 were Plantanus × acerifolia ‘Bloodgood’ (London plane tree), while those in T2 and T4 were Acer × freemanii ‘Armstrong’ (Freeman’s maple). The bottom of the infiltration bed was lined with a layer of sand 15 cm thick. Approximately 2494 m² of road surface area drained into the trench, yielding an 11.8:1 ratio of directly-connected impervious area to treatment bed area. Two inlet structures (GI1 and GI2) collected runoff water from the street and a perforated distribution pipe delivered water collected by the inlet structures into the infiltration bed. The system was sized such that a 4.75 cm storm could be contained in the media’s void space (Chris Bergerson, Philadelphia Water Department, pers. comm.). Given that it was designed statically and that, at the time of its installation, GI systems in Philadelphia were required to retain water from a 2.54 cm storm, we strongly suspected that it was overdesigned. Runoff entering the bottom of the infiltration bed was intended to rise to the level of the soil pits such that it would provide water to the trees. Additional information about the site and tree trench system can be found in earlier works involving this system [24,25].

2.2. Hydrological Characterization

A time-series dataset of water depth in the trench was used to quantify the frequency that stormwater reached the bottom of each tree’s soil pit. The dataset spanned March 2015 to April 2018, with data collected at 5-min intervals. A HOBO pressure transducer (Onset Computer Corporation, Bourne, USA) recorded water depth in the infiltration bed; it was set into an observation well in the center of the trench (Figure 1). Volumetric soil moisture content (θ) was measured at 5-min intervals in each soil pit using HydraProbe sensors (Stevens Water Monitoring Systems, Portland, USA) located at 10 and 35 cm depths. Two additional sensors were installed at 60 cm in T2 and T4; the 60-cm sensor in T4 was the deepest by elevation. A weather station installed at the site monitored precipitation and other meteorological conditions; details are provided by Tu and Traver [24].

2.3. Plant Water Stress

The response of tree water relations to varying soil moisture conditions was characterized from a dataset on mid-day leaf water potential (Ψ_md) and stomatal conductance (g_s) collected in 2015. Procedures for data collection are described in detail elsewhere [25], but briefly, Ψ_md and g_s were measured in each of the five trees between 1100–1300 h, 1–2 times per week from May through October. A leaf porometer (SC-1, METER Environment, Pullman, USA) was used to measure g_s and a Scholander-type pressure chamber (PMS Instruments, Albany, USA) was used to measure Ψ_md. Records of the times when each physiological data point was collected were used to extract soil moisture data from an imputed time series representing levels at the 35-cm depth. Pearson correlation statistics (denoted $\rho$) were used to quantify the strength of the relationship between each water relations variable and soil moisture level.

2.4. Simulated Runoff Test

A simulated runoff test (SRT) was performed on 1 August 2017 to investigate tree and trench dynamics under relatively extreme inflow conditions. Runoff water was provided by a street hydrant connected to a valve so that the release rate could be adjusted to increase the water depth gradually. Water was applied via a pair of hoses (approx. 10 cm diameter) to the street surface so that it would flow towards the pair of inlets (Figure 1) and enter the tree trench via the same pathway taken by stormwater runoff. The time series of outflow from the hoses was recorded via a flow meter. The SRT began after a set of baseline measurements of tree performance was completed (see below) and proceeded for approximately 3.5 h. Soil moisture, water depth, and associated hydrological data were collected throughout.

Trees’ water-use responses to the SRT were determined using measurements of g_s. Measurements spanned five time periods: one immediately prior to the SRT, three during the SRT, and one the morning after the SRT. In addition to the five trees in the focal tree trench, a P. × acerifolia tree in an adjacent GI system of the same design (but that did not experience the SRT) was also measured to provide a reference for diurnal changes in g_s. To account for variation in g_s within each tree’s canopy, measurements were taken from at least three randomly selected leaves from both exterior and interior portions of the canopy (n = 6–14 measurements per tree per period).

A statistical analysis was performed to determine how g_s changed during the course of the SRT, if this differed from the tree in the adjacent trench, and whether responses differed between species. A mixed-effects linear regression model was used; fixed effects included species identity, GI identity (i.e., SRT or non-SRT), canopy position (i.e., measurements taken in either the interior or exterior portion of the canopy), and measurement period (a discrete variable with five levels), as well as all possible two-way interactions except GI identity × species (because data were only available for a single species from the non-SRT GI). A random effect for tree identity (discrete with six levels) was included to account for repeated measurements of individual trees. All hierarchically complete models were fit using maximum likelihood estimation via the lme4 library [26] in R version 3.6.0 [27]. Binary variables were coded ± 0.5 and g_s was centered and divided by two standard deviations [28]. Model-averaged coefficients were then determined for all models with an ΔAIC_c < 4; coefficients for terms not present in a model were taken to be zero for the purpose of averaging. This process yielded robust coefficients (denoted $\beta$) proportional to each term’s effect on g_s, as well as their unconditional standard errors and 95% confidence intervals [29]. The model term for the first period defined the intercept of the model, while that terms for Periods 2–5 represented deviations from it.

2.5. Hydrological Modeling

A hydrological model was used to evaluate the response of soil moisture to wetting by stormwater from the infiltration bed. The model was generated in HYDRUS-2D and simulated water movement in variably saturated and unsaturated soil media by solving the Richards equation [30]. It was parameterized for a vertical plane through the T4 soil pit so that it intersected the position of the 60-cm soil moisture sensor (0.92 × 1.22 m; dashed line in Figure 2). This location was selected because it allowed a direct comparison between empirical and modeled soil moisture time series. In effect, the model provided an independent means of quantifying soil moisture at that location during the SRT and, thus, an ability to infer which characteristics of the GI system likely influenced the soil moisture response (or lack thereof) during a large storm.

In the model, water inputs came from the time series of hydrant outflow recorded during the SRT. Boundaries of the soil pit that fell below the highest water level reached during the SRT were designated as having “variable head” conditions. The remaining side walls were designated as “seepage faces”, because the pits were surrounded by gravel subject to atmospheric pressure [31]. No flow was assumed at the top boundary.

Water retention parameters of the soil in the tree pits were derived empirically using a pair of intact cores. Pressure potentials and their corresponding water content values were measured with a HYPROP and WP4C (METER Environment, Pullman, USA). Parameters were determined by fitting the van Genuchten function [32] to the combined datasets, and parameter values from the two curves were averaged (

Table 1. Parameters of the engineered soil’s water retention curve and saturated hydraulic conductivity as used in HYDRUS-2D.

Parameter	Unit	Meaning	Value
θr	m3 m−3	Residual water content	0.029
θs	m3 m−3	Saturated water content	0.479
α	cm−1	Air entry suction parameter	0.040
n	dimensionless	Pore size distribution parameter	1.344
Ks	cm min−1	Saturated hydraulic conductivity	0.296

). At the outset of the model runs, soil moisture was set to match the value recorded by the soil moisture sensors (0.16 m³ m⁻³). The saturated hydraulic conductivity of the media was also used in the model, having been measured from the same cores using a KSAT device (METER Environment, Pullman, USA).

Model calibration was not performed. Calibration of the soil moisture time series would have precluded using the output as an independent estimate of soil water levels. Moreover, calibration was not required since water inputs, soil pit dimensions, and water retention parameters were empirically defined. Also, the geotextile was not simulated in the model. Given its permeability (0.274 cm s⁻¹) and thickness (0.15 cm), even if the flow velocity through the geotextile was equal to the soil’s saturated hydraulic conductivity (0.296 cm s⁻¹), the head loss generated by the geotextile would have been negligible (0.16 cm). If the geotextile had become partially clogged during its four-year lifespan, the head loss would have been greater and the elevation of the actual wetting front would have been lower than observed [33].

3. Results

3.1. Hydrological Characterization

Of the 119 recorded storms between March 2015 and April 2018, 66 yielded enough water to be detectable in the infiltration bed. These events had an average depth of 23.2 mm and an average intensity of 3.4 mm hr⁻¹ (

Table 2. Attributes of storms that occurred at the focal tree trench during the study period (March 2015 to April 2018).

Storm Set	Count	Length (hr)	Depth (mm)	Intensity (mm hr−1)	Peak Intensity (mm 5-min−1)
All storms	119	11.9	20.0	3.9	2.6
Detectable in infiltration bed	66	11.5	23.2	5.5	3.4

). Excluding the SRT, none of these storms caused water to rise sufficiently high enough in the infiltration bed to reach the bottom of any tree pit (Figure 3). The maximum observed water depth was associated with a 69-mm storm and caused water to rise to 0.63 m. This was 0.03 m lower than the bottom of the T5 soil pit and 0.63 m lower than the bottom of the T1 soil pit.

3.2. Plant Water Stress

Both species exhibited less favorable leaf water potential as soil water declined (Figure 4a). The relationship was approximately linear in both species, but the relationship was weaker for P. × acerifolia ($\rho$ = 0.50) than for A. × freemanii ($\rho$ = 0.66). Moreover, Ψ_md was below the level typically indicative of hydraulic damage to plant tissue (−1.5 MPa) more frequently in A. × freemanii than in P. × acerifolia (39% vs 4% of measurements, respectively). A large portion of these observations occurred when θ was below 0.20 m³ m⁻³. Stomatal conductance varied weakly with soil moisture in P. × acerifolia ($\rho$ = 0.24; Figure 4b), but the relationship was slightly stronger for A. × freemanii ($\rho$ = 0.34), especially when θ was below 0.20 m³ m⁻³ ($\rho$ = 0.54).

3.3. Simulated Runoff Test

Tree-level means of $g_s$ remained between approximately 200 and 400 mmol m⁻² s⁻¹ during all measurement periods (Figure 5). This was the case for both trees that did and did not experience the SRT. Statistical modeling showed that g_s in the non-SRT GI was marginally greater ($\beta$ = −0.144 with 95% CI including zero;

Table 3. Statistical modeling results for a linear mixed-effects model of stomatal conductance. Bold depicts model terms with relatively strong influence ($\left|\beta \right|>0.1$). Only terms in models with a ΔAIC_c < 4 are shown.

Model Term	$\mathbf{Coefficient}\left(\mathit{\beta }\right)$	SE	95% CI
Period 2	0.019	0.069	(−0.116, 0.155)
Period 3	−0.176	0.075	(−0.324, -0.029)
Period 4	−0.038	0.070	(−0.176, 0.099)
Period 5	0.098	0.070	(−0.040, 0.236)
Canopy position	−0.375	0.055	(−0.483, −0.268)
Species	0.427	0.100	(0.232, 0.622)
GI identity	−0.144	0.075	(−0.290, 0.003)
Period 2 × Species	0.022	0.119	(−0.211, 0.255)
Period 3 × Species	−0.251	0.200	(−0.643, 0.140)
Period 4 × Species	0.002	0.119	(−0.232, 0.236)
Period 5 × Species	−0.135	0.146	(−0.421, 0.151)
Canopy position × Species	−0.205	0.110	(−0.420, 0.010)
Canopy position × GI identity	−0.016	0.068	(−0.149, 0.118)

), likely because the non-SRT GI only contained P. × acerifolia. The greatest source of variation in $g_s$ was species identity, with P. × acerifolia having substantially greater rates than A. × freemanii ($\beta$ = 0.427). Canopy position was the second-strongest source of variation in g_s, with leaves from the exterior portions of canopies having greater g_s than those from canopy interiors ($\beta$ = −0.375), as expected [34].

The primary case in which g_s differed among measurement periods was a decline from baseline during Period 3 (1130–1230 h; $\beta$ = −0.176 for the main effect). The change was potentially greater for P. × acerifolia ($\beta$ = −0.251 for the interaction), though the coefficient’s 95% CI included zero. This decline was likely a result of trees restricting water loss in response to high evaporative demand during the middle part of the day, a phenomenon that has been observed in many studies previously [35]. Rates returned to baseline in Period 4 ($\beta$ = −0.038), at least for three of the four P. × acerifolia trees (including that in the non-SRT GI). There was also some evidence that mean $g_s$ increased over baseline the following day (Period 5; $\beta$ = 0.098) with A. × freemanii contributing disproportionately to this increase ($\beta$ = −0.135).

3.4. Hydrological Modeling

The HYDRUS-2D model indicated that, when the gravel bed’s water level rose to the highest point it reached during the SRT (and therefore during the lifetime of the GI system), the soil media was near saturation (θ = 0.450 − 0.479 m³ m⁻³) up to approximately a 10-cm depth (Figure 6). Above the saturation zone, θ exhibited a sharp vertical gradient through an additional, approximately 10-cm-thick capillary zone, decreasing from near saturation to 0.16 m³ m⁻³. The effect of water contacting the soil pit, therefore, had no effect on the level of the 60-cm soil moisture sensor, and θ modeled at the sensor varied minimally during the simulation, mimicking the empirical time series (Figure 5).

4. Discussion

4.1. Overdesign & Plant Water Stress

The tree trench system on which this study was based was unquestionably overdesigned with respect to its capacity to store water. Water in the infiltration bed did not reach the bottom of even the lowest-elevation soil pit during any of the natural storm events that the system experienced in the four-year period considered. While this had no ill effects on the system’s primary function of water removal, it hydraulically isolated the soil pits from the infiltration bed. Therefore, soil media received water primarily via direct reception of rainfall (i.e., through the 1.22 × 1.22 m openings in the sidewalk surface (Figure 7)). Moreover, the hydraulic properties of the media compounded the effects of overdesign. Although water did reach the bottom of the modeled soil pit during the SRT, the media exerted insufficient capillary force to retain an appreciable amount of water at pressure potentials over which it would be accessible to plants (−33 to −1500 kPa [36]) and was therefore rapidly lost to the underlying gravel bed. This can likely be attributed to the high sand content of the media (87.6%), with the implication that stormwater entering from the sidewalk would be similarly poorly retained. In combination, the absence of the intended subsurface water supply, restricted surface inputs, and rapidly draining media meant that soil pits contained far less than the intended amount of soil water during rain-free periods.

The implications of limited water availability in soil pits to the trees were strongly species-dependent. In the case of A. × freemanii, water stress (low Ψ_md) occurred frequently through the growing season, especially when soil water availability was reduced, and was presumably the factor responsible for strong restrictions in water use. Unless mitigated by other factors, this phenomenon could be expected to occur in many overdesigned GI systems, ultimately leading to poorer tree health and mortality [37]. In contrast to A. × freemanii, P. × acerifolia exhibited water stress infrequently through the growing season, likely contributing to its ability to maintain high g_s. In addition, the rebound in g_s for P. × acerifolia during Period 4 of the SRT is also consistent with it responding to an increase in water availability, as weather conditions (notably vapor pressure deficit) had not changed since the decline that occurred during Period 3.

A parsimonious explanation for the contrasting water relations of the two species is that P. × acerifolia had an alternative subsurface water source that buffered it from changes in soil moisture in tree pit soil, while A. × freemanii relied almost exclusively on soil water within the soil pits themselves. Evidence that P. × acerifolia had gained access to water below (or possibly at the bottom of) the infiltration bed includes direct observations of roots in the distribution pipe, reports of deep-rooting in other Platanus species, and the larger size of P. × acerifolia trees. Specifically, roots were evident along nearly the full length of the distribution pipe in videos recorded during a maintenance investigation (Figure 8). These observations confirm that roots had extended beyond the primary impediment, namely the geotextile lining the soil pits, though A. × freemanii roots may have been among those observed. The inference that most of the deeply proliferated roots were from P. × acerifolia (aside from its more consistent water status) derives from prior observations of Platanus spp. roots extending below 2 m [38,39] in combination with the fact that P. × acerifolia stems and canopies were appreciably larger than those of A. × freemanii (Figure 7). Positive associations between rooting depth and the above-ground size of woody plants are common in water-limited systems [40]. Moreover, a study of street trees found that the growth of Platanus species was accelerated in sandy soil while that of Acer species was hindered [41]; it is likely that a similar pattern arose in the focal trench given the high sand content of its soil pits. The fact that A. × freemanii responded minimally to the SRT but increased g_s following the overnight rain event also suggests that soil pits were its dominant source of water.

4.2. Implications for Design

Ideally, vegetated GI systems would be deliberately designed to minimize plant water stress while still meeting stormwater management goals. This is likely to be less difficult in cases where vegetation is smaller in stature and therefore has lower water requirements than do trees, though trees are preferred in many settings given their aesthetic and ability to provide services like shade [42]. Trees’ rates of water use are also typically greater than those of smaller-stature plants [19,43], enhancing their utility in GI. In designing GI systems for which trees are desired but their soil pits are at risk of hydraulic isolation (notably, tree trenches), the results of this study suggest that several modifications to typical designs could help to minimize the frequency and intensity of water stress events.

First, designers should restrict overdesign so that water captured in infiltration beds during small to moderate storms thoroughly wets the soil provided to plants. In most cases, achieving an appropriate distribution of water depths over time would entail carefully optimizing design parameters (notably catchment depth); this might include accounting for exfiltration from the gravel bed during storms rather than using a static sizing approach. Such efforts may be particularly important when the infiltration capacity of the native soil is moderate or greater (such as with the focal trench; Figure 9). While reducing the depth (or other dimensions) of infiltration beds may reduce their capacity for stormwater retention, this is likely to be problematic only rarely during the lifespan of the GI system, such as when large storms occur in succession [44]. In tree trenches, the ability of stormwater to exfiltrate through side walls (in addition to the bottom surface) appears to further reduce the probability of overflow [45,46]. This suggests that trenches could be much shallower than those calculated under the assumption that exfiltration occurs strictly through the bottom. Accordingly, it may be possible to make simple adjustments to the dimensions of infiltration beds so as to increase the water available to plants during rain-free periods, ultimately improving plant health and survival.

Second, the capacity of soil media to draw water upward by capillary force should be considered carefully. If insufficient, a situation like that observed during this study’s SRT can arise in which most water accumulates at the bottom of the soil pit and the capillary zone is quite narrow (10 cm in this study; Figure 6). Using media with a greater capacity for capillary uptake than that used in the focal trench could significantly increase water retention in the plant-available range and decrease the frequency and intensity of water stress events. Adjusting clay and organic matter components of soil media may be inexpensive means of achieving this, though amendments such as water-absorbing polymers and biochar could also be considered. Increasing the amount of stormwater entering soil pits from the sidewalk surface (e.g., using porous pavement, curb cuts, or shaping sidewalk surfaces to direct water to soil pits) could also help to reduce the effects of hydraulic isolation.

Third, tree species and cultivars should be selected that are suited to the unique hydrologic regime of the GI system, although this may be a somewhat different set than is suitable for non-GI street trees. Choosing species after an empirical evaluation of hydrologic conditions in a GI made during installation could minimize the chances of a mismatch, though this may not be possible in many cases. Another important aspect of species selection in tree trench settings may be whether the proliferation of roots outside soil pits can be tolerated or if it should be avoided. If root proliferation can be tolerated, it may be possible to select species likely to find alternative water sources before the trees grow to a size where hydraulic isolation imposes severe physiological stress. Otherwise, it may be beneficial to select species that can tolerate limited water availability or to enact the abovementioned strategies of increasing soil water availability. Using root barriers may also be particularly important in these cases.

5. Conclusions

Whether done inadvertently or deliberately, overdesign can be an issue in GI systems that are intended to deliver water to plants by raising the level of stored water high enough to contact overlying soil. In such systems, the frequency that soils are wetted is likely to be lower than intended and, in the periods between rain events, plants may experience moderate to severe water stress. A number of other factors can influence the dynamics of this process and could potentially be attended to during the design phase (e.g., soil water retention properties and the availability of pathways for water to contact soils directly). Notably, even among street trees and common landscaping plants, taxa may have extremely different responses to water shortages due to functional traits like rooting depth. In combination with advances in large-scale planning methods [47], efforts to improve GI’s ability to support vegetation at the site-scale could substantially expand the performance of GI systems both in managing stormwater and in greening cities.