Use of Global Sensitivity and Data-Worth Analysis for an Efficient Estimation of Soil Hydraulic Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Laboratory Experiment
2.2. Numerical Model
2.3. Global Sensitivity Analysis
2.4. Bayesian Parameter Inference
3. Results and Discussion
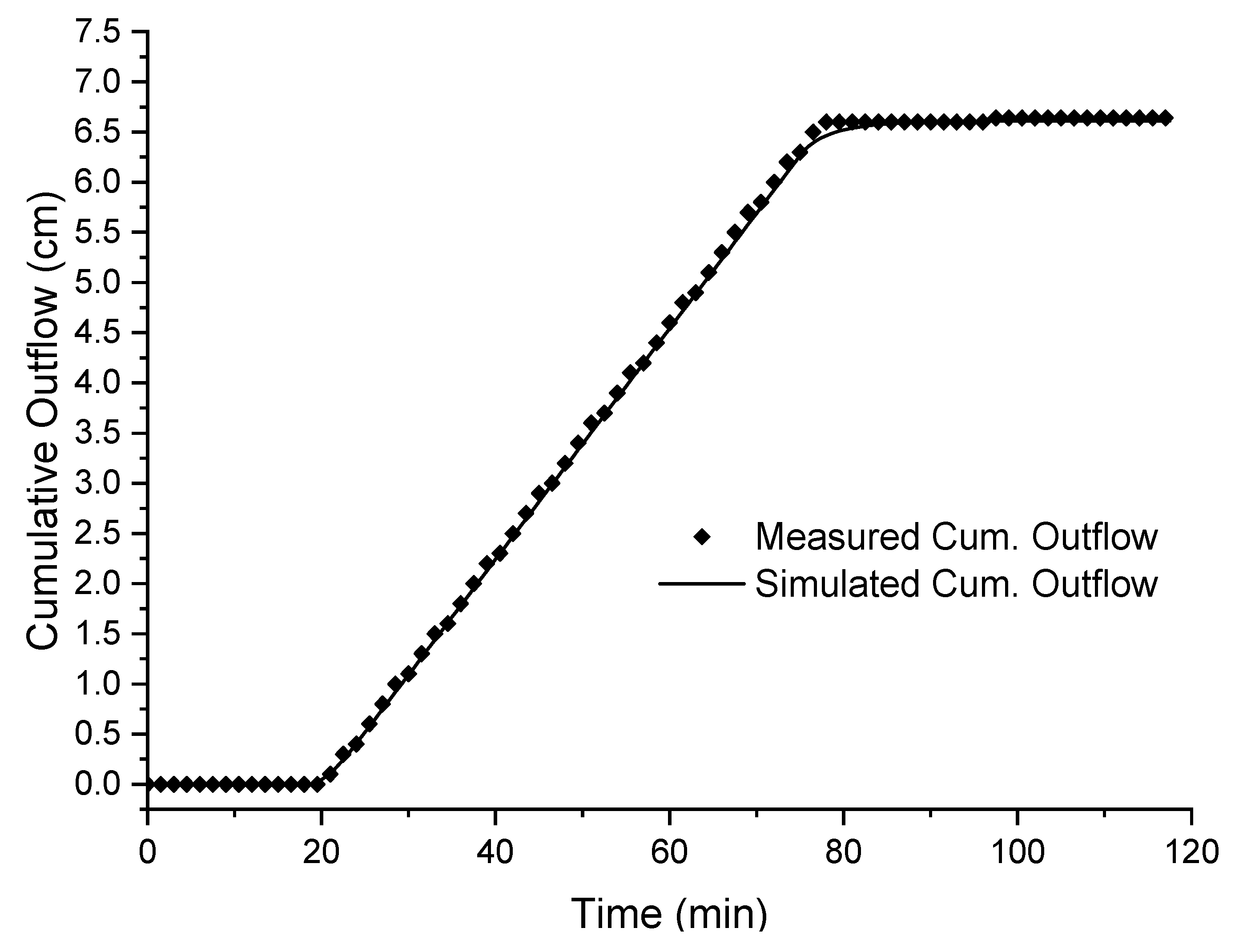
3.1. Inversion Using Cumulative Outflow Measurements
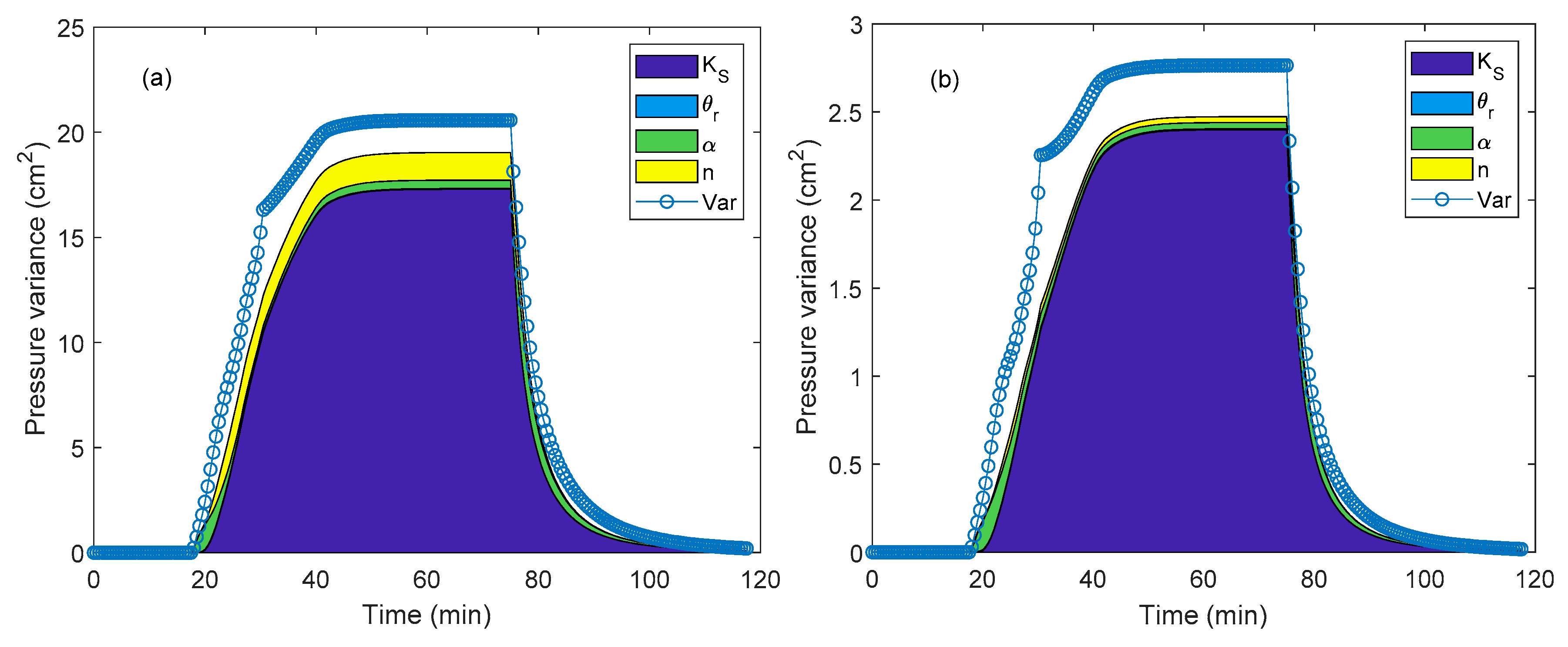
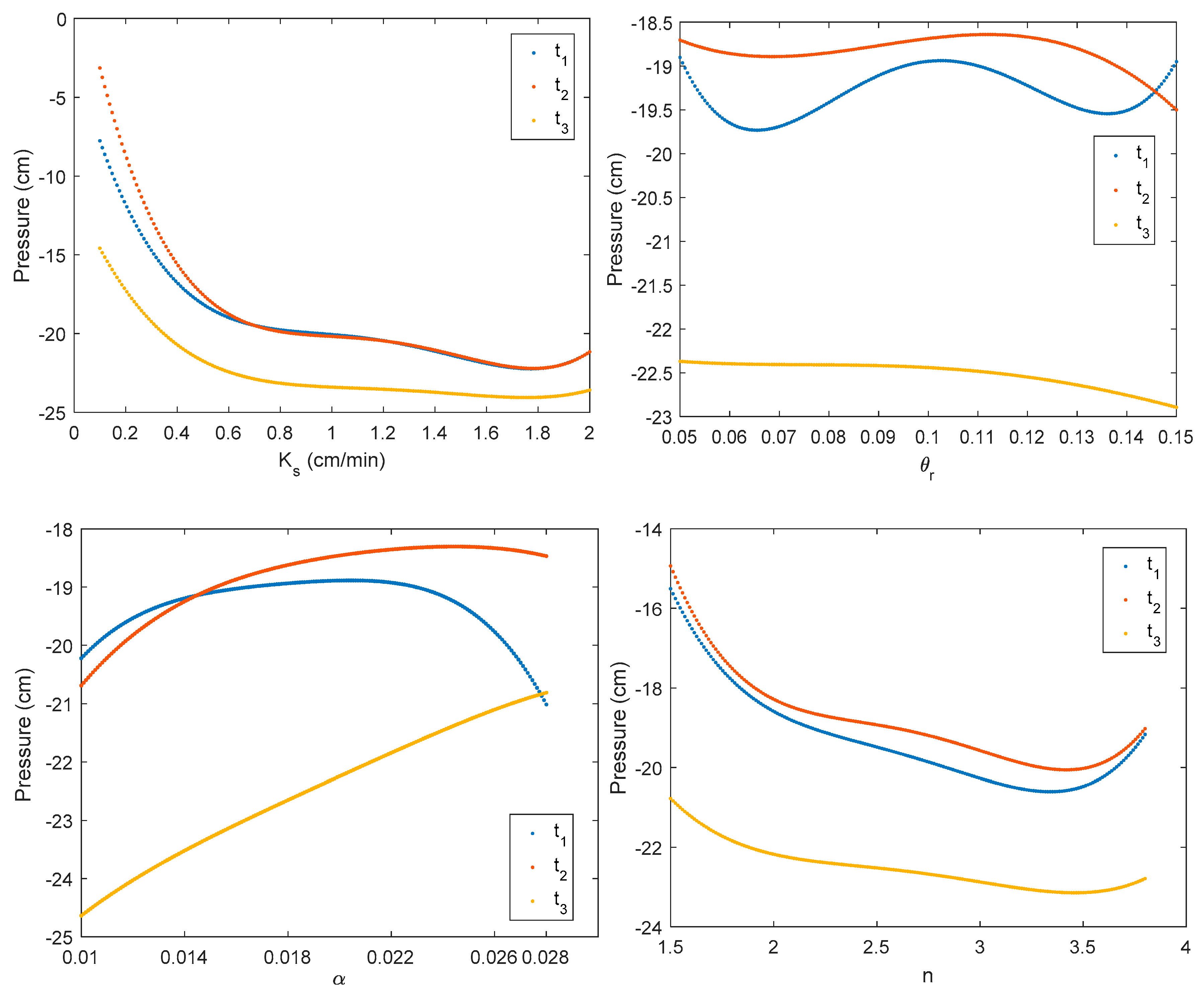
3.2. Global Sensitivty Analysis Results
- (i)
- The pressure head prediction was driven by hydraulic parameters and thus, the accuracy of the soil parameters may improve if the pressure data are also considered for calibration.
- (ii)
- If one has to install a single tensiometric sensor for collecting pressure head measurements, it is better to install it near the soil surface (near the top of the column).
- (iii)
- The parameter cannot be estimated from the pressure head measurements regardless to the position of the tensiometric sensor.
3.3. Data Worth Analysis Results
- (i)
- The numerical model was used to generate synthetic pressure head data at 18.5 cm using the mean parameter values obtained earlier from the calibration of the cumulative outflow data (Table 2, column 3).
- (ii)
- Then, the simulated pressure values were noised with Gaussian noises of 0.5 cm standard deviation and used as fictive new observations.
- (iii)
- The new fictive pressure observations were supplemented to the real cumulative outflow observations and used for a new Bayesian calibration of the hydraulic parameters.
3.4. Inversion Using Real Cumulative Outflow and Pressure Measurements
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kool, J.B.; Parker, J.C.; van Genuchten, M.T. Determining Soil Hydraulic Properties from One-step Outflow Experiments by Parameter Estimation: I. Theory and Numerical Studies1. Soil Sci. Soc. Am. J. 1985, 49, 1348. [Google Scholar] [CrossRef] [Green Version]
- Parker, J.C.; Kool, J.B.; van Genuchten, M.T. Determining Soil Hydraulic Properties from One-step Outflow Experiments by Parameter Estimation: II. Experimental Studies1. Soil Sci. Soc. Am. J. 1985, 49, 1354. [Google Scholar] [CrossRef]
- Van Dam, J.C.; Stricker, J.N.M.; Droogers, P. Inverse method to determine soil hydraulic functions from multistep outflow experiments. Soil Sci. Soc. Am. J. 1994, 58, 647–652. [Google Scholar] [CrossRef]
- Durner, W.; Schultze, B.; Zurmühl, T. State-of-the-Art in Inverse Modeling of Inflow/Outflow Experiments; University of California: Riverside, CA, USA, 1999. [Google Scholar]
- Puhlmann, H.; Von Wilpert, K.; Lukes, M.; Dröge, W. Multistep outflow experiments to derive a soil hydraulic database for forest soils. Eur. J. Soil Sci. 2009, 60, 792–806. [Google Scholar] [CrossRef]
- Beydoun, H.; Lehmann, F. Expériences de drainage et estimation de paramètres en milieu poreux non saturé. Comptes Rendus Geosci. 2006, 338, 180–187. [Google Scholar] [CrossRef]
- Younes, A.; Mara, T.A.; Fajraoui, N.; Lehmann, F.; Belfort, B.; Beydoun, H. Use of Global Sensitivity Analysis to Help Assess Unsaturated Soil Hydraulic Parameters. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Mishra, S.; Parker, J.C. Parameter estimation for coupled unsaturated flow and transport. Water Resour. Res. 1989, 25, 385–396. [Google Scholar] [CrossRef]
- Younes, A.; Zaouali, J.; Fahs, M.; Slama, F.; Grunberger, O.; Mara, T.A. Bayesian soil parameter estimation: Results of percolation-drainage vs. infiltration laboratory experiments. J. Hydrol. 2018, 565, 770–778. [Google Scholar] [CrossRef]
- Durner, W.; Iden, S.C. Extended multistep outflow method for the accurate determination of soil hydraulic properties near water saturation. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Wendroth, O.; Ehlers, W.; Hopmans, J.W.; Kage, H.; Halbertsma, J.; Wösten, J.H.M. Reevaluation of the evaporation method for determining hydraulic functions in unsaturated soils. Soil Sci. Soc. Am. J. 1993, 57, 1436–1443. [Google Scholar] [CrossRef]
- Kumar, S.; Sekhar, M.; Reddy, D.V.; Mohan Kumar, M.S. Estimation of soil hydraulic properties and their uncertainty: Comparison between laboratory and field experiment. Hydrol. Process. 2010, 24, 3426–3435. [Google Scholar] [CrossRef]
- Schelle, H.; Iden, S.C.; Durner, W. Combined transient method for determining soil hydraulic properties in a wide pressure head range. Soil Sci. Soc. Am. J. 2011, 75, 1681–1693. [Google Scholar] [CrossRef]
- Moreira, P.H.S.; van Genuchten, M.T.; Orlande, H.R.B.; Cotta, R.M. Bayesian estimation of the hydraulic and solute transport properties of a small-scale unsaturated soil column. J. Hydrol. Hydromech. 2016, 64, 30–44. [Google Scholar] [CrossRef] [Green Version]
- Younes, A.; Mara, T.; Fahs, M.; Grunberger, O.; Ackerer, P. Hydraulic and transport parameter assessment using column infiltration experiments. Hydrol. Earth Syst. Sci. 2017, 21, 2263–2275. [Google Scholar] [CrossRef] [Green Version]
- Younes, A.; Mara, T.A.; Voltz, M.; Guellouz, L.; Musa Baalousha, H.; Fahs, M. A new efficient Bayesian parameter inference strategy: Application to flow and pesticide transport through unsaturated porous media. J. Hydrol. 2018, 563, 887–899. [Google Scholar] [CrossRef]
- Younes, A.; Zaouali, J.; Kanzari, S.; Lehmann, F.; Fahs, M. Bayesian Simultaneous Estimation of Unsaturated Flow and Solute Transport Parameters from a Laboratory Infiltration Experiment. Water 2019, 11, 1660. [Google Scholar] [CrossRef] [Green Version]
- Mboh, C.M.; Huisman, J.A.; Zimmermann, E.; Vereecken, H. Coupled Hydrogeophysical Inversion of Streaming Potential Signals for Unsaturated Soil Hydraulic Properties. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Younes, A.; Zaouali, J.; Lehmann, F.; Fahs, M. Sensitivity and identifiability of hydraulic and geophysical parameters from streaming potential signals in unsaturated porous media. Hydrol. Earth Syst. Sci. 2018, 22, 3561–3574. [Google Scholar] [CrossRef] [Green Version]
- Pan, F.; Zhu, J.; Ye, M.; Pachepsky, Y.A.; Wu, Y.S. Sensitivity analysis of unsaturated flow and contaminant transport with correlated parameters. J. Hydrol. 2011, 397, 238–249. [Google Scholar] [CrossRef]
- Brunetti, G.; Šimůnek, J.; Turco, M.; Piro, P. On the use of global sensitivity analysis for the numerical analysis of permeable pavements. Urban Water J. 2018, 15, 269–275. [Google Scholar] [CrossRef] [Green Version]
- van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Fajraoui, N.; Ramasomanana, F.; Younes, A.; Mara, T.A.; Ackerer, P.; Guadagnini, A. Use of global sensitivity analysis and polynomial chaos expansion for interpretation of nonreactive transport experiments in laboratory-scale porous media. Water Resour. Res. 2011, 47, W02521. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 964–979. [Google Scholar] [CrossRef]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Sobol′, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Kaipio, J.; Somersalo, E. Statistical and Computational Inverse Problems; Applied Mathematical Sciences; Springer: New York, NY, USA, 2004; p. 160. [Google Scholar]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, M.; Doherty, J. Parameter estimation and uncertainty analysis for a watershed model. Environ. Model. Softw. 2007, 22, 1000–1020. [Google Scholar] [CrossRef]
- Kahl, G.M.; Sidorenko, Y.; Gottesbüren, B. Local and global inverse modelling strategies to estimate parameters for pesticide leaching from lysimeter studies: Inverse modelling to estimate pesticide leaching parameters from lysimeter studies. Pest Manag. Sci. 2015, 71, 616–631. [Google Scholar] [CrossRef] [PubMed]
- Vrugt, J.A.; Bouten, W. Validity of first-order approximations to describe parameter uncertainty in soil hydrologic models. Soil. Sci. Soc. Am. J. 2002, 66, 1740–1751. [Google Scholar] [CrossRef] [Green Version]
- Hindmarsh, A.C. LSODE and LSODI, two new initial value ordinary differential equation solvers. ACM Signum Newsl. 1980, 15, 10–11. [Google Scholar] [CrossRef]
- Miller, C.T.; Abhishek, C.; Farthing, M.W. A spatially and temporally adaptive solution of Richards’ equation. Adv. Water Resour. 2006, 29, 525–545. [Google Scholar] [CrossRef]
- Farthing, M.W.; and Ogden, F.L. Numerical solution of Richards’ equation: A review of advances and challenges. Soil Sci. Soc. Am. J. 2017, 81, 1257–1269. [Google Scholar] [CrossRef] [Green Version]
- Fahs, M.; Younes, A.; Lehmann, F. An easy and efficient combination of the Mixed Finite Element Method and the Method of Lines for the resolution of Richards’ Equation. Environ. Modell. Softw. 2009, 24, 1122–1126. [Google Scholar] [CrossRef]
- Mara, T.A.; Tarantola, S. Application of global sensitivity analysis of model output to building thermal simulations. Build. Simul. 2008, 1, 290–302. [Google Scholar] [CrossRef] [Green Version]
- Fajraoui, N.; Mara, T.A.; Younes, A.; Bouhlila, R. Reactive transport parameter estimation and global sensitivity analysis using sparse polynomial chaos expansion. Water Air Soil Poll. 2012, 223, 4183–4197. [Google Scholar] [CrossRef]
- Shao, Q.; Younes, A.; Fahs, M.; Mara, T.A. Bayesian sparse polynomial chaos expansion for global sensitivity analysis. Comput. Methods Appl. Mech. Eng. 2017, 318, 474–496. [Google Scholar] [CrossRef] [Green Version]
- Younes, A.; Delay, F.; Fajraoui, N.; Fahs, M.; Mara, T.A. Global sensitivity analysis and Bayesian parameter inference for solute transport in porous media colonized by biofilms. J. Contam. Hydrol. 2016, 191, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Mara, T.A.; Belfort, B.; Fontaine, V.; Younes, A. Addressing factors fixing setting from given data: A comparison of different methods. Environ. Modell. Softw. 2017, 87, 29–38. [Google Scholar] [CrossRef] [Green Version]
- Xiu, D.; Karniadakis, G.E. A new stochastic approach to transient heat conduction modeling with uncertainty. Int. J. Heat Mass Tran. 2003, 46, 4681–4693. [Google Scholar] [CrossRef]
- Laloy, E.; Vrugt, J.A. High-dimensional posterior exploration of hydrologic models using multiple-try DREAM (ZS) and high-performance computing. Water Resour. Res. 2012, 48, W01526. [Google Scholar] [CrossRef] [Green Version]
- Hayek, M.; Younes, A.; Zouali, J.; Fajraoui, N.; Fahs, M. Analytical solution and Bayesian inference for interference pumping tests in fractal dual-porosity media. Computat. Geosci. 2018, 22, 413–421. [Google Scholar] [CrossRef]
- Linde, N.; Ginsbourger, D.; Irving, J.; Nobile, F.; Doucet, A. On uncertainty quantification in hydrogeology and hydrogeophysics. Adv. Water Resour. 2017, 110, 166–181. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stren, H.S.; Rubin, D.B. Bayesian Data Analysis; Chapmann and Hall: London, UK, 1997. [Google Scholar]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Statist. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]



| Parameter | Lower Bound | Upper Bound |
|---|---|---|
| [cm/min] | 0.10 | 2.0 |
| [-] | 0.05 | 0.15 |
| [cm−1] | 0.005 | 0.15 |
| [-] | 1.5 | 13. |
| Unit | Mean Value | 99% Confidence Interval | Size of the 99% Confidence Interval | |
|---|---|---|---|---|
| (cm/min) | 1.37 | [0.1–2.0] | 1.9 | |
| - | 0.104 | [0.05–0.15] | 0.1 | |
| (cm−1) | 0.019 | [0.01–0.029] | 0.028 | |
| - | 2.19 | [0.6–3.8] | 3.2 |
| Unit | Reference Value | Mean Value | 99% Confidence Interval | Size of the 99% CI | |
|---|---|---|---|---|---|
| (cm/min) | 1.37 | 1.59 | [0.9–2.3] | 1.3 | |
| - | 0.104 | 0.106 | [0.05–0.15] | 0.1 | |
| (cm−1) | 0.0187 | 0.02 | [0.017–0.025] | 0.007 | |
| - | 2.19 | 2.19 | [1.56–2.64] | 1.08 |
| Unit | Reference Value | Mean Value | 99% Confidence Interval | Size of the 99% CI | |
|---|---|---|---|---|---|
| (cm/min) | 0.2 | 0.19 | [0.18–0.2] | 0.02 | |
| - | 0.104 | 0.07 | [0.05–0.15] | 0.1 | |
| (cm−1) | 0.0187 | 0.0132 | [0.012–0.014] | 0.002 | |
| - | 2.19 | 2.64 | [2.4–2.8] | 0.4 |
| Unit | Mean Value | 99% Confidence Interval | Size of the 99% CI | |
|---|---|---|---|---|
| (cm/min) | 0.231 | [0.22–0.24] | 0.022 | |
| - | 0.07 | [0.05–0.15] | 0.1 | |
| (cm−1) | 0.012 | [0.01–0.013] | 0.003 | |
| - | 2.26 | [2–2.5] | 0.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Younes, A.; Shao, Q.; Mara, T.A.; Baalousha, H.M.; Fahs, M. Use of Global Sensitivity and Data-Worth Analysis for an Efficient Estimation of Soil Hydraulic Properties. Water 2020, 12, 736. https://doi.org/10.3390/w12030736
Younes A, Shao Q, Mara TA, Baalousha HM, Fahs M. Use of Global Sensitivity and Data-Worth Analysis for an Efficient Estimation of Soil Hydraulic Properties. Water. 2020; 12(3):736. https://doi.org/10.3390/w12030736
Chicago/Turabian StyleYounes, Anis, Qian Shao, Thierry Alex Mara, Husam Musa Baalousha, and Marwan Fahs. 2020. "Use of Global Sensitivity and Data-Worth Analysis for an Efficient Estimation of Soil Hydraulic Properties" Water 12, no. 3: 736. https://doi.org/10.3390/w12030736








