Nonlinear Dynamic Modeling of Urban Water Consumption Using Chaotic Approach (Case Study: City of Kelowna)
Abstract
1. Introduction
1.1. Background
1.2. Problem Statement
1.3. Objective
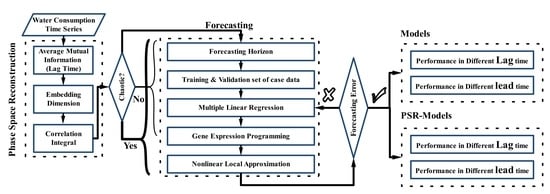
2. Materials and Methods
2.1. Phase Space Reconstruction
2.2. Correlation Dimension
2.3. Nonlinear Local Approximation
2.4. Largest Lyapunov Exponent
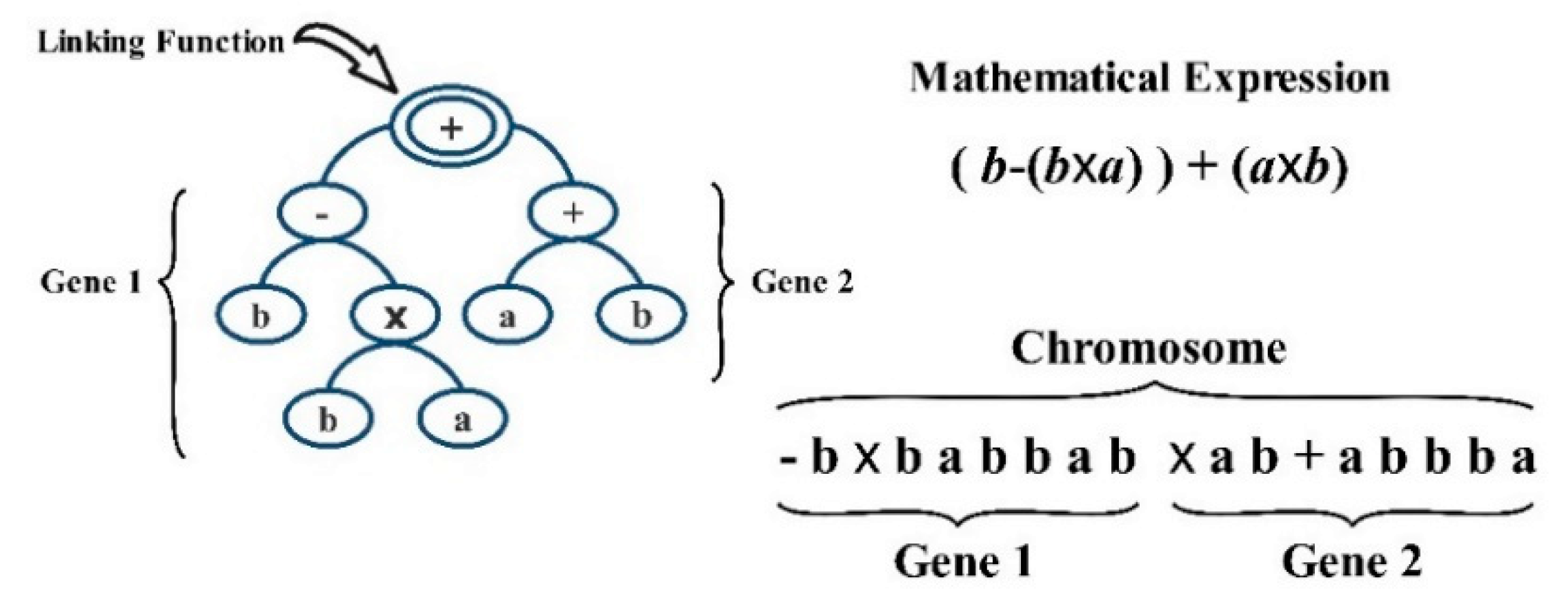
2.5. Gene Expression Programming
2.6. Multiple Linear Regression
2.7. Models Selection Criteria
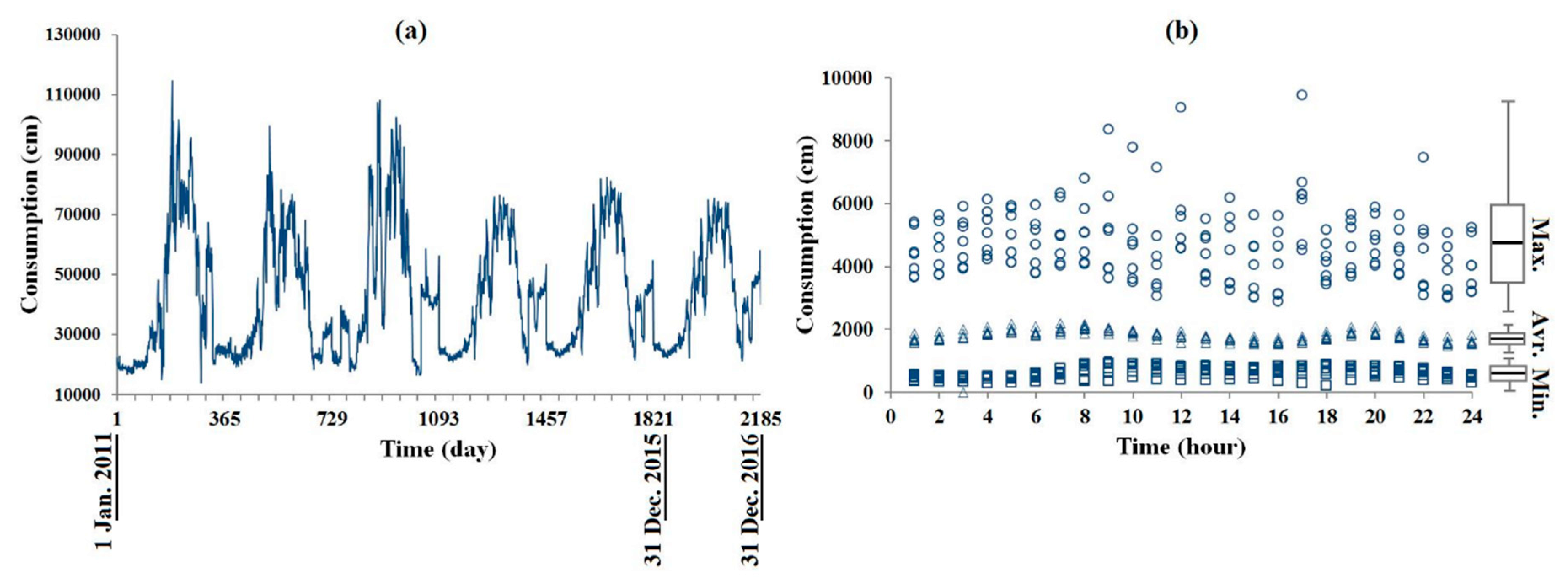
2.8. Test Case
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yousefi, P. Integrated Management Plan of Water Distribution Systems: Forecasting Approach. Ph.D. Thesis, University of British Columbia, Kelowna, BC, Canada, 2020. [Google Scholar] [CrossRef]
- Xenochristou, M.; Kapelan, Z.; Hutton, C. Using Smart Demand-Metering Data and Customer Characteristics to Investigate Influence of Weather on Water Consumption in the UK. J. Water Resour. Plan. Manag. 2020, 146, 4019073. [Google Scholar] [CrossRef]
- Water Conflict—World’s Water. Available online: https://www.worldwater.org/water-conflict/ (accessed on 14 February 2019).
- Billings, R.B.; Jones, C.V. Forecasting Urban Water Demand; American Water Works Association: Denver, CO, USA, 2008. [Google Scholar]
- Ghalehkhondabi, I.; Ardjmand, E.; Young, W.A.; Weckman, G.R. Water demand forecasting: Review of soft computing methods. Environ. Monit. Assess. 2017, 189, 313. [Google Scholar] [CrossRef]
- Sastri, T.; Valdes, J.B. Rainfall Intervention Analysis for On-Line Applications. J. Water Resour. Plan. Manag. 2008, 115, 397–415. [Google Scholar] [CrossRef]
- Odan, F.K.; Reis, L.F.R. Hybrid Water Demand Forecasting Model Associating Artificial Neural Network with Fourier Series. J. Water Resour. Plan. Manag. 2012, 138, 245–256. [Google Scholar] [CrossRef]
- Iwanek, M.; Kowalska, B.; Hawryluk, E.; Kondraciuk, K. Distance and time of water effluence on soil surface after failure of buried water pipe. Laboratory investigations and statistical analysis. Eksploat. I Niezawodn. Maint. Reliab. 2016, 18, 278–284. [Google Scholar] [CrossRef]
- Ghiassi, M.; Zimbra, D.K.; Saidane, H. Urban Water Demand Forecasting with a Dynamic Artificial Neural Network Model. J. Water Resour. Plan. Manag. 2008, 134, 138–146. [Google Scholar] [CrossRef]
- Jayawardena, A.W.; Gurung, A.B. Noise reduction and prediction of hydrometeorological time series: Dynamical systems approach vs. stochastic approach. J. Hydrol. 2000, 228, 242–264. [Google Scholar] [CrossRef]
- Lisi, F.; Villi, V. CHAOTIC FORECASTING OF DISCHARGE TIME SERIES: A CASE STUDY. J. Am. Water Resour. Assoc. 2001, 37, 271–279. [Google Scholar] [CrossRef]
- Cominola, A.; Giuliani, M.; Piga, D.; Castelletti, A.; Rizzoli, A.E. Benefits and challenges of using smart meters for advancing residential water demand modeling and management: A review. Environ. Model. Softw. 2015, 72, 198–214. [Google Scholar] [CrossRef]
- Oshima, N. Information Integration Type Chaos Theory-Based Demand Forecasting for Predictive Control of Waterworks. Water Purify Technol. 2015, 164, 6–12. [Google Scholar]
- Jain, A.; Ormsbee, L.E. Short-term water demand forecast modeling techniques—Conventional methods versus AI. J. Am. Water Work Assoc. 2002, 94, 64–72. [Google Scholar] [CrossRef]
- Kame’enui, A.E. Water Demand Forecasting in the Puget Sound Region: Short and long-Term Models. 2003, pp. 1–97. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.461.405&rep=rep1&type=pdf (accessed on 18 February 2019).
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Yousefi, P.; Naser, G.; Mohammadi, H. Surface Water Quality Model: Impacts of Influential Variables. J. Water Resour. Plan. Manag. 2018, 144, 4018015. [Google Scholar] [CrossRef]
- Shabani, S.; Yousefi, P.; Adamowski, J.; Naser, G. Intelligent Soft Computing Models in Water Demand Forecasting. In Water Stress in Plants; IntechOpen: London, UK, 2016. [Google Scholar] [CrossRef]
- Miaou, S.-P. A stepwise time series regression procedure for water demand model identification. Water Resour. Res. 1990, 26, 1887–1897. [Google Scholar] [CrossRef]
- Jain, A.; Kumar Varshney, A.; Chandra Joshi, U. Short-Term Water Demand Forecast Modelling at IIT Kanpur Using Artificial Neural Networks. Water Resour. Manag. 2001, 15, 299–321. [Google Scholar] [CrossRef]
- Gato, S.; Jayasuriya, N.; Roberts, P. Temperature and rainfall thresholds for base use urban water demand modelling. J. Hydrol. 2007, 337, 364–376. [Google Scholar] [CrossRef]
- Bougadis, J.; Adamowski, K.; Diduch, R. Short-term municipal water demand forecasting. Hydrol. Process. 2005, 19, 137–148. [Google Scholar] [CrossRef]
- Adamowski, J.; Fung Chan, H.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Zhou, S.L.; McMahon, T.A.; Walton, A.; Lewis, J. Forecasting daily urban water demand: A case study of Melbourne. J. Hydrol. 2000, 236, 153–164. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Akber, A.; Al-Awadi, E. Analysis of freshwater consumption patterns in the private residences of Kuwait. Urban. Water. 2001, 3, 53–62. [Google Scholar] [CrossRef]
- Dos Santos, C.C.; Pereira Filho, A.J. Water Demand Forecasting Model for the Metropolitan Area of São Paulo, Brazil. Water Resour. Manag. 2014, 28, 4401–4414. [Google Scholar] [CrossRef]
- Brekke, L.; Larsen, M.D.; Ausburn, M.; Takaichi, L. Suburban Water Demand Modeling Using Stepwise Regression. J. Am. Water Works Assoc. 2002, 94, 65–75. [Google Scholar] [CrossRef]
- Polebitski, A.S.; Palmer, R.N. Seasonal Residential Water Demand Forecasting for Census Tracts. J. Water Resour. Plan. Manag. 2010, 136, 27–36. [Google Scholar] [CrossRef]
- Lee, S.-J.; Wentz, E.A.; Gober, P. Space–time forecasting using soft geostatistics: A case study in forecasting municipal water demand for Phoenix, Arizona. Stoch. Environ. Res. Risk Assess. 2010, 24, 283–295. [Google Scholar] [CrossRef]
- Adamowski, J.; Karapataki, C. Comparison of Multivariate Regression and Artificial Neural Networks for Peak Urban Water-Demand Forecasting: Evaluation of Different ANN Learning Algorithms. J. Hydrol. Eng. 2010, 15, 729–743. [Google Scholar] [CrossRef]
- Cutore, P.; Campisano, A.; Kapelan, Z.; Modica, C.; Savic, D. Probabilistic prediction of urban water consumption using the SCEM-UA algorithm. Urban. Water J. 2008, 5, 125–132. [Google Scholar] [CrossRef]
- Adamowski, J.F. Peak Daily Water Demand Forecast Modeling Using Artificial Neural Networks. J. Water Resour. Plan. Manag. 2008, 134, 119–128. [Google Scholar] [CrossRef]
- Zhou, T.; Wang, F.; Yang, Z. Comparative Analysis of ANN and SVM Models Combined with Wavelet Preprocess for Groundwater Depth Prediction. Water 2017, 9, 781. [Google Scholar] [CrossRef]
- Firat, M.; Yurdusev, M.A.; Turan, M.E. Evaluation of Artificial Neural Network Techniques for Municipal Water Consumption Modeling. Water Resour. Manag. 2009, 23, 617–632. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Long, Z.; Chen, Y. A Novel Dual-Scale Deep Belief Network Method for Daily Urban Water Demand Forecasting. Energies 2018, 11, 1068. [Google Scholar] [CrossRef]
- Msiza, I.S.; Nelwamondo, F.V.; Marwala, T. Artificial neural networks and support vector machines for water demand time series forecasting. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007; pp. 638–643. [Google Scholar] [CrossRef]
- Msiza, I.S.; Nelwamondo, F.V.; Marwala, T. Water demand prediction using artificial neural networks and support vector regression. J. Comput. 2008, 3, 1–8. [Google Scholar] [CrossRef]
- Shabani, S.; Yousefi, P.; Naser, G. Support Vector Machines in Urban Water Demand Forecasting Using Phase Space Reconstruction. Procedia Eng. 2017, 186, 537–543. [Google Scholar] [CrossRef]
- Yousefi, P.; Shabani, S.; Mohammadi, H.; Naser, G. Gene Expression Programing in Long Term Water Demand Forecasts Using Wavelet Decomposition. Procedia Eng. 2017, 186, 544–550. [Google Scholar] [CrossRef]
- Shabani, S. Water Demand Forecasting: A Flexible Approach. Ph.D. Thesis, University of British Columbia, Kelowna, BC, Canada, 2018. [Google Scholar] [CrossRef]
- Ambrosio, J.K.; Brentan, B.M.; Herrera, M.; Luvizotto, E.; Ribeiro, L.; Izquierdo, J. Committee Machines for Hourly Water Demand Forecasting in Water Supply Systems. Math. Probl. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Yousefi, P.; Naser, G.; Mohammadi, H. Application of Wavelet Decomposition and Phase Space Reconstruction in Urban Water Consumption Forecasting: Chaotic Approach (Case Study). In Wavelet Theory and Its Applications; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Yousefi, P.; Naser, G.; Mohammadi, H. Hybrid Wavelet and Local Approximation Method for Urban Water Demand Forecasting—Chaotic Approach. In Proceedings of the WDSA Conference, Kingstone, ON, Canada, 23–25 July 2018. [Google Scholar]
- Azadeh, A.; Neshat, N.; Hamidipour, H. Hybrid Fuzzy Regression–Artificial Neural Network for Improvement of Short-Term Water Consumption Estimation and Forecasting in Uncertain and Complex Environments: Case of a Large Metropolitan City. J. Water Resour. Plan. Manag. 2011, 138, 71–75. [Google Scholar] [CrossRef]
- Ahmadi, S.; Alizadeh, S.; Forouzideh, N.; Yeh, C.H.; Martin, R.; Papageorgiou, E. ICLA imperialist competitive learning algorithm for fuzzy cognitive map: Application to water demand forecasting. In Proceedings of the IEEE International Conference on Fuzzy Systems, Beijing, China, 6–11 July 2014; pp. 1041–1048. [Google Scholar] [CrossRef]
- Navarrete-López, C.; Herrera, M.; Brentan, B.; Luvizotto, E.; Izquierdo, J. Enhanced Water Demand Analysis via Symbolic Approximation within an Epidemiology-Based Forecasting Framework. Water. 2019, 11, 246. [Google Scholar] [CrossRef]
- Yousefi, P.; Naser, G.; Mohammadi, H. Estimating High Resolution Temporal Scale of Water Demand Time Series—Disaggregation Approach (Case Study). In Proceedings of the 13th International Conference on Hydroinformatics (HIC 2018), Palermo, Italy, 1–6 July 2018; Volume 3, pp. 2408–2416. [Google Scholar] [CrossRef]
- Kozłowski, E.; Kowalska, B.; Kowalski, D.; Mazurkiewicz, D. Water demand forecasting by trend and harmonic analysis. Arch. Civ. Mech. Eng. 2018, 18, 140–148. [Google Scholar] [CrossRef]
- Campisi-Pinto, S.; Adamowski, J.; Oron, G. Forecasting Urban Water Demand Via Wavelet-Denoising and Neural Network Models. Case Study: City of Syracuse, Italy. Water Resour. Manag. 2012, 26, 3539–3558. [Google Scholar] [CrossRef]
- Casdagli, M. Chaos and Deterministic Versus Stochastic Non-Linear Modelling. J. R Stat. Soc. Ser. B 1992, 54, 303–328. [Google Scholar] [CrossRef]
- Lorenz, E.N. Atmospheric Predictability as Revealed by Naturally Occurring Analogues. J. Atmos. Sci. 2004, 26, 636–646. [Google Scholar] [CrossRef]
- Sivakumar, B.; Jayawardena, A.W.; Li, W.K. Hydrologic complexity and classification: A simple data reconstruction approach. Hydrol. Process. 2007, 21, 2713–2728. [Google Scholar] [CrossRef]
- Ng, W.W.; Panu, U.S.; Lennox, W.C. Chaos based Analytical techniques for daily extreme hydrological observations. J. Hydrol. 2007, 342, 17–41. [Google Scholar] [CrossRef]
- Regonda, S.K.; Sivakumar, B.; Jain, A. Temporal scaling in river flow: Can it be chaotic? Hydrol. Sci. J. 2004, 49, 373–385. [Google Scholar] [CrossRef]
- Salas, J.D.; Kim, H.S.; Eykholt, R.; Burlando, P.; Green, T.R. Aggregation and Sampling in Deterministic Chaos: Implications for Chaos Identification in Hydrological Processes. June 2005. Available online: https://hal.archives-ouvertes.fr/hal-00302625/ (accessed on 29 July 2019).
- Elshorbagy, A.; Simonovic, S.P.; Panu, U.S. Estimation of missing streamflow data using principles of chaos theory. J. Hydrol. 2002, 255, 123–133. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Simonovic, S.P.; Panu, U.S. Noise reduction in chaotic hydrologic time series: Facts and doubts. J. Hydrol. 2002, 256, 147–165. [Google Scholar] [CrossRef]
- Sivakumar, B.; Wallender, W.W. Predictability of river flow and suspended sediment transport in the Mississippi River basin: A non-linear deterministic approach. Earth Surf. Process. Landforms. 2005, 30, 665–677. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M. Investigating Chaos and Nonlinear Forecasting in Short Term and Mid-term River Discharge. Water Resour. Manag. 2016, 30, 1851–1865. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Khatibi, R.; Danandeh Mehr, A.; Asadi, H. Chaos-based multigene genetic programming: A new hybrid strategy for river flow forecasting. J. Hydrol. 2018, 562, 455–467. [Google Scholar] [CrossRef]
- Sivakumar, B. A phase-space reconstruction approach to prediction of suspended sediment concentration in rivers. J. Hydrol. 2002, 258, 149–162. [Google Scholar] [CrossRef]
- Sivakumar, B.; Jayawardena, A.W. An investigation of the presence of low-dimensional chaotic behaviour in the sediment transport phenomenon. Hydrol. Sci. J. 2002, 47, 405–416. [Google Scholar] [CrossRef]
- Ghorbani, M.; Khatibi, R.; Asadi, H.; Yousefi, P. Inter-Comparison of an Evolutionary Programming Model of Suspended Sediment Time-Series with Other Local Models. In Genetic Programming—New Approaches and Successful Applications; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef]
- Petkov, B.H.; Vitale, V.; Mazzola, M.; Lanconelli, C.; Lupi, A. Chaotic behaviour of the short-term variations in ozone column observed in Arctic. Commun. Nonlinear Sci. Numer. Simul. 2015, 26, 238–249. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Kisi, O.; Aalinezhad, M. A probe into the chaotic nature of daily streamflow time series by correlation dimension and largest Lyapunov methods. Appl. Math. Model. 2010, 34, 4050–4057. [Google Scholar] [CrossRef]
- Khatibi, R.; Ghorbani, M.A.; Aalami, M.T.; Kocak, K.; Makarynskyy, O. Dynamics of hourly sea level at Hillarys Boat Harbour, Western Australia: A chaos theory perspective. Ocean Dyn. 2011, 61, 1797–1807. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Febres De Power, B.; Sharifi, M.B.; Georgakakos, K.P. Chaos in rainfall. Water Resour. Res. 1989, 25, 1667–1675. [Google Scholar] [CrossRef]
- Jayawardena, A.W.; Lai, F. Analysis and prediction of chaos in rainfall and stream flow time series. J. Hydrol. 1994, 153, 23–52. [Google Scholar] [CrossRef]
- Sivakumar, B.; Berndtsson, R.; Olsson, J.; Jinno, K.; Kawamura, A. Dynamics of monthly rainfall-runoff process at the Gota basin: A search for chaos. Hydrol. Earth Syst. Sci. 2000, 4, 407–417. [Google Scholar] [CrossRef][Green Version]
- Maskey, M.L.; Puente, C.E.; Sivakumar, B. Temporal downscaling rainfall and streamflow records through a deterministic fractal geometric approach. J. Hydrol. 2019, 568, 447–461. [Google Scholar] [CrossRef]
- Wang, J.; Shi, Q. Short-term traffic speed forecasting hybrid model based on Chaos–Wavelet Analysis-Support Vector Machine theory. Transp. Res. Part. C Emerg. Technol. 2013, 27, 219–232. [Google Scholar] [CrossRef]
- Ravi, V.; Pradeepkumar, D.; Deb, K. Financial time series prediction using hybrids of chaos theory, multi-layer perceptron and multi-objective evolutionary algorithms. Swarm Evol. Comput. 2017, 36, 136–149. [Google Scholar] [CrossRef]
- Abdechiri, M.; Faez, K.; Amindavar, H.; Bilotta, E. The chaotic dynamics of high-dimensional systems. Nonlinear Dyn. 2017, 87, 2597–2610. [Google Scholar] [CrossRef]
- Li, M.W.; Geng, J.; Han, D.F.; Zheng, T.J. Ship motion prediction using dynamic seasonal RvSVR with phase space reconstruction and the chaos adaptive efficient FOA. Neurocomputing 2016, 174, 661–680. [Google Scholar] [CrossRef]
- Kalra, R.; Deo, M.C. Genetic programming for retrieving missing information in wave records along the west coast of India. Appl. Ocean. Res. 2007, 29, 99–111. [Google Scholar] [CrossRef]
- Ustoorikar, K.; Deo, M.C. Filling up gaps in wave data with genetic programming. Mar. Struct. 2008, 21, 177–195. [Google Scholar] [CrossRef]
- Gaur, S.; Deo, M.C. Real-time wave forecasting using genetic programming. Ocean. Eng. 2008, 35, 1166–1172. [Google Scholar] [CrossRef]
- Aytek, A.; Kişi, Ö. A genetic programming approach to suspended sediment modelling. J. Hydrol. 2008, 351, 288–298. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming in Problem Solving. In Soft Computing and Industry; Springer: London, UK, 2002; pp. 635–653. [Google Scholar] [CrossRef]
- Ferreira, C. Function Finding and the Creation of Numerical Constants in Gene Expression Programming. In Advances in Soft Computing; Springer: London, UK, 2003; pp. 257–265. [Google Scholar] [CrossRef]
- Nasseri, M.; Moeini, A.; Tabesh, M. Forecasting monthly urban water demand using Extended Kalman Filter and Genetic Programming. Expert Syst. Appl. 2011, 38, 7387–7395. [Google Scholar] [CrossRef]
- Shabani, S.; Candelieri, A.; Archetti, F.; Naser, G. Gene Expression Programming Coupled with Unsupervised Learning: A Two-Stage Learning Process in Multi-Scale, Short-Term Water Demand Forecasts. Water 2018, 10, 142. [Google Scholar] [CrossRef]
- Gutzler, D.S.; Nims, J.S. Interannual Variability of Water Demand and Summer Climate in Albuquerque, New Mexico. J. Appl. Meteorol. 2006, 44, 1777–1787. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.A.; Soyer, R.; Alan Roberson, J. Urban Water Demand Forecasting: Review of Methods and Models. J. Water Resour. Plan. Manag. 2012, 140, 146–159. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M.; Marinelli, A. A short-term, pattern-based model for water-demand forecasting. J. Hydroinformatics 2006, 9, 39–50. [Google Scholar] [CrossRef]
- Sivakumar, B.; Berndtsson, R.; Olsson, J.; Jinno, K. Evidence of chaos in the rainfall-runoff process. Hydrol. Sci. J. 2001, 46, 131–145. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar] [CrossRef]
- Sivakumar, B. Forecasting monthly flow dynamics in the western united states: A nonlinear dynamical approach. J. Environ. Model. Softw. 2003, 17, 721–728. [Google Scholar] [CrossRef]
- Khatibi, R.; Sivakumar, B.; Ghorbani, M.A.; Kisi, O.; Koçak, K.; Farsadi Zadeh, D. Investigating chaos in river stage and discharge time series. J. Hydrol. 2012, 414–415, 108–117. [Google Scholar] [CrossRef]
- Meng, Q.; Peng, Y. A new local linear prediction model for chaotic time series. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2007, 370, 465–470. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Holzfuss, J.; Mayer-Kress, G. An Approach to Error-Estimation in the Application of Dimension Algorithms. In Dimensions and Entropies in Chaotic Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 114–122. [Google Scholar] [CrossRef]
- Hegger, R.; Kantz, H.; Schreiber, T. Practical implementation of nonlinear time series methods: The TISEAN package. Chaos Interdiscip. J. Nonlinear Sci. 1999, 9, 413–435. [Google Scholar] [CrossRef] [PubMed]
- Zounemat-Kermani, M.; Kisi, O. Time series analysis on marine wind-wave characteristics using chaos theory. Ocean. Eng. 2015, 100, 46–53. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Phys. D Nonlinear Phenom. 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Islam, M.N.; Sivakumar, B. Characterization and prediction of runoff dynamics: A nonlinear dynamical view. Adv. Water Resour. 2002, 25, 179–190. [Google Scholar] [CrossRef]
- Tongal, H.; Berndtsson, R. Impact of complexity on daily and multi-step forecasting of streamflow with chaotic, stochastic, and black-box models. Stoch. Environ. Res. Risk Assess. 2017, 31, 661–682. [Google Scholar] [CrossRef]
- Farmer, J.D.; Sidorowich, J.J. Predicting chaotic time series. Phys. Rev. Lett. 1987, 59, 845–848. [Google Scholar] [CrossRef] [PubMed]
- Itoh, K.-I. A method for predicting chaotic time-series with outliers. Electron. Commun. Jpn. Part III Fundam Electron. Sci. 1995, 78, 44–53. [Google Scholar] [CrossRef]
- Porporato, A.; Ridolfi, L. Nonlinear analysis of river flow time sequences. Water Resour. Res. 1997, 33, 1353–1367. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Shang, P.; Li, X.; Kamae, S. Chaotic analysis of traffic time series. Chaos Solitons Fractals 2005, 25, 121–128. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms and the optimal allocation of trials. In Evolutionary Computation: The Fossil Record; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1998; Volume 2, pp. 443–460. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Strategic Value Solution. Kelowna Integrated Water Suply Plan. Kelowna. 2017. Available online: https://www.kelowna.ca/city-services/water-wastewater/ (accessed on 26 February 2020).
- Ruelle, D. The Claude Bernard Lecture, 1989. Deterministic Chaos: The Science and the Fiction. Proc. R Soc. A Math. Phys. Eng. Sci. 1990, 427, 241–248. [Google Scholar] [CrossRef]

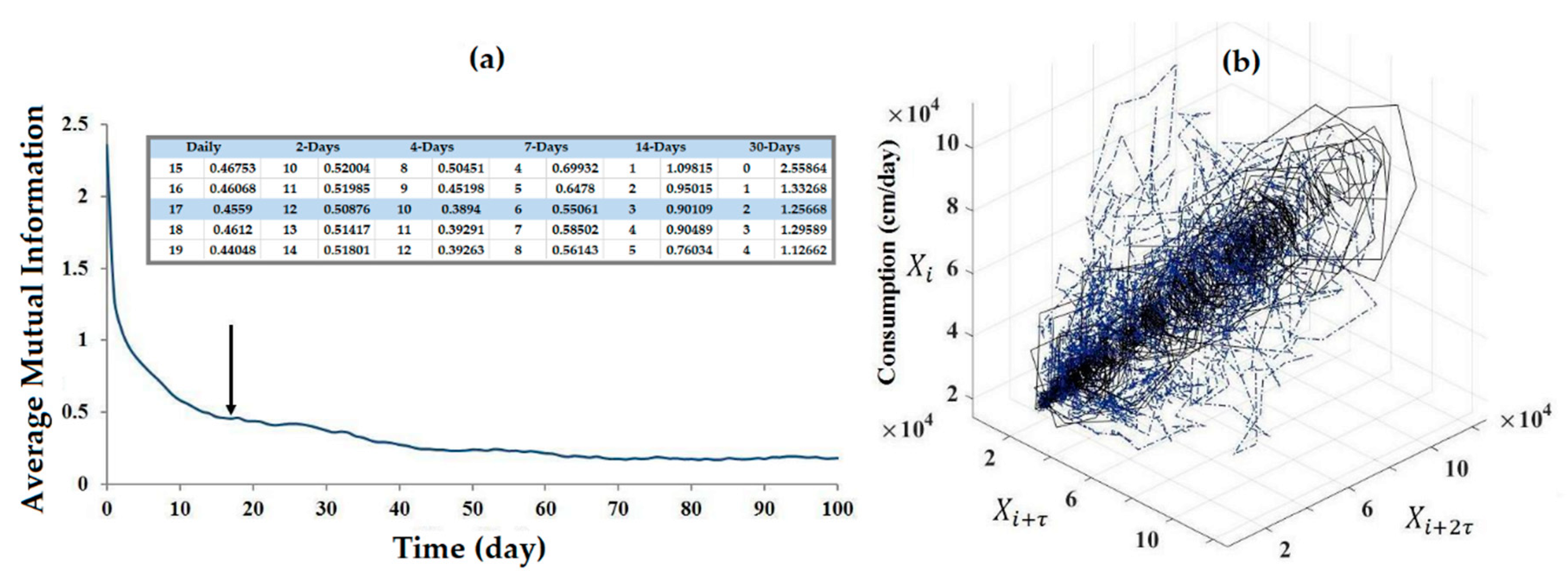





| Property | Daily | 2-Day | 4-Day | 7-Day | 14-Day | Monthly |
|---|---|---|---|---|---|---|
| Number of Data | 2186 | 1092 | 552 | 312 | 156 | 72 |
| Max. value (m3) | 114,597.2 | 210,740.3 | 410,428.3 | 656,173.6 | 1,255,211 | 2,475,026 |
| Min. value (m3) | 14124 | 31,477.3 | 69,655.5 | 124,112.9 | 252,704.1 | 557,066.8 |
| Average (m3) | 43,046.4 | 86,102 | 170,332.4 | 301,357.3 | 602,714.7 | 1,291,944 |
| Standard deviation (m3) | 20,074.5 | 39,897 | 79,304.3 | 136,626.8 | 268,733.2 | 552,701.5 |
| Coefficient of variation | 0.46 | 0.46 | 0.46 | 0.45 | 0.44 | 0.42 |
| Skew | 0.73 | 0.71 | 0.72 | 0.66 | 0.63 | 0.54 |
| Kurtosis | −0.38 | −0.45 | −0.51 | −0.63 | −0.79 | −0.91 |
| Time Scale | AMI | Ce | 2LogN > Ce |
|---|---|---|---|
| Daily | 17 | 3.50 | 6.67 |
| 2-Day | 12 | 3.37 | 6.07 |
| 4-Day | 10 | 3.74 | 5.48 |
| 7-Day | 6 | 3.94 | 4.98 |
| 14-Day | 3 | 3.83 | 4.38 |
| 30-Day | 2 | 3.49 | 3.71 |
| NLA, τ = 1, T = 1 | PSR-NLA, τ = 17, T = 1 | τ = 1, m = 18 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| m | CC | RMSE * | MAE | m | CC | RMSE * | MAE | T | CC | RMSE * | MAE |
| 1 | 1 | 0.9842 | 2855.6 | 43.07 | |||||||
| 2 | 0.9759 | 3532.1 | 47.85 | 2 | 0.9751 | 3581.7 | 49.09 | 2 | 0.9783 | 3351.6 | 48.02 |
| 3 | 0.9771 | 3424.8 | 47.34 | 3 | 0.9773 | 3425.3 | 48.01 | 4 | 0.9331 | 5883.5 | 63.03 |
| 4 | 0.9762 | 3495.5 | 47.74 | 4 | 0.9789 | 3302.9 | 47.30 | 7 | 0.8932 | 7445.8 | 72.49 |
| 5 | 0.9785 | 3332.0 | 47.08 | 5 | 0.9785 | 3331.7 | 47.10 | 14 | 0.7877 | 10555.0 | 87.76 |
| 6 | 0.9795 | 3248.6 | 46.13 | 6 | 0.9795 | 3257.8 | 46.79 | 30 | 0.6735 | 13307.6 | 100.44 |
| 7 | 0.9802 | 3187.3 | 45.49 | 7 | 0.9829 | 2967.1 | 45.80 | 60 | 0.2523 | 20189.1 | 129.71 |
| 8 | 0.9805 | 3176.4 | 45.65 | 8 | 0.9838 | 2887.9 | 45.22 | τ = 17, m = 19 | |||
| 9 | 0.9806 | 3164.1 | 45.65 | 9 | 0.9849 | 2792.8 | 43.95 | T | CC | RMSE * | MAE |
| 10 | 0.9803 | 3193.6 | 45.09 | 10 | 0.9846 | 2828.2 | 44.52 | 1 | 0.9852 | 2772.8 | 43.83 |
| 11 | 0.9813 | 3098.7 | 44.56 | 11 | 0.9850 | 2792.2 | 43.95 | 2 | 0.9898 | 2295.7 | 39.59 |
| 12 | 0.9763 | 3495.1 | 48.11 | 12 | 0.9804 | 3189.4 | 46.69 | 4 | 0.9415 | 5504.2 | 61.47 |
| 13 | 0.9752 | 3578.0 | 48.11 | 13 | 0.9768 | 3457.4 | 48.32 | 7 | 0.9002 | 7211.2 | 71.46 |
| 14 | 0.9779 | 3378.9 | 47.14 | 14 | 0.9788 | 3303.6 | 47.65 | 14 | 0.8048 | 10147.5 | 86.61 |
| 15 | 0.9806 | 3169.7 | 46.06 | 15 | 0.9790 | 3290.2 | 47.23 | 30 | 0.6776 | 13265.1 | 95.31 |
| 16 | 0.9765 | 3491.0 | 47.24 | 16 | 0.9796 | 3250.2 | 46.70 | 60 | 0.4363 | 17784.9 | 118.53 |
| 17 | 0.9810 | 3139.6 | 45.21 | 17 | 0.9825 | 2995.5 | 45.95 | ||||
| 18 | 0.9842 | 2855.6 | 43.07 | 18 | 0.9838 | 2894.0 | 45.21 | * m3 | |||
| 19 | 0.9685 | 4088.5 | 44.69 | 19 | 0.9852 | 2772.8 | 43.83 | ||||
| 20 | 0.9661 | 4209.2 | 45.29 | 20 | 0.9846 | 2833.1 | 44.43 | ||||
| Tot | 0.9775 | 3394.2 | 46.30 | Tot | 0.9807 | 3142.9 | 46.34 | ||||
| Best | 0.9842 | 2855.6 | 43.07 | Best | 0.9852 | 2772.8 | 43.83 | ||||
| EM | 18 | 18 | 18 | EM | 19 | 19 | 19 | ||||
| GEP, τ = 1, T = 1 | PSR-GEP, τ = 17, T = 1 | τ = 1, m = 4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| m | CC | RMSE * | MAE | m | CC | RMSE * | MAE | T | CC | RMSE * | MAE |
| 1 | 1 | 0.9764 | 3486.6 | 47.83 | |||||||
| 2 | 0.9757 | 3543.7 | 48.14 | 2 | 0.9789 | 3636.9 | 48.57 | 2 | 0.9494 | 5112.2 | 57.92 |
| 3 | 0.9761 | 3517.8 | 47.91 | 3 | 0.9788 | 3644.6 | 48.59 | 4 | 0.9130 | 6716.4 | 67.48 |
| 4 | 0.9764 | 3486.6 | 47.83 | 4 | 0.9789 | 3647.1 | 48.56 | 7 | 0.8652 | 8376.4 | 76.57 |
| 5 | 0.9760 | 3519.0 | 47.95 | 5 | 0.9789 | 3635.5 | 48.68 | 14 | 0.7810 | 10,734.8 | 88.95 |
| 6 | 0.9760 | 3520.5 | 48.37 | 6 | 0.9788 | 3649.5 | 48.71 | 30 | 0.6548 | 13,649.0 | 97.03 |
| 7 | 0.9760 | 3500.9 | 47.91 | 7 | 0.9788 | 3649.0 | 48.70 | 60 | 0.2345 | 20411.3 | 130.23 |
| 8 | 0.9760 | 3521.4 | 47.97 | 8 | 0.9789 | 3631.6 | 48.62 | τ = 17, m = 8 | |||
| 9 | 0.9760 | 3511.9 | 47.89 | 9 | 0.9788 | 3653.9 | 48.63 | T | CC | RMSE * | MAE |
| 10 | 0.9760 | 3514.7 | 47.89 | 10 | 0.9788 | 3650.6 | 48.73 | 1 | 0.9789 | 3631.6 | 48.62 |
| 11 | 0.9760 | 3514.6 | 47.88 | 11 | 0.9788 | 3656.6 | 48.65 | 2 | 0.9553 | 5267.3 | 58.52 |
| 12 | 0.9760 | 3514.7 | 47.89 | 12 | 0.9787 | 3657.4 | 48.69 | 4 | 0.9227 | 6894.5 | 68.47 |
| 13 | 0.9760 | 3510.1 | 47.91 | 13 | 0.9789 | 3645.4 | 48.55 | 7 | 0.8713 | 8848.2 | 78.11 |
| 14 | 0.9760 | 3516.6 | 47.91 | 14 | 0.9787 | 3655.7 | 48.69 | 14 | 0.7782 | 11,571.8 | 91.84 |
| 15 | 0.9760 | 3510.4 | 47.86 | 15 | 0.9788 | 3650.5 | 48.61 | 30 | 0.6334 | 14,631.5 | 105.98 |
| 16 | 0.9760 | 3498.7 | 47.88 | 16 | 0.9789 | 3644.4 | 48.54 | 60 | 0.3864 | 18,670.2 | 126.20 |
| 17 | 0.9759 | 3515.1 | 47.89 | 17 | 0.9789 | 3638.9 | 48.56 | ||||
| 18 | 0.9760 | 3509.7 | 47.85 | 18 | 0.9789 | 3646.6 | 48.57 | * m3 | |||
| 19 | 0.9759 | 3514.8 | 47.93 | 19 | 0.9787 | 3650.6 | 48.74 | ||||
| 20 | 0.9759 | 3514.2 | 47.90 | 20 | 0.9789 | 3642.5 | 48.51 | ||||
| Tot | 0.9759 | 3519.0 | 47.96 | Tot | 0.9788 | 3646.5 | 48.62 | ||||
| Best | 0.9764 | 3486.6 | 47.83 | Best | 0.9789 | 3631.6 | 48.51 | ||||
| EM | 4 | 4 | 4 | EM | 8 | 8 | 20 | ||||
| MLR, τ = 1, T = 1 | PSR-MLR, τ = 17, T = 1 | τ = 1, m = 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| m | CC | RMSE * | MAE | m | CC | RMSE * | MAE | T | CC | RMSE * | MAE |
| 1 | 1 | 0.9789 | 3638.9 | 48.56 | |||||||
| 2 | 0.7825 | 11658.6 | 92.37 | 2 | 0.9758 | 3763.4 | 50.48 | 2 | 0.9494 | 5139.4 | 58.65 |
| 3 | 0.9790 | 3762.3 | 49.89 | 3 | 0.9809 | 3336.0 | 48.17 | 4 | 0.9130 | 6701.6 | 68.26 |
| 4 | 0.9790 | 3792.3 | 50.19 | 4 | 0.9811 | 3443.9 | 49.41 | 7 | 0.8595 | 8511.9 | 77.68 |
| 5 | 0.9790 | 3814.1 | 50.42 | 5 | 0.9766 | 3905.5 | 52.04 | 14 | 0.7595 | 11204.4 | 91.66 |
| 6 | 0.9790 | 3958.0 | 52.11 | 6 | 0.9148 | 22846.5 | 145.73 | 30 | 0.6447 | 13707.5 | 101.02 |
| 7 | 0.9790 | 4133.6 | 54.24 | 7 | 0.9765 | 3568.2 | 48.60 | 60 | 0.2282 | 20211.2 | 129.01 |
| 8 | 0.9790 | 4187.1 | 54.85 | 8 | 0.9764 | 3811.2 | 51.08 | τ = 17, m = 3 | |||
| 9 | 0.9791 | 4432.7 | 57.65 | 9 | 0.9766 | 3568.2 | 48.71 | T | CC | RMSE * | MAE |
| 10 | 0.9792 | 5024.0 | 63.46 | 10 | 0.9766 | 3680.4 | 49.81 | 1 | 0.9809 | 3336.0 | 48.17 |
| 11 | 0.9792 | 5576.0 | 68.14 | 11 | 0.9767 | 3610.6 | 49.13 | 2 | 0.9555 | 5336.5 | 59.61 |
| 12 | 0.9792 | 5921.4 | 70.92 | 12 | 0.9767 | 3603.9 | 49.04 | 4 | 0.9232 | 6889.3 | 69.17 |
| 13 | 0.9793 | 6276.8 | 73.59 | 13 | 0.9766 | 3601.4 | 49.13 | 7 | 0.8723 | 8841.9 | 78.12 |
| 14 | 0.9793 | 7267.0 | 80.61 | 14 | 0.9767 | 3584.5 | 48.92 | 14 | 0.7790 | 11549.8 | 91.70 |
| 15 | 0.9794 | 9128.5 | 92.30 | 15 | 0.9769 | 3560.6 | 48.79 | 30 | 0.6344 | 14504.2 | 104.84 |
| 16 | 0.9794 | 10115.3 | 97.81 | 16 | 0.9769 | 3550.4 | 48.73 | 60 | 0.3859 | 18351.2 | 125.12 |
| 17 | 0.9789 | 3638.9 | 48.56 | 17 | 0.9769 | 3550.5 | 48.73 | ||||
| 18 | 0.9794 | 10114.2 | 97.80 | 18 | 0.9769 | 3560.4 | 48.81 | * m3 | |||
| 19 | 0.9794 | 10115.3 | 97.81 | 19 | 0.9768 | 3561.6 | 48.87 | ||||
| 20 | 0.9795 | 9618.8 | 95.07 | 20 | 0.9769 | 3610.5 | 49.39 | ||||
| Tot | 0.9595 | 6709.6 | 72.00 | Tot | 0.9738 | 4579.2 | 54.20 | ||||
| Best | 0.9795 | 3638.8 | 48.56 | Best | 0.9811 | 3336.0 | 48.17 | ||||
| EM | 20 | 17 | 17 | EM | 4 | 3 | 3 | ||||
| Property | Observed | NLA τ = 1, m = 18 | PSR-NLA τ = 17, m = 19 | GEP τ =1, m = 4 | PSR-GEP τ = 17, m = 8 | MLR τ = 1, m =1 7 | PSR-MLR τ = 17, m = 3 |
|---|---|---|---|---|---|---|---|
| Max. value | 75,620.26 | ✓ | |||||
| Min. value | 21,313.72 | ✓ | |||||
| Average | 42,500.82 | ✓ | |||||
| Standard deviation | 16,117.34 | ✓ | |||||
| Coefficient of variation | 0.38 | ✓ | |||||
| Skew | 0.43 | ✓ | |||||
| Kurtosis | −1.13 | ✓ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousefi, P.; Courtice, G.; Naser, G.; Mohammadi, H. Nonlinear Dynamic Modeling of Urban Water Consumption Using Chaotic Approach (Case Study: City of Kelowna). Water 2020, 12, 753. https://doi.org/10.3390/w12030753
Yousefi P, Courtice G, Naser G, Mohammadi H. Nonlinear Dynamic Modeling of Urban Water Consumption Using Chaotic Approach (Case Study: City of Kelowna). Water. 2020; 12(3):753. https://doi.org/10.3390/w12030753
Chicago/Turabian StyleYousefi, Peyman, Gregory Courtice, Gholamreza Naser, and Hadi Mohammadi. 2020. "Nonlinear Dynamic Modeling of Urban Water Consumption Using Chaotic Approach (Case Study: City of Kelowna)" Water 12, no. 3: 753. https://doi.org/10.3390/w12030753
APA StyleYousefi, P., Courtice, G., Naser, G., & Mohammadi, H. (2020). Nonlinear Dynamic Modeling of Urban Water Consumption Using Chaotic Approach (Case Study: City of Kelowna). Water, 12(3), 753. https://doi.org/10.3390/w12030753