Precipitation Characteristic Analysis of the Zhoushan Archipelago: From the View of MSWEP and Rainfall Merging

Abstract

Based on the long series of gauge rainfall data from 1979 to 2015, the performance of Multi-Source Weighted-Ensemble Precipitation (MSWEP) precipitation dataset in the Zhoushan Archipelago and its surrounding sea area in Southeast China was evaluated from a variety of perspectives, and then the Cressman scheme was used to merge MSWEP with surface gauge measurements. It was found that at the spatial scale of 0.1° × 0.1°, MSWEP correctly detected most of the daily rainfall events in the study area. The surface precipitation was generally underestimated, with a relative deviation no more than 10%, but there was a fairly high miss reporting on heavy precipitation. The performance of MSWEP is also obviously characterized with seasonal fluctuation. Compared with the gauge records interpolation results, the accuracy statistics of rainfall dataset generated by merging MSWEP with gauge observations is improved to a certain degree. Especially its comprehensive identification ability of the dry and wet state for daily precipitation has been obviously raised. In addition, the merged data has the mixed characteristics of rain gauge observations and MSWEP in spatial structure. This paper has deepened the understanding of the performance of MSWEP in islands and sea areas, and also strengthened the understanding of the marginal effect of merging gauge data with MSWEP, even other global precipitation datasets.

1. Introduction

Precipitation is one of the most basic meteorological and hydrological elements. Under the combined influenced by atmospheric motion and underlying surface, precipitation has complex spatial variability. Acquisition of detailed precipitation spatial distribution is of great significance for a series of applications including natural disaster prevention and control, water resources management and regulation, infrastructure operation and maintenance, and ecological environment protection. For a long time, rain gauge networks have been the main way to obtain the spatial distribution of precipitation. Later, in order to make up for the deficiency of the rain gauge network in spatial coverage, representativeness and timeliness, weather radar, meteorological satellite, atmospheric numerical model, and other precipitation acquisition technologies were developed. The existing precipitation acquisition methods are different in the principle of observation way, accuracy, spatial and time resolution, and coverage, but they are theoretically complementary to some extent [1]. Therefore, integration and merging of precipitation information from different sources and with different nature has become the frontier of quantitative precipitation estimation. At present, a series of rainfall merging algorithms have been proposed, and they can be roughly summarized into three types, namely initial field correction, interpolation with auxiliary information, and optimal matching [2]. On the basis of these algorithms, literatures have extensively integrated ground rainfall gauge data with radar, satellite, reanalysis and other non-traditional precipitation data, and developed several global or regional precipitation merged datasets, the fairly famous ones including the Global Precipitation Climatology Project (GPCP) [3], the Climate Prediction Center (CPC) Merged Analysis (CMAP) [4], Tropical Rainfall Measuring Mission 3B42 (TRMM 3B42) [5], Global Satellite Mapping of Precipitation (GSMaP) Moving Vector with Kalman-filter(GSMaP-MVK) [6], and Integrated Multi-satellite Retrievals for GPM (IMERG) [7]. A lot of studies have been carried out on the accuracy assessment and hydrological application of merged rainfall. Relevant literatures show that the marginal effect of merging gauge measurements with other precipitation data depends on the quality of data source, gauge density, geographical and climatic conditions, and other factors [2].

Multi-Source Weighted-Ensemble Precipitation (MSWEP) is a global precipitation dataset recently developed by Beck et al. [8,9], it merges the surface rain gauge and various satellite and reanalysis precipitation information and adopts runoff and potential evapotranspiration data in some catchments for the calibration. MSWEP has the spatial resolution of 0.1° × 0.1°, and time resolution of 3 h, with a data series length from 1979 to the present. Since its release, MSWEP has attracted extensive attention in related scientific fields such as meteorology and hydrology. Beck et al. [8] evaluated the accuracy of MSWEP in 9053 river catchments around the world by using both the precipitation measurements from rain gauge network and hydrological simulation method. Through comparison with TMPA 3B42 V7 and other merging data, the advantages of MSWEP were demonstrated preliminarily. Beck et al. [9] also used rain gauge-radar precipitation data within the United States to compare the performance of 11 kinds of global or quasi-global precipitation data (including 1 purely gauge based data and 10 merged data) at daily scale, and found that MSWEP had the highest accuracy among all the data; Alijanian et al. [10] obtained similar results in a comparative study in Iran. Nair and Indu [11] found that MSWEP had a strong identification ability for daily precipitation in India, but they also found that this data had deficiency in monitoring heavy or extreme precipitation. Awange et al. [12] pointed out that MSWEP underestimated precipitation in northern and northwestern Australia and was unable to reflect major extreme hydroclimatic events in the west, east, and south of Africa. Deng et al. [13] believed that MSWEP performed differently both in time and space in China mainland, with overestimation for weak precipitation and underestimation for heavy precipitation events, respectively. Xu et al. [14] analyzed the applicability of MSWEP V2.1 to drought monitoring in China mainland, and pointed out that MSWEP was superior to TMPA 3B42V7 and CMORPH BLD in areas where surface rainfall measurements were lacking, but the performance of MSWEP was better in humid areas than in arid and semi-arid areas.

In general, existing literatures have shown that MSWEP has a strong ability for discerning surface precipitation, and its accuracy is often better than other global precipitation dataset. Thus, this dataset undoubtedly has a strong potential in meteorological and hydrological researches and application. However, in general, as a global rainfall dataset recently developed, the evaluation of MSWEP and its combination with other rainfall dataset is not fully developed yet. Moreover, existing assessment and verification of MSWEP and even other global precipitation datasets are mainly carried out in land area. There is rare investigation for islands and sea areas where surface precipitation data are rather scarce or even lacking. Furthermore, similar to other multi-source merged rainfall data, MSWEP have integrated precipitation information from ten thousands of rain gauges, satellite, reanalysis and others worldwide, but in many areas, the rain gauges used in the process of developing MSWEP is quite sparse or even non-existent. Therefore, in specific areas, MSWEP and local ground rainfall data can be further merged to improve the quality of precipitation spatial estimation and deepen the understanding of regional precipitation distribution characteristics. For example, Woldemeskel et al. [15] pointed out that the marginal effect of the merging of TRMM 3B42 data and rain gauge data in Australia was related to the rain gauge network density. Nerini et al. [16] used a variety of algorithms in Peru to combine gauge rainfall with TRMM 3B42 on a daily time scale. Wang et al. [17] used generalized additive model to merge gauge observation with MSWEP in the Three-Gorge Reservoir area of China, and pointed out that MSWEP and gauge precipitation information were complementary with each other to some extent. Motivated by the existing studies, this paper takes Zhoushan Archipelago and their surrounding sea area in southeast China as the study area, to investigate the merging of ground rain gauge observations with MSWEP. We have two main objectives in this paper. Firstly, to verify and evaluate the accuracy of MSWEP in the Zhoushan Archipelago, and deepen the understanding of the accuracy characteristics of MSWEP in the southeast coastal region of China. Secondly, to test and analyze the marginal gains of MSWEP and local gauge data combination. Multi-source rainfall merging is fairly hot in the field of quantitative precipitation estimation. However, its additional gain with respect to gauge observation interpolation is not fully illustrated yet. We expect that based on long series of rainfall records, this study will promote the rational application of global precipitation datasets including MSWEP in areas where surface precipitation data are sparse and deepen the understanding of the precipitation characteristics of the similar regions to provide scientific basis for strengthening water resource management and rainwater utilization in the island areas. It should be pointed that the main purpose of this paper is not to develop a new rainfall merging method or validate any sophisticated method. Thus, we choose the Cressman scheme for rainfall spatial estimation. Although this method is traditional and somewhat simple, in the study area it is more feasible than other sophisticated methods. It is both adequate for rainfall merging and interpolation and thus provides convenience for analyze the marginal effect of adding more information to rainfall spatial estimation.

The article is organized as follows. In Section 2, we briefly introduce the study area and the rainfall datasets used. Then, in Section 3, the statistics for evaluating the performance of MSWEP and the algorithm used to merge MSWEP and gauge rainfall data are stated. In the next section, the differences among three rainfall datasets, namely the original MSWEP, the gauge interpolation data and the dataset combining gauges rainfall and MSWEP are compared and illustrated at various time scales. Finally, In Section 5, the marginal benefit of merging global rainfall with local gauge rainfall is especially discussed and some conclusions are drawn.

2. Study Area and Data

2.1. Study Area

The Zhoushan Archipelago is located in the Pacific Ocean at the south side of the Yangtze River estuary and the outer edge of Hangzhou Bay, between 121°30’–123°25’E and 29°32’–31°04’N (see Figure 1), under the administration of Zhejiang Province and adjacent to Shanghai City. The total area of the main islands of the Zhoushan Archipelago and their adjacent water area is 22,216 km², including a land area of 1371 km². The Zhoushan Archipelago is the largest archipelago in China, accounting for 20% of the total islands of this country. In this archipelago, fifty-eight islands are with area over 1 km², accounting for 96.9% of the total land area. Among these islands, the Central Zhoushan Island is the largest island with an area of 502.65 km², which is the fourth largest island in China. Large islands are densely distributed in the southwest of the study area, and small islands mainly scattered in the northeast.

Located in the subtropical marine monsoon climate region. Long winter and summer, short spring and autumn, four distinct seasons, warm and moist, and abundant sunlight. Compared with inland cities and counties with similar latitudes, it has the climatic characteristics of no intense heat in summer, no severe winter, and small temperature difference between winter and summer. The average temperature over the years is around 15.5–16.7 °C, the extreme maximum temperature is 39.1 °C (6 August 1966), and the extreme minimum temperature is −7.9 °C (31 January 31 1981). The over-years average rainfall is between 980.7 and 1355.2 mm, which is 70–500 mm lower than that of the continental area at the same latitude. The over-years water-surface evaporate is 1208.7–1466.2 mm, which is 100–300 mm higher than the later. These results in the annual runoff depth about 44% less than that in continental areas of the same latitude. The precipitation is unevenly distributed throughout the year. Affected by the plum rain and typhoons, the precipitation in June to September generally accounts for about 45% that of the whole year. Affected by cold air in winter and low air pressure in spring, more sea fog in spring and more typhoons in summer and autumn, 110 days of gale days above the average annual level of 8. The winter is with the characters of less ice and snow, about 296 days of frost-free period, rich sunlight.

The Zhoushan Archipelago is with low hilly terrain. The highest peak on the south islands is 544.4 m above the sea level, while the rest are mostly 200–400 m. As most of the islands are with small catchments, it is difficult to effectively collect surface runoff. In addition, due to the shallow soil cover, sparse vegetation, and hard rock, the groundwater utilization is rather difficult. In terms of permanent population, the water resource per capita in this archipelago is only about half of the country. Therefore, people there have to unitedly rely on local water source, water transferred from the mainland and seawater desalination to meet the living and production water needs.

2.2. Rainfall Data

2.2.1. Rain Gauge Observations

Daily rainfall records of eight gauges from 1979 to 2015 were collected, and their locations and basic information are shown in

Table 1. Rain gauges location and basic information over the study area.

No.	Name	Type	Data Collection Periods	Longitude (°E)	Latitude (°N)	Annual Average Precipitation (mm)	Annual Precipitation Variation Range (mm)
1	Shengsi	WS	1979–2015	122°27′E	30°43′N	1135.6	681.1–1459.4
2	Qushan	RG	1979–1984, 2007–2015	122°20′E	30°26′N	1042.0	621.3–1478.5
3	Daishan	RG	1979–1984, 2007–2015	122°11′E	30°17′N	1131.1	639.1–1782.5
4	Dasha	RG	1979–1984, 2007–2015	122°01′E	30°08′N	1194.7	668.2–1759.0
5	Dinghai	WS	1975–2015	122°05′E	30°03′N	1581.7	925.1–2139.3
6	Jintang	RG	1979–1984, 2007–2015	121°52′E	30°01′N	1220.2	674.7–1948.0
7	Shenjiamen	RG	1979–1984, 2007–2015	122°18′E	29°57′N	1277.2	744.6–1686.5
8	Liuheng	RG	1979–1984, 2007–2015	122°07′E	29°45′N	1275.6	729.4–1868.8

. Among them, Shengsi and Dinghai are weather stations measuring rainfall and other metrological variables (with type denoted by “WS”), and the data of Qushan and other five stations just observe rainfall (with type denoted by “RG”). Rainfall data observed by all gauges were subject to strict quality control, and suspicious and erroneous data were manually checked and corrected. Table 1 shows that the rainfall data from Shengsi and Dinghai are continuous, but are missing within certain period for other gauges.

For the missing rainfall records in the six gauges, a linear regression relationship for the daily precipitation between these gauges and Shengsi or Dinghai was established, and then the missing data were interpolated. Figure 2 shows the example of the Shenjiamen station. The daily rainfall data from 1979 to 1984 and from 2007 to 2015 were used to establish a linear regression relationship between this station and Dinghai or Shengsi. We could see that that Shenjiamen and Dinghai had a better correlation than Shenjiamen and Shengsi. Then at Shejiamen, daily rainfall data recorded during 1985 to 2006 were interpolated using Shejiamen other than Shengsi, and finally the continuous daily rainfall data from 1979 to 2015 were obtained. The interpolation method of rainfall data in other rain gauges is similar to that of Shenjiamen.

2.2.2. MSWEP Data

MSWEP-V2.1 data corresponding to the study area during 1979 to 2015 were downloaded from the Internet (url: http://www.gloh2o.org/). The original data had spatial resolution of 0.1° × 0.1°, and time resolution of 3 h. In this paper, the 3-hour rainfall was accumulated to obtain the MSWEP rainfall on a corresponding day, month, and other duration.

3. Methodology

3.1. Precipitation Evaluation Indices

The accuracy of MSWEP at daily and monthly time scales was assessed. For the daily scale, both categorical and quantitative statistics are used simultaneously, while for the monthly scale, only quantitative statistics are used.

The categorical indices are used to describe the ability of MSWEP to identify the occurrence of precipitation events are Probability of Detection (POD), Frequency of Hit (FH), and Heidke’Skill Score (HSS). Among them, POD and FH are respectively used to describe the degree of missing and false alarm of daily precipitation events. The closer they are near to 1, the lower degree of missing and false alarm of precipitation events. HSS is a comprehensive index reflecting the identification ability of precipitation events. If it is higher than zero, the identification ability of precipitation events is better than random estimation, and its optimal value is 1. Formulas of the three categorical indices are as follows:

$$\mathrm{POD}=\frac{n_{11}}{n_{11}+n_{01}}$$

(1)

$$\mathrm{FH}=\frac{n_{11}}{n_{11}+n_{10}}$$

(2)

$$\mathrm{HSS}=\frac{2(n_{11}{n}_{00}-n_{10}{n}_{01})}{(n_{11}+n_{01})(n_{01}+n_{00})+(n_{11}+n_{10})(n_{10}+n_{00})}$$

(3)

where, $n_{11}$ represents the number of rain days both detected by the estimation and the reference (i.e., the gauge observation, the same for below); $n_{10}$ represents the frequency of rain days by the estimation but no rain by the reference; $n_{01}$ represents the frequency of no rain days by the estimation but rainy by the reference; and $n_{00}$ represents the frequency of no rain days both by the estimation and the reference. The threshold value of rain and no rain for daily precipitation event is 0.1 mm/d.

Quantitative statistics include Relative bias (RBIAS), Standardized Root Mean Square Error (SRMSE), Root Mean Square Error (RMSE), Determination Coefficient (R²), and Correlation Coefficient (CC). RBIAS describes the average deviation (relative value) of the estimation from the reference [18]; RMSE is used to measure the average error of the estimation and SRMSE reflects the relative dispersion degree of error; R² reflects the interpretation ability of the reference variance by the estimation; and CC refers to the correlation between the estimation and the reference. Formulas calculating the five quantitative statistics are as follows:

$$\mathrm{RBIAS}=\frac{1}{n}\times {\displaystyle {\sum }_{i=1}^n\frac{\left(\left(S_i+\epsilon \right)-\left(G_i+\epsilon \right)\right)}{\left(G_i+\epsilon \right)}}$$

(4)

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{(S_i-G_i)}^2}}$$

(5)

$$\mathrm{SRMSE}=(\sqrt{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{(S_i-G_i)}^2}})/\overline{G}$$

(6)

$${\mathrm{R}}^2=1-{\displaystyle {\sum }_{i=1}^n{(S_i-G_i)}^2/}{\displaystyle {\sum }_{i=1}^n{(G_i-\overline{G})}^2}$$

(7)

$$\mathrm{CC}=\frac{{\displaystyle \sum _{i=1}^n(S_i-\overline{S})(G_i-\overline{G})}}{\sqrt{{\displaystyle \sum _{i=1}^n{(G_i-\overline{G})}^2}}\sqrt{{\displaystyle \sum _{i=1}^n{(S_i-\overline{S})}^2}}}$$

(8)

In Equations (4)–(8): $G_i$ and $S_i$ stand for the gauge measured and the estimated precipitation respectively; $\overline{G}$ and $\overline{S}$ respectively represent the mean value of the gauge measured and estimated precipitation, and n represents the number of samples. $\epsilon =0.01$ is required in the event of $G_i=0$; $\epsilon =0$ is required in the event of $G_i\ne 0$ [18].

3.2. Rainfall Merging Algorithms

The Cressman scheme is adopted to merge surface gauge rainfall and MSWEP data. This method is traditional and somewhat simple. However, it is a practical objective analysis method, widely used in the field of climate diagnosis and analysis [19,20]. Rain gauges are sparse and irregular in space in the study area. Thus, the Cressman scheme is more feasible for the study area than other sophisticated methods such as geostatistics, Bayesian, and so on [21]. In addition, there is another advantage for using this scheme. It is adequate for both rainfall merging and interpolation and thus provides much convenience for analyze the marginal effect of adding MSWEP information to rainfall spatial estimation.

The Cressman method takes MSWEP data as the first initial field of precipitation, and then uses the gauge observations to iteratively correct the initial field, until the error metric between the obtained analysis field and the observation field no longer changes. For a spatial variable α, supposing the corrected value at the grid point (i, j) is $\Delta {\alpha }_{ij}$, $\Delta {\alpha }_{ij}$ is the weighted average of the difference between the observed values and the analyzed values within a certain radius D, and its specific calculation formula is following [22]:

$$\Delta {\alpha }_{ij}=\frac{{\displaystyle {\sum }_{k=1}^K(W_{ijk}^2\Delta {\alpha }_k)}}{{\displaystyle {\sum }_{k=1}^K{W}_{ijk}}}$$

(9)

where $\Delta {\alpha }_k$ is the difference between the observed value and analyzed value at the observation location denoted by $k$; $W_{ijk}$ is the weight ranging from 0.0–1.0; and K is the number of observations within the influence radius D. The key of Cressman method is to determine the weight, and it is generally in the form as follows:

$$W_{ijk}=\{\begin{array}{cc}\frac{D^2-d^2{}_{ijk}}{D^2+d^2{}_{ijk}},& (d_{ijk}<D)\\ 0,& (d_{ijk}\ge D)\end{array}$$

(10)

where $d_{ijk}$ is the distance between the grid point (i, j) and the kth observation point within the influence radius [15].

There is a small number of rain gauges in the area of Zhoushan Archipelago, and they are unevenly distributed in space. When the Cressman method is used for spatial estimation, if the influence radius D is set too small, it is likely that measured data correction cannot be made for some locations. Conversely, it may make the analysis value too smooth. Therefore, a dynamic influence radius method for the Cressman scheme is adopted by Zhang et al. [23], and a larger influence radius is adopted in areas with low gauge density and a smaller influence radius in areas with high gauge density, so as to ensure that there are at least three gauges for each grid to be calibrated.

4. Results and Analysis

Using the Cressman scheme, at three different time scales of daily, monthly, and yearly, in the study area precipitation dataset based on gauges and MSWEP rainfall combination (denoted by CMSWEP for convenience) during 1979–2015 were obtained, with a spatial resolution of 0.1° × 0.1°. In addition, the gauge-interpolated precipitation (briefly expressed with GIP) with a spatial resolution of 0.1° × 0.1° was produced. Thus, there are totally three precipitation datasets with a spatial resolution of 0.1° × 0.1° in the Zhoushan Archipelago, namely MSWEP, GIP, and CMSWEP. Choosing the pointwise gauge measurements as the benchmark, the three sets of precipitation data are evaluated and compared from different aspects.

4.1. Precipitation Performance at Different Time Scales

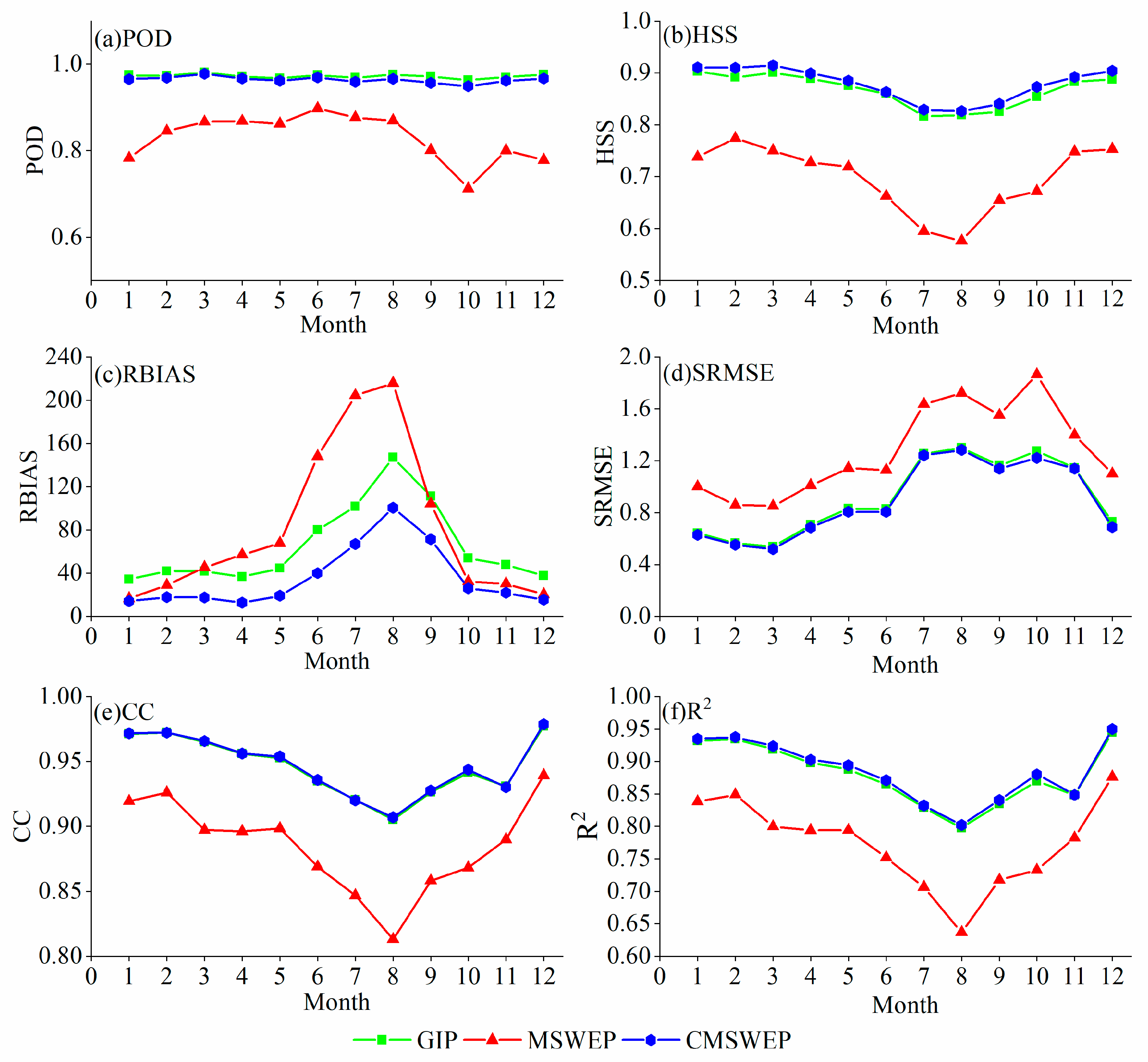
4.1.1. Accuracy of Daily Rainfall

Figure 3 shows the scatter plots between GIP, MSWEP, and CMSWEP and the benchmark rainfall at the daily time scale during 1979–2015. In this Figure, the two accuracy indices, R² and SRMSE, are also presented.

Table 2. Daily accuracy indices for the three rainfall datasets during 1979 to 2015.

				Indices
Rainfall Datasets	POD	FH	HSS	RBIAS	SRMSE	RMSE (mm)	R2	CC
GIP	0.97	0.80	0.82	8.12	1.049	3.49	0.862	0.929
MSWEP	0.84	0.79	0.70	10.15	1.435	4.77	0.743	0.864
CMSWEP	0.96	0.89	0.88	4.42	1.026	3.41	0.868	0.933

presents the categorical accuracy and quantitative statistics.

As can be seen from Table 2, most of the daily rainfall events that occurred during 1979–2015 were successfully detected by the three kinds of datasets (with POD > 0.8 in all), also with a high FH above 0.79, which indicates a low degree of false alarm. Therefore, they have a strong identification ability on the dry and wet status of daily rainfall. Among them, CMSWEP has the highest classification accuracy. POD corresponding to CMSWEP are generally equal to GIP, but FH is significantly higher than the later, so its HSS is also significantly improved compared with the later However, the comprehensive ability of MSWEP to identify precipitation events is some low compared with the other two datasets. Compared with GIP, the main problem with MSWEP is that there is a large degree of missed reporting. For MSWEP, the R² is over 0.74, while CC is over 0.86, indicating that this data had a well interpretation ability for daily rainfall in the Zhoushan Archipelago, but its quantitative error is still remarkable, with RBIAS close to 10.15 and the RMSE and SRMSE are the highest among the three kinds of data. The surface daily precipitation was generally underestimated by MSWEP.

In general, at the daily time scale, the accuracy of MSWEP in Zhoushan Archipelago is lower than GIP based on sparse and unevenly distributed rain gauges. However, after merging with the rain gauge data, all the quantitative accuracy indices are improved to a certain degree. Overall, the performance of CMSWEP is not only higher than MSWEP, but also higher than GIP.

4.1.2. Accuracy of Monthly Rainfall

Figure 4 is the scatter plot of GIP, MSWEP, and CMSWEP and the gauge measurements at the monthly time scale.

Table 3. Monthly accuracy indices for the three rainfall datasets during 1979 to 2015.

		Indices
Rainfall Datasets	RBIAS	RMSE (mm)	SRMSE	R2	CC
GIP	0.57	23.89	0.236	0.879	0.944
MSWEP	−0.19	26.67	0.263	0.880	0.939
CMSWEP	0.36	22.93	0.227	0.894	0.948

shows the relevant quantitative accuracy indices. As can be seen from this table, GIP and CMSWEP have small systematic deviations at the monthly scale, with RBIAS being 0.57 and 0.36, respectively. MSWEP shows relatively significant underestimation of monthly rainfall, and its RBIAS value is about−0.19, lower to the results of the other two data, which is due to the fact that no monthly precipitation is zero. By comparing Figure 3 and Figure 4, it can be seen that relative to the daily scale, at the monthly scale the interpretation ability of the three rainfall datasets for the benchmark has been significantly enhanced, with R² exceeding 0.87. CMSWEP had the highest R², reaching 0.894, followed by GIP. The correlation of the three datasets with the benchmark has also been significantly improved, with CC exceeding 0.9 in all, among which CMSWEP is the highest, about 0.95. At the same time, compared with the daily scale, the SRMSE of the three kinds of data at the monthly scale has significantly reduced, being 0.236, 0.263, and 0.227, respectively, and RMSE has also decreased to 23.89 mm, 26.67 mm, and 22.93 mm, respectively. It can also be found that at the monthly scale, all accuracy indices of CMSWEP are better than those of GIP and MSWEP. This indicates that the blending of MSWEP data with gauge data enhances the interpretation ability for the monthly surface rainfall.

4.1.3. Seasonal Changes of the Accuracy Statistics

Figure 5 shows the daily accuracy indices fluctuation of GIP, MSWEP, and CMSWEP within a year in the study area. It can be known from this figure that, except for POD, the accuracy indices of the three dataset at the daily time scale all show significant seasonal fluctuation. In terms of RBIAS, the systematic error of MSWEP from June to September is lower than that of other periods of the year, but HSS, CC, R², and SRMSE are all poor in this period, indicating that in this period the overall performance of MSWEP is relatively low. MSWEP significantly underestimates the benchmark during January–March and October–December by as much as about 15%. The performance of GIP and CMSWEP are both significantly better than MSWEP in each month of the year. The POD, HSS, and RBIAS of GIP and CMSWEP have no obvious seasonal change in the year, but other indices from June to October are poorer than other months.

Figure 6 shows the distribution of monthly accuracy indices within a year for the three rainfall datasets. In terms of RBIAS, the systematic error of MSWEP from January–June is lower than other months (RBIAS is the highest in November); and SRMSE is similar, the deviation from January to June is significantly lower than July to December, and the deviation is the largest from July to October. For MSWEP, CC, and R2 show no distinct change pattern. For GIP and CMSWEP, the seasonal change of RBIAS is not remarkable. Except September, it differs little in other months; the trend of SRMSE is basically the same as MSWEP’s, showing an inverted "U" shape. From July–November, SRMSE is significantly higher than other months for the two datasets. However, there is no fixed change rule for other indices in each month of the year. Therefore, the seasonal characteristics of the three precipitation datasets in terms of accuracy indices at the monthly scale are apparently different from those at the daily scale.

4.2. Comparison of Rainfall Spatial Distribution

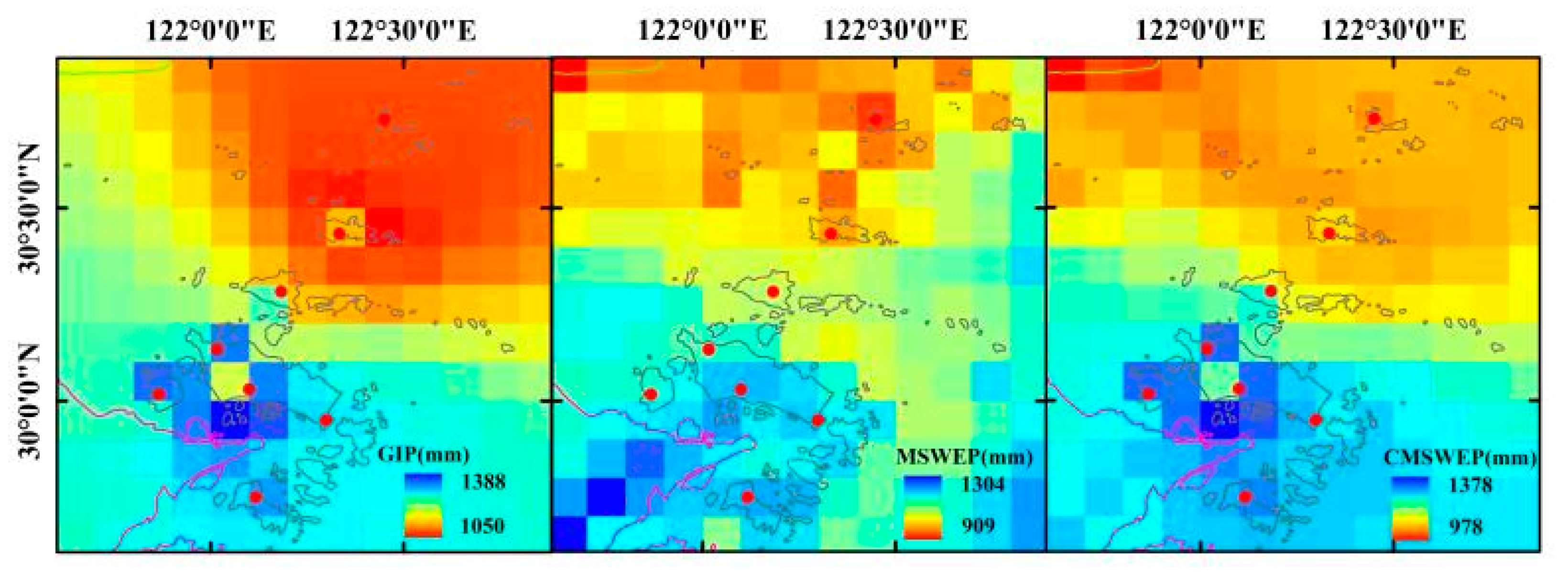
4.2.1. Annual Rainfall

In addition to the statistics, the difference of three kinds of rainfall datasets and the influence of rainfall merging on the spatial estimation results are further explained from the rainfall spatial distribution over the Zhoushan Archipelago. Figure 7 shows the gridded multi-year averaged annual precipitation corresponding to GIP, MSWEP, and CMSWEP with 0.1° × 0.1° spatial resolution. It can be known from the figure that, both GIP and MSWEP reflect that the mean annual rainfall is higher in the Central Zhoushan Island and its adjacent ocean in the south of the study area, but is lower in the Shengsi Island and its surrounding ocean in the north. For these two datasets, the mean annual rainfall decreases gradually from the southwest to the north on the whole. However, there are substantial differences in spatial distribution pattern of annual rainfall between GIP and MSWEP. Firstly, in terms of the range of annual rainfall amount at the grid scale, MSWEP underestimates the surface annual rainfall to a certain degree, and the lowest and highest annual rainfall of all the grids are both lower than those of GIP. Secondly, grids distribution with high annual mean rainfall is not completely consistent. For GIP, the high mean annual rainfalls are mainly located in the vicinity of the Central Zhoushan Island, while for MSWEP they are mainly distributed to the southwest of the Central Zhoushan Island. Thirdly, for GIP, the annual rainfall spatial distribution is relatively smooth, while for MSWEP, the annual rainfall distribution is relatively diverse and shows more detailed characteristics. CMSWEP has the mixed features from GIP and MSWEP. For this dataset, in terms of the spatial distribution pattern of annual rainfall, the original gauge data take a dominant role in the south of the study area, i.e., the Zhoushan Island and its adjacent sea area with some high density of rain gauge, while in the Shengsi Island and its surrounding sea area in the northeast with relatively sparse rain gauges, MSWEP plays a more significant role. The range of annual mean rainfall of CMSWEP grids is close to that of GIP, indicating that the systematic error of MSWEP has been effectively reduced by observations.

Table 4. Comparison of the mean annual precipitation and flood season precipitation over the main inhabited islands among the three rainfall datasets from 1979 to 2015.

Island	Land Area (km2)	Population (person)	Data	Flood Season Precipitation (mm)	Mean Annual Precipitation (mm)
Zhoushan Island	486.2	489,509	GIP	706.9	1278.5
			MSWEP	660.0	1169.1
			CMSWEP	705.6	1271.6
Daishan Island	105.0	103,396	GIP	644.5	1179.7
			MSWEP	606.1	1072.6
			CMSWEP	641.8	1168.8
Liuheng Island	93.5	58,432	GIP	728.0	1301.8
			MSWEP	682.8	1189.9
			CMSWEP	726.9	1296.0
Qushan Island	59.8	50,408	GIP	593.3	1107.1
			MSWEP	554.5	993.0
			CMSWEP	584.5	1081.2
Jintang Island	77.4	41,135	GIP	735.4	1324.5
			MSWEP	675.2	1142.7
			CMSWEP	731.9	1313.2
Siqiao Island	22.5	31,619	GIP	568.0	1069.0
			MSWEP	517.8	948.5
			CMSWEP	562.4	1055.4
Zhujiajian Island	61.8	26,512	GIP	709.1	1279.2
			MSWEP	661.9	1160.2
			CMSWEP	706.6	1262.3
Xiazhi Island	17.0	18,372	GIP	718.5	1275.8
			MSWEP	679.4	1190.3
			CMSWEP	717.0	1274.5
Taohua Island	40.7	16,574	GIP	714.3	1274.5
			MSWEP	661.7	1160.4
			CMSWEP	711.3	1269.7
Dayangshan Island	4.9	11,303	GIP	594.1	1115.5
			MSWEP	528.5	954.2
			CMSWEP	576.1	1061.5

further presents the mean annual precipitation and flood season precipitation corresponding to the three rainfall datasets over the islands with a population no less than 10,000 (the locations of each island are shown in Figure 1). It can be realized that the annual precipitation corresponding to MSWEP is lower than that of GIP for all the inhabited islands, but the degree of underestimation is less than 10%. However, CMSWEP is fairly close to the GIP.

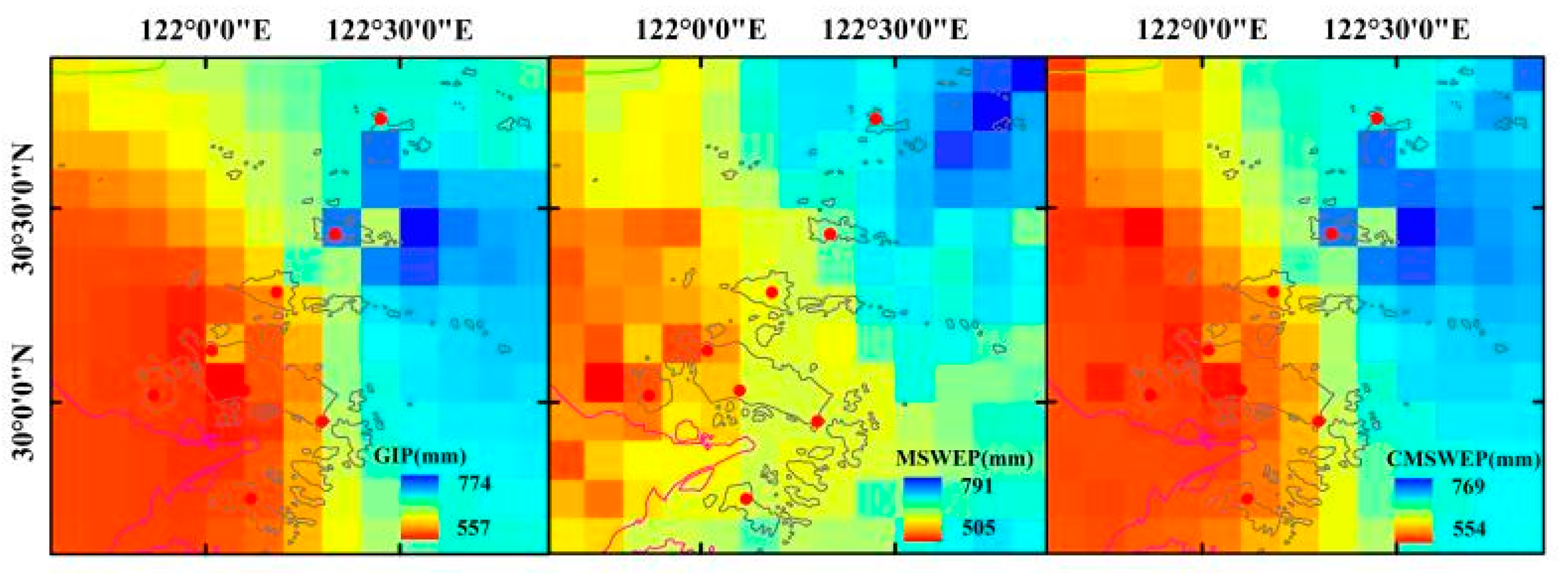
4.2.2. Flood Season Rainfall

Figure 8 shows the spatial distribution of multi-year mean flood season precipitation (during May to September) corresponding to the three datasets in the study area. According to the Figure, GIP and MSWEP both reflect that the flood season precipitation in the northeast sea area of the Zhoushan Archipelago is significantly higher than that in other sub-areas, while the flood season precipitation in the west area is relatively low, which is obviously different from the annual precipitation. The flood season precipitation distribution corresponding to MSWEP obviously shows stronger spatial diversity and details, while GIP is relatively monotone. This is related to the density of the rain gauges in the study area and also the characteristics of Cressman method. When the gauge density is low and the spatial distribution is uneven, this scheme is likely to produce an excessively smooth estimation result when it is applied to spatial interpolation. Meanwhile, the minimum value of the gridded flood season precipitation corresponding to MSWEP is less than GIP, while the maximum value is slightly higher than the latter. The range of flood season precipitation of CMSWEP data is close to GIP. Meanwhile, CMSWEP blends the spatial distribution characteristics of MSWEP and GIP. For the main inhabited islands, the comparison of multi-year mean flood season precipitation during 1979–2015 among the three datasets is shown in Table 4. It can be seen that MSWEP underestimates the flood season precipitation of all the islands by less than 10%, while CMSWEP is close to GIP.

4.2.3. Accumulated Days with Daily Rainfall Exceeding 50 mm

Located in the southeast coastal region of China affected by the plum rain and typhoons, the Zhoushan Archipelago is prone to high intensity precipitation events, which may produce important impacts on the economy and society development. Therefore, this paper pays more attention to the spatial distribution of the rainstorm days in this region obtained by different precipitation datasets. Figure 9 is the 0.1° × 0.1° gridded accumulated rainstorm days (days with daily precipitation over 50 mm) during 1979–2015 for the three precipitation datasets. It can be seen that the rainstorm days for MSWEP is significantly lower than GIP and CMSWEP, indicating that MSWEP has underestimated the heavy precipitation to a large extent, missing quite a number of rainstorm events. This agrees with the finding by Deng et al. [17]. In addition, the spatial distribution of accumulated rainstorm days between MSWEP and GIP is also significantly different. For GIP, the regions with high cumulative rainstorm days are mainly distributed in Central Zhoushan Island and the adjacent sea area in the south. However, MSWEP has two areas with high cumulative rainstorm days. For MSWEP, besides the islands in the south and their surrounding sea area, the northeast sea area is also with high cumulative rainstorm days. At the grid scale, the cumulative rainstorm days for CMSWEP ranges from 53 to 132 days, and its maximum value is close to GIP, but its minimum value is still significantly lower than GIP. The cumulative rainstorm days of CMSWEP are with two distinct zones, reflecting high and low value respectively. In the third map of Figure 9, the high value zone mainly corresponds to GIP, while the low value zone reflects the influence of MSWEP.

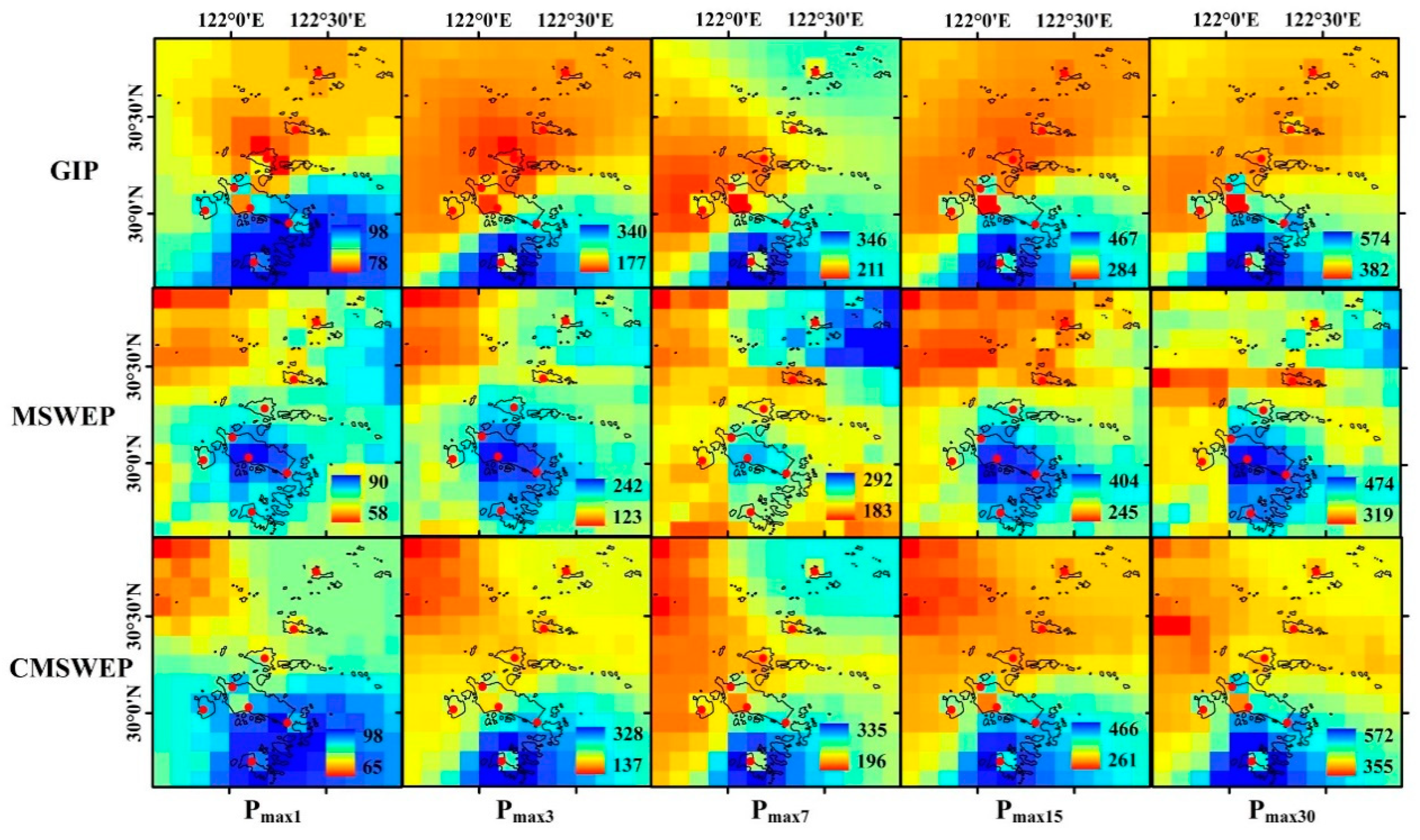
4.2.4. Maximum Rainfall of Different Duration

Further comparison was made on the ability of the three precipitation datasets to describe the five kinds of characteristic precipitations, including 1-day, 3-day, 7-day, 15-day, and 30-day maximum precipitation in the year (respectively denoted as Pmax1, Pmax3, Pmax7, Pmax15 and Pmax30). Figure 10 shows the spatial distribution of the multi-year mean of various maximum precipitation at the grid scale during 1979–2015.

It can be seen from Figure 10 that the maximum precipitation range for the three datasets is different to some extent. The high value area of GIP is relatively concentrated, with the highest value near the Zhoushan Island and the adjacent sea area in the south. Due to the underestimation of heavy precipitation, for MSWEP the maximum precipitation is significantly lower than GIP on the whole. Additionally, MSWEP data not only reflect the maximum precipitation center surrounding the Central Zhoushan Island in the south, but also shows a second maximum precipitation center in the sea area to the east of the Shengsi Island. Especially for Pmax7, the second center of MSWEP is even more remarkable than the first one. CMSWEP has the characteristics of both GIP and MSWEP. For this merged dataset, the lowest value of the various maximum precipitation is significantly higher than MSWEP, while the highest value is relatively close to the latter.

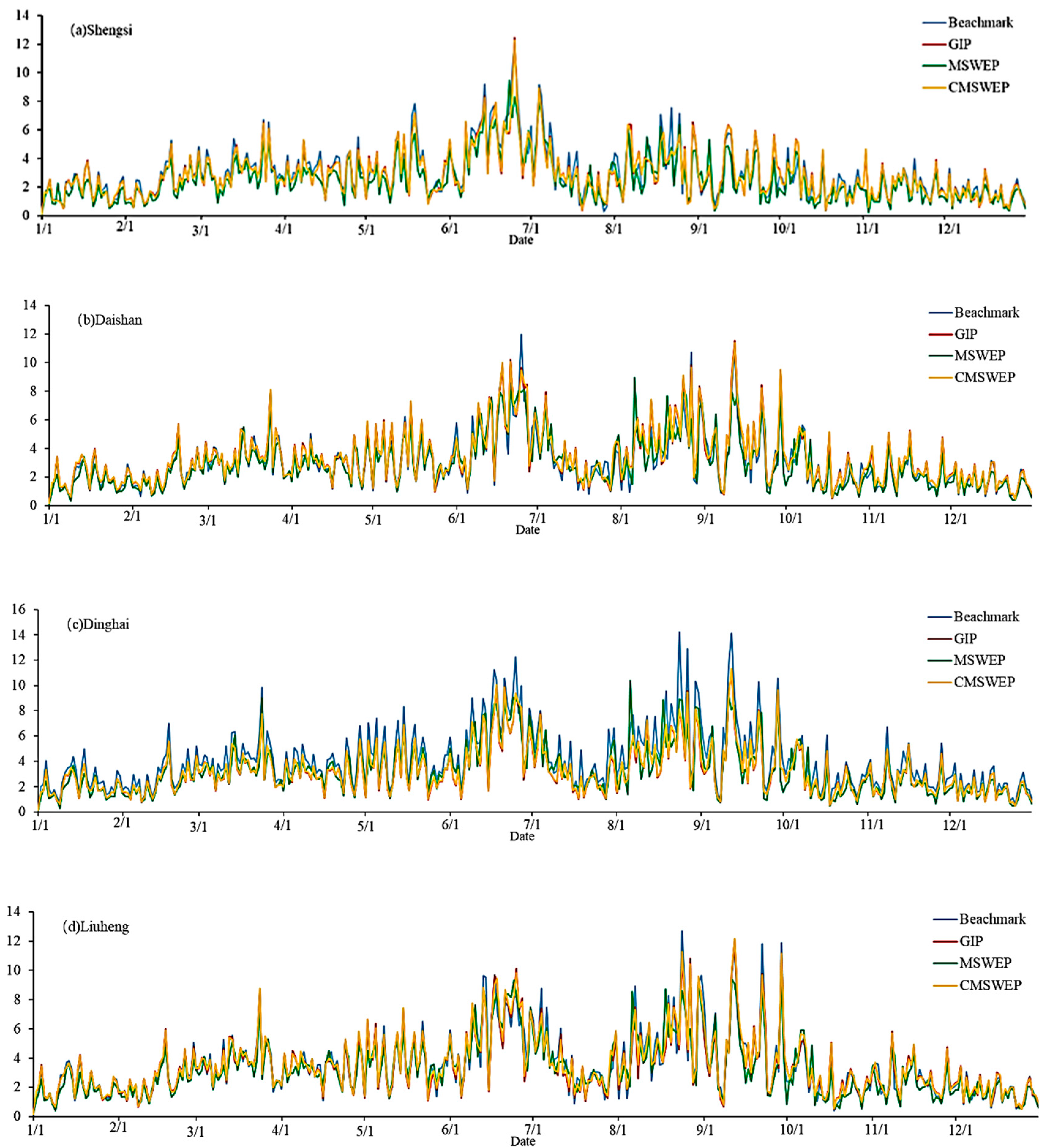
4.3. Analysis of Daily Rainfall Process

At the same time, the multi-year mean daily rainfall processes corresponding to the three precipitation datasets were compared. Figure 11 gives the specific situation of four rain gauges including Shengsi, the other four gauges are not shown due to limited space, but the situation is similar. It can be seen from the Figure that the multi-year mean daily rainfall process of GIP, MSWEP, and CMSWEP, as well as measurements by the rain gauge are fairly similar, all reflecting that precipitation is relatively concentrated from mid-June to mid-July and from mid-August to late September in the year. The daily rainfall process corresponding to GIP and CMSWEP is fairly close to the gauge measurements, while the difference between the gauge measurements and MSWEP is some apparent, and the underestimation is obvious in some periods of the year.

5. Discussion and Conclusions

Based on the surface rain gauge records in the Zhoushan Archipelago from 1979 to 2015, the accuracy evaluation results of MSWEP and CMSWEP at different time scales are given from different perspectives in the above sections. At the same time, the characteristics of MSWEP and CMSWEP on the spatial distribution pattern of different precipitation elements have been analyzed. This section will focus on two issues. One is to discuss the performance of MSWEP and other global precipitation data in islands and sea areas; and the second is to discuss the marginal effect of merging global precipitation data with local gauge measurements.

At present, the evaluation of global precipitation data is mostly implemented on land, but still there are several explorations focused on the accuracy evaluation of TRMM, CMORPH, and other datasets in islands and sea areas. Through the comparison of existing literatures and this paper, the accuracy improvement of MSWEP compared with other global precipitation data and its potentiality in offshore meteorological and hydrological monitoring can be further explained. Tian and Peters-Lidard [24] once evaluated the global uncertainty of six kinds of precipitation data, such as TRMM3B42 and CMORPH, and pointed out that the accuracy of these data was generally higher in the sea area than in the land area, but even so, the accuracy of these data in the coastal area of China was still over 30%. Yong et al. [25] pointed out that at the daily time scale, the POD of four gauge adjusted precipitation datasets including TRMM V7, GSMaP_Gauge, CMORPH-CRT, and PERSIANN-CDR did not exceed 0.70 in Taiwan Island of China and Okinawa Islands of Japan, with the false alarm ratio (FAR) at 0.36 and the RBIAS close to 20%. Considering that the climate characteristics of this region are close to the Zhoushan Archipelago, this study has actually provided more relevant evidence for performance comparison between MSWEP and other precipitation data. Among the available global precipitation data, GSMaP_MVK performs relatively well in east Asia. However, according to Setiawati and Miura [26], GSMaP_MVK underestimated rainy season precipitation in Kyushu Island of Japan by 46.78%, as compared with HSS of only 0.67. Therefore, according to existing literatures, MSWEP has obviously higher ability to identify precipitation events than TRMM 3B42 and other precipitation datasets at the daily time scale, which fully demonstrated the advantages of MSWEP. Of course, MSWEP still hasn’t completely overcome one of the obvious limitations of global rainfall data, that is, the poor identification ability of heavy precipitation. Like other global precipitation data, MSWEP has a high degree of miss reporting of heavy precipitation. Due to the influence of plum rain and typhoon in the Zhoushan Archipelago and other coastal areas, heavy precipitation events are fairly frequent, which should be fully noted when MSWEP and other global precipitation data are used.

At present, there are many studies on the global precipitation data, especially the merging of satellite precipitation data with surface rain gauge data. Rainfall merging is not only a process of integrating and matching different precipitation information, but also a process of balancing the errors. Rainfall merging, while providing the precipitation analysis results, often provides the metric of the uncertainty of the estimated results. Existing literatures involve not only the merging of pure satellite precipitation data and rain gauge data [27,28], but also the re-merging of gauge adjusted global precipitation with the local rain gauge data [15,17]. Global satellite precipitation data can make up for the deficiency of spatial representation of the latter, while rain gauge data has high local accuracy. Theoretically, the merging of the two can give full play to their respective advantages and obtain better estimation results than any of the original data. Presently, a large number of literatures have pointed out that the accuracy of global precipitation data is significantly improved after calibration with surface rainfall data [2,15,27,29]. However, it is still necessary to discern and evaluate the gain of rainfall merging choosing the rain gauge interpolation data as the benchmark. Only in this way can the marginal effect of rainfall merging be fully illustrated. Researchers from Australia and other countries have conducted some in-depth discussions on this issue. Li and Shao [29] proposed a merging algorithm based on non-parametric estimation, to indicate that by merging TRMM 3B42 with rain gauge data, the accuracy of spatial precipitation estimation in Australia has been indeed improved in a statistical sense compared with the interpolation results of gauge data using Ordinary Kriging (OK). The investigation by Woldemeskel et al. [15] on this issue further made clear that the improvement of precipitation accuracy was mainly demonstrated in areas with sparse rain gauges. Renzullo et al. [30] discussed the marginal effect of merging the Australian rain gauge data with TRMM 3B42RT, and found that when the gauges were more than one in each 2500 km² area, the merging of TRMM 3B42RT with rain gauge data had no obvious effect and even probably reduced the estimation accuracy. Rozante et al. [31] also had a similar conclusion in South America and pointed out that only when the data of surface gauge network was sparse, the effect of merging rain gauge data with TRMM 3B42RT was relatively obvious. Chappell et al. [32] studied the merging effect of TRMM 3B42RT data with rain gauge data in Australia, and stated that in terms of conventional statistics, the combination of the two has no obvious positive effect and may even produce negative effect, but it can effectively reduce the estimation variance. Therefore, in general, the marginal effect of merging global precipitation data with surface rainfall data is affected by a series of factors, such as the type of global precipitation data, the density of surface rain gauges and their spatial configuration, and is also related to the geographic and climatic background. The merging of MSWEP data with rain gauge data in the Zhoushan Archipelago has shown a certain degree of improvement at both daily and monthly time scales, as compared with the pure interpolation results of rain gauge data, but its marginal effect is rather limited. The results of this paper are based on the long series data from 1979 to 2015, so it is undoubtedly more reliable. In addition, it is consistent with previous studies, and also inherent with the original intention of developing the global precipitation datasets. These types of datasets were originally oriented to the regions lacking in surface rainfall observation. At the same time, considering that MSWEP data has high spatial resolution and relatively low error among the existing global precipitation data, this paper is also of considerable reference significance for the merging of other global precipitation data with gauge data. Of course, the authors also agree with Chappell et al. [32] that if we only view the effects in light of the conventional statistics, rainfall merging may not produce obvious effect, but it may have other benefits. For the Zhoushan Archipelago, MSWEP data can demonstrate the information of the precipitation spatial structure not reflected by sparse gauge observations, and the precipitation fields obtained by multi-source merging are of more detailed features.

In general, based on the long series of surface rainfall data, this paper evaluated the performance of MSWEP and its combination with surface rainfall gauge data in the Zhoushan Archipelago from a variety of aspects. Our investigation deepened the understanding of the performance of MSWEP in coastal regions, and also the understanding of the marginal effect of combining MSWEP with surface precipitation data. Main conclusions could be drawn as follows:

MSWEP data can correctly identify most daily precipitation events in Zhoushan Archipelago during 1979–2015, so it has a strong ability to discern dry and wet states. MSWEP generally underestimates precipitation in the Zhoushan Archipelago, but its relative deviation is less than 10%. Like other global precipitation datasets, MSWEP has a high degree of miss reporting of heavy precipitation.

• The precipitation data CMSWEP by merging MSWEP with surface rainfall data not only has a significant improvement in accuracy compared with MSWEP, but also has a certain degree of improvement compared with the gauge interpolation data GIP. At the daily time scale, the advantage of CMSWEP over GIP is mainly shown in the comprehensive identification ability of the dry and wet state of daily rainfall.
• At the daily time scale, the accuracy indices of GIP, MSWEP, and CMSWEP have significant seasonal changes except POD. GIP and CMSWEP are significantly better than MSWEP in terms of accuracy indices in each month of the year. At the monthly scale, there are also certain seasonal changes for the accuracy indices of the three datasets, but they are obviously different from those at the daily scale.
• For various precipitation elements including multi-year mean precipitation, multi-year mean flood season precipitation, cumulative rainstorm days, and maximum precipitation, MSWEP and CMSWEP can demonstrate the spatial distribution characteristics that sparse surface rainfall data cannot describe. For various precipitation elements of MSWEP and GIP, the location of the center with high value is not completely consistent. Meanwhile, the spatial distribution is relatively smooth with GIP, while MSWEP shows more details. CMSWEP has spatial structure characteristics of both GIP and MSWEP.
• Although the spatial distribution characteristics of precipitation statistics such as annual precipitation and extreme precipitation in Zhoushan Archipelago are displayed by ARCGIS in this paper, the precipitation statistics indicators are not further processed. In order to describe the precipitation characteristics of Zhoushan Archipelago in more detail, the authors will use copulas non-parametric statistical method to conduct on the spatial distribution of the probability index of regional rainfall height [33,34,35,36]. At the same time, the time resolution of MSWEP data is 3 h, but the accuracy below the daily time scale of MSWEP data has not been evaluated in this paper. In the future, the accuracy of MSWEP below the daily time scale will be further analyzed, so as to explore the ability of MSWEP to identify short-duration rainfall and rainfall diurnal variation. Despite of the high spatial resolution of MSWEP, the merging of the data with surface rain gauge data is still faced with the problem of space scale transformation. Thus, in future the merging of different precipitation data will be realized on the basis of spatial downscaling of MSWEP, and the effect of the data spatial resolution on estimation results will be analyzed. We will extend this study from the Zhoushan Archipelago to other coastal or inland areas lacking in surface rainfall observations.